On contiguous and non-contiguous parallel task scheduling

Abstract

In this paper we study differences between contiguous and non-contiguous parallel task schedules. Parallel tasks can be executed on more than one processor simultaneously. In the contiguous schedules, indices of the processors assigned to a task must be a sequence of consecutive numbers. In the non-contiguous schedules, processor indices may be arbitrary. Optimum non-preemptive schedules are considered. Given a parallel task instance, the optimum contiguous and non-contiguous schedules can be of different lengths. We analyze minimal instances where such a difference may arise, provide bounds on the difference of the two schedules lengths, and prove that deciding whether the difference in schedule length exists is NP-complete.

1 Introduction

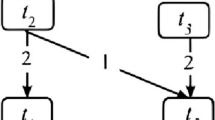
Parallel tasks may require more than one processor simultaneously. The processors are granted either contiguously or non-contiguously. In the contiguous case, indices of the processors are a range of consecutive integers. In the opposite case the indices may be arbitrarily scattered in the processor pool. In this paper we analyze the cases when for a parallel task instance, the lengths of the optimum non-preemptive contiguous and non-contiguous schedules are different. Non-contiguous schedules may be shorter because a contiguous schedule is also a feasible non-contiguous schedule, but not vice versa. We will call such a situation a c/nc-difference. An example of the c/nc-difference is shown in Fig. 1.

Fig. 1

Example of the c/nc-difference. a Instance data, b optimum non-contiguous schedule, c optimum contiguous schedule

More formally our problem can be formulated as follows: We are given set $\mathcal{P}=\{P_1,\ldots , P_m\}$ of $m$ parallel identical processors, and set $\mathcal{T}=\{T_1,\ldots ,T_n\}$ of $n$ parallel tasks. Each task $T_j\in \mathcal{T}$ is defined by its processing time $p_j$ and the number of required processors $size_j$, where $size_j\in \{1,\ldots ,m\}$. For conciseness, we will be calling $p_j$ task $T_j$ length and $size_j$ task $T_j$ size, or width. Both processing times and task sizes are positive integers. We study two versions of the problem: either tasks are scheduled contiguously, or non-contiguously. In the former case the indices of the processors assigned to a task must be consecutive. In the latter case, processor indices can be arbitrary in the range $[1,m]$. Scheduling is non-preemptive and migration is disallowed. It means that task $T_j$ started at time $s_j$ must be executed continuously until time $s_j+p_j$ on the same set of processors. Schedule length (i.e., makespan) is the optimality criterion. Unless stated to be otherwise throughout the paper we refer to the optimum schedule lengths. We will denote by $C_\mathrm{max}^\mathrm{c}$ contiguous and by $C_\mathrm{max}^\mathrm{nc}$ non-contiguous optimum schedules lengths for the given instance. In this paper we study the cases when $C_\mathrm{max}^\mathrm{c}>C_\mathrm{max}^\mathrm{nc}$.

Since task widths $size_j$ are given and cannot be changed, we consider here a subclass of parallel task scheduling model called rigid tasks (Feitelson et al. 1997). Our scheduling problem has been denoted $P|size_j|C_\mathrm{max}$ in Veltman et al. (1990) and Drozdowski (2009) without making distinction between the contiguous and the non-contiguous case. This problem is NP-hard in both variants, which follows from the complexity of the classic problem $P2||C_\mathrm{max}$. Parallel task scheduling has been studied already in the early 1980s Lloyd (1981) also as a problem of packing rectangles on infinite strip (Coffman et al. 1980), but its origins can be traced back at least into 1960 (Codd 1960). The problem of scheduling various types of parallel task systems and the strip-packing problem have been tackled in hundreds of publications and reporting them here is beyond the size and scope of this paper. Therefore, we direct an interested reader to, e.g., Dutot et al. (2004), Drozdowski (2009), Ntene and Vuuren (2009), and Amoura et al. (2002). A polynomial-time approximation scheme (PTAS) has been proposed for non-contiguous version of the problem and fixed number of processors $m$ in Amoura et al. (2002). To the best of our knowledge, for the contiguous version of the problem, there is an asymptotic fully polynomial-time approximation scheme (AFPTAS) by Kenyon and Rémila (2000) and the problem is $5/3+\varepsilon$-approximable (Harren et al. 2014). The difference between contiguous and non-contiguous schedules has been first demonstrated in 1992 (Turek et al.) on an instance with $n=8$ tasks, $m=23$ processors, $C^\mathrm{nc}_\mathrm{max}=17, C^\mathrm{c}_\mathrm{max}=18$. Its existence has been acknowledged in Dutot et al. (2004), and Baille et al. (2008). However, to the best of our knowledge, the consequences of applying contiguous and non-contiguous schedules to the same instance have not been studied before.

The difference between contiguous and non-contiguous schedules has practical consequences in parallel processing. Parallel applications are composed of many threads running simultaneously and communicating frequently. It is advantageous to assign the threads of a single application to processors within a short network distance because communication delays are shorter and there are fewer opportunities for network contention with other communications (Bokhari and Nicol 1997, Bunde et al. 2004, Lo et al. 1997). In certain network topologies, processor numbering schemes have been proposed to aid allocation of processors which are close to each other. In such network topologies ranges of consecutive processor indices correspond to locally connected processors. These can be various buddy processor allocation systems for 1-, 2-dimensional meshes, hypercubes, and $k$-ary $n$-cube interconnection networks (Chen and Shin 1987; Li and Cheng 1991; Drozdowski 2009). Also other, more sophisticated processor numbering schemes have been proposed for this purpose (Leung et al. 2002). As a result, contiguous schedules correspond to assigning tasks to tightly connected processors. Thus, contiguous schedules are favorable for the efficiency of parallel processing. However, contiguous schedules are less desirable when managing many parallel tasks. It may be impossible to pack the tasks on the processors in a schedule of a given makespan if the tasks cannot be split between several groups of available processors. Consequently, resource utilization may be lower. Hence, it is necessary to understand the difference between contiguous and non-contiguous schedules: When such a difference may arise and how much makespan may be gained by going from a contiguous to a non-contiguous schedule.

In the domain of harbor logistics, the berth assignment problem (BAP) is one of the most studied problems in container terminal operations (Lim 1998; Bierwirth and Meisel 2010). In the discrete BAP, a quay is partitioned into berths. In a common case one berth may serve one ship at a time and one ship requires several contiguous berths. After relaxing some other constraints, the BAP reduces to a contiguous scheduling problem. A berth corresponds to a processor and a ship corresponds to a job. Depending on its size, a ship requires a given number of berths. A job processing time is given by the corresponding ship handling duration. This duration may be fixed or may depend on the berths. Since vessels cannot be partitioned into several pieces, non-contiguous schedules are not practically relevant. However, non-contiguous makespan values provide lower bounds on contiguous schedules and thus lower bounds for the relaxed versions of BAP.

Further organization of this paper is the following: In Sect.  2 minimal instances for which a c/nc-difference may exist are analyzed. Section 3 contains a proof that deciding if a c/nc-difference appears is NP-complete. In Sect.  4 it is shown that the ratio of contiguous and non-contiguous schedule lengths is bounded. In Sect.  5 we report on the simulations conducted to verify whether c/nc-difference is a frequent phenomenon on average. The last section is dedicated to conclusions.

2 Minimal instances

Here we study conditions under which a c/nc-difference can arise. We start with a couple of observations. Obviously, $C^\mathrm{nc}_\mathrm{max}\le C^\mathrm{c}_\mathrm{max}$ because each contiguous schedule is also a valid non-contiguous schedule, but not vice versa. In the following discussion we use “up”/“down” directions to refer to shifting tasks toward bigger/smaller processor indices. By “renumbering” a pair of processors we mean swapping the whole schedules on the two processors.

Observation 1

For c/nc-difference to arise, there must be at least three tasks with $size_j>1$.

If there is only one task $T_j$ with $size_j>1$, then it is possible to renumber processors in an optimum non-contiguous schedule such that $T_j$ is executed contiguously. If there are exactly two tasks $T_i,T_j:size_i,size_j>1$, then in the optimum non-contiguous schedule $T_i,T_j$ either share some processors or they do not. In the latter case it is again possible to renumber processors such that $T_i, T_j$ are scheduled contiguously. If $T_i, T_j$ share processors, then they are executed sequentially. Therefore, it is also possible to renumber processors such that the processors used only by $T_i$ are assigned contiguously above the shared processors, the shared processors are assigned contiguously, while the processors used only by $T_j$ are assigned contiguously below the shared processors. Thus, a contiguous schedule of the same length would be obtained. An instance with c/nc-difference and exactly three non-unit size tasks is shown in Fig. 2.

Fig. 2

C/nc-difference for three tasks with $size_j>1$. a Optimum non-contiguous schedule, b optimum contiguous schedule

Observation 2

For c/nc-difference to arise, there must be at least three tasks with $p_j>1$.

If $\forall ~T_j, p_j=1$, then it is always possible to rearrange tasks in the optimum non-contiguous schedule into contiguous allocations by sorting task indices in each time unit of a schedule. Similar procedure can be applied if there is exactly one task $T_j$ with $p_j>1$ and all other tasks have unit execution time. Task $T_j$ should be moved, e.g., to the lowest processor indices in the interval in which it is scheduled, then the indices of the unit execution time tasks should be sorted in their time intervals. Suppose there are exactly two tasks $T_i, T_j:p_i,p_j>1$ and all other tasks have unit processing time. If $T_i, T_j$ are executed in different time intervals, then each of them can be treated as in the case of one task with non-unit processing time. If the intervals of processing $T_i, T_j$ overlap, then $T_i$ can be moved to the bottom and $T_j$ up to the ceiling of the schedule and unit processing time tasks should be reassigned by sorting in their respective unit time intervals (cf. Fig. 4c). An instance with c/nc-difference and exactly three non-unit length tasks is shown in Fig. 3.

Fig. 3

C/nc-difference for three tasks with $p_j>1$. a Optimum non-contiguous schedule, b optimum contiguous schedule

Fig. 4

Example of converting a non-contiguous schedule of length $C_\mathrm{max}^\mathrm{nc}=3$ to a contiguous schedule. a Initial schedule. b Shifting tasks with $p_j=3$. c Shifting tasks with $p_j=2$. d Rearranging tasks into contiguous allocations

Theorem 3

For c/nc-difference to arise, the non-contiguous schedule length must be at least $C_\mathrm{max}^\mathrm{nc}=4$.

Proof

First we will show that all non-contiguous schedules of length $C_\mathrm{max}^\mathrm{nc}\le 3$ can be rearranged to contiguous schedules of the same length. Then, we show that there is an instance which non-contiguous schedule has $C_\mathrm{max}^\mathrm{nc}=4$ and the contiguous schedule has $C_\mathrm{max}^\mathrm{c}=5$.

For $C_\mathrm{max}^\mathrm{nc}=1$ rearrangement into a contiguous schedule is always possible by Observation 2. If $C_\mathrm{max}^\mathrm{nc}=2$, then tasks must have lengths $p_j\in \{1,2\}$. The tasks with $p_j=2$ can be reassigned contiguously on the lowest processor numbers, and the remaining tasks with $p_j=1$ are handled as in Observation 2. For $C_\mathrm{max}^\mathrm{nc}=3$ processing times are $p_j\in \{1,2,3\}$. The tasks with $p_j=3$ can be moved down to the lowest processor numbers (cf. Fig. 4a, b). The tasks with $p_j=2$ can be shifted down or up by swapping whole intervals of the schedule on the processors. The tasks executed in time units 1, 2 are moved down (just above any tasks with $p_j=3$), and the tasks executed in time units 2,3 are shifted up to the biggest processor numbers (Fig. 4c). After these transformations we obtained a schedule in which tasks that run in the same interval are stacked one on another without being interleaved by the tasks from other intervals. Consequently, it is possible to rearrange the tasks in their time intervals to be executed contiguously (Fig. 4d). Hence, we have $C_\mathrm{max}^\mathrm{c}=C_\mathrm{max}^\mathrm{nc}=3$.

In Fig. 5 a schedule of length $C_\mathrm{max}^\mathrm{nc}=4$ is shown. It can be verified that there is no contiguous schedule shorter than $C_\mathrm{max}^\mathrm{nc}=5$ as, e.g., presented in Fig. 5b.$\square$

Fig. 5

C/nc-difference with the shortest possible $C_\mathrm{max}^\mathrm{nc}.$ a Optimum non-contiguous schedule, b optimum contiguous schedule

A practical consequence of Theorem 3 is that if it is possible to build schedules in pieces of short length (at most 3 units of time), then rearrangement into a contiguous schedule of the same length is always possible.

Theorem 4

For c/nc-difference to arise, at least $m=4$ processors are required.

Proof

For $m=2$ processors no task can be scheduled non-contiguously. For $m=3$ a non-contiguous schedule can be converted to a contiguous schedule of the same length. The converting procedure scans a non-contiguous schedule from the beginning to the end for tasks scheduled on $P_1,P_3$ and then reschedules them such that they are executed on $P_1,P_2$ or $P_2,P_3$. Suppose $T_j$ is the first task executed on $P_1,P_3$ (cf. Fig. 6). We search for the latest task $T_i$ preceding $T_j$ and executed on two processors (or for the beginning of the schedule if such a task does not exist). Task $T_i$ is scheduled contiguously (because $T_j$ is the first task scheduled non-contiguously). We search for the earliest task $T_k$ succeeding $T_j$ and executed on the same processors as $T_i$ (or for the end of the schedule if such a task does not exist). Then, we swap the intervals between $T_i,T_k$ (Fig. 6b). Consequently, all tasks until $T_j$ are scheduled contiguously. The procedure proceeds until the last task executed on $P_1,P_3$.

Fig. 6

Transforming a non-contiguous schedule on $m=3$ to a contiguous schedule

In Fig. 1 an instance with c/nc-difference on $m=4$ processors is given.$\square$

We finish this section with a conjecture motivated by the instance in Fig. 1 with the c/nc-difference for as few tasks as $n=7$. No smaller instance have been found in our simulations (cf. Sect.  5).

Conjecture 1

For c/nc-difference to arise, at least $n=7$ tasks are required.

3 Complexity of c/nc-difference

In this section we demonstrate that determining if a c/nc-difference exists is NP-complete. Informally speaking, given an instance of our scheduling problem checking if loosening or tightening processor-assignment rule results in a shorter/longer schedule, is computationally hard. More formally, the c/nc-difference problem may be defined as follows:

Table 1 Task set for the proof of Theorem 5

c/nc-difference

Instance: Processor set $\mathcal{P}$, set $\mathcal{T}$ of parallel tasks, non-contiguous schedule $\sigma ^\mathrm{nc}$ for $\mathcal{P}$, $\mathcal{T}$.

Question: Does there exist a contiguous schedule $\sigma ^c$ for $\mathcal{P}$ and $\mathcal{T}$ at most as long as $\sigma ^\mathrm{nc}$?

Theorem 5

C/nc-difference is NP-complete.

Proof

C/nc-difference is in NP because NDTM may guess the contiguous schedule $\sigma ^c$ and compare its length with the length of $\sigma ^\mathrm{nc}$. Without loss of generality we can restrict our considerations to active schedules. In active schedules each task starts either at time zero, or at the end of some other task. In a non-contiguous schedule a task may be assigned to arbitrary processors available at its start time. Hence, a string of length $O(n)$ encoding a task permutation is sufficient to determine a non-contiguous schedule. For a contiguous schedule it is enough to determine a task permutation and the lowest processor index used by each task. Then a string encoding a contiguous schedule has length $O(n\log m)$. Thus, a non-contiguous schedule can be encoded in a string of polynomial size in the size of the input. We will use polynomial transformation from the partition problem defined as follows:

Partition

Instance: Set $A=\{a_1,\ldots ,a_k\}$ of integers, such that $\sum _{j=1}^{k}a_j=2B$.

Question: Is it possible to partition $A$ into disjoint subsets $A_1,A_2$ such that $\sum _{i\in A_1}a_i=\sum _{i\in A_2}a_i=B$?

For the simplicity of exposition we assume that $\forall ~i,a_i>2$. The transformation from partition to c/nc-difference is defined as follows: $m=2B+1, n=7+k$. The tasks are defined in Table 1 and schedule $\sigma ^\mathrm{nc}$ of length $C_\mathrm{max}^\mathrm{nc}=15$ is shown in Fig. 7.

Fig. 7

Schedule for the proof of Theorem 5

If the answer to the partition problem is positive, then an optimum contiguous schedule of length $C_\mathrm{max}^\mathrm{c}=15$ as shown in Fig. 7 can be constructed. Note that tasks $T_8,\ldots ,T_n$ can be scheduled contiguously in interval [13,15] either on processors $P_1,\ldots ,P_B$ or $P_{B+1},\ldots ,P_{2B+1}$ because the answer to partition problem is positive. Schedules $\sigma ^c,\sigma ^\mathrm{nc}$ are optimum because they have no idle time. Hence, $C_\mathrm{max}^\mathrm{c}=C_\mathrm{max}^\mathrm{nc}$ and the answer to c/nc-difference is also positive.

Suppose now that the answer to c/nc-difference is positive, i.e., $C_\mathrm{max}^\mathrm{nc}=C_\mathrm{max}^\mathrm{c}$. We will show that the answer to partition problem must be also positive. In the following sequence of observations we will ascertain that the pattern of tasks depicted in Fig. 7 is necessary for $C_\mathrm{max}^\mathrm{c}=15$. The position of task $T_6$ is crucial for the proof because $T_6$ divides the range of available processors into two equal parts. We will argue that tasks $T_2,T_3,T_6$ must be executed sequentially.

• $T_1$ cannot be scheduled sequentially (i.e., one after another) with any of tasks $T_2,\ldots ,T_6$, otherwise $C_\mathrm{max}^\mathrm{c}>15=C_\mathrm{max}^\mathrm{nc}$. Hence, $T_1$ and $T_2,\ldots ,T_6$ must be executed at least partially in parallel.

• $T_2$ must be executed sequentially with $T_3,T_4,T_5,T_7$, otherwise more than $m$ processors would run in parallel. Since $T_1$ and $T_2$ must run in parallel and $T_6$ cannot be run sequentially with $T_1$ then also $T_6$ with $T_2$ must be executed sequentially.

• Considering sequential execution of $T_2,T_4$, task $T_4$ cannot be scheduled sequentially with any of tasks $T_3,T_5,T_6$ (otherwise $C_\mathrm{max}^\mathrm{c}>15=C_\mathrm{max}^\mathrm{nc}$). Hence, $T_4$ must be executed at least partially in parallel with each of tasks $T_3,T_5,T_6$.

• Since $T_1$ must run in parallel with $T_3,\ldots ,T_6$ and $T_4$ in parallel with $T_3,T_5,T_6$, then $T_3$ and pair $T_5,T_6$ must be executed sequentially (otherwise more than $m$ processors would run in parallel).

• Consequently, $T_2,T_3,T_6$ are executed sequentially and $T_2$ cannot be the second in the sequence because $T_4$ would have to be preempted or $C_\mathrm{max}^\mathrm{c}>15=C_\mathrm{max}^\mathrm{nc}$.

• Since the non-contiguous schedule has no idle time, then also the contiguous schedule of length $C_\mathrm{max}^\mathrm{c}=C_\mathrm{max}^\mathrm{nc}$ has no idle time.

• $T_1$ must be scheduled sequentially with $T_7$ and on the same set of processors because $p_1=12$, $C_\mathrm{max}^\mathrm{c}=15$ and all $p_j$ except $p_4,p_6,p_7$ are even (otherwise there is an idle time on the processors running $T_1$). Moreover, $T_1,T_4,T_6$ must run in parallel.

• Since $T_1,T_7$ are scheduled sequentially, task $T_6$ cannot be the second in the sequence of $T_2,T_3,T_6$. For example, in sequence $(T_2,T_6,T_3)$ task $T_7$ would have to be scheduled in parallel with $T_2$ or with pair $T_3, T_4$ and more than $m$ processors would be used in the interval of executing $T_7$. Similar reasoning applies to sequence $(T_3,T_6,T_2)$.

• Thus, only two sequences are feasible: either $(T_2,T_3,T_6)$, or $(T_6,T_3,T_2)$.

• Assuming sequence $(T_2,T_3,T_6)$, task $T_7$ must be executed after $T_1$. Consequently, $T_7$ runs in parallel with $T_6$. As $T_6$ runs in parallel also with $T_4$, task $T_6$ must be executed on processor $P_{B+1}$, otherwise some tasks would be scheduled non-contiguously.

• This creates a box of 11 time units and $B$-processor wide for $T_4$ after $T_2$. There must be some subset of tasks from $T_8,\ldots ,T_n$ in this box (otherwise there is an idle time on the processors running $T_4$).

• Since the schedule is non-preemptive, contiguous, without migration and idle time, the tasks selected from $T_8,\ldots ,T_n$, executed in the box require simultaneously exactly $B$ processors. Thus, the answer to partition problem must be also positive.

• Sequence $(T_6,T_3,T_2)$ results in a (vertical) mirror symmetry of the schedule. Also horizontal mirror symmetry is possible. Both cases can be handled analogously to the above described procedure.$\square$

It follows from the above theorem that it is hard to decide whether $C^\mathrm{c}_\mathrm{max}/C^\mathrm{nc}_\mathrm{max}<1+1/15$ (Garey and Johnson 1979). However, stronger bounds on approximability of $C^\mathrm{c}_\mathrm{max}/C^\mathrm{nc}_\mathrm{max}$ can be given. On the one end, no polynomial algorithm can give better approximation than $3/2C^\mathrm{c}_\mathrm{max}$ which follows from partition (and hence verifying whether a schedule of length $C^\mathrm{c}_\mathrm{max}=2$ exists for problem $P|size_j,p_j=1|C_\mathrm{max}$). On the other end, a $5/3+\varepsilon$-approximation algorithm exists for the contiguous version (Harren et al. 2014). Moreover, the non-contiguous version admits a PTAS for fixed $m$ (Amoura et al. 2002). Hence, for fixed $m$ ratio $C^\mathrm{c}_\mathrm{max}/C^\mathrm{nc}_\mathrm{max}$ can be approximated in range $[3/2,5/3+\varepsilon ]$. Let us note that approximating $C^\mathrm{c}_\mathrm{max}/C^\mathrm{nc}_\mathrm{max}$ for a particular instance is a different issue than determining the range of possible values of this ratio for all possible instances.

4 The ratio of c/nc schedule lengths

In this section we study bounds on the worst case ratio of the non-contiguous and contiguous schedules for a given instance. Let $\Pi$ denote our problem as the set of all pairs ($\mathcal{P,T}$) and let $I$ be an instance of $\Pi$.

Theorem 6

$5/4\le \sup _{I\in \Pi }\{C^\mathrm{c}_\mathrm{max}/C^\mathrm{nc}_\mathrm{max}\}\le 2$.

Proof

The instance shown in Fig. 5 demonstrates that the maximum ratio for c/nc-different schedule lengths is at least 5/4. To show that it is bounded from above by 2 a proof has been given in Błądek et al. (2013) which constructs a contiguous schedule at most twice as long as any given non-contiguous schedule. A reader interested in converting a non-contiguous schedule to a contiguous one may find an algorithm in the above report. However, a simpler proof is possible here. The contiguous parallel task scheduling problem is equivalent to the strip-packing problem. Our range of $m$ processors is equivalent to the fixed dimension of the strip (say width) and our schedule length is equivalent to the minimized strip length. For the strip-packing an algorithm exists (Steinberg 1997) which strip length $C^s_\mathrm{max}$, in terms of our problem, can be bounded by

$$\begin{aligned} C^s_\mathrm{max}\le \frac{1}{m}\!\sum _{j=1}^np_jsize_j\!+\!\max \left\{ \frac{1}{m}\!\sum _{j=1}^np_jsize_j,\max _{j=1}^n\big \{p_j\big \}\right\} . \end{aligned}$$

Since $C^s_\mathrm{max}$ is an upper bound on the length of the optimum contiguous schedule, and since $\sum _{j=1}^n(p_jsize_j)/m\le C^\mathrm{nc}_\mathrm{max}$, $\max _{j=1}^n\{p_j\}\le C^\mathrm{nc}_\mathrm{max}$ we have: $C^\mathrm{c}_\mathrm{max}\le C^s_\mathrm{max}\le 2C^\mathrm{nc}_\mathrm{max}$. $\square$

Theorem 6 has practical consequences. If one constructs a schedule while disregarding possible non-contiguity of the assignments, then to be sure that a conversion to a contiguous schedule is always feasible a margin in time of [25 %, 100 %] of non-contiguous schedule length should be included. However, in the simulations described in the next section, no difference exceeding 25 % of non-contiguous schedule length was found. Hence, we finish this section with a conjecture:

Conjecture 2

$\sup _{I\in \Pi }\big \{C^\mathrm{c}_\mathrm{max}/C^\mathrm{nc}_\mathrm{max}\big \}=5/4$.

5 Simulations

In this section we study by simulation whether c/nc-difference is a frequent phenomenon and how big is the difference between contiguous/non-contiguous schedule lengths.

Two branch and bound algorithms were constructed to solve contiguous and non-contiguous versions of the problem. Branching schemes of both algorithms assume that a schedule consists of two parts: a part that is already constructed and a part still remaining to be built. The branching schemes enumerate all possible completions of the existing partial schedule with the yet unscheduled tasks. Both in the contiguous and in the non-contiguous version, a branch with a partial schedule not shorter than the best known schedule was eliminated. Consider a partial non-contiguous schedule. The set of optimum schedules comprises active schedules, i.e., the schedules in which a task starts at time zero or at the end of some other task. To schedule task $T_j$ feasibly $size_j$ arbitrary processors must be available. Hence, given some partial schedule it is enough to know the earliest moment $s_j$ when $size_j$ processors are available to determine starting time of $T_j$. If scheduling of $T_j$ creates an idle interval before $s_j$ on some processor(s) which could have been exploited by some other task $T_i$, then a schedule in which $T_i$ is using this interval is constructed by considering $T_i$ before $T_j$. Thus, in order to define a non-contiguous schedule, it is enough to determine a permutation of the tasks.

In the contiguous case the branching scheme must determine not only the sequence of the tasks but also the processors executing a task, e.g., by defining the smallest index of a processor used by each task $T_j$. Fortunately, enumeration of the processors ranges may be limited. Consider, the area in time$\times$processor space that can be reached by the lower-left corner of $T_j$ in the optimum schedule. The border of this area will be called an envelope for $T_j$. If $size_j$ contiguous processors are free in front of $T_j$, then it is possible to shift $T_j$ to the earliest moment $s_j$ when these processors are free contiguously without increasing schedule length. Hence, $T_j$ can be scheduled in contact with its envelope. Suppose that more than $size_j$ processors are free contiguously at time $s_j$. Then it is possible to shift $T_j$ to the set of processors with the smallest, or the biggest indices without increasing schedule length. Thus, the reference point of $T_j$ is in a corner of the envelope because it touches the envelope from the right and either from above or from below. We will call such a task assignment a corner-contact. Hence, it is not necessary to enumerate all processor assignments one by one because there are optimum contiguous schedules such that each task is in corner-contact with its envelope. It remains to show that there exists a permutation of the tasks such that assigning each task in its turn in one of the possible corner-contacts with the current partial schedule leads to the optimum schedule. Existence of such a permutation and corner-contact positions can be verified in a thought experiment in which we dismantle optimum corner-contact schedule. By taking away, one by one, the rightmost and topmost task it is possible to dismantle the optimum schedule such that at each intermediate step the remaining tasks are in corner-contact. Thus, there is a permutation which leads from an optimum corner-contact schedule to an empty schedule via partial corner-contact schedules. And vice versa there must be a task permutation and a set of corner-contact locations which reassemble the optimum schedule. The branching scheme enumerates all task permutations, and for a given partial permutation, task assignments in all feasible corner-contacts are verified.

The experiments were conducted on a cluster of 30 PCs with Intel Core 2 Quad CPU Q9650 running at 3.00 GHz, with 8 GB RAM memory, and OpenSuSE Linux. The algorithms were implemented in GNU C++. Two series of experiments were conducted. In the first series, task numbers $n$ were increasing from $n=5$ to $n=11$. The processor numbers were $m\in \{10,20,50,100,200,500\}$. Processing times of the tasks were chosen with discrete uniform distribution $U[1,100]$. Tasks widths were generated with discrete uniform distribution $U[1,size_\mathrm{max}]$ with two ranges: $size_\mathrm{max}\in \{\lceil m/2\rceil ,m-1\}$. For each combination of $n,m$ and $size_\mathrm{max}$ at least 1E4 instances were generated and solved.

The relative frequency of the c/nc-difference in the instance population is shown in Fig. 8a versus task number $n$ and in Fig. 8b versus processor number $m$. In Fig. 8b, results for instances with $n\ge 7$ are shown for better readability. It can be verified in Fig. 8 that on average the emergence of c/nc-difference depends on the sizes of the tasks. If task sizes are dispersed (Fig. 8a, $size_\mathrm{max}=m-1$) then fewer than 0.8 % instances had c/nc-difference in our simulations. If task sizes are more restricted (Fig. 8a, $size_\mathrm{max}=\lceil m/2\rceil$) then c/nc-difference is more frequent and nearly as many as 5 % of instances had it. Our results support Conjecture 1 because no c/nc-differences were observed for $n\le 6$. The frequency is increasing with $n$ and decreasing with $m$. It remains an open question whether the frequency of c/nc-differences tends to 100 % with growing $n$ (Fig. 8a).

Fig. 8

Frequency in % of c/nc-differences in simulation. a versus $n$ b versus $m$

The magnitude of c/nc-differences, measured as the ratio of contiguous to non-contiguous schedule lengths, is shown versus $n$ in Fig. 9a and versus $m$ in Fig. 9b. In both figures the boxplots show quartiles of values. Only instances with $n\ge 7$ are depicted in Fig. 9b. It can be seen that the biggest ratio of schedule lengths is $\approx$1.15 which is far below 1.25 observed in Fig. 5. Thus, the results support Conjecture 2. On average the difference between contiguous and non-contiguous schedule lengths decreases with the number of tasks $n$ from 2.1 % difference median at $n=7$ to 1 % at $n=11$ (Fig. 9a). No apparent tendency can be observed in the ratios of the c/nc-different schedule lengths versus $m$ (Fig. 9b).

Fig. 9

Dispersion of c/nc-different schedule lengths. a versus $n$, b versus $m$

Intuitively, the tendencies in Figs. 8, 9 can be justified in the following way: On the one hand, the number of opportunities for creating c/nc-difference is growing with the number of the tasks. Hence, the frequency of c/nc-differences is growing (Fig. 8a). On the other hand, also the flexibility of constructing contiguous schedules is growing with the number of the tasks. Therefore, the difference in contiguous/non-contiguous schedule lengths is decreasing with $n$ (Fig. 9a). With growing number of processors $m$, the relative differences between task sizes (e.g., $size_j/m-size_i/m$, for tasks $T_i, T_j$) have more and more possible realizations in the stochastic process defining the instances. This gives more flexibility and makes enforcing c/nc-difference more difficult with growing $m$. Consequently, with growing $m$, fewer c/nc-different instances were generated (Fig. 8b). Yet, when a c/nc-difference arises then ratio $C^\mathrm{c}_\mathrm{max}/C^\mathrm{nc}_\mathrm{max}$ is ruled by the relative lengths of the tasks. It does not depend on $m$ and hence no tendency is visible in Fig. 9b.

In the second series of experiments we took a closer look at the impact of $size_j$ and $p_j$ distributions on the frequency of c/nc-difference and ratios of the schedule lengths. Here $m=100$, while $n$ was generated with uniform discrete probability from $U[7,11]$. Task widths were generated from $U[1,size_\mathrm{max}]$, where $size_\mathrm{max}$ increased from 10 to 100 with progress of 10. Processing times were generated from $U[1,p_\mathrm{max}]$, where $p_\mathrm{max}\in \{25,50,100,200,400,800\}$. For each pair of $size_\mathrm{max},p_\mathrm{max}$ at least 1E4 instances were generated and solved. As it can be seen in Fig. 10 the c/nc-difference becomes quite frequent for certain $p_j, size_j$ distributions. On the one hand, if $size_\mathrm{max}$ is small then the total number of required processors $\sum _{j=1}^n size_j$ hardly ever exceeds $m$ and all tasks are executed in parallel. On the other hand, if $size_\mathrm{max}$ is big then many tasks require $size_j>m/2$ processors and must be executed sequentially. Consequently, the greatest chance for c/nc-difference arises when task sizes are moderate, i.e., around $m/4$ on average. The ratios of c/nc-different schedule lengths (not shown here) revealed only that for smaller $p_\mathrm{max}$ optimum schedules are shorter and hence schedule length ratios are bigger on average.

Fig. 10

Frequency in % of c/nc-differences in simulation versus range of $size_j$ and range of $p_j$

6 Conclusions

In this paper we analyzed differences between optimum non-preemptive contiguous and non-contiguous schedules for parallel tasks. The requirements on the minimal instances allowing the c/nc-difference were pointed out. Determining whether a c/nc-difference emerges is computationally hard. However, all non-contiguous schedules have a valid contiguous counterpart at most twice as long as the original schedule. Since the two variants of the problem are apparently different, one should distinguish them in the $\alpha |\beta |\gamma$ notation. For example, by adding c, nc to the $size_j$ phrase: $P|size_j\!-\!c|C_\mathrm{max}$ versus $P|size_j\!-\!nc|C_\mathrm{max}$. We leave a few open questions: What is the minimum number of tasks necessary for c/nc-difference to arise (Conjecture 1)? Is it always possible to build a contiguous schedule not longer than 125 % of the non-contiguous schedule length for the same instance (Conjecture 2)? Does the frequency of c/nc-differences tends to 100 % with growing $n$ (Fig. 8a)?