1 Introduction

Currently, among the various limitations to be solved during the development of superconducting materials, there are still pendant tasks to overcome such as achieving temporal stability of superconductivity behavior at several experimental conditions [1], getting vortex creep [2], and avoiding the aging effect and environmental degradation [3,4,5,6,7]. In particular, it is well known that the superconductivity property of cuprate superconductors degrades or destroys with time [8]. Thus, understanding the aging effect of the cuprate superconductors is vital for industrial applications.

Among high critical temperature cuprate superconductors (HTSC), YBa2Cu3O7 (YBCO) is one of the most studied and promising for industrial applications. Previous studies about the aging effect on YBCO reports that it reacts with surrounding air if the sample is kept unprotected for a long time. This leads to the degradation of the superconducting properties [9]. Nonetheless, at relative short-time, the YBCO does not show any major change in ambient air [10]. For long-term applications it is important to protect any device made from YBCO superconductor by coating or controlling the surrounding atmosphere.

On the other hand, double-site-doped YBCO with rare earths or lanthanides has been extensively studied for both, understanding the origin of the superconductivity and to increase the TC in YBCO. In particular, studies about YBCO doped with Ca and BO3: [Y1−xCax]SrBaCu2.80(BO3)0.20O7 with \(0.10\;\le\;x\;\le\;0.50\) has been demonstrated that the superconducting transition occurs at TC = 77 K, being this value independent of the calcium content [11].

However, there is lack of information about the aging effect in double-site-doped YBCO such as [Y1−xCax]SrBaCu2.80(BO3)0.20O7 with \(0.10\;\le\;x\;\le\;0.50\) which could provide information about the stability of the bonding between doped rare earth and ions into the YBCO structure with time. The present work reports the changes occurred in the crystalline structure and superconducting properties in [Y1−xCax]SrBaCu2.80(BO3)0.20O7 powder samples due to the aging effect for more than 20 years.

2 Experimental

The pristine superconducting samples were prepared in 2000 by following the solid-state reaction method [11]. In brief, stoichiometric amounts of Y2O3, BaO2, SrCO3, CaCO3, CuO, and H3BO3 were grinded and sintered at 1273 K for 16 h in air and O2. The pristine samples were characterized and then stored under normal laboratory environmental conditions for 24 years.

The crystallization of the aged samples was studied by X-ray diffraction (XRD) technique. The data were collected from 8 to 80° (0.01° step) using a powder universal diffractometer Bruker D8 with Cu Kα1 radiation (λ = 1.54056 Å). The crystallite size was estimated from the basic Scherrer’s formula, neglecting peak broadening caused by residual stresses in the films [12].

$$D\;=\;\frac{K\lambda }{{\beta }_{hkl}\;{\text{cos}}\;{\theta }_{hkl}}$$
(1)

where \(D\) is the average crystallite size, \(\lambda\) is the wavelength of the applied X-ray (λCu-Kα1 = 0.154056 nm), \({\theta }_{hkl}\) is the Bragg’s angle, \({\beta }_{hkl}\) is the width of the x-ray peak on the \(2\theta\) axis, which can be easily found by measuring the full width at the half maximum (FWHM) of the reflection, and \(K\) is the so-called Scherrer Constant. \(K\) depends of the crystallite shape and the size distribution, indices of the diffraction line, and the actual definition used for \(\beta\) whether FWHM or integral breadth [13]. \(K\) can have values from 0.62 and 2.08. In the present work, \(K\) = 0.916 is used.

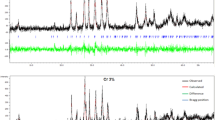
The powder diffraction patterns were refined using the Rietveld refinement method using the FullProf Suite program (January 2021 version). The background of the powder X-ray diffraction was refined using a linear interpolation between a set of background points with refinable heights. A pseudo-Voigt function [14] was used to describe the reflection profiles. No corrections for absorption or micro-absorption were applied. The R values (Rp, Rwp, Rexp, RBragg, and RF) as well as the S parameter were used as numerical convergence criteria for the refinement. The definition of the R parameters is described in reference [15]. To ensure the convergence of the structural parameters, the Rietveld refinement was performed following the order described in reference [16].

Temperature dependence of the magnetization was measured by using a Quantum Design DC Magnetic Property Measurement System (DC-MPMS-SQUID) magnetometer equipped with a 7-T superconducting magnet. The data were collected in zero field cooling (ZFC) and field cooling (FC) modes at applied magnetic fields from 10 Oe and 20 kOe for superconducting and normal state, respectively. The magnetization hysteresis loops were measured using the same DC-MPMS-SQUID equipment. All the M(H) measurements were done under applied magnetic fields from − 5 to + 5 T and at 10 K.

Critical current density \({J}_{C}\) values were estimated using the critical state Bean model, according to the relation between the irreversible magnetization Mirr and \({J}_{C}\) (see Eq. (2)) [17]:

$${J}_{C}\;=\;\left[\frac{30\Delta M}{d}\right]$$
(2)

where \({M}^{+}\mathrm\;{and }\;{M}^{-}\) are the magnetization branches in the fully penetrated state for decreasing and increasing applied fields, respectively, and \(\Delta M\;=\;{M}^{-}\;-\;{M}^{+}\). The unit of \(\Delta M\) is emu/cm3, and \(d\) is the crystallite diameter of each superconducting sample.

3 Results and Discussion

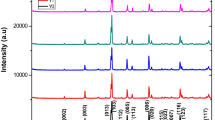
Figure S1 shows the XRD pattern for each sample with 0.1≤ \(x\)  ≤ 0.5 for the Ca composition. The presence of the peaks (103), (104), (113), (200), (116), (220), and (310) corresponds to the superconductor phase, in agreement with the XRD pristine samples [11]. Additionally, carbonate barium BaCO3 reflections were detected, being its presence product of the interaction between the samples and the environment along the years. However, the presence of BaCO3 reflections is not clearly observed in the sample with x = 0.3. As complement for the XRD characterization for the aged samples, some SEM micrographs together with their respective EDX analysis are presented in Fig. S2. Regarding the carbon presence, Tables S1–S5 reveal C in all the aged samples, corroborating the presence of BaCO3.

The Rietveld refinement of the two series is shown in the Fig. 1. The raw data were analyzed in the tetragonal structure with P4/mmm symmetry by Rietveld refinement technique to obtain the structural parameters. At the initial stage of refinements for the main phase of YBCO, it is assumed that the occupancies for the sites Ba (1/2, ½, zBa), Cu(2) (0, 0, zCu(2)), O(2) (0, 0, zO(2)), and O(3) (0,0, zO(3)) are all set to 1. The Ca atom was assumed to occupy at Y-site. Also, the oxyanion BO3 was assumed to occupy at Cu(1) site. Oxygen atoms were assumed to occupy at O(1), O(2), O(3), O(4), and O(5) sites. The oxygens O(4) and O(5) were employed to link the B atom. Moreover, the occupancies of oxygen atoms sited at O(1), O(4), and O(5) were refined. The fractional coordinates oxygen atoms sited at O(4) and O(5) were inaccurate due to the weak X-ray scattering power for oxygen atoms. For this reason, the fractional coordinates were fixed. The structural parameters for the samples were refined so that the calculated pattern fits the observed one very well. A summary of the refined atomic parameters for both series is given in Tables 1 and 2.

Fig. 1
figure 1

Rietveld refinement of XRD patterns (in logarithmical scale) of the a pristine and b aged [Y1−xCax]SrBaCu2.80(BO3)0.20O7 with \(0.10\;\le\;x\;\le\;0.50\) samples

Full size image
Table 1 Refined structural parameters for the pristine [Y1−xCax]SrBaCu2.80(BO3)0.20O7 with \(0.10\;\le\;x\;\le\;0.50\) samples
Full size table
Table 2 Refined structural parameters for aged [Y1−xCax]SrBaCu2.80(BO3)0.20O7 with \(0.10\le x \le 0.50\) samples
Full size table

The lattice parameters versus Ca content, x, are plotted in Fig. 2 for the pristine and the aged samples. Due to the ionic radii of the calcium atom (0.99 Å) being bigger than the yttrium atom (0.93 Å), the cell unit volume increases as more calcium atoms enter the structure replacing the yttrium atom. This increase is also observed in the cell parameters like a- and c-axes despite the difference in the ionic between calcium and yttrium; calcium (Ca2+) has a lower valence value than yttrium (Y3+). This fact is exposed in the cell unit volume where the valence reaches the balance with x = 0.20 for the pristine samples (Fig. 2b) and x = 0.40 for aged samples (Fig. 2d). The jumps observed in the lattice parameters is caused by the competition between two local inner stress in the unit cell, ionic radii, and atom valence. Moreover, CuO and BaCuO3 spurious phase percentage in the pristine and aged samples is shown in Fig. 2e, f, respectively. These two phases were found in a major percentage in the aged samples than in the pristine ones.

Fig. 2
figure 2

a, b Lattice parameters of the pristine sample. c, d Lattice parameters of the aged samples. e, f CuO and BaCuO3 spurious phase percentage in pristine and aged [Y1−xCax]SrBaCu2.80(BO3)0.20O7 with \(0.10\le x\le 0.50\) samples, respectively

Full size image

With the aim of quantify the aging and environmental effect in the superconducting properties, Fig. 3 shows the temperature dependence of the zero-field cooling susceptibility in the two samples series. Figure 3a shows a clear diamagnetic response measured under applied magnetic field of 10 Oe for the x = 0.20, 0.30, 0.40, and 0.50 of the aged samples, with Tc = 75.33, 75.30, 79.40, and 73.35, respectively. These Tc values are obtained from the \(d\chi /dT\) curves shown in the inset of Fig. 3a. Despite the long time, it does not show appreciable changes compared with the non-aged samples (see Fig. 3c) [11]. According to Fig. 3a, the sample with Ca concentration x = 0.1 does not show diamagnetic signal and therefore does not exhibit the superconducting phenomena. However, at temperatures below 10 K, the susceptibility values decay, which suggests that there is a diamagnetic component in the sample. The ZFC \(\mathrm{\chi vs}. T\) plot at under a higher magnetic field, 20 kOe, is shown in Fig. 3b. Interestingly, under this Hext, the powder with x = 0.10 shows diamagnetic response, corresponding to the superconducting behavior, similar to the x = 0.10 pristine sample. However, under the same applied field, the curve corresponding to the Ca-content x = 0.5 begins to lose its superconductor response. This might indicate that the value of the applied Hext is close to the Hc2 and thus the superconductivity is destroyed. In addition, the presence of the CuO and BaCO3 secondary phases affects the superconducting transition, as noted by comparing Fig. 3a and b. This is clearly distinguished at low T in both cases, which arise in a positive contribution signal. For the pristine samples, the diamagnetic signal reaches saturated values for all Ca content.

Fig. 3
figure 3

Zero-field cooling DC susceptibility vs. temperature plots under a 10 Oe applied field a and 20 kOe b for the aged samples, and under 10 Oe for the pristine samples c. c Reprinted from reference [11] with permission from Elsevier

Full size image

Figure 4 shows the temperature-dependence of the inverse magnetic DC susceptibility in the normal state, at the temperature range 100 to 300 K and under Hext = 20 kOe. The plots show a typical Curie-Weiss behavior in all the cases. However, for x = 0.3 and 0.4 in the aged samples (see Fig. 4a), two (positive and negative) \({\theta }_{c}\) values are discovered, indicating two (ferromagnetic and antiferromagnetic) coupling contributions. Since the pristine samples showed only antiferromagnetic coupling under the same applied magnetic field [11], the aging effect has produced the appearance of a ferromagnetic signal. For x = 0.2 and 0.5, the new coupling observed corresponds to ferromagnetic with positive \({\theta }_{c}\) values. Table 3 summarizes the \({T}_{{\text{c}}}\) and \({\theta }_{{\text{c}}}\) values found for the two series samples.

Fig. 4
figure 4

Inverse magnetic DC susceptibility versus temperature plots measured at Hext = 20 kOe for the aged a and pristine samples b. All the plots show a typical Curie-Weiss behavior. b Reprinted from reference [11] with permission from Elsevier

Full size image
Table 3 A comparison of the characteristic temperatures at normal (\({\theta }_{c}\)) and superconducting (\({T}_{c}\)) state for the pristine and aged-doped YBCO powder samples
Full size table

To check if the aged samples are suitable for potential application, the critical current density \({J}_{C}(H)\) isothermal curves were indirectly estimated from the hysteresis loops (see Fig. 5a) by using the Bean model. Figure 5b shows the \({J}_{C}\) values for each aged powder at 10 K. The results indicate that for x = 0.1, \({J}_{C}\) reaches the highest values (around 106 A/cm2) at 10 K ( \({\mu }_{0}\) Hext = 0.5 T). However, for all cases, a rapid decay of the \({J}_{C}\) values is observed. Nevertheless, considering its age, these presented \({J}_{c}\) values indicate that the samples are suitable for potential application. The presence of the carbonate barium (BaCO3) does not affect the transport capabilities of the studied samples.

Fig. 5
figure 5

a Hysteresis loops measurements at 10 K for the aged samples. b Critical current density vales estimated by using the critical Bean model in the M(H) loops

Full size image

4 Conclusions

The aging effect in [Y1−xCax]SrBaCu2.80(BO3)0.20Oy powder samples stored for 20 years at normal conditions of pressure and temperature was studied. The structural characterization, made by XRD and Rietveld refinement, revealed that barium carbonate BaCO3 has been formed during the stored period. This is corroborated by SEM-EDS that shows the presence of carbon in all the EDS spectra and on several sites. The aging and environmental effect in the superconducting properties was studied by temperature dependence of the zero-field cooling susceptibility plots under 10 Oe and 20 kOe applied magnetic fields. The powders show superconducting behavior in agreement with the pristine samples 24 years ago without any appreciable change of Tc. Critical current density values were estimated by the critical Bean model, evidencing that despite the morphological degradation, the samples still present \({J}_{c}\) potentially applicable values. Overall, the presence of the formed BaCO3 should have affect the superconducting properties of the sample.