1 Introduction

Second-generation high-temperature superconducting (HTS) tapes, known as REBCO coated conductors (REBCO-CCs), have advantages of high critical magnetic field and strong current-carrying capacity. Meanwhile, it is not practical to gain a high magnetic field or high transport current with a single HTS tape. As a result, cabling methods of HTS tapes to achieve a powerful electro-magnetic application have been proposed [1,2,3]. The conductor on round core (CORC) cable is one of them, and it is composed of a round former and layers of helically wound REBCO-CCs. It is remarkable in the power density and mechanical adaptability, and those transposed superconductors in each layer make the CORC cable effective in coupling current reduction.

There have been some studies on the AC loss characteristics of CORC cables. Wang et al. [4] and Sheng et al. [5] investigated the cable’s magnetisation in TA formulation and H formulation, respectively. They explored the effects of magnetic shielding, winding direction and multi-layer layout. Also, Šouc et al. [6] and Vojenčiak et al. [7] found that CORC cables wound with striated superconducting tapes could reduce the magnetisation loss at a high magnetic field, and the filaments in superconductors proved to be useful. Furthermore, Terzioǧlu et al. [8] experimentally examined both the magnetisation loss and the transport loss of the CORC cable, and the metallic former is tested to increase the total loss in this case. Correspondingly, Ye et al. [9] probed the influence of the electrical properties of the core former on the cable loss, showing both magnetisation loss and transport loss decreased with lower conductivity of the former. However, most of the cable samples used above have only a single layer, and the complex electro-magnetic behaviours inside a multi-layer CORC have not been fully revealed.

Therefore, this paper mainly aims to study the transport loss of a two-layer CORC cable and compare it with a single-layer structure. A 3D finite-element cable model is first introduced. Then, measurements on the transport loss of an assembled cable are carried out to verify the numerical modelling. Next, the loss distribution, the eddy current density and magnetic field characteristics among different layers are analysed in the simulation. Moreover, simulated results of a single-layer cable is presented. Finally, the normalised transport loss of the two-layer and the single-layer CORC cable are quantitatively compared with a reference of straight HTS tapes.

2 Sample Description

The studied CORC sample, shown in Fig. 1, is manufactured by Advanced Conductor Technologies. It is a two-layer structure consisting of six REBCO-CCs. Voltage taps are soldered inside each terminal, and they are brought together as twisted pairs to eliminate the inductive voltage component. The detailed parameters of the cable can be found in Table 1.

Fig. 1
figure 1

Photograph of a two-layer CORC cable. The insulation maintains tape tension against the former

Full size image
Table 1 Specifications of the Two-Layer CORC Cable
Full size table

The solid former is made from copper, and the pitch length (\(L\)) is 27.2 mm with a winding angle (\(\alpha\)) of 60°. Both parameters approximately have the following relationship,

$$\mathrm{tan}\ \alpha =\frac{L}{\pi d}$$
(1)

where \(d\) is the diameter of the core former.

Due to the helical layout of the CORC cable, a full pitch of 3D geometry is adopted rather than just a 2D plane. This structure is drawn in Solidworks before being imported into the COMSOL/Multiphysics. The schematic of the finished 3D model is shown in Fig. 2. It is worth noting that no metal components are included, and the thickness of the superconducting layer is thickened to \(100 \mu m\) in order to reduce the meshing elements.

Fig. 2
figure 2

Schematic of the studied CORC cable model

Full size image

3 Numerical Method

3D H formulation is implemented here to solve the required Maxwell equations [10, 11]. The non-linear resistivity of the superconductors is characterised by the classic power law, while that of the copper former is a constant in the model. They are expressed as follows,

$$\rho =\left\{\begin{array}{ll}\frac{{E}_{c}}{{J}_{c}\left(B,\theta \right)}{\left(\frac{{J}_{norm}}{{J}_{c}\left(B,\theta \right)}\right)}^{n-1} & for\ superconductors\\ {\rho }_{c} & for\ copper\ former\end{array}\right.$$
(2)

where \({E}_{c}=1\times {10}^{-4} V\ {m}^{-1}\), \({J}_{norm}=\sqrt{{J}_{x}^{2}+{J}_{y}^{2}+{J}_{z}^{2}}\), \(n=31\) and \({\rho }_{c}=5\times {10}^{-9}\Omega \cdot m\).

As an input, \({J}_{c}\left(B,\theta \right)\) is incorporated by Kim model [12], written in Eq. (3),

$${J}_{c}\left(B, \theta \right)={J}_{c}\left({B}_{\parallel },{B}_{\perp }\right)=\frac{{J}_{c0}}{{\left[1+\sqrt{{\left(k{B}_{\parallel }\right)}^{2}+{{B}_{\perp }}^{2}}/{B}_{c}\right]}^{b}}$$
(3)

where \({J}_{c0}\) is the critical current density in self-field at \(77 K\); \(k=0.25\), \(b=0.7\), \({B}_{c}=0.1 T\) [12, 13]. \({B}_{\parallel }\), \({B}_{\perp }\) stand for the magnetic field that is parallel and perpendicular to the tape surface, respectively.

With the helical structure of the CORC cable, the above two magnetic field components can be calculated by the cylinder coordinate system, as expressed in Eq. (4). Meanwhile, the conversion matrix between the Cylindrical \(\left(x, y,z\right)\) and the Cartesian coordinate \(\left(r, \theta ,z\right)\) system is shown in Eq. (5).

$$\left\{\begin{array}{c}{B}_{\parallel }=\sqrt{{{B}_{\theta }}^{2}+{{B}_{z}}^{2}}\\ {B}_{\perp }={B}_{r}\end{array}\right.$$
(4)
$$\left[\begin{array}{c}{B}_{r}\\ {B}_{\theta }\\ {B}_{z}\end{array}\right]=\left[\begin{array}{ccc} cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0\\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{c}{B}_{x}\\ {B}_{y}\\ {B}_{z}\end{array}\right]$$
(5)

A sinusoidal transport current \({I}_{a}sin\left(2\pi ft\right)\) is imposed by employing a constraint function in the finite-element software package. Also, with the geometric symmetry in the axial direction, periodic conditions are applied as boundary conditions to simplify the modelling.

4 Results and Discussion

4.1 Model Validation

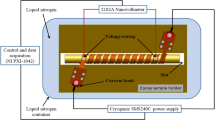
In order to validate the developed model, the measurement on the AC transport loss of the sample shown in Fig. 1 is carried out. The experimental schematic is shown in Fig. 3. The adjustable compensation coil is utilised to compensate the inductive component of the CORC sample. The transport loss can be calculated by electrical method, which is expressed as the following,

$$Q=\frac{{I}_{rms}\cdot {V}_{rms}}{f}$$
(6)

where \({I}_{rms}\) is the RMS value of the AC current flowing through the cable, and \({V}_{rms}\) is the RMS value of the voltage measured on the sample; \(f\) is the frequency of the AC current.

Fig. 3
figure 3

Experimental schematic of the transport loss measurement using electrical method

Full size image

In the meanwhile, the transport loss in the cable simulation is gained using the power density integration,

$$Q=2{\int }_{T/2}^{2}{\int }_{V}\ J\cdot E\ dV\ dt$$
(7)

where \(T\) is the period of the transport current; \(J\) and \(E\) is the current vector and electric field vector; V is the integration area that contains all the superconductors and the copper former.

The transport loss with respect to the current amplitude for three groups of frequency is measured, and the comparison between experiment and simulation is plotted in Fig. 4. The loss here is along the axial direction, and its unit is \(J/cycle/m\). It is witnessed that the measured and the simulated results generally match, which validates the modelling method. The frequency dependency is significant before the transport current goes to \(250A\). As a result of the power capacity limitation of the experimental equipment, the maximum amplitude of the applied current is \(250A\). Hence, the loss characteristics in the situation where the imposed current is larger is examined by the following simulation.

Fig. 4
figure 4

Measured (symbols) and simulated (lines) AC transport loss in \(J/cycle/m\) (cable length) of the two-layer CORC sample

Full size image

4.2 AC Transport Loss Analysis of Two-Layer CORC Cable

To further reveal the loss distribution in the two-layer CORC cable, Fig. 5 plots the trend of loss respectively generated in the inner layer, the outer layer and the former under an increasing transport loss for different frequency groups.

Fig. 5
figure 5

Simulated AC transport loss in \(J/cycle/m\) (cable length) of the inner layer, outer layer and former in the two-layer CORC sample

Full size image

Simulated results indicate that the loss of the superconducting layers basically does not change with frequency, while the eddy current loss in the former goes up with the frequency rising. Also, the induced core loss is much greater than the transport loss in superconductors with a relatively small current. When the transported current arrives at around \(300A\), the loss caused by the outer superconducting layer can overtake the eddy current loss; the loss generated in all the superconducting layers starts to become more dominant in the total cable loss. This frequency dependence tends to be no longer significant with a higher current until the two-layer cable’s maximum critical current, \(140\times 6=840\ A\).

Figure 6 then illustrates the eddy current density distribution in the copper former with a typical transport current (\(f=72 Hz\), \({I}_{a}=400\ A\)) at the time point when the transport current reaches its maximum amplitude (\(2\pi ft=3\pi /2\)). It can be seen that the eddy current here is mainly concentrated in the gap where the two layers are aligned and the interval between the inner superconducting tapes.

Fig. 6
figure 6

Distribution of eddy current density in the copper former of the two-layer CORC sample at selected instant (\(2\pi ft=3\pi /2\)) under a sinusoidal transport current (\(f=72 Hz\), \({I}_{a}=400\ A\))

Full size image

The eddy current distribution on the former surface indicates the shielding effect among the two superconducting layers and the copper core. Figure 7 further draws the magnetic flux density distribution between the two superconducting layers in the same instant of the sinusoidal current (\(2\pi ft=3\pi /2\)). One can see that the magnetic field in the inner superconductors is much lower than that of the outer layer. The magnetic field of the part covered by the outer layer on the inner layer is also lower than the gap exposed in the air space. Thus, while the inner layer is shielding the former, it is also shielded by the outer superconducting tapes. This shielding effect also explains the loss deviation between the two superconducting layers in Fig. 5. Consequently, the eddy current loss in the former is not only restrained by the cancellation of the self-field of the opposite-wound layers, but also due to the shielding effect of the inner superconducting tape.

Fig. 7
figure 7

Distribution of magnetic flux density in the superconductors of the two-layer CORC sample at selected instant (\(2\pi ft=3\pi /2\)) under a sinusoidal transport current (\(f=72 Hz\), \({I}_{a}=400\ A\)). (a) outer layer; (b) inner layer

Full size image

Additionally, when a transport current passes through an actual CORC cable, its assembled superconducting tapes usually present an inhomogeneous current. This was attributed to the non-uniform contact resistance [14]. Now, it can be concluded that the electro-magnetic interaction between the inner and outer layers should also be taken into account.

4.3 AC Transport Loss Analysis of Single-Layer CORC Cable

Furthermore, we remove the three superconductors in the outer layer of the cable model and calculate the AC transport loss of this typical single-layer structure. Likewise, the total loss under the increasing current amplitude for three groups of frequency is calculated, as shown in Fig. 8.

Fig. 8
figure 8

Simulated AC transport loss in \(J/cycle/m\) (cable length) of the single-layer CORC sample

Full size image

This figure shows that the total transport loss is dependent on the frequency. In contrast with the case in the two-layer CORC cable, the frequency dependence can be observed until the transported current close to the single-layer cable’s maximum critical current, \(140\times 3=420\ A\).

Subsequently, the power of the cable loss over a cycle of the transport current (\(f=72 Hz\), \({I}_{a}=200\ A\)) is displayed in Fig. 9a, which proves that the eddy current loss from the copper former is overwhelmingly more outstanding than the AC loss of the remaining HTS tapes. This is different from the results of the two-layer cable, whose loss from the core can be dramatically reduced due to the inside shielding effect and the outer superconducting tapes wound in the opposite direction.

Fig. 9
figure 9

Simulated AC transport loss of the single-layer CORC cable at \(f=72 Hz\) and \({I}_{a}=200\ A\): (a) loss power in \(W/m\) (cable length) of superconductors and the former over one cycle; (b) current density distribution in the former at \(t=7.5 ms\), Current streamlines are plotted with white arow-style lines; (c) distribution of magnetic flux density in the superconductors

Full size image

Besides, if taking the time point around the peak value of the eddy current loss (\(t=7.5 ms\)) as an example, the cross-sectional view of the eddy current density in the former is illustrated in Fig. 9b.

The streamline in the graph demonstrates that the eddy current in the former is mainly along the circumferential direction, which is consistent with the helical structure of the configurated superconducting tapes. As a result of Lenz’s law, the closer to the former surface, the greater the current density.

Meanwhile, Fig. 9c shows the magnetic flux density in the superconductors at the same time point. It can be seen that the magnetic field in the single-layer CORC cable is symmetrically distributed on both sides of the superconductors along the winding direction.

4.4 Comparison of Two-Layer and Single-Layer CORC Cable

Finally, the simulated transport losses of the above two-layer and the single-layer CORC cable are compared with the theoretical values derived from the strip equations of the Norris model [15], as shown in Fig. 10. For better comparison, the transport loss here means the average loss normalised to the length of superconducting tapes, and the conversion is expressed as follows,

$${Q}_{average}=\frac{{Q}_{cable}}{N}\mathrm{sin}\ \alpha$$
(8)

where \(N\) is the number of tapes of the cable; \(\alpha\) is the winding angle. Meanwhile, without considering the terminal contact resistance, the theoretical maximum current of the cable is taken as the reference of the cable’s critical current. Here, it is respectively \(840\ A\) and \(420\ A\) for the two-layer and the single-layer structure. The critical current of the HTS tape is \(140\ A\).

Fig. 10
figure 10

Normalized AC transport loss in \(J/cycle/m\) (tape length) of the two-layer CORC sample and the single-layer CORC sample, with a reference of the analytical solutions of Norris strip model

Full size image

The graph shows that the normalised loss of a single-layer cable is greater than that of a single HTS tape for most situations; only when the current is close to the critical current, its loss becomes less than the latter. What’s worse, the higher the frequency, the greater the transport loss in the single-layer structure. In comparison, the two-layer cable not only gets rid of frequency dependence before the current reaching \(0.4{I}_{c}\), but also its loss trend is always under the curve of the Norris model.

Therefore, if the CORC cable fabricated into an multi-layer structure with the winding direction of the adjacent layer opposite to the previous layer, the inside shielding effect and the even-numbered layer structure can significantly offset the loss effect of the self-field on the copper former and achieve a more efficient space use of HTS tapes.

5 Conclusion

This paper mainly investigated the AC transport of CORC cables subjected to sinusoidal transport current, and the cases of a two-layer and a single-layer cables are analysed and compared.

The studied model was built in COMSOL/Multiphysics based on 3D H formulation, and measurements on transport loss verified its validity. Then, a two-layer structure was first studied. The transport loss among different layers and the core former were analysed, indicating that the eddy current loss in the former tended to be less significant with the transported current increasing. Meanwhile, the distribution of current density and magnetic flux density in those components was analysed, and the shielding effect was found out, which also contributes to the current inhomogeneity between layers of the multi-layer cable.

Next, a single-layer CORC cable was subsequently modelled, demonstrating that most of the transport loss of the cable came from the eddy current loss in the copper former, and the eddy current was more concentrated on the outer surface.

Finally, the normalised transport losses of cables over the length of an HTS tape are compared with Norris theoretical data, showing that the two-layer CORC cable with opposite-winding direction exhibited minimal transport loss among them.

Overall, the modelling method and analysis process presented can provide an essential reference for the practical design of CORC cable.