1 Introduction

Recently, nanoparticles [1–3], nanofilms [4–6], nanotubes [7], and nanowires [8–12] have attracted considerable attention. The motivation in these studies is mainly because nanomaterials have many peculiar physical properties compared with those of bulk materials. There are many potential applications where nanomaterials may become very important such as in information storage, sensors [13], and medical applications [14]. Under certain conditions, there is in ferrimagnets an interesting possibility of the existence of the compensation temperature. The compensation behavior has potential applications in the field of thermomagnetic recording [15–17]. Significantly, the coercivity has been proven to show strong temperature dependence near the compensation point. It can be applied to achieve a direct erasable ability with a local heating by a focused laser beam in magnetic optical recording media [18, 19].

The nanomaterials have been studied, both experimentally and theoretically, within various models and techniques, rich critical, and magnetic properties were found. In refs [20, 21], the magnetic properties of a cubic nanowire, a multilayer and multisublattice cubic nanowire with mixed spin (1,3/2) have been examined by the effective field theory (EFT). It was found that two compensation points can exist for certain values of the system parameters. In ref. [22], the authors have studied the magnetic behavior of a mixed spin (1,3/2) ferrimagnetic spherical nanoparticle using Monte Carlo simulations. The results found present rich variety of phase diagrams with first-order and second-order phase transitions. By using Monte Carlo simulations [23], the dynamic phase transition properties of a single spherical ferrimagnetic core-shell nanoparticle have been investigated. It has been found that the dynamic phase boundaries strongly depend on the Hamiltonian parameters such as the high amplitude and the period of the external field. In ref [24], the authors have investigated the magnetic properties of the cubic nanowire, which consists of a ferromagnetic core of spin-1 atoms and a ferromagnetic shell of spin −3/2 atoms with ferrimagnetic interface coupling, using the effective-field theory with correlations(EFT). They have found that two compensation points can appear for appropriate values of the system parameters. In ref. [25], the phase diagrams and compensation behaviors of a mixed spin (1/2,1) hexagonal Ising nanowire with core-shell structure have been studied by using the effective-field theory with correlations. It has been found that the system shows many rich phenomena such as first-order and second-order phase transitions and tricritical points. Recently, in ref. [26], Monte Carlo simulation has been used to study the magnetic properties of a mixed spin (5/2,2) ferrimagnetic Ising model on a honeycomb lattice. The system displays very rich critical behaviors, including the first- and second-order phase transitions, the tricritical points and the compensation points. Using a continuum approach, the magnetic configurations of barcode-type magnetic nanostructures consisting of alternate ferromagnetic and nonmagnetic layers arranged within a multilayer nanotube structure are investigated in ref. [27]. The authors found that the lines separating the magnetic phases and, in particular, the triple point, are very sensitive to the geometry of the barcode-type nanostructures. Experimentally, magnetic NiFe/Au barcode nanowires with self-powered motion is investigated [28]. The approach used of synthesize these nanowire demonstrates how sophistication in barcode nanoarchitecture can be used to synthesize a wide range of hybrid materials.

Despite these studies, as far as we know, the phase diagrams and the compensation behavior of a mixed spin (3/2,1) hexagonal Ising nanowire with alternate layers have not been investigated. Given their potential technological applications linked with the existence of a compensation phenomena, nanowires with alternate layers have been attracted considerable interest. Therefore, in this paper, we have used Monte Carlo simulations, to study the phase diagrams of a hexagonal ferrimagnetic nanowire with alternate layers structure consisting of σ-layers with the spin σ = 3/2 and S-layers with the spin S = 1. The outline of the paper is organized as follows: in Section 2, we briefly present our model and the related formulation. The results and discussions are presented in Section 3 and finally Section 4 is devoted to our conclusions.

2 Model and Formalism

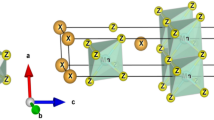
We consider a ferrimagnetic nanowire composed of alternate spin-1 ferromagnetic S-layers and spin-3/2 ferromagnetic σ-layers coupled with an antiferrimagnetic interface coupling as shown in Fig. 1. The Hamiltonian of our hexagonal Ising nanowire is given by:

$$\begin{array}{@{}rcl@{}} \mathcal{H} &=& - J_{\text{s}} \sum\limits_{\left\langle {ij} \right\rangle } {S_{\text{i}} S_{\text{j}} } - J_{\sigma} \sum\limits_{\left\langle {kl} \right\rangle } {\sigma_{\text{k}} \sigma_{\text{l}} } - J_{\text{Int}} \sum\limits_{\left\langle {ik} \right\rangle } {S_{\text{i}} \sigma_{\text{k}} } \\&&- D\left( \sum\limits_{{i} } {S_{\text{i}} }^{2}+\sum\limits_{\text{ {k} }} {\sigma_{\text{k}} }^{2}\right) \end{array} $$
(1)

where S i = ±1,0 and σ k = ±3/2,±1/2 denote the usual Ising variables. J s, J σ , and J Int are the exchange interaction parameters between the two nearest-neighboring spins located at the S-layer, σ-layer, and between S-layer and σ-layer, respectively; D stands for the single-ion anisotropy (i.e., crystal field). The summation index <i j>, <k l>, and <i k> denote a summation over all pairs of neighboring spins S − S, σ − σ, and S − σ, respectively. We have fixed the value of J s throughout the simulation. Using the Monte Carlo simulation based on Metropolis [29] algorithm, we apply periodic boundary conditions in the z-direction, free boundary conditions are applied in the x and y-directions. Data were generated over 20–40 realizations by using 50,000 Monte Carlo steps per site after discarding the first 25,000 steps. Our program calculates the following parameters, namely:

  • The sublattice magnetizations per site

    $$\begin{array}{@{}rcl@{}} M_{\text{s}} =\frac{1} {N.L/2} \left< \sum\limits_{\text{i}} {S_{\text{i}}} \right >\end{array} $$
    (2)

    and

    $$\begin{array}{@{}rcl@{}} M_{\sigma} = \frac{1}{N.L/2} \left < \sum\limits_{i} {\sigma_{\text{i}}} \right >\end{array} $$
    (3)

  • The total magnetization per site

    $$\begin{array}{@{}rcl@{}} M_{\text{T}} =\frac { (M_{\text{s}}+M_{\sigma}) } {2} \end{array} $$
    (4)

  • The magnetic susceptibility of the nanowire

    $$\begin{array}{@{}rcl@{}} \chi_{\text{T}} =\beta.N \left( \left < {M_{\text{T}}^{2}} \right > - \left < M_{\text{T}} \right >^{2}\right) \end{array} $$
    (5)

  • and we have also calculated the internal energy per site

    $$\begin{array}{@{}rcl@{}} E =\frac{1}{ 2.N.L}< \mathcal{H}>\end{array} $$
    (6)

where \(\beta =\frac {1}{k_{B}T}\), T is the absolute temperature and k B is the Boltzmann factor (here k B = 1). N denotes the number of spins in each layer and L denotes the length of the nanowire.

Fig. 1
figure 1

Schematic representation of a hexagonal nanowire with alternate layers; S-layers of spin-1 and σ-layers of spin-3/2

Full size image

To determine the compensation temperature T comp from the computed magnetization data, the intersection point of the absolute values of the sublattice magnetizations was found using

$$\begin{array}{@{}rcl@{}} \mid M_{s}(T_{comp})\mid=\mid M_{\sigma}(T_{comp}) \mid \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} sign(M_{s}(T_{comp}))=-sign (M_{\sigma}(T_{comp})) \end{array} $$
(8)

with T c o m p <T c , T c is the critical temperature i.e. Néel temperature [30]. Equations (7) and (8) indicate that the sign of the sublattice magnetitizations is different; however, absolute values of them are equal to each other at the compensation point.

The second-order phase transition is determined from the maxima of the susceptibility curves, and the first-order phase transition is obtained by locating the discontinuities of the magnetization and internal energy curves.

3 Results and Discussions

In this section, we will discuss the thermal and magnetic properties of the system for some selected values of the Hamiltonian parameters. Throughout the simulation, we have tacked L = 200 (the total number of layers) and each layer of the nanowire consists four rings. A number of additional simulations were performed for L = 250 and L = 300, but no significant differences were found from the results presented here.

Figure 2 shows the effects of the temperature on the magnetic properties of the nanowire for J σ /J s = 0.1, D/J s = 0.0 and for selected value of J Int/J s = −0.2, −0.4, −0.6, and −0.8. In Fig. 2(a), we present the total magnetization versus the reduced temperature T/J s; it is seen that the magnetization curves present two zeros. The first one corresponds to the temperature value at which the total magnetization of the nanowire M T reduces to zero, whereas the sublattice ones M s and M σ are different from zero, it corresponds to the compensation temperature. The second zero denotes the temperature at which the magnetizations M T, M s, and M σ depress to zero; it corresponds to the critical temperature of the system. Furthermore, we can see that both compensation and critical temperatures of the system increase as the absolute value of J Int/J s increases. In Fig. 2b, the variation of the sublattice magnetizations M s and M σ with the temperature are plotted. One can observe that, as the temperature increases, the magnetization of the S-layers increases slowly from its minimum value −1, whereas the magnetization M σ of the σ layers decreases monotonically from its maximum value 1.5; both magnetizations fall to zero at the critical temperature. The temperature dependence of the total susceptibility χ T is shown in Fig. 2c, it is clear that the susceptibility-temperature curves present a peaks at T c; and that, as increasing the absolute value of J Int/J s, the position of the peak shifts to higher temperatures which means that the critical temperature increases. The temperature dependence of the internal energy E is presented in Fig. 2d, we can see that the internal energy increases rapidly with increasing the temperature and decreases with J Int/J s.

Fig. 2
figure 2

The temperature dependencies of a the total magnetization, b the S-layers and σ-layers magnetizations M S, M σ , c the susceptibility of the system, and d the internal energy E, for D/J s = 0.0 and J σ /J s = 0.1 and for different values of J Int/J s

Full size image

In order to investigate the influence of J Int/J s on both critical and compensation temperatures of the nanowire, the phase diagram of the system is plotted, in Fig. 3, in the (T, J Int/J s) plane for D/J s = 0.0 and J σ /J s = 0.1. One can notice that, as the absolute value of J Int/J s increases, the critical temperature T c increases progressively; concerning the compensation one (T comp), it exists only when J Int/J s is less than a threshold value (J Int/J s = 1.2) and it increases linearly with J Int/J s.

Fig. 3
figure 3

Phase diagram of the system in (T, J Int/J s) plane for D/J s = 0.0 and J σ /J s = 0.1

Full size image

In order to study the effect of the exchange interaction J σ /J s on both critical and compensation behaviors, we have plotted in Fig. 4 the phase diagrams in the (T, J σ /J s) plane for selected values of the crystal field D (D/J s = 3.0,−2.0,−2.75, and −3.4) with J Int/J s = −0.1 (Fig. 4a), and for selected values of J Int/J s (J Int/J s = −0.1,−0.6, and −1.6) with D/J s = 0.0 (Fig. 4b). In Fig. 4a, we can see that, depending on the value of D/J s, the critical and compensation behaviors change; that is, for D/J s≤−3.4, the phase diagrams, consist only, on a line of second-order phase transition which separates the ordered and the disordered phases and which is independent of the value of D/J s, this line increases almost linearly when we increase J σ /J s. We can also notice that, in the range −3.4<D/J s<3.0, for a given value of D/J s, the critical temperature T c remains constant below a threshold value of J σ /J s and increases linearly above it. In this range of D/J s, it is worthwhile to notice that the phase diagrams are very sensitive to the change of D/J s; that is, when we increase D/J s, this threshold value of J σ /J s shifts to lower values of J σ /J s, in contrast the critical temperature increases with D/J s. It is important to mention that in this range also, we can have two kinds of phase diagrams, in the first one (D/J s = −2.0), we have only one line of second-order phase transition, while in the second kind (D/J s = −2.75), we have a line of first-order phase transition for low values of J σ /J s which is linked with a second-order critical one at a tricritical point which is located at (J σ /J s = 0.675, T/J s = 0.27). For D/J s≥3, we have only one line of second-order phase transition which is independent of the value of D/J s, this line increases in an exponential like with J σ /J s. Concerning the compensation behavior, it is important to notice that we have a compensation point only when D/J s≥−3.4 and that, in the interval −3.4<D/J s<3.0, the range of J σ /J s where the compensation temperature exists depends on the value of D/J s, above the interval (D/J s≥3.0), the range where T comp exists is constant and is equal to 0<J σ /J s<0.24. It is interesting to emphasize that, for D/J s = −2.75, the nanowire can exhibits two compensation points in a narrow range of J σ /J s, this fact is well shown in Fig. 5, where we plot the thermal variations of the magnetization for D/J s = −2.75, J Int/J s = −0.1, and J σ /J s = 0.94. This type of behavior of compensation point has been observed in ref. [31], where the effective field theory has been used to study spin-3/2 cylindrical Ising nanotube system. In Fig. 4b, it is shown that we have two types of phase diagrams, the first one is obtained for J Int/J s≤−1.45 and consists an a line of second-order phase transitions with a constant T c below a threshold value of J σ /J s and above this threshold value, T c increases linearly with J σ /J s. It is also remarked that the threshold value is strongly dependent on the value of J Int/J s, that is it decreases with decreasing J Int/J s. The second type is obtained for J Int/J s>−1.45 and it consists on a line of second-order phase transitions with increasing T c. It is worthwhile to notice that T c increases as we decrease the value of J Int/J s. Concerning the compensation temperature T comp, it exists only when J σ /J s≥−1.45 and the range where we have T comp decreases with decreasing J Int/J s. This result is similar with those obtained in ref. [32], where the authors have studied the phase diagrams of the magnetic spin-1 Ising nanowire.

Fig. 4
figure 4

Phase diagrams of the nanowire in (T, J σ /J s) plane for different values of D/J s with J Int/J s = −0.1 (a), and for different values of J Int/J s with D/J s = 0.0 (b)

Full size image
Fig. 5
figure 5

The total magnetization versus the temperature for D/J s = −2.75, J Int/J s = −0.1, and J σ /J s = 0.94

Full size image

In Fig. 6, we present the variations of the critical and compensation temperatures T c and T comp with the crystal field D/J s for J Int/J s = −0.1 and for J σ /J s = 0.1 (Fig. 6a), J σ /J s = 0.6 (Fig. 6b) and J σ /J s = 1.2 (Fig. 6c). It is interesting to note that the phase diagrams are very rich and are strongly sensitive to the variations of J σ /J s, that is, depending on the value of J σ /J s, we can have three types of phase diagrams. In the first one, Fig. 6a, in the low temperature region, we have two lines of first-order transitions. The first one, which separates the paramagnetic phase from the ferrimagnetic phase (1/2,−1), is connected to a second-order transition line at a tricritical point . The coordinates of the tricritical point are (D/J s = −2.65, T/J s = 0.73). The second first-order line, which separates the ferrimagnetic (1/2,−1) phase from the other ferrimagnetic phase (3/2,−1), terminates at an isolated critical point (•) located at (D/J s = −0.39, T/J s = 0.12). For higher temperatures, we have a second-order transition line, which increases from the tricritical point to reach a saturation value \((T_{c_{sat}}=2.5)\) for large values of D/J s. This line separates the ordered phase from the disordered one. The second type of phase diagrams, Fig. 6b, consists in two lines of first-order transitions and two lines of second-order ones with the appearance of a new ferrimagnetic phase (1/2,0) and the narrowness of the area of the (1/2,−1) ferrimagnetic phase. For large negative values of D/J s, we have a second-order transition line with a constant critical temperature (T c = 0.29), which separates the new ferrimagnetic phase (1/2,0) from the paramagnetic one. This line terminates at a critical end point denoted by the symbol \((\square )\) and located at (D/J s = −2.78, T/J s = 0.29). The second line of second-order phase transitions is connected to a first-order transition line at a tricritical point which is located at (D/J s = −2.67, T/J s = 0.66) and separates the paramagnetic phase from the ferrimagnetic one. In the low temperature region, we have a second line of first-order phase transitions. This line which separates the two ferrimagnetic phases (1/2,−1) and (3/2,−1) emerges from D/J s = −1.73 and increases vertically to an isolated critical point located at (D/J s = −1.73, T/J s = 0.46). In the third type of phase diagrams, Fig. 6c, we have only two phase transition lines, one of the second order and the other of first order with the disappearance of the (1/2,−1) ferrimagnetic phase. The second-order line separates the ordered phase from the disordered one, and as it is seen, as increasing D/J s, the critical temperature is constant \((T_{c_{sat}}=0.64)\) for large negative values of D/J s, increases with D/J s to reach a saturation value for large positive values of D/J s \((T_{c_{sat}}=5.84)\). In the low temperature region, the first-order transition line emerges from D/J s = −2.87, increases vertically to terminates at an isolated critical point located at (D/J s = −2.87, T/J s = 0.61). This line separates the two ferrimagnetic phases (1/2,0) and (3/2,−1). Concerning the compensation temperature, it exists only when J σ /J s is less than 1.1, and the range of D/J s where we have a compensation behavior decreases with increasing the value of J σ /J s to disappears from J σ /J s≥1.1. It is noted that the tricritical point appears in the spin-1 nanowire or nanotube systems, whereas the critical end point is not found in these systems [32, 33].

Fig. 6
figure 6

The phase diagrams of the system in the (T, D/J s) plane for J Int/J s = −0.1 and for J σ /J s = 0.1 (a), J σ /J s = 0.6 (b) and J σ /J s = 1.2 (c)

Full size image

In order to complete the discussion of the above phase diagrams, we have plotted in Fig. 7, the magnetizations (a–c) and the internal energy (e–d) as a function of D/J s for J Int/J s = −0.1 and J σ /J s = 0.6, and for selected values of the temperature (T/J s = 0.9,0.4 and 0.1). For T/J s = 0.9 (Fig. 7a,d), it is seen that the system presents a continuous passage between the ferrimagnetic phase and the paramagnetic one at D/J s = −2.51. In Fig. 7b,e (T/J s = 0.4), it is clear that the compensation point appears when the two sublattice magnetizations are equal at D/J s = −1.71, since the sublattice magnetization has opposite signs at this crystal field value. It is also clear that the sublattice magnetization curves exhibit a first-order point at D/J s = −2.66 between the ferrimagnetic phase and the paramagnetic one. For a low temperature value (T/J s = 0.1), it is found that the system exhibits two first-order transitions between three ferrimagnetic phases at two values of D (D/J s = −2.82 and D/J s = −1.77) (see Fig 7c,f).

Fig. 7
figure 7

The variation of the nanowire magnetization and the internal energy with D/J s for the same parameters as in Fig. 6b and for selected values of the temperature (a,d) T/J s = 0.9, (b,e) T/J s = 0.4, (c,f) T/J s = 0.1

Full size image

4 Conclusion

In this work, we have used Monte Carlo simulation employing Metropolis algorithm to investigate the phase diagrams, thermal, and magnetic properties of a ferrimagnetic nanowire with alternate layers; S-layer of spin-1, and σ-layer of spin-3/2. The two sublattices interact antiferromagnetically. We have investigated the influences of the crystal field interactions, interfacial and exchange interaction coupling on the critical, and compensation behaviors of the nanowire. It is found that, depending on the set of the Hamiltonian parameters, we can have different types of phase diagrams topology with many interesting phenomena such as, tricritical points, critical end points, and isolated critical points. Concerning the compensation temperature, we have shown that it exists only in a certain range of the system parameters, these range is closely dependant on the Hamiltonian parameters. It was also found that the system can even exhibits two compensation points in a narrow range of J σ /J s.