Induction Infrared Thermography for Non-destructive Evaluation of Welding-Induced Sensitization in Stainless Steels

Abstract

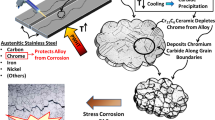
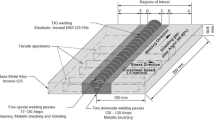
For medium- and high-carbon stainless steels, welding can induce sensitization in the heat affected zone (HAZ) adjacent to the weld, where chromium carbide $(\hbox {Cr}_{23}\hbox {C}_{6})$ precipitates out of the bulk metal and accumulates at the grain boundaries. This chromium depletion and precipitate accumulation at grain boundaries makes the alloy susceptible to intergranular corrosion, environmentally assisted cracking, and broader fracture. In this paper, we investigate the efficacy of using induction infrared thermography (IIRT) as a non-destructive method for detecting welding-induced sensitization, using the AISI 440C steel as an example. We start by presenting a laboratory experiment to demonstrate this approach, using a radio frequency function generator, an induction wand, and a FLIR SC8203 infrared camera. We use traditional metallography techniques and scanning electron microscopy (SEM) to identify the location of any sensitized regions and characterize the corresponding microstructure. The IIRT experimental results reveal a distinguishable heat signature, with higher temperature observed within the sensitized regions. Next, we present a computational study to simulate the IIRT experiment and investigate the underlying physics. We adopt a three-dimensional thermo-electro-magnetic model including Fourier’s law of heat conduction and Maxwell’s equations for predicting the electromagnetic field caused by a sinusoidal excitation current flowing through the induction coil. We solve the system of governing equations using the commercial solver COMSOL Multiphysics. To numerically investigate the possible causes of the disproportionate heating within the sensitized regions, we realistically vary the values of electrical resistivity and magnetic permeability therein. The simulated results indicate that the heat signature observed in the laboratory experiment may result from the increase of both electrical resistivity and magnetic permeability in the HAZ. The possible physical relationships between sensitization and the variation of these two properties are discussed.

Appendix: Additional Details on the Governing Electromagnetic Equation and the Impedance Boundary Condition

One of the primary governing equations comes in the form of the magnetic vector potential formulation of the electromagnetic diffusion equation derived from Maxwell’s equations.

$$\begin{aligned} i\omega \sigma \mathbf {A} - \frac{1}{\mu }\nabla ^2\mathbf {A} = \mathbf {J}_s. \end{aligned}$$

(13)

To arrive at this result, the following derivation is undertaken.

From Maxwell’s Law of Induction, the curl of an electric field ($\mathbf {E}$) is equal to the negative time derivative of the magnetic field ($\mathbf {B}$), i.e.

$$\begin{aligned} \nabla \times \mathbf {E} = -\frac{\partial \mathbf {B}}{\partial t}. \end{aligned}$$

(14)

From Gauss’s Law for Magnetism,

$$\begin{aligned} \nabla \cdot \mathbf {B} = 0. \end{aligned}$$

(15)

Therefore, the magnetic field $\mathbf {B}$ can be written in terms of $\mathbf {A}$, the magnetic vector potential:

$$\begin{aligned} \mathbf {B} = \nabla \times \mathbf {A}. \end{aligned}$$

(16)

Substituting (16) into (14) yields

$$\begin{aligned} \nabla \times \mathbf {E} = - \frac{\partial }{\partial t}\big (\nabla \times \mathbf {A}\big ) = -\nabla \times \frac{\partial \mathbf {A}}{\partial t}, \end{aligned}$$

(17)

or equivalently,

$$\begin{aligned} \nabla \times \Big (\mathbf {E}+\frac{\partial \mathbf {A}}{\partial t}\Big ) = 0. \end{aligned}$$

(18)

Because the curl of a gradient of a vector field is 0, one possible solution to (18) is given by

$$\begin{aligned} \mathbf {E} = -\frac{\partial \mathbf {A}}{\partial t} - \nabla \varphi , \end{aligned}$$

(19)

where $\varphi$ is the electric scalar potential. This expression can be interpreted as a combination of an induced electric field ($\mathbf {E}_i$) and an applied (i.e. source) electric field ($\mathbf {E}_s$), i.e.

$$\begin{aligned} \mathbf {E}=-\frac{\partial \mathbf {A}}{\partial t} - \nabla \varphi = \mathbf {E}_{i} + \mathbf {E}_{s}. \end{aligned}$$

(20)

Multiplying the electric field by the electrical conductivity ($\sigma$), the result relates current density ($\mathbf {J}$) to the magnetic vector potential (the continuum form of Ohm’s law):

$$\begin{aligned} \mathbf {J} = \sigma \mathbf {E} = -\sigma \frac{\partial \mathbf {A}}{\partial t} - \sigma \nabla \varphi = -\sigma \frac{\partial \mathbf {A}}{\partial t} + \mathbf {J}_s. \end{aligned}$$

(21)

By Ampere’s law,

$$\begin{aligned} \mathbf {J} = \nabla \times \frac{1}{\mu }\mathbf {B}, \end{aligned}$$

(22)

where $\mu$ denotes the material’s magnetic permeability, assumed here to be a constant. Combining Eqs. (16), (21), and (22), we obtain

$$\begin{aligned} \frac{1}{\mu }\nabla \times \nabla \times \mathbf {A} = -\sigma \frac{\partial \mathbf {A}}{\partial t} + \mathbf {J}_s. \end{aligned}$$

(23)

Through a vector identity, (23) can be re-written as

$$\begin{aligned} \frac{1}{\mu }\Big (\nabla (\nabla \cdot \mathbf {A}) - \nabla ^2\mathbf {A}\Big ) = -\sigma \frac{\partial \mathbf {A}}{\partial t} + \mathbf {J}_s. \end{aligned}$$

(24)

By imposing the Coulomb gauge condition,

$$\begin{aligned} \nabla \cdot \mathbf {A} = 0, \end{aligned}$$

(25)

we arrive at the final form of the diffusion equation in the time domain,

$$\begin{aligned} -\frac{1}{\mu }\nabla ^2\mathbf {A} = -\sigma \frac{\partial \mathbf {A}}{\partial t} + \mathbf {J}_s. \end{aligned}$$

(26)

Assuming $\mathbf {J}_s$ and $\mathbf {A}$ are harmonic, the above equation can be moved from the time domain to the frequency domain through a phase transformation, i.e.

$$\begin{aligned} \mathbf {J}_s = \mathbf {J}_{s0} e^{i\omega t},~~~~\mathbf {A} = \mathbf {A}_0 e^{i\omega t}. \end{aligned}$$

(27)

Employing (27) into (26), and dropping the subscript “0”, we obtain

$$\begin{aligned} i\omega \sigma \mathbf {A} - \frac{1}{\mu }\nabla ^2\mathbf {A} = \mathbf {J}_{s}. \end{aligned}$$

(28)

The final magnetic vector potential, $\mathbf {A}$, is found by solving this diffusion equation in the frequency domain. Upon finding the solution for the magnetic vector potential, the eddy currents in the plate are described by

$$\begin{aligned} \mathbf {J} = -i\omega \sigma \mathbf {A}. \end{aligned}$$

(29)

At a surface with impedance $\eta$, the electric field ($\mathbf {E}$) and the magnetic field ($\mathbf {H}$) are related through

$$\begin{aligned} \mathbf {n}\times (\mathbf {n}\times \mathbf {E}) = -\eta \mathbf {n}\times \mathbf {H}, \end{aligned}$$

(30)

where $\mathbf {n}$ denotes the unit surface normal. For example, for a planar surface in the x-y plane, Eq. (30) gives

$$\begin{aligned} E_x&= -\eta H_y \end{aligned}$$

(31)

$$\begin{aligned} E_y&= \eta H_x. \end{aligned}$$

(32)

Again, the electric field $\mathbf {E}$ can be written as the combination of an induced field and an applied source field, i.e.

$$\begin{aligned} \mathbf {E} = \mathbf {E}_i + \mathbf {E}_s. \end{aligned}$$

(33)

Substituting (33) into (30) yields

$$\begin{aligned} \mathbf {n}\times (\mathbf {n}\times \mathbf {E}_i) + \mathbf {n}\times (\mathbf {n}\times \mathbf {E}_s) = -\eta \mathbf {n}\times \mathbf {H}. \end{aligned}$$

(34)

Applying vector identity

$$\begin{aligned} \mathbf {a}\times (\mathbf {b}\times \mathbf {c}) = (\mathbf {a}\cdot \mathbf {c})\mathbf {b} - (\mathbf {a}\cdot \mathbf {b})\mathbf {c},~~~~\forall \mathbf {a},\mathbf {b},\mathbf {c}, \end{aligned}$$

(35)

Equation (34) becomes

$$\begin{aligned} (\mathbf {n}\cdot \mathbf {E}_i)\mathbf {n} - \mathbf {E}_i + (\mathbf {n}\cdot \mathbf {E}_s)\mathbf {n} - \mathbf {E}_s = -\eta \mathbf {n}\times \mathbf {H}. \end{aligned}$$

(36)

Therefore, with surface impedance ([35])

$$\begin{aligned} \eta = -\sqrt{\frac{\mu }{\varepsilon -\frac{i\sigma }{\omega }}}, \end{aligned}$$

(37)

we obtain the impedance boundary condition adopted in the COMSOL simulations, i.e.

$$\begin{aligned} \sqrt{\displaystyle \frac{\mu }{\varepsilon -\frac{i\sigma }{\omega }}} \mathbf {n}\times \mathbf {H} + \mathbf {E}_i - (\mathbf {n}\cdot \mathbf {E}_i)\mathbf {n} = (\mathbf {n}\cdot \mathbf {E}_s)\mathbf {n} - \mathbf {E}_s. \end{aligned}$$

(38)