A Highly Efficient Numerical Method for the Time-Fractional Diffusion Equation on Unbounded Domains

Abstract

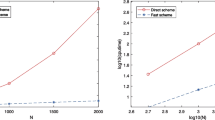
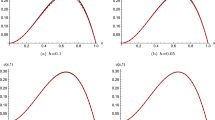
In this paper, we propose a fast high order method for the time-fractional diffusion equation on unbounded spatial domains. The proposed numerical method is a combination of a time-stepping scheme and spectral method for the spatial discretization. First, we reformulate the unbounded domain problem into a bounded domain problem by introducing suitable artificial boundary conditions. Then the time fractional derivatives involved in the equation and the artificial boundary condition are discretized using the so-called L2 formula and sum-of-exponentials (SOE) approximation. The former has been a popular formula for discretization of the Caputo fractional derivative, while the latter is a computational cost reducing technique frequently employed in recent years for convolution integrals. The spatial discretization makes use of the standard Legendre spectral method. The stability and the accuracy of the full discrete problem are analyzed. Our obtained theoretical results include a rigorous proof of the convergence order for both uniform mesh and graded mesh, and a stability proof for the uniform mesh. Finally, several numerical examples are provided to validate the theoretical results and to demonstrate the efficiency of the proposed method.

Appendix

To prove Lemma 3.3, the following Lemma presenting properties of the coefficients $d^{k,\alpha }_{k-j}$ will be needed, we refer to [36] for proof.

Lemma 7.1

For any $0<\alpha <1$, $k\ge 3$, $n\ge k$, the coefficients $d^{k,\alpha }_{k-j}$ in (3.16) satisfy

• (1) $\displaystyle 0< d^{k,\alpha }_{k-1} < \frac{4}{3};$    

• (2) $\displaystyle -\frac{1}{2}< d^{k,\alpha }_{k-2}<\frac{1}{3}$;    

• (3) $\displaystyle d^{k,\alpha }_{k-j} > 0,j=3,\dots ,k;$    

• (4) $\displaystyle \sum ^{k}_{j=1}d^{k,\alpha }_{k-j}=1;$

• (5) $\displaystyle \sum ^{n}_{k=2}{d}^{k,\alpha }_{0}\le (2-\alpha )(n-1)^{1-\alpha };$

• (6) $\displaystyle \sum ^{n}_{k=2}{d}^{k,\alpha }_{1}\le \displaystyle \frac{4}{3}+(2-\alpha )(n-2)^{1-\alpha };$

• (7) $\displaystyle \sum ^{n}_{k=j+1}{d}^{k,\alpha }_{j}\le 1, \ j=2,\dots , n-2$;

• (8) $d^{k,\alpha }_{k-j}=d^{k+1,\alpha }_{k-j+1}, j=1,\ldots ,k-2$.

Proof of Lemma 3.3

We start with proving (i). We only prove (i.1) since (i.2)–(i.5) can be proved in a similar way as Lemma 3.2.

• For $k\ge 4$, it follows from (3.2) (3.3) and (3.18) that

  $$\begin{aligned} \displaystyle \overline{d}^{k,{\alpha /2}}_{k-1}= & {} {d}^{k,{\alpha /2}}_{k-1} -\frac{1}{2}{d}^{k,\alpha }_{k-1}=3-\frac{{\alpha /2}+4}{{\alpha /2}+2}{\big (\frac{3}{2}\big )}^{1-{\alpha /2}} -\frac{1}{2}\Big [3-\frac{\alpha +4}{\alpha +2}{\big (\frac{3}{2}\big )}^{1-\alpha }\Big ],\\ \displaystyle \overline{d}^{k,{\alpha /2}}_{k-2}= & {} {d}^{k,{\alpha /2}}_{k-2}+\eta ({d}^{k,{\alpha /2}}_{k-1}-\eta )\\= & {} \displaystyle \frac{\alpha +8}{\alpha +4}{\big (\frac{3}{2}\big )}^{2-{\alpha /2}} +\frac{1}{2}\frac{\alpha +8}{\alpha +2}{\big (\frac{3}{2}\big )}^{2-3{\alpha /2}} -\frac{1}{4}{\big (\frac{\alpha +4}{\alpha +2}\big )}^2{\big (\frac{3}{2}\big )}^{2-2\alpha }\\{} & {} -\frac{3}{4} -\frac{\alpha +12}{\alpha +4}2^{1-{\alpha /2}}. \end{aligned}$$

  Now we show $\overline{d}^{k,{\alpha /2}}_{k-i}>0 \ (i=1,2)$ one by one. Let $\displaystyle g(x)=3-\frac{x+4}{x+2}{\big (\frac{3}{2}\big )}^{1-x}$, since the derivative function $\displaystyle g'(x)={(\frac{3}{2})}^{1-x}\Big [\frac{2}{{(x+2)}^2}+\frac{x+4}{x+2}\ln \frac{3}{2}\Big ]$ is decreasing on [0, 1], then

  $$\begin{aligned}\displaystyle \overline{d}^{k,{\alpha /2}}_{k-1}=g({\alpha /2})-\frac{1}{2}g(\alpha ) =g(\frac{\alpha +0}{2})-\frac{g(\alpha )+g(0)}{2}>0.\end{aligned}$$

  Next, a careful calculation shows

  $$\begin{aligned}{} & {} \displaystyle 2^{3+\alpha /2}(\alpha +2)^2(\alpha +4)\overline{d}^{k,{\alpha /2}}_{k-2}\\{} & {} \quad =\displaystyle 2^{{\alpha /2}}\big [18{(\alpha +2)}^2(\alpha +8)\big (\frac{3}{2}\big )^{-{\alpha /2}} +9(\alpha +2)(\alpha +4)(\alpha +8)\big (\frac{3}{2}\big )^{-3{\alpha /2}}\\{} & {} \qquad \displaystyle -\frac{9}{2}{(\alpha +4)}^3\big (\frac{3}{2}\big )^{-2\alpha }-6{(\alpha +2)}^2(\alpha +4)\big ] -16{(\alpha +2)}^2(\alpha +12)\\{} & {} \quad \ge \displaystyle \big (1+\frac{\alpha }{3}+\frac{1}{13}{\alpha }^2+\frac{1}{255}{\alpha }^3\big )\Big \{18{(\alpha +2)}^2(\alpha +8) \big [1+\sum _{i=1}^9\frac{(-\frac{\alpha }{2})\cdots (-\frac{\alpha }{2}-i+1)}{i!}\frac{1}{2^i}\big ]\\{} & {} \qquad +\displaystyle 9(\alpha +2)(\alpha +4)(\alpha +8)\big [1+\sum _{i=1}^9 \frac{(-\frac{3\alpha }{2})\cdots (-\frac{3\alpha }{2}-i+1)}{i!}\frac{1}{2^i}\big ]\\{} & {} \qquad \displaystyle -\frac{9}{2}{(\alpha +4)}^3\big [1+\sum _{i=1}^{10} \frac{(-2\alpha )\cdots (-2\alpha -i{+}1)}{i!}\frac{1}{2^{i}}\big ] -6{(\alpha +2)}^2(\alpha +4)\Big \}-16{(\alpha +2)}^2(\alpha +12)\\{} & {} \quad =\displaystyle \frac{89}{14}\alpha -\frac{1017593}{436800}\alpha ^2+\alpha ^3\Big (\frac{6796887131}{712857600}-\frac{75894521561}{17108582400}\alpha -\frac{74831376457}{26320896000}\alpha ^2\\{} & {} \qquad -\frac{1623224922073}{1368686592000}\alpha ^3-\frac{3521490017653}{5474746368000}\alpha ^4\\{} & {} \displaystyle -\frac{2854730671973}{10949492736000}\alpha ^5-\frac{75386416843}{912457728000}\alpha ^6-\frac{10640668967}{521404416000}\alpha ^7-\frac{20152333777}{5152702464000}\alpha ^8\\{} & {} \qquad -\frac{99934568449}{175191883776000}\alpha ^9\displaystyle -\frac{10839693427}{175191883776000}\alpha ^{10}-\frac{817537909}{175191883776000}\alpha ^{11}\\{} & {} \qquad -\frac{1439423}{6488588288000}\alpha ^{12}-\frac{1}{205632000}\alpha ^{13}\Big )\\\ge & {} \displaystyle \frac{89}{14}\alpha -\frac{1017593}{436800}\alpha ^2 \ge \alpha >0. \end{aligned}$$

  Furthermore, it can be verified that

  $$\begin{aligned} \overline{d}^{k,{\alpha /2}}_{k-j}={d}^{k,{\alpha /2}}_{k-j}+\eta \overline{d}^{k,{\alpha /2}}_{k-j+1}, \quad j=3,\ldots ,k. \end{aligned}$$

  Then it follows from Lemma 7.1(3) that $\overline{d}^{k,{\alpha /2}}_{k-j}>0$, $j=3,\ldots ,k$.

• For $k=3$. We find from (3.2) that ${d}^{3,{\alpha /2}}_{2}={d}^{4,{\alpha /2}}_{3}$, ${d}^{3,{\alpha /2}}_{1}>{d}^{4,{\alpha /2}}_{2}$, ${d}^{3,{\alpha /2}}_{0}>0$. As a consequence,

  $$\begin{aligned} \begin{array}{lcl} &{}&{}\overline{d}^{3,{\alpha /2}}_{2}=\overline{d}^{4,{\alpha /2}}_{3}>0,\\ &{}&{}\overline{d}^{3,{\alpha /2}}_{1}={d}^{3,{\alpha /2}}_{1}+\eta ({d}^{3,{\alpha /2}}_{2}-\eta )>{d}^{4,{\alpha /2}}_{2}+\eta ({d}^{4,{\alpha /2}}_{3}-\eta )=\overline{d}^{4,{\alpha /2}}_{2}>0,\\ &{}&{}\overline{d}^{3,{\alpha /2}}_{0}={d}^{3,{\alpha /2}}_{0}+\eta \overline{d}^{3,{\alpha /2}}_{1}>0. \end{array} \end{aligned}$$

• For $k=2$, a direct calculation using (3.2) gives

  $$\begin{aligned}{} & {} \overline{d}^{2,{\alpha /2}}_{1}={d}^{2,{\alpha /2}}_{1}-\eta \ge \frac{2\alpha ^2}{(\alpha +2)(\alpha +4)}>0,\\{} & {} \overline{d}^{2,{\alpha /2}}_{0} ={d}^{2,{\alpha /2}}_{0}+\eta \overline{d}^{2,{\alpha /2}}_{1} \ge {d}^{2,{\alpha /2}}_{0} =\frac{4-3\alpha }{4+\alpha }>0. \end{aligned}$$

(ii) By (3.18), we get $\displaystyle \overline{d}^{k,\beta }_{0}=\sum ^{k}_{j=1}\eta ^{k-j}{d}^{k,\beta }_{k-j}-\eta ^{k}$. Using Lemma 7.1(5)(6)(7), and noticing that $\displaystyle \eta =\frac{1}{2}\big [3-\frac{\alpha +4}{\alpha +2}(\frac{3}{2})^{1-\alpha }\big ]\in (0,\frac{2}{3})$, we obtain

$$\begin{aligned} \begin{array}{lcl} \displaystyle \sum ^{n}_{k=2}\overline{d}^{k,\beta }_{0} &{}=&{}\displaystyle \sum ^{n}_{k=2}\sum ^{k}_{j=1}\eta ^{k-j}{d}^{k,\beta }_{k-j}-\sum ^{n}_{k=2}\eta ^k =\sum ^{n}_{k=2}{d}^{k,\beta }_{0}+\sum ^{n-1}_{j=1}\sum ^{n}_{k=j+1}\eta ^j{d}^{k,\beta }_{j} -\sum ^{n}_{k=2}\eta ^k\\ &{}\le &{}\displaystyle \sum ^{n}_{k=2}{d}^{k,\beta }_{0}+\eta \sum ^{n}_{k=2}{d}^{k,\beta }_{1} +\sum ^{n-2}_{j=2}\eta ^j\sum ^{n}_{k=j+1}{d}^{k,\beta }_{j} +\eta ^{n-1}{d}^{n,\beta }_{n-1}-\sum ^{n}_{k=2}\eta ^k\\ &{}\le &{}\displaystyle \sum ^{n}_{k=2}{d}^{k,\beta }_{0}+\eta \sum ^{n}_{k=2}{d}^{k,\beta }_{1} +\eta ^{n-1}{d}^{n,\beta }_{n-1}-\eta ^{n-1}-\eta ^{n} \le \displaystyle \sum ^{n}_{k=2}{d}^{k,\beta }_{0}+\eta \sum ^{n}_{k=2}{d}^{k,\beta }_{1}\\ &{}\le &{}\displaystyle \frac{4}{3}\eta +(1+\eta )(2-\beta )(n-1)^{1-\beta } \le \frac{8}{9}+\frac{5}{3}(2-\beta )(n-1)^{1-\beta }. \end{array} \end{aligned}$$

(iii) Noticing $\displaystyle \overline{d}^{k,\beta }_{1}=\sum ^{k-1}_{j=1}\eta ^{k-j-1}{d}^{k,\beta }_{k-j} -\eta ^{k-1}$, we follow similar lines as (ii) to deduce:

$$\begin{aligned} \begin{array}{lcl} \displaystyle \sum ^{n}_{k=2}\overline{d}^{k,\beta }_{1} &{}=&{}\displaystyle \sum ^{n}_{k=2}\sum ^{k-1}_{j=1}\eta ^{k-j-1}{d}^{k,\beta }_{k-j}-\sum ^{n-1}_{k=1}\eta ^k \le \sum ^{n-1}_{j=1}\sum ^{n}_{k=j+1}\eta ^{j-1}{d}^{k,\beta }_{j}-\sum ^{n-1}_{k=1}\eta ^k\\ &{}=&{}\displaystyle \sum ^{n}_{k=2}{d}^{k,\beta }_{1}+\sum ^{n-2}_{j=2}\eta ^{j-1}\sum ^{n}_{k=j+1}{d}^{k,\beta }_{j} +\eta ^{n-2}{d}^{n,\beta }_{n-1}-\sum ^{n-1}_{k=1}\eta ^k\\ &{}\le &{}\displaystyle \sum ^{n}_{k=2}{d}^{k,\beta }_{1}+\eta ^{n-2}{d}^{n,\beta }_{n-1}-\eta ^{n-2}-\eta ^{n-1} \le \displaystyle \sum ^{n}_{k=2}{d}^{k,\beta }_{1} \le \displaystyle \frac{4}{3}+(2-\beta )(n-2)^{1-\beta }. \end{array} \end{aligned}$$

(iv) According to Lemma 7.1(8) and the definition of $\overline{d}^{k,\beta }_{k-j}$ in (3.18), it is seen that

$$\begin{aligned}\overline{d}^{k,\beta }_{k-j}=\overline{d}^{k+1,\beta }_{k+1-j}, \ j=1,\ldots ,k-2, \ k\ge 3, \ \forall \beta \in (0,1).\end{aligned}$$

Then using Lemma 3.2(1) and (3), Lemma 3.3(i.1) and (i.3), we obtain: for $j=2,\dots ,n-1$,

$$\begin{aligned} \sum ^{n}_{k=j+1}\overline{d}^{k,\beta }_{j} =\sum ^{n}_{k=j+1}\overline{d}^{n,\beta }_{n-k+j} =\sum ^{n-1}_{k=j}\overline{d}^{n,\beta }_{k} \le \sum ^{n-1}_{k=2}\overline{d}^{n,\beta }_{k} \le 1-\overline{d}^{n,\beta }_{0}-\overline{d}^{n,\beta }_{1}. \end{aligned}$$

(v) and (vi) can be derived directly from Lemma 3.3(i.4) and (i.5). $\square$