A Numerical Method for Singularly Perturbed Convection-diffusion Problems Posed on Smooth Domains

Abstract

A finite difference method is constructed to solve singularly perturbed convection-diffusion problems posed on smooth domains. Constraints are imposed on the data so that only regular exponential boundary layers appear in the solution. A domain decomposition method is used, which uses a rectangular grid outside the boundary layer and a Shishkin mesh, aligned to the curvature of the outflow boundary, near the boundary layer. Numerical results are presented to demonstrate the effectiveness of the proposed numerical algorithm.

1 Introduction

The numerical solution of singularly perturbed elliptic problems, of convection-diffusion type, posed on smooth domains presents several challenges. In order to generate a pointwise accurate global approximation to the solution using piecewise polynomial basis functions, the grid needs to insert mesh points into the layer regions, where the derivatives of the solution depend inversely on the magnitude of the singular perturbation parameter. To avoid the dimension of the discrete problem depending on the inverse of the singular perturbation parameter, a quasi-uniform discretization of the continuous domain will not suffice [3]. Outside the layer regions one only needs a coarse mesh and within the layers one requires a fine mesh. However, spurious oscillations will appear on a coarse mesh, unless some particular discretization is used to preserve the inverse monotoniticity of the differential operator [2, 5]. Finite element discretizations using triangles are well suited to discretizing domains with smooth geometries; but it is difficult to generate an inverse-monotone system matrix to a singularly perturbed convection-diffusion problem using triangular elements [1, 4]. Upwinded finite difference operators (or finite volumes [15]) can be used to guarantee stability, but it is not easy to work with these constructions over anisotropic meshes posed on a smooth domain.

In addition to these complications, our objective is to design a parameter-uniform numerical method [3], which will be accurate both for the classical case (where the singular perturbation parameter is large) and the singularly perturbed case (where the singular perturbation parameter is very small), and will also deal with all the intermediate values of the singular perturbation parameter. Moreover, given that boundary layers will be present, we are only interested in global approximations that are pointwise accurate at all points in the domain. Hence, although we use a finite difference formulation, our focus is not primarily on the nodal accuracy of the numerical method, but on the global accuracy of the interpolated approximation generated by the numerical algorithm.

The presence of a regular boundary layer [3] near a curved boundary requires a coordinate transformation so that the layer region can be mapped to a rectangular computational region, on which a suitable mesh can be aligned to the direction of steepest descent. In the special case of a domain that is a circle [7] or an annulus [8], this coordinate transformation exists. However, for a general smooth domain, it is difficult to apply such a coordinate transformation across the entire domain. Hence, we need to use a mixture of coordinate systems. In the case of singularly perturbed elliptic problems on smooth domains which are of reaction-diffusion type, mixed coordinate systems have been applied to get energy norm error bounds [16,17,18] or pointwise $L_\infty$ error bounds [10, 11]. In the case of convection-diffusion problems, the interaction between the outer solution and the boundary layer function is more significant than in the case of reaction-diffusion and the mixing of coordinate systems can be more challenging.

To circumvent the difficulties mentioned above, we employ a domain decomposition algorithm. The domain is first covered with a rectangle to generate an initial approximation to the solution. On this rectangle, we simply use an upwinded finite difference operator on a tensor product of uniform meshes. This classical method will produce an accurate and stable approximation outside of the boundary layers. A correction within the layers is generated across a subdomain that is aligned to the curved outflow boundary of the original domain [16, 17]. Across this subdomain, a coordinate transformation is used and a piecewise-uniform Shishkin mesh [3] is employed in the normal direction to the boundary.

On any closed domain, there will be characteristic points on the boundary, where the tangent to the boundary is parallel to the convective direction, which is associated with the characteristics of the reduced first order problem. In order to establish the theoretical error bound in Theorem 2 below, we impose constraints on the data via three assumptions. The first assumption prevents characteristic boundary layers forming; the second assumption ensures that the solution is sufficiently regular for the numerical analysis within the paper to apply and the final assumption prevents internal layers emerging within the solution. The numerical results in Sect. 4 suggest that these theoretical constraints are excessive, as the numerical method continues to display first order parameter-uniform under significantly weaker constraints. The identification of necessary data constraints to retain the error bound in Theorem 2 remains an open question.

In Sect. 2, the continuous problem is discussed and the solution is decomposed into a regular and a singular component. Pointwise bounds on the derivatives (up to third order) of these components are deduced. In Sect. 3, a numerical method is constructed and an asymptotic error bound is deduced in Theorem 2. Numerical results for three sample problems are presented in the final section.

Notation If D is the domain of some function f and $D \subset D^*$, then throughout we denote the extension of the function to the larger domain by $f^*$. In addition, $f(x,y) = {\tilde{f}} (r,t)$, where (r, t) is a co-ordinate system aligned to the boundary of the domain. Thoughout the paper C denotes a generic constant that is independent of both the singular perturbation parameter $\varepsilon$ and the discretization parameter N.

2 Continuous Problem

Let $\Omega$ be a two dimensional domain with a smooth closed boundary $\partial \Omega$. The origin is located within the domain. As in [11] we introduce a local curvilinear coordinate system associated with the boundary. Let the boundary $\partial \Omega$ be parameterized by

$$\begin{aligned} \partial \Omega := \{ (x, y)\ \vert \ x =\phi (t), y =\psi (t),\ 0 \le t \le T \}, \quad \gamma (t) :=(\phi (t), \psi (t)); \end{aligned}$$

where $(\phi (0), \psi (0)) = (\phi (T), \psi (T))$. As the variable t increases, the boundary points move in an anti-clockwise direction. At any point on the boundary, the magnitude of the tangent vector $(\phi ', \psi ')$ is denoted by $\tau (t)$ and the curvature of the boundary by $\vert \kappa (t) \vert$, which are given by

$$\begin{aligned} \tau (t) := \sqrt{(\phi ' )^2 + (\psi ' )^2} \quad \hbox {and} \quad \kappa (t) := \frac{\phi ' \psi '' - \psi ' \phi ''}{\tau ^3}. \end{aligned}$$

A curvilinear local coordinate system (r, t) is defined by

$$\begin{aligned} x=\phi (t) +rn_1(t), \ n_1 := \frac{-\psi '}{\tau }; \qquad y=\psi (t) +rn_2(t), \ n_2 := \frac{\phi '}{\tau }. \end{aligned}$$

(1)

Note that $\vec n = (n_1,n_2)$ is the inward unit normal and

$$\begin{aligned} n_1'=-\phi ' \kappa =-\kappa \tau n_2,\quad n_2'=-\psi ' \kappa =\kappa \tau n_1. \end{aligned}$$

These coordinates are orthogonal in the sense that

$$\begin{aligned} \left( \frac{\partial x }{\partial r} , \frac{\partial y }{\partial r}\right) \cdot \left( \frac{\partial x }{\partial t} , \frac{\partial y }{\partial t}\right) = (n_1,n_2) \cdot (\phi '+rn_1', \psi '+rn_2') =0. \end{aligned}$$

In these coordinates , the transformed Laplacian will contain no mixed second order derivative and we have [11,  Lemma 2.1]

$$\begin{aligned} \triangle u = \eta ^{-1} \frac{\partial }{\partial r} \left( \eta \frac{\partial {\tilde{u}} }{\partial r} \right) + \zeta \frac{\partial }{\partial t} \left( \zeta \frac{\partial {\tilde{u}} }{\partial t} \right) , \quad \hbox {where} \quad \zeta := \frac{1}{\tau \eta }, \ \eta := 1- \kappa r. \end{aligned}$$

(2)

Consider the singularly perturbed convection-diffusion elliptic problem¹

$$\begin{aligned} Lu\equiv & {} -\varepsilon \triangle u+ au_x +bu=f, \quad (x,y) \in \Omega , \end{aligned}$$

(3a)

$$\begin{aligned} u= & {} 0, \ (x,y) \in \partial \Omega ,\quad a> \alpha >0,\ b \ge 0, \quad a,b,f \in C^{5, \gamma }({{\bar{\Omega }}} ) . \end{aligned}$$

(3b)

We define the inflow boundary $\partial \Omega _I$ and the outflow boundary $\partial \Omega _O$ by

$$\begin{aligned} \partial \Omega _I:= \{(\phi ,\psi ) \ \vert \ n_1 > 0 \} \quad \hbox {and} \quad \partial \Omega _O:= \{(\phi ,\psi )\ \vert \ n_1 < 0 \}. \end{aligned}$$

If $\psi '(t_C) =0$ (i.e., $\vec n=(0,\pm 1)$), then this will correspond to a characteristic point $(\phi (t_C) ,\psi (t_C))$ on the boundary. To exclude the presence of parabolic boundary layers [3,  Chapter 6] and [9,  Chap. 4, §1], we assume that there is only a finite number of isolated characteristic points on the boundary. We confine the discussion to characteristic points where the component $n_1$ changes sign.

Assumption 1

Assume that there is a finite number of characteristic points on the boundary $\partial \Omega$. Moreover, at each characteristic point $t=t_C$ assume that there exists a $\delta >0$ and a neighbourhood $t_C\in I_C: = (t_0, t _1)$ such that $\vert \psi '(t_0) \vert = 2\delta = \vert \psi '(t_1) \vert$ and

$$\begin{aligned} \psi '' (t) >0 \quad \hbox {or} \quad \psi '' (t) <0, \ \forall t \in I_C. \end{aligned}$$

(4)

We identify three subintervals of $I_C=I^\delta _O\cup I^\delta _C \cup I^\delta _I.$, associated with each characteristic point $(\phi (t_C) ,\psi (t_C))$:

$$\begin{aligned} I^\delta _O(t_C):= & {} \{ t \in I_C\ \vert \ 2\delta >\psi ' (t) \ge \delta \} , \end{aligned}$$

(5a)

$$\begin{aligned} I^\delta _I(t_C):= & {} \{ t \in I_C\ \vert \ -2\delta < \psi ' (t) \le -\delta \}, \end{aligned}$$

(5b)

$$\begin{aligned} I^\delta _C (t_C):= & {} \{ t \in I_C \ \vert \ \vert \psi ' (t) \vert <\delta \}. \end{aligned}$$

(5c)

As the domain is closed, there will be at least two distinct characteristic points on the boundary $\partial \Omega$. If the domain has an internal tangent to the boundary at $t=t_C$ and $n_1$ changes sign at this point, then we shall call $(\phi (t_C) ,\psi (t_C))$ an internal characteristic point. Otherwise, if $n_1$ changes sign at $t=t_C$, we call $(\phi (t_C) ,\psi (t_C))$ an external characteristic point [9,  Chap. 4].

In the local coordinate system, the differential equation transforms into:

$$\begin{aligned} -\varepsilon \left( \eta ^{-1} \frac{\partial }{\partial r} \left( \eta \frac{\partial {\tilde{u}} }{\partial r} \right) + \zeta \frac{\partial }{\partial t} \left( \zeta \frac{\partial {\tilde{u}} }{\partial t} \right) \right) + {\tilde{a}} n_1{\tilde{u}}_r+ {\tilde{a}} \zeta n_2 {\tilde{u}}_t +{\tilde{b}} {\tilde{u}}={\tilde{f}}. \end{aligned}$$

Let us partition the domain $\Omega$ into a finite number of non-overlapping subdomains $\{ D_i \} _{i=1}^n$ such that

$$\begin{aligned} D_i \cap D_j = \emptyset , \ i \ne j, \quad {{\bar{\Omega }}} = \cup _{i=1}^n {\bar{D}}_i \quad \hbox {and} \quad \Gamma _{i,j} := \bar{D}_i \cap {\bar{D}}_j. \end{aligned}$$

Let $\frac{\partial u }{\partial n _i}$ denote the outward normal derivative of each subdomain $D_i$ and define the jump in the normal derivative across an interface $\Gamma _{i,j}$ to be

$$\begin{aligned} \left[ \frac{\partial u }{\partial n} \right] _{\Gamma _{i,j}} := \frac{\partial u }{\partial n_i} \Bigg \vert _{\Gamma _{i,j}} + \frac{\partial u }{\partial n_j} \Bigg \vert _{\Gamma _{i,j}}. \end{aligned}$$

Using the usual proof by contradiction argument (with a separate argument for the interfaces $\Gamma _{i,j}$) we can establish the following

Theorem 1

If $w,v \in C^0({{\bar{\Omega }}} ) \cap (\cup _{i=1}^n C^2(D_i ))$ is such that for all i, $L w (x,y)\ge L v (x,y), \ \forall (x,y) \in D_i$; for all i, j: $\bigl [ \frac{\partial w }{\partial n} \bigr ] _{\Gamma _{i,j}} \ge \bigl [ \frac{\partial v }{\partial n} \bigr ] _{\Gamma _{i,j}}$ and $w \ge v$ on the boundary $\partial \Omega$, then $w (x,y) \ge v(x,y),\ \forall (x,y) \in {{\bar{\Omega }}}$.

We next assume that the data a, b, f is sufficiently regular and the boundary $\partial \Omega$ sufficiently smooth so that $u \in C^{3,\gamma }({\overline{\Omega }})$. See [6,  pg. 94] for definition of smooth domain and boundary. Also see [6,  Theorem 6.14] and [6,  Theorem 6.19] to justify the following assumption.

Assumption 2

Assume that $\Omega$ is a $C^{3,\gamma }$ domain and the data $a,b, f \in C^{1,\gamma }({{\bar{\Omega }}} )$, so that

$$\begin{aligned} u \in C^{3,\gamma }({\overline{\Omega }}) . \end{aligned}$$

(6)

As the problem is linear, there is no loss in generality in dealing with homogeneous boundary data. Nevertheless, below we decompose the solution into regular and layer components, which satisfy a singularly perturbed differential equation with inhomogeneous boundary data. Hence, we state a result on a priori bounds on the derivatives of the solution of the more general problem: find z such that

$$\begin{aligned} Lz = p(x,y), \quad (x,y) \in \Omega , \quad z =q(x,y),\ (x,y) \in \partial \Omega , \end{aligned}$$

(7)

where the data and the boundary $\partial \Omega$ are sufficiently smooth so that $z \in C^{3, \gamma }({\bar{\Omega }})$.

Using stretched variables $\zeta =x/\varepsilon , \tau = y/\varepsilon$ and bounds from [12], one can establish the following result (see the argument in [14,  Appendix A] or [13,  Theorem 3.2]).

Lemma 1

Assume $a,b, p \in C^{1, \gamma }({\bar{\Omega }})$ and $q\in C^{3, \gamma }(\partial {\Omega })$. The solution z of (7) satisfies

$$\begin{aligned} ||z||\le & {} C||p||+ ||q||_{\partial \Omega } , \\ |{z}|_{1} + \varepsilon ^{\gamma } \lceil {z}\rceil _{1, \gamma }\le & {} C\varepsilon ^{-1} ||z|| + C\left( |{p}|_{0}+ \varepsilon ^{\gamma }\lceil {p}\rceil _{0,\gamma } + \sum _{i=0}^2 \varepsilon ^{i-1}| {q}|_{i}+ \varepsilon ^{1+ \gamma } \lceil q \rceil _{2,\gamma , \partial \Omega } \right) , \end{aligned}$$

and for $l = 0,1$

$$\begin{aligned} | z |_{2+l} + \varepsilon ^ \gamma \lceil z \rceil _{l+2, \gamma }\le & {} C\varepsilon ^{-(2+l)}||z|| + C\left( \sum _{i=0}^l \varepsilon ^{i-(1+l)}|{p}|_{i}+ \sum _{i=0}^l \varepsilon ^{ \gamma -1}\lceil {p}\rceil _{i,\gamma }\right) \\&+ C\left( \sum _{i= 0}^{l} \varepsilon ^{i-l-2}|q|_{i} + \varepsilon ^{ \gamma } \sum _{i= 0}^{l} \lceil q \rceil _{2+i, \gamma }\right) . \end{aligned}$$

From these bounds, we have the crude bounds on the solution u of (3)

$$\begin{aligned} \vert u \vert _ i \le C\varepsilon ^{-i},\quad i =0,1,2,3. \end{aligned}$$

(8)

The solution u of problem (3) can be decomposed into the sum $u=v+w$, where v is a regular component and w is a boundary layer function associated with the outflow boundary. The reduced solution $v_0$ is defined as the solution of the first order problem

$$\begin{aligned} a(v_0)_x+bv_0=f, \ (x,y) \in {{\bar{\Omega }}} {\setminus } \partial \Omega _I,\quad v_0(x,y) =0, \ (x,y) \in \partial \Omega _I; \end{aligned}$$

(9)

and the first correction $v_1$ is defined as the solution of

$$\begin{aligned} a(v_1)_x+bv_1=\triangle v_0,\ (x,y) \in {{\bar{\Omega }}} {\setminus } \partial \Omega _I,\quad v_1(x,y) =0, \ (x,y) \in \partial \Omega _I. \end{aligned}$$

(10)

Our next assumption guarantees that only regular boundary layers appear near the outflow boundary.

Assumption 3

At each characteristic point $(x_C,y_C)=(\phi (t_C), \psi (t_C))$, define the rectangle

$$\begin{aligned} Q_\delta (x_C,y_C) := \bigl ((-\infty , x_C+\delta ] \times [y_C-\delta , y_C +\delta ]\bigr ) \cap {{\bar{\Omega }}}. \end{aligned}$$

Assume that $a,b, f \in C^{5,\gamma }({\overline{\Omega }})$ and that there exists some $\delta >0$ such that

$$\begin{aligned} f(x,y) \equiv 0 \quad \hbox {for all} \quad (x,y) \in Q_\delta (x_C,y_C), \quad \forall (x_C,y_C). \end{aligned}$$

(11)

Remark 1

At any external characteristic point $\vec p$, assumption (11) constrains the data in a $O(\delta ^2)$ neighbourhood of $\vec p$. If the characteristic point $\vec p$ is an internal characteristic point, then assumption (11) constrains the data in a $O(\delta )$ neighbourhood of $\vec p$.

As $v_0,v_1$ are solutions of a first order differential equation (either (9) or (10)), it follows from Assumption 3 that

$$\begin{aligned} v_0(x,y) \equiv v_1(x,y) \equiv 0, \quad \hbox {for all} \quad \vert y - y_C \vert < \delta . \end{aligned}$$

The regular component v is defined as the solution of the problem: Find v such that

$$\begin{aligned} Lv= & {} f, \quad (x,y) \in \Omega , \end{aligned}$$

(12a)

$$\begin{aligned} v= & {} v_0+\varepsilon v_1,\ (x,y) \in \partial \Omega _O, \quad v=0, \ (x,y) \in \partial \Omega {\setminus } \partial \Omega _O. \end{aligned}$$

(12b)

Note that, if $z=v- (v_0+\varepsilon v_1)$, then z satisfies

$$\begin{aligned} Lz=\varepsilon ^2 \triangle v_1 \ (x,y) \in \Omega , \quad z= 0,\ (x,y) \in \partial \Omega . \end{aligned}$$

As in [14,  Appendix A] and since Assumption 3 eliminates any regularity difficulties at the characteristic points, we then have $v_0 \in C^{5, \gamma }({{\bar{\Omega }}} ),\ v_1 \in C^{3, \gamma }({{\bar{\Omega }}} )$ and $z \in C^{3, \gamma }({{\bar{\Omega }}} )$. Using Lemma 1, we deduce that

$$\begin{aligned} \Vert z \Vert \le C\varepsilon ^2, \quad \vert z \vert _i \le C (1+\varepsilon ^{2-i}), \ 1 \le i \le 3. \end{aligned}$$

Hence, we have the following bounds on the regular component

$$\begin{aligned} \Vert v \Vert \le C, \quad \vert v \vert _i + \varepsilon ^{\gamma }\lceil v \rceil _{i,\gamma } \le C (1+\varepsilon ^{2-i}), \ 1 \le i \le 3. \end{aligned}$$

(13)

Assumption (11) also prevents any internal characteristic layers emerging from any internal characteristic points.

The boundary layer component w is the solution of the problem: Find w such that

$$\begin{aligned} Lw= & {} 0, \quad (x,y) \in \Omega , \end{aligned}$$

(14a)

$$\begin{aligned} w= & {} (u-v) (x,y), \ (x,y) \in \partial \Omega _O \quad w(x,y)=0, \ (x,y) \in \partial \Omega {\setminus } \partial \Omega _O. \end{aligned}$$

(14b)

From assumption (6), it follows that for all characteristic points

$$\begin{aligned} w(x,y) =0, \quad \hbox {if} \ (x,y) \in \partial \Omega _O \quad \hbox {and} \quad \vert y - y_C \vert < \delta . \end{aligned}$$

In other words, the boundary layer function is not only zero on the inflow boundary, but also on those parts of the outflow boundary near the characteristic points.

For some fixed $R=O(1)$, we define the strip

$$\begin{aligned} \Omega _S:= \{ (r, t) \in \Omega \ \vert \ \psi '(t) >0,\ r \in (0,R) \}, \quad R < \min \{ \delta , \Vert \kappa \Vert _{\partial \Omega _O} ^{-1}\} , \end{aligned}$$

(15)

which is aligned to the outer boundary $\partial \Omega _O$. The width R of this strip $\Omega _S$ is further limited in (24). Note that if there are internal characteristic points, then $\Omega _S$ will not be a connected set. The outer boundary $\partial \Omega \cap \partial \Omega _S$ of the strip will have characteristic points as end-points. At each of these characteristic points, the strip $\Omega _S$ will have a vertical boundary of the form $\{ (x_C,y) \vert \vert y-y_C \vert \le R\}$. If $R < \delta$ then the boundary layer function $w\equiv 0$ along these vertical boundaries of $\Omega _S$, by (6).

In the next lemma, we show that the boundary layer function decreases exponentially in the radial direction as one moves away from the outer boundary. To establish this result, we assume that $\varepsilon \le \varepsilon _*=O(1)$, where $\varepsilon _*$ is sufficiently small and depends on the problem data $f,a,b, \phi , \psi$ and in particular on $\delta$.

Lemma 2

Assume (4), (6), (11) and $\varepsilon \le \varepsilon _*=O(1)$ is sufficiently small. If w is the solution of (14) then within the strip $\Omega _S$ (15),

$$\begin{aligned} \vert {\tilde{w}} (r,t) \vert \le Ce^{-\frac{\alpha \theta r}{ \varepsilon } }+ Ce^{-\frac{\mu \alpha \theta R}{ \varepsilon } },\ 0 \le r \le R; \ \theta := \min _{\psi ' \ge \delta >0} \vert n_1 \vert , \ \mu < 1; \end{aligned}$$

(16)

and exterior to the strip $\vert w (x,y)\vert \le Ce^{-\frac{\mu \alpha \theta R}{ \varepsilon } }, \quad (x,y) \in \Omega {\setminus } \Omega _S.$

Proof

Associated with the neighbourhood $I_C$ (5) of each characteristic point, we construct a cut-off function $\Psi _C(t;2\delta ) \in C^2[0,T]$ such that

$$\begin{aligned} 0< & {} \Psi _C(t;2\delta ) < 1,\ t \in I_O^\delta ; \end{aligned}$$

(17a)

$$\begin{aligned} \Psi _C(t;2\delta )\equiv & {} 1,\ t \in \partial \Omega _O {\setminus } I_C; \quad \Psi _C(t;2\delta )\equiv 0, \ t \in \partial \Omega _I \cup I^\delta _C. \end{aligned}$$

(17b)

Consider the barrier function

$$\begin{aligned} {\tilde{B}}(r,t) :=\Psi _C(t;2\delta )\left( \frac{e^{-\frac{\alpha \theta r}{ \varepsilon } } -e^{-\frac{\alpha \theta R}{ \varepsilon }}}{1 -e^{-\frac{\alpha \theta R}{ \varepsilon }}}\right) , \quad (r,t) \in \bar{\Omega }_S. \end{aligned}$$

Observe that $\psi ' (t) \ge \delta , \ \vert \Psi '_C(t) \vert + \vert \Psi ''_C(t) \vert \le C, \ t \in I_0^\delta$ and $\Psi _C (t) \equiv 0, \ t \in I_C {\setminus } I_O^\delta$. Then, for $\varepsilon$ sufficiently small and $(r,t) \in \Omega _S$, using the definition of $\theta$ we have

$$\begin{aligned} {\tilde{L}} {\tilde{B}} =\frac{\alpha \theta }{\varepsilon } \left( \tilde{a} \frac{\psi ' (t)}{\tau (t)} -\alpha \theta + O(\varepsilon ) \right) \tilde{B}(r,t) > \frac{\alpha ^2\theta }{\varepsilon }(-n_1 -\theta ) {\tilde{B}}(r,t) \ge 0. \end{aligned}$$

Observe that ${\tilde{B}} = \Psi _C(t;2\delta )$ on the outer boundary $\partial \Omega _O$ and ${\tilde{B}} =0$ on the other three boundaries of the strip. This function ${\tilde{B}}(r,t)$ is currently only defined on the strip ${{\bar{\Omega }}} _S$. We extend this function to ${{\bar{\Omega }}}$ as follows:

$$\begin{aligned} B(x,y) := \left\{ \begin{array}{ll} {\tilde{B}}(r,t),&{}\quad (x,y) \in {{\bar{\Omega }}} _S\\ 0,&{}\quad (x,y) \in \Omega {\setminus } {{\bar{\Omega }}} _S \end{array},\right. \end{aligned}$$

such that at the inner boundary $\partial \Omega _S^-:= \partial \Omega _S \cap \Omega$,

$$\begin{aligned} \frac{ \partial B}{\partial n _S} = \frac{ \partial \tilde{B}}{\partial r}= -\frac{\Psi _C(t;2\delta )}{\varepsilon } \frac{\alpha \theta e^{-\frac{\alpha \theta R}{ \varepsilon } } }{1 -e^{-\frac{\alpha \theta R}{ \varepsilon }}} < 0 \quad \hbox {and} \quad \frac{ \partial B}{\partial n _O}=0, \end{aligned}$$

where $\frac{ \partial B}{\partial n _S} , \frac{ \partial B}{\partial n _O}$ denote, respectively, the normal derivative to $\Omega _S, \Omega _O$. We define a second barrier function of the form

$$\begin{aligned} B_1(x,y) := \left\{ \begin{array}{ll} \phi (t) - m_x +0.5(r+R)n_1(t), &{}\qquad (x,y) \in {{\bar{\Omega }}} _S \\ x - m_x,&{}\qquad (x,y) \in \Omega {\setminus } {{\bar{\Omega }}} _S \end{array} ,\right. \end{aligned}$$

where $m_x := \min _{0\le t \le T} \phi (t)$. On the strip, for $\varepsilon$ sufficiently small,

$$\begin{aligned} {\tilde{L}} {\tilde{B}}_1 \ge \frac{{\tilde{a}}}{2} \left( 1 + \frac{\zeta }{\tau } (\phi ')^2(1-R\kappa ) \right) + O(\varepsilon ) > 0. \end{aligned}$$

At the inner boundary of the strip $\partial \Omega _S^-$, we have

$$\begin{aligned} \frac{ \partial B_1}{\partial n _O} = - \frac{ \partial \tilde{B}_1}{\partial r} =\frac{\psi '}{\tau } \frac{ \partial B_1 }{\partial x} |_{\partial \Omega ^-_S } =\frac{\psi '}{\tau } \quad \hbox {and} \quad \frac{ \partial B_1}{\partial n _S} = -\frac{\psi '}{2\tau }. \end{aligned}$$

We complete the proof by forming the barrier function

$$\begin{aligned} B_2(x,y) := B(x,y) + \frac{2\Vert \tau \Vert }{\delta } \frac{\alpha \theta }{ \varepsilon }e^{-\frac{\alpha \theta R}{ \varepsilon } } B_1(x,y) . \end{aligned}$$

By the design of this barrier function, we see that on the inner boundary

$$\begin{aligned} \frac{ \partial B_2 }{\partial n _S} + \frac{ \partial B_2 }{\partial n _O} \ge 0. \end{aligned}$$

Complete the proof using the inequality

$$\begin{aligned} te^{-t} \le (1- \mu )^{-1} e ^{-\mu t}, \quad \mu <1, t \ge 0 \end{aligned}$$

and the comparison principle in Theorem 1. $\square$

The crude bounds

$$\begin{aligned} \vert w \vert _{{{\bar{\Omega }}} , i } \le C\varepsilon ^{- i } ,\quad i =0,1,2,3. \end{aligned}$$

(18)

on the derivatives of the layer function follow from (8). We can further decompose the boundary layer function within the strip:

$$\begin{aligned} {\tilde{w}}= & {} {\tilde{w}}_0 + {\tilde{w}}_1, \quad (r,t) \in {{\bar{\Omega }}} _S, \qquad \hbox {where} \\ {\tilde{L}} {\tilde{w}}_0= & {} {\tilde{L}} {\tilde{w}}_1 =0, \quad (r,t) \in \Omega _S, \qquad w_0(x_C,y) = w_1(x_C,y) =0; \\ {\tilde{w}}_0(0,t)= & {} {\tilde{w}}(0,t), \ {\tilde{w}}_0(R,t) = 0, \qquad {\tilde{w}}_1(0,t) = 0,\ {\tilde{w}}_1(R,t) = {\tilde{w}}(R,t). \end{aligned}$$

By Lemma 2 and the maximum principle, $\Vert \tilde{w}_1 \Vert _{ \Omega _S} \le Ce^{-\frac{\alpha \mu \theta R}{ \varepsilon } }$. Moreover, from the bounds in (18),

$$\begin{aligned} \Bigl \Vert \frac{\partial ^i {\tilde{w}}_0}{ \partial r^i} \Bigr \Vert _{ \Omega _S}\le C(1+\varepsilon ^{-i}), \quad i \le 3. \end{aligned}$$

(19)

Consider the function ${\tilde{z}}(r,t) = {\tilde{w}}_0(r,t) - \Phi (r,t),$ where, for each t, $\Phi (r,t)$ is the solution of the problem

$$\begin{aligned} -\varepsilon \Phi _{rr} + \frac{{\tilde{a}}(0,t) \psi '(t) }{ \tau (t) } \Phi _{r} =0, \ r \in (0,R), \quad \Phi (0,t)={\tilde{w}}(0,t),\ \Phi (R,t)= 0. \end{aligned}$$

Then ${\tilde{z}} \equiv 0$ on $\partial \Omega _S$ and we can check that

$$\begin{aligned} \vert {\tilde{L}} {\tilde{z}}(r,t) \vert \le C\varepsilon ^{-1} e^{-\frac{{\tilde{a}}(0,t) \psi '(t) r}{ \tau (t) \varepsilon } },\ (r,t) \in \Omega _S. \end{aligned}$$

Applying the arguments from [14,  Theorem 12.4], we deduce that

$$\begin{aligned} \Bigl \Vert \frac{\partial ^j {\tilde{w}}_0}{ \partial t^j} \Bigr \Vert _{ \Omega _S}\le C(1+\varepsilon ^{1-j}), \quad j \le 3 . \end{aligned}$$

(20)

Let ${{\bar{\Omega }}} \subset \Omega ^*$ be an extended smooth closed domain that encloses ${{\bar{\Omega }}}$ and is constructed so that any characteristic point $(x_C,y_C) \in \partial \Omega$ is extended to $(x_C,y^*_C) \in \partial \Omega ^*$ and $\vert y_C^*\vert \ge \vert y_C\vert$. In this way, all the points on the inflow boundary $\partial \Omega _I$ are extended to the inflow boundary $\partial \Omega _I^*$ and likewise for the outflow boundaries. With each point $\vec p \in \partial \Omega$ on the boundary, we associate $\vec p_* \in \partial \Omega ^*$ as the point lying on the outward normal to $\partial \Omega$ and passing through $\vec p$. If the the two boundaries intersect, then $\vec p_* = \vec p$. We define the width of the extension to be

$$\begin{aligned} \delta _E:= \max _{\vec p \in \partial \Omega } \vert \vec p - \vec p_* \vert . \end{aligned}$$

(21)

Let the boundary of this extended domain be parameterized by

$$\begin{aligned} \partial \Omega ^*:= \{ (x, y)\ \vert \ x =\phi ^* (t), y =\psi ^*(t),\ 0 \le t \le T \}, \quad \gamma ^* (t) :=(\phi ^*(t), \psi ^* (t)); \end{aligned}$$

and $a^*,f^*$ are smooth extensions of a, f from $\Omega$ to $\Omega ^*$. Define $v^*, w^*$ as the solutions of

$$\begin{aligned} L^*v^*= & {} f^*, \ (x,y) \in \Omega ^*,\quad v^* =0,\ (x,y) \in \partial \Omega _I^*,\ v^* = v_0^*+\varepsilon v_1^*, \ (x,y) \in \partial \Omega ^*_O,\\ L^*w^*= & {} 0, \ (x,y) \in \Omega ^*,\quad w^* =0,\ (x,y) \in \partial \Omega _I^*,\ w^* =u^*-v^*, \ (x,y) \in \partial \Omega _O^*. \end{aligned}$$

As $v_0, v_1, v^*_0, v^*_1$ are solutions of first order problems (9), (10) and $\Vert v_0^* \Vert _{\partial \Omega _I} \le C \delta _E, \Vert v^*_1 \Vert _{\partial \Omega _I} \le C \delta _E$ , then

$$\begin{aligned} \Vert (v_0^*+\varepsilon v^*_1) - (v_0+\varepsilon v_1) \Vert _{{{\bar{\Omega }}}} \le C \delta _E. \end{aligned}$$

Then, using a comparison principle for the elliptic operator L

$$\begin{aligned} \Vert v^* - v \Vert _{{{\bar{\Omega }}}} \le C \delta _E (x+C_1) \le C \delta _E. \end{aligned}$$

Hence, on any subdomain $D \subset {{\bar{\Omega }}}$, we have

$$\begin{aligned} \Vert v^* - u \Vert _{D} \le \Vert v^* - v - w \Vert _{D} \le C \delta _E + \Vert w \Vert _{D}. \end{aligned}$$

We define an approximation $u_1$ to u on the strip $\Omega _S$ as the solution of

$$\begin{aligned} {\tilde{L}} {\tilde{u}}_1={\tilde{f}}, (r,t) \in \Omega _S,\ {\tilde{u}}_1(0,t)={\tilde{u}}(0,t)= 0, \ {\tilde{u}}_1(R,t)=\tilde{v}^*(R,t),\ t \in I_O, \end{aligned}$$

where $I_O$ denotes the subinterval of [0, T] where $\psi '(t) >0$. Outside the strip $u_1:=v^*, (x,y) \in \Omega {\setminus } \Omega _S$. Then

$$\begin{aligned} \Vert u -u_1 \Vert _\Omega \le C\delta _E+ \Vert w \Vert _{\Omega {\setminus } \Omega _S}. \end{aligned}$$

In the next section, we describe a numerical method which initially generates an approximation ${\bar{U}}_0$ to $v^*$ across $\bar{\Omega }$ and, using ${\bar{U}}_0$ along the inner boundary $\Omega ^-_S$, it corrects this initial approximation within the strip using a piecewise-uniform Shishkin mesh.

3 Numerical Method

A global approximation ${\bar{U}}$ is generated in this section, using a two-step numerical procedure. An initial approximation $\bar{U}_0$ is generated across a rectangular domain ${\bar{Q}}_E$, which contains the original domain ${{\bar{\Omega }}}$. In the second stage, an approximation ${\bar{U}}_1$ is generated in the strip $\Omega _S$, which is adjacent to the outflow boundary $\partial \Omega _O$. The initial approximation ${\bar{U}}_0$ is used as a boundary condition along the inner boundary $\partial {{\tilde{\Omega }}} _S \cap \Omega$. The approximation ${\bar{U}}$ corresponds to ${\bar{U}}_1$ within the strip and to ${\bar{U}}_0$ outside of the strip.

Enclose the domain with a rectangle ${\bar{Q}}_E:= [m_x,M_x] \times [m_y,M_y],$ where

$$\begin{aligned} m_x\le & {} \min _{t\in [0,T]} \phi (t) , \quad M_x \ge \max _{t\in [0,T]} \phi (t) , \quad L_x := M_x-m_x; \end{aligned}$$

(22a)

$$\begin{aligned} m_y\le & {} \min _{t\in [0,T]} \psi (t) , \quad M_y \ge \max _{t\in [0,T]} \psi (t) ,\quad L_y := M_y-m_y. \end{aligned}$$

(22b)

Set $u(x,y) \equiv 0, \ (x,y) \in {\bar{Q}}_E {\setminus } \Omega$ for points outside $\Omega$, then solve the problem (3) using upwinding on a uniform rectangular mesh

$$\begin{aligned} {\bar{Q}}^{N} := \left\{ (x_i,y_j)\ \vert \ x_i=m_x+i\frac{L_x}{N},\ y_j=m_y+ j\frac{L_y}{N}\ \right\} _{i,j=0}^N. \end{aligned}$$

That is, find $U_0$ such that²

$$\begin{aligned} L^N U_0(x_i,y_j)= & {} f(x_i,y_j), \quad (x_i,y_j) \in \Omega \cap Q^{N}; \end{aligned}$$

(23a)

$$\begin{aligned} U_0(x_i,y_j)= & {} 0, \quad (x_i,y_j) \in {\bar{Q}}^{N} {\setminus } \Omega ; \end{aligned}$$

(23b)

$$\begin{aligned} \hbox {where} \qquad L^N:= & {} -\varepsilon (\delta _x^2 +\delta ^2_y) + aD_x^-+bI. \end{aligned}$$

(23c)

Use bilinear interpolation to form an initial global approximation ${\bar{U}}_0$ to u, defined as

$$\begin{aligned} {\bar{U}}_0 (x,y) = \sum _{i,j=1}^{N-1} U_0(x_i,y_j) \phi _i(x) \phi ^j(y), \quad (x,y) \in {{\bar{\Omega }}}, \end{aligned}$$

where $\phi _i(x)$ ($\phi ^j(y)$) is the standard piecewise linear hat functions centered at $x=x_i (y=y_j)$. Since we are using upwinding, the numerical solution will be stable; in the sense that the operator $L^N$ satisfies a discrete comparison principle of the form: If $Z(x_i,t_j) \ge 0, (x_i,t_j) \in {\bar{Q}}^{N} {\setminus } \Omega$ and $L^NZ(x_i,t_j) \ge 0, (x_i,t_j) \in Q^{N}$, then $Z(x_i,t_j) \ge 0, (x_i,t_j) \in {\bar{Q}}^{N}$. However, the layers at the outflow will be smeared and ${\bar{U}}_0$ will not be accurate in the boundary layer region.

We correct this approximation in the strip (15), where the width of the strip is such that

$$\begin{aligned} R < \min \left\{ M_x , \vert m_y \vert , M_y , \frac{1}{\Vert \kappa \Vert _{ \partial \Omega _O}} \right\} . \end{aligned}$$

(24)

On the strip, we will use the following upwinded finite difference operator

$$\begin{aligned} {\tilde{L}}^N {\tilde{Z}}(r_i,t_j)&:= \Bigl ( -\varepsilon \eta _{i,j}^{-1} {\bar{h}}_i^{-1}\bigl (\eta _{i+1/2,j} D^+_r-\eta _{i-1/2,j} D^-_r \bigr ) + ( {\tilde{a}} n_1)_{i,j} D_r ^\pm \\&\quad -\varepsilon \zeta _{i,j} {\bar{k}}_j^{-1}\bigl ( \zeta _{i,j+1/2} D^+_t - \zeta _{i,j-1/2} D^-_t\bigr ) + ( {\tilde{a}} n_2\zeta )_{i,j} D_t ^\pm + {\tilde{b}} _{i,j} I \Bigr ) {\tilde{Z}}(r_i,t_j); \end{aligned}$$

where ${\tilde{Z}}$ is any mesh function,

$$\begin{aligned} h_i&:=r_i-r_{i-1},\ {\bar{h}}_i:=\frac{h_{i+1}+h_i}{2}; \quad k_j:= t_j - t _{j-1}, \ {\bar{k}}_j:=\frac{k_{j+1}+k_j}{2}; \\ \eta _{i,j}&:= \eta (r_i, t_j), \quad \hbox {and} \quad \eta _{i+1/2,j} := \eta \left( \frac{r_i+r_{i+1}}{2}, t_j\right) . \end{aligned}$$

The operator ${\tilde{L}}^N$ again satisfies a discrete comparison principle on the strip. Over $\Omega _S$, we generate a Shishkin mesh [3] in the r coordinate and a uniform mesh in the t direction. The interval $[0,R]= [0, \sigma ] \cup [\sigma , R]$ and the Shishkin transition point [3] is taken to be

$$\begin{aligned} \sigma := \min \left\{ \frac{R}{2} , C_*\frac{\varepsilon }{\alpha } \ln N \right\} , \ C_*> \frac{1}{\theta },\quad \theta = \min _{\psi ' \ge \delta >0} \vert n_1 \vert . \end{aligned}$$

(25)

Remark 2

In the neighbourhood of each characteristic point $t=t_C$, consider the parabola

$$\begin{aligned} y-y_C= \kappa (t_C)(x-x_C)^2, \quad \hbox {on which} \quad \vert n_1(t) \vert = \frac{2\vert \kappa (t_C) t\vert }{\sqrt{1+(2 \kappa (t_C) t)^2}}. \end{aligned}$$

If we choose the parameter $\delta$ in Assumption 3 such that $\vert \kappa ( t_C) \vert ^{-1}> \delta \ge (m \vert \kappa ( t_C) \vert )^{-1},\ m > 1$ and if the boundary $\partial \Omega$ coincided with this parabola then $\theta \ge \frac{2}{\sqrt{4+m}}.$ Based on this observation, we shall take $C_*=2$ in (25) in our numerical experiments.

The mesh on the strip will be denoted by ${{\tilde{\Omega }}} ^N_S$ and the mesh points on the boundary of the strip will be denoted by $\partial {{\tilde{\Omega }}} ^N_S$. Solve for the corrected approximation in the transformed co-ordinates

$$\begin{aligned} {\tilde{L}} ^N{\tilde{U}}_1(r_i,t_j)= & {} {\tilde{f}}(r_i,t_j) , \quad (r_i,t_j) \in {{\tilde{\Omega }}} ^N_S, \end{aligned}$$

(26a)

$$\begin{aligned} {\tilde{U}}_1(r_i,t_j)= & {} 0, \ (r_i,t_j) \in \partial {{\tilde{\Omega }}} ^N_S \cap \partial \Omega _O, \ {\tilde{U}}_1= {\tilde{U}}_0, \ (r_i,t_j) \in \partial {{\tilde{\Omega }}} ^N_S {\setminus } \partial \Omega _O. \end{aligned}$$

(26b)

Use bilinear interpolation within the strip to form ${\bar{U}}_1$. Our corrected numerical approximation ${\bar{U}}$ is defined by

$$\begin{aligned} {\bar{U}} (x,y)= \left\{ \begin{array}{ll} {\bar{U}}_1(x,y),\ (x,y) \in {{\bar{\Omega }}} _S, \\ {\bar{U}}_0(x,y), (x,y) \in \Omega {\setminus } \Omega _S\end{array}\right. . \end{aligned}$$

(27)

Theorem 2

Assume (4), (6), (11) and that the strip width $R < \delta$. If U is the corrected numerical solution (27) and u is the continuous solution of (3) then

$$\begin{aligned} \Vert {\bar{U}} -u \Vert \le CN^{-1} (\ln N)^2. \end{aligned}$$

Proof

In the first phase of the numerical algorithm, we solve on the rectangular mesh ${\bar{Q}}^{N}$. For each vertical height $y=y_j$, we identify the external mesh points $S^j := {\bar{Q}}^{N}{\setminus } {{\bar{\Omega }}}$ and the edge co-ordinates

$$\begin{aligned} x_{0,j} := \max _{ S^j} \{ x_i <0\} \quad \hbox {and} \quad x_{N,j} := \min _{ S^j} \{ x_i >0\}. \end{aligned}$$

A smooth curve $\partial \Omega ^*$ can be created to pass through these edge mesh points $\{(x_{0,j}, y_j), (x_{N,j}, y_j)\} _{j=0}^N$, which will define the boundary of an extension $\Omega ^*$ of the domain $\Omega$. Note that the width of this extension (21) is such that $\delta _E \le C N^{-1}.$ If $\varepsilon$ is sufficently large such that $\varepsilon \ln N >C_0$ or $\varepsilon > \varepsilon _*=O(1)$, then using the derivative bounds (8) we can deduce that

$$\begin{aligned} \Vert {\bar{U}}_0 -u \Vert \le CN^{-1} (\ln N)^2, \quad \hbox {if} \quad \varepsilon \ln N > C_0. \end{aligned}$$

(28)

In the other case where $\varepsilon \ln N \le C_0$, we decompose the initial approximation $U_0=V_0+W_0$, where the regular and singular components are defined as the solutions of

$$\begin{aligned} L^N V_0= & {} f(x_i,y_j), \ (x_i,y_j) \in \Omega , \ V_0=v^*, \quad (x_i,y_j) \in {\bar{Q}}^{N} {\setminus } \Omega ,\\ L^N W_0= & {} 0, \ (x_i,y_j) \in \Omega , \quad W_0=w^*, \quad (x_i,y_j) \in {\bar{Q}}^{N} {\setminus } \Omega . \end{aligned}$$

Let us first bound the error in the regular component $V_0$. The truncation error and the interpolation error on the boundary yield

$$\begin{aligned} \left| L^N (V_0 -v)(x_i,y_j) \right|= & {} \left| (L^Nv -Lv) (x_i,y_j) \right| \le CN^{-1}, \quad (x_i,y_j) \in \Omega , \\ \vert (V_0 -v) (x_i,y_j) \vert= & {} \vert (v^*-v) (x_i,y_j) \vert \le CN^{-1}, \quad (x_i,y_j) \in {\bar{Q}}^{N} {\setminus } \Omega . \end{aligned}$$

Hence,

$$\begin{aligned} \Vert {\bar{V}}_0 -v \Vert \le CN^{-1}. \end{aligned}$$

(29)

observe that

$$\begin{aligned} \vert W_0(x_i,y_j) \vert \le C \left( 1+\frac{\alpha H}{\varepsilon }\right) ^{i-N} \le C \left( 1+\frac{\alpha L_x}{N\varepsilon }\right) ^{-pN}, \qquad x_i \le (1-p)N, \ p <1. \end{aligned}$$

As in [14,  Lemma 5.1], we have the inequality,³

$$\begin{aligned} \left( 1+\frac{q\ln N}{N}\right) ^{-pN} \le N^{-pq }, \quad \forall N \ge 1,\ p,q >0. \end{aligned}$$

If $\varepsilon \ln N \le C_0:=pq,\ 0<p< 1,\ q:=\alpha L_x$, then for all $x_i \le (1-p)N, p <1$,

$$\begin{aligned} \vert W_0(x_i,y_j) \vert \le C \left( 1+\frac{q}{N\varepsilon }\right) ^{-pN} \le \left( 1+\frac{\ln N}{pN}\right) ^{-pN} \le CN^{-1}. \end{aligned}$$

Then, in the outer domain $\Omega _O:= \Omega {\setminus } \Omega _S$, for $\varepsilon \ln N \le pq$, we have the bound

$$\begin{aligned} \Vert {\bar{U}}_0 -u\Vert _{ \Omega _0} \le \Vert {\bar{V}}_0 -v\Vert _{ \Omega _0} + \Vert w \Vert _{ \Omega _0}+ \Vert {\bar{W}}_0 \Vert _{ \Omega _0} \le CN^{-1}, \end{aligned}$$

where we have used the bound (16) from Lemma 2. Hence, in all cases, outside the strip

$$\begin{aligned} \Vert {\bar{U}}_0 -u\Vert _{ \Omega _0} \le CN^{-1} (\ln N)^2. \end{aligned}$$

We next examine the error $\Vert {\bar{U}}_1 -u\Vert$ on the strip.

In the case of functions a(r), u(r) of a single variable, over the interval $I_i:=[r_{i-1},r_{i+1}]$ with $H_i := \max \{h_i, h_{i+1} \}$, we have that

$$\begin{aligned}&\frac{h_i}{{\bar{h}}_i} D_r^-(a(r_{i+1/2}) D^+_ru(r_i)) \\&\quad =\frac{1}{{\bar{h}}_i} \Bigl ( \frac{a(r_{i+1/2})}{h_{i+1}} \int _{s=r_i} ^{r_{i+1}} u'(s) \ ds - \frac{a(r_{i-1/2})}{h_{i}} \int ^{r_i} _{s=r_{i-1}} u'(s) \ ds \Bigr ) \\&\quad = \frac{a(r_{i+1/2})-a(r_i)}{{\bar{h}}_ih_{i+1}} \int _{s=r_i} ^{r_{i+1}} \int _{t=r_i} ^{s} u''(t) \ dt \ ds +(a'u')(r_i) + a(r_i) \delta ^2_r u(r_i) \\&\qquad - \frac{a(r_{i-1/2})-a(r_i)}{{\bar{h}}_ih_{i}} \int ^{r_i} _{s=r_{i-1}} \int _{t=r_i} ^{s} u''(t) \ dt \ ds + \frac{u'(r_i)}{{\bar{h}}_i} \int _{s=r_{i-1/2}} ^{r_{i+1/2}} \int _{t=r_i} ^{s}a''(t) \ dt \ ds \ \\&\quad = \frac{a(r_{i+1/2})-a(r_i)}{{\bar{h}}_i h_{i+1}} \int _{s=r_i} ^{r_{i+1}} \int _{t=r_i} ^{s} \int _{w=r_i} ^{t} u'''(w) \ dw\ dt \ ds +(a'u')(r_i)\\&\qquad - \frac{a(r_{i-1/2})-a(r_i)}{{\bar{h}}_i h_{i}} \int ^{r_i} _{s=r_{i-1}} \int _{t=s} ^{r_i} \int _{w=r_i} ^{t} u'''(w) \ dw\ dt \ ds + a(r_i) \delta ^2_r u(r_i)\\&\qquad + \frac{u''(r_i)}{{\bar{h}}_i}\bigl (\frac{h_{i+1}}{2} \int _{s=r_{i}} ^{r_{i+1/2}} \int _{t=r_{i}} ^{s} a''(t) \ dt \ ds - \frac{h_{i}}{2} \int _{s=r_{i-1/2}} ^{r_{i}} \int _{t=r_{i}} ^{s} a''(t) \ dt \ ds\bigr ) \\&\qquad + \frac{u'(r_i)}{{\bar{h}}_i} \int _{s=r_{i-1/2}} ^{r_{i+1/2}} \int _{t=r_i} ^{s} \int _{w=r_i} ^{t} a'''(t) \ dw \ dt \ ds +\frac{(u'a''+2u''a')(r_i)}{4}(h_{i+1}-h_i) . \end{aligned}$$

From this expression, we have the following truncation error bound,

$$\begin{aligned}&\left| (au_r)_r(r_i)- \frac{h_i}{{\bar{h}}_i} D_r^-(a(r_{i+1/2}) D^+_ru(r_i) \right| \\&\quad \le C \vert h_{i+1} -h_i\vert \sum _{k=1}^3 \left| \frac{\partial ^{3-k} a}{\partial r^{3-k}} (r_i) \right| \cdot \left| \frac{\partial ^k u}{\partial r^k} (r_i) \right| \\&\qquad +\, CH_i^2 \sum _{k=1}^2 \left\| \frac{\partial ^{4-k} a}{\partial r^{4-k}} \right\| _{I_i} \cdot \left| \frac{\partial ^k u}{\partial r^k} (r_i) \right| +CH_i\min \left\{ \left\| \frac{\partial ^3 u}{\partial r^3} \right\| _{I_i}, H_i\sum _{k=3}^4 \left\| \frac{\partial ^k u}{\partial r^k} \right\| _{I_i} \right\} . \end{aligned}$$

By the choice of transition point (25), we can identify the following barrier function

$$\begin{aligned} {\tilde{E}}(r_i) := \frac{\Pi _{n=1}^i (1+\frac{\alpha \theta h_i}{\varepsilon })}{\Pi _{n=1}^N (1+\frac{\alpha \theta h_i}{\varepsilon })},\quad \hbox {so that} \quad {\tilde{L}} {\tilde{E}} (r_i) \ge 0, \ 0<r_i <R. \end{aligned}$$

(30)

The proof is completed using the arguments in [14,  Chapter 13], the barrier function (30), Lemma 2, the above truncation error bounds coupled with the bounds on the derivatives in (8) and (20). The first case of $\varepsilon \ln N > \frac{\alpha R}{2C_*}$, when the mesh is uniform, uses the truncation error bound

$$\begin{aligned} \Vert {\tilde{L}}( {\tilde{U}}_1- {\tilde{u}})(r_i,t_j) \Vert \le CN^{-1}\varepsilon ^{-2} \le CN^{-1} (\ln N)^2, \end{aligned}$$

coupled with the boundary value $\Vert ({\tilde{U}}_1 - \tilde{u})(R,t_j) \Vert \le CN^{-1} (\ln N)^2$ to deduce that $\Vert \tilde{U}_1- {\tilde{u}}\Vert \le CN^{-1} (\ln N)^2$ in the classical case of $\varepsilon$ large. In the other case of $2C_*\varepsilon \ln N \le \alpha R$, the discrete solution ${\tilde{U}}_1$ is again decomposed into a regular ${\tilde{V}}_1$ and singular component ${\tilde{W}}_1$, defined as the solutions of

$$\begin{aligned} {\tilde{L}} ^N{\tilde{V}}_1(r_i,t_j)= & {} {\tilde{f}}(r_i,t_j),\ {\tilde{L}} ^N{\tilde{W}}_1(r_i,t_j) =0 \quad (r_i,t_j) \in {{\tilde{\Omega }}} ^N_S, \\ {\tilde{V}}_1(r_i,t_j)= & {} {\tilde{v}}(r_i,t_j) ,\ {\tilde{W}}_1(r_i,t_j) = {\tilde{w}}(r_i,t_j) , \quad (r_i,t_j) \in \partial {{\tilde{\Omega }}} ^N_S. \end{aligned}$$

The errors $\Vert {\tilde{V}}_1- {\tilde{v}}\Vert _{\Omega _S}, \Vert {\tilde{W}}_1- {\tilde{w}}\Vert _{\Omega _S}$ are then bounded as in the case of the outer errors $\Vert V_0 -v\Vert _{\Omega _O}, \Vert W_0 -w\Vert _{\Omega _O}$. $\square$

Remark 3

Recall that throughout this paper, we have assumed that the boundary $\partial \Omega$ is smooth. This assumption is implicitly used in the Proof of Theorem 2 as all the derivatives $\frac{\partial ^i \zeta }{\partial t^i}, \frac{\partial ^i \eta }{\partial t^i}, \ 0\le i \le 3$ (see the definitions in (2)) are assumed to be bounded within the strip. Hence, for the error analysis, the smoothness of the outflow boundary $\partial \Omega _O$ is of particular importance in the error analysis.

4 Numerical Results

The following set of examples are all related to the following: Let $\beta >0$ and

$$\begin{aligned} \partial \Omega&:= \{ (\rho \cos t, \rho \sin t) \} \quad \hbox {or} \quad \partial \Omega := \{ (\rho \sin t, \rho \cos t) \}, \\ \ \rho (t)&:= \beta \pm t^ i \sin ^2 t \quad \hbox {or} \quad \rho (t) := \beta \pm t^ i\cos ^2 t\quad \hbox {with}\quad i=0,1,2 . \end{aligned}$$

Once $\phi , \psi$ are smooth functions, the level of smoothness of the boundary $\partial \Omega$ will be determined by identifying the value of p for which $\phi ^{(i)} (0)= \phi ^{(i)} (2\pi ), \ \psi ^{(i)} (0)= \psi ^{(i)} (2\pi ), 0 \le i \le p$. (See Example 2 below).

To numerically estimate the order of convergence of the numerical method as it is applied to several test problems, we use the double-mesh method [3]. Denote the mesh points on the rectangular grid ${\bar{Q}}^N$ , which lie within the domain $\bar{\Omega }$ by ${\bar{Q}}_I^N:= {\bar{Q}}^N \cap {{\bar{\Omega }}}$. For each particular value of $\varepsilon \in R_\varepsilon :=\{ 2^{-i}, i=0,1,2,\ldots 20 \}$ and $N \in R_N: =\{ 2^{-j}, j=3,4,5\ldots 10 \}$, let $U^N$ be the computed solutions numerical solution (27), where N denotes the number of mesh elements used in each co-ordinate direction within the rectangle ${\bar{Q}}^N$ and within the strip ${{\bar{\Omega }}} _S$. Define the maximum local two-mesh global differences $D^N_\varepsilon$ and the parameter-uniform two-mesh global differences $D^N$ by

$$\begin{aligned} D^N_\varepsilon := \max \{ \Vert {\bar{U}}_0^N-{\bar{U}}_0^{2N}\Vert _{(Q_I^N \cup Q_I^{2N}) {\setminus } \Omega _S}, \Vert {\bar{U}}_1^N-{\bar{U}}_1^{2N}\Vert _{{{\tilde{\Omega }}} ^N_S \cup {{\tilde{\Omega }}}_S^{2N}} \} ; D^N:= \max _{ \varepsilon \in R_\varepsilon } D^N_\varepsilon . \end{aligned}$$

Then, for any particular value of $\varepsilon$ and N, the local orders of global convergence are denoted by ${\bar{p}} ^{N}_\varepsilon$ and, for any particular value of N and all values of $\varepsilon$, the parameter-uniform global orders of convergence ${\bar{p}} ^N$ are defined, respectively, by

$$\begin{aligned} {\bar{p}}^N_\varepsilon := \log _2\left( \frac{D^N_\varepsilon }{D^{2N}_\varepsilon } \right) \quad \hbox {and} \quad {\bar{p}}^N := \log _2\left( \frac{D^N}{D^{2N}} \right) . \end{aligned}$$

In implementing the numerical method, we will apply the method to problems which do not satisy the assumptions (4), (6) and (11). Hence, unless otherwise indicated, we simply take $R=0.1$ (for the width of the strip) and $C_*=2$ (in (25)).

Example 1

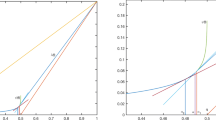
Consider $\partial \Omega _1:=\{(\phi (t), \psi (t)) \} = \{ (\rho \cos t, \rho \sin t) \}$, with $\rho := \beta + \sin ^2 t$. The domain is displayed in Fig. 1 for the case of $\beta =0.5$. The outflow is all points on the boundary where $x >0$ and the inflow is for the boundary points where $x<0$. There are two external characteristic points at $(0, \pm (1+ \beta ))$ and no internal characteristic points. The curvature at the two characteristic points is $\kappa = (3+\beta )(1+\beta )^{-2}$ and the upper bound in (24) is $R < \frac{1}{6}$.

Fig. 1

Domain $\Omega _1$ with $\beta =0.5$

Table 1 Computed double-mesh global orders of convergence $\bar{p}_\varepsilon ^N$ for the corrected approximations ${\bar{U}}$ for problem (31) and $\beta =0.5$

Fig. 2

Computed solution of problem (31) for $\varepsilon =10^{-3}$ and $N=1024$ on the domain $\Omega _1$ with $\beta =0.5$

In Table 1 we present orders for the following test problem:

$$\begin{aligned} -\varepsilon \triangle u+ u_x +u=(1+\beta )^2-y^2, \ (x,y) \in \Omega _1, \quad u=0, \ (x,y) \in \partial \Omega _1. \end{aligned}$$

(31)

A sample computed solution is displayed in Fig. 2.

Remark 4

In determining the double-mesh global orders of convergence, we note that we can underestimate the orders due to a potential overestimate of the maximum two mesh differences. This overestimate is caused by the fact that the interpolant ${\bar{U}}_0$ over the rectangular grid, will use mesh points lying within the strip ${{\bar{\Omega }}} _S$. This overspill is visible in Fig. 3. An overestimate can occur when the maximum two mesh differences are located near the inner boundary of the strip.

Fig. 3

Example 1: Location of mesh points used in the calculation of ${\bar{U}}_0(x,y),\ (x,y) \in \Omega {\setminus } \Omega _S$, with $N=128$ on the rectangular grid

Example 2

The boundary is $\partial \Omega _2:=\{ (\rho \sin t, \rho \cos t) \}$, with $\rho := 2.5\pi ^2 +\beta -t^2 \sin ^2 t$. In this case the orientation of the curve is clockwise as the parameter t increases and the domain is not symmetrical. The domain is displayed in Fig. 4 for the case of $\beta =0.5$. This domain does not have a smooth boundary at $t=0$, where there is a jump ($\vert [ \kappa ] (0) \vert \approx 0.1246$) in the curvature. However, this point does not lie within the outflow boundary and hence it does not have any adverse effect on the rates of convergence. There are two external characteristic points at $(0, \pm M_y), M_y= 2.5\pi ^2+\beta$. Also $M_x = 2.25 \pi ^2+\beta$ and the upper bound in (24) is $R \approx 14.28$. In Table 2 we present global orders for the test problem, with $R=1$:

$$\begin{aligned} -\varepsilon \triangle u+ u_x +u=\left( \left( 1- \frac{y^2}{M_y^2}\right) \left( \frac{x}{M_x}\right) \right) ^4, \ (x,y) \in \Omega _2,\ u=0, \ (x,y) \in \partial \Omega _2 .\qquad \end{aligned}$$

(32)

A sample computed solution is displayed in Fig. 5.

Fig. 4

Domain $\Omega _2$ with $\beta =0.5$

Table 2 Computed double-mesh global orders of convergence $\bar{p}_\varepsilon ^N$ for the corrected approximations ${\bar{U}}$, using a strip of width $R=1$, for problem (32) and $\beta =0.5$

Fig. 5

Computed solution of problem (32) for $\varepsilon =2^{-10}$ and $N=1024$ on the domain $\Omega _2$ with $\beta =0.5$

Fig. 6

Domain $\Omega _3$ with $\beta =0.5$

Table 3 Computed double-mesh global orders of convergence $\bar{p}_\varepsilon ^N$ for the corrected approximations ${\bar{U}}$ for problem (33) and $\beta =0.5$

Fig. 7

Computed solution of problem (33) for $\varepsilon =2^{-10}$ and $N=1024$ on the domain $\Omega _3$ with $\beta =0.5$

Example 3

The boundary is $\partial \Omega _3:=\{(\phi (t), \psi (t)) \} = \{ (\rho \cos t, \rho \sin t) \}$, where $\rho := \beta + \cos ^2 t$ and $0< \beta <2$ and the domain $\Omega _3$ is displayed in Fig. 6 for the case of $\beta =0.5$. The inflow boundary is disjointed and corresponds to the intervals (in the t variable)

$$\begin{aligned} (0,\theta ) \cup (\pi /2,\pi -\theta ) \cup (\pi +\theta , 3\pi /2) \cup (2\pi -\theta , 2\pi ), \quad \theta = \arcsin \sqrt{\frac{1+\beta }{3}}. \end{aligned}$$

The domain has four exterior characteristic points (where for $\beta =0.5, \kappa = 3/(2\sqrt{2})$) at

$$\begin{aligned} (\pm P, \pm Q), \quad P:= \frac{2(1+\beta )}{3} \sqrt{\frac{2-\beta }{3}} \quad Q:=\frac{2(1+\beta )}{3} \sqrt{\frac{1+\beta }{3}} \end{aligned}$$

and two interior characteristic points (where for $\beta =0.5, \kappa = 2$) at $(0, \pm \beta )$. In Table 3 we present global orders for the test problem (with $R=1$):

$$\begin{aligned} -\varepsilon \triangle u+ u_x +u= & {} \left( 1-\frac{y}{\beta }\right) ^4\left( 1+\frac{y}{\beta }\right) ^4H(y-\beta ) H(y+\beta ), \ (x,y) \in \Omega _3, \nonumber \\ u= & {} 0, \ (x,y) \in \partial \Omega _3; \end{aligned}$$

(33)

where $H(\cdot )$ is the Heaviside unit step function. A sample computed solution is displayed in Fig. 7.

Remark 5

The data in test problem (33) has been chosen to satisfy Assumption 3, with $\delta =0.5$. The data in the test problems (31) and (32) do not satisfy the compatibility constraints in Assumption 3 for any choice of $\delta >0$. Nevertheless, for all three test problems we observe parameter-uniform convergence in each of the corresponding tables of orders of convergence. However, if the test problem (33) is modified so that $f=(1-\frac{y}{\beta })^4(1+\frac{y}{\beta })^4$ then the numerical method will fail to converge due to insufficient compatibility being imposed at the characteristic points.