Residual Estimates for Post-processors in Elliptic Problems

Abstract

In this work we examine a posteriori error control for post-processed approximations to elliptic boundary value problems. We introduce a class of post-processing operator that “tweaks” a wide variety of existing post-processing techniques to enable efficient and reliable a posteriori bounds to be proven. This ultimately results in optimal error control for all manner of reconstruction operators, including those that superconverge. We showcase our results by applying them to two classes of very popular reconstruction operators, the Smoothness-Increasing Accuracy-Conserving filter and superconvergent patch recovery. Extensive numerical tests are conducted that confirm our analytic findings.

1 Introduction

Post-Processing techniques are often used in numerical simulations for a variety of reasons from visualisation purposes [4] to designing superconvergent approximations [5] through to becoming fundamental building blocks in constructing numerical schemes [6, 12, 13]. Another application of these operators is that they are a very useful component in the a posteriori analysis for approximations of partial differential equations (PDEs) [2, 33]. The goal of an a posteriori error bound is to computationally control the error committed in approximating the solution to a PDE. In order to illustrate the ideas, let u denote the solution to some PDE and let $u_h$ denote a numerical approximation. Then, the simplest possible use of post-processing in a posteriori estimates is to compute some $u^{*}$ from $u_h$ and to use

$$\begin{aligned} \parallel {u-u_h}\parallel \approx \parallel {u^{*}-u_h}\parallel \end{aligned}$$

as an error estimator.

However, a key observation here (and in several more sophisticated approaches) is that $u^*$ must be at least as good of an approximation of the solution u as $u_h$ is. In fact, in many cases, $u^*$ is actually expected to be a better approximation. This raises a natural question: If an adaptive algorithm computes (on any given mesh) not only $u_h$ but also $u^*$ and $u^*$ is a better approximation of u than $u_h$ is, why is $u_h$ and not $u^*$ considered as the “primary” approximation of u? Indeed, the focus of this paper is to consider $u^*$ as the primary approximation of u. We are therefore interested in control of the error $\parallel {u-u^*}\parallel$ and in adaptivity based on an a posteriori estimator for $\parallel {u-u^*}\parallel$. Specifically, we aim to provide reliable and efficient error control for $\parallel {u-u^*}\parallel$.

Note that our goal is not to try to construct “optimal” superconvergent post-processors. Rather we try to determine, from the a posteriori viewpoint, the accuracy of some given post-processed solution and to determine how this is useful for the construction of adaptive numerical schemes based on an error tolerance for $u - u^*$.

There are several examples of superconvergent post-processors, including SIAC and superconvergent patch recovery. More details on the history, properties and implementation of these methods will be provided in Sects. 4.1 and 4.2 . However, our a posteriori analysis, aims at being applicable for a wide variety of post-processors and, therefore, we avoid special assumptions that are only valid for specific post-processors. Indeed, our analysis makes only very mild assumptions on the post-processing operator. Specifically, we only require that:

• 1. The post-processed solution $u^*$ belongs to a finite dimensional space that contains piecewise polynomials, although it does not necessarily need to be piecewise polynomial itself.

• 2. The post-processed solution should be piecewise smooth over the same triangulation, or a sub-triangulation, of the finite element approximation.

Given a post-processor, $u^*$ that satisfies these rather mild assumptions, we perturb it slightly and call the result $u^{**}$. This is to ensure an orthogonality condition holds which then allows us to show various desirable properties including:

• 1. The orthogonal post-processor provides a better approximation than the original post-processor, i.e. $\parallel {u-u^{**}}\parallel _{\mathscr {A} _h} \le \parallel {u-u^*}\parallel _{\mathscr {A} _h}$ in the energy norm, see Lemma 3.4.

• 2. The orthogonal post-processor has an increased convergence order in the ${\text {L}} ^{2}$ norm. Practically, this is not always the case for the original post-processor, see Lemma 3.6.

• 3. Efficient and reliable a posteriori bounds are available for the error committed by the orthogonal post-processor.

This, motivates us to consider $u^{**}$ (and not $u^*$ or $u_h$) as the primary approximation. Since the improved accuracy of $u^{**}$, compared to $u_h$, stems from superconvergence it is much more sensitive with respect to smoothness of the exact solution, i.e. in regions where the exact solution is $C^\infty$ we expect $u^{**}$ to be much more accurate than $u_h$ whereas in places where the exact solution is less regular, e.g. has kinks, $u_h$ and $u^{**}$ are expected to have similar accuracy. Therefore, meshes constructed based on error estimators for $u-u_h$ will usually not be optimal when used for computing $u^{**}$ in the sense that the ratio of degrees of freedom to error $\Vert u- u_h\Vert$ would be much better for other meshes, this is elaborated upon in Sect. 5.

We will demonstrate the good approximation properties of our modification strategy for post-processors and the benefits of basing mesh adaptation on an estimator for $\Vert u- u_h\Vert$ in a series of numerical experiments. In order to highlight the versatility of our approach, we conduct experiments based on two popular post-processing techniques: The Smoothness Increasing Accuracy Conserving (SIAC) filter and superconvergent patch recovery (SPR). Background on these methods is provided in Sects. 4.1 and 4.2 respectively.

The rest of the paper is structured as follows: In Sect. 2 we introduce the model elliptic problem and its dG approximation. We also recall some standard results for this method. In Sect. 3, for a given reconstruction, we perturb it so it satisfies Galerkin orthogonality and show some a priori type results. We then study a posteriori results and give upper and lower bounds for a residual type estimator. In Sect. 4 we describe the two families of post-processor that we consider in this work. Finally, in Sect. 5 we perform extensive numerical tests on the SIAC and SPR post-processors to show the performance of the a posteriori bounds, the effect of smoothness of the solution on the post-processors and to study adaptive methods driven by these estimators.

2 Problem Setup and Notation

Let $\Omega \subset \mathbb R ^d$, $d=1,2,3$ be bounded with Lipschitz boundary $\partial \Omega$. We denote by ${\text {L}} ^{p}(\Omega )$, $p\in [1,\infty ]$, the standard Lebesgue spaces and ${\text {H}} ^{s}(\Omega )$, the Sobolev spaces of real-valued functions defined over $\Omega$. Further we denote ${\text {H}} ^{1}_0(\Omega )$ the space of functions in ${\text {H}} ^{1}(\Omega )$ with vanishing trace on $\partial \Omega$.

For $f \in {\text {L}} ^{2}(\Omega )$ we consider the problem

$$\begin{aligned} \begin{aligned} - {\text {div}}\!\left( {{\varvec{{\mathfrak {D}}}}\nabla u}\right)&=f \text { in } \Omega \\ u&=0 \text { on } \partial \Omega , \end{aligned} \end{aligned}$$

(2.1)

where ${\varvec{{\mathfrak {D}}}}:\Omega \rightarrow \mathbb R ^{d\times d}$ is a uniformly positive definite diffusion tensor and ${\varvec{{\mathfrak {D}}}}\in \!\left[ {{\text {H}} ^{1}(\Omega )\cap {\text {L}} ^{\infty }(\Omega )}\right] ^{d\times d}$. Weakly, the problem reads: find $u\in {\text {H}} ^{1}_{0}(\Omega )$ such that

$$\begin{aligned} \mathscr {A} \!\left( {u,v}\right) := \int _\Omega {\varvec{{\mathfrak {D}}}}\nabla u \cdot \nabla v \,\mathrm {d}{\varvec{x}} = \int _\Omega f v \,\mathrm {d}{\varvec{x}} \quad \,\forall \,v\in {\text {H}} ^{1}_{0}(\Omega ). \end{aligned}$$

(2.2)

Let $\mathscr {T} ^{}$ be a triangulation of $\Omega$ into disjoint simplicial or box-type (quadrilateral/hexahedral) elements $K\in \mathscr {T} ^{}$ such that $\overline{\Omega }=\bigcup _{K\in \mathscr {T} ^{}} \overline{K}$. Let $\mathscr {E}$ be the set of edges which we split into the set of interior edges $\mathscr {E} _i$ and the set of boundary edges $\mathscr {E} _b$.

We introduce the standard broken Sobolev spaces. For $s \in \mathbb N _0$ we define

$$\begin{aligned} {\text {H}} ^{s}(\mathscr {T} ^{}) := \{ v \in {\text {L}} ^{2}(\Omega ) \, : \, v|_K \in {\text {H}} ^{s}(K) \, \quad \,\forall \,K \in \mathscr {T} ^{}\}, \end{aligned}$$

(2.3)

and we will use the notation

$$\begin{aligned} \parallel {v}\parallel _{{\text {H}} ^{s}(\mathscr {T} ^{})} = \!\left( {\sum _{K\in \mathscr {T} ^{}} \parallel {v}\parallel _{{\text {H}} ^{s}(K)}^2}\right) ^{1/2} \end{aligned}$$

(2.4)

as an elementwise norm for the broken space.

For $p\in \mathbb N$ we denote the set of all polynomials over K of total degree at most p by $\mathbb P ^{p}(K)$. For $p \ge 1$, we consider the finite element space

$$\begin{aligned} \mathbb {V}_{h}^{p} := \{ \phi \in {\text {L}} ^{2}(\Omega ) : v|_{K} \in \mathbb P ^{p}(K), K\in \mathscr {T} ^{} \}. \end{aligned}$$

(2.5)

Let $v\in {\text {H}} ^{1}(\mathscr {T} ^{})$ be an arbitrary scalar function. For any interior edge $e \in \mathscr {E} _i$ there are two adjacent triangles $K^-, K^+$ and we can consider the traces $v^\pm$ of v from $K^\pm$ respectively. We denote the outward normal of $K^\pm$ by ${\varvec{n}}^\pm$ and define average and jump operators for one $\mathscr {E} _i$ by

$$\begin{aligned} \begin{aligned} \lbrace \!\!\lbrace \! v \! \rbrace \!\!\rbrace&:= {\frac{1}{2}\!\left( { v^+ + v^-}\right) }:= \frac{1}{2}\!\left( {\lim _{s \searrow 0} v(\cdot + s {\varvec{n}}^+) + \lim _{s \searrow 0} v(\cdot + s {\varvec{n}}^-)}\right) , \\ [\![ v]\!]&:= {\!\left( {v^- {\varvec{n}}^- + v^+{\varvec{n}}^+}\right) }:= \lim _{s \searrow 0} v(\cdot + s {\varvec{n}}^-) {\varvec{n}}^- +\lim _{s \searrow 0} v(\cdot + s{\varvec{n}}^+) {\varvec{n}}^+. \end{aligned} \end{aligned}$$

(2.6)

For boundary edges there is only one trace of v and one outward pointing normal vector ${\varvec{n}}$ and we define

$$\begin{aligned} \lbrace \!\!\lbrace \! v \! \rbrace \!\!\rbrace := v \qquad [\![ v]\!] := v {\varvec{n}}. \end{aligned}$$

(2.7)

For vector valued functions ${\varvec{v}}\in [{\text {H}} ^{1}(\mathscr {T} ^{})]^d$ we define jumps and averages on interior edges by

$$\begin{aligned} \lbrace \!\!\lbrace \! {\varvec{v}} \! \rbrace \!\!\rbrace := \frac{1}{2} {\varvec{v}}^+ + \frac{1}{2} {\varvec{v}}^- , \quad [\![ {\varvec{v}}]\!] := {\!\left( {{\varvec{v}}^- \cdot {\varvec{n}}^- + {\varvec{v}}^+ \cdot {\varvec{n}}^+}\right) }. \end{aligned}$$

(2.8)

As before, for boundary edges, we define jumps and averages using traces from the interior only. Note that $[\![ {\varvec{v}}]\!],\lbrace \!\!\lbrace \! v \! \rbrace \!\!\rbrace \in {\text {L}} ^{2}(\mathscr {E})$ and $[\![ v]\!], \lbrace \!\!\lbrace \! {\varvec{v}} \! \rbrace \!\!\rbrace \in [{\text {L}} ^{2}(\mathscr {E})]^d$.

For any triangle $K \in \mathscr {T} ^{}$ we define $h_K:= {\text {diam}}{K}$ and collect these values into an element-wise constant function $h:\Omega \rightarrow \mathbb R$ with $h|_K = h_K$. We denote the radius of the largest ball inscribed in K by $\rho _K$. For every edge e we denote by $h_e = \lbrace \!\!\lbrace \! h \! \rbrace \!\!\rbrace$, i.e., the mean of diameters of adjacent triangles. For our analysis we will assume that $\mathscr {T} ^{}$ belongs to a family of triangulations which is quasi-uniform and shape-regular. Let us briefly recall the definitions of these two notions: The triangulation $\mathscr {T} ^{}$ is called

• shape-regular if there exists $C>0$ so that

  $$\begin{aligned} h_K < C \rho _K \quad \,\forall \,K \in \mathscr {T} ^{} \end{aligned}$$

  (2.9)

• quasi-uniform if there exists $C>0$ so that

  $$\begin{aligned} \max _{K \in \mathscr {T} ^{}} h_K < C h_K \quad \,\forall \,K \in \mathscr {T} ^{}. \end{aligned}$$

  (2.10)

Note that for shape-regular triangulations we have inverse and trace inequalities [10, Lemmas 1.44, 1.46]. Note that the quasi-uniformity assumption is only required for the first part of our analysis, in Sect. 3.1 and can be relaxed in Sect. 3.2.

In this work we will consider a standard interior penalty method to approximate solutions of (2.2). We consider the Galerkin method to seek $u_h \in \mathbb {V}_h^p$ such that

$$\begin{aligned} \mathscr {A} _{h}\!\left( {u_h,v_h}\right) = \int _\Omega f v_h\,\mathrm {d}{\varvec{x}} \quad \,\forall \,v_h\in \mathbb {V}_h^p, \end{aligned}$$

(2.11)

where $\mathscr {A} _h: {\text {H}} ^{2}(\mathscr {T} ^{}) \times {\text {H}} ^{2}(\mathscr {T} ^{}) \rightarrow \mathbb R$ is given by

$$\begin{aligned} \mathscr {A} _{h}\!\left( {u,v}\right) = \int _{\mathscr {T} ^{}} {\varvec{{\mathfrak {D}}}}\nabla u \cdot \nabla v - \int _\mathscr {E} [\![ v]\!] \cdot \lbrace \!\!\lbrace \! {\varvec{{\mathfrak {D}}}}\nabla u \! \rbrace \!\!\rbrace - \int _\mathscr {E} [\![ u]\!] \cdot \lbrace \!\!\lbrace \! {\varvec{{\mathfrak {D}}}}\nabla v \! \rbrace \!\!\rbrace + \int _\mathscr {E} \sigma h_e^{-1} [\![ u]\!] \cdot [\![ v]\!]\nonumber \\ \end{aligned}$$

(2.12)

Note that the bilinear form (2.12) is stable provided $\sigma = \sigma ({\varvec{{\mathfrak {D}}}})$ is large enough, see [1].

Remark 2.1

(Continuous Galerkin methods). Note that if we restrict test and trial functions to $\mathbb {V}_h^p \cap {\text {H}} ^{1}(\Omega )$ then all jumps on interior edges vanish and (2.11), (2.12) reduces to a (continuous) finite element method with weakly enforced boundary data. Our analysis is equally valid in this case.

We introduce two dG norms

$$\begin{aligned} \begin{aligned} \parallel {v}\parallel _{dG}^2&:= \parallel {\nabla v}\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})}^2 + \parallel {h_e^{-\frac{1}{2}} [\![ v]\!]}\parallel _{{\text {L}} ^{2}(\mathscr {E})}^2 \\ \parallel {v}\parallel _{\mathscr {A} _h}^2&:= \mathscr {A} _{h}\!\left( {v,v}\right) , \end{aligned} \end{aligned}$$

(2.13)

which are equivalent provided $\sigma >0$ is sufficiently large and conclude this section by stating a-priori estimates for the Galerkin method as is standard in the literature [1, 17].

Theorem 2.2

(Error bounds for the dG approximation). Let $u\in {\text {H}} ^{s}(\Omega )$ for $s\ge 2$ be the solution of (2.1) and $u_h\in \mathbb {V}_h^p$ be the unique solution to the problem (2.11). Then,

$$\begin{aligned} \parallel {u-u_h}\parallel _{{\text {L}} ^{2}(\Omega )} + h\parallel {u-u_h}\parallel _{dG} \le C_1 h^{\min \,\!\left( {p+1,s}\right) } \left| u\right| _{{\text {H}} ^{s}(\Omega )}. \end{aligned}$$

(2.14)

Further, for $u\in {\text {H}} ^{1}(\Omega )$, we have the a posteriori error bound

$$\begin{aligned} \parallel { u - u_h}\parallel _{dG} \le C_2 R_h := C_2 \!\left( { \sum _{K\in \mathscr {T} ^{}} \!\left( { \eta _K^2 + \frac{1}{2} \sum _{e \in \partial K} \eta _e^2 }\right) }\right) ^{\frac{1}{2}}, \end{aligned}$$

(2.15)

where

$$\begin{aligned} \begin{aligned} \eta _K^2&:= \parallel {h_K ( f + {\text {div}}\!\left( {{\varvec{{\mathfrak {D}}}}\nabla u_h}\right) )}\parallel _{{\text {L}} ^{2}(K)}^2 \\ \eta _e^2&:= \parallel {h_e^{\frac{1}{2}} [\![ {\varvec{{\mathfrak {D}}}}\nabla u_h]\!]}\parallel _{{\text {L}} ^{2}(e)}^2 + \parallel {h_e^{-\frac{1}{2}} [\![ u_h]\!] }\parallel _{{\text {L}} ^{2}(e)}^2, \end{aligned} \end{aligned}$$

(2.16)

and $C_1$ is a constant depending on the shape-regularity and quasi-uniformity constants of $\mathscr {T} ^{}$ and $C_2$ depends only upon the shape-regularity. Here $R_h$ is a computable residual that we refer to during our numerical simulations.

3 The Orthogonal Reconstruction, a priori and a posteriori Error Estimates

In this section, we derive robust and efficient error estimates. We make the assumption that we have access to a computable reconstruction, $u^{*}\in \mathbb {V}_h^* \subset {\text {H}} ^{2}(\mathscr {T} ^{})$ generated from our numerical solution $u_h$, where $\mathbb {V}_h^*$ is required to contain the original finite element space, that is $\mathbb {V}_h^p \subset \mathbb {V}_h^*$. We are unable to provide reliable a posteriori error estimates for $u^{*}$ directly, but we can modify, and, as we shall demonstrate, improve any such reconstruction such that a robust and efficient error estimate can be obtained for the modified reconstruction.

We split this section into two parts, the first subsection contains the definition of the improved reconstruction and some of its properties. In particular, we study this from an a priori viewpoint, show that it satisfies Galerkin orthogonality as well as some desirable a priori bounds. Throughout this subsection we assume that $u\in {\text {H}} ^{2}(\Omega )$ and the underlying mesh is quasi-uniform. In the second part we derive reliable and efficient a posteriori estimates under the weaker assumption that $u\in {\text {H}} ^{1}(\Omega )$ and the mesh is shape regular.

3.1 Improved Reconstruction

In the following assume that $u\in {\text {H}} ^{2}(\Omega )$ solves (2.2) and let $u^{*}\in \mathbb {V}_h^* \subset {\text {H}} ^{2}(\mathscr {T} ^{})$ be a reconstruction of the discrete solution $u_h$, e.g. a SIAC reconstruction as described in Sect. 4.1 or obtained by some patch recovery operator as described in Sect. 4.2.

Definition 3.1

Let $R: {\text {H}} ^{2}(\mathscr {T} ^{}) \rightarrow \mathbb {V}_h^p$ denote the Ritz projection with respect to $\mathscr {A} _{h}\!\left( {\cdot ,\cdot }\right)$, i.e.,

$$\begin{aligned} \mathscr {A} _{h}\!\left( {Rv,\phi _h}\right) = \mathscr {A} _{h}\!\left( {v,\phi _h}\right) \quad \,\forall \,\phi _h \in \mathbb {V}_h^p. \end{aligned}$$

(3.1)

We define the improved reconstruction as

$$\begin{aligned} u^{**}:= u^{*}- Ru^{*}+ u_h \in \mathbb {V}_h^* \end{aligned}$$

(3.2)

Remark 3.2

We make the following remarks:

• 1. The finite element approximation from (2.11) satisfies $u_h = R u$.

• 2. We work under the assumption that a post-processor $u^{*}$ is already being computed. To realise $u^{**}$ we are required to solve the original elliptic problem a second time with a different forcing term. This means the improved reconstruction $u^{**}$ is computable at a small additional cost to $u^{*}$. Once $u^{*}$ has been computed, $u^{**}$ can be computed by solving a discrete elliptic problem over $\mathbb {V}_h^p$. A typical scenario is that the user already has a good scheme for computing $u_h$, and that the cost of computing $u^{**}$ (after the post-processing to obtain $u^*$) is just that of solving the same system as that for $u_h$ with a different right hand side. This means the assembly and preconditioning, perhaps ILU or AMG, can be reused without change.

  Estimating the cost of computing $u^*$ is more complicated and will depend on the method used and the implementation. While our implementation for solving $u_h$ and the correction are optimized (and implemented in C++) the computation of $u^{**}$ is a proof of concept implementation in Python and is therefore not competitive.

• 3. Note that

  $$\begin{aligned} u - u^{**}= u - u_h - u^{*}+ R u^{*}= (id - R)( u - u^{*}), \end{aligned}$$

  (3.3)

  where id is the identity mapping, i.e., the error of $u^{**}$ is the Ritz-projection of the error of $u^{*}$ onto the orthogonal complement of $\mathbb {V}_h^p$.

• 4. Even if $u^{*}$ is continuous, this does not necessarily hold for $u^{**}$ as $\mathbb {V}_h^p$ may contain discontinuous functions.

One of the key properties of the improved reconstruction is that it satisfies a Galerkin orthogonality result.

Lemma 3.3

(Galerkin orthogonality). The reconstruction $u^{**}$ from (3.2) satisfies Galerkin orthogonality, i.e.,

$$\begin{aligned} \mathscr {A} _{h}\!\left( {u - u^{**}, v_h}\right) =0 \quad \forall v_h \in \mathbb {V}_h^p. \end{aligned}$$

(3.4)

Proof

For any $v_h \in \mathbb {V}_h^p$, we have using (3.3)

$$\begin{aligned} \begin{aligned} \mathscr {A} _{h}\!\left( {u - u^{**}, v_h}\right)&= \mathscr {A} _{h}\!\left( { (id - R)( u - u^{*}) ,v_h}\right) =0 \end{aligned} \end{aligned}$$

(3.5)

by definition of the Ritz projection, as required. $\square$

Now, we show that with respect to $\parallel {\cdot }\parallel _{\mathscr {A} _h}$ the new reconstruction $u^{**}$ indeed improves upon $u^{*}$:

Lemma 3.4

(Better approximation of the improved reconstruction). Let $u^{**}$ be defined by (3.2), then the following holds:

$$\begin{aligned} \parallel { u - u^{**}}\parallel _{\mathscr {A} _h} \le \parallel { u - u^{*}}\parallel _{\mathscr {A} _h}. \end{aligned}$$

(3.6)

In (3.6) the inequality is an equality if and only if $u^{**}=u^{*}$, i.e., if the original reconstruction $u^{*}$ itself satisfies Galerkin orthogonality.

Proof

Since the images of R and $(id - R)$ are orthogonal with respect to $\mathscr {A} _{h}\!\left( {\cdot ,\cdot }\right)$, Pythagoras’ theorem implies

$$\begin{aligned}&\parallel {u - u^{*}}\parallel _{\mathscr {A} _h}^2 = \parallel {(id-R)(u-u^{*})+R(u-u^{*})}\parallel _{\mathscr {A} _h}^2 \nonumber \\&\quad \ge \parallel {(id-R)(u-u^{*})}\parallel _{\mathscr {A} _h}^2 = \parallel {u-u^{**}}\parallel _{\mathscr {A} _h}^2 \end{aligned}$$

(3.7)

We have used (3.3) in the third step. Note that if $u^{*}$ is not Galerkin orthogonal then

$$\begin{aligned} \parallel {R(u-u^{*})}\parallel _{\mathscr {A} _h} > 0 \end{aligned}$$

leading to a strict inequality in the first step. This completes the proof. $\square$

Remark 3.5

One appealing feature of the new reconstruction that results from Galerkin orthogonality is that if the reconstruction $u^{*}$ has some superconvergence properties in the energy norm this is inherited by $u^{**}$ and also immediately implies an additional order of accuracy in ${\text {L}} ^{2}$. This results from an Aubin-Nitsche trick being available.

Lemma 3.6

(Dual bounds). Let $\Omega$ be a convex polygonal domain and let $u^{**}$ be defined by (3.2), then there exists a constant $C>0$ (only depending on the shape regularity of the mesh) such that

$$\begin{aligned} \parallel {u - u^{**}}\parallel _{{\text {L}} ^{2}(\Omega )} \le Ch \parallel {u - u^{**}}\parallel _{\mathscr {A} _h}. \end{aligned}$$

(3.8)

Proof

Let $\psi \in {\text {H}} ^{2}(\Omega ) \cap {\text {H}} ^{1}_{0}(\Omega )$ solve

$$\begin{aligned} - {\text {div}}\!\left( {{\varvec{{\mathfrak {D}}}}\nabla \psi }\right) = u - u^{**}\end{aligned}$$

which implies

$$\begin{aligned} \int _{\mathscr {T} ^{}} {\varvec{{\mathfrak {D}}}}\nabla \psi \cdot \nabla v - \int _\mathscr {E} [\![ v]\!] \cdot \lbrace \!\!\lbrace \! {\varvec{{\mathfrak {D}}}}\nabla \psi \! \rbrace \!\!\rbrace = \int _\Omega (u - u^{**}) v \quad \forall v \in {\text {H}} ^{1}(\mathscr {T} ^{}). \end{aligned}$$

(3.9)

Thus, by choosing $v = u - u^{**}$ in (3.9) we obtain

$$\begin{aligned} \begin{aligned} \parallel {u - u^{**}}\parallel _{{\text {L}} ^{2}(\Omega )}^2&= \int _{\mathscr {T} ^{}} {\varvec{{\mathfrak {D}}}}\nabla \psi \cdot \nabla (u - u^{**}) - \int _\mathscr {E} [\![ u - u^{**}]\!] \cdot \lbrace \!\!\lbrace \! {\varvec{{\mathfrak {D}}}}\nabla \psi \! \rbrace \!\!\rbrace \\&= \mathscr {A} _{h}\!\left( {\psi ,u - u^{**}}\right) \\&= \mathscr {A} _{h}\!\left( {\psi - \psi _h,u - u^{**}}\right) \end{aligned} \end{aligned}$$

(3.10)

for any $\psi _h \in \mathbb {V}_h^p$ where the last equality follows from Galerkin orthogonality (3.4). Thus, choosing $\psi _h$ as the best approximation of $\psi$ in the piecewise linear subspace of $\mathbb {V}_h^p$, we obtain

$$\begin{aligned} \begin{aligned} \parallel {u - u^{**}}\parallel _{{\text {L}} ^{2}(\Omega )}^2&\le \parallel {\psi - \psi _h}\parallel _{\mathscr {A} _h} \parallel {u - u^{**}}\parallel _{\mathscr {A} _h} \\&\le Ch \parallel {u - u^{**}}\parallel _{\mathscr {A} _h} \parallel {\nabla ^2 \psi }\parallel _{{\text {L}} ^{2}(\Omega )} \\&\le C h \parallel {u - u^{**}}\parallel _{{\text {L}} ^{2}(\Omega )} \parallel {u - u^{**}}\parallel _{\mathscr {A} _h}, \end{aligned} \end{aligned}$$

(3.11)

by elliptic regularity of the dual problem, concluding the proof. $\square$

3.2 A Posteriori Error Estimates

Now that we have shown some fundamental results on the improved reconstruction, we relax the regularity requirements on u in this subsection allowing for weak solutions to (2.1), that is, $u\in {\text {H}} ^{1}(\Omega )$. With that in mind we modify the definition of $\mathscr {A} _{h}\!\left( {\cdot ,\cdot }\right)$ such that it is a suitable extension over ${\text {H}} ^{1}(\mathscr {T} ^{})\times {\text {H}} ^{1}(\mathscr {T} ^{})$ to

$$\begin{aligned} \mathscr {A} _{h}\!\left( {u,v}\right) := \int _{\mathscr {T} ^{}} {\varvec{{\mathfrak {D}}}}\nabla u \cdot \nabla v - r_{h}^{*}([\![ v]\!]) \cdot {\varvec{{\mathfrak {D}}}}\nabla u - r_{h}^{*}( [\![ u]\!] ) \cdot {\varvec{{\mathfrak {D}}}}\nabla v + \int _\mathscr {E} \sigma h_e^{-1} [\![ u]\!] \cdot [\![ v]\!],\nonumber \\ \end{aligned}$$

(3.12)

for $u,v \in {\text {H}} ^{1}(\mathscr {T} ^{})$ and where $r_{h}^{*}: [{\text {L}} ^{2}(\mathscr {E})]^d \rightarrow \!\left[ {\mathbb {V}_h^*}\right] ^d$ is the lifting operator that we recall from [10, Section 4.3.1]

$$\begin{aligned} \int _\Omega r_{h}^{*}(\varphi ) \cdot {\varvec{{\mathfrak {D}}}}{\varvec{\psi }}_h = \int _\mathscr {E} \varphi \cdot \lbrace \!\!\lbrace \! {\varvec{{\mathfrak {D}}}}{\varvec{\psi }}_h \! \rbrace \!\!\rbrace \quad \quad \,\forall \,{\varvec{\psi }}_h \in \!\left[ {\mathbb {V}_h^*}\right] ^d. \end{aligned}$$

(3.13)

The lifting operators satisfy the stability estimate, [10, Lemma 4.34],

$$\begin{aligned} \parallel {r_{h}^{*}(\varphi )}\parallel _{{\text {L}} ^{2}(\Omega )} \le C \parallel { h_e^{-\frac{1}{2}} \varphi }\parallel _{{\text {L}} ^{2}(\mathscr {E})}, \end{aligned}$$

(3.14)

For test and trial functions in $\mathbb {V}_h^*$ (which contains $\mathbb {V}_h^p$ by assumption) the new definition of $\mathscr {A} _{h}\!\left( {\cdot ,\cdot }\right)$ is equivalent to the one given in (2.12). Therefore for any function $v^*\in \mathbb {V}_h^*$ the Ritz projection given in Definition 3.1 remains the same still satisfying $\mathscr {A} _{h}\!\left( {Rv^*,\phi _h}\right) = \mathscr {A} _{h}\!\left( {v^*,\phi _h}\right)$ for all $\phi _h \in \mathbb {V}_h^p$. But note that we no longer have $u_h=Ru$ and Galerkin orthogonality for $u^{**}$ no longer holds in general, it only holds for a ${\text {H}} ^{1}(\Omega )$ conforming subspace of $\mathbb {V}_h^p$:

Lemma 3.7

For $u\in {\text {H}} ^{1}(\Omega )$ and $z_h\in \mathbb {V}_h^p\cap {\text {H}} ^{1}_0(\Omega )$ it holds that

$$\begin{aligned} \mathscr {A} _{h}\!\left( {u^{**}- u,z_h}\right) = 0. \end{aligned}$$

(3.15)

Proof

By definition of $u^{**}$ we have that

$$\begin{aligned} \begin{aligned} \mathscr {A} _{h}\!\left( {u^{**}- u,z_h}\right)&= \mathscr {A} _{h}\!\left( {u^{*}- R u^{*}+ u_h - u,z_h}\right) \\&= \mathscr {A} _{h}\!\left( {u^{*}- Ru^{*},z_h}\right) + \mathscr {A} _{h}\!\left( {u_h - u,z_h}\right) \\&= \mathscr {A} _{h}\!\left( {u_h - u,z_h}\right) , \end{aligned} \end{aligned}$$

(3.16)

since $u^{*}\in \mathbb {V}_h^*$. Now, notice that by definition

$$\begin{aligned} \mathscr {A} _{h}\!\left( {u_h - u,z_h}\right) = \left\langle {f,z_h}\right\rangle - \int _{\mathscr {T} ^{}} {\varvec{{\mathfrak {D}}}}\nabla u \cdot \nabla z_h - r_{h}^{*}([\![ z_h]\!]) \cdot {\varvec{{\mathfrak {D}}}}\nabla u = 0 \end{aligned}$$

(3.17)

as $z_h$ is an element of $\mathbb {V}_h^p\cap {\text {H}} ^{1}_0(\Omega )$ and, hence, continuous, as required. $\square$

Let a quantity of interest be given by the linear functional $\mathscr {J} \in {\text {H}} ^{-1}(\mathscr {T} ^{})$, the dual space of ${\text {H}} ^{1}_0(\mathscr {T} ^{})$. Note that ${\text {H}} ^{-1}(\mathscr {T} ^{}) \subset {\text {H}} ^{-1}(\Omega )$ where the latter is the dual space of ${\text {H}} ^{1}_0(\Omega )$. We begin by deriving an error representation formula. Following [15], we split $u^{**}$ into a continuous part $u^{**}_C \in \mathbb {V}_h^{*} \cap {\text {H}} ^{1}_0(\Omega )$ and a discontinuous part $u^{**}_\perp \in \mathbb {V}_h^{*}$ so that

$$\begin{aligned} u^{**}= u^{**}_C + u^{**}_\perp \quad \text { and } \quad \mathscr {A} _{h}\!\left( { u^{**}_\perp ,\psi _h}\right) = 0 \quad \,\forall \,\psi \in \mathbb {V}_h^{*}\cap {\text {H}} ^{1}_0(\Omega ). \end{aligned}$$

(3.18)

Theorem 3.8

(Dual error representation). Let $u\in {\text {H}} ^{1}_0(\Omega )$ be the solution of (2.2) and let $u^{**}$ be given by (3.2), then

$$\begin{aligned} \mathscr {J} (u - u^{**}) = \langle f, z - z_h \rangle - \mathscr {A} _{h}\!\left( {u^{**},z - z_h}\right) + \mathscr {A} _{h}\!\left( {u^{**}_\perp ,z}\right) - \mathscr {J} (u^{**}_\perp ) \end{aligned}$$

(3.19)

where $\langle \cdot ,\cdot \rangle$ denotes the ${\text {L}} ^{2}$ scalar product and $z \in {\text {H}} ^{1}_{0}(\Omega )$ is the solution of the dual problem

$$\begin{aligned} \mathscr {A} \!\left( {v,z}\right) = \mathscr {J} ( v ) \quad \,\forall \,v\in {\text {H}} ^{1}_{0}(\Omega )\end{aligned}$$

(3.20)

and $z_h$ is an arbitrary function in $\mathbb {V}_h^p\cap {\text {H}} ^{1}_0(\Omega )$.

Proof

By definition of z, we have, for any $z_h \in \mathbb {V}_h^p\cap {\text {H}} ^{1}_0(\Omega )$,

$$\begin{aligned} \begin{aligned} \mathscr {J} (u - u^{**})&= \mathscr {J} (u- u^{**}_C - u^{**}_\perp ) \\&= \mathscr {J} (u- u^{**}_C) - \mathscr {J} (u^{**}_\perp ) \\&= \mathscr {A} \!\left( {u-u^{**}_C, z}\right) - \mathscr {J} (u^{**}_\perp ) \\&= \langle f,z\rangle - \mathscr {A} _{h}\!\left( {u^{**}_C,z}\right) - \mathscr {J} (u^{**}_\perp ) \\&= \langle f,z\rangle - \mathscr {A} _{h}\!\left( {u^{**},z}\right) + \mathscr {A} _{h}\!\left( {u^{**}_\perp ,z}\right) - \mathscr {J} (u^{**}_\perp ) \\&= \langle f,z\rangle - \mathscr {A} _{h}\!\left( {u^{**},z-z_h}\right) - \mathscr {A} _{h}\!\left( {u^{**},z_h}\right) + \mathscr {A} _{h}\!\left( {u^{**}_\perp ,z}\right) - \mathscr {J} (u^{**}_\perp ) \\&= \langle f,z-z_h\rangle - \mathscr {A} _{h}\!\left( {u^{**},z-z_h}\right) + \mathscr {A} _{h}\!\left( {u^{**}_\perp ,z}\right) - \mathscr {J} (u^{**}_\perp ), \end{aligned} \end{aligned}$$

(3.21)

where we made use of Galerkin orthogonality, Lemma 3.7, in the last step. $\square$

Theorem 3.9

(Primal error estimate). There exists some constant $C_A >0$ depending on mesh geometry and polynomial degree such that

$$\begin{aligned} \parallel { u - u^{**}}\parallel _{dG} \le C_A R^{**} := C_A \!\left( { \sum _{K\in \mathscr {T} ^{}} \!\left( { (\eta ^{**}_K)^2 + \frac{1}{2} \sum _{e \in \partial K} (\eta ^{**}_e)^2 }\right) }\right) ^{\frac{1}{2}}, \end{aligned}$$

(3.22)

where

$$\begin{aligned} \begin{aligned} (\eta ^{**}_K)^2&:= \parallel {h_K ( f + {\text {div}}\!\left( {{\varvec{{\mathfrak {D}}}}\nabla u^{**}}\right) )}\parallel _{{\text {L}} ^{2}(K)}^2 \\ (\eta ^{**}_e)^2&:= \parallel {h_e^{\frac{1}{2}} [\![ {\varvec{{\mathfrak {D}}}}\nabla u^{**}]\!]}\parallel _{{\text {L}} ^{2}(e)}^2 + \parallel {h_e^{-\frac{1}{2}} [\![ u^{**}]\!] }\parallel _{{\text {L}} ^{2}(e)}^2 \end{aligned} \end{aligned}$$

(3.23)

Proof

Since

$$\begin{aligned} \parallel { u - u^{**}}\parallel _{dG} \le C \left( \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\!\left( {\nabla u - \nabla u^{**}}\right) }\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})}^2 + \sum _{e \in \mathscr {E}} \parallel {h_e^{-\frac{1}{2}} [\![ u^{**}]\!]}\parallel _{{\text {L}} ^{2}(e)}^2 \right) ^{\frac{1}{2}}, \end{aligned}$$

(3.24)

where C is some constant depending on ${\varvec{{\mathfrak {D}}}}$ only, it is sufficient to show that

$$\begin{aligned} \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\!\left( {\nabla u - \nabla u^{**}}\right) }\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})} \end{aligned}$$

is bounded by the right hand side of (3.22).

In Theorem 3.8 we may choose

$$\begin{aligned} \mathscr {J} (v):= \int _{\mathscr {T} ^{}} {\varvec{{\mathfrak {D}}}}(\nabla u - \nabla u^{**}) \nabla v. \end{aligned}$$

(3.25)

Note that, by definition, $z \in {\text {H}} ^{1}_{0}(\Omega )$ so that, if $\mathbb {V}_h^p$ contains discontinuous functions, $z \not = u - u^{**}$. Nevertheless, z satisfies the stability estimate

$$\begin{aligned} \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla z}\parallel _{{\text {L}} ^{2}(\Omega )} \le \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\!\left( {\nabla u - \nabla u^{**}}\right) }\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})}. \end{aligned}$$

(3.26)

Then, for any $z_h \in \mathbb {V}_h^p \cap {\text {H}} ^{1}_{0}(\Omega )$, Theorem 3.8 implies

$$\begin{aligned} \begin{aligned}&\parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla \!\left( {u - u^{**}}\right) }\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})}^2 \\&\quad = \mathscr {J} (u - u^{**}) \\&\quad = \langle f,z-z_h\rangle - \mathscr {A} _{h}\!\left( {u^{**},z-z_h}\right) + \mathscr {A} _{h}\!\left( {u^{**}_\perp ,z}\right) - \mathscr {J} (u^{**}_\perp ) \\&\quad = \langle f,z-z_h\rangle - \int _{\mathscr {T} ^{}} (\nabla u^{**}- r_{h}^{*}([\![ u^{**}]\!])) {\varvec{{\mathfrak {D}}}}\nabla (z - z_h) \\&\qquad + \mathscr {A} _{h}\!\left( {u^{**}_\perp ,z}\right) - \mathscr {J} (u^{**}_\perp ). \end{aligned} \end{aligned}$$

(3.27)

Integrating by parts in (3.27) and using (3.14) we obtain

$$\begin{aligned} \begin{aligned}&\parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla \!\left( {u - u^{**}}\right) }\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})}^2\\&\quad = \int _{\mathscr {T} ^{}} (f + {\text {div}}\!\left( {{\varvec{{\mathfrak {D}}}}\nabla u^{**}}\right) )(z - z_h ) - \int _\mathscr {E} [\![ {\varvec{{\mathfrak {D}}}}\nabla u^{**}]\!] ( z - z_h ) \\&\qquad + \int _{\mathscr {T} ^{}} r_{h}^{*}([\![ u^{**}]\!]) {\varvec{{\mathfrak {D}}}}\nabla (z - z_h) + \mathscr {A} _{h}\!\left( {u^{**}_\perp ,z}\right) - \mathscr {J} (u^{**}_\perp ) \\&\quad \le \sum _K h_K \parallel {f + {\text {div}}\!\left( {{\varvec{{\mathfrak {D}}}}\nabla u^{**}}\right) }\parallel _{{\text {L}} ^{2}(K)} h_K^{-1}\parallel {z - z_h }\parallel _{{\text {L}} ^{2}(K)} \\&\qquad + \frac{1}{2} \sum _{e \in \partial K} h_e^{\frac{1}{2}} \parallel {[\![ {\varvec{{\mathfrak {D}}}}\nabla u^{**}]\!]}\parallel _{{\text {L}} ^{2}(e)} h_e^{- \frac{1}{2}} \parallel {z - z_h }\parallel _{{\text {L}} ^{2}(e)} \\&\qquad + C \parallel {h_e^{-\frac{1}{2}}[\![ u^{**}]\!] }\parallel _{{\text {L}} ^{2}(\mathscr {E})} \parallel { {\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla (z - z_h)}\parallel _{{\text {L}} ^{2}(\Omega )} \\&\qquad + C \parallel {u^{**}_\perp }\parallel _{dG} \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla \!\left( {z - z_h}\right) }\parallel _{{\text {L}} ^{2}(\Omega )} + \parallel {\mathscr {J}}\parallel _{{\text {H}} ^{-1}(\Omega )} \parallel {u^{**}_\perp }\parallel _{dG} \end{aligned} \end{aligned}$$

(3.28)

From [14, Theorem 5.3] we obtain

$$\begin{aligned} \parallel {u^{**}_\perp }\parallel _{dG} \le C_P \parallel {h_e^{-\frac{1}{2}} [\![ u^{**}]\!]}\parallel _{{\text {L}} ^{2}(\mathscr {E})} \end{aligned}$$

(3.29)

with a constant $C_P>0$ which is independent of h but depends on the shape regularity of the mesh and the polynomial degree and we also note that

$$\begin{aligned} \parallel {\mathscr {J}}\parallel _{{\text {H}} ^{-1}(\Omega )} \le C\parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}} \nabla \!\left( {u - u^{**}}\right) }\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})}. \end{aligned}$$

(3.30)

We insert (3.29) and (3.30) into (3.28) and apply trace inequality and Cauchy-Schwarz inequality and obtain

$$\begin{aligned} \begin{aligned} \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla \!\left( {u - u^{**}}\right) }\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})}^2&\le \left( \sum _K \left( (\eta ^{**}_K)^2 + C \sum _{e \in \partial K} (\eta ^{**}_e)^2 \right) \right) ^{\frac{1}{2}} \parallel {h^{-1} (z - z_h) }\parallel _{{\text {L}} ^{2}(\Omega )} \\&\qquad + C \left( \sum _K \sum _{e \in \partial K} (\eta ^{**}_e)^2 \right) ^{\frac{1}{2}} \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla (z - z_h) }\parallel _{{\text {L}} ^{2}(\Omega )}. \end{aligned} \end{aligned}$$

(3.31)

Now, we choose $z_h \in \mathbb {V}_h^p \cap {\text {H}} ^{1}_{0}(\Omega )$ as the Clément interpolant of z so that

$$\begin{aligned} \begin{aligned} \parallel {h^{-1} (z - z_h) }\parallel _{{\text {L}} ^{2}(\Omega )} + \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla (z - z_h) }\parallel _{{\text {L}} ^{2}(\Omega )}&\le C \parallel {\nabla z }\parallel _{{\text {L}} ^{2}(\Omega )} \\&\le C \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}} \nabla \!\left( {u - u^{**}}\right) }\parallel _{{\text {L}} ^{2}(\mathscr {T} ^{})}, \end{aligned} \end{aligned}$$

(3.32)

and insert (3.32) into (3.31) to obtain the assertion of the theorem. $\square$

The error estimator, derived in Theorem 3.9, is locally efficient in the following sense:

Theorem 3.10

(Local efficiency). Assume f and ${\varvec{{\mathfrak {D}}}}$ are piecewise polynomial on $\mathscr {T} ^{}$. Then, there exists a constant $C>0$ independent of h such that for any $K \in \mathscr {T} ^{}$ and any $e \in \mathscr {E}$ the following estimates hold:

$$\begin{aligned} \eta ^{**}_K \le C \parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}} \nabla \!\left( {u - u^{**}}\right) }\parallel _{{\text {L}} ^{2}(K)} \end{aligned}$$

(3.33)

and

$$\begin{aligned} \eta ^{**}_e \le C\parallel {{\varvec{{\mathfrak {D}}}}^{\tfrac{1}{2}}\nabla \!\left( {u - u^{**}}\right) }\parallel _{{\text {L}} ^{2}(K_e)} \end{aligned}$$

(3.34)

where $K_e$ denotes the union of cells sharing common edge e.

Proof

Both proofs are standard and follow [33]. $\square$

Remark 3.11

(Data oscillation). In case f or ${\varvec{{\mathfrak {D}}}}$ are not polynomial the right hand side of (3.33) contains additional data oscillation terms.

4 Post-processors

In order to show the versatility of our results, we consider two families of reconstruction operators. Namely, the Smoothness-Increasing Accuracy-Conserving (SIAC) post-processing [5, 30, 32] as well as patch reconstruction via the Zienkiewicz and Zhu [37, 39] Superconvergent Patch Recovery (SPR) technique. Below we outline the procedure for performing these reconstructions as well as error estimates for the ideal case.

4.1 SIAC Post-processors

One example of a superconvergent post-processor that we examine is the Smoothness Increasing Accuracy Conserving (SIAC) filter. The SIAC filter has its roots in an accuracy-enhancing post-processor developed by Bramble and Schatz [5]. The original analysis was done for finite element approximations for elliptic equations. This technique has desirable qualities including its locality, allowing for efficient parallel implementations, and its effectiveness in almost doubling the order of accuracy rather than increasing the order of accuracy by one or two orders. This post-processor was also explored from a Fourier perspective and for derivative filtering by Thomeé [32] and Ryan and Cockburn [29].

SIAC filters are an extension of the above ideas and have traditionally been used to reduce the error oscillations and recover smoothness in the solution and its derivatives for visualization purposes [24, 31, 34] or to extract accuracy out of existing code [28]. It has been extended to a variety of PDEs as well as meshes [16]. A quasi-interpolant perspective on SIAC can be found in [26]. The important property of these filters is that, in addition to increasing the smoothness, for smooth initial data and linear problems, the filtered solution is more accurate than the DG solution. To combat the high computational cost of the tensor-product nature of the multi-dimensional kernel, a line filter was introduced in [11].

For ease of presentation the following discussion only details the design of the filter and presents a-priori error estimates for the case of a smooth solution. Although the discussion is limited to one-dimension, it can be extended to Cartesian meshes in more than one space dimension using a tensor product approach. More advanced applications of the multi-dimensional SIAC post-processor are the Hexagonal SIAC [22] or Line SIAC [11].

The basic idea is that the reconstruction is done via convolution post-processing:

$$\begin{aligned} u^{*}({\bar{x}})=K^{2r+1,m+1}_{H} * u_h = \frac{1}{H}\int _{-\infty }^{\infty }\, K\left( \frac{{\bar{x}}-y}{H}\right) u_h(y)\, dy, \end{aligned}$$

where h is the mesh size of the numerical scheme and H is the scaling of the post-processor. The convolution kernel, $K^{2r+1,m+1}(\cdot ),$ is defined as

$$\begin{aligned} K^{2r+1,m+1}(x) = \sum _{\gamma =-r}^{r}c_{\gamma }^{2r+1,m+1}\psi ^{(m+1)}\left( x-\gamma \right) . \end{aligned}$$

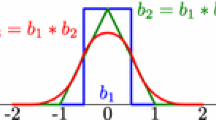
This is a linear combination of $2r+1$ shifted copies of some function, $\psi ^{(m+1)}(x).$ The function weights are real scalars, $c_{\gamma }^{2r+1,m+1} \in {\mathbb {R}}.$ For the kernel, r is chosen to satisfy consistency as well as 2r moment requirements, $\text { i.e., }$ polynomial reproduction conditions, which are necessary for preserving the accuracy of the Galerkin scheme and m is chosen for smoothness requirements. We focus on kernels built from B-splines which are defined via the B-Spline recurrence relation:

$$\begin{aligned} \begin{aligned} \psi ^{(1)}&= \chi _{[-1/2,1/2]} \\ \psi ^{(m+1)}&= \frac{1}{m}\left[ \left( x+\frac{m+1}{2}\right) \psi ^{(m)}\left( x+\frac{1}{2}\right) +\left( \frac{m+1}{2}-x\right) \psi ^{(m)}\left( x-\frac{1}{2}\right) \right] , \end{aligned} \end{aligned}$$

(4.1)

for $m\ge 1$.

Remark 4.1

(Kernel scaling.). For cartesian grids, the kernel scaling is typically chosen to be the element size, $H=h$. In adaptive meshes or structured triangular meshes and tetrahedral meshes, H is typically chosen to be the length of the mesh pattern [21]. For Line SIAC, the kernel scaling is taken to be the element diagonal [11], for unstructured meshes, the kernel scaling is taken to be largest element side [23, 25].

It can be shown that when the solution is sufficiently smooth the post-processed numerical solution $u^{*}$ is a superconvergent approximation.

In particular, if $u\in {\text {C}} ^{\infty }(\Omega )$, then the Galerkin solution converges in Theorem 2.2 as

$$\begin{aligned} \parallel { u - u_h}\parallel _{{\text {L}} ^{2}(\Omega )} = {\text {O}}(h^{p+1}). \end{aligned}$$

(4.2)

If we choose $r=p$ and $m = p-2$ then

$$\begin{aligned} \parallel { u - u^{*}}\parallel _{{\text {L}} ^{2}(\Omega )} = {\text {O}}(h^{2p}), \end{aligned}$$

(4.3)

see Theorem 1 in [5, 32], which for $p \ge 2$ constitutes an improvement. It is possible to obtain the same estimates in ${\text {H}} ^{1}$ by taking higher order B-Splines.

In this paper, in order to apply the post-processor globally, we mirror the underlying approximation as an odd function at the boundary as discussed in [5].

Remark 4.2

(Impact of in-cell regularity of $u^{**}$). If $u^{*},u^{**}\not \in {\text {H}} ^{2}(\mathscr {T} ^{})$ Theorem 3.9 does not hold. Still, as long as $u^{*}\in {\text {H}} ^{1}(\mathscr {T} ^{})$ similar results can be obtained by slightly modifying the proof of Theorem 3.9. One interesting example is SIAC reconstruction with $m=0$. In this case, for any $K \in \mathscr {T} ^{}$ the restriction $u^{**}|_K$ contains several kinks, i.e. there are hypersurfaces (points for $d=1$, lines for $d=2$) across which u is continuous but not differentiable. However, for any K there exists a triangulation $\mathscr {T} ^{}_K$ of K, such that $u^{**}|_K \in {\text {H}} ^{2}(\mathscr {T} ^{}_K)$. If we follow the steps of the proof of Theorem 3.9 we realise that integration by parts can only be carried out on elements of $\cup _{K \in \mathscr {T} ^{}} \mathscr {T} ^{}_K$ and each term $\parallel {h_K ( f + \Delta u^{**})}\parallel _{{\text {L}} ^{2}(K)}^2$ in the error bound needs to be replaced by

$$\begin{aligned} \sum _{T \in \mathscr {T} ^{}_K} \parallel {h_K ( f + \Delta u^{**})}\parallel _{{\text {L}} ^{2}(T)}^2 + \frac{1}{2}\sum _{e \in \mathscr {E} _K}\parallel {h_K^{\frac{1}{2}} [\![ \nabla u^{**}]\!] }\parallel _{{\text {L}} ^{2}(e)}^2, \end{aligned}$$

(4.4)

where $\mathscr {E} _K$ denotes the set of interior edges of $\mathscr {T} ^{}_K$. Efficiency of this modified estimator can be shown along the same lines as in Theorem 3.10 but bubble functions with respect to the elements and edges in the sub-triangulation $\mathscr {T} ^{}_K$ need to be used.

4.2 Superconvergent Patch Recovery

The second post-processing operator we study is based on the superconvergent patch recovery (SPR) technique. This was originally studied numerically and showed a type of superconvergence for elliptic equations using finite element approximations [36]. The mathematical theory behind this recovery technique was addressed by Zhang and Zhu [38] for the two-point boundary value problems and for two-dimensional problems and extended to parabolic problems in [18, 19]. The superconvergent patch recovery method works by recovering the derivative approximation values for one element from patches surrounding the nodes of that element using a least squares fitting of the superconvergent values at the nodes and edges. In typical derivative recovery, the derivative approximation is a continuous piecewise polynomial of some given degree. For overlapping patches, the recovered derivative is just an average of the approximations obtained on the surrounding patches. Unlike SIAC post-processing, this recovery technique does not rely on translation invariance for the high-order recovery. The superconvergent patch recovery technique has been shown to work well for elliptic equations that have a smooth solution, and for less smooth solutions with a suitably refined mesh.

The usual application of this technique is for gradient recovery. However, in this article we apply this technique to recover function values.

As mentioned, we suitably modify the algorithm to construct a function $u^{*}\in \mathbb {V}_h^*$ with $\mathbb {V}_h^*=\mathbb {V}_h^{2p+1}\cap C^0(\Omega )$. The construction of $u^{*}$, given some finite element function $u_h$, is carried out in two steps:

• 1. Construct a polynomial $q_i$ of order 2p at each node $v_i$ of the mesh using a least squares fitting of function values of $u_h$ evaluated at suitable points in elements surrounding $v_i$.

• 2. Given an element K we use linear interpolation of the values of $q_i$ for the three nodes of K to compute $u^{*}\in \mathbb {V}_h^*$.

There are many approaches for constructing the polynomials $q_i$ in the first step at a given node $v_i$ with surrounding triangles $K'$. For our experiments, we use the following approach. For $p=1$, we construct a quadratic polynomial $q_i$ by fitting the values of $u_h$ at the nodes of all $K'$. For a piecewise quadratic $u_h$ ($p=2$) we also use the midpoints of all edges of the $K'$. Finally for our tests with $p=3$ we evaluate $u_h$ at two points on each edge chosen symmetrically around the midpoint of the edge (we use the Lobatto points with local coordinates $\frac{1}{2}\pm \frac{\sqrt{5}}{10}$) and also add the value of $u_h$ at the barycentre of the $K'$. This is depicted in Fig. 1. To guarantee that we have enough function values to compute the least squares fits, we add a second layer of triangles around $v_i$ if necessary, e.g., at boundary nodes.

Note that this procedure is similar, although not the same, as the approach investigated in [35]. Another related procedure was proposed in [27].

Fig. 1

Evaluation points of $u_h$ used for the least squares fit of a polynomial at node $v_i$ for $p=1,2,3$ (from left to right)

5 Numerical Results

In this section we study the numerical behaviour of the error indicators proposed for the SIAC and SPR post-processing operators. We compare this behaviour with the true error on some typical model problems. The computational work was done in the DUNE package [3] based on the new Python frontend for the DUNE-FEM module [8, 9].

5.1 Smoothness-Increasing Accuracy-Conserving Post-processors

The implementation of the post-processor is done through simple matrix-vector multiplication and is discussed in [20].

We first investigate the behaviour of the error and the residual estimator for the problem (2.1) in one space dimension with ${\varvec{{\mathfrak {D}}}}= 1$, i.e. the Laplace problem

$$\begin{aligned} \begin{aligned} - u''&= f \text { in } \Omega \\ u&=0 \text { on } \partial \Omega , \end{aligned} \end{aligned}$$

(5.1)

where the forcing function f is chosen so that the exact solution is

$$\begin{aligned} u(x)={\text {sin}}\left( 6\pi x\right) ^2{\text {cos}}\left( \frac{9}{2}\pi x\right) \end{aligned}$$

(5.2)

on the interval (0, 1). We show both the ${\text {L}} ^{2}$ and ${\text {H}} ^{1}$ errors for the Galerkin approximation $u_h$, the SIAC postprocessed approximation, $u^{*}$ and the orthogonal postprocessor, $u^{**}$. We also show the two residual indicators $R_h$ (from Theorem 2.2) and $R^{**}$ from (Theorem 3.9). For the basis we consider the continuous Lagrange polynomials for $u_h$ and impose the boundary conditions weakly with a penalty parameter $\frac{10p^2}{h}$, where p is the polynomial degree and h is the grid spacing. Additional experiments were conducted using a discontinuous Galerkin approximation, but no significant differences in the outcome where found and therefore do not include the results. We solve the resulting linear system using an exact solver [7] to avoid issues with stopping tolerances.

We will mainly focus on $p=2$ but also show results for $p=1$ and $p=3$. The SIAC postprocessing is constructed using a continuous B-spline, $m=1,$ as well as setting $r=\lceil {\frac{p+1}{2}}\rceil .$ This leads to an inner stencil of $2\lceil {r+\frac{1}{2}-1}\rceil +1 = 2\lceil {\frac{p+1}{2}+3}\rceil$ elements. We also tested other choices of $r,\, m$ for $p=2$ but the above choice provided the best results and these are the results shown.

In Fig. 2 we show the errors for $p=2$ for a series of grid refinement levels starting with 20 intervals and doubling that number on each level. In Fig. 2 we plot the corresponding Experimental Orders of Convergence (EOCs). As can clearly be seen, SIAC postprocessing ($u^{*}$) improves the convergence rate in ${\text {H}} ^{1}$ from 2 to 3 and in ${\text {L}} ^{2}$ from 3 to 4. While in ${\text {H}} ^{1}$ the Galerkin orthogonality trick only leads to a small improvement in the error, in ${\text {L}} ^{2}$ we see an improvement of a full order leading to a convergence rate of 5. As expected from the theory the residual indicators follow the ${\text {H}} ^{1}$ errors of $u_h$ and $u^{**}$ closely. The efficiency index is comparable between $R_h$ and $R^{**}$.

For a better understanding of how the error is reduced by utilizing SIAC postprocessing and the Galerkin orthogonality treatment, we show the pointwise errors of the approximations in Fig. 3. It is evident that the function values are much smoother when applying SIAC. The move from $u^{*}$ and $u^{**}$ does reintroduce small scale errors, but at a far lower level compared to the original approximation, $u_h$. As expected from the errors, the differences in ${\text {H}} ^{1}$ are less pronounced.

Fig. 2

Errors and convergence rates for ${\text {H}} ^{1}$ (left two) and ${\text {L}} ^{2}$ (right two) for polynomial degree $p=2$ using a SIAC reconstruction

Fig. 3

Pointwise errors for the three different solutions on the right half of the interval, evaluating the function in a number of points per interval. These are results with $p=2$ and $h=1/320$ showing the errors in the gradient (left) and in the function values (right)

In Fig. 4 we show errors and EOCs for $p=3$. Due to the very low errors on the final grid the actual convergence rates for $u^{*}$ and $u^{**}$ is not clear. However, the improvement due to the Galerkin orthogonality trick, especially in ${\text {L}} ^{2}$ is quite noticable as it reduced the error by two orders of magnitude.

Fig. 4

Errors and convergence rates for ${\text {H}} ^{1}$ (left two) and ${\text {L}} ^{2}$ (right two) for polynomial degree $p=3$ using SIAC reconstruction

Fig. 5

Errors and convergence rates for ${\text {H}} ^{1}$ (left two) and ${\text {L}} ^{2}$ (right two) for polynomial degree $p=1$ using SIAC reconstruction

Fig. 6

Errors and convergence rates for ${\text {H}} ^{1}$ (left two) and ${\text {L}} ^{2}$ (right two) for polynomial degree $p=2$ with hyperpenalty at the boundary

We next show results for $p=1$ in Fig. 5. Again, there is a clear reduction in the values of the errors from $u_h$ to $u^{*}$ to $u^{**}$ in ${\text {H}} ^{1}$ together with an improvement in the convergence rate due to the SIAC postprocessing. This improvement in the convergence rate is about 1 order. While the convergence rate going from $u_h$ to $u^{**}$ seems to only be half an order on the higher grid resolution, it is important to note that the error using $u^{**}$ is still significantly smaller than the error between the exact solution and $u^{*}$ by at least a factor of 2. Hence the results do not contradict the theory. In ${\text {L}} ^{2}$, SIAC leads to no improvement while the convergence rate of the error using $u^{**}$ is at least half an order higher. Overall the improvement in the convergence rate is not quite as good as for the higher polynomial degrees. The following tests summarized in Fig. 6 show that the weak form of the boundary conditions is responsible for the reduced order improvement. The figure shows results using a hyperpenalty of the form $\frac{10p^2}{h^2}$. Applying this hyperpenalty term leads to improvements that are again more in line with our observations for higher order polynomials. We note that strong enforcement of the boundary conditions also lead to similar results.

We summarize our results for the smooth problem in Table 1. It can be clearly seen that the step from $u^{*}$ to $u^{**}$, which requires solving one additional low order problem, is quite advantageous and increases the convergence rate in the ${\text {L}} ^{2}$ norm by at least one. In the linear case this improves by two and by one in the ${\text {H}} ^{1}$ norm. This makes it highly efficient in this case, at least when implementing the hyperpenalization or strong constraints to enforce the Dirichlet boundary conditions. The reason for this restriction will be investigated further in future work. For $p=3$ the actual EOCs of the postprocessed solutions are difficult to determine and therefore we provide approximate numbers. In this case, SIAC shows a higher order in ${\text {L}} ^{2}$ compared to the ${\text {H}} ^{1}$ norm. The Galerkin orthogonalty trick does not improve the rate further, but note that the overall error is still a factor of 100 smaller. Additionally note that in the other cases where there is no improvement in the rate, the error is reduced by enforcing Galerkin orthogonality, e.g., in the ${\text {H}} ^{1}$ norm with $p=2$ the error is still reduced by about a factor of two. In addition, the orthogonality of $u^{**}$ allows us to compute a reliable and efficient error estimator with a comparable efficiency index to the error estimator for $u_h$ using $R_h$.

Table 1 Experimental rates of convergence for the smooth problem using different values for the polynomial degree p. The convergence rates are shown for the three approximations, i.e., $u_h,u^{*},u^{**}$

We conclude our investigations of the SIAC reconstruction and the residual estimates by studying problems with less smooth solutions. We change the forcing function so that the exact solution is of the form

$$\begin{aligned} u(x)&= {\left\{ \begin{array}{ll} w\left( \frac{x-0.3}{0.4}\right) &{} x\in (0.3,0.7)~, \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} w(s)={\text {sin}}\left( 6\pi s\right) ^2{\text {cos}}\left( \frac{9}{2}\pi s\right) \end{aligned}$$

(5.3)

is the smooth function from previous studies. We show results for polynomial degree $p=2$. We again implement a simple $O(h^{-1})$ penalty term at the boundary. Note that the solution is in ${\text {C}} ^{2}{\setminus } {\text {C}} ^{3}$ at $x=0.7$ and only in ${\text {C}} ^{1}{\setminus } {\text {C}} ^{2}$ for $x=0.3$. Overall the solution is an element of ${\text {H}} ^{2}(0,1)$ but not of ${\text {H}} ^{3}(0,1)$, i.e., it is not smooth enough to achieve optimal convergence rates for $p=2$ when the mesh is not aligned. Even when the mesh is aligned, as in our experiments, we do not expect an increase of the convergence rate using the SIAC reconstruction as can be seen in Fig. 7. The local loss of regularity at $x=0.3$ and $x=0.7$ is clearly visible for the pointwise errors of the two reconstructions as shown in Fig. 8. Examining the errors in the original approximation, $u_h$, the reduced smoothness is hardly visible. However, in both of the reconstructions a jump in the error is clearly visible. At $x=0.7$, where the solution is still in ${\text {C}} ^{2}$ the error in $u^{**}$ increases approximately by two orders while at $x=0.3$ it is close to four orders of magnitude larger since the solution is only ${\text {C}} ^{1}$ at this point. The lack of smoothness is also identified by the residual indicator $R^{**}$, the spatial distribution of which is shown in Fig. 9 together with the distribution of $R_h$. It is worthwhile to note that the region of the ’reduced smoothness’ is better isolated by $R^{**}$ than by $R_h$. Hence it would be easier for an adaptive algorithm to separate these different smoothness regions which would lead to more optimal meshes. The picture clearly shows that $R_h$ does not ’see’ the kink so that an adaptive algorithm would either refine the whole non-constant region or nothing at all depending on the tolerance. In contrast, with $R^{**}$ (and the right algorithm) refinement could be isolated to the kinks.

Fig. 7

Errors and convergence rates for ${\text {H}} ^{1}$ (left two) and ${\text {L}} ^{2}$ (right two) for polynomial degree $p=2$ using SIAC for solution with reduced smoothness

Fig. 8

Pointwise errors of the three different approximations for the piecewise smooth problem. Top row shows the difference in the solution values around $x=0.3$ (left) and around $x=0.7$ (right). The bottom row shows gradient errors in the same two regions. These are results with $p=2$ and $h=1/320$

Fig. 9

Elementwise residual indicators using $u_h$ and $u^{**}$ for the piecewise smooth problem around $x=0.3$ (left) and around $x=0.7$ (right). bottom row shows gradient errors in the same two regions. These are results with $p=2$ and $h=1/320$

5.2 Superconvergent Patch Recovery

In the following we solve

$$\begin{aligned} -{\text {div}}\!\left( {{\varvec{{\mathfrak {D}}}}\nabla u}\right) = f \end{aligned}$$

(5.4)

in a two dimensional domain $\Omega$ where the forcing function f is chosen by prescribing an exact solution u. This function is also used to prescribe Dirichlet boundary conditions on all of $\partial \Omega$. In the first example we chose a smooth exact solution u with a scalar diffusion coefficient ${\varvec{{\mathfrak {D}}}}=I_2\!\left( {|x|^2+\frac{1}{2}}\right)$, while for the second test we use a solution with a corner singularity and ${\varvec{{\mathfrak {D}}}}= I_2$.

In the following we show results using a DG scheme on a triangular grid. The grid is refined by splitting each element into four elements. In the final examples with local adaptivity, this leads to a grid with hanging nodes. We also carried out experiments using a continuous ansatz space with very simular results.

Note that in all figures depicting errors and EOCs, the x-axis shows the number of degrees of freedom for $u_h$. While the other approximations have a larger number of degrees of freedom, the global problem that has to be solved, i.e. solving the linear system for $u_h$ and for $Ru^{*}$, scales with the number of degrees of freedom for $u_h$ and thus this seems a reasonable indication of the computational complexity.

For our first test we choose $u(x,y) = {\text {sin}}\left( \pi x/(0.25+xy)\right) {\text {sin}}\left( \pi (x+y)\right)$, and $\Omega =(0,1)^2$. We start with an initial grid which is slightly irregular as shown in Fig. 10. This is to avoid any superconvergence effects due to a structured layout of the triangles.

Fig. 10

Macro grid and exact solution u for smooth problem. Note that the solution has been scaled down by a factor of 4

Fig. 11

$L^2$ errors and EOC (top two rows) and $H^1$ errors and EOC (bottom two rows) for the smooth problem with $p=1,2,3$ (left to right)

Figure 11 shows ${\text {L}} ^{2}$ and ${\text {H}} ^{1}$ errors and EOCs for the three approximations $u_h,u^{*},u^{**}$ with polynomial degrees $p=1,2,3$. It can be seen that, in general, the postprocessor $u^{*}$ improves the EOC by an order of 1 in the ${\text {H}} ^{1}$ norm and that the EOC of the improved postprocessor $u^{**}$ is at least as good. While the actual error of $u^{*}$ can be larger on coarser grids than the error computed with $u_h$, the error using $u^{**}$ is significantly better in all cases. Focusing now on the ${\text {L}} ^{2}$ norm, we see that when computing the error using $u^{**}$, the EOC is one order better then the convergence rate in the ${\text {H}} ^{1}$ norm, as expected. For $p=2,3$, this is also true when using $u^{*}$, while for $p=1$ the EOC is only 2 in this case, and an increase to 3 is only achieved with the improved postprocessor $u^{**}$. The same observation can be made when using the SIAC postprocessor in the previous section.

Using the same problem setting, we investigate the performance of an adaptive algorithm in Fig. 12. We use a modified equal distribution strategy where elements are marked for refinement when the local indicator $\eta _K$ exceeds $\frac{\sum \eta _K}{{{\#elements}}}$. We compute the local indicator on either $u_h$ or on the improved reconstruction $u^{**}$. The advantage of basing the marking strategy on $u^{**}$ is clearly demonstrated. While marking with respect to $u_h$ and then using the postprocessor only on the final solution (filled upward triangles) leads to a significant reduction of the final error, the difference in the convergence rate between $R_h$ and $R^{**}$ results in a finer grid than necessary for a given tolerance. A reduction in the number of degrees of freedom by a factor of 10 to 100 can be easily achieved by using $R^{**}$.

Fig. 12

$H^1$ errors and residuals for smooth problem with $p=1,2,3$ (left to right). Results are shown for an adaptive mesh using a tolerance of 0.2, 0.01, 0.001 for $p=1,2,3$, respectively

Fig. 13

Errors (right) and EOCs (left) for a simple corner problem. From top to bottom: ${\text {L}} ^{2}$ with $p=1,2$ and ${\text {H}} ^{1}$ with $p=1,2$

Fig. 14

${\text {H}} ^{1}$ errors and residuals for simple corner problem with $p=1$ (left) and $p=2$ (right). Results are shown for an adaptive mesh using a tolerance of 0.01

For our final test we study a reentrant corner type problem, i.e., $\Omega =(-1,1)^2{\setminus }([0,1]\times [-1,0])$ using a regular triangulation. First we choose the well known exact solution $u\in {\text {H}} ^{\frac{3}{2}}$ leading to $f=0$. Since the solution is not even ${\text {H}} ^{2}$ we can not expect the postprocessed solution to have an increased convergence rate. This is confirmed by our numerical tests summarized in Fig. 13. Due to the reduced smoothness and the simplicity of the solution away from the corner, the postprocessing does not only not improve the EOC but can even lead to a slight increase in the overall error clearly noticeable in the ${\text {H}} ^{1}$ error for the $p=2$ case. This is even more obvious when the postprocessor, $u^{*}$, is used directly. Alternatively, going from $u^{*}$ to $u^{**}$ leads to an approximation which is very close to the original $u_h$ in all cases. Although the results for the globally refined grid are not that promising, the postprocessing nevertheless has considerable benefits when adapting the grid using the residual indicator based on $u^{**}$. Indeed Fig. 14 shows that, for a given number of dofs, mesh adaptation based on $R^{**}$ produces an approximation $u^{**}$ which has a much smaller error than $u_h$ (on a mesh constructed using $R_h$).

For a more challenging test, especially for $p=3$, we construct the forcing function so that the exact solution is $u(x,y)=\omega (x,y)u_{\mathrm{corner}}(x,y)$, where $u_{\mathrm{corner}}$ is the solution to the above corner problem and $\omega (x,y)=-{\text {sin}}\left( \frac{3}{2}\pi (1-x^2)(1-y^2)\right)$. The function u still has the same corner singularity but is also smooth. However, the challenging nature of this solution is that it has large gradients towards the outer boundaries. Results for $p=2,3$ are summarized in Figs. 15 and 17 . The final grids for $p=3$ are shown in Fig. 16 using $R_h$ and $R^{**}$ to mark cells for refinement. In both cases 22 steps were needed and the resulting grids have 1597 and 4540 cells (20725 and 7381 degrees of freedom), respectively. While the corner is highly refined in both cases, the regions that are smooth but strongly varying in their solution are far less refined when using $R^{**}$. When using $R_h$ the final errors are $\Vert u-u_h\Vert _{dG}\approx 7.4\cdot 10^{-4}$ and $\Vert u-u^{**}\Vert _{dG}\approx 6.8\cdot 10^{-4}$ while adaptivity based on $R^{**}$ results in errors of the size $\Vert u-u_h\Vert _{dG}\approx 3.9\cdot 10^{-3}$ and $\Vert u-u^{**}\Vert _{dG}\approx 7.0\cdot 10^{-4}$. Because of the corner singularity, using the postprocessor after finishing the refinement (based on $R_h$) does not lead to a significant improvement while basing the adaptive process on $R^{**}$ leads to an almost identical error while requiring only $35\%$ of the cells.

Fig. 15

Errors (right) and EOCs (left) for the extended corner problem. From top to bottom: ${\text {L}} ^{2}$ with $p=2,3$ and ${\text {H}} ^{1}$ with $p=2,3$

Fig. 16

${\text {H}} ^{1}$ errors and residuals for extended corner problem with $p=2$ (left) and $p=3$ (right). Results are shown for an adaptive mesh using a tolerance of 0.01

Fig. 17

Discrete solution and adapted grid for extended corner problem with $p=2$ using $R_h$ (left) and $R^{**}$ (right) for marking. The iterate is chosen so that the resulting errors satisfty $e_h\approx e^{**}\approx 0.013$

Figure 18 shows the efficiency index for all three test cases on globally refined grids. The results seem to indicate that there is only a slight increase in the efficiency index $\frac{R^{**}}{\Vert \nabla (u^{**}-u)\Vert }$ compared to $\frac{R_h}{\Vert \nabla (u_h-u)\Vert }$.

Fig. 18

Efficiency index on globally refined grids for smooth problem with $p=1,2,3$ (left), simple corner problem with $p=1,2$ (middle), and extended corner problem with $p=2,3$ (right)

6 Summary Discussion

In this article, we provide a strategy for improving existing post-processing strategies for numerical solutions of a model elliptic problem. The main idea is to modify the post-processed solution so that it satisfies Galerkin orthogonality. We prove various a priori type results showing desirable convergence properties of the orthogonal post-processor including an increased order of accuracy in the ${\text {L}} ^{2}$ norm. We supported the analysis with numerical examples using two types of post-processors – that of SIAC and SPR – approximating smooth and non-smooth solutions.

In addition to the a priori results, we provide a reliable and efficient a posteriori error estimator for the orthogonal post-processed solution, it should be noted that no such estimator is available for $u - u^*$. We demonstrate in several examples that much more efficient meshes are obtained when adaptation is based on $R^{**}$ than when refinement is based on $R_h$ and the post-processor is only applied to the numerical solution on the final mesh.