1 Introduction

The most common domain decomposition procedures involve formulating a general class of partial differential equations on a single domain, followed by an equivalent multidomain formulation. The multidomain formulation is used to construct an iterative scheme which can be employed using different discretization methods. Notable contributors using this technique include [14] and [11]. Various approaches exist depending on if the subdomains overlap [3] or not [6], but as a rule, the methods are iterative. There are exceptions, such as the finite difference based domain decomposition algorithm in [2], and the explicit-implicit domain decomposition methods in [15].

Our approach is similar to the one used in [2] in the following ways: It is non-iterative and uses non-overlapping subdomains. Subdomain intercommunication is limited to the problem of computing interface components, whence interior and boundary points may be computed in parallel. Key differences arise in the treatment of boundary and initial conditions, which in our schemes is done weakly through penalty terms. Also, our time integration is fully implicit, whereas [2] uses explicit time-stepping for the interface components.

Since our schemes are formulated in terms of general discrete differential operators known as Summation-by-Parts (SBP) operators, we gain most of the convenience commonly associated with them. For example, it is trivial to adjust the order of the derivative approximations in our schemes by simply switching the operators. Furthermore, the theoretical properties of SBP operators—augmented with Simultaneous Approximation Terms (SATs) for weakly enforcing boundary conditions—provide a general and straightforward way to prove stability for a multitude of discretized problems by mimicking continuous energy estimates [1, 9].

Traditionally, the SBP-SAT technique has been used in space to formulate high-order semi-discrete schemes. Such schemes typically generate a linear system of ordinary differential equations, which is integrated in time using explicit methods. The groundwork for employing SBP-SAT also as a method of time integration was laid in [10]. However, naive usage of SBP in time produces schemes that, while provably stable and high order accurate, lead to large systems which are difficult to solve efficiently in multiple dimensions. For a comprehensive review of the SBP-SAT technique, see [13].

This article is an initial attempt at combining SBP in time and domain decomposition in order to address this efficiency problem. We consider provably stable SBP based domain decomposition methods for a two-dimensional advection–diffusion problem, where local solutions are coupled at the subdomain interfaces using SATs. The coupling procedure follows the ideas in [1], with adjustments to account for the use of SBP in time [7, 10]. Our scheme involves isolating a linear system consisting only of interface components by solving independent, subdomain sized systems. This allows us to solve for the interface components separately, which are used to build the full solution.

The scheme is proved stable using established SBP-SAT procedures. By using the spectral properties of the temporal and spatial operators we are also able prove that our scheme is invertible, ensuring unique and convergent solutions.

In Sect. 2 we outline the continuous problem to be solved. Section 3 introduces SBP operators in multiple dimensions. These are used in Sects. 4 and 5 to formulate stable discretizations of the continuous problem. A system reduction algorithm based on the construction of an interface system is described in Sect. 6. The procedure is further justified by proofs of invertibility in Sect. 7. Section 8 contains an outline of the method for an arbitrary number of subdomains, together with an example illustrating how the system sizes shrink compared to a single domain scheme. A convergence and efficiency study based on a Matlab implementation of the scheme is presented in Sect. 9. Section 10 contains a brief summary of our work and future research directions.

2 The Advection–Diffusion Problem

Let \(a = (a_1, a_2) \in \mathbb {R}^2\), \(\epsilon > 0\), \(T > 0\) and consider the following advection–diffusion problem on a rectangular domain \(\varOmega \):

$$\begin{aligned} \begin{aligned} u_t + a \cdot \nabla u&= \epsilon \varDelta u, \text { for } (x,y) \in \varOmega , \, 0< t < T \\ { \left. u \phantom {\big |} \right| _{t=0} }&= f, \text { on } \varOmega \\ -\,a \cdot n u + \epsilon \nabla u \cdot n&= g, \text { on } \varGamma _\text {in} \\ \epsilon \nabla u \cdot n&= h, \text { on } \varGamma _\text {out} \, . \end{aligned} \end{aligned}$$
(1)

Here n is the outward pointing unit normal of \(\partial \varOmega \); \(\varGamma _\text {in} = \partial \varOmega \cap \{ n \cdot a < 0 \}\) is the inflow part of the boundary, and \(\varGamma _\text {out} = \partial \varOmega \cap \{ n \cdot a \ge 0 \}\) is the outflow part of the boundary (see Fig. 1).

Fig. 1
figure 1

The domain \(\varOmega \) with highlighted inflow and outflow boundaries

Full size image

It can be shown that this problem is well-posed. Furthermore, the single domain problem (1) is equivalent to the following multidomain (see Fig. 2) formulation

$$\begin{aligned} \begin{aligned} u_t + a \cdot \nabla u&= \epsilon \varDelta u, \text { for } (x,y) \in \varOmega _L, \, 0< t< T \, ,\\ { \left. u \phantom {\big |} \right| _{t=0} }&= f, \text { on } \varOmega _L \, ,\\ -\,a \cdot n u + \epsilon \nabla u \cdot n&= g, \text { on } \varGamma _\text {in} \cap \partial \varOmega _L \, ,\\ \epsilon \nabla u \cdot n&= h, \text { on } \varGamma _\text {out} \cap \partial \varOmega _L \, ,\\ \\ v_t + a \cdot \nabla v&= \epsilon \varDelta v, \text { for } (x,y) \in \varOmega _R, \, 0< t < T \, ,\\ { \left. v \phantom {\big |} \right| _{t=0} }&= f, \text { on } \varOmega _R \, ,\\ -\,a \cdot n v + \epsilon \nabla v \cdot n&= g, \text { on } \varGamma _\text {in} \cap \partial \varOmega _R \, ,\\ \epsilon \nabla v \cdot n&= h, \text { on } \varGamma _\text {out} \cap \partial \varOmega _R \, ,\\ \\ u&= v, \text { on } \varGamma ^I \, ,\\ u_x&= v_x, \text { on } \varGamma ^I \, . \end{aligned} \end{aligned}$$
(2)
Fig. 2
figure 2

The decomposed domain \(\varOmega = \varOmega _L \cup \varOmega _R\) with highlighted inflow and outflow boundaries

Full size image

In the coming sections we will propose a stable and parallelizable discretization of problem (2) based on the SBP-SAT technique.

3 Summation-by-Parts Operators

We begin with a brief introduction to multidimensional Summation-by-Parts (SBP) operators on rectangular grids. Consider first a smooth, real-valued function u on the unit interval. Given an equidistant discretization \(x_k = \frac{k}{N_x}\) of the unit interval, an SBP operator is a matrix \(D_x\) such that if we form the vectors \(\mathbf {u}\) and \(\mathbf {u}_x\) by evaluating u and \(u_x\) at the grid points, then \(D_x \mathbf {u}\approx \mathbf {u}_x\). Furthermore, there is a diagonal, positive definite matrix \(P_x\) such that if u, v are smooth functions, then

$$\begin{aligned} \langle \mathbf {u}, \mathbf {v}\rangle _{P_x} := \mathbf {u}^\top P_x \mathbf {v}\approx \int _0^1 u v dx \end{aligned}$$

and

$$\begin{aligned} \langle \mathbf {u}, D_x \mathbf {v}\rangle _{P_x} = u_{N_x} v_{N_x} - u_0 v_0 - \langle D_x \mathbf {u}, \mathbf {v}\rangle _{P_x} \, . \end{aligned}$$
(3)

Equation (3) is a discrete analogue of the integration by parts formula

$$\begin{aligned} \int _0^1 u v_x dx = u(1)v(1) - u(0)v(0) - \int _0^1 u_x v dx \, . \end{aligned}$$

SBP operators are classified by their order of accuracy. An SBP operator \(D_x\) is called an SBP(p, r) operator if its order of accuracy is p in the interior and r at the boundary. For details, see [13].

Next we consider smooth, time-dependent functions of two spatial variables. Let \(\varOmega = [0,1] \times [0,1]\) and \(u : [0, T] \times \varOmega \rightarrow \mathbb {R}\) be such a function. The temporal and spatial intervals are discretized using equidistant grids \(t_i = iT/N_t\), \(x_j = j/N_x\), \(y_k = k/N_y\), and we define the three-dimensional field \(\mathbf {U}= (u_{ijk})\), where \(u_{ijk} = u(t_i, x_j, y_k)\). Furthermore, let \(D_t\), \(D_x\) and \(D_y\) be SBP operators in each dimension. To be able to operate on dimensions separately using matrix-vector multiplications, we form the vector

$$\begin{aligned} \mathbf {u}= (u_0, u_1, \dots , u_{N_t})^\top \end{aligned}$$

where

$$\begin{aligned} u_i = (u_{i0}, u_{i1}, \dots , u_{iN_x}), \quad u_{ij} = (u_{ij0}, u_{ij1}, \dots , u_{ijN_y}) \, . \end{aligned}$$

Furthermore we define the discrete partial differential operators

$$\begin{aligned} \mathbf {D}_t = D_t \otimes I_x \otimes I_y, \quad \mathbf {D}_x = I_t \otimes D_x \otimes I_y, \quad \mathbf {D}_y = I_t \otimes I_x \otimes D_y \, . \end{aligned}$$

Here \(I_t\), \(I_x\), and \(I_y\) are identity matrices of sizes corresponding to the discretization. With this structure it follows that

$$\begin{aligned} \mathbf {D}_t \mathbf {u}\approx \mathbf {u}_t, \quad \mathbf {D}_x \mathbf {u}\approx \mathbf {u}_x, \quad \mathbf {D}_y \mathbf {u}\approx \mathbf {u}_y \, . \end{aligned}$$

The quadrature matrices \(P_t\), \(P_x\), and \(P_y\) can be combined to form various integral approximations. Three types of integration are of particular importance: Integration over the entire domain \([0,T] \times \varOmega \); integration over the spatial domain at particular times; and integration at the spatial boundaries during all times.

The quadrature matrix for integration over the entire domain is defined as \(\mathbf {P}= P_t \otimes P_x \otimes P_y\) and

$$\begin{aligned} \langle \mathbf {u}, \mathbf {v}\rangle _\mathbf {P}:= \mathbf {u}^\top \mathbf {P}\mathbf {v}\approx \iiint \limits _{[0,T] \times \varOmega } uv dxdydt \, . \end{aligned}$$

To integrate over the spatial domain at a particular time \(t_i\) we let \(E_t^i = e_i e_i^\top \), where \(e_i\) is the standard basis vector in \(\mathbb {R}^{N_t+1}\) (this matrix has a 1 at position (i, i) and zeros everywhere else). The quadrature matrix for integration over the spatial domain at time \(t_i\) is defined as \(\mathbf {P}_\varOmega ^i = E_t^i \otimes P_x \otimes P_y\), and we have

$$\begin{aligned} \langle \mathbf {u}, \mathbf {v}\rangle _{\mathbf {P}_\varOmega ^i} := \mathbf {u}^\top \mathbf {P}_\varOmega ^i \mathbf {v}\approx \iint _{\varOmega } { \left. uv \phantom {\big |} \right| _{t=t_i} } dxdy \, . \end{aligned}$$

We define quadrature matrices for the spatial boundaries in a similar manner. Let \(E_x^j = e_j e_j^\top \), \(E_y^k = e_k e_k^\top \), and

$$\begin{aligned} \mathbf {P}_w&= P_t \otimes E_x^0 \otimes P_y, \quad \mathbf {P}_e = P_t \otimes E_x^{N_x} \otimes P_y \\ \mathbf {P}_s&= P_t \otimes P_x \otimes E_y^0, \quad \mathbf {P}_n = P_t \otimes P_x \otimes E_y^{N_y} \, . \end{aligned}$$

Then

$$\begin{aligned} \langle \mathbf {u}, \mathbf {v}\rangle _{\mathbf {P}_w} := \mathbf {u}^\top \mathbf {P}_w \mathbf {v}\approx \int _0^T \int _0^1 { \left. uv \phantom {\big |} \right| _{x = 0} } dx dt \, . \end{aligned}$$

The remaining boundary quadratures are defined analogously, with the subscripts w, e, s, n denoting the west, east, south and north boundary respectively (see Fig. 3).

Fig. 3
figure 3

Left: An equidistant discretization of the unit square with labelled boundaries. Right: An example grid function \(\mathbf {u}\). The time integral of the red area is approximated by the numerical boundary integral \(\mathbf {1}^\top \mathbf {P}_w \mathbf {u}\)

Full size image

The SBP property is inherited from the one-dimensional operators in the sense that

$$\begin{aligned} \begin{aligned} \langle \mathbf {u}, \mathbf {D}_t \mathbf {v}\rangle _\mathbf {P}&= \langle \mathbf {u}, \mathbf {v}\rangle _{\mathbf {P}_\varOmega ^{N_t}} - \langle \mathbf {u}, \mathbf {v}\rangle _{\mathbf {P}_\varOmega ^0} - \langle \mathbf {D}_t \mathbf {u}, \mathbf {v}\rangle _\mathbf {P}\\ \langle \mathbf {u}, \mathbf {D}_x \mathbf {v}\rangle _\mathbf {P}&= \langle \mathbf {u}, \mathbf {v}\rangle _{\mathbf {P}_e} - \langle \mathbf {u}, \mathbf {v}\rangle _{\mathbf {P}_w} - \langle \mathbf {D}_x \mathbf {u}, \mathbf {v}\rangle _\mathbf {P}\\ \langle \mathbf {u}, \mathbf {D}_y \mathbf {v}\rangle _\mathbf {P}&= \langle \mathbf {u}, \mathbf {v}\rangle _{\mathbf {P}_n} - \langle \mathbf {u}, \mathbf {v}\rangle _{\mathbf {P}_s} - \langle \mathbf {D}_y \mathbf {u}, \mathbf {v}\rangle _\mathbf {P}\, , \end{aligned} \end{aligned}$$
(4)

where the corresponding identities in the continuous setting are

$$\begin{aligned} \begin{aligned} \iiint \limits _{[0,T] \times \varOmega } uv_t dxdydt&= \iint \limits _\varOmega { \left. uv \phantom {\big |} \right| _{t = T} } dxdy - \iint \limits _\varOmega { \left. uv \phantom {\big |} \right| _{t = 0} } dxdy - \iiint \limits _{[0,T] \times \varOmega } u_t v dxdydt \\ \iiint \limits _{[0,T] \times \varOmega } uv_x dxdydt&= \int \limits _0^T \int \limits _0^1 { \left. uv \phantom {\big |} \right| _{x = 1} } dydt - \int \limits _0^T \int \limits _0^1 { \left. uv \phantom {\big |} \right| _{x = 0} } dydt - \iiint \limits _{[0,T] \times \varOmega } u_x v dxdydt \\ \iiint \limits _{[0,T] \times \varOmega } uv_y dxdydt&= \int \limits _0^T \int \limits _0^1 { \left. uv \phantom {\big |} \right| _{y = 1} } dxdt - \int \limits _0^T \int \limits _0^1 { \left. uv \phantom {\big |} \right| _{y = 0} } dxdt - \iiint \limits _{[0,T] \times \varOmega } u_y v dxdydt \, , \end{aligned} \end{aligned}$$

respectively.

4 Single Domain Discretization

It is natural to first discuss a single domain scheme, since the handling of the boundary and initial conditions will carry over to the two-domain case. We restrict problem (1) to the unit square \(\varOmega = [0,1]^2\) and discretize it. A bound on the energy of the solution to problem (1) with homogenous boundary data can be found by using the energy method: We multiply the differential equation by 2u and integrate over the spatial domain. Integration by parts then yields

$$\begin{aligned} \frac{\partial }{\partial }{t}\Vert u\Vert _{L^2(\varOmega )}^2 = -\oint _{\partial \varOmega } (u^2 a - 2 \epsilon u \nabla u) \cdot n ds - 2 \epsilon \iint _\varOmega |\nabla u|^2 dxdy \, . \end{aligned}$$

The energy rate above is controlled by the boundary conditions. Indeed, by inserting the homogeneous boundary conditions we get

$$\begin{aligned} \frac{\partial }{\partial }{t}\Vert u\Vert _{L^2(\varOmega )}^2 = \oint \limits _{\{ a \cdot n < 0 \}} a \cdot n u^2 ds -\oint \limits _{\{ a \cdot n \ge 0 \}} a \cdot n u^2 ds - 2 \epsilon \iint _\varOmega |\nabla u|^2 dxdy \le 0 \, . \end{aligned}$$

Integrating in time results in a bound in terms of initial data,

$$\begin{aligned} \Vert { \left. u \phantom {\big |} \right| _{t = T} }\Vert _{L^2(\varOmega )}^2 + 2 \epsilon \int _0^T \Vert \nabla u\Vert ^2 dxdy \le \Vert f\Vert _{L^2(\varOmega )}^2 \, . \end{aligned}$$
(5)

The bound (5) implies that

Proposition 1

Problem (1) is well-posed.

Our goal is now to construct a discrete scheme which controls indefinite terms in a similar manner. Consider first the linear system

$$\begin{aligned} \mathbf {D}_t \mathbf {u}+ a_1 \mathbf {D}_x \mathbf {u}+ a_2 \mathbf {D}_y \mathbf {u}- \epsilon (\mathbf {D}_x^2 \mathbf {u}+ \mathbf {D}_y^2 \mathbf {u}) = 0 \, . \end{aligned}$$
(6)

If u solves problem (1), then (6) holds approximately. What we want, however, is the converse—a system with a unique solution \(\mathbf {u}\) which approximates the solution to (1). In order to achieve this we introduce penalty terms to the right-hand side which impose the boundary and initial conditions weakly. The necessary form of these penalty terms can be derived by studying the terms that arise from applying the discrete energy method to the left-hand side in (6). That is, we perform the discrete analogue of multiplying the differential equation by 2u and integrating in space and time—we multiply (6) by \(2\mathbf {u}^\top \mathbf {P}\):

$$\begin{aligned} 2\langle \mathbf {u}, \mathbf {D}_t \mathbf {u}\rangle _\mathbf {P}+ 2a_1 \langle \mathbf {u}, \mathbf {D}_x \mathbf {u}\rangle _\mathbf {P}+ 2a_2 \langle \mathbf {u}, \mathbf {D}_y \mathbf {u}\rangle _\mathbf {P}- 2\epsilon (\langle \mathbf {u}, \mathbf {D}_x^2 \mathbf {u}\rangle _\mathbf {P}+ \langle \mathbf {u}, \mathbf {D}_y^2 \mathbf {u}\rangle _\mathbf {P}) = 0 \, . \end{aligned}$$

Each term can be rewritten using the summation by parts properties (4):

$$\begin{aligned} 2\langle \mathbf {u}, \mathbf {D}_t \mathbf {u}\rangle _\mathbf {P}&= \Vert \mathbf {u}\Vert _{\mathbf {P}_\varOmega ^{N_t}}^2 - \Vert \mathbf {u}\Vert _{\mathbf {P}_\varOmega ^0}^2 \end{aligned}$$
(7)
$$\begin{aligned} 2 a_1 \langle \mathbf {u}, \mathbf {D}_x \mathbf {u}\rangle _\mathbf {P}&= a_1 \Vert \mathbf {u}\Vert _{\mathbf {P}_e}^2 - a_1 \Vert \mathbf {u}\Vert _{\mathbf {P}_w}^2 \end{aligned}$$
(8)
$$\begin{aligned} 2 a_2 \langle \mathbf {u}, \mathbf {D}_y \mathbf {u}\rangle _\mathbf {P}&= a_2 \Vert \mathbf {u}\Vert _{\mathbf {P}_n}^2 - a_2 \Vert \mathbf {u}\Vert _{\mathbf {P}_s}^2 \end{aligned}$$
(9)
$$\begin{aligned} 2 \epsilon \langle \mathbf {u}, \mathbf {D}_x^2 \mathbf {u}\rangle _\mathbf {P}&= 2 \epsilon \langle \mathbf {u}, \mathbf {D}_x \mathbf {u}\rangle _{\mathbf {P}_e} - 2 \epsilon \langle \mathbf {u}, \mathbf {D}_x \mathbf {u}\rangle _{\mathbf {P}_w} - 2 \epsilon \Vert \mathbf {D}_x \mathbf {u}\Vert _\mathbf {P}^2 \end{aligned}$$
(10)
$$\begin{aligned} 2 \epsilon \langle \mathbf {u}, \mathbf {D}_y^2 \mathbf {u}\rangle _\mathbf {P}&= 2 \epsilon \langle \mathbf {u}, \mathbf {D}_y \mathbf {u}\rangle _{\mathbf {P}_n} - 2 \epsilon \langle \mathbf {u}, \mathbf {D}_y \mathbf {u}\rangle _{\mathbf {P}_s} - 2 \epsilon \Vert \mathbf {D}_y \mathbf {u}\Vert _\mathbf {P}^2 \, . \end{aligned}$$
(11)

The terms in the equations above end up being dissipative depending on the signs of \(a_1\) and \(a_2\). Assume for simplicity that \(a_1, a_2 > 0\). By combining (8)–(11), each of the four boundaries will have an associated indefinite boundary term that we must control with corresponding penalty terms. The indefinite terms are

  • West: \(a_1 \Vert \mathbf {u}\Vert _{\mathbf {P}_w}^2 - 2 \epsilon \langle \mathbf {u}, \mathbf {D}_x \mathbf {u}\rangle _{\mathbf {P}_w}\) .

  • East: \(2 \epsilon \langle \mathbf {u}, \mathbf {D}_x \mathbf {u}\rangle _{\mathbf {P}_e}\) .

  • South: \(a_2 \Vert \mathbf {u}\Vert _{\mathbf {P}_s}^2 - 2 \epsilon \langle \mathbf {u}, \mathbf {D}_y \mathbf {u}\rangle _{\mathbf {P}_s}\) .

  • North: \(2 \epsilon \langle \mathbf {u}, \mathbf {D}_y \mathbf {u}\rangle _{\mathbf {P}_n}\) .

The corresponding penalty terms are constructed such that they approximate the boundary conditions (and hence are sufficiently small), and when multiplied by \(2 \mathbf {u}^\top \mathbf {P}\), they eliminate the indefinite terms above. We choose

  • West: \(-\mathbf {P}^{-1} \mathbf {P}_w (a_1 \mathbf {u}- \epsilon \mathbf {D}_x \mathbf {u}- \mathbf {g}_w)\) .

  • East: \(-\mathbf {P}^{-1} \mathbf {P}_e (\epsilon \mathbf {D}_x \mathbf {u}- \mathbf {h}_e)\) .

  • South: \(-\mathbf {P}^{-1} \mathbf {P}_s (a_2 \mathbf {u}- \epsilon \mathbf {D}_y \mathbf {u}- \mathbf {g}_s)\) .

  • North: \(-\mathbf {P}^{-1} \mathbf {P}_n (\epsilon \mathbf {D}_y \mathbf {u}- \mathbf {h}_n)\) .

Here \(\mathbf {g}_w\), \(\mathbf {h}_e\), \(\mathbf {g}_s\) and \(\mathbf {h}_n\) is the data injected into the boundary grid points. Note that when multiplied by \(2 \mathbf {u}^\top \mathbf {P}\), the penalty terms turn into boundary integrals.

For example, with homogeneous boundary data, the east penalty becomes

$$\begin{aligned} -2 \epsilon \mathbf {u}^\top \mathbf {P}_e \mathbf {D}_x \mathbf {u}= -2 \epsilon \langle \mathbf {u}, \mathbf {D}_x \mathbf {u}\rangle _{\mathbf {P}_e} \, , \end{aligned}$$

and eliminate the east indefinite term.

Finally we must enforce the initial condition \({ \left. u \phantom {\big |} \right| _{t = 0} } = f\). This is done with the penalty term

$$\begin{aligned} -\mathbf {P}^{-1} \mathbf {P}_\varOmega ^0 ( \mathbf {u}- \mathbf {f}) \, , \end{aligned}$$
(12)

which will control the term \(\Vert \mathbf {u}\Vert _{\mathbf {P}_\varOmega ^0}^2\) from Eq. (7). Multiplying (12) by \(2 \mathbf {u}^\top \mathbf {P}\), adding \(\Vert \mathbf {u}\Vert _{\mathbf {P}_\varOmega ^0}^2\) and completing the square yields

$$\begin{aligned} -\Vert \mathbf {u}\Vert _{\mathbf {P}_\varOmega ^0}^2 + 2 \langle \mathbf {u}, \mathbf {f}\rangle _{\mathbf {P}_\varOmega ^0} = -\Vert \mathbf {u}- \mathbf {f}\Vert _{\mathbf {P}_\varOmega ^0}^2 + \Vert \mathbf {f}\Vert _{\mathbf {P}_\varOmega ^0}^2 \, . \end{aligned}$$

By defining a discrete gradient and Laplacian we can write the full scheme in a complete, but compact form. Let

$$\begin{aligned} \nabla \mathbf {u}&= (\mathbf {D}_x \mathbf {u}, \mathbf {D}_y \mathbf {u}) \\ \varDelta \mathbf {u}&= \mathbf {D}_x^2 \mathbf {u}+ \mathbf {D}_y^2 \mathbf {u}\, . \end{aligned}$$

With this notation, the scheme can be written as

$$\begin{aligned} \begin{aligned} \mathbf {D}_t \mathbf {u}+ a \cdot \nabla \mathbf {u}- \epsilon \varDelta \mathbf {u}&= {} - \mathbf {P}^{-1} \mathbf {P}_\varOmega ^0 ( \mathbf {u}- \mathbf {f}) \\&\phantom {{} = {}} - \mathbf {P}^{-1} \mathbf {P}_w (a_1 \mathbf {u}- \epsilon \mathbf {D}_x \mathbf {u}- \mathbf {g}_w) \\&\phantom {{} = {}} - \mathbf {P}^{-1} \mathbf {P}_e (\mathbf {D}_x \mathbf {u}- \mathbf {h}_e) \\&\phantom {{} = {}} - \mathbf {P}^{-1} \mathbf {P}_s (a_2 \mathbf {u}- \epsilon \mathbf {D}_y \mathbf {u}- \mathbf {g}_s) \\&\phantom {{} = {}} - \mathbf {P}^{-1} \mathbf {P}_n (\mathbf {D}_y \mathbf {u}- \mathbf {h}_n) . \end{aligned} \end{aligned}$$
(13)

It can be shown that the scheme above yields the following bound when using homogeneous boundary data

$$\begin{aligned} \Vert \mathbf {u}\Vert _{\mathbf {P}_\varOmega ^{N_t}} + 2 \epsilon \Vert \nabla \mathbf {u}\Vert _\mathbf {P}^2 \le \Vert \mathbf {f}\Vert _{\mathbf {P}_\varOmega ^0} \, . \end{aligned}$$
(14)

That is, the energy of the numerical solution at the final time and the integral of the gradients is bounded by the energy of the initial data. We have therefore proved the following proposition.

Proposition 2

The scheme (13) is stable.

Remark 1

The bound (14) is a discrete analogue of the continuous bound (5).

Remark 2

The scheme (13) is implicit in time. It is generally not prudent to solve up to time T using a single system (it will be too large)—instead we solve for a small number of time points successively, until we reach T. The initial data for each time-slab is given by the last solution from the previous time-slab. The procedure (multi-block in time) is explained in detail in [7].

5 Two-Domain Discretization

Fig. 4
figure 4

A two-block grid of the partitioned domain \(\varOmega = \varOmega _L \cup \varOmega _R\)

Full size image

We partition the domain \(\varOmega = [0,2] \times [0,1]\) into a left subdomain \(\varOmega _L\) and a right subdomain \(\varOmega _R\), each discretized by a uniform grid (see Fig. 4). We associate to \(\varOmega _L\) a numerical solution \(\mathbf {u}\) and to \(\varOmega _R\) a numerical solution \(\mathbf {v}\). The problem (2) is for the most part discretized as in the previous section. The imposition of the boundary and initial conditions is handled as in (13), and the conditions \(u = v\) and \(\partial u / \partial n = \partial v / \partial n\) at the interface are imposed in a similar weak manner. The combined scheme can be written

$$\begin{aligned} \begin{aligned} \mathbf {D}_t \mathbf {u}+ a \cdot \nabla \mathbf {u}- \epsilon \varDelta \mathbf {u}&= \phantom {{} + {}} \sigma _L^I \mathbf {P}^{-1} \mathbf {P}_e ( \mathbf {u}- \mathbf {E}_{we} \mathbf {v}) \\&\phantom {{} = {}} + \sigma _L^V \epsilon \mathbf {P}^{-1} \mathbf {P}_e ( \mathbf {D}_x \mathbf {u}- \mathbf {E}_{we} \mathbf {D}_x \mathbf {v}) \\&\phantom {{} = {}} + \text {External Penalties} \\ \mathbf {D}_t \mathbf {v}+ a \cdot \nabla \mathbf {v}- \epsilon \varDelta \mathbf {v}&= \phantom {{} + {}} \sigma _R^I \mathbf {P}^{-1} \mathbf {P}_w ( \mathbf {v}- \mathbf {E}_{ew} \mathbf {u}) \\&\phantom {{} + {}} + \sigma _R^V \epsilon \mathbf {P}^{-1} \mathbf {P}_w ( \mathbf {D}_x \mathbf {v}- \mathbf {E}_{ew} \mathbf {D}_x \mathbf {u}) \\&\phantom {{} = {}} + \text {External Penalties} \, . \end{aligned} \end{aligned}$$
(15)

Here the “External Penalties” terms contain the penalty terms described in the previous section to enforce the boundary and initial conditions. The matrices \(\mathbf {E}_{we}\) and \(\mathbf {E}_{ew}\) are reordering operators, moving components between the west and east boundary. This is necessary because the interface components of \(\mathbf {u}\) (i.e. the east boundary of \(\varOmega _L\)) do not appear in the same positions as the interface components of \(\mathbf {v}\) (i.e. the west boundary of \(\varOmega _R\)). More precisely: Let \(e_j\) be the standard basis in \(\mathbb {R}^{N_x+1}\) and \(E_x^{N_x 0} = e_{N_x} e_0^\top \). Then \(\mathbf {E}_{we} = I_t \otimes E_x^{N_x 0} \otimes I_y\) and \(\mathbf {E}_{ew} = \mathbf {E}_{we}^\top \).

Note that because the subdomains \(\varOmega _L\) and \(\varOmega _R\) are discretized with uniform grids and the same number of grid points, we can use the same SBP operators and quadratures on both subdomains. This is done only for simplicity, and is not necessary. To simplify the stability proof of Proposition 3 the quadratures used for integration at the interface should match.

Remark 3

The simplifying requirement that the grid points must match at the interface can be relaxed by using so called SBP preserving interpolation operators, see [8].

The right-hand side in (15) is a stable coupling for appropriate choices of \(\sigma _L^I, \sigma _L^V, \sigma _R^I, \sigma _R^V\). Indeed, by arguments similar to those in [1], the following proposition can be proved.

Proposition 3

A positive number \(\xi \) exists such that if

$$\begin{aligned} \sigma _R^I = \sigma _L^I - a_1, \quad \sigma _R^V = \sigma _L^V + 1, \quad \sigma _L^I \le \frac{a_1}{2} - \epsilon \frac{\left( \sigma _L^V\right) ^2 + \left( \sigma _R^V\right) ^2}{4\xi }, \end{aligned}$$
(16)

then the scheme (15) is stable.

This is proved in [1] for the semi-discrete case, and is here extended to the fully discrete case. The proof is given in “Appendix A”.

6 System Reduction

Our goal is now to split the problem (15) into two smaller, independent subproblems. To this end we rewrite (15) as

$$\begin{aligned} \begin{bmatrix} \mathbf {A}_L&\varvec{\Sigma }_L \\ \varvec{\Sigma }_R&\mathbf {A}_R \end{bmatrix} \begin{bmatrix} \mathbf {u}\\ \mathbf {v}\end{bmatrix} =\begin{bmatrix} \mathbf {b}_L \\ \mathbf {b}_R \end{bmatrix} \, . \end{aligned}$$
(17)

Here \(\varvec{\Sigma }_L = \sigma _L^I \mathbf {P}^{-1} \mathbf {P}_e \mathbf {E}_{we} + \sigma _L^V \mathbf {P}^{-1} \mathbf {P}_e \mathbf {E}_{we} \mathbf {D}_x\) and \(\varvec{\Sigma }_R = \sigma _R^I \mathbf {P}^{-1} \mathbf {P}_w \mathbf {E}_{ew} + \sigma _R^V \mathbf {P}^{-1} \mathbf {P}_w \mathbf {E}_{ew} \mathbf {D}_x\). The matrix \(\mathbf {A}_L\) is the sum of all the factors in front of \(\mathbf {u}\) (including the external penalty terms) in the top equation of (15), and the matrix \(\mathbf {A}_R\) is the sum of all the factors in front of \(\mathbf {v}\) in the bottom equation of (15). The right-hand side \(\mathbf {b}_L\) and \(\mathbf {b}_R\) contains data from the initial and boundary conditions.

Parallelization opportunities can now be illuminated by a few key observations. First, the full system (15) is equivalent to

$$\begin{aligned} \begin{bmatrix} I&\mathbf {A}_L^{-1} \varvec{\Sigma }_L \\ \mathbf {A}_R^{-1} \varvec{\Sigma }_R&I \end{bmatrix} \begin{bmatrix} \mathbf {u}\\ \mathbf {v}\end{bmatrix} =\begin{bmatrix} \mathbf {A}_L^{-1} \mathbf {b}_L \\ \mathbf {A}_R^{-1} \mathbf {b}_R \end{bmatrix} \, . \end{aligned}$$
(18)

This formulation has the desirable property of being easily reduced to involve only interface components, as we shall soon demonstrate. Three major questions must be answered. Is it possible to construct (18), i.e. are the involved matrices invertible? How do we solve for the interface components? And how do we build the full solution once the interface components are known?

Let us discuss these questions in order. To build the system (18) we must compute the products \(\mathbf {A}_L^{-1} \varvec{\Sigma }_L\) and \(\mathbf {A}_R^{-1} \varvec{\Sigma }_R\) (the invertibility of \(\mathbf {A}_L\) and \(\mathbf {A}_R\) is shown in Sect. 7). Due to the sparse structure of \(\varvec{\Sigma }_L\) and \(\varvec{\Sigma }_R\) this is equivalent to solving \(2 k N_t N_y\) independent linear systems of subdomain size. The parameter k depends on the size of the boundary stencil of the SBP operator (using a standard second order operator implies \(k = 2\), fourth order implies \(k = 4\) etc.). The right-hand side in (18) is in general time dependent and must be computed for each implicit time-integration step.

Once the matrix on the left-hand side of (18) and the vector on the right-hand side is known we can reduce the system to involve only interface components. Let us study a small example to illustrate the procedure. The left-hand side matrix in (18) is a block matrix with identities on the diagonal. The off-diagonal blocks have nonzero columns in positions corresponding to the interface components. This will allow us to eliminate rows and columns corresponding to non-interface components. In the example below we can think of \(u_0\) and \(v_2\) as non-interface components, and \(u_1,u_2,v_0,v_1\) as interface components to be isolated from the full system. The reduction is schematically depicted below.

$$\begin{aligned} \begin{bmatrix} 1&0&0&*&*&0 \\ 0&1&0&*&*&0 \\ 0&0&1&*&*&0 \\ 0&*&*&1&0&0 \\ 0&*&*&0&1&0 \\ 0&*&*&0&0&1 \end{bmatrix} \begin{bmatrix} u_0 \\ u_1 \\ u_2 \\ v_0 \\ v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ b_3 \\ b_4 \\ b_5 \end{bmatrix} \end{aligned}$$
(19)
figure a
$$\begin{aligned} \begin{bmatrix} 1&0&*&* \\ 0&1&*&* \\ *&*&1&0 \\ *&*&0&1 \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \\ v_0 \\ v_1 \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \end{bmatrix} \end{aligned}$$
(21)

Finally, once (21) has been solved for the interface components, the remaining unknowns \(u_0\) and \(v_2\) can be computed by using the top and bottom rows in (19). While the system above is too small to be the result of a real discretization, both its structure and the elimination procedure is analogous in realistic cases.

In conclusion, the following solution algorithm for (15) can be set up by precomputing the products \(\mathbf {A}_L^{-1} \varvec{\Sigma }_L\) and \(\mathbf {A}_R^{-1} \varvec{\Sigma }_R\):

  1. 1.

    Compute \(\mathbf {A}_L^{-1} \mathbf {b}_L\) and \(\mathbf {A}_R^{-1} \mathbf {b}_R\).

  2. 2.

    Build and solve the interface system.

  3. 3.

    Build the full solution from the interface components.

  4. 4.

    Repeat using previous solution as initial data until time T is reached.

Remark 4

This type of algorithm is beneficial also for a sequential code because of the non-linear growth of the memory cost for solving linear systems. That is, solving a single-domain discretization with a given grid size may be impossible due to memory constraints, while the multidomain scheme is solvable due to the reduced system sizes.

Remark 5

For linear problems with time-independent coefficients, the matrices \(\mathbf {A}_L\) and \(\mathbf {A}_R\) can be LU-decomposed ahead of simulation to increase efficiency. For non-linear problems, or problems with time dependent coefficients, the matrices \(\mathbf {A}_L\) and \(\mathbf {A}_R\) will change with time, and must be LU-decomposed in each time slab.

7 Invertibility

The procedure described in the previous section requires that the subsystems are invertible, and that the full system (17) has a unique solution. To prove that this is the case we study the spectral properties of the spatial discretization and the temporal discretization separately. The overarching idea is to

  1. 1.

    Establish that the discrete temporal and spatial differential operators commute.

  2. 2.

    Show that the eigenvalues of the temporal operator have strictly positive real parts.

  3. 3.

    Show that the eigenvalues of the spatial operator have non-negative real parts.

  4. 4.

    Note that the eigenvalues of the sum of commuting operators are the sums of their respective eigenvalues and conclude therefore that zero is not an eigenvalue of the full operator, implying that it is invertible.

Point 2 is proven for the second order case, but remains an open question for high order operators. However, extensive numerical studies corroborate this hypothesis (see [7]). We consider Point 2 in the form of a conjecture.

Conjecture 1

The eigenvalues of the matrix \(\tilde{D}_t = D_t + P_t^{-1} E^0_t = P_t^{-1} (Q_t + E^0_t)\) have strictly positive real parts.

Point 1 is a simple consequence of properties of the Kronecker product. The discrete differential operator \(\mathbf {A}_L\) in (17) is the sum of a temporal part \(\tilde{D}_t \otimes I_x \otimes I_y\) and a spatial part \(I_t \otimes \tilde{D}_x \otimes I_y + I_t \otimes I_x \otimes \tilde{D}_y\) (here the tilde symbols indicate the sum of an SBP operator and penalty terms). Clearly the temporal part commutes with the spatial part. The same is true for \(\mathbf {A}_R\).

Next we study the spectrum of \(\mathbf {A}_L\) and \(\mathbf {A}_R\) by considering the semi-discrete version

$$\begin{aligned} \begin{bmatrix} \mathbf {u}\\ \mathbf {v}\end{bmatrix}_t + \begin{bmatrix} A_L&\varSigma _L \\ \varSigma _R&A_R \end{bmatrix} \begin{bmatrix} \mathbf {u}\\ \mathbf {v}\end{bmatrix} = \begin{bmatrix} \mathbf {b}_L \\ \mathbf {b}_R \end{bmatrix} \end{aligned}$$
(22)

of (17). Here \(A_L\) and \(A_R\) are the same as \(\mathbf {A}_L\) and \(\mathbf {A}_R\), sans the temporal discretization—i.e. \(A_L = \tilde{D}_x \otimes I_y + I_x \otimes \tilde{D}_y\) and \(A_R = \hat{D}_x \otimes I_y + I_x \otimes \hat{D}_y\) (here again the tilde and hat symbols indicate that penalty terms have been added to the SBP operators). Similarly \(\varSigma _L\) and \(\varSigma _R\) are as in Sect. 6, sans the temporal discretization. The semi-discrete system (22) is stable under the conditions of Proposition 3 (the proof is essentially the same). This allows us to prove the following lemma.

Lemma 1

Under the stability conditions of Proposition 3, the eigenvalues of the matrices \(A_L\) and \(A_R\) have non-negative real parts.

Proof

We have established that the semidiscrete system (22) is stable, or, equivalently, with \(P = P_x \otimes P_y\),

$$\begin{aligned} \begin{bmatrix} \mathbf {u}\\ \mathbf {v}\end{bmatrix}^\top \left[ \begin{bmatrix} P A_L&P \varSigma _L \\ P \varSigma _R&P A_R \end{bmatrix} + \begin{bmatrix} A_L^\top P&\varSigma _R^\top P \\ \varSigma _L^\top P&A_R^\top P \end{bmatrix} \right] \begin{bmatrix} \mathbf {u}\\ \mathbf {v}\end{bmatrix} \ge 0 \end{aligned}$$
(23)

for all \(\mathbf {u}, \mathbf {v}\). It follows that \(P A_L + A_L^\top P\) and \(P A_R + A_R^\top P\) are positive semi-definite. To see this, assume that \(P A_L + A_L^\top P\) is not positive semi-definite. Then there is a vector \(\tilde{u}\) such that \(\tilde{u}^\top (P A_L + A_L^\top P) \tilde{u} < 0\). But this contradicts (23) if we set \(\mathbf {u}= \tilde{u}\) and \(\mathbf {v}= 0\). Hence \(P A_L + A_L^\top P\) is positive semi-definite, and by a similar argument, so is \(P A_R + A_R^\top P\).

Furthermore, if \((\lambda , z)\) is an eigenpair of \(A_L\), then

$$\begin{aligned} A_L z = \lambda z \implies P A_L z = \lambda P z \implies z^* P A_L z = \lambda z^* P z \, . \end{aligned}$$

By adding the conjugate transpose of the rightmost equation above it follows that

$$\begin{aligned} z^* [ P A_L + (P A_L)^\top ] z = 2 \text {Re} (\lambda ) z^* P z \, . \end{aligned}$$

Hence the eigenvalues of \(A_L\) (and \(A_R\)) have non-negative real parts. \(\square \)

Using Lemma 1 it is straightforward to prove invertibility of \(\mathbf {A}_L\) and \(\mathbf {A}_R\).

Proposition 4

The stability conditions of Proposition 3 imply that the matrices \(\mathbf {A}_L\) and \(\mathbf {A}_R\) are invertible.

Proof

We prove invertibility of \(\mathbf {A}_L\) only—the proof for \(\mathbf {A}_R\) is the same.

From the discussion above we know that the temporal term \(\tilde{D}_t \otimes I_x \otimes ~I_y\) and the spatial term \(I_t \otimes \tilde{D}_x \otimes I_y + I_t \otimes I_x \otimes \tilde{D}_y\) of \(\mathbf {A}_L\) commute, and that the eigenvalues of the temporal term have strictly positive real parts. Furthermore, from Lemma 1, the eigenvalues of the spatial part has non-negative real parts. It follows that the eigenvalues of \(\mathbf {A}_L\)—being sums of the eigenvalues of the temporal and spatial parts—have strictly positive real parts (see [4, p. 117]). Then, since all its eigenvalues are nonzero, \(\mathbf {A}_L\) is invertible. \(\square \)

It follows in a similar manner that the full system (17) has a unique solution.

Proposition 5

The stability conditions of Proposition 3 imply that the system (17) has a unique solution.

Proof

Again we split the matrix into a temporal and a spatial part:

$$\begin{aligned} \begin{bmatrix} \mathbf {A}_L&\varvec{\Sigma }_L \\ \varvec{\Sigma }_R&\mathbf {A}_R \end{bmatrix} = \underbrace{ \begin{bmatrix} \tilde{\mathbf {D}}_t&\\&\tilde{\mathbf {D}}_t \end{bmatrix} }_{\mathbf {T}} + \underbrace{ \begin{bmatrix} I_t \otimes A_L&I_t \otimes \varSigma _L \\ I_t \otimes \varSigma _R&I_t \otimes A_R \end{bmatrix} }_{\mathbf {S}} \end{aligned}$$

where \(\tilde{\mathbf {D}}_t = \tilde{D}_t \otimes I_x \otimes I_y\). The matrix \(\mathbf {S}\) is the blockwise Kronecker product of \(I_t\) and the matrix in (22). Since (22) is stable, it follows that the eigenvalues of \(\mathbf {S}\) have non-negative real parts [5, p. 178]. Furthermore, by Conjecture 1, the eigenvalues of \(\mathbf {T}\) have strictly positive real parts. But then, since \(\mathbf {T}\) and \(\mathbf {S}\) commute (this follows from the Kronecker product structure), the eigenvalues of the sum \(\mathbf {T} + \mathbf {S}\) have strictly positive real parts. It follows that the system (17) has a unique solution. \(\square \)

Finally, the invertibility of the interface system is an immediate consequence of Propositions 4 and 5.

Proposition 6

The stability conditions of Proposition 3 imply that the interface system described in Sect. 6 has a unique solution.

Proof

The equations of the interface system is a subset of the equations of the full system (18). By Propositions 4 and 5, the system (18) has a unique solution. Hence, the interface system has a unique solution. \(\square \)

8 N-Domain Discretization

The procedure for two domains discussed above can be straightforwardly extended to an arbitrary number of subdomains, leading to systems defined by matrices of the form

$$\begin{aligned} \begin{bmatrix} \mathbf {A}_1&\varvec{\Sigma }_{12}&\cdots&\varvec{\Sigma }_{1N} \\ \varvec{\Sigma }_{21}&\mathbf {A}_2&\cdots&\varvec{\Sigma }_{2N} \\ \varvec{\Sigma }_{31}&\varvec{\Sigma }_{32}&\cdots&\varvec{\Sigma }_{3N} \\ \vdots&\vdots&\cdots&\vdots \\ \varvec{\Sigma }_{N1}&\varvec{\Sigma }_{N2}&\cdots&\mathbf {A}_N \end{bmatrix} \, , \end{aligned}$$

where \(\varvec{\Sigma }_{ij}\) is nonzero if and only if the subdomains i and j share an interface. An interface system is then constructed as in the two-domain case by solving linear systems of subdomain size.

9 Numerical Experiments

Our domain decomposition scheme is readily extended to curvilinear blocks. To verify that our code produces solutions that converge with design order of accuracy we consider (1) with \(a = (1,1)\) and \(\epsilon = 0.01\), posed on the domain \(\varOmega \) shown in Fig. 5. Data is given by the manufactured solution

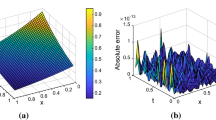
$$\begin{aligned} u = \cos (-\,2.5\pi x + 2.1\pi y + t) \, . \end{aligned}$$
(24)

We compute approximate solutions at time \(T=1\) for increasingly fine grids and for different order SBP operators in space. The equation is integrated in time using an SBP(2, 1) operator with 3 points per temporal block and \(\varDelta t\) small enough to not influence the spatial error. Convergence rates and \(L^2\) errors in space are shown in Table 1, verifying that the schemes converge with the correct order.

Fig. 5
figure 5

An irregular domain decomposed into three subdomains

Full size image
Table 1 \(L^2\) errors at time \(T=1\) and convergence rates for different spatial SBP operators
Full size table
Fig. 6
figure 6

The domain \(\varOmega = (0,1)^2\) divided into 9 subdomains, each discretized by a \(10 \times 10\) grid

Full size image

We investigate the efficiency of our method by comparing against both explicit Runge–Kutta time integration and the single-domain (SD) formulation described in Sect. 4. The square domain \(\varOmega = (0,1)^2\) is partitioned into 9 blocks as in Fig. 6, and we again set \(a = (1,1)\), \(\epsilon = 0.01\), and use data from (24). The multidomain formulation described in Sect. 5 is easily made semi-discrete by only discretizing in space, leaving the time dimension continuous. This yields a system of ODEs which we solve using the Matlab routine ode45—a Runge–Kutta based explicit integrator with adaptive step size. Both our implicit methods use an SBP(2, 1) operator in time with \(\varDelta t = 0.005\) and 3 points per temporal block. All methods use SBP(4, 2) operators in space. The test is performed as follows.

For \(N = 10, 11, \dots , 30\):

  • Partition the domain \(\varOmega = (0,1)^2\) into 9 uniform subdomains.

  • Discretize each subdomain by an \(N \times N\) grid.

  • Compute the solution using explicit time integration. Record the execution time and spatial error at the final time.

  • Compute the solution using our proposed implicit multi-domain algorithm. Record the execution time and spatial error at the final time.

Using the 9 subdomain grid structure in Fig. 6 gives a total spatial resolution of \((3N - 2) \times (3N - 2)\) (because the interface nodes are shared). Hence, for the single-domain algorithm:

  • Discretize the domain \(\varOmega = (0,1)^2\) by a \((3N - 2) \times (3N - 2)\) grid.

  • Compute the solution using implicit integration as described in Sect. 4. Record the execution time and spatial error at the final time.

The execution times are plotted against the spatial errors at time \(T=1\) in Fig. 7. Our implicit domain decomposition based integrator is an order of magnitude faster than both the explicit integrator and the single-domain implicit integrator (and several orders of magnitude faster for finer grids). As the grid resolution increases, the implicit single-domain algorithm becomes inefficient due to the size of the system that must be solved in each time step. This makes the single-domain algorithm memory intensive, and for fine grids the method breaks down due to memory limitations (this is why the single-domain algorithm has fewer measurement points in Fig. 7; for high resolutions we simply run out of memory). The explicit solver, while not very memory intensive, requires very small time steps for stability, making it computationally expensive.

Fig. 7
figure 7

Execution times for solving (1) on the unit square using our proposed scheme (Implicit MD), the single-domain scheme from Sect. 4 (Implicit SD), and explicit Runge–Kutta (Explicit RK)

Full size image

Remark 6

The above comparison is between Matlab implementations running on a single desktop machine. The bulk of the computations consist of matrix–vector addition and multiplication, and solving linear systems. These are all operations which are heavily parallelized in Matlab. Large scale parallelization using computer clusters will be done in a future paper.

Remark 7

In our domain decomposition implementation, both the interface system and the subdomain systems are solved by direct methods. This is particularly suitable for linear problems with time independent coefficients, because it allows us to LU-decompose the systems ahead of simulation. At higher resolutions this becomes infeasible and one should instead use iterative solvers, like for example GMRES.

Execution times for the domain decomposition scheme can be optimized by appropriately choosing the number of subdomains. The size of the subproblems increase with grid refinement, ultimately resulting in systems that cannot be solved efficiently. By increasing the number of subdomains, we reduce the sizes of the subsystems, but increase the size of the interface system. Hence there is an optimal number of subdomains for producing solutions at a given accuracy in the least amount of time. To illustrate this effect we compute solutions on the unit square, with increasing number of subdomains. More precisely, a reference accuracy is set by computing a solution at time \(T=1\) using the single-domain algorithm [with \(\varDelta t = 0.05\) and data from (24)] on a \(48 \times 48\) grid. Next, solutions are computed using \(M^2\) subdomains, where \(M = 1,2,3,4,5\). The execution time needed to achieve equal or higher accuracy than the reference accuracy is recorded. This is typically achieved by using grid size \(\approx (48/M) \times (48/M)\) for each subdomain. In this case the optimal execution time is reached at \(3^2\) blocks. The results are shown in Fig. 8.

A basic heuristic for determining the optimal number of subdomains can be constructed by balancing the sizes of the interface and subdomain problems. This is done by deriving expressions for the number of interface and subdomain nodes in terms of the total resolution and the number of subdomains. In our unit square example, if the total resolution is \(N \times N\) and we use \(M^2\) subdomains, then each subdomain comprises \((N/M)^2\) nodes, while the interfaces comprise \(2(M-1)N\) nodes in total. By letting these quantities be equal we can solve for M:

Fig. 8
figure 8

The execution time needed to achieve a given accuracy depends on the number of subdomains. This plot shows execution times for different partitions of the unit square. In this case, optimal execution time is achieved at 9 subdomains

Full size image
$$\begin{aligned} (N/M)^2 = 2(M-1)N \Leftrightarrow M^3 - M^2 - N/2 = 0 \, . \end{aligned}$$
(25)

In general, the solution will not be an integer, so the best we can do is to round off to the nearest integer. For \(N = 48\), the solution to Eq. (25) is \(M \approx 3.26\), which indicates that \(3^2 = 9\) subdomains should be optimal, which is what we find in our computations as well.

For problems with high temporal variation and low spatial variation we can benefit from raising the order of accuracy in time. We will illustrate this with data from the manufactured solution

$$\begin{aligned} u = \cos (-\,0.5\pi x + 0.1\pi y + 2\pi t) \, . \end{aligned}$$
(26)

The domain \(\varOmega = (0,1)^2\) is discretized as in Fig. 6 (i.e. the spatial resolution is fixed). We compute solutions at time \(T=1\) for increasingly fine temporal resolutions using both SBP(2, 1) and SBP(4, 2) operators in time (and SBP(4, 2) in space). Naturally the SBP(2, 1) operator requires smaller time steps than the SBP(4, 2) operator in order to reach the optimal spatial error for the chosen grid. The downside of raising the order of accuracy in time is that it increases the system size (since the stencil is larger we need more time points per implicit time step). However in this case the harsher time step requirements of the SBP(2, 1) operator incurs higher computational cost than the increased system size of the SBP(4, 2) operator, resulting in slower execution times. The results can be seen in Fig. 9.

Fig. 9
figure 9

Temporal resolution and execution times needed to achieve optimal spatial accuracy at time \(T=1\), using the grid shown in Fig. 6 and data from (26)

Full size image

Finally we illustrate our procedure by an example. We compute the solution with homogeneous boundary and forcing data, Gaussian initial data, \(\epsilon = 0.01\), \(a = (0,0.3)\), \(\varDelta x = 1/24\), \(\varDelta t = 1/20\), \(T = 10\). The simulation uses the grid shown in Fig. 10 with 4th order operators in space and a 2nd order operator in time. Color plots of the solution at different times are shown in Fig. 11. The solution slowly advects to the right and diffuses, without oscillations.

Fig. 10
figure 10

A multiblock grid

Full size image
Fig. 11
figure 11

A solution with homogeneous boundary and forcing data, and Gaussian initial data

Full size image

10 Conclusions

We have formulated an efficient, fully discrete and provably stable domain decomposition scheme for the advection–diffusion equation using SBP-SAT in space and time. The single-domain problem is reduced to a set of subdomain-sized problems along with a linear system comprising the interface components. Using the stability of the scheme together with the spectral properties of the SBP operators we proved that the scheme is invertible, i.e. for any given set of data, the scheme will produce a unique convergent solution.

By numerical experiments we showed significant efficiency gain compared to both implicit single-domain and explicit multi-block solvers. Due to the stiffness of the equation, explicit time integration is crippled by the small time steps required for stability. The implicit single-domain solver does not require small time steps, but becomes inefficient with grid refinement as the size of the linear system grows.

The ideas presented here provide both theoretical and practical paths for further research into the connection between SBP-SAT based discretizations and domain decomposition. In future papers we intend to elaborate on the method used on non-trivial domains using curvilinear grids. The viability of the method should also be further explored through parallelized implementations and research related to applications using variable coefficient as well as non-linear problems.