Super-Convergence in Maximum Norm of the Gradient for the Shortley–Weller Method

Abstract

We prove in this paper the second-order super-convergence in $L^{\infty }$-norm of the gradient for the Shortley–Weller method. Indeed, this method is known to be second-order accurate for the solution itself and for the discrete gradient, although its consistency error near the boundary is only first-order. We present a proof in the finite-difference spirit, using a discrete maximum principle to obtain estimates on the coefficients of the inverse matrix. The proof is based on a discrete Poisson equation for the discrete gradient, with second-order accurate Dirichlet boundary conditions. The advantage of this finite-difference approach is that it can provide pointwise convergence results depending on the local consistency error and the location on the computational domain.

A Numerical Illustration: Corners and Regularity of the Solution

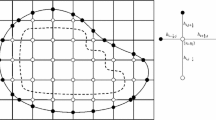
We illustrate here the possible loss of regularity of the solution in the case of corners, that was evocated in Sect. 2. Depending on the angles of this corners, the solution can indeed be less than $C^1$ near the boundary, even if the source term and the boundary conditions are very smooth.

Fig. 4

Example of domains with corners

On Fig. 4, we consider two domains that are only piecewise smooth: the diamond-shaped one, denoted by $\varOmega _1$, and its complementary, denoted by $\varOmega _2$. The angles of the first one do not exceed the value $\pi$, while some of the second one do actually.

We solve numerically the following problem

$$\begin{aligned} \left\{ \begin{array}{c} -\triangle u = 1 \text{ on } \varOmega , \\ u = 0 \text{ on } \varGamma . \end{array} \right. \end{aligned}$$

(17)

in these two domains: $\varOmega = \varOmega _1$ and $\varOmega = \varOmega _2$, with the Shortley–Weller method. The numerical solution is in fact the sum of all the discrete Green functions associated to grid points in the numerical domain. In this paper, to obtain the estimate (10) on the discrete Green function, we make the assumption that the solution u of problem (17) is at least $C^1$ near the boundary, so that it satisfies $u(x) = O(h)$ for points located at a distance O(h) of the domain boundary.

We compute in both cases, the $L^{\infty }$-norm of the numerical solution on grid points in $\varOmega _h^*$ (that is, irregular grid points). The Tables 1 and 2 present these results. We observe that for domain $\varOmega _1$, the numerical solution on $\varOmega _h^*$ converges to zero at order one. For domain $\varOmega _2$, the convergence order is strictly smaller than one, which means that the discrete Green functions do not satisfy the property that we need for our convergence estimates.

Table 1 Convergence to zero for irregular grid points for problem (17) in domain $\varOmega _1$

Table 2 Convergence to zero for irregular grid points for problem (17) in domain $\varOmega _2$