1 Introduction

For electronic transitions in heavy ion-atom collisions at intermediate and high impact energies E, single capture (SC) and double capture (DC) are of high relevance not only in fundamental atomic physics, but also in X-ray astronomy, plasma physics, thermonuclear fusion, particle transport physics, design of heavy ion accelerators, etc. As an example, consider a beam of \(\alpha -\)particles traversing a gaseous medium in e.g. a cloud chamber. For most of their track, the \(\alpha -\)particle projectiles steadily keep their initial charge equal to 2. The stopping power distribution (energy loss per traversed distance) is mainly flat from the entrance to the medium all the way toward the \(\alpha -\)particle range \(R_{\text{B}}\), which depends on the initial value of E. However, as the maximal penetration depth or range \(R_{\text{B}}\) is approached, the situation becomes more involved.

Alpha particles are sufficiently slowed down close to the range \(R_{\text{B}}\), where they deposit most of their remaining energies. This is manifested by the appearance of a sharply maximized stopping power in the lineshape form of a characteristic peak, called the Bragg peak. Near this maximum energy loss, the produced track contains helium singly charged ions \({\text{He}}^{+}\) and neutral helium atoms \({\text{He}}\). These are respectively due to SC and DC by \(\alpha -\)particles from the surrounding gas. Moreover, at the end of the track, as shown by Henderson [1,2,3], Rutherford [4] and Jacobsen [5], while colliding with the medium, the \({\text{He}}^{+}\) ions, formed by SC, are converted to alpha particles. The latter process, known as electron loss (projectile ionization) alternates with electron capture thousands of times in the immediate vicinity of the Bragg peak.

Ultimately, the neutral helium atoms would prevail within barely the last couple of centimeters of the track. These helium atoms can be created by two different events. For instance, one encounter through DC can occur when \(\alpha -\)particles scatter on an atom/molecule G contained in the rest gas of the traversed medium as \(\mathrm{He^{2+}+G\rightarrow He+G^{2+}}\). Another pathway is through two sequential SC collisions, first as \(\mathrm{He^{2+}+G\rightarrow He^{+}+G^{+}}\) and subsequently as \(\mathrm{He^{+}+G^+\rightarrow He+G^{2+}}\). Instead of the latter process, formation of helium atoms can be due to collisions of the \(\mathrm{He^{+}}\) projectiles and another target (say \( \widetilde{\text{G}}^+\)) via \(\mathrm{He^{+}+\widetilde{\text{G}}^+\rightarrow He+\widetilde{\text{G}}^{2+}}\).

Ever since these first cutting edge experiments with rearrangement collisions [1,2,3,4,5], all the subsequent measurements of DC in e.g. the \(\mathrm{He^{2+}+He}\) collisions, had to rule out the contributions due to SC by \({\text{He}}^{+}\) from the background gases. It is possible that this issue could be at least partly responsible for an unusually large discrepancy by a factor of 20 between the total cross sections Q for DC by \(\alpha -\)particles from helium atoms measured at 4.0 and 4.08 MeV in the experiments by Schuch et al. [6] and Afrosimov et al. [7], respectively.

More recently, Zastrow et al. [8] reported on an experiment on DC in the \(\text{He}^{+}+\text{He}\) collisions. They developed a procedure for discriminating between the mentioned two channels for DC. This was done at the Joint European Torus (JET) tokamak by injecting neutral helium beam into the helium plasma.Footnote 1 By analyzing the emitted X-ray lines, these authors concluded that their cross section datum Q measured at \(E=\)118 keV was solely due to the resonant transition (ground-to-ground state \(1\,s^2\rightarrow 1\,s^2\)) as \(\mathrm{{}^4He^{+}+{}^4He(ground)\rightarrow {}^4He(ground)+{}^4He^{2+}}\) with no detectable contribution from the process \(\mathrm{{}^4He^{+}+{}^4He(ground)\rightarrow {}^4He(excited)+{}^4He^{2+}}\).

The result for Q obtained by Zastrow et al. [8] is about 2 to 3 times larger than the data of e.g. DuBois [9, 10] from an ’ion beam into gas experiments’ for \(\mathrm{{}^4He^{2+}+{}^4He(ground)\rightarrow {}^4He}(\Sigma )+{}^4{\text{He}}^{2+}\), where \(\Sigma \) denotes the sum of the helium final states (ground and excited). The cross section Q from Ref. [8] is in fair agreement with the four-body boundary-corrected first Born (CB1-4B) method [11], but overestimates the corresponding result by the close-coupling (CC) method [12] by a factor between 2 to 3. The CB1-4B method is a perturbative method valid at intermediate and high energies, implying that its good performance at \(E=\)118 keV might be fortuitous. Another surprise here is the inability of the non-perturbative CC method (applicable at intermediate energies) to reproduce the measured cross section at \(E=\)118 keV [8].

Cross sections for charge exchange are essential for diagnostics of fusion plasmas through determining the ion temperature, collective velocities and impurity density. An enhanced accuracy of these critical parameters impacts strongly on the estimates of the cooling rate of the tokamak plasmas. In particular, charge exchange spectroscopy (CXS) helps interpret and understand the structures in the generated X-ray spectral lines from the laboratory fusion plasmas found routinely in the JET and in the Tokamak Fusion Test Reactor (TFTR) [13, 14], as well as in the non-terrestrial sources (e.g. in the Sun, the Moon, Venus and comets) [15,16,17,18,19,20,21,22]. For example, in X-ray astrophysics (one of the newest branches of astrophysics), it has been recognized for about a quarter of a century now that SC by energetic multiply charged heavy ions (in the solar wind) from neutral atoms or molecules (in comets) represents the dominant process for the cometary X-ray emission [15].

In the JET tokamak plasmas, using the injected helium neutral beams, besides the plasma ions \({\text{He}}^{+}\) and \({\text{He}}^{2+}\), it occurs that DC may also involve the partially or fully ionized impurity ions. One of the major concerns in fusion research is the presence of the bare ion impurities in the core of tokamak plasmas. In the core environment, the impurity light ions of nuclear charges below 10 are fully ionized. However, the problem is that the bare ion impurities cannot be detected directly. Nevertheless, there is an indirect way of detection. This is where atomic rearrangement collisions come to the rescue by means of CXS, as one of the two most effective experimental methods for detecting the bare ion impurities in the core plasma (the other method is based on three-body recombination).

As stated, the ionic impurities too can capture electrons from the injected neutral atom beams (one electron from H, one or two electrons from He). After capture, the formed multiply charged ion impurities are in their excited states. Detection of the ensuing X-ray spectral lines resulting from radiative decays of these unstable states is a signature of the presence of the bare ion impurities in the plasma core. This indirect detection of bare ion impurities clearly illustrates the inverse problem nature of the pertinent measurement, the proper understanding/interpretation of which necessitates a theory. Herein, the effect (detection of X-ray emission line spectra) is known, but its cause is unknown. Thus, it is the theory that identifies the cause (creation of excited states by the mechanism of electron capture) which, through decays, produces the observed X-ray emission lines.

To emphasize, measurements of total cross sections (state-selective, state-summed) are enabled by detecting and subsequently parametrizing the emitted X-rays from the excited states formed by charge exchange. This is a meeting point of charge exchange collisions and spectroscopy, as transpired in the name ’charge exchange spectroscopy’, CXS. An absorptive pure Lorentzian-shaped resonance spectral line is quantified by the main three parameters. These are the position (energy or frequency), width (inversely proportional to the lifetime of the decaying excited state) and height or intensity (proportional to the Lorentzian area), which itself is directly proportional to the abundance or concentration or density of the atomic systems that emitted the rays.

This remark brings us to one of the essential features of fusion plasma. It is the determination of the temperature and density of the bare ion impurities. Such plasma characteristics can be extracted from the just mentioned parameters of the emitted X-ray lines (widths and intensities). Thus, the estimated intensities and Doppler-broadened widths of the spectral lines provide the sought temperature and density of the bare ion impurities, respectively.

High-temperature tokamak fusion plasmas are maintained by nuclear collisions involving fusion of deuterium and tritium nuclei with production of energetic \(\alpha -\)particles and neutrons. Of particular importance is to obtain adequate information about the \(\alpha -\)particle distributions and confinement in hot tokamak plasmas from nuclear fusion reactors. This can be provided by DC in e.g. the \(\mathrm{He^{2+}+Li}\) collisions. Further, DC events invoking multiply charged nitrogen as well as neon ions in the \(\text{N}^{q+}+{\text{He}}\) and \(\text{Ne}^{q+}+{\text{He}}\) collisions, respectively, are currently examined by means of CXS in the Axially Symmetric Divertor Experiment (ASDEX) and ASDEX-Upgrade (ASDEXU or AUG). The overall umbrella of this endeavor, the International Thermonuclear Experimental Reactor (ITER), located in Southern France, represents the culmination of more than 100 fusion reactors built since the 1950s. The plasma temperature in the ITER must be about 150 million \({}^\text{o}\text{C}\), which is ten times higher than the temperature of the core of the Sun.

By late 2025, the ITER is projected to achieve a ten-fold gain in the output thermal power of the fusion plasma. About 50 MW of thermal power absorbed in the input by the plasma is anticipated to yield about 500 MW of the output heat from fusion for nearly 500 s. As a fusion-based new source of energy, the ITER is a terrestrial replica of a similar process, which powers the Sun and other stars. According to the theory of Bethe [23,24,25,26], the intense heat at the core of the Sun forces light nuclei to fuse together, after overcoming the repulsive Coulomb barrier by way of quantum-mechanical tunneling. No less than 35 nations across the world participate to research on the ITER during the last 35 years. This can also be appreciated from the recent overview of the results (obtained at the ASDEXU tokamak), as published by more than 400 authors from 20 different countries (Europe, America, Asia) [14].

While fusing together in the core (center) of the Sun, the sum of the masses of e.g. two hydrogen nuclei does not give the mass of the formed helium nucleus (alpha particle). Rather, the outcome is about 99.3% of the mass of an alpha particle. The missing 0.7% of the combined mass is converted to energy. This is dictated by the Einstein relation \(E=mc^2\), according to which any loss of mass m must be compensated by creation of the corresponding energy E (where c is the speed of light). Given this fact and the enormous density of protons in the core of the Sun, it follows that about 4.26 million tons of the Sun mass are converted into energy and heat every second. The ensuing mass-energy conversion rate (luminosity) amounts to \(3.846\times 10^{26}\)W, as produced by the Sun in merely one second. This is sufficient to supply the energy needs of the entire World for nearly 8 days. Most of this emitted Solar energy is in the visible and infrared part of the electromagnetic spectrum of radiation, with about 1% shared by the radio, ultraviolet and X-ray spectral bands.

It is also important that, prior to being ionized, a large fraction of the injected neutral beam (e.g. H, He) reaches the core of the tokamak. This is possible when the injected neutral beam does not interact too much with the cold plasma near the wall of the tokamak. Such a condition is secured by neutral beams of sufficiently high impact energy E. However, for CXS to be effective, charge exchange cross sections Q should be detectable (i.e. not too small). These cross sections decrease rapidly beyond the adiabatic Massey peak (i.e. above about 100 keV/amu). Therefore, the impact energies E of the injected neutral beams of hydrogen and helium atoms should optimally be between 100 keV/amu up to a few MeV/amu. Precisely this energy span (100 keV–10 MeV) is of the main relevance to the presently addressed four-body quantum-mechanical perturbative distorted wave theories for DC in the \(\alpha -{\text{He}}\) collisions.

Many inputs to the unprecedented ’fusion quest’ for a new sustainable, carbon-free, global energy supply through plasma physics proved to be essential. Among these, atomic collision physics with its CXS diagnostic methodology ranks high. Such a status should serve as an impetus for further advances in theoretical modelings of charge exchange phenomena at intermediate and high impact energies. One of the goals of atomic collision physics within the fusion plasmas and other mentioned cross-disciplinary applications is to enhance the accuracy of the cross section data bases. The sought accuracy is especially missing for DC in both theory and measurements [27,28,29,30]. For DC, the existing quantum-mechanical four-body (4B) distorted wave perturbative theories are in large mutual disparity. Quite unexpectedly, some of these methods, known as successful for SC, are in sharp disagreement with the measured total cross sections for DC.

Besides the CB1-4B method, we shall also consider the continuum distorted wave (CDW-4B) [31], the boundary-corrected continuum intermediate state (BCIS-4B) [32] and the Born distorted wave (BDW-4B) methods [33]. For arbitrary charges of the projectile and target nuclei, these four theories have both the initial and final scattering functions with the correct outgoing and incoming spherical wave boundary conditions at infinitely large inter-particle distances. The goal of the present study is to examine the quantitative extent of the actual influence of the Coulomb distortions on the unperturbed channel wave functions as a function of E. To that end, the original nuclear charges are modified.

The perturbation strength, which is gauged by the Sommerfeld factor (a ratio of a nuclear charge and an incident velocity \(v\)) is gradually diminished. The net effect on Q caused by this weakening of the Coulomb distorted waves is monitored as a function of E. This has two goals:

  • (i) To allow a smooth passage from one to another method (BCIS-4B \(\rightarrow \) CB1-4B, CDW-4B \(\rightarrow \) BDW-4B), thus permitting the cross-validation of different computing programs that should give the same numerical results for Q in the pertinent limiting cases.

  • (ii) To determine the energy region where it is essential to retain the electronic Coulomb logarithmic phases. These phases are the purely electronic parts of the distortions due to the relative motion of heavy scattering aggregates, associated with the charge of a free nucleus and the net charge of the heliumlike system.

Atomic units will be used throughout unless noted otherwise.

2 Theory

We examine the problem of double capture or DC by a nucleus P of charge \(Z_\mathrm{\scriptscriptstyle P}\) and mass \(M_\mathrm{\scriptscriptstyle P}\gg 1\) from a heliumlike atom with a nucleus T of charge \(Z_\mathrm{\scriptscriptstyle T}\) of mass \(M_\mathrm{\scriptscriptstyle T}\gg 1\), as schematized by the process:

$$\begin{aligned} Z_\mathrm{\scriptscriptstyle P}+(Z_\mathrm{\scriptscriptstyle T};e_1,e_2)_i\longrightarrow (Z_\mathrm{\scriptscriptstyle P};e_1,e_2)_f+Z_\mathrm{\scriptscriptstyle T}, \end{aligned}$$
(1)

where \(e_k\) is the \(k\,\)th electron \((k=1,2).\) The small parentheses indicate the bound states with the usual sets of the quantum numbers \(\{i,f\}.\)

The two-electron initial and final bound states with their corresponding energies are \(\{\varphi _i(\varvec{x}_1,\varvec{x}_2),\, \varphi _f(\varvec{s}_1,\varvec{s}_2)\}\) and \(\{E^\mathrm{\scriptscriptstyle T}_i,\, E^\mathrm{\scriptscriptstyle P}_f\}\), respectively. Here, \(\varvec{x}_k\) and \(\varvec{s}_k\) are the position vectors of the \(k\,\)th electron relative to \(Z_\mathrm{\scriptscriptstyle T}\) and \(Z_\mathrm{\scriptscriptstyle P}\), respectively. The position vector of \(Z_\mathrm{\scriptscriptstyle P}\) relative to \(Z_\mathrm{\scriptscriptstyle T}\) is \(\varvec{R}\), which is connected to the electronic coordinates by \(\varvec{R}=\varvec{x}_1-\varvec{s}_1=\varvec{x}_2-\varvec{s}_2.\)

Further, let \(\varvec{r}_i\) and \(\varvec{r}_f\) be the position vectors of P and T relative to the centers-of-masses of the atomic systems \((Z_\mathrm{\scriptscriptstyle T};e_1,e_2)_i\) and \((Z_\mathrm{\scriptscriptstyle P};e_1,e_2)_f\), respectively. In the entrance and exit channels, the initial and final unperturbed states of the whole system are \(\Phi _i=\varphi _i\text{e}^{i\varvec{k}_i\cdot \varvec{r}_i}\) and \(\Phi _f=\varphi _f\text{e}^{-i\varvec{k}_f\cdot \varvec{r}_f}\), respectively. The momentum vector of P with respect to \((Z_\mathrm{\scriptscriptstyle T};e_1,e_2)_i\) is \(\varvec{k}_i\) and the momentum vector of \((Z_\mathrm{\scriptscriptstyle P};e_1,e_2)_f\) relative to T is \(\varvec{k}_f\).

Taking the target to be at rest, the relative velocity of the two colliding aggregates becomes the incident velocity of \(Z_\mathrm{\scriptscriptstyle P}\). The incident velocity vector \(\varvec{v}\) is directed along the unit vector \({\hat{\varvec{Z}}}\) of the Z-axis (\(\varvec{v}=v\hat{\varvec{Z}}\)) in the arbitrary Galilean XOYZ coordinate system. Thus, vector \(\varvec{R}\) acquires its two-component form as \(\varvec{R}=\{\varvec {\rho },\varvec{Z}\}=\varvec {\rho }+Z\hat{\varvec{v}}\) with vector \(\varvec {\rho }\) lying in the collisional XOY plane so that \(\varvec {\rho }\cdot \varvec{v}=0\). The vectorial projection \(\varvec {\rho }\) of \(\varvec{R}\) onto the XOY plane should not be confused with the impact parameter since we treat the nuclear motion quantum-mechanically as opposed to using classical straight-line trajectories.

In distorted wave theories for process (1), the unperturbed states \(\Phi _{i,f}\) are modified by the correlation effects between the two scattering aggregates. Such correlations lead to the Coulomb distortions of \(\Phi _{i,f}\). This amounts to multiplying \(\Phi _{i,f}\) by the Coulomb distortion factors. The actual distortion can come from the Coulomb interactions between the free nuclear charges and the electrons or from the nuclear-nuclear Coulomb potential (or both) in one or two channels. The electron-nucleus attractive Coulomb potentials \(\{-Z_\mathrm{\scriptscriptstyle P}/s_k,\,-Z_\mathrm{\scriptscriptstyle T}/x_k\}\, (k=1, \, 2)\) in the entrance and exit channels yield the full Coulomb wave functions that multiply \(\Phi _{i,f}\), respectively.

The repulsive nucleus-nucleus Coulomb potential \(V_\mathrm{\scriptscriptstyle PT}=Z_\mathrm{\scriptscriptstyle P}Z_\mathrm{\scriptscriptstyle T}/R\) also leads to the full Coulomb wave functions. They too, as a part of the overall correlation effect, multiply the unperturbed states \(\Phi _{i,f}\). Such nuclear Coulomb wave functions reduce to their logarithmic phases \(\text{e}^{\pm i(Z_\mathrm{\scriptscriptstyle P}Z_{\mathrm{\scriptscriptstyle T}}/v){\text{ln}}(\mu vR\mp \mu \varvec{v}\cdot \varvec{R})}\). These latter phases are valid at all distances because of the heavy reduced mass \(\mu =M_\mathrm{\scriptscriptstyle P}M_\mathrm{\scriptscriptstyle P}/(M_\mathrm{\scriptscriptstyle P}+M_\mathrm{\scriptscriptstyle P})\gg 1\) of nuclei P and T colliding predominantly in the forward (eikonal) direction. We explicitly checked numerically for process (1) with \(Z_\mathrm{\scriptscriptstyle P}=Z_\mathrm{\scriptscriptstyle T}=2\) that computations with the full internuclear Coulomb waves and their eikonal phases give the same total cross sections Q to within 2-3 decimal places.

The same type of the mentioned reduction also applies to the asymptotic forms \(Z_\mathrm{\scriptscriptstyle P}(Z_\mathrm{\scriptscriptstyle T}-2)/R\) and \(Z_\mathrm{\scriptscriptstyle T}(Z_\mathrm{\scriptscriptstyle P}-2)/R\) of the initial and final perturbation potentials \(V_i=Z_\mathrm{\scriptscriptstyle P}Z_\mathrm{\scriptscriptstyle T}/R-Z_\mathrm{\scriptscriptstyle P}/s_1-Z_\mathrm{\scriptscriptstyle P}/s_2\) and \(V_f=Z_\mathrm{\scriptscriptstyle P}Z_\mathrm{\scriptscriptstyle T}/R-Z_\mathrm{\scriptscriptstyle T}/x_1-Z_\mathrm{\scriptscriptstyle T}/x_2\), respectively. Here, the screened nuclear charges \(Z_\mathrm{\scriptscriptstyle T}-2\) and \(Z_\mathrm{\scriptscriptstyle P}-2\) are the net charges of the two-electron systems \((Z_\mathrm{\scriptscriptstyle T};e_1,e_2)_i\) and \((Z_\mathrm{\scriptscriptstyle P};e_1,e_2)_f\) in the entrance and exit channels, respectively. The Coulomb phase for the relative motion of heavy scattering aggregates \(\{Z_\mathrm{\scriptscriptstyle P},(Z_\mathrm{\scriptscriptstyle T};e_1,e_2)_i\}\) and \(\{(Z_\mathrm{\scriptscriptstyle P};e_1,e_2)_f,Z_\mathrm{\scriptscriptstyle T}\}\) is \(\{\text{e}^{i[Z_{\mathrm{\scriptscriptstyle P}}(Z_{\text{T}}-2)/v]{\text{ln}}(\mu vR-\mu \varvec{v}\cdot \varvec{R})}, \text{e}^{-i[Z_{\mathrm{\scriptscriptstyle T}}(Z_{\mathrm{\scriptscriptstyle P}}-2)/v]{\text{ln}}(\mu vR+\mu \varvec{v}\cdot \varvec{R})}\}\), respectively.

From the product \(\text{e}^{i[Z_{\mathrm{\scriptscriptstyle P}}(Z_{\text{T}}-2)/v]{\text{ln}}(\mu vR-\mu \varvec{v}\cdot \varvec{R})} \text{e}^{i[Z_{\mathrm{\scriptscriptstyle T}}(Z_{\mathrm{\scriptscriptstyle P}}-2)/v]{\text{ln}}(\mu vR+\mu \varvec{v}\cdot \varvec{R})}\) contained in the transition amplitude and total cross section Q, the part \(\text{e}^{i(Z_{\mathrm{\scriptscriptstyle P}}Z_{\text{T}}/v){\text{ln}}(\mu vR-\mu \varvec{v}\cdot \varvec{R})} \text{e}^{i(Z_{\mathrm{\scriptscriptstyle T}}Z_{\mathrm{\scriptscriptstyle P}})/v){\text{ln}}(\mu vR+\mu \varvec{v}\cdot \varvec{R})}\) due to \(V_\mathrm{\scriptscriptstyle PT}\) disappears [27]. The remainders in that product are the purely electronic logarithmic phases \(\text{e}^{-i(2Z_{\mathrm{\scriptscriptstyle P}}/v){\text{ln}}(vR-\varvec{v}\cdot \varvec{R})}\) and \(\text{e}^{i(2Z_{\mathrm{\scriptscriptstyle T}}/v){\text{ln}}(vR+\varvec{v}\cdot \varvec{R})}\). Herein, as well as in the other similar Coulomb logarithmic terms, mass \(\mu \) can be left out because it leads to an unimportant phase of unit amplitude. In the phases \(\{\text{e}^{-i(2Z_{\mathrm{\scriptscriptstyle P}}/v){\text{ln}}(vR-\varvec{v}\cdot \varvec{R})},{\text{e}}^{i(2Z_{\mathrm{\scriptscriptstyle T}}/v){\text{ln}}(vR+\varvec{v}\cdot \varvec{R})}\}\) the doubled Sommerfeld factors \(2Z_{\mathrm{\scriptscriptstyle P}}/v\) and \(2Z_{\mathrm{\scriptscriptstyle T}}/v\) appear because of the presence of two electrons in heliumlike atoms.

For convenience, regarding the general hetero-nuclear case of process (1) with \(Z_\mathrm{\scriptscriptstyle P}\ne Z_\mathrm{\scriptscriptstyle T}\), the post CB1-4B and BCIS-4B methods as well as the prior BDW-4B and CDW-4B methods will be addressed. Generally, there is a post-prior discrepancy, i.e. the inequality of the post and prior cross sections (\(Q^+_{if}\ne Q^-_{if}\)). However, the illustrations from Sect. 3 are for the homo-nuclear case (\(Z_\mathrm{\scriptscriptstyle P}=Z_\mathrm{\scriptscriptstyle T}\)), dealing specifically with completely symmetric DC in the \(\alpha +{\text{He}}(1s^2)\rightarrow {\text{He}}(1s^2)+\alpha \) collisions. In this circumstance, there is no post-prior discrepancy, when the same type of the ground-state helium wave function is used in the entrance and exit channels. This is confirmed presently using the computer programs from the CB1-4B, BCIS-4B, BDW-4B and CDW-4B methods.

The extent of the Coulomb distortion effect is quantified by the perturbation strength, which represents the Sommerfeld factors \(Z_{\mathrm{\scriptscriptstyle P}}/v\) and \(Z_{\mathrm{\scriptscriptstyle T}}/v\). We want to find out how these distortions vary with changes in the perturbation strengths. To that end, \(Z_{\mathrm{\scriptscriptstyle P}}/v\) and \(Z_{\mathrm{\scriptscriptstyle T}}/v\) are replaced by \(\lambda Z_{\mathrm{\scriptscriptstyle P}}/v\) and \(\lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) (\(\lambda \ge 0\)) in the initial and final Coulomb distortions, respectively. Such changes are made in the BCIS-4B, BDW-4B and CDW-4B methods, but not in the CB1-4B method.

Moreover, \(\Phi _{i,f}\) and \(V_{i,f}\) are intact, i.e. they do not depend on \(\lambda \). Further, there is no \(\lambda -\)dependence either in the perturbation potentials \(Z_\mathrm{\scriptscriptstyle P}(2/R-1/s_1-1/s_2)\) and \(Z_\mathrm{\scriptscriptstyle T}(2/R-1/x_1-1/x_2)\) from the prior and post forms of the transition amplitudes in the BCIS-4B method. This particular design permits to formally recover the exact numerical values of the cross sections in the CB1-4B method by utilizing the independent computer program in the BCIS-4B method to which the limit \(\lambda \rightarrow 0\) is applied. In the same limit \(\lambda \rightarrow 0\), it should also be possible to obtain the cross sections in the BDW-4B method from the separate computer program in the CDW-4B method.

As stated in Sect. 1, the present goal is twofold: (i) to assess the overall effect of the perturbation strengths in the Coulomb distortion factors at different impact energies and (ii) to verify whether the same cross sections can be obtained when passing from one to another distorted wave method by using different computer programs. Such a task can be accomplished by monitoring the sensitivity of the predicted total cross sections Q to variation of the scaling parameter \(\lambda \) in the interval \(0\le \lambda \le 1\). This can be done in any distorted wave theory. To exemplify, the current illustrations are reported using the \(\lambda -\)modified BCIS-4B, BDW-4B and CDW-4B methods.

In the post form of the transition amplitude \(T^\mathrm{(BCIS-4B)+}_{if}\), the Sommerfeld factor \(Z_{\mathrm{\scriptscriptstyle P}}/v\) is present in each of the two full electronic Coulomb wave functions in the entrance channel through the Gauss confluent hypergeometric functions (the Kummer functions) and the corresponding Euler gamma functions in the normalization constants. These Coulomb distortions of \(\Phi _i\) are due to the potentials \(-Z_\mathrm{\scriptscriptstyle P}/s_1\) and \(-Z_\mathrm{\scriptscriptstyle P}/s_2\), i.e. to the interactions between \(Z_\mathrm{\scriptscriptstyle P}\) and \(e_k\, (k=1,2)\). The other Coulomb distortion of \(\Phi _i\) comes from the internuclear potential \(Z_\mathrm{\scriptscriptstyle T}Z_\mathrm{\scriptscriptstyle P}/R\). As mentioned, in the heavy mass limit \(M_\mathrm{\scriptscriptstyle P.T}\gg 1\), this latter distortion is given by the logarithmic phase \(\text{e}^{i(Z_{\mathrm{\scriptscriptstyle P}}Z_{\mathrm{\scriptscriptstyle T}}/v)\ln {(vR-\varvec{v}\cdot \varvec{R}\,)}}\).

In the exit channel described by \(T^\mathrm{(BCIS-4B)+}_{if}\), the Sommerfeld factor \(2Z_{\mathrm{\scriptscriptstyle T}}/v\) appears in the electronic Coulomb logarithmic phase \(\text{e}^{i(2Z_{\mathrm{\scriptscriptstyle T}}/v)\ln {(vR+\varvec{v}\cdot \varvec{R}\,)}}\). As noted, this distortion of \(\Phi _f\) stems from the final compound distortion \(\text{e}^{-i[Z_{\mathrm{\scriptscriptstyle T}}(Z_{\mathrm{\scriptscriptstyle P}}-2)/v]\ln {(vR+\varvec{v}\cdot \varvec{R}\,)}}\) due the asymptote \(Z_\mathrm{\scriptscriptstyle T}(Z_\mathrm{\scriptscriptstyle P}-2)/R\) of \(V_f\) at \(R\rightarrow \infty \). Thus, the latter Coulomb logarithmic phase describes the relative motion of the heavy scattering aggregates \(Z_\mathrm{\scriptscriptstyle T}\) and \((Z_P;e_1,e_2)_f\) in the final state of the complete system.

In the transition amplitude \(T^\mathrm{(BCIS-4B)+}_{if}\), there appears the following product of the initial and the complex-conjugated final logarithmic phases:

$$\begin{aligned}{} & {} \text{e}^{i(Z_{\mathrm{\scriptscriptstyle P}}Z_{\mathrm{\scriptscriptstyle T}}/{v})\ln {(vR-\varvec{v}\cdot \varvec{R}\,)}}\text{e}^{i[Z_{\mathrm{\scriptscriptstyle T}}(Z_{\mathrm{\scriptscriptstyle P}}-2)/v]\ln {(vR+\varvec{v}\cdot \varvec{R}\,)}}\nonumber \\{} & {} \quad =(\rho v)^{2i\nu _\mathrm{\scriptscriptstyle PT}}\text{e}^{-2i(Z_{\mathrm{\scriptscriptstyle T}}/v)\ln {(vR+\varvec{v}\cdot \varvec{R}\,)}},\,\,\nu _\mathrm{\scriptscriptstyle PT}=\frac{Z_\mathrm{\scriptscriptstyle P}Z_{\mathrm{\scriptscriptstyle T}}}{v}. \end{aligned}$$
(2)

The factor \((\rho {v})^{2i\nu _{\mathrm{\scriptscriptstyle PT}}}\) is the only contribution from the Coulomb internuclear potential \(Z_\mathrm{\scriptscriptstyle P}Z_\mathrm{\scriptscriptstyle T}/R\). The phase \((\rho {v})^{2i\nu _{\mathrm{\scriptscriptstyle PT}}}\) disappears from the total cross section \(Q^\mathrm{(BCIS-4B)+}_{if}\). As such, this cross section is computed from the pure electronic matrix element. It is therein that the Sommerfeld factors \(Z_{\mathrm{\scriptscriptstyle P}}/v\) and \(2Z_{\mathrm{\scriptscriptstyle T}}/v\) are replaced by their modified counterparts \(\lambda Z_{\mathrm{\scriptscriptstyle P}}/v\) and \(2\lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) in the pertinent distortions that are the initial two full Coulomb waves and the final \(\varvec{R}-\)dependent Coulomb logarithmic phase, respectively. Thus, for process (1), in order to compute \(Q^\mathrm{(BCIS-4B)+}_{if}\), we can employ the matrix element \(R^\mathrm{(BCIS-4B)+}_{if}\), which differs from \(T^\mathrm{(BCIS-4B)+}_{if}\) only in the absence of the nucleus-nucleus eikonal phase \((\rho {v})^{2i\nu _{\mathrm{\scriptscriptstyle PT}}}\).

There exists a product of the type (2) also in \(T^\mathrm{(CB1-4B)+}_{if}\). Specifically, this transition amplitude contains the logarithmic Coulomb phase distortions \(\text{e}^{i[Z_{\mathrm{\scriptscriptstyle P}}(Z_{\mathrm{\scriptscriptstyle T}}-2)/v]\ln {(vR-\varvec{v}\cdot \varvec{R}\,)}}\) and \(\text{e}^{-i[Z_{\mathrm{\scriptscriptstyle T}}(Z_{\mathrm{\scriptscriptstyle P}}-2)/v]\ln {(vR+\varvec{v}\cdot \varvec{R}\,)}}\) of \(\Phi _i\) and \(\Phi _f\), respectively. The former and the latter distortions stem from the descriptions of the relative motions of heavy collision aggregates \(\{Z_\mathrm{\scriptscriptstyle P},\,(Z_\mathrm{\scriptscriptstyle T};e_1,e_2)_i\}\) and \(\{(Z_\mathrm{\scriptscriptstyle P};e_1,e_2)_f,\,Z_\mathrm{\scriptscriptstyle T}\}\) in the entrance and exit channels, respectively. These distortions appear in \(T^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}\) through the product:

$$\begin{aligned}{} & {} \text{e}^{i[Z_{\mathrm{\scriptscriptstyle P}}(Z_{\mathrm{\scriptscriptstyle T}}-2)/v]\ln {(vR-\varvec{v}\cdot \varvec{R}\,)}} \text{e}^{i[Z_{\mathrm{\scriptscriptstyle T}}(Z_{\mathrm{\scriptscriptstyle P}}-2)/v]\ln {(vR+\varvec{v}\cdot \varvec{R}\,)}}\nonumber \\{} & {} \quad =(\rho v)^{2i\nu _i}\text{e}^{-2i\xi \ln {(vR+\varvec{v}\cdot \varvec{R}\,)}},\,\,\xi =\frac{Z_{\mathrm{\scriptscriptstyle T}}-Z_\mathrm{\scriptscriptstyle P}}{v},\,\,\,\nu _i=\frac{Z_{\mathrm{\scriptscriptstyle P}}(Z_{\mathrm{\scriptscriptstyle T}}-2)}{v}. \end{aligned}$$
(3)

In \(Q^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}\), the factor \((\rho {v})^{2i\nu _i}\) vanishes and \(T^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}\) is reduced to \(R^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}\), which is the electronic matrix element in the CB1-4B method.

In the same vein, the cross sections \(Q^\mathrm{(BDW-4B)-}_{if}\) and \(Q^\mathrm{(CDW-4B)-}_{if}\) are computed by means of the corresponding electronic matrix elements \(R^\mathrm{(BDW-4B)-}_{if}\) and \(R^\mathrm{(CDW-4B)-}_{if}\), respectively. These matrix elements differ from the original transition amplitudes \(T^\mathrm{(BDW-4B)-}_{if}\) and \(T^\mathrm{(CDW-4B)-}_{if}\) merely in dropping the non-contributing phases \((\rho {v})^{2iZ_{\mathrm{\scriptscriptstyle P}}(Z_{\mathrm{\scriptscriptstyle T}}-2)/v}\) and \((\rho {v})^{2iZ_{\mathrm{\scriptscriptstyle P}}Z_{\mathrm{\scriptscriptstyle T}}/v}\), respectively [27].

The matrix elements \(R^\mathrm{(CB1-4B)+}_{if}\), \(R^\mathrm{(BCIS-4B)+}_{if}\), \(R^\mathrm{(BDW-4B)-}_{if}\) and \(R^\mathrm{(CDW-4B)-}_{if}\) share the following common exponential term from the product of the plane waves in \(\Phi _i\Phi ^\star _f\) [27,28,29,30]:

$$\begin{aligned} {{\mathcal {E}}}_{if}= & {} \text{e}^{i\varvec{k}_i\cdot \varvec{r}_i+i\varvec{k}_f\cdot \varvec{r}_f}\nonumber \\= & {} \text{e}^{i\varvec{\alpha }\cdot ({\varvec{s}}_1+{\varvec{s}}_2)+i\varvec{\beta }\cdot ({\varvec{x}}_1+{\varvec{x}}_2)} =\text{e}^{2i\varvec{\beta }\cdot \!\varvec{R}-i\varvec{v}\cdot (\varvec{s}_1+\varvec{s}_2)} =\text{e}^{-2i\varvec{\alpha }\cdot \varvec{R}-i\varvec{v}\cdot (\varvec{x}_1+\varvec{x}_2)}, \end{aligned}$$
(4)
$$\begin{aligned} \left. \begin{array}{c} {\displaystyle { \varvec{\alpha }=\frac{\varvec{\eta }-{v}^+\varvec{v}}{2},\, \varvec{\beta }=-\frac{\varvec{\eta }+{v}^-\varvec{v}}{2} ,\, \varvec{\alpha }+\varvec{\beta }=-\varvec{v} }}\\ \\ {\displaystyle { {v}^+=1+\frac{\mathrm{\Delta }E_{if}}{{v}^2}\,\,,\,\,{v}^-=1-\frac{\mathrm{\Delta }E_{if}}{{v}^2}\,\,,\,\,\mathrm{\Delta }E_{if} =E^\mathrm{\scriptscriptstyle P}_f-E^\mathrm{\scriptscriptstyle T}_i }} \end{array}\right\} . \end{aligned}$$
(5)

Here, \(\varvec{\eta}\) is the transverse momentum vector, which is perpendicular to the incident velocity (\(\varvec{\eta}\cdot \varvec{v}=0\)). In (4), the electronic translation factor (ETF) for \(e_{1,2}\) are \(\varvec{v}\cdot (\varvec{s}_1+\varvec{s}_2)\) and \(\varvec{v}\cdot (\varvec{x}_1+\varvec{x}_2)\). They cannot be neglected and their importance rapidly increases with the augmented incident velocity \(v\). After these preliminary remarks, we can pass now to the main working formulae for the CB1-4B, BCIS-4B, BDW-4B and CDW-4B methods.

2.1 The post form of the CB1-4B method

$$ Q^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}(a^2_0)=\int\!\!{\text{d}}\varvec{\eta }\left| \frac{R^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}(\varvec{\eta }\,)}{2\pi {v}}\right| ^2, $$
(6)
$$\begin{aligned}{} &{} R^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}(\varvec{\eta }\,)=\int\!\!\int\!\!\int\!\!{\text {d}}\varvec{x}_1{\text {d}}\varvec{x}_2{\text {d}}\varvec{R}\, ({v}R+\!\varvec{v}\cdot \varvec{R})^{-2i\xi }{{\mathcal {E}}}_{if}\mathcal {B}^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}, \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \mathcal {B}^\mathrm{\scriptscriptstyle {(CB1-4B)}+}_{if}=\varphi ^\star _f(\varvec{s}_1,\varvec{s}_2\,) \left[Z_\mathrm{\scriptscriptstyle T}\left( \frac{2}{R}-\frac{1}{x_1}-\frac{1}{x_2}\right) \right]\varphi _i(\varvec{x}_1,\varvec{x}_2\,). \end{aligned}$$
(8)

Here, the original nuclear charges \(Z_\mathrm{\scriptscriptstyle P,T}\) for processes (20) and (21) with no scaling parameter \(\lambda\) are used and thus the Sommerfeld factor \(\xi\) from (7) is given by (3). Stated equivalently, if \(Z_\mathrm{\scriptscriptstyle P,T}\) were respectively replaced by \(\lambda Z_\mathrm{\scriptscriptstyle P,T}\) in the CB1-4B method, then its exact version would correspond to \(\lambda=1\).

2.2 The post form of the BCIS-4B method

$$ Q^\mathrm{\scriptscriptstyle {(BCIS-4B)}+}_{if,\lambda }(a^2_0)= \int\!\!{\text {d}}\varvec{\eta }\left| \frac{R^\mathrm{\scriptscriptstyle {(BCIS-4B)}+}_{if,\lambda }(\varvec{\eta }\,)}{2\pi {v}}\right| ^2, $$
(9)
$$\begin{aligned}{} & {} R^\mathrm{\scriptscriptstyle {(BCIS-4B)}+}_{if,\lambda }(\varvec{\eta }\,)\!=\!N_{\mathrm{\scriptscriptstyle P},\lambda } \!\!\int\!\!\int\!\!\int\!\!{\text {d}}\varvec{s}_1{\text {d}}\varvec{s}_2{\text {d}}\varvec{R} \, ({v}R\!+\!\varvec{v}\!\cdot \!\varvec{R})^{-2i\lambda \nu _\mathrm{\scriptscriptstyle T}}{{\mathcal {E}}}_{if}\mathcal {B}^\mathrm{\scriptscriptstyle {(BCIS-4B)}+}_{if,\lambda }, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \mathcal {B}^\mathrm{\scriptscriptstyle {(BCIS-4B)}+}_{if,\lambda } =\varphi ^\star _f(\varvec{s}_1,\varvec{s}_2\,) \left[Z_\mathrm{\scriptscriptstyle T}\left( \frac{2}{R}-\frac{1}{x_1}-\frac{1}{x_2}\right) \right]\varphi _i(\varvec{x}_1,\varvec{x}_2\,)\nonumber \\{} & {} \quad \times {}_1F_1(i\lambda \nu _\mathrm{\scriptscriptstyle P},1,i{v}s_1+i\varvec{v}\!\cdot {\varvec{s}}_1)\, {}_1F_1(i\lambda \nu _\mathrm{\scriptscriptstyle P},1,i{v}s_2+i\varvec{v}\cdot {\varvec{s}}_2), \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \left. \begin{array}{c} {\displaystyle {N_{\mathrm{\scriptscriptstyle P},\lambda }=\left| N^{-\star }(\lambda \nu _\mathrm{\scriptscriptstyle P})\right| ^2}}\\ \\ {\displaystyle {N^-(\lambda \nu _\mathrm{\scriptscriptstyle P})={\text{ e }}^{\pi \lambda \nu _\mathrm{\scriptscriptstyle P}/2}\mathrm{\Gamma }(1+i\lambda \nu _\mathrm{\scriptscriptstyle P}) \,\,,\,\,\nu _\mathrm{\scriptscriptstyle P}=\frac{Z_{\mathrm{\scriptscriptstyle P}}}{v}\,\,, \,\,\nu _\mathrm{\scriptscriptstyle T}=\frac{Z_{\mathrm{\scriptscriptstyle T}}}{v} }} \end{array}\right\} . \end{aligned}$$
(12)

2.3 The prior form of the BDW-4B method

$$ Q^\mathrm{\scriptscriptstyle {(BDW-4B)}-}_{if,\lambda }(a^2_0) =\int\!\!{\text {d}}\varvec{\eta }\left| \frac{R^\mathrm{\scriptscriptstyle {(BDW-4B)}-}_{if,\lambda }(\varvec{\eta }\,)}{2\pi {v}}\right| ^2, $$
(13)
$$\begin{aligned}{} & {} R^\mathrm{\scriptscriptstyle {(BDW-4B)}-}_{if,\lambda }(\varvec{\eta }\,)\!=\!-N_\mathrm{\scriptscriptstyle P,1}\!\int\!\!\int\!\!\int\!\!{\text {d}}\varvec{x}_1{\text {d}}\varvec{x}_2{\text {d}}\varvec{R} \,({v}R\!+\!\varvec{v}\cdot \varvec{R})^{-2i\lambda \nu _\mathrm{\scriptscriptstyle T}}{{\mathcal {E}}}_{if}\mathcal {B}^\mathrm{\scriptscriptstyle {(BDW-4B)}-}_{if,1 }, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \mathcal {B}^\mathrm{\scriptscriptstyle {(BDW-4B)}-}_{if,1 } =\varphi ^\star _f({\varvec{s}}_1,{\varvec{s}}_2) \nonumber \\{} & {} \quad \times \left\{ {}_1F_1(i\nu _\mathrm{\scriptscriptstyle P},1,i{v}s_2+i\varvec{v}\cdot {\varvec{s}}_2){\varvec{\nabla }}_{x_{1}}\varphi _i({\varvec{x}}_1,{\varvec{x}}_2)\cdot {\varvec{\nabla }}_{s_{1}} \,{}_1F_1(i\nu _\mathrm{\scriptscriptstyle P},1,i{v}s_1+i\varvec{v}\cdot {\varvec{s}}_1) \right. \nonumber \\{} & {} \quad +\!\left. \, \,{}_1F_1(i\nu _\mathrm{\scriptscriptstyle P},1,i{v}s_1+i\varvec{v}\cdot {\varvec{s}}_1){\varvec{\nabla }}_{x_{2}}\varphi _i({\varvec{x}}_1,{\varvec{x}}_2)\cdot {\varvec{\nabla }}_{s_{2}} \,{}_1F_1(i\nu _\mathrm{\scriptscriptstyle P},1,i{v}s_2+i\varvec{v}\cdot {\varvec{s}}_2) \right\} .\nonumber \\ \end{aligned}$$
(15)

2.4 The prior form of the CDW-4B method

$$ Q^\mathrm{\scriptscriptstyle {(CDW-4B)}-}_{if,\lambda }(a^2_0) =\int\!\!{\text {d}}\varvec{\eta }\left| \frac{R^\mathrm{\scriptscriptstyle {(CDW-4B)}-}_{if,\lambda }(\varvec{\eta }\,)}{2\pi {v}}\right| ^2, $$
(16)
$$\begin{aligned}{} & {} R^\mathrm{\scriptscriptstyle {(CDW-4B)}-}_{if,\lambda }(\varvec{\eta }\,)=-N_\mathrm{\scriptscriptstyle P,1}N_{\mathrm{\scriptscriptstyle T},\lambda }\int\!\!\int\!\!\int\!\!{\text {d}}{\varvec{x}}_1 {\text {d}}{\varvec{x}}_2{\text {d}}{\varvec{R}} \,{{\mathcal {E}}}_{if}{\mathcal B}^\mathrm{\scriptscriptstyle {(CDW-4B)}-}_{if,\lambda }, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \mathcal {B}^\mathrm{\scriptscriptstyle {(CDW-4B)}-}_{if,\lambda }=\varphi ^\star _f({\varvec{s}}_1,{\varvec{s}}_2) \nonumber \\{} & {} \quad \times {}_1F_1(i\lambda \nu _\mathrm{\scriptscriptstyle T},1,i{v}x_1+i\varvec{v}\cdot {\varvec{x}}_1) \,{}_1F_1(i\lambda \nu _\mathrm{\scriptscriptstyle T},1,i{v}x_2+i\varvec{v}\cdot {\varvec{x}}_2) \nonumber \\{} & {} \quad \times \left\{ {}_1F_1(i\nu _\mathrm{\scriptscriptstyle P},1,ivs_2+i\varvec{v}\cdot {\varvec{s}}_2){\varvec{\nabla }}_{{x}_{1}}\varphi _i({\varvec{x}}_1,{\varvec{x}}_2)\cdot {\varvec{\nabla }}_{{s}_{1}} \,{}_1F_1(i\nu _\mathrm{\scriptscriptstyle P},1,i{v}s_1+i\varvec{v}\cdot {\varvec{s}}_1) \right. \nonumber \\{} & {} \qquad +\left. \,{}_1F_1(i\nu _\mathrm{\scriptscriptstyle P},1,i{v}s_1+i\varvec{v}\cdot {\varvec{s}}_1){\varvec{\nabla }}_{{x}_{2}}\varphi _i({\varvec{x}}_1,{\varvec{x}}_2)\cdot {\varvec{\nabla }}_{{s}_{2}} \,{}_1F_1(i\nu _\mathrm{\scriptscriptstyle P},1,i{v}s_2+i\varvec{v}\cdot {\varvec{s}}_2) \right\} , \end{aligned}$$
(18)
$$\begin{aligned}{} & {} N_{\mathrm{\scriptscriptstyle T},\lambda }=\left| N^{-\star }(\lambda \nu _\mathrm{\scriptscriptstyle T})\right| ^2,\quad N^-(\lambda \nu _\mathrm{\scriptscriptstyle T})={\text{ e }}^{\pi \lambda \nu _\mathrm{\scriptscriptstyle T}/2}\mathrm{\Gamma }(1+i\lambda \nu _\mathrm{\scriptscriptstyle T}). \end{aligned}$$
(19)

3 Results and discussion

We shall now illustrate the theme from Sect. 2 in the exemplified case of DC by \(\alpha -\)particles from helium targets at intermediate and high impact energies E:

$$\begin{aligned} \mathrm{{}^4 He^{2+}+{}^4He(1s^2)\longrightarrow {}^4He(1s^2)+{}^4He^{2+}}. \end{aligned}$$
(20)

The presently employed CB1-4B, BCIS -4B, BDW-4B and CDW-4B methods for process (20) use the one-parameter wave functions of Hylleraas [34] for the initial \(\varphi _i=(1.6875/\pi )\text{e}^{-1.6875(x_1+x_2)}\) and the final \(\varphi _f=(1.6875/\pi )\text{e}^{-1.6875(s_1+s_2)}\) ground states of helium atoms. The multiple numerical integrations in the cross sections \(Q^\mathrm{(CB1-4B)+}_{if}\), \(Q^\mathrm{(BCIS-4B)+}_{if}\), \(Q^\mathrm{(BDW-4B)-}_{if}\) and \(Q^\mathrm{(CDW-4B)-}_{if}\) are computed by means of the adaptive Gauss-Legendre quadrature rule. The same number of the quadrature points is used per axis with no division of the integration bounds. In the CDW-4B methods, the Gauss-Mehler quadrature rule is employed for the azimuthal angle \(\phi \in [0,2\pi ]\) of vectors in the momentum state representation of the integrand.

In the literature, only two reports [8, 35] give the experimental data on total cross sections Q for the ground-to-ground state transition in process (20). All the other available measured cross sections Q are for the state-summed transitions with no information on any of the final bound states [6, 7, 9, 10, 36,37,38,39,40,41,42,43,44,45]:

$$\begin{aligned} \mathrm{{}^4 He^{2+}+{}^4He(1s^2)\longrightarrow {}^4He(\Sigma )+{}^4He^{2+}}. \end{aligned}$$
(21)

Symbol \(\Sigma \) denotes the contribution from the sum of all the final bound states of the newly formed helium atom in the exit channel of process (21).

The theme of Sect. 2 is the perturbation strength sensitivity of \(Q^\mathrm{(BCIS-4B)+}_{if}\), \(Q^\mathrm{(BDW-4B)-}_{if}\) and \(Q^\mathrm{(CDW-4B)-}_{if}\). The perturbation strength sensitivity of these cross sections is monitored by gradual changes in the Sommerfeld factors \(\lambda Z_{\mathrm{\scriptscriptstyle P}}/v\) and \(\lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) (\(\lambda \ge 0\)) from the Coulomb distortions in the entrance and exit channels, respectively. By definition, the BCIS-4B and CB1-4B methods become identical for \(\lambda =0\) for process (20) because the Sommerfeld factor \(\xi \) from (3) is equal to zero for all homo-nuclear collisions (\(Z_\mathrm{\scriptscriptstyle P}=Z_\mathrm{\scriptscriptstyle T}\)). Moreover, in the case of arbitrary \(Z_\mathrm{\scriptscriptstyle P}\) and \(Z_\mathrm{\scriptscriptstyle T}\) in process (1), the CDW-4B and BDW-4B methods must coincide for \(\lambda =0\). The specific values of the non-negative parameter \(\lambda \) are selected from the interval \(0\le \lambda \le 1\).

The results of the computations are presented in Table 1 and Figs. 1-6. Figures 1 and 2 as well as 4 and 5 are on the theoretical results alone. On the other hand, Figs. 3 and 6 are on both theories and measurements. The BCIS-4B and CB1-4B methods are in Table 1 as well as on Figs. 1-3. The CDW-4B and BDW-4B methods are on Figs. 4-6.

Fig. 1
figure 1

Total cross sections \(Q(\text{cm}^2)\) as a function of impact energy \(E(\text{keV})\) for double capture \((\alpha +{\text{He}})\) in process (20). Quantities \(\text{D}^+_{i,\lambda ;\mathrm{\scriptscriptstyle BCIS-4B}}\) and \(\text{D}^+_{f,\lambda ;\mathrm{\scriptscriptstyle BCIS-4B}}\) are from the full electronic Coulomb wave functions and the electronic Coulomb logarithmic phase, respectively. This figure is on the relationship between the post cross sections \(Q^\mathrm{\scriptscriptstyle (BCIS-4B)+}_{if}\) and \(Q^\mathrm{\scriptscriptstyle (CB1-4B)+}_{if}\). The general program for the BCIS-4B method is modified only in the Sommerfeld factors \(Z_{\mathrm{\scriptscriptstyle P}}/v\rightarrow \lambda Z_{\mathrm{\scriptscriptstyle P}}/v\) (in the initial two electronic full Coulomb waves) and \(2Z_{\mathrm{\scriptscriptstyle T}}/v\rightarrow 2\lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) (in the final electronic Coulomb phase). The exact BCIS-4B method is with \(\lambda =1\) (full black line). The BCIS-4B method for \(\lambda \) between 0 and 1 is with \(\lambda =0.75\) (full blue line), \(\lambda =0.5\) (full cyan line) and \(\lambda =0.001\) (circles, the same also with \(\lambda = 0\)). The BCIS-4B method for \(\lambda =0.001\) (circles) coincides with the exact CB1-4B method (full red line). For details, see the main text (Color figure online)

Full size image
Fig. 2
figure 2

Total cross sections \(Q(\text{cm}^2)\) as a function of impact energy \(E(\text{keV})\) for double capture \((\alpha +{\text{He}})\) in process (20). Quantities \(\text{D}^+_{i,\lambda ;\mathrm{\scriptscriptstyle BCIS-4B}}\) and \(\text{D}^+_{f,\lambda ;\mathrm{\scriptscriptstyle BCIS-4B}}\) are from the full electronic Coulomb wave functions and the electronic Coulomb logarithmic phase, respectively. This figure is on the relationship between the post cross sections \(Q^\mathrm{\scriptscriptstyle (BCIS-4B)+}_{if}\) and \(Q^\mathrm{\scriptscriptstyle (CB1-4B)+}_{if}\). The general program for the BCIS-4B method is modified only in the Sommerfeld factors \(Z_{\mathrm{\scriptscriptstyle P}}/v\rightarrow \lambda Z_{\mathrm{\scriptscriptstyle P}}/v\) (in the initial two electronic full Coulomb waves) and \(2Z_{\mathrm{\scriptscriptstyle T}}/v\rightarrow 2\lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) (in the final electronic Coulomb phase). The exact BCIS-4B method is with \(\lambda =1\) (full black line). The BCIS-4B method for \(\lambda \) between 0 and 1 is with \(\lambda =0.75\) (full blue line), \(\lambda =0.5\) (full cyan line) and \(\lambda =0.001\) (circles, the same also with \(\lambda \equiv 0\)). The BCIS-4B method for \(\lambda =0.001\) (circles) coincides with the exact CB1-4B method (full red line). Figure 2 is the enlarged panel (d) of Fig. 1. For details, see the main text (Color figure online)

Full size image
Fig. 3
figure 3

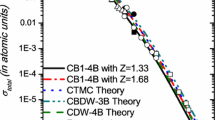
Total cross sections \(Q(\text{cm}^2)\) as a function of impact energy \(E(\text{keV})\) for double capture in the \(\alpha +{\text{He}}\) collisions. Theoretical results are for process (20) for which the initial and final ground state helium wave functions are represented by the one-parameter wave function of Hylleraas [34]. This is the case only in two measurements of Zastrow et al. [8] and Schöffler et al. [35]. All the remaining measured cross sections are for capture into any final bound non-autoionizing state of helium in process (21). The lines (specified on the figure itself) represent the theoretical results from the BCIS-4B and CB1-4B methods. Experimental data: \(\square \) [6], \(\bullet \) [7], \(\boxplus \) [8], \(\oplus \) [9], \(\triangledown \) [10], \(\bigstar \) [35], [35], \(\lozenge \) [36], \(\vartriangle \) [37], \(\blacksquare \) [38], \(\blacktriangle \) [39], \(\blacktriangledown \) [40], \(\blacklozenge \) [41], \(\circ \) [42], \(\blacktriangleleft \) [43], \(\triangleleft \) [44], \(\triangleright \) [45]. Only the symbols \(\boxplus \) [8] and (filled small red circles) [35] are for process (20): \({\text{He}}(1s^2)\rightarrow{\text{He}}(1s^2)\), whereas all the other symbols are for process (21): \({\text{He}}(1s^2)\rightarrow{\text{He}}(\Sigma)\). For details, see the main text (Color figure online)

Full size image
Fig. 4
figure 4

Total cross sections \(Q(\text{cm}^2)\) as a function of impact energy \(E(\text{keV})\) for double capture (\(\alpha +{\text{He}}\)) in process (20). Quantities \(\text{D}^+_{i;\mathrm{\scriptscriptstyle CDW-4B}}\), \(\text{D}^+_{i;\mathrm{\scriptscriptstyle BDW-4B}}\) and \(\text{D}^-_{f;\lambda ,\mathrm{\scriptscriptstyle CDW-4B}}\) are from the full electronic Coulomb wave functions, whereas \(\text{D}^-_{f;\lambda ,\mathrm{\scriptscriptstyle BDW-4B}}\) is the electronic Coulomb logarithmic phase. This figure is on the relationship between the prior cross sections \(Q^\mathrm{\scriptscriptstyle (CDW-4B)-}_{if}\) and \(Q^\mathrm{\scriptscriptstyle (BDW-4B)-}_{if}\). The general programs for the CDW-4B and BDW-4B methods are modified only in the Sommerfeld factors \(Z_{\mathrm{\scriptscriptstyle T}}/v\rightarrow \lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) (in the final two electronic full Coulomb waves) and \(2Z_{\mathrm{\scriptscriptstyle T}}/v\rightarrow 2\lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) (in the final electronic Coulomb phase), respectively. The exact CDW-4B and BDW-4B methods are with \(\lambda =1\) on (a, c): full red line and on (b, c): full blue line, respectively. The CDW-4B and BDW-4B methods with \(\lambda =0.00001\) are on (a, d): dashed red line and on (b, d): dashed blue line, respectively. On (d) with \(\lambda =0.00001\), the CDW-4B method (dashed red line) coincides with the BDW-4B method (dashed blue line) (Color figure online)

Full size image
Fig. 5
figure 5

Total cross sections \(Q(\text{cm}^2)\) as a function of impact energy \(E(\text{keV})\) for double capture (\(\alpha +{\text{He}}\)) in process (20). Quantities \(\text{D}^+_{i;\mathrm{\scriptscriptstyle CDW-4B}}\), \(\text{D}^+_{i;\mathrm{\scriptscriptstyle BDW-4B}}\) and \(\text{D}^-_{f,\lambda ;\mathrm{\scriptscriptstyle CDW-4B}}\) are from the full electronic Coulomb wave functions, whereas \(\text{D}^-_{f;\lambda ,\mathrm{\scriptscriptstyle BDW-4B}}\) is the electronic Coulomb logarithmic phase. This figure is on the relationship between the prior cross sections \(Q^\mathrm{\scriptscriptstyle (CDW-4B)-}_{if}\) and \(Q^\mathrm{\scriptscriptstyle (BDW-4B)-}_{if}\). The general programs for the CDW-4B and BDW-4B methods are modified only in the Sommerfeld factors \(Z_{\mathrm{\scriptscriptstyle T}}/v\rightarrow \lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) (in the final two electronic full Coulomb waves) and \(2Z_{\mathrm{\scriptscriptstyle T}}/v\rightarrow 2\lambda Z_{\mathrm{\scriptscriptstyle T}}/v\) (in the final electronic Coulomb phase), respectively. The exact CDW-4B and BDW-4B methods are with \(\lambda =1\) as the dashed red line and the full blue line, respectively. For \(\lambda =0.00001\), the CDW-4B method (full red line) coincides with the BDW-4B method (circles) (Color figure online)

Full size image
Fig. 6
figure 6

Total cross sections \(Q(\text{cm}^2)\) as a function of impact energy \(E(\text{keV})\) for double capture in the \(\alpha +{\text{He}}\) collisions. Theoretical results are for process (20) for which the initial and final ground state helium wave functions are represented by the one-parameter wave function of Hylleraas [34]. This is the case only in two measurements of Zastrow et al. [8] and Schöffler et al. [35]. All the remaining measured cross sections are for capture into any final bound non-autoionizing state of helium in process (21). The lines (specified on the figure itself) represent the theoretical results from the CDW-4B and BDW-4B methods. Experimental data: \(\square \) [6], \(\bullet \) [7], \(\boxplus \) [8], \(\oplus \) [9], \(\triangledown \) [10], \(\bigstar \) [35], [35], \(\lozenge \) [36], \(\vartriangle \) [37], \(\blacksquare \) [38], \(\blacktriangle \) [39], \(\blacktriangledown \) [40], \(\blacklozenge \) [41], \(\circ \) [42], \(\blacktriangleleft \) [43], \(\triangleleft \) [44], \(\triangleright \) [45]. Only the symbols \(\boxplus \) [8] and (filled small red circles) [35] are for process (20): \({\text{He}}(1s^2)\rightarrow{\text{He}}(1s^2)\), whereas all the other symbols are for process (21): \({\text{He}}(1s^2)\rightarrow{\text{He}}(\Sigma)\). For details, see the main text (Color figure online)

Full size image
Table 1 Total cross sections \(Q(\text{cm}^2)\) as a function of impact energy \(E(\text{keV})\) for double charge exchange \(\mathrm{{{}^4He^{2+}+{}^4He({}^1\,S)\rightarrow {}^4He({}^1\,S)+{}^4He^{2+}}}\) as in process (20). This table is on deducing \(Q^\mathrm{\scriptscriptstyle (CB1-4B)+}_{if}\) (exact) from the independent computer program for \(Q^\mathrm{\scriptscriptstyle (BCIS-4B)+}_{if}\) in which the original Sommerfeld factors \(Z_\text{P}/{v}\) and \(2Z_\text{T}/{v}\) are replaced by \(\lambda Z_\text{P}/{v}\) and \(2\lambda Z_\text{T}/{v}\), respectively. The values of \(\lambda \) are: 1, 0.75, 0.5, 0.001 and 0.00001. The results for \(Q^\mathrm{\scriptscriptstyle (BCIS-4B)+}_{if}\) \((\lambda =0.00001)\) and \(Q^\mathrm{\scriptscriptstyle (CB1-4B)+}_{if}\) (exact) are in perfect agreement at 100-7000 keV. Notation 2.3431,-17 means \(2.3431\times 10^{-17}\)
Full size table

The case with \(\lambda =1\) corresponds to the exact BCIS-4B method (no scaling of nuclear charges). By gradually diminishing parameter \(\lambda \), it should be possible to assess the rate of convergence of \(Q^\mathrm{(BCIS-4B)+}_{if}\) to the exact values of \(Q^\mathrm{(CB1-4B)+}_{if}\). This is shown in Table 1 for \(\lambda \in \{1.0,\,0.75,\, 0.5, \,0.001, \,0.00001\}\) as well as in Figs. 1-3 for \(\lambda \in \{1.0,\,0.75,\, 0.5, \,0.001\}\). The number of the Gauss-Legendre integration points per axis was 192 (BCIS-4B, CB1-4B: \(\lambda =1\)) and 96 (BCIS-4B: \(\lambda \ne 1\)).

The results for \(Q^\mathrm{(BCIS-4B)+}_{if}\, (\lambda =0.00001)\) and \(Q^\mathrm{(CB1-4B)+}_{if}\) (exact) in the 6th and 7th columns of Table 1, respectively, are in full agreement to within the displayed 3-4 decimal places. Corroborated with Table 1, the curves for \(\lambda \in (0,1)\) in Figs. 1 and 2 display the deviations of \(Q^\mathrm{(BCIS-4B)+}_{if}\, (\lambda \ne 1)\) from \(Q^\mathrm{(BCIS-4B)+}_{if}\, (\lambda =1).\) The farther the parameter \(\lambda \) from 1, the closer the cross section \(Q^\mathrm{(BCIS-4B)+}_{if}\, (\lambda \ne 1)\) to the exact \(Q^\mathrm{(CB1-4B)+}_{if}\). In particular, the circles for the BCIS-4B method (\(\lambda =0.00001\)) are seen in Figs. 1 and 2 to completely coincide with the full red line for the exact CB1-4B method (the same circles are obtained also for \(\lambda =0.001\)). This outcome cross-validates the adequacy of the different computer programs from the BCIS-4B and CB1-4B methods.

Figure 3 is similar to Fig. 2 except for inclusion of the experimental data from various measurements. Overall, as has previously been established [27,28,29,30, 32], the BCIS-4B method (exact, \(\lambda =1\)) compares more favorably with the experimental data than the CB1-4B method (exact). The situation observed in the BCIS-4B method for e.g. \(\lambda =0.5\) at 100-2000 keV suggests that it might be of interest to consider some effective nuclear charges \(Z^\text{eff}_\mathrm{\scriptscriptstyle P,T}\) dependent on the incident velocity \(v\). Below 1000 keV, this could improve the standing of the BCIS-4B method relative to the experimental data.

As announced, Figs. 4-6 are on the relationship between the CDW-4B and BDW-4B methods. The subject is the passage from \(Q^\mathrm{(CDW-4B)-}_{if}\) to \(Q^\mathrm{(BDW-4B)-}_{if}\) as a function of \(\lambda \) for the given energy E. The displayed results refer to \(\lambda =1\) and \(\lambda =0.00001\). Both the BDW-4B and CDW-4B methods employ the same number of the Gauss-Legendre integration points per axis: 192 (\(\lambda =1\)) and 96 (\(\lambda =0.00001\)). It is seen in Figs. 4 and 5 that the CDW-4B method is much more sensitive than the BDW-4B method to changes in the perturbation strengths. Therein, a marked difference exists between \(Q^\mathrm{(CDW-4B)-}_{if}\) (\(\lambda =1\)) and \(Q^\mathrm{(CDW-4B)-}_{if}\) (\(\lambda =0.00001\)) at all energies E. On the other hand, above 1000 keV, the cross sections \(Q^\mathrm{(BDW-4B)-}_{if}\) (\(\lambda =1\)) and \(Q^\mathrm{(BDW-4B)+}_{if}\) (\(\lambda =0.00001\)) are in excellent agreement. For \(\lambda =0.00001\), Figs. 4 and 5 show that the CDW-4B and BDW-4B methods give the indistinguishable total cross sections. Such a finding establishes the reliability of the different computer programs for the CDW-4B and BDW-4B methods.

Finally, Fig. 6 is an adaptation of Fig. 5 with an added aspect consisting of comparisons of theories and experimental data. Here too, at 100-2000 keV, it might be beneficial for the BDW-4B method to choose some effective nuclear charges \(Z^\text{eff}_\mathrm{\scriptscriptstyle P,T}\) as a function of \(v\). This might be especially influential in the CDW-4B method which exhibits a very strong dependence on the Sommerfeld factors on the incident velocity. Of course, all the potential modelings of the nuclear charges \(Z^\text{eff}_{\mathrm{\scriptscriptstyle P,T}}(v)\) in the Coulomb distortions should duly respect the correct boundary conditions. These critical conditions are not preserved in Fig. 6 for \(\lambda =0.00001\) in the CDW-4B and BDW-4B methods. The implication is that in such a case the favorable performance of these methods relative to the measurements should be considered as fortuitous.

Similarly, as per Fig. 4 at 100–2000 keV, the BCIS-4B method fares better with measurements for e.g. \(\lambda=0.5\) than for \(\lambda=1\), even though the former value of the scaling parameter violates the correct boundary conditions. This outcome in the BCIS-4B method with the fictitious value \(\lambda=0.5\) in the Sommerfeld factor for the perturbation strength should also be viewed as fortuitous.

It is not merely a good performance of a theory relative to measurements that should be of relevance for validation of the predictions. Prior to testing against measurements, it should be secured that theoretical methods obey the first principles of physics. One such principle is preservation of the initial and final correct boundary conditions for both the total scattering wave functions and the corresponding perturbation potentials, as is indeed the case for the physical value \(\lambda=1\) in the presently examined theories.

Although the scaling parameter \(\lambda\) in the fictitious nuclear charges \(\lambda Z_\mathrm{\scriptscriptstyle P,T}\) modifies the Coulomb distorted waves and disregards the correct boundary conditions, it is nevertheless instructive. Besides cross-validating the different algorithms in the CB1-4B, BCIS-4B, BDW-4B and CDW-4B methods, parameter \(\lambda\) informs about the energy region where the Coulomb distortions are numerically influential for total cross sections \(Q\).

Above 1000 keV (Fig. 6), the experimental data agree well with the BDW-4B method, which gives the indistinguishable values of \(Q\) for \(\lambda=1\) and \(\lambda=0.00001\) or \(\lambda=0\). In (13)–(15), the values \(\lambda=1\) and \(\lambda=0.00001\) (or \(\lambda=0\)) correspond respectively to including and excluding the electronic \(\varvec{R}\)-dependent Coulomb logarithmic phase, i.e. to obeying and disobeying the correct boundary conditions. In many past applications of a number of distorted wave methods, due mainly to computational complexities, the electronic \(\varvec{R}\)-dependent Coulomb logarithmic phases have often been ignored from the onset. The previous attempts for ‘justifying’ these omissions at all impact energies failed as they relied solely upon the relatively larger nuclear charges in asymmetric collisions.

In fact, as the present study shows, it is the given perturbation strength, through the associated Sommerfeld factor, that is of relevance for determining the energy region where the electronic \(\varvec{R}\)-dependent Coulomb logarithmic phases appreciably impact on total cross sections \(Q\). As per Fig. 6, in the BDW-4B method for processes (20) and (21), the electronic \(\varvec{R}\)-dependent Coulomb logarithmic phase strongly modifies \(Q\) below 1000 keV, i.e., within a large portion of intermediate energies. This modification consists of suppressing the probability for double capture in the case for \(\lambda=1\) relative to \(\lambda=0\). Coulomb distortions in a transient ionizing stage of collision suppress the transition probability because such intermediate channels are not occupied by the two electrons in the final configuration of double charge exchange.

4 Conclusion

In the past research on energetic rearrangement collisions, the three-body first Born (B1-3B) method [46,47,48,49,50], as the simplest perturbative formalism, was attractive due to relatively easy computations. The relevant matrix element consists of integrals over the initial and final unperturbed states weighted with the pertinent interaction potentials. However, the cross sections computed by the B1-3B method often tend to be too large with the decreased impact energy E. Moreover, they are not adequate either in the limit of high E. The main unphysical feature of the B1-3B method is in neglecting the correct boundary conditions for any collision with some remaining Coulomb potentials at infinitely large inter-particle separations.

These drawbacks motivated the innovation of the alternative perturbative methods. The most obvious attempt was to introduce another transition amplitude, similar to the B1-3B method, but with certain judicious modifications. For instance, in a preassigned manner, the unperturbed channel wave functions were perturbed or “distorted”. This is how the notion of distorted wave methodology emerged. For single charge exchange, distorted wave methods are usually effective in improving the B1-3B method by about the right extent to become concordant with measurements. The prime example of a very successful theory for single charge exchange is the three-body boundary-corrected first Born (CB1-3B) method [51,52,53].

Also for single charge exchange, the physically well-founded three-body second-order perturbative theories with successful descriptions of experimental data are the continuum distorted wave (CDW-3B) [51, 54], boundary-corrected intermediate state (BCIS-3B) and Born distorted wave (BDW-3B) methods. On the other hand, for double charge exchange, the four-body versions of these theories, i.e. the CB1-4B, CDW-4B, BCIS-4B and BDW-4B methods, exhibit a pronounced uneven performance when compared to measurements. This points to an enhanced sensitivity of double charge exchange to the choice of distorted waves.

To peer into the nature of this marked sensitivity, we opt to gradually alter the perturbation strength in the distorted waves. Thus, the present focus is on the purely numerical aspects of the relationships between the CB1-4B and BCIS-4B methods as well as between the BDW-4B and CDW-4B methods. To that end, we perform several numerical experiments for double charge exchange in the symmetric \(\alpha -{\text{He}}\) collisions at 100-10000 keV. The basic idea is to vary the perturbation strengths of the Coulomb distortions of the unperturbed channel states. This is reflected in changing the Sommerfeld factors from the pertinent two electronic Coulomb wave functions (at all distances) and in the electronic Coulomb logarithmic phases (at asymptotic distances). Such changes are made through multiplication of the original Sommerfeld factors by a scaling parameter \(\lambda \), which takes on its values in the interval \(0\le \lambda \le 1\).

Therefore, a sequence of approximations to the exact total cross sections \(Q^\mathrm{(CB1-4B)}_{if}\) should be obtainable from the general program for \(Q^\mathrm{(BCIS-4B)}_{if}\) by allowing the \(\lambda -\)dependent Sommerfeld factors to gradually approach the zero values. As an outcome, the tabular results for \(Q^\mathrm{(CB1-4B)}_{if}\) are reproduced to within 3-4 decimal places from the independent algorithm for \(Q^\mathrm{(BCIS-4B)}_{if}\) at all the considered impact energies. This, in turn, cross-validates the different computer programs for the CB1-4B and BCIS-4B methods.

Quite a similar pattern is observed for the link between the BDW-4B and CDW-4B methods. These two theories also give the same total cross sections for \(\lambda \rightarrow 0\). Such a finding confirms the consistency and accuracy of the different computer programs for \(Q^\mathrm{(BDW-4B)}_{if}\) and \(Q^\mathrm{(CDW-4B)}_{if}\). Further, throughout 100-10000 keV, it is noted that the CDW-4B method is extremely sensitive to the varying perturbation strengths. In contradistinction, above 1000 keV, the situation is more gratifying with the BDW-4B method, which is basically insensitive to changes in the perturbation strengths from the Coulomb distortions of the initial and final states.