1 Introduction

Quantum entanglement is one of the fundamental properties of quantum mechanics [1] and also a core resource in the field of quantum information and quantum computing [2,3,4]. However, relevant theories and experiments have confirmed that quantum entanglement is not the only quantum correlation. Even if a non-entangled system, there might still exist some other kind of quantum correlations in it. One of them is the quantum discord (QD), which is introduced by Olivier and Zurek based on von Neumann entropy [5]. Owing to QD significance and pervasiveness, its characterization, quantification, and functions have been extensively investigated. But the calculations of QD require minimization procedures, which makes the calculations difficult. It had been calculated specifically only for a rather limited quantum states, and definition for more general quantum states is still not known. To avoid this difficulty, Dakic et al. [6, 7] introduced the concept of geometric quantum discord (GQD), which greatly simplifies the calculation process and gives us a better way to understand and study QD. However, GQD is analyzed in a lot of theoretical models, such as a non-interacting simplest type of qubits [8, 9], these researches shown GQD can be controlled by the bath and initial state.

Among many physical systems in which quantum correlation states can be prepared via various methods, the charge qubit encoded by the electron occupied states in a double quantum dot system has attracted much attention due to its controllability and some unique characteristics in the fields of quantum information and quantum control [10,11,12]. As a scalable solid-state system, it is also a hopeful candidate for quantum computing. However, like many other solid-state systems, a practical double quantum dot system is an open system, which is inevitably affected by the surrounding electronic bath, whose influence cannot be ignored. In an open quantum system, the state of the system and the environment are entangled, and the state vector cannot accurately describe the state of the system. Therefore, in the open quantum system theory, the state of the system is described by the density operator. The equation of motion of the density operator is also called the master equation, which contains all the dynamic characteristics of an open quantum system. Recently, with the applications of principles and methods of quantum decay to superconducting devices, applications and implications in quantum thermodynamics setups are discussed in [13]. Steady state thermodynamics of two qubits strongly coupled to bosonic environments are analyzed to show that heat conduction in non-equilibrium steady states can be suppressed in the strong coupling limit [14].

Based on the reversibility of the process, the dynamics of an open quantum system is defined as Markovian or non-Markovian. While the Markov evolution is an irreversible process, in the case of non-Markovian dynamics, the system energy (or phase information) dissipated into the environment may flow back to the system within a certain time interval and restore its historical state. Relevant studies have proved that the dynamic evolution of a double quantum dot system is a non-Markovian process [15, 16]. Decoherence dynamics of a double quantum dot charge qubit is analyzed using the Feynman-Vernon influence functional path-integral method [16]. Compared to the path-integral method, the non-Markovian quantum state diffusion (NMQSD) method proposed by Diosi et al. [17, 18] has shown its unique computational characteristics in the study of non-Markovian dynamics of various solid-state systems coupled to the bosonic or fermionic bath [19,20,21,22,23,24]. In this article, we use the fermionic NMQSD method to obtain the non-Markovian exact master equation of a double quantum dot system strongly coupled to two independent non-zero temperature electronic bath (source and drain). And with the master equation, we study the dynamic evolution characteristics of the GQD in the double quantum dot charge qubit system. The present study of GQD in simple examples will help us to understand the non-Markovian behavior of GQD and will demonstrate the quantum correlation in double quantum dot systems can be manipulated with the help of non-Markovianity, inter-dot coupling and the fermionic bath temperature. In particular, these results may be helpful in the fields of quantum information as far as the GQD in double quantum dot charge qubits is considered as a resource.

The paper is organized as follows: In Sec. II, the model of a double quantum dot system coupled to two independent non-zero temperature electronic bath is introduced, and then, the formal exact master equation of the total system is derived using the fermionic NMQSD method. In Sec. III, after a brief introduction of GQD, the numerical simulations of GQD dynamics in the double quantum dot based on the exact master equation are provided. Finally, a brief conclusion is presented in Sec. IV.

2 System Model and Master Equation

There are many factors competing to play the consequent physics in the double quantum dot system. In this paper, we focus on the effects induced by the dot-bath coupling, inter-dot coupling, and bath temperature on the resulted non-Markovian dynamical properties of this charge qubit. For the double quantum dot charge qubit, the electronic occupied state is a \(\left| {1} \right\rangle\) state, and empty state is a \(\left| {0} \right\rangle\) state. The double quantum dot is designed in the strong Coulomb blockade regime such that only one electron is allowed in the double quantum dot, and each dot only contains one energy level. Hence, a complete basis of the Hilbert space can be formed by the following \(\left| {{00}} \right\rangle\),\(\left| {{01}} \right\rangle\),\(\left| {{10}} \right\rangle\) states, on which an arbitrary state can be always written as

$$\left| {\psi \left( t \right)} \right\rangle = a\left| {00} \right\rangle + b\left| {10} \right\rangle + c\left| {01} \right\rangle$$
(1)

where \(\left| a \right|^{2} + \left| b \right|^{2} + \left| c \right|^{2} = 1\).

The total Hamiltonian of the system is consisted of three parts: the double quantum dot HD, the electronic bath HB and the interaction term Hint and can be written as (setting \(\hbar { = }1\))

$$\begin{gathered} H_{D} = E_{1} a_{1}^{\dag } a_{1} + E_{2} a_{2}^{\dag } a_{2} + g(a_{1}^{\dag } a_{2} + a_{2}^{\dag } a_{1} ) \hfill \\ H_{B} = \sum\limits_{\lambda k} {\omega_{\lambda k} b_{\lambda k}^{\dag } b_{\lambda k} } \hfill \\ H_{{\text{int}}} = \sum\limits_{\lambda k} {(f_{\lambda k} a_{\eta }^{\dag } b_{\lambda k} + h.c.)} \hfill \\ \end{gathered}$$
(2)

Here, \(a_{\eta }^{\dag } ,a_{\eta } (\eta = 1,2)\) are the creation and annihilation operators for the electrons in the quantum dot with energy level Eη, and g is the inter-dot coupling strength. \(b_{\lambda k}^{\dag } ,b_{\lambda k} \left( {\lambda = s,d} \right)\) are the creation and annihilation operators for electrons in the source and drain at k’th mode, which satisfy the anti-commutation relations \(\left\{ {b_{\lambda k} ,b_{{\lambda^{^{\prime}} k^{^{\prime}} }}^{\dag } } \right\} = \delta_{{\lambda k,\lambda^{^{\prime}} k^{^{\prime}} }}\), and \(\omega_{\lambda k}\) is energy of the bath electrons. The first (second) quantum dot is coupled to the source (drain) by the tunneling strength \(f_{\lambda k}\), which corresponds to a tunneling rate \(\Gamma_{\lambda k} { = 2}\pi \rho_{\lambda k} \left| {f_{\lambda k} } \right|^{2}\), where \(\rho_{\lambda k}\) is the density operator of the bath.

In the NMQSD method, to conveniently represent the environmental degrees of freedom with the coherent state basis, environments are required to be initially at zero temperature. As for the initially finite temperature bath, we can introduce a fictitious bath term \(H_{C} = \sum\limits_{\lambda k} { - \omega_{\lambda k} c_{\lambda k}^{\dag } } c_{\lambda k}\) to transform the finite temperature case into an effective zero by applying the Bogoliubov transformation [23, 24].

After the Bogoliubov transformation

$$\begin{gathered} b_{\lambda k} = \sqrt {1 - \overline{n}_{\lambda k} } d_{\lambda k} - \sqrt {\overline{n}_{\lambda k} } e_{\lambda k}^{\dag } \hfill \\ c_{\lambda k} = \sqrt {1 - \overline{n}_{\lambda k} } e_{\lambda k} + \sqrt {\overline{n}_{\lambda k} } d_{\lambda k}^{\dag } \hfill \\ \overline{n}_{\lambda k} = {1 \mathord{\left/ {\vphantom {1 {(e^{{{{(\omega_{\lambda k} - \mu_{\lambda k} )} \mathord{\left/ {\vphantom {{(\omega_{\lambda k} - \mu_{\lambda k} )} {k_{B} T}}} \right. \kern-\nulldelimiterspace} {k_{B} T}}}} + 1)}}} \right. \kern-\nulldelimiterspace} {(e^{{{{(\omega_{\lambda k} - \mu_{\lambda k} )} \mathord{\left/ {\vphantom {{(\omega_{\lambda k} - \mu_{\lambda k} )} {k_{B} T}}} \right. \kern-\nulldelimiterspace} {k_{B} T}}}} + 1)}} \hfill \\ \end{gathered}$$
(3)

The total system Hamiltonian in the interaction picture read as

$$H_{tot}^I(t) = {H_S} + \sum\limits_{\lambda k,\eta } {(\sqrt {{{\bar n}_{\lambda k}}} f_{\lambda k}^ * {a_\eta }e{{_\lambda ^{}}_k}{e^{i{\omega _{\lambda k}}t}} + \sqrt {1 - {{\bar n}_{\lambda k}}} {f_{\lambda k}}a_\eta ^\dag {d_{\lambda k}}{e^{ - i{\omega _{\lambda k}}t}}} + h.c.)$$
(4)

where \(\overline{n}_{\lambda k}\) is the average number of electrons in the k’th state of the source and drain with chemical potential \(\mu_{\lambda }\). The fermionic operators \(d_{\lambda k} ,e_{\lambda k}^{{}}\) satisfy \(\left\{ {d_{\lambda k} ,d_{{\lambda^{^{\prime}} k^{^{\prime}} }}^{\dag } } \right\} = \left\{ {e_{\lambda k} ,e_{{\lambda^{^{\prime}} k^{^{\prime}} }}^{\dag } } \right\} = \delta_{{\lambda \lambda^{^{\prime}} ,kk^{^{\prime}} }}\).

We use Grassmann-Bargmann coherent states \(\left| {z_{\lambda k} } \right\rangle\),\(\left| {w_{\lambda k} } \right\rangle\) to describe the state of electronic bath HB and fictitious bath term HC. The coherent states are defined as

$$\begin{gathered} d_{\lambda k} \left| {z_{\lambda k}^{{}} } \right\rangle = z_{\lambda k} \left| {z_{\lambda k}^{{}} } \right\rangle \hfill \\ e_{\lambda k} \left| {w_{\lambda k}^{{}} } \right\rangle = w_{\lambda k} \left| {w_{\lambda k}^{{}} } \right\rangle \hfill \\ \end{gathered}$$
(5)

where \(z_{\lambda k}\),\(w_{\lambda k}\) are the Grassmann variables, satisfy \(\left\{ {z_{\lambda i} ,z_{\lambda j} } \right\} = \left\{ {w_{\lambda i} ,w_{\lambda j} } \right\} = 0\) and \({\text{M}}\left[ {z_{\lambda } w_{\lambda } } \right] = \int {\prod\limits_{\lambda } {e^{{ - z_{\lambda }^{ * } z_{\lambda } - w_{\lambda }^{ * } w_{\lambda } }} z_{\lambda } w_{\lambda } dz_{\lambda }^{2} } } dw_{\lambda }^{2} = 0\). \({\text{M}}\left[ \bullet \right] = \int {\prod\limits_{\lambda } {e^{{ - z_{\lambda }^{ * } z_{\lambda } - w_{\lambda }^{ * } w_{\lambda } }} \left[ \bullet \right]dz_{\lambda }^{2} } } dw_{\lambda }^{2}\) is the statistical mean over the Grassmann Gaussian noise variables. The time-local fermionic NMQSD equation can then be written as

$$\begin{array}{l}\frac{\partial }{{\partial t}}\left| {{\psi _t}\left( {z_\lambda ^ * ,w_\lambda ^ * } \right)} \right\rangle = - i{H_S}\left| {{\psi _t}\left( {z_\lambda ^ * ,w_\lambda ^ * } \right)} \right\rangle - \sum\limits_{\lambda ,\eta } {\left[ {{a_\eta }z_\lambda ^ * {\rm{ + }}a_\eta ^\dag w_\lambda ^ * } \right.} \\\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ + }}a_\eta ^\dag {{\bar O}_\lambda }\left( {t,z_L^ * } \right){\rm{ + }}a_\eta ^{}{{\bar Q}_\lambda }\left( {t,w_L^ * } \right)} \right]\left| {{\psi _t}\left( {z_\lambda ^ * ,w_\lambda ^ * } \right)} \right\rangle \end{array}$$
(6)

where \(z_{\lambda k}^{ * }\),\(w_{\lambda k}^{ * }\) are the Grassmann Gaussian noise. \(O_{\lambda }\),\(Q_{\lambda }\) are the operators defined as

$$\begin{array}{l}{O_\lambda }\left( {t,s,z_\lambda ^ * } \right)\left| {{\psi _t}\left( {z_\lambda ^ * } \right)} \right\rangle {\rm{ = }}\frac{\delta }{{\delta z_\lambda ^ * \left( s \right)}}\left| {{\psi _t}\left( {z_\lambda ^ * } \right)} \right\rangle \\{Q_\lambda }\left( {t,s,w_\lambda ^ * } \right)\left| {{\psi _t}\left( {w_\lambda ^ * } \right)} \right\rangle {\rm{ = }}\frac{\delta }{{\delta w_\lambda ^ * \left( s \right)}}\left| {{\psi _t}\left( {w_\lambda ^ * } \right)} \right\rangle \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\bar O}_\lambda }\left( {t,z_\lambda ^ * } \right){\rm{ = }}\int_0^t {ds} {\alpha _\lambda }\left( {t,s} \right){O_\lambda }\left( {t,s,z_\lambda ^ * } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\overline Q _\lambda }\left( {t,w_\lambda ^ * } \right){\rm{ = }}\int_0^t {ds} {\beta _\lambda }\left( {t,s} \right){Q_\lambda }\left( {t,s,w_\lambda ^ * } \right)\end{array}$$
(7)

where \(\alpha_{\lambda } \left( {ts} \right){ = }\sum\limits_{k} {\left( {1 - \overline{n}_{\lambda k} } \right)\left| {f_{\lambda k} } \right|}^{2} e^{{ - i\omega_{\lambda k} \left( {t - s} \right)}}\),\(\beta_{\lambda } \left( {ts} \right){ = }\sum\limits_{k} {\overline{n}_{\lambda k} \left| {f_{\lambda k} } \right|}^{2} e^{{i\omega_{\lambda k} \left( {t - s} \right)}}\) are the environment correlation functions, which can be derived from the correlation function

$$\begin{gathered} \alpha_{\lambda } \left( {ts} \right){ = }\sum\limits_{k} {\left| {f_{\lambda k} } \right|}^{2} \left[ {\coth \left( {\frac{{\omega_{\lambda k} }}{{2k_{B} T}}} \right)\cos \left[ {\omega_{\lambda k} \left( {t - s} \right)} \right] - i\sin \left[ {\omega_{\lambda k} \left( {t - s} \right)} \right]} \right] \hfill \\ \beta_{\lambda } \left( {ts} \right){ = }\sum\limits_{k} {\left| {f_{\lambda k} } \right|}^{2} \left[ {\coth \left( {\frac{{\omega_{\lambda k} }}{{2k_{B} T}}} \right)\cos \left[ {\omega_{\lambda k} \left( {t - s} \right)} \right] + i\sin \left[ {\omega_{\lambda k} \left( {t - s} \right)} \right]} \right] \hfill \\ \end{gathered}$$
(8)

With the noise correlation function, Eq. (8), which is realized for the Drude, Lorentz, and Brownian cases (and combinations thereof), one can obtain the reduced equations of motion as the hierarchial equations of motion, by which quantum heat transport phenomena was investigated intensively [25,26,27].

By substituting the fermionic NMQSD equation (Eq. (6)) into the following relation

$$\frac{{\partial P_{t} }}{\partial t}{ = }\frac{{\partial \left| {\psi_{t} \left( {z_{\lambda }^{ * } ,w_{\lambda }^{ * } } \right)} \right\rangle }}{\partial t}\left\langle {\psi_{t} \left( { - z_{\lambda }^{{}} , - w_{\lambda }^{{}} } \right)} \right| + \left| {\psi_{t} \left( {z_{\lambda }^{ * } ,w_{\lambda }^{ * } } \right)} \right\rangle \frac{{\partial \left\langle {\psi_{t} \left( { - z_{\lambda }^{{}} , - w_{\lambda }^{{}} } \right)} \right|}}{\partial t}$$
(9)

where \(P_{t} { = }\left| {\psi_{t} \left( {z_{\lambda }^{ * } ,w_{\lambda }^{ * } } \right)} \right\rangle \left\langle {\psi_{t} \left( { - z_{\lambda }^{{}} , - w_{\lambda }^{{}} } \right)} \right|\) as the stochastic density operator, the non-Markovian exact master equation of the double quantum dot system strongly coupled to two independent non-zero temperature electronic bath with memory effect can be written as

$$\begin{array}{c}\frac{\partial }{{\partial t}}\rho = - i\left[ {{H_S},\rho } \right] + \left( {\left[ {{a_1},{\rm M}\left[ {{P_t}\bar O_s^\dag } \right]} \right]{\rm{ + }}\left[ {{a_2},{\rm{M}}\left[ {{P_t}\bar O_d^\dag } \right]} \right]} \right.\\\left. {\;\; + \left[ {a_1^\dag ,M\left[ {{P_t}\bar Q_s^\dag } \right]} \right] + \left[ {a_2^\dag ,{\rm{M}}\left[ {{P_t}\bar Q_d^\dag } \right]} \right] + h.c.} \right)\end{array}$$
(10)

In the subsequent sections, we will use the above non-perturbative master equation to numerically study the non-Markovian dynamics of double quantum dot charge qubit GQD (Fig. 1).

Fig. 1
figure 1

The sketch of double quantum dot system (Color figure online).

Full size image

3 Data Analysis and Discussion

According to the definition of GQD, the general two-qubit state can be written as [28]

$$\rho = \frac{1}{4}\left( {I \otimes I + \sum\limits_{{i{ = }1}}^{3} {x_{i} \sigma_{i}^{A} \otimes I + } \sum\limits_{{i{ = }1}}^{3} {I \otimes y_{i} \sigma_{i}^{B} + \sum\limits_{{i,j{ = }1}}^{3} {R_{ij} \sigma_{i}^{A} \otimes \sigma_{j}^{B} } } } \right)$$
(11)

where \(x_{i} = Tr\left( {\rho \sigma_{i}^{A} \otimes I} \right)\),\(y_{i} = Tr\left( {\rho I \otimes \sigma_{i}^{B} } \right)\),\(R_{ij} = Tr\left( {\rho \sigma_{i}^{A} \otimes \sigma_{j}^{B} } \right)\), and \(\sigma_{i} \left( {\sigma_{j} } \right)\) being Pauli matrices. According to the Eq. (11), GQD is calculated as [6]

$$GQD\left( \rho \right) = \frac{1}{4}\left( {\left\| x \right\|^{2} + \left\| R \right\|^{2} - k_{\max } } \right)$$
(12)

where \(\left\| x \right\|^{2} { = }\sum\limits_{{i{ = }1}}^{3} {x_{i}^{2} }\),\(\left\| R \right\|^{2} { = }\sum\limits_{{i,j{ = }1}}^{3} {R_{ij}^{2} }\),\(k_{\max }\) is the maximum eigenvalue of the matrix \(xx^{T} + RR^{T}\). The maximum value of GQD is 0.5 and the minimum value is 0. For the X-state quantum system, the GQD analytic expression can be written as [9]

$$\begin{array}{c}GQD\left( \rho \right) = \frac{1}{4}\left[ {{\rm{8}}\left( {{{\left| {{\rho _{{\rm{14}}}}} \right|}^{\rm{2}}} + {{\left| {{\rho _{{\rm{23}}}}} \right|}^{\rm{2}}}} \right) + {\rm{2}}{{\left( {\left( {\left| {{\rho _{{\rm{11}}}}} \right| - \left| {{\rho _{{\rm{33}}}}} \right|} \right)} \right.}^{\rm{2}}}} \right.\\\;\; \quad + \left. {\left. {{{\left( {\left| {{\rho _{{\rm{22}}}}} \right| - \left| {{\rho _{{\rm{44}}}}} \right|} \right)}^{\rm{2}}}} \right) - \max \left\{ {{k_1},{k_2},{k_3}} \right\}} \right]\end{array}$$
(13)

where \(k_{1} = 4\left( {\left| {\rho_{23} } \right| - \left| {\rho_{14} } \right|} \right)^{2}\),\(k_{2} = 4\left( {\left| {\rho_{23} } \right| + \left| {\rho_{14} } \right|} \right)^{2}\),\(k_{3} = 2\left( {\left( {\left| {\rho_{11} } \right| - \left| {\rho_{33} } \right|} \right)^{2} + \left( {\left| {\rho_{22} } \right| - \left| {\rho_{44} } \right|} \right)^{2} } \right)\) are the eigenvalues of the matrix k. In the strong Coulomb blockade regime, the Eq. (13) can be written as

$$GQD\left( \rho \right) = \frac{1}{4}\left[ {{8}\left| {\rho_{{{23}}} } \right|^{{2}} + {2}\left( {\left( {\left| {\rho_{{{11}}} } \right| - \left| {\rho_{{{33}}} } \right|} \right)} \right.^{{2}} } \right. + \left. {\left. {\left| {\rho_{{{22}}} } \right|^{{2}} } \right) - \max \left\{ {k_{1} ,k_{2} ,k_{3} } \right\}} \right]$$
(14)

The double quantum dot system rate equations are reduced to [16]

$$\begin{gathered} \frac{\partial }{\partial t}\rho_{11} = \left( {{1} - \overline{n}_{s} } \right)\Gamma_{s} \rho_{22} + \left( {{1} - \overline{n}_{d} } \right)\Gamma_{d} \rho_{33} - \left( {\overline{n}_{s} \Gamma_{s} + \overline{n}_{d} \Gamma_{d} } \right)\rho_{11} \hfill \\ \frac{\partial }{\partial t}\rho_{22} = \overline{n}_{s} \Gamma_{s} \rho_{11} + ig(\rho_{23} - \rho_{32} ) - \left( {{1} - \overline{n}_{s} } \right)\Gamma_{s} \rho_{22} \hfill \\ \frac{\partial }{\partial t}\rho_{33} = \overline{n}_{d} \Gamma_{d} \rho_{11} - ig(\rho_{23} - \rho_{32} ) - \left( {{1} - \overline{n}_{d} } \right)\Gamma_{d} \rho_{33} \hfill \\ \frac{\partial }{\partial t}\rho_{23} = \left[ { - i\left( {E_{1} - E_{2} } \right) - \frac{1}{2}\left( {{1} - \overline{n}_{s} } \right)\Gamma_{s} - \frac{1}{2}\left( {{1} - \overline{n}_{d} } \right)\Gamma_{d} } \right]\rho_{23} + ig(\rho_{22} - \rho_{33} ) \hfill \\ \end{gathered}$$
(15)

Based on the Eqs. (10), (12), (14) and (15), we next numerically simulate the non-Markovian dynamics of the double quantum dot charge qubit GQD. We will focus on the coherent manipulation regime where the double dot is set up symmetrically \(E_{1} = E_{2} = 25\mu eV\) and the chemical potentials of the electron reservoirs are aligned above the energy levels of two dots with zero-bias voltage \(\mu_{1} = \mu_{2} = 20\mu eV\). For simplicity, we also choose the symmetric case of the same tunneling rate as \(\Gamma_{S} = \Gamma_{d} { = 100}\mu eV\). Moreover, the correlation functions are modeled as the Ornstein–Uhlenbeck process

$$\begin{gathered} \alpha_{\lambda } \left( {ts} \right) = \left( {1 - \overline{n}_{\lambda } } \right)\frac{\gamma }{2}e^{{ - \gamma \left| {t - s} \right|}} \hfill \\ \beta_{\lambda } \left( {ts} \right) = \overline{n}_{\lambda } \frac{\gamma }{2}e^{{\gamma \left| {t - s} \right|}} \hfill \\ \end{gathered}$$
(16)

where γ−1 is memory time of the environment. When γ approaches to zero, it will manifest a strong non-Markovian effect, while \(\gamma \to \infty\) corresponds to a white noise situation, approaching the Markov limit. For the zero temperature electronic bath (\(\overline{n}_{\lambda k} = 0\)), the correlation functions are \(\alpha_{\lambda } \left( {ts} \right) = \frac{\gamma }{2}e^{{ - \gamma \left| {t - s} \right|}}\),\(\beta_{\lambda } \left( {ts} \right) = 0\).

We first consider effect of the environmental non-Markovianity on the double quantum dot charge qubit GQD. In Fig. 2a, b and c, we plot the GQD dynamics for separable initial states \(\left| {00} \right\rangle\),\(\left| {10} \right\rangle\),\(\left| {01} \right\rangle\), respectively. The numerical simulation results show that GQD is generated only when the electron is allowed to enter at least one of the quantum dots. Moreover, for the \(\left| {10} \right\rangle\),\(\left| {01} \right\rangle\) states, we can see that the degree of the repeatedly regenerated GQD depends on the value of the parameter γ. When γ = 0.1, which is a strong non-Markovian regime for the environment, the charge qubit GQD exhibits a strong oscillation pattern before completely disappears. But when the environment recovers to the Markov limit γ = 1, it leads to a faster converging of GQD to the ground state. In Fig. 2d, the initial state of the charge qubit is prepared to be in the maximal GQD. We note that when the environment is in the Markov limit (γ = 1), the charge qubit GQD sharply decays to the zero, accompanied by exponential decoherence. In a strongly non-Markovian regime (γ = 0.1), the non-Markovian time-dependent decay rate leads to a slower decay compared to the Markovian exponential one without dropping to the ground state for a definite time scale. Moreover, the decay process can be partially reversed due to the negative values of the decay rates. These show that the environment non-Markovianity can significantly enhance the generation and re-coherence of charge qubit GQD.

Fig. 2
figure 2

(Color online) The dynamics of GQD with different memory capacity parameter γ. The initial states are a \(\left| {00} \right\rangle\), b \(\left| {10} \right\rangle\), c \(\left| {01} \right\rangle\), d \({{\left( {\left| {{0}1} \right\rangle + \left| {10} \right\rangle } \right)} \mathord{\left/ {\vphantom {{\left( {\left| {{0}1} \right\rangle + \left| {10} \right\rangle } \right)} {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}\). Other parameters are \(g = {45}\mu eV\), T = 0

Full size image

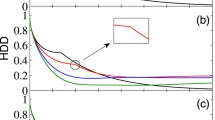
The inter-dot strength coupling is the crucial parameter that directly affects the properties of the double quantum dot system. When the dots are coupled through an ionic-like bond (weak coupling), the electron is localized on the individual dots, and when the coupling is covalent-like bonds (strong coupling), an electron can tunnel many times between the two dots in a phase-coherent way, which can be regarded as a coherent wave that is delocalized over the two dots [29, 30]. In Fig. 3a, we plot the dynamic evolution of the charge qubit GQD with different coupling strength parameters g. As can be seen, the stronger the inter-dot coupling (\(g = {80}\mu eV\)), the more robust the GQD is. This shows the non-classical coherence of the strong coupled dots can inhibit the decay of charge qubit GQD. Another parameter that will affect the double quantum dot properties is the temperature of the bath. In Fig. 3b, as an expected result, in the low temperature electronic bath, the charge qubit GQD is enhanced and exhibits a stronger non-Markovian oscillation pattern compared to the case of high temperature electronic bath due to the more dominant non-Markovianity at low temperature. This is due to the fact that the thermal movement of electrons in the bath can be suppressed by the low temperature so that the information feedback from reservior to the system is less influenced by the thermal fluctuation.

Fig. 3
figure 3

(Color online) The dynamics of GQD with different strength couplings g and different temperatures T: a is for different g when T = 0, and b is for different T when \(g = {65}\mu eV\). γ = 0.1, and the initial state is \(\left| a \right|^{2} = {0}\),\(\left| b \right|^{2} = \left| c \right|^{2} = 1/{2}\) for all cases

Full size image

4 Conclusion

In this paper, using the non-perturbative NMQSD equation, we derived the exact master equation of the double quantum dot system coupled to two independent non-zero temperature electronic baths directly from the microscopic Hamiltonian. Based on the master equation, we carried out numerical simulations of non-Markovian dynamics of the double quantum dot charge qubit GQD. Our results show that due to the non-Markovian environment memory, the historical phase information is recovered to some level leading to the regeneration of GQD. Moreover, the strong inter-dot coupling resulting in coherent tunneling and low bath temperature causing more dominant non-Markovianity both make a more robust charge qubit GQD. These theoretical investigations on the non-Markovian dynamics of double quantum dot charge qubit GQD may be helpful when it comes to use the system in quantum information processing.