Thermodynamic Properties of a GaAs Quantum Dot with an Effective-Parabolic Potential: Theory and Simulation

Abstract

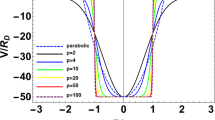
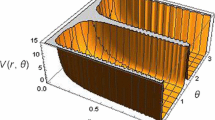
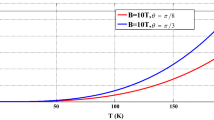
In this work, we have studied the thermodynamic properties of a GaAs quantum dot (QD) with an effective-parabolic potential. We have analytically obtained entropy, heat capacity and average energy of the QD in the presence of a magnetic field and its interaction with the electron spin using the canonical ensemble approach. According to the results, it is found that the entropy is an increasing function of temperature. At low temperatures, the entropy increases monotonically with increasing the temperature for all values of the magnetic field and it is independent of the magnetic field. But, the entropy depends on the magnetic field at high temperatures. The entropy is also decreased with increasing magnetic field. The average energy of the system is increased by enhancing temperature and magnetic field. At low temperatures, the average energy appears weakly dependent on magnetic field. It is nearly independent of magnetic field. The heat capacity increases with enhancing temperatures for all considered values of magnetic fields, and it approaches a saturation value at high temperatures. The heat capacity decreases with increasing the magnetic field for all considered values of temperatures. There is an interesting behavior in heat capacity as a function of magnetic field. The heat capacity does not change much at high temperatures like T = 200 K and 300 K. However, at relatively lower temperatures like T = 100 K, the heat capacity reduces with increasing magnetic field. We have also calculated the magnetization of the system. The magnitude of the magnetization $\left( {\left| M \right|} \right)$ increases with the magnetic field and the confinement range.

Appendix

We know that $H = H_{0} + H_{1}$. To obtain the total Hamiltonian, we add Eqs. (6) and (8) as

$$ H = - \frac{{\hbar^{2} }}{{2m^{*} }}\nabla_{r}^{2} + \frac{1}{2}m^{*} \varOmega^{2} r^{2} + \frac{1}{2}\hbar \omega_{c} \left( {\hat{L}_{z} + g\hat{S}_{z} } \right) - V_{0} + \alpha \left[ {\frac{{V_{0} }}{{r^{2} }} - \frac{1}{2}m^{*} \omega^{2} - \frac{{V_{0} }}{{r^{2} }}\text{sech}^{2} \left( {\frac{r}{R}} \right)} \right]r^{2} $$

(A1)

Therefore, we have

$$ H = - \frac{{\hbar^{2} }}{{2m^{*} }}\nabla_{r}^{2} + \frac{1}{2}m^{*} \varOmega^{2} r^{2} - \alpha \frac{1}{2}m^{*} \omega^{2} r^{2} + \frac{1}{2}\hbar \omega_{c} \left( {\hat{L}_{z} + g\hat{S}_{z} } \right) - V_{0} + \alpha \frac{{V_{0} }}{{r^{2} }}r^{2} - \alpha \frac{{V_{0} }}{{r^{2} }}r^{2} \left\langle {\text{sech}^{2} \left( {\frac{r}{R}} \right)} \right\rangle $$

(A2)

Using the relation $\varOmega^{2} = \omega^{2} + \frac{{\omega_{c}^{2} }}{4}$, the second and third terms can be written as

$$ \frac{1}{2}m^{*} \varOmega^{2} r^{2} - \alpha \frac{1}{2}m^{*} \omega^{2} r^{2} = \frac{1}{2}m^{*} r^{2} \left[ {\varOmega^{2} - \alpha \omega^{2} } \right] = \frac{1}{2}m^{*} r^{2} \left[ {\left( {1 - \alpha } \right)\omega^{2} + \frac{{\omega_{c}^{2} }}{4}} \right] $$

(A3)

Now, we should calculate the expectation value $r^{2}$ and $\left\langle {\text{sech}^{2} \left( {\frac{r}{R}} \right)} \right\rangle$ with respect to ground state wave function of the harmonic oscillator of frequency $\varOmega$. After obtaining the expectation values, we have inserted the values in Eq. (A2). Thus, we obtain the following equation

$$ H = - \frac{1}{{2m^{*} }}\nabla^{2} + \frac{1}{2}m^{*} \varpi^{2} r^{2} + \frac{1}{2}\hbar \omega_{c} \left( {\hat{L}_{z} + g\hat{S}_{z} } \right) - V_{0} $$

where

$$ \varpi^{2} = \left[ {\left( {1 - \alpha } \right)\omega^{2} + \frac{{\omega_{c}^{2} }}{4} + 2\alpha V_{0} \frac{\varOmega }{{\hbar + m^{*} \varOmega R^{2} }}} \right]. $$