Convex envelopes of bivariate functions through the solution of KKT systems

Abstract

In this paper we exploit a slight variant of a result previously proved in Locatelli and Schoen (Math Program 144:65–91, 2014) to define a procedure which delivers the convex envelope of some bivariate functions over polytopes. The procedure is based on the solution of a KKT system and simplifies the derivation of the convex envelope with respect to previously proposed techniques. The procedure is applied to derive the convex envelope of the bilinear function xy over any polytope, and the convex envelope of functions $x^n y^m$ over boxes.

Appendices

Convex envelope and polyhedral subdivision for the bilinear function

We make a separate discussion for each of the three cases discussed in Sect. 4.

1.1 $J=\{i,j,k\}$ and $\Omega _i, \Omega _j,\Omega _k\in V(P)$

Let $\mathbf{v}^i, \mathbf{v}^j, \mathbf{v}^k\in V(P)$ be the three vertices $\Omega _i, \Omega _j,\Omega _k$ such that no pair of these vertices lies along a line with positive slope. In this case the computation of the convex envelope is rather simple: the convex envelope is the affine function interpolating xy at the three vertices, i.e.,

$$\begin{aligned} conv_{f,P}(\mathbf{x})=\mathbf{p}^T \mathbf{x}+p_0, \end{aligned}$$

(26)

where $\mathbf{p}^T \mathbf{v}^h +p_0= v_{x}^h v_{y}^h$ for each $h\in J$. Moreover, the set $\Gamma _J$ is defined in the following observation.

Observation A.1

If $f(\mathbf{x})=xy$ and $J=\{i,j,k\}$, then

$$\begin{aligned} \Gamma _J=chull\{\mathbf{v}^i, \mathbf{v}^j, \mathbf{v}^k\}. \end{aligned}$$

1.2 $J=\{i,j\}$ and $\Omega _i\in V(P)$, $\Omega _j\in \bar{E}(P)$

We denote by $\mathbf{v}=(v_x,v_y)$ the vertex $\Omega _i\in V(P)$. We will omit in what follows the dependency of $x_j$ from $\varvec{\alpha }$. Recalling (22), system (20) is equivalent to

$$\begin{aligned} \begin{aligned}&\lambda x_j +(1-\lambda ) v_x = x \\&\lambda (m_jx_j+q_j) +(1-\lambda ) v_y = y \\&-m_j x_j^2 - b q_j = v_x v_y - a v_x - b v_y. \end{aligned} \end{aligned}$$

The parametric solution of this system is easy to derive. It follows from (21) that $a=2 m_j x_j + q_j - m_j b$. Then, the system can be rewritten as follows

$$\begin{aligned} \begin{aligned}&\lambda x_j +(1-\lambda ) v_x = x \\&\lambda (m_jx_j+q_j) +(1-\lambda ) v_y = y \\&m_j x_j^2 - 2 m_j x_j v_x-q_jv_x+ b(q_j+m_j v_x -v_y) + v_x v_y =0. \end{aligned} \end{aligned}$$

The first two equations lead to

$$\begin{aligned} \begin{aligned} \lambda&=\frac{x-v_x}{x_j-v_x} \\ \lambda&=\frac{y-v_y}{m_j x_j +q_j -v_y}, \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} x_j=\frac{x(v_y-q_j)-v_x(y-q_j)}{m_j(x-v_x)+v_y-y}. \end{aligned}$$

(27)

Then

$$\begin{aligned} \begin{aligned} \lambda (\mathbf{x})&=\frac{m_j(x-v_x)+v_y-y}{v_y-q_j-m_j v_x} \\ b(\mathbf{x})&=\frac{m_j x_j^2-2 m_j v_x x_j -q_j v_x+v_x v_y}{v_y-m_jv_x -q_j} \\ a(\mathbf{x})&=2 m_j x_j +q_j - m_j b(\mathbf{x}). \end{aligned} \end{aligned}$$

(28)

The convex envelope is equal to

$$\begin{aligned} conv_{f,P}(\mathbf{x})=v_x v_y+ \varvec{\alpha }_J(\mathbf{x})^T(\mathbf{x}-\mathbf{v}), \end{aligned}$$

(29)

where $\varvec{\alpha }_J(\mathbf{x})=(a(\mathbf{x}), b(\mathbf{x}))$, over the set

$$\begin{aligned} \begin{aligned} \Gamma _J&=\left\{ {} \mathbf{x}\in P\ :\ \eta _r(\varvec{\alpha }_J(\mathbf{x}))\ge \eta _k(\varvec{\alpha }_J(\mathbf{x})),\ \forall r\not \in J,\ k\in J,\right. \\&\quad \left. \lambda ^J(\mathbf{x})\in [0,1],\ \ \ \varvec{\alpha }_J(\mathbf{x})\in D_j\right\} . \end{aligned} \end{aligned}$$

Note that, according to definition (9) $\varvec{\alpha }_J(\mathbf{x})\in D_j$ can also be written as $x_j^1\le x_j \le x_j^2$. In the following observation we derive a simplified definition of the set $\Gamma _J$. It will turn out that the restrictions $\eta _r(\varvec{\alpha }_J(\mathbf{x}))\ge \eta _k(\varvec{\alpha }_J(\mathbf{x})),\ \forall r\not \in J,\ k\in J$, can be replaced by simple restrictions on the values of $x_j$. We assume that $\Omega _j\in \bar{E}^u(P)$ (the analysis for the case $\Omega _j\in \bar{E}^{\ell }(P)$ is analogous).

Observation A.2

Let $\Omega _j\in \bar{E}^u(P)$. Then, the following holds.

• If $P\cap \{\varvec{\xi }\ :\ \xi _x>v_x,\xi _y<v_y\}\ne \emptyset$, then $\Gamma _J=\emptyset$;

• If $P\subseteq \{\varvec{\xi }\ :\ \xi _x\le v_x,\xi _y\ge v_y\}$, then

  $$\begin{aligned} \Gamma _J=\left\{ \mathbf{x}\in P\ :\ \lambda ^J(\mathbf{x})\in [0,1],\ \ x_j^1\le x_j \le x_j^2\right\} . \end{aligned}$$

  (30)

• If $P\cap \{\varvec{\xi }\ :\ \xi _x>v_x,\xi _y\ge v_y\}\ne \emptyset$, then we need to add the restriction

  $$\begin{aligned} x_j \le \min \left\{ x_j^2,-\frac{q_j}{m_j+\sqrt{m_j m_k}}\right\} , \end{aligned}$$

  in the definition (30) of $\Gamma _J$.

• If $P\cap \{\varvec{\xi }\ :\ \xi _x<v_x,\ \xi _y\le v_y\}\ne \emptyset$, then we need to add the restriction

  $$\begin{aligned} x_j \ge \max \left\{ x_j^1,-\frac{q_j}{m_j+\sqrt{m_j m_h}}\right\} , \end{aligned}$$

  in the definition (30) of $\Gamma _J$.

Proof

We will assume in what follows that $v_x=v_y=0$. This is without loss of generality since it can always be made true by a translation. Since $\Omega _j\in \bar{E}^u(P)$ and $(v_x,v_y)=(0,0)$, it holds that $q_j>0$ and

$$\begin{aligned} a(\mathbf{x})=\frac{(m_j x_j +q_j)^2}{q_j}\ge 0,\ \ \ b(\mathbf{x})=-\frac{m_j x_j^2}{q_j}\le 0. \end{aligned}$$

Moreover, $x_j\le 0, y_j=m_jx_j+q_j\ge 0$, otherwise the bilinear function is strictly convex along the segment between (0, 0) and $(x_j,y_j)$, which can not hold in view of Corollary 3.2. Thus, we can impose $-\frac{q_j}{m_j}\le x_j \le 0$. Next, we need to impose that for each $\varvec{\xi }\in P$,

$$\begin{aligned} \xi _x\xi _y -\varvec{\alpha }^T \varvec{\xi }\ge \eta _i(\varvec{\alpha }(\mathbf{x}))=0. \end{aligned}$$

(31)

We remark that we could restrict the attention to $\varvec{\xi }\in \Omega _k$, for all $\Omega _k\in G(P)$, but this would not simplify the following analysis. The inequality (31) can be rewritten as follows

$$\begin{aligned} m_j x_j^2(\xi _y-m_j \xi _x)-2 m_j q_j \xi _x x_j + q_j\xi _x(\xi _y-q_j)\ge 0. \end{aligned}$$

(32)

If we consider the above inequality as a quadratic inequality with respect to $x_j$, then its determinant is

$$\begin{aligned} m_jq_j\xi _x\xi _y(m_j \xi _x+q_j-\xi _y). \end{aligned}$$

This is $< 0$ for $\xi _x\xi _y<0$ and $\varvec{\xi }\not \in \Omega _j$. Thus, if $\xi _x\xi _y< 0$ and $\xi _y-m_j \xi _x<0$, i.e., $\xi _x\xi _y< 0,\ \xi _y< 0,\ \xi _x> 0$, for some $\varvec{\xi }\in P$, then $\Gamma _J=\emptyset$. Otherwise, if $\xi _x\xi _y\le 0$ and $\xi _y-m_j \xi _x\ge 0$, i.e., $\xi _x\xi _y\le 0,\ \xi _y\ge 0,\ \xi _x\le 0$ for all $\varvec{\xi }\in P$, then

$$\begin{aligned} \Gamma _J=\left\{ \mathbf{x}\in P\ :\ \lambda ^J(\mathbf{x})\in [0,1],\ \ x_j^1\le x_j \le x_j^2\right\} . \end{aligned}$$

Next, let us assume that $\xi _x>0,\ \xi _y\ge 0$ for some $\varvec{\xi }\in P$. In this case the origin is the vertex of an edge of P lying along a line $y=m_k x$ for some $m_k\ge 0$. Moreover, $P\subseteq \{\mathbf{x} :\ y\ge m_k x\}$. Thus, since $b(\mathbf{x})\le 0$, we have

$$\begin{aligned} \xi _x\xi _y -\varvec{\alpha }^T \varvec{\xi }\ge \xi _x\xi _y -a(\mathbf{x}) \xi _x - b(\mathbf{x})m_k \xi _x. \end{aligned}$$

Taking into account the definitions of $a(\mathbf{x})$ and $b(\mathbf{x})$ we have that, in view of $\xi _x>0$, (31) is satisfied if

$$\begin{aligned} \xi _y \ge \frac{(m_j x_j +q_j)^2}{q_j} -\frac{m_j m_k x_j^2}{q_j}, \end{aligned}$$

Since $\xi _y\ge 0$, $q_j>0$, $x_j\le 0$, and $y_j=m_jx_j+q_j\ge 0$, the above inequality is satisfied if

$$\begin{aligned} m_j x_j +q_j +\sqrt{m_j m_k} x_j\le 0, \end{aligned}$$

or, equivalently

$$\begin{aligned} x_j \le -\frac{q_j}{m_j+\sqrt{m_j m_k}}, \end{aligned}$$

which, combined with $x_j\le x_j^2$ proves the result.

Finally, let us assume that $\xi _x<0,\ \xi _y\le 0$ for some $\varvec{\xi }\in P$. In this case the origin is the vertex of an edge of P lying along a line $y=m_h x$ for some $m_h\ge 0$. Moreover, $P\subseteq \{\mathbf{x}\ :\ y\ge m_h x\}$. Thus, since $b(\mathbf{x})\le 0$, we have

$$\begin{aligned} \xi _x\xi _y -\varvec{\alpha }^T \varvec{\xi }\ge \xi _x\xi _y -a(\mathbf{x}) \xi _x - b(\mathbf{x})m_h \xi _x. \end{aligned}$$

Taking into account the definitions of $a(\mathbf{x})$ and $b(\mathbf{x})$ we have that, in view of $\xi _x<0$, (31) is satisfied if

$$\begin{aligned} \xi _y \le \frac{(m_j x_j +q_j)^2}{q_j} -\frac{m_j m_h x_j^2}{q_j}, \end{aligned}$$

Since $\xi _y\le 0$, $q_j>0$, $x_j\le 0$, and $y_j=m_jx_j+q_j\ge 0$, the above inequality is satisfied if

$$\begin{aligned} m_j x_j +q_j +\sqrt{m_j m_h} x_j\ge 0, \end{aligned}$$

or, equivalently

$$\begin{aligned} x_j \ge -\frac{q_j}{m_j+\sqrt{m_j m_h}}, \end{aligned}$$

which, combined with $x_j\ge x_j^1$ proves the result. $\square$

1.3 $J=\{i,j\}$ and $\Omega _i,\Omega _j \in \bar{E}(P)$

We will assume that $\Omega _j \in \bar{E}^{\ell }(P)$, $\Omega _i \in \bar{E}^{u}(P)$, so that

$$\begin{aligned} y\ge m_j x+q_j,\ \ y\le m_ix+q_i\ \ \ \forall \mathbf{x}\in P. \end{aligned}$$

(33)

System (20) becomes (once again we omit the dependency of $x_i$ and $x_j$ from $\varvec{\alpha }$)

$$\begin{aligned} \begin{aligned}&\lambda x_j +(1-\lambda )x_i = x \\&\lambda (m_jx_j+q_j) +(1-\lambda )(m_ix_i+q_i) = y \\&m_j x_j^2 + b q_j = m_i x_i^2 + b q_i. \end{aligned} \end{aligned}$$

The case $m_i=m_j$ is a simpler one for which a solution of the system is easily derived. Indeed, in this case it follows from (21) that

$$\begin{aligned} x_j=x_i+\frac{q_i-q_j}{2m_i}. \end{aligned}$$

The first two equations lead to

$$\begin{aligned} \begin{aligned} \lambda&=\frac{2m_i(x-x_i)}{q_i-q_j} \\ \lambda&=\frac{2(y-m_ix_i-q_i)}{q_j-q_i}, \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} x_i=\frac{y+m_ix-q_i}{2m_i}. \end{aligned}$$

The third equation reduces to

$$\begin{aligned} b(\mathbf{x})=x_i+\frac{q_i-q_j}{4}, \end{aligned}$$

while (21) implies

$$\begin{aligned} a(\mathbf{x})=2 m_i x_i-m_i b(\mathbf{x})+q_i. \end{aligned}$$

If $m_i\ne m_j$ the solution of the system is a bit more cumbersome although always based on standard computations. It follows from (21) that

$$\begin{aligned} \begin{aligned} b&=\frac{2 m_j x_j +q_j - 2 m_i x_i-q_i}{m_j-m_i} \\ a&= 2 m_j x_j + q_j - m_j b. \end{aligned} \end{aligned}$$

(34)

The first two equations lead to

$$\begin{aligned} \begin{aligned} \lambda&=\frac{x-x_i}{x_j-x_i} \\ \lambda&=\frac{y-m_ix_i-q_i}{m_j x_j +q_j -m_i x_i-q_i}. \end{aligned} \end{aligned}$$

The system can be rewritten as follows

$$\begin{aligned} \begin{aligned}&(m_i-m_j) x_i x_j + x_i(y-m_ix - q_j)+x_j(m_j x+q_i - y)+(q_j-q_i)x = 0 \\&\left( \sqrt{m_i}x_i+\sqrt{m_j}x_j\right) \left( \sqrt{m_j}x_j - \sqrt{m_i}x_i\right) =(q_i-q_j)\frac{2 m_j x_j +q_j - 2 m_i x_i-q_i}{m_j-m_i}. \end{aligned} \end{aligned}$$

In order to solve it parametrically with respect to $\mathbf{x}$, it is worthwhile to make the following change of variables

$$\begin{aligned} \begin{aligned} Z&=\sqrt{m_j}x_j-\sqrt{m_i}x_i \\ W&=\sqrt{m_j}x_j+\sqrt{m_i}x_i. \end{aligned} \end{aligned}$$

After that, the system is rewritten as follows

$$\begin{aligned} \begin{aligned}&(m_i-m_j)\frac{W^2-Z^2}{ 4 \sqrt{m_im_j}} + \frac{W-Z}{2\sqrt{m_i}} (y-q_j-m_ix) \\&\quad +\frac{W+Z}{2\sqrt{m_j}}(-y+q_i+m_jx)+(q_j-q_i)x= 0 \\&\left[ \left( \sqrt{m_j}+\sqrt{m_i}\right) Z+q_j-q_i\right] \left[ \left( \sqrt{m_j}- \sqrt{m_i}\right) W+q_j-q_i\right] =0. \end{aligned} \end{aligned}$$

It is immediately seen that the possible solutions of the second equation are

$$\begin{aligned} Z=\frac{q_i-q_j}{\sqrt{m_i}+\sqrt{m_j}}, \end{aligned}$$

(35)

or

$$\begin{aligned} W=\frac{q_i-q_j}{\sqrt{m_j}-\sqrt{m_i}}. \end{aligned}$$

(36)

If (35) holds, then, after a few computations, it can be seen that the solutions of the first equation are

$$\begin{aligned} W_1=2 \ell _1(\mathbf{x})+\frac{q_i-q_j}{\sqrt{m_i}-\sqrt{m_j}}\ \ \text{ or }\ \ \ W_2=\frac{q_i-q_j}{\sqrt{m_j}-\sqrt{m_i}}, \end{aligned}$$

where

$$\begin{aligned} \ell _1(\mathbf{x})=\frac{\sqrt{m_i}(m_jx-y+q_i)-\sqrt{m_j}(m_ix-y+q_j)}{m_j-m_i}. \end{aligned}$$

Solution $W_2$ can be discarded. Indeed, in this case both Z and W do not depend from x, y and

$$\begin{aligned} x_i=x_j=\frac{q_i-q_j}{m_j-m_i}. \end{aligned}$$

This is only possible if $(x_j,y_j)\equiv (x_i,y_i)$ and the point is the intersection of the two lines $y=m_jx+q_j$ and $y=m_ix+q_i$, so that we can discard this case. If we consider the solution $W_1$, we have

$$\begin{aligned} \begin{aligned} x_i&= \frac{y+\sqrt{m_im_j}x-q_i}{\sqrt{m_i}\left( \sqrt{m_i}+\sqrt{m_j}\right) } \\ x_j&=\frac{y+\sqrt{m_im_j}x-q_j}{\sqrt{m_j}\left( \sqrt{m_i}+\sqrt{m_j}\right) }. \end{aligned} \end{aligned}$$

(37)

Next, let us assume that (36) holds. In this case we have the two solutions

$$\begin{aligned} Z_1=-2 \ell _2(\mathbf{x})+\frac{q_j-q_i}{\sqrt{m_i}+\sqrt{m_j}}\ \ \text{ or }\ \ \ Z_2=\frac{q_i-q_j}{\sqrt{m_i}+\sqrt{m_j}}, \end{aligned}$$

where

$$\begin{aligned} \ell _2(\mathbf{x})=\frac{\sqrt{m_i}(y-m_jx-q_i)-\sqrt{m_j}(m_ix-y+q_j)}{m_i-m_j}. \end{aligned}$$

Once again, $Z_2$ can be discarded. If we consider $Z_1$ we end up with

$$\begin{aligned} \begin{aligned} x_i&= \frac{y-\sqrt{m_im_j}x-q_i}{\sqrt{m_i}\left( \sqrt{m_i}-\sqrt{m_j}\right) } \\ x_j&=\frac{-y+\sqrt{m_im_j}x+q_j}{\sqrt{m_j}\left( \sqrt{m_i}-\sqrt{m_j}\right) }. \end{aligned} \end{aligned}$$

However, in this case we observe that (33) implies that for each $\mathbf{x}\in P\setminus [\Omega _i\cup \Omega _j] \, x_i,x_j< x$ if $m_i>m_j$, or $x_i,x_j> x$ if $m_i<m_j$ (note that over $\Omega _i$ and over $\Omega _j$ the convex envelope is equal to the restriction of the bilinear function to that edge and we do not need to consider these points). Then, $\lambda (\mathbf{x})\not \in [0,1]$, so that we can discard this solution. In conclusion, the only acceptable solution of the system is (37). Then, we can derive $\varvec{\alpha }_J(\mathbf{x})=(a(\mathbf{x}), b(\mathbf{x}))$ from (34). We have

$$\begin{aligned} conv_{f,P}(\mathbf{x})=g(\mathbf{x})=-m_j x_j^2- b(\mathbf{x}) q_j + \varvec{\alpha }_J(\mathbf{x})^T\mathbf{x}, \end{aligned}$$

(38)

over the set

$$\begin{aligned} \begin{aligned} \Gamma _J&=\left\{ {} \mathbf{x}\in P\ :\ \eta _r(\varvec{\alpha }_J(\mathbf{x}))\ge \eta _k(\varvec{\alpha }_J(\mathbf{x})),\ \forall r\not \in J,\ k\in J\right. \\&\quad \left. \lambda ^J(\mathbf{x})\in [0,1],\ \ \varvec{\alpha }_J(\mathbf{x})\in D_i\cap D_j\right\} . \end{aligned} \end{aligned}$$

In fact, the following observation gives a simplified definition of the set $\Gamma _J$, showing that we can omit $\eta _r(\varvec{\alpha }_J(\mathbf{x}))\ge \eta _k(\varvec{\alpha }_J(\mathbf{x} )),\ \forall r\not \in J,\ k\in J$.

Observation A.3

We have that

$$\begin{aligned} \Gamma _J=\{\mathbf{x}\in P\ :\ \lambda ^J(\mathbf{x})\in [0,1],\ \ \varvec{\alpha }_J(\mathbf{x})\in D_i\cap D_j\}. \end{aligned}$$

(39)

Proof

Let $P'=chull(\Omega _i\cup \Omega _j)\subseteq P$. It turns out that $conv_{f,P'}(\mathbf{x})$ is equal to the function g defined in (38) over the set $\Gamma _J\subseteq P'$ defined in (39). This is an immediate consequence of the fact that in this case $r\not \in J$ implies that $\Omega _r$ is a vertex of one of the two edges $\Omega _i$ and $\Omega _j$ of $P'$, and $\eta _r(\varvec{\alpha }_J(\mathbf{x}))\ge \eta _i(\varvec{\alpha }_J(\mathbf{x}))$ for all $r\not \in J$ follows from $\varvec{\alpha }_J(\mathbf{x})\in D_i\cap D_j$. What we will prove now is that g is a convex underestimator of f over the whole polytope P. Then, by definition of convex envelope as the largest convex underestimator of f over P and observing that $P'\subseteq P$ implies $conv_{f,P'}(\mathbf{x})\ge conv_{f,P}(\mathbf{x}) \, \forall \mathbf{x}\in P'$, we must have $conv_{f,P}(\mathbf{x})=conv_{f,P'}(\mathbf{x})=g(\mathbf{x})$ over $\Gamma _J$.

In what follows we will omit the dependency of $\varvec{\alpha }=(a,b)$ from J. In order to see that g is a convex underestimator of f over the whole polytope P, we need to check whether

$$\begin{aligned} g(\mathbf{x})=-m_j x_j^2- b(\mathbf{x}) q_j + \varvec{\alpha }^T \mathbf{x}\le xy\ \ \ \forall \mathbf{x}\in P. \end{aligned}$$

We rewrite this as

$$\begin{aligned} -m_j x_j^2- b(\mathbf{x}) q_j + a(\mathbf{x}) x + b(\mathbf{x}) (y + m_j x -q_j) + b(\mathbf{x}) q_j - b(\mathbf{x}) m_j x- xy\le 0, \end{aligned}$$

or, equivalently

$$\begin{aligned} -m_j x_j^2+(a(\mathbf{x})+ m_j b(\mathbf{x})) x + b(\mathbf{x}) (y - m_j x -q_j) - xy\le 0. \end{aligned}$$

Since $a(\mathbf{x})+ m_j b(\mathbf{x})=2 m_j x_j + b(\mathbf{x})q_j$, and after adding and subtracting $m_j x^2$, we end up, after a few elementary computations, with

$$\begin{aligned} m_j(x_j-x)^2\ge (x-b(x,y))(m_jx+q_j-y). \end{aligned}$$

By definition of $x_j$ and $b(\mathbf{x})$ the inequality reduces to

$$\begin{aligned} y-m_i x -q_i\le 0, \end{aligned}$$

which always holds over P. $\square$

1.4 An example

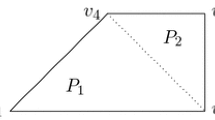
In order to illustrate the results of this section we consider the following example taken from [19]. Let

$$\begin{aligned} P=\{\mathbf{x}\ :\ x,y\ge 0,\ x\le 5,\ y\le x+1\}, \end{aligned}$$

i.e., P is the polytope with vertices $\mathbf{v}_1=(0,0)$, $\mathbf{v}_2=(5,0)$, $\mathbf{v}_3=(0,1)$, and $\mathbf{v}_4=(5,6)$. We set $\Omega _i=\{\mathbf{v}_i\}$, $i=1,\ldots ,4$. We have that $\bar{E}^u(P)$ is made up by the edge $\Omega _5=[\mathbf{v}_3,\mathbf{v}_4]$, while $\bar{E}^\ell (P)=\emptyset$. The only set J with cardinality three which needs to be considered is $J=\{1,2,3\}$, from which we have

$$\begin{aligned} conv_{xy,P}(\mathbf{x})=0\ \ \ \forall \ \mathbf{x}\in chull\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}. \end{aligned}$$

The only set with cardinality two which needs to be considered is $J=\{2,5\}$. Following the development of Sect. A.2, we have from (27) that

$$\begin{aligned} x_j=\frac{x+5y-5}{y+5-x}, \end{aligned}$$

(40)

from (28) that

$$\begin{aligned} \begin{aligned} \lambda (\mathbf{x})&=\frac{y+5-x}{6} \\ b(\mathbf{x})&=-\frac{x_j^2-10x_j-5}{6} \\ a(\mathbf{x})&=x_j+1 - b(\mathbf{x}), \end{aligned} \end{aligned}$$

so that it follows from (29) that

$$\begin{aligned} conv_{xy,P}(\mathbf{x})=-\frac{x_j^2-10x_j-5}{6}(y-x+5)+(2 x_j+1)(x-5), \end{aligned}$$

over $\Gamma _J$. In order to define $\Gamma _J$, we notice that: (i) $\lambda (\mathbf{x})\in [0,1] \, \forall \mathbf{x}\in P$; (ii) after translating $\mathbf{v}_2$ into the origin, we remark that we are in the second subcase of Observation A.2. Thus,

$$\begin{aligned} \Gamma _J=\{\mathbf{x}\ :\ 0\le x_j\le 5\}. \end{aligned}$$

Recalling the definition (40) of $x_j$, and observing that $y-x+5\ge 0$ over P, we conclude that

$$\begin{aligned} conv_{xy,P}(\mathbf{x})=\left\{ \begin{array}{ll} 0 &{} x+5y-5\le 0 \\ \frac{y(5y+x-5)}{y+5-x} &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

Figure 4 reports polytope P and the corresponding polyhedral subdivision.

Fig. 4

Polyhedral subdivision for the convex envelope of $f(\mathbf{x})=x y$ over P

Convex envelope and polyhedral subdivision for $x^n y^m$ over a box

As already mentioned in Sect. 5, we restrict the attention to $\mathbf{x}\in \mathcal{B}^u$ since the case $\mathbf{x}\in \mathcal{B}^{\ell }$ is analogous. We remark that, according to Observation 3.1

$$\begin{aligned} \begin{aligned} 1,7&\in J\ \ \Rightarrow \ \ x_1(a)=\bar{x}_1^1\\ 2,5&\in J\ \ \Rightarrow \ \ y_2(b)=\bar{y}_2^1, \end{aligned} \end{aligned}$$

and, equivalently

$$\begin{aligned} \begin{aligned} 1,7&\in J\ \ \Rightarrow \ \ a=\bar{a}=n u_y^m \left[ \bar{x}_1^1\right] ^{n-1}\\ 2,5&\in J\ \ \Rightarrow \ \ b=\bar{b}=m u_x^n \left[ \bar{y}_2^1\right] ^{m-1}. \end{aligned} \end{aligned}$$

Now, let us consider the two triples $\{1,5,7\}$ and $\{2,5,7\}$. In both cases $\eta _5(\varvec{\alpha })=\eta _7(\varvec{\alpha })$, so that

$$\begin{aligned} b=\frac{a (u_x-l_x)+l_x^nu_y^m-u_x^nl_y^m}{u_y-l_y}. \end{aligned}$$

(41)

If $J=\{1,5,7\}$, then

$$\begin{aligned} \eta _2(\varvec{\alpha })\ge \eta _5(\varvec{\alpha })\ \ \ \Rightarrow \ \ \ b\le \bar{b},\ \ \eta _1(\varvec{\alpha })= \eta _7(\varvec{\alpha })\ \ \ \Rightarrow \ \ \ a= \bar{a}, \end{aligned}$$

(42)

while if $J=\{2,5,7\}$, then

$$\begin{aligned} \eta _1(\varvec{\alpha })\ge \eta _7(\varvec{\alpha })\ \ \ \Rightarrow \ \ \ a\le \bar{a},\ \ \eta _2(\varvec{\alpha })= \eta _5(\varvec{\alpha })\ \ \ \Rightarrow \ \ \ b= \bar{b}. \end{aligned}$$

(43)

Due to (41), (42) and (43) can hold at the same time only if $\eta _1(\varvec{\alpha })=\eta _2(\varvec{\alpha })=\eta _5(\varvec{\alpha })=\eta _7(\varvec{\alpha })$. In all the other cases, only one of the two triples is acceptable. In particular, if

$$\begin{aligned} \frac{\bar{a} (u_x-l_x)+l_x^nu_y^m-u_x^nl_y^m}{u_y-l_y}<\bar{b}, \end{aligned}$$

(44)

then, we can restrict our attention to $J=\{1,5,7\}$, while if

$$\begin{aligned} \frac{\bar{a} (u_x-l_x)+l_x^nu_y^m-u_x^nl_y^m}{u_y-l_y}>\bar{b} \end{aligned}$$

(45)

then, we can restrict our attention to $J=\{2,5,7\}$. In fact, the two conditions (44) and (45) allow to restrict the attention to a collection $\mathcal{J}$ made up by only four sets. For instance, if (44) holds, then $J=\{2,7\}$ can be removed. Indeed, in such case

$$\begin{aligned} \eta _1(\varvec{\alpha })>\eta _7(\varvec{\alpha })\ \Rightarrow \ a<\bar{a},\ \ \ \eta _5(\varvec{\alpha })>\eta _2(\varvec{\alpha })\ \Rightarrow \ b>\bar{b}, \end{aligned}$$

while

$$\begin{aligned} \eta _2(\varvec{\alpha })=\eta _7(\varvec{\alpha })\ \Rightarrow (1-m)u_x^n[y_2(b)]^m+b u_y=a(u_x-l_x)+l_x^n u_y^m. \end{aligned}$$

The left-hand side is an increasing function with respect to a, so that the above equation implies that b is an increasing function with respect to a. Moreover, for $b=\bar{b}$ the equation reduces to

$$\begin{aligned} \bar{b}=\frac{a (u_x-l_x)+l_x^nu_y^m-u_x^nl_y^m}{u_y-l_y}, \end{aligned}$$

which, in view of (44) implies $a>\bar{a}$, but that is not possible. In a similar way it can be seen that if (44) holds, then we can remove the set $J=\{1,2,7\}$. In conclusion, if (44) holds, then we can restrict our attention to the four sets

$$\begin{aligned} \{1,5,7\},\ \ \{1,5\},\ \ \{1,2,5\},\ \ \{1,2\}, \end{aligned}$$

while in an analogous way it can be seen that if (45) holds, we can restrict our attention to the four sets

$$\begin{aligned} \{2,5,7\},\ \ \{2,7\},\ \ \{1,2,7\},\ \ \{1,2\}. \end{aligned}$$

The case

$$\begin{aligned} \frac{\bar{a} (u_x-l_x)+l_x^nu_y^m-u_x^nl_y^m}{u_y-l_y}=\bar{b} \end{aligned}$$

is a rather peculiar one where

$$\begin{aligned} conv_{f,\mathcal{B}}(\mathbf{x})= l_xu_y-\bar{a}x-\bar{b}y,\ \ \ \forall \mathbf{x}\in chull\{A,C,K,L\}, \end{aligned}$$

while over $chull\{B,K,L\}$ the convex envelope can be computed by solving the system associated to the set $J=\{1,2\}$.

In what follows we only discuss the case where (44) holds, since the other cases are analogous. Figure 5 displays the polyhedral subdivision induced by the convex envelope in this case.

Fig. 5

Polyhedral subdivision for the convex envelope of $f(\mathbf{x})=x^n y^m$ over $\mathcal{B}^u$ if (45) holds

1.1 Set $\{1,5,7\}$

In this case

$$\begin{aligned} \eta _1(\varvec{\alpha })=\eta _7(\varvec{\alpha })\ \Rightarrow \ a=\bar{a},\ \ \eta _2(\varvec{\alpha })>\eta _5(\varvec{\alpha })\ \Rightarrow \ b<\bar{b}. \end{aligned}$$

The solution of the system (19) is

$$\begin{aligned} a_1=\bar{a},\ \ \ \ b_1=\frac{a_1 (u_x-l_x)+l_x^nu_y^m-u_x^nl_y^m}{u_y-l_y}<\bar{b}. \end{aligned}$$

We should also check whether $\eta _3(\varvec{\alpha }),\eta _4(\varvec{\alpha }),\eta _8(\varvec{\alpha }) \ge \eta _5(\varvec{\alpha })$. It is enough to observe that $a_1>0$ and that $b_1>0$. The latter follows by observing that

$$\begin{aligned} a_1 (u_x-l_x)+l_x^nu_y^m=u_y^m \left[ n\left[ \bar{x}_1^1\right] ^{n-1}(u_x-l_x)+l_x^n\right] >0. \end{aligned}$$

In view of the definition (25) of $\bar{x}_1^1$, this is equivalent to prove that

$$\begin{aligned} n\left[ \bar{x}_1^1\right] ^{n-1}u_x +(1-n)\left[ \bar{x}_1^1\right] ^{n}>0, \end{aligned}$$

or, equivalently

$$\begin{aligned} n u_x > (n-1) \bar{x}_1^1, \end{aligned}$$

which certainly holds. Then, $a_1\in D_3^+$ and $b_1\in D_4^+$. Indeed, $D_3$ and $D_4$ only contain negative a and b values, respectively. Thus, for these a and b values it holds that $\eta _8(\varvec{\alpha })>\eta _3(\varvec{\alpha })=\eta _4(\varvec{\alpha })= \eta _5(\varvec{\alpha })=\eta _7(\varvec{\alpha })$.

In conclusion, we have $\Gamma _J=chull\{A,C,K\}$, and

$$\begin{aligned} conv_{f,\mathcal{B}}(\mathbf{x})=u_x^n l_y^m -a_1 (u_x-x) - b_1( l_y-y) \ \ \ \forall \mathbf{x}\in \Gamma _J. \end{aligned}$$

1.2 Set $\{1,2,5\}$

In this case

$$\begin{aligned} \eta _7(\varvec{\alpha })>\eta _1(\varvec{\alpha })\ \Rightarrow \ a>\bar{a},\ \ \eta _2(\varvec{\alpha })=\eta _5(\varvec{\alpha })\ \Rightarrow \ b=\bar{b}, \end{aligned}$$

and the solution of the system (19) is

$$\begin{aligned} b_2=\bar{b},\ \ \ a_2=\frac{b_2 (u_y-l_y)-l_x^nu_y^m+u_x^nl_y^m}{u_x-l_x}>\bar{a}. \end{aligned}$$

Then, after defining $M=(x_1(a_2),u_y)$, we have $\Gamma _J=chull\{A,M,L\}$, and

$$\begin{aligned} conv_{f,\mathcal{B}}(\mathbf{x})=u_x^n l_y^m -a_2 (u_x-x) - b_2 (l_y-y) \ \ \ \forall \mathbf{x}\in \Gamma _J. \end{aligned}$$

Note that also in this case we should check whether $\eta _3(\varvec{\alpha }),\eta _4(\varvec{\alpha }),\eta _8(\varvec{\alpha }) \ge \eta _5(\varvec{\alpha })$, but the proof is analogous to the one in the previous case.

1.3 Set $\{1,5\}$

In this case (20) is

$$\begin{aligned} \begin{aligned}&\lambda x_1(a)+(1-\lambda ) u_x= x \\&\lambda u_y+(1-\lambda )l_y= y \\&(1-n)u_y^m[x_1(a)]^n+a u_x = u_x^n l_y^m + b(u_y- l_y), \end{aligned} \end{aligned}$$

whose solution (parametric with respect to $\mathbf{x}$) is

$$\begin{aligned} \begin{aligned} \lambda _3(\mathbf{x})&=\frac{y-l_y}{u_y-l_y} \\ a_3(\mathbf{x})&=n u_y^m\left[ \frac{u_xy-u_xu_y+u_yx-l_yx}{y-l_y}\right] ^{n-1}\ \ \ \left( \text{ follows } \text{ from }\ \ x_1(a)=u_x-\frac{u_x-x}{\lambda }\right) \\ b_3(\mathbf{x})&=\frac{(1-n)u_y^m \left[ \frac{u_xy-u_xu_y+u_yx-l_yx}{y-l_y}\right] ^n+a_3(x,y) u_x - u_x^n l_y^m}{u_y-l_y}. \end{aligned} \end{aligned}$$

Then, $\Gamma _J=chull\{A,M,K\}$, and

$$\begin{aligned} conv_{f,\mathcal{B}}(\mathbf{x})=u_x^n l_y^m -a_3(\mathbf{x}) (u_x-x) - b_3(\mathbf{x}) (l_y-y) \ \ \ \forall \mathbf{x}\in \Gamma _J \end{aligned}$$

(we omit to prove that $\eta _3(\varvec{\alpha }),\eta _4(\varvec{\alpha }),\eta _8(\varvec{\alpha }) \ge \eta _5(\varvec{\alpha })$).

1.4 Set $\{1,2\}$

In this case (20) is

$$\begin{aligned} \begin{aligned}&\lambda x_1(a)+(1-\lambda ) u_x= x \\&\lambda u_y+(1-\lambda )y_2(b)= y \\&(1-n)u_y^m[x_1(a)]^n+a u_x = (1-m) u_x^n[y_2(b)]^m + bu_y. \end{aligned} \end{aligned}$$

(46)

If we denote by $\lambda _4(\mathbf{x}), a_4(\mathbf{x}), b_4(\mathbf{x})$ the parametric solution of the system, then $\Gamma _J=chull\{B,M,L\}$, and $\forall \mathbf{x}\in \Gamma _J$

$$\begin{aligned} conv_{f,\mathcal{B}}(\mathbf{x})=[x_1(a_4(\mathbf{x}))]^n [y_2(b_4(\mathbf{x}))]^m -a_4(\mathbf{x}) (x_1(a_4(\mathbf{x}))-x) - b_4(\mathbf{x}) (y_2(b_4(\mathbf{x}))-y) \end{aligned}$$

(again, we omit to prove that $\eta _3(\varvec{\alpha }),\eta _4(\varvec{\alpha }),\eta _8(\varvec{\alpha }) \ge \eta _1(\varvec{\alpha })$). If $m\ne n$, we are not able to derive a closed form formula for the parametric solution of the system (46). Thus, $a_4, b_4$ are implicitly defined as solutions of the system (46). If $m=n$ (the case already discussed in [14]), then it turns out that the last equation in (46) is equivalent to

$$\begin{aligned} y_2(b)=\frac{u_y}{u_x}x_1(a), \ \ \ b=\frac{u_x}{u_y}a. \end{aligned}$$

Thus, the first two equations become

$$\begin{aligned} \begin{aligned} \lambda x_1(a)+(1-\lambda ) u_x&= x \\ \lambda u_y+(1-\lambda )\frac{u_y}{u_x}x_1(a)&= y, \end{aligned} \end{aligned}$$

or, equivalently

$$\begin{aligned} \begin{aligned} \lambda&=\frac{u_x-x}{u_x- x_1(a)}&\\ \lambda&=\frac{u_x y-u_y x_1(a)}{u_x u_y-u_y x_1(a)},&\end{aligned} \end{aligned}$$

and, consequently

$$\begin{aligned} x_1(a)=\frac{u_xy+u_yx-u_xu_y}{u_y}, \ \ \ y_2(b)=\frac{u_xy+u_yx-u_xu_y}{u_x}. \end{aligned}$$

In view of the definition of $x_1(a)$ and $y_2(b)$ we also have

$$\begin{aligned} \begin{aligned} a_4(\mathbf{x})&=m u_y\left[ u_xy+u_yx-u_xu_y\right] ^{m-1} \\ b_4(\mathbf{x})&=m u_x\left[ u_xy+u_yx-u_xu_y\right] ^{m-1}. \end{aligned} \end{aligned}$$