Skip to main content
SpringerLink
Log in

PAINT–SiCon: constructing consistent parametric representations of Pareto sets in nonconvex multiobjective optimization

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

We introduce a novel approximation method for multiobjective optimization problems called PAINT–SiCon. The method can construct consistent parametric representations of Pareto sets, especially for nonconvex problems, by interpolating between nondominated solutions of a given sampling both in the decision and objective space. The proposed method is especially advantageous in computationally expensive cases, since the parametric representation of the Pareto set can be used as an inexpensive surrogate for the original problem during the decision making process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. For a comprehensive survey on well established multiobjective optimization algorithms see [1] and the references therein.

  2. Further technical details on the PAINT algorithm are given in Sect. 2 of the Supplementary Material (SM).

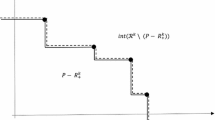
  3. The Pareto critical set is the set of points satisfying the first order necessary conditions for optimality (see [24]).

  4. By generic property, we mean a property that holds for an open and dense set, or more generally on a residual set, i.e., a set which is a countable intersection of open and dense sets. Notice that the sets we are dealing with are function spaces, i.e., we are saying that a generic property holds for “almost all” functions in a suitable sense. See, among others, [24, 30] and the references therein.

  5. A stratified set can be thought as a differentiable manifold with boundary, where the boundary is a collection of differentiable manifolds of lower dimension, and the same holds for the boundary of those manifolds. See the SM for more details.

  6. A tubular neighborhood of a set \(S\subset X\) with radius \(r>0\) is defined as \(T_{S,r}:=\left\{ x\in X: d(x,S)<r\right\} \).

  7. See also Fig. 3b.

  8. See also Fig. 4.

  9. Note that, all the simplexes are now line segments.

References

  1. Miettinen, K.: Nonlinear Multiobjective Optimization. Kluwer Academic Publishers, Boston (1999)

    MATH  Google Scholar 

  2. Hwang, C., Masud, A.S.M.: Multiple Objective Decision Making—Methods and Applications: A State-of-the-Art Survey. Springer, Berlin (1979)

    Book  MATH  Google Scholar 

  3. Pareto, V.: Manuale di economia politica con una introduzione alla scienza sociale. Piccola biblioteca scientifica. Società editrice libraria, Milan (1906)

  4. Benson, H.P., Sayin, S.: Towards finding global representations of the efficient set in multiple objective mathematical programming. Naval Res. Logist. 44, 47–67 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  5. Karasakal, E., Köksalan, M.: Generating a representative subset of the nondominated frontier in multiple criteria decision making. Oper. Res. 57, 187–199 (2009)

    Article  MATH  Google Scholar 

  6. Klamroth, K., Miettinen, K.: Integrating approximation and interactive decision making in multicriteria optimization. Oper. Res. 56, 222–234 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  7. Noor, E., Milo, R.: Efficiency in evolutionary trade-offs. Science 336, 1114–1115 (2012)

    Article  Google Scholar 

  8. Shoval, O., Sheftel, H., Shinar, G., Hart, Y., Ramote, O., Mayo, A., Dekel, E., Kavanagh, K., Alon, U.: Evolutionary trade-offs, Pareto optimality, and the geometry of phenotype space. Science 336, 1157–1160 (2012)

    Article  Google Scholar 

  9. Ruzika, S., Wiecek, M.M.: Approximation methods in multiobjective programming. J. Optim. Theory Appl. 126, 473–501 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  10. Hillermeier, C.: Nonlinear Multiobjective Optimization: A Generalized Homotopy Approach. Birkhäuser, Basel (2001)

    Book  Google Scholar 

  11. Hillermeier, C.: Generalized homotopy approach to multiobjective optimization. J. Optim. Theory Appl. 110, 557–583 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  12. Schütze, O., Dell’Aere, A., Dellnitz, M.: On Continuation methods for the numerical treatment of multi-objective optimization problems. In: Practical Approaches to Multi-objective Optimization. IBFI, Schloss Dagstuhl, Germany (2005)

  13. Hartikainen, M., Miettinen, K., Wiecek. M. M.: Pareto front approximations for decision making with inherent non-dominance. In: New State of MCDM in the 21st Century, pp. 35–46. Springer, Berlin (2011)

  14. Hartikainen, M., Miettinen, K., Wiecek, M.M.: Constructing a Pareto front approximation for decision making. Math. Methods Oper. Res. 73, 209–234 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  15. Rakowska, J., Haftka, R.T., Watson, L.T.: Multi-objective control–structure optimization via homotopy methods. SIAM J. Optim. 3, 654–667 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  16. Askar, S., Tiwari, A.: Multi-objective optimisation problems: a symbolic algorithm for performance measurement of evolutionary computing techniques. In: Ehrgott, M. (ed.) EMO 2009, pp. 169–182. Springer, Berlin (2009)

    Google Scholar 

  17. Das, I., Dennis, J.E.: Normal-boundary intersection: a new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J. Optim. 8, 631–657 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  18. Grünbaum, B.: Convex Polytopes. Interscience Publishers, London (1967)

    MATH  Google Scholar 

  19. Lovison, A.: Global search perspectives for multiobjective optimization. J. Global Optim. 57(2), 385–398 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  20. Lovison, A.: Singular continuation: generating piecewise linear approximations to Pareto sets via global analysis. SIAM J. Optim. 21, 463–490 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  21. Hartikainen, M., Miettinen, K., Wiecek, M.M.: PAINT: Pareto front interpolation for nonlinear multiobjective optimization. Comput. Optim. Appl. 52, 845–867 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  22. Deb, K., Thiele, L., Laumanns, M., Zitzler, E.: Scalable multi-objective optimization test problems. IEEE Int. Conf. E-Comm. Technol. 1, 825–830 (2002)

    Google Scholar 

  23. Wierzbicki, A.P.: On the completeness and constructiveness of parametric characterizations to vector optimization problems. OR Spectr. 8, 73–87 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  24. Smale, S.: Global analysis and economics. I. Pareto optimum and a generalization of Morse Theory. In: Dynamical systems (Proceedings Symposium, Univ. Bahia, Salvador, 1971), pp. 531–544. Academic Press, New York (1973)

  25. de Melo, W.: Stability and optimization of several functions. Topology 15, 1–12 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  26. Wan, Y.H.: On the algebraic criteria for local Pareto optima. I. Topology 16, 113–117 (1977)

    Article  MATH  MathSciNet  Google Scholar 

  27. Allgower, E.L., Georg, K.: Piecewise linear methods for nonlinear equations and optimization. J. Comput. Appl. Math. 124, 245–261 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  28. Edelsbrunner, H.: Shape reconstruction with delaunay complex. In: Lucchesi, C.L., Moura, A.V. (eds.) LATIN’98: Theoretical Informatics, pp. 119–132. Springer, Berlin (1998)

    Chapter  Google Scholar 

  29. Goodman, J.E., O’Rourke, J. (eds.): Discrete and Computational Geometry. CRC Press, Boca Raton (1997)

    MATH  Google Scholar 

  30. Golubitsky, M., Guillemin, V.: Stable Mappings and Their Singularities. Graduate Texts in Mathematics, vol. 14. Springer, New York (1973)

    Book  Google Scholar 

  31. Lovison, A., Pecci, F.: Hierarchical stratification of Pareto sets. Submitted (2014)

  32. de Melo, W.: On the structure of the Pareto set of generic mappings. Boletim da Sociedade Brasileira de Matemática 7, 121–126 (1976)

    Article  MATH  Google Scholar 

  33. Thom, R.: Les singularités des Applications Différentiables. Ann. l’inst. Fourier 6, 43–87 (1956)

    Article  MATH  MathSciNet  Google Scholar 

  34. Edelsbrunner, H., Mücke, E.P.: Simulation of simplicity: a technique to cope with degenerate cases in geometric algorithms. ACM Trans. Graph. 9, 66–104 (1990)

    Article  MATH  Google Scholar 

  35. Anstreicher, K.: Linear programming in O([n3/ln n]L) operations. SIAM J. Optim. 9, 803–812 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  36. Eaton, J.W.: GNU Octave Manual. Network Theory Limited (2002)

  37. Mather, J.: Notes on topological stability. Bull. Am. Math. Soc. (New Ser.) 49, 475–506 (2012)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

This research has been partially supported by the Fondazione CaRiPaRo Project “Nonlinear Partial Differential Equations: models, analysis, and control-theoretic problems”.

Author information

Authors and Affiliations

  1. Department of Mathematical Information Technology, University of Jyväskylä, PO Box 35 (Agora), 40014, Jyväskylä, Finland

    Markus E. Hartikainen

  2. Dipartimento di Matematica, Università degli Studi di Padova, Via Trieste, 63, 35121, Padova, Italy

    Alberto Lovison

Authors
  1. Markus E. Hartikainen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alberto Lovison
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alberto Lovison.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 198 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hartikainen, M.E., Lovison, A. PAINT–SiCon: constructing consistent parametric representations of Pareto sets in nonconvex multiobjective optimization. J Glob Optim 62, 243–261 (2015). https://doi.org/10.1007/s10898-014-0232-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-014-0232-9

Keywords

Search

Navigation