A Lagrangian–Eulerian Method on Regular Triangular Grids for Hyperbolic Problems: Error Estimates for the Scalar Case and a Positive Principle for Multidimensional Systems

Abstract

In this work, we design a new class of fully discrete Lagrangian–Eulerian schemes on triangular grids to approximate nonlinear multidimensional initial value problems for scalar models and multidimensional systems of conservation. The numerical approach is based on the improved concept of multidimensional no-flow curves. We also provide a convergence proof towards the entropy solution to the scalar problem $u_{t}(t,{\textbf{x}})+$div$({\textbf{f}}(u(t,{\textbf{x}})))=0$, with $u_{0} \in L^{\infty }({\mathbb {R}}^{2})$, which is analyzed in the effective setting of the properties of uniqueness and regularity of the entropy process solutions in the $L_{t}^{\infty }(L_{{\textbf{x}}}^{1})$-norm and linked to the entropy measure-valued solutions. Additionally, we obtain optimal a priori error estimates as ${\mathcal {O}}(h^{\frac{1}{2}})$ on equilateral triangular meshes. In the general context of multidimensional hyperbolic systems of conservation laws, we show that the Lagrangian–Eulerian scheme on triangular grids also satisfies the positivity principle proposed by Lax and Liu (J Comput Phys 5(2):133–156, 1996; J Comput Phys 187:428–440, 2003) and a type of weak positivity principle. We found a connection (given in the “Appendix”) between the notion of no-flow curves (viewed as a vector field with locally bounded $\Gamma ^{M}{-}variation$) and the results of Bressan in the context of (local) existence and continuous dependence for discontinuous O.D.E.’s as introduced in Bressan (Proc Am Math Soc 104(3):772–778, 1988) and Bressan and Colombo (Boll Un Mat Ital 4(2):295–311, 1990). We present numerical solutions for nontrivial 2D hyperbolic problems, e.g., 4 by 4 compressible Euler equations (Double Mach Reflection problem and Mach 3 wind tunnel flow), a nonclassical 2 by 2 three-phase flow system of nonstrictly hyperbolic conservation laws (with a resonance/umbilic point), and the 3 by 3 shallow-water system (with and without bottom topography), and also 8 by 8 Orszag-Tang vortex system in magnetohydrodynamics.

Appendix A: Construction of No-Flow Curves Via Discontinuous O.D.E.’s

1.1 The Lagrangian–Eulerian Numerical Flux Function Based on the No-Flow Curves Free of (Exact and Approximate) Eigenvalues

Following [28], consider the 1D scalar initial value problem

$$\begin{aligned} \frac{\partial u}{\partial t}+ \frac{\partial H(u)}{\partial x} = 0, \quad x \in [a,b], \quad t > 0, \quad \quad \quad u(0,x) = u_0(x), \end{aligned}$$

(100)

where $H \in C^{1}(\Omega )$, $H:\Omega \rightarrow {\mathbb {R}}$, $u_{0}(x) \in L^{\infty }([a,b])$ and $u=u(t,x): \mathbb {R^+} \times {\mathbb {R}} \longrightarrow \ \Omega \subset {\mathbb {R}}.$

As in [6,7,8,9, 18, 28, 29], we assume that $\left[ \begin{array}{c} u \\ H(u) \end{array}\right] \cdot \vec {\textit{n}} = 0$ with oriented normal $\vec {\textit{n}}$ from $\nabla _{t,x} \cdot [u \,\,\, H(u)]^{\top }=0$ over the local space-time domain

$$\begin{aligned} D_j^{n,n+1}(t,x) = \{(t,x) \,\, | \,\, \sigma _j^n(t) \le x \le \sigma _{j+1}^n(t), \,\,t^n \le t \le t^{n+1}\}, \end{aligned}$$

(101)

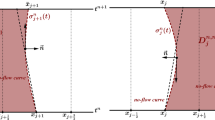
and, applying the divergence theorem in Eq. (100), we obtain (with $h_j^{n+1}={\overline{x}}_{j +1}^{n+1}-{\overline{x}}_{j}^{n+1}$)

$$\begin{aligned} \int _{{\overline{x}}_{j}^{n+1}}^{{\overline{x}}_{j +1}^{n+1}} u(t^{n+1},x) \,\, dx= & {} \int _{x_j^n}^{x_{j+1}^n} u(t^n,x) \,\, dx, \qquad \text {or} \qquad \nonumber \\ \displaystyle \frac{1}{h_j^{n+1}}{\int _{{\overline{x}}_{j}^{n+1}}^{{\overline{x}}_{j+1}^{n+1}}} u(t^{n+1},x) \,dx= & {} \displaystyle \frac{1}{h_j^{n+1}} {\int _{x_j^n}^{x_{j+1}^n}} \!\!u(t^n,x) \,dx. \end{aligned}$$

(102)

To construct the dynamic parametric no flow curves $\sigma _j^n(t)$ $\forall \,\, j$ governing the space-time $D_j^{n,n+1}$, we consider $\Upsilon _j(\xi )=(x(\xi ),t(\xi ))_j$ for each curve $\sigma _j^n(t)$ and formally write $\frac{d\Upsilon _j(\xi )}{d\xi } =\left( \frac{dx(\xi )}{d\xi },\frac{dt(\xi )}{d\xi }\right) _j$. By assuming $\left[ \begin{array}{c} H(u) \\ u \end{array}\right] \cdot \vec {\textit{n}} = 0$ over $D_j^{n,n+1}(x,t)$ from (101) for $t^n \le t \le t^{n+1}$, we might conclude that, for each $D_j^{n,n+1}(x,t)$, we have ${\frac{d\Upsilon _j^n(\xi )}{d\xi } \bot \,\vec {\textit{n}}}$ and ${\frac{d\Upsilon _{j+1}^n(\xi )}{dt}\bot \, \vec {\textit{n}}}$ since the slope $(\frac{dx(\xi )}{d\xi },\frac{dt(\xi )}{d\xi })$ is proportional to the slope of vector $[H(u),u]^{\top }$ over curves ${\sigma _{j}^n(t)}$ and $\sigma _{j+1}^n(t)$. The change in variable $\sigma (t)=x(\xi (t))$, noticing that (for any real number $\omega \ne 0$) the relations hold

$$\begin{aligned} \displaystyle \frac{dx(\xi )}{d\xi }=\omega \,H(u) \quad \text {and} \quad \displaystyle \frac{dt(\xi )}{d\xi }=\omega \,u, \end{aligned}$$

(103)

and also noticing that $\frac{d\sigma (t)}{dt}\!= \frac{dx(\xi )}{dt} = \frac{\frac{dx(\xi )}{d\xi }}{\frac{dt(\xi )}{d\xi }}$ allow us to write the system of O.D.E.’s

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{d\sigma _j^n(t)}{dt} = \displaystyle \frac{H(u(t,\sigma _{j}^{n}(t)))}{u(t,\sigma _{j}^{n}(t))}, \qquad t^n < t \le t^{n+1}, \\ \sigma _j^n(t^n) = x_j^n, \end{array}\right. } \end{aligned}$$

(104)

where $\sigma _j^0(t^0) = x_j^0$ and $u(t^0, \sigma _j^0(t^0)) = u_0(x_j^0)$ for all $j{\mathbb {Z}}$, which is simply the initial data $u(x,0) = u_0(x)$ at the initial time. Thus, under the appropriate hypotheses of the Divergence Theorem, the above calculations show that the original problem given by (100) is equivalent to Eqs. (102a) and (104), along with the relevant definitions given by (101) and (102.b). Based on the above formalism of the no-flow curves, fully discrete monotone-type schemes [7,8,9] and semi-discrete schemes [28, 29] were designed and analyzed for solving initial value problems for scalar models and multidimensional systems of conservation laws.

1.2 The Existence and Uniqueness of No-Flow Curves

In this “Appendix”, we discuss the existence and uniqueness of no-flow curves using some results of A. Bressan as originally presented in [1].

In [1] (see also [2]), Bressan was concerned with the problem of uniqueness and continuous dependence of a very important class of discontinuous differential equations related to the fundamental Cauchy problem,

$$\begin{aligned} {\dot{x}}={\textbf{f}}(t,x(t)), \quad x(t_0)=x_0, \,\, x_0 \in {\mathbb {R}}^{n}, \end{aligned}$$

(105)

where the vector field ${\textbf{f}}$ may be discontinuous with respect to both variables t, x. In [1], Bressan proved that, if the total variation of f along certain directions is locally finite, then the existence of a unique solution holds, depending continuously on the initial data.

In [1], Bressan considered a much weaker condition, which does not imply the continuity of f. For a fixed $M > 0$, consider the cone

$$\begin{aligned} \Gamma ^{M}=\left\{ (t,x) \in {\mathbb {R}}^{n+1}: \left\| x \right\| \le Mt \right\} . \end{aligned}$$

(106)

Let $\preceq$ be the partial ordering on ${\mathbb {R}}^{n+1}$ induced by cone $\Gamma ^{M}$:

$$\begin{aligned} (t,x) \preceq (t^{\prime },x^{\prime }) \quad \text { iff } \quad || (x^{\prime }-x) || \le M \, (t^{\prime }-t). \end{aligned}$$

(107)

Using this ordering, one can define a class of vector fields with bounded “directional variation.”

Definition 1

A vector field ${\textbf{f}}: {\mathbb {R}}^{n+1} \rightarrow {\mathbb {R}}^{n}$ has bounded $\Gamma ^{M}{-}variation$ if there exists a constant C such that

$$\begin{aligned} \displaystyle \sum ^{N}_{i=1} || {\textbf{f}}(t_i,x_i) - {\textbf{f}}(t_{i-1},x_{i-1}) || \le C, \end{aligned}$$

(108)

for every finite sequence $(t_i,x_i)$, $i=0, 1, \cdots , N$, with $(t_0,x_0) \preceq (t_1,x_1) \preceq \cdots \preceq (t_N,x_N)$.

Definition 2

A vector field ${\textbf{f}}: {\mathbb {R}}^{n+1} \rightarrow {\mathbb {R}}^{n}$ has locally bounded $\Gamma ^{M}{-}variation$ if, for every $(t_0,x_0) \in {\mathbb {R}}^{n+1}$, there exist $\delta > 0$ and a constant C such that

$$\begin{aligned} \displaystyle \sum ^{N}_{i=1} || {\textbf{f}}(t_i,x_i) - {\textbf{f}}(t_{i-1},x_{i-1}) || \le C, \end{aligned}$$

(109)

for every finite sequence $(t_i,x_i)$, $i=1, \cdots , N$, satisfying

$$\begin{aligned} (t_0,x_0) \preceq (t_1,x_1) \preceq \cdots \preceq (t_N,x_N), \quad t_N < t_0+\delta . \end{aligned}$$

(110)

The main result in Bressan’s study ([1]) shows that, if f has locally bounded directional variation, then the solution of (105) is unique:

Theorem A.1

Let ${\textbf{f}}: {\mathbb {R}}^{n+1} \rightarrow {\mathbb {R}}^{n}$ be a vector field with locally bounded $\Gamma ^{M}{-}variation$. If $|| {\textbf{f}}(t,x)|| \le L < M$ for all t, x, then the Cauchy problem (105) has a unique forward solution $x(\cdot )$, which is defined on $[t_0,\infty )$. Moreover, the restriction of $x(\cdot )$ to any bounded internal $[t_0,T]$ depends continuously on the initial value $x_0$.

Note that Eq. (105) is solved along with variable x. We utilize Theorem A.1 to prove the existence and uniqueness of no-flow curves. The construction of these curves is performed using a given mesh: for a fixed $t^n$, we consider the points $(x_i,t^n)$ along the mesh. Equation (104) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{d\sigma _j^n(t)}{dt} = \displaystyle {{\textbf{f}}(u(t,\sigma _{j}^{n}(t)))}, \qquad t^n < t \le t^{n+1}, \\ \sigma _j^n(t^n) = x_j^n, \end{array}\right. } \end{aligned}$$

(111)

where ${\textbf{f}}(u)=H(u)/u$. We can extend the construction of the no-flow curve for $t\in [0,T]$ for some T, as follows (see Fig. 19.b):

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{d\sigma _j(t)}{dt} = \displaystyle {{\textbf{f}}(u(t,\sigma _{j}(t)))}, \qquad 0=t^0<t \le T, \\ \sigma _j(t^0) = x^0_j. \end{array}\right. } \end{aligned}$$

(112)

According to Definition 1, Definition 2, and Theorem 1, the cone condition $\Gamma ^{M}$ in (107) satisfies (see Fig. 19.a)

$$\begin{aligned} \displaystyle \frac{|| (x^{\prime }-x) ||}{(t^{\prime }-t)} \le M. \end{aligned}$$

(113)

On the other hand, from the analysis of previous works (see, e.g., [28, 29]), we propose the weak CFL-condition (for $f(u)\equiv \displaystyle \frac{H(u)}{u}$, where u and H(u) are given by (100))

$$\begin{aligned} \beta \frac{\Delta t}{\Delta x}\,\, \underset{u}{\text {Sup}} \left| f(u) \right| \le 1 \end{aligned}$$

(114)

for solving the 1D model problem in (100).

For any sequence $(x^i,t^i)\in {\mathbb {R}}\times {\mathbb {R}}^+$, we define the partial order $(x^i,t^i)\preceq (x^{i+1},t^{i+1})$ as (see Fig. 19.a)

$$\begin{aligned} (t^i,x^i)\preceq (t^{i+1},x^{i+1})\quad \text { iff } \quad || x^{i+1}-x^{i} || \le M \, (t^{i+1}-t^i). \end{aligned}$$

(115)

Fig. 19

(a) Left: partial order $(t^i,x^i)\preceq (t^{i+1},x^{i+1})$. (b) Right: solution of (112) satisfying the cone condition

Note that Eq. (112) is different from (105) since the solution of $\sigma _j^n(t)$ depends on variable u(x, t). However, for the scalar case, we can utilize Kruzhkov’s results (see [15]). First, we can see that u(x, t) is a function of variables x and t, and the main result is that for the problem in (100). Second, we have that $TV(u(t))\le TV(u_0)$, where TV(u(t)) represents the total variation of u(x, t) for time t.

Here, we give the following condition for the solution of u(x, t) (and thus for flux f):

Condition A: Assume that, for each point $(t^i,x^i)$ of any sequence with partial order given by (115), there is a curve $(t,\tau ^i(t))$ satisfying

$$\begin{aligned} u(t,\tau ^i(t))=u(t^i,x^i)\quad \quad \text { for all } t^0=0\le t \le t^{i}. \end{aligned}$$

(116)

Fig. 20

(a) Left: curve $(t,\tau ^i(t))$. (b) Right: projection of no-flow curve for each step onto the mesh points

Note that Condition A states the existence of a curve in which the solution is constant. For states far from shocks, this curve represents characteristic waves. In more general cases, we can consider the generalized characteristic in Dafermos’ theory [16] (see also [15]).

We also assume the following condition for flux $f:{\mathbb {R}}\longrightarrow {\mathbb {R}}$.

Condition B: Function $f:{\mathbb {R}}\longrightarrow {\mathbb {R}}$, with $f(u)=H(u)/u$, is a locally Lipschitz continuous function with constant $B>0$, i.e., there is an interval $[c,d]\subset {\mathbb {R}}$ such that

$$\begin{aligned} |f(b)-f(a)|=B|b-a|, \text { for } a, b \in [c,d]. \end{aligned}$$

(117)

We can prove, in the following result, that we can construct the no-flow curve from $t=0$ to $t=T$ in such a way that we can obtain sequences $(x^i,t^i)$ satisfying (115).

Theorem A.2

Let $f: {\mathbb {R}} \rightarrow {\mathbb {R}}$ be a function satisfying Condition B and the u(x, t) solution of (100) with initial data $u_0(x)\in L^\infty ({\mathbb {R}})$ satisfying $TV(u_0(x))\le {\tilde{C}}$, for some ${\tilde{C}}>0$. For a fixed j, assume that Condition A is satisfied for $t^N=T$. If $|| f(u(t,x))|| \le L < M$ for all t, x, then the Cauchy problem (112) has a unique forward solution $\sigma _j(\cdot )$, which is defined on $[t_0,\infty )$. Moreover, $\sigma _j(\cdot )$ restricted to any bounded internal $[t_0,T]$ depends continuously on the initial value $x_j^0$.

Proof

For the proof of Theorem A.2, it is enough to prove that the conditions of Theorem A.1 are verified. Since we are interested in the construction of each curve, here we denote $x_j^i$ only as $x^i$. The only condition that we need to verify is that f satisfies Eq. (109) for some $C>0$. From Kruzhkov’s results, we get $TV(u(t)\le TV(u_0)\le {\tilde{C}}$. Now, using Condition A, we have

$$\begin{aligned} f(u(t^i,x^{i}))-f(u(t^{i-1},x^{i-1}))=f(u(0,\tau ^i(0)))-f(u(0,\tau ^{i-1}(0))). \end{aligned}$$

(118)

Taking the absolute value in (118) and taking into account that f satisfies Condition B, we have

$$\begin{aligned} |f(u(t^i,x^{i}))-f(u(t^{i-1},x^{i-1}))|&= |f(u(0,\tau ^i(0)))-f(u(0,\tau ^{i-1}(0))|\nonumber \\&\le B_i|u(0,\tau ^i(0))-u(0,\tau ^{i-1}(0))|, \end{aligned}$$

(119)

for some positive $B_i$. By summing (119) from $i=1$ to N, we obtain

$$\begin{aligned} \sum _{i=1}^N|f(u(x^{i},t^i))-f(u(x^{i-1},t^{i-1}))|\le \sum _{i=1}^N B_i|u(\tau ^i(0),0)-u(\tau ^{i-1}(0),0)|. \end{aligned}$$

(120)

Taking $B=\underset{i}{\max }\ \; B_{i}$ and considering that $u_0(x)$ is bounded, we obtain

$$\begin{aligned} \sum _{i=1}^N|f(u(t^i,x^{i}))-f(u(t^{i-1},x^{i-1}))|\le B\sum _{i=1}^N |u(0,\tau ^i(0))-u(0,\tau ^{i-1}(0))|\le B \, TV(u_0). \end{aligned}$$

(121)

Thus, the condition in (108) is satisfied, and the conditions of Theorem A.1 are verified. Then, Theorem A.2 is proved. $\square$

Since $f(u)=H(u)/u$ and it is necessary that $|f(u)|\le L$ to obtain the solution, we need to define f(u) for $u=0$. In this case, we assume that

$$\begin{aligned} \lim _{u\longrightarrow 0} \frac{H(u)}{u} \end{aligned}$$

(122)

exists, and we define f(0) as this limit. Thus, the condition $|| f(u(t,x))|| \le L$ (for some $L>0$) is verified because $u_0(x)$ is bounded, and, therefore, the solution to u(x, t) is also bounded through Kruzhkov’s theory.

Although Theorem A.2 is proved for the scalar case, if conditions similar to those of Theorem A.2 are verified, it is possible to prove a similar result for multidimensional systems.

Note that Condition A may be difficult to verify over long times. In our method, we utilize the strategy of construction of no-flow curves by solving (111) only for two consecutive times $t^i$ and $t^{i+1}$ in the mesh grid. As a result, we obtain the curve $(\sigma _j^i(t),t)$ for $t^i\le t \le t^{i+1}$, and then we project the point $\sigma _j^i(t^{i+1})$ onto mesh point $x_j$ again (see Fig. 20.b).

In this case, to guarantee Condition A, it is enough to use the CFL condition (114). As we are assuming that $|f(u)|\le L$ for all the solutions to u, condition (114) becomes

$$\begin{aligned} \beta \frac{\Delta t}{\Delta x} L\le 1. \end{aligned}$$

(123)

From condition (113), we have that

$$\begin{aligned} \frac{\Delta x}{\Delta t}\le M. \end{aligned}$$

(124)

Equations (123) and (124) lead to

$$\begin{aligned} \beta \le \frac{M}{L}. \end{aligned}$$

(125)

In particular, since $M>L$, we can take $\beta =1$, and, in this case, we can construct the wave satisfying Condition A.