The Minkowski Billiard Characterization of the EHZ-Capacity of Convex Lagrangian Products

Abstract

We rigorously state the connection between the EHZ-capacity of convex Lagrangian products $K\times T\subset \mathbb {R}^n\times \mathbb {R}^n$ and the minimal length of closed (K, T)-Minkowski billiard trajectories. This connection was made explicit for the first time by Artstein–Avidan and Ostrover under the assumption of smoothness and strict convexity of both K and T. We prove this connection in its full generality, i.e., without requiring any conditions on the convex bodies K and T. This prepares the computation of the EHZ-capacity of convex Lagrangian products of two convex polytopes by using discrete computational methods.

1 Introduction and Main Result

Simply put, this paper is about the connection between the symplectic size of certain convex bodies in $\mathbb {R}^{2n}$, $n\ge 1$, and the length of certain minimal periodic billiard trajectories on that convex bodies, more precisely, it is about the connection between the EHZ-capacity of convex Lagrangian products

$$\begin{aligned} K\times T\subset \mathbb {R}^n\times \mathbb {R}^n \end{aligned}$$

and the minimal $\ell _T$-length of closed (K, T)-Minkowski billiard trajectories.

Let us first introduce these two quantities one by one.

1.1 The EHZ-Capacity of Convex Lagrangian Products

The EHZ-capacity of a convex set $C\subset \mathbb {R}^{2n}$ is

$$\begin{aligned} c_{EHZ}(C)=\min \{\mathbb {A}(x):x \text { closed characteristic on }\partial C\}, \end{aligned}$$

where a closed characteristic on $\partial C$ is an absolutely continuous loop in $\mathbb {R}^{2n}$ satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)\in J\partial H_{C}(x(t))\quad \text {a.e.} \\ H_{C}(x(t)):=\frac{1}{2}\mu _{C}(x(t))^2=\frac{1}{2}\quad \forall t\in \mathbb {R}/\mathbb {Z}\end{array}\right. } \end{aligned}$$

(1)

where is the symplectic matrix, $\partial$ the subdifferential-operator, and

$$\begin{aligned} \mu _C(x)=\min \{s\ge 0 : x \in sC\}, \; x\in \mathbb {R}^{2n}, \end{aligned}$$

the Minkowski functional. By $\mathbb {A}(x)$ we denote the loop’s action given by

$$\begin{aligned} \mathbb {A}(x)= -\frac{1}{2}\int _{\mathbb {R}/\mathbb {Z}} \langle J\dot{x}(t),x(t)\rangle \;dt.\end{aligned}$$

We remark that the above definition of the E(keland)H(ofer)Z(ehnder)-capacity is the outcome of a historically grown study of symplectic capacities. More precisely, it is the generalization (to the non-smooth case) by Künzle in [14] of a symplectic capacity that originally represented the coincidence of the Ekeland–Hofer- and Hofer–Zehnder-capacities constructed in [9] and [13], respectively.

Let us clarify the notion of Lagrangian products in $\mathbb {R}^{2n}$.

On $\mathbb {R}^{2n}$ there exists a natural symplectic structure such that $x\in \mathbb {R}^{2n}$ can be written as

$$\begin{aligned} x=(q_1,...,q_n;p_1,...,p_n), \end{aligned}$$

where $q=(q_1,..,q_n)$ represent the local and $p=(p_1,...,p_n)$ the momentum coordinates in the classical physical phase space

$$\begin{aligned} \mathbb {R}^n_q\times \mathbb {R}^n_p. \end{aligned}$$

This phase space is equipped with the standard symplectic  2-form $\omega _0$ which satisfies

$$\begin{aligned} \omega _0(q,p)=\sum _{j=1}^n dp_j \wedge dq_j=\langle Jq,p\rangle . \end{aligned}$$

The Hamiltonian “vector” field

$$\begin{aligned} X_{H_C}=J\partial H_C \end{aligned}$$

of the Hamiltonian differential inclusion (1) is determined by

$$\begin{aligned} \iota _{X_{H_C}}\omega _0=-\partial H_C \end{aligned}$$

and the action of a closed curve $\gamma$ by

$$\begin{aligned} \mathbb {A}(\gamma )=\int _\gamma \lambda ,\quad \omega _0=d\lambda . \end{aligned}$$

Now, a product $K\times T\subset \mathbb {R}^{2n}$ is called Lagrangian if $K\subset \mathbb {R}^n_q$ and $T\subset \mathbb {R}^n_p$.

1.2 Minkowski billiards

Minkowski billiards are the natural extensions of Euclidean billiards to the Finsler setting.

Euclidean billiards are associated to the local Euclidean billiard reflection rule: The angle of reflection equals the angle of incidence (assuming that the relevant normal vector as well as the incident and the reflected ray lie in the same two-dimensional affine flat). This local Euclidean billiard reflection rule follows from the global least action principle. For a reflection on a hyperplane this principle means that a billiard trajectory segment $(q_{j-1},q_j,q_{j+1})$ minimizes the Euclidean length in the space of all paths connecting $q_{j-1}$ and $q_{j+1}$ via a reflection at this hyperplane.

In Finsler geometry, the notion of length of vectors in $\mathbb {R}^n$ is given by a convex body $T\subset \mathbb {R}^n$, i.e., a compact convex set in $\mathbb {R}^n$ which has the origin in its interior (in $\mathbb {R}^n$). The Minkowski functional $\mu _T$ determines the distance function, where we recover the Euclidean setting when T is the n-dimensional Euclidean unit ball. Then, heuristically, billiard trajectories are defined via the global least action principle with respect to $\mu _T$, because in Finsler geometry, there is no useful notion of angles.

Here, convexity of $T\subset \mathbb {R}^n$ means that for every boundary point $z\in \partial T$ there is a hyperplane H with its associated open half spaces $\mathring{H}^+$ and $\mathring{H}^-$ of $\mathbb {R}^n$ such that either $T\cap \mathring{H}^+=\emptyset$ or $T\cap \mathring{H}^-=\emptyset$. We call $T\subset \mathbb {R}^n$ strictly convex if for every boundary point $z\in \partial T$ and every unit vector in the outer normal cone

$$\begin{aligned} N_T(z)=\left\{ n\in \mathbb {R}^n : \langle n,y-z\rangle \le 0 \text { for all } y\in T\right\} \end{aligned}$$

the hyperplane H in $\mathbb {R}^n$ containing z and normal to n satisfies $H\cap T =\{z\}$.

Let us precisely define Minkowski billiard trajectories. As we have shown in [16], it makes sense to differentiate between weak and strong Minkowski billiard trajectories.

Definition 1

(Weak Minkowski billiard trajectories) Let $K\subset \mathbb {R}^n$ be a convex body. Let $T\subset \mathbb {R}^n$ be another convex body and

$$\begin{aligned} T^\circ = \left\{ x\in \mathbb {R}^n : \langle x,y\rangle \le 1 \; \forall y\in T \right\} \subset \mathbb {R}^n \end{aligned}$$

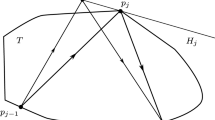
its polar body. We say that a closed polygonal curve¹ with vertices $q_1,...,q_m$, $m\in \mathbb {N}_{\ge 2}$, on the boundary of K is a closed weak (K, T)-Minkowski billiard trajectory if for every $j\in \{1,...,m\}$, there is a K-supporting hyperplane $H_j$ through $q_j$ such that $q_j$ minimizes

$$\begin{aligned} \mu _{T^\circ }(\bar{q}_j-q_{j-1})+\mu _{T^\circ }(q_{j+1}-\bar{q}_j) \end{aligned}$$

(2)

over all $\bar{q}_j\in H_j$ (see Fig. 1). We encode this closed weak (K, T)-Minkowski billiard trajectory by $(q_1,...,q_m)$ and call its vertices bouncing points. Its $\ell _T$-length is given by

$$\begin{aligned} \ell _T((q_1,...,q_m))=\sum _{j=1}^m \mu _{T^\circ }(q_{j+1}-q_j). \end{aligned}$$

Fig. 1

The weak Minkowski billiard reflection rule: $q_j$ minimizes (2) over all $\bar{q}_j\in H_j$, where $H_j$ is a K-supporting hyperplane through $q_j$

We call a boundary point $q\in \partial K$ smooth if there is a unique K-supporting hyperplane through q. We say that $\partial K$ is smooth if every boundary point is smooth (we also say K is smooth while we actually mean $\partial K$).

We remark that, in general, the K-supporting hyperplanes $H_j$ in Definition 1 are not uniquely determined. One can prove that this is only the case for smooth and strictly convex T (see [16]).

We note that the weak Minkowski billiard reflection rule does not only generalize the Euclidean billiard reflection rule to Finsler geometries, it also extends the classical understanding of billiard trajectories–which are usually understood as trajectories with bouncing points in smooth boundary points (billiard table cushions) while they terminate in non-smooth boundary points (billiard table pockets)–to non-smooth billiard table boundaries. To the author’s knowledge, the papers [5] (’89), [10] (’04), and [6] (’09) were among the first suggesting a detailed study of these generalized billiard trajectories.

In the case when $T^\circ$ is smooth and strictly convex, Definition 1 yields a geometric interpretation of the billiard reflection rule: On the basis of Lagrange’s multiplier theorem, one derives the condition

$$\begin{aligned} \nabla _{\bar{q}_j}\varSigma _j(\bar{q}_j)_{\vert \bar{q}_j=q_j}=\nabla \mu _{T^\circ }(q_j-q_{j-1})-\nabla \mu _{T^\circ }(q_{j+1}-q_j)= \mu _j n_{H_j}, \end{aligned}$$

where $\mu _j>0$, since the strict convexity of $T^\circ$ implies

$$\begin{aligned} \nabla \mu _{T^\circ }(q_j-q_{j-1}) \ne \nabla \mu _{T^\circ }(q_{j+1}-q_j), \end{aligned}$$

and where $n_{H_j}$ is the outer unit vector normal to $H_j$. This implies that the weak Minkowski billiard reflection rule can be illustrated as within Fig. 2. For smooth, strictly convex, and centrally symmetric $T^ \circ \subset \mathbb {R}^n$, this interpretation is due to [11, Lemma 3.1, Corollary 3.2 and Lemma 3.3] (this interpretation has also been referenced in [2]). For the extension to just smooth and strictly convex $T^\circ \subset \mathbb {R}^n$, it is due to [7, Lemma 2.1]. However, from the constructive point of view, this interpretation has its limitations.

Fig. 2

$T^\circ$ is a smooth and strictly convex body in $\mathbb {R}^2$ and its boundary plays the role of the indicatrix, i.e., the set of vectors of unit Finsler (with respect to $T^\circ$) length, which therefore is an 1-level set of $\mu _{T^\circ }$. Note that the two $T^\circ$-supporting hyperplanes intersect on $H_j$ due to the condition $\nabla \mu _{T^\circ }(q_j-q_{j-1})-\nabla \mu _{T^\circ }(q_{j+1}-q_j)= \mu _j n_{H_j}$

Definition 2

(Strong Minkowski billiards) Let $K,T\subset \mathbb {R}^n$ be convex bodies. We say that a closed polygonal curve q with vertices $q_1,...,q_m$, $m\in \mathbb {N}_{\ge 2}$, on $\partial K$ is a closed strong  (K, T)-Minkowski billiard trajectory if there are points $p_1,...,p_m$ on $\partial T$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} q_{j+1}-q_j \in N_T(p_j), \\ p_{j+1}-p_j \in - N_K(q_{j+1})\end{array}\right. } \end{aligned}$$

(3)

is satisfied for all $j\in \{1,...,m\}$. We call $p=(p_1,...,p_m)$ a closed dual billiard trajectory in T. We denote by $M_{n+1}(K,T)$ the set of closed (K, T)-Minkowski billiard trajectories with at most $n+1$ bouncing points.

Definition 2 appeared implicitly in [11, Theorem 7.1], then later the first time explicitly in [3]. It yields a different interpretation of the billiard reflection rule. Without requiring a condition on T, the billiard reflection rule can be represented as within Fig. 3. From the constructive point of view, this interpretation is much more appropriate in comparison to the one for weak Minkowski billiards.

Fig. 3

The pair (q, p) satisfies (3), namely: $q_j-q_{j-1}\in N_T(p_{j-1})$, $q_{j+1}-q_j\in N_T(p_j)$, $p_j-p_{j-1}\in -N_K(q_j)$, and $p_{j+1}-p_j\in - N_K(q_{j+1})$

The natural follow-up question concerns the relationship between weak and strong Minkowski billiards. In [16, Theorem 1.3], we have shown the following for convex bodies $K,T\subset \mathbb {R}^n$: Every closed strong (K, T)-Minkowski billiard trajectory is a weak one. If T is strictly convex, then every closed weak (K, T)-Minkowski billiard trajectory is a strong one. This is a sharp result in the following sense: One can construct convex bodies $K,T\subset \mathbb {R}^n$ (where T is not strictly convex) and a closed weak (K, T)-Minkowski billiard trajectory which is not a strong one (see Example A in [16]).

In the following–if the risk of confusion is excluded–we will call strong Minkowski billiards trajectories just Minkowski billiard trajectories.

1.3 Main Result

For a convex body $K\subset \mathbb {R}^n$, we define the set $F_{n+1}^{cp}(K)$ as the set of all closed polygonal curves $q=(q_1,...,q_m)$ with $m\le n+1$ that cannot be translated into $\mathring{K}$.

Our main result concerning the connection between the minimal $\ell _T$-length of closed (K, T)-Minkowski billiard trajectories and the EHZ-capacity of convex Lagrangian products $K\times T$ reads:

Theorem 1

Let $K,T\subset \mathbb {R}^n$ be convex bodies such that $K\times T\subset \mathbb {R}^{2n}$ is a convex Lagrangian product. Then, we have

$$\begin{aligned} c_{EHZ}(K\times T) = \min _{q\in F_{n+1}^{cp}(K)}\ell _T(q) = \min _{p\in F_{n+1}^{cp}(T)}\ell _K(p) = \min _{q \in M_{n+1}(K,T)} \ell _T(q). \end{aligned}$$

We note that under the condition of strict convexity of T, the statement of Theorem 1 also holds for $\ell _T$-minimizing closed weak (K, T)-Minkowski billiard trajectories. In the general case, this is not true. When T is not strictly convex, then one can have

$$\begin{aligned} \min _{q \text { cl.}\,\text {weak }(K,T)\text {-Mink.}\,\text {bill}.\,\text {traj.}} \ell _T(q) < \min _{q \text { cl}.\,\text {strong }(K,T)\text {-Mink.}\,\text {bill.}\,\text {traj.}} \ell _T(q) \end{aligned}$$

(see [16, Example E], where $q=(q_1,q_2,q_3)$ is a closed weak Minkowski billiard trajectory which is shorter than any closed strong Minkowski billiard trajectory), and it even can happen that there is no $\ell _T$-minimizing closed weak (K, T)-Minkowski billiard trajectory at all (see [16, Example G]; while in Example E instead, there exists a minimizer).

In order to classify Theorem 1 against the background of current research, we note that the relationship between action-minimizing closed characteristics on $\partial (K\times T)$ and $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectories was made explicit for the first time by Artstein-Avidan and Ostrover in [3]. However, two points in particular must be taken into account here: First, they showed this relationship only under the assumption of smoothness and strict convexity of both K and T. In particular, if one intends to compute the length-minimizing trajectories (as we have described in [16] for the 4-dimensional case), this is not so effective, since for this, one would typically use convex polytopes, which are neither smooth nor strictly convex. Secondly, their definition of closed (K, T)-Minkowki billiard trajectories slightly differed from ours. They used the notion of closed Minkowski billiard trajectories for closed trajectories which arised within their characterization of closed characteristics on $\partial (K\times T)$. As consequence, they had to take trajectories into account, for example, which intuitively had no relation to billiard trajectories and could produce ugly behaviour (see [12])–they called them gliding billiard trajectories. As part of our approach, we were able to avoid considering such trajectories, allowing us to focus entirely on trajectories that are commonly understood as billiard trajectories and which, in the case of strict convexity of T, i.e., when weak and strong Minkowski billiards coincide, in fact can be traced back to the classical least action principle.

Besides what has been proved by Artstein-Avidan and Ostrover, Alkoumi and Schlenk indicated in [2] Theorem 1 for the case $K,T\subset \mathbb {R}^2$, where T is additionally assumed to be smooth and strictly convex. Balitskiy showed in [4] the first equality of the statement in Theorem 1 under the assumption of smoothness of T.

We note that the generality of Theorem 1 is central to understand the different characterizations of action-minimizing closed characteristics in more detail. For instance, it will be our starting point when analyzing Viterbo’s conjecture for Lagrangian products in [17]. The generality of this theorem is essential for being able to apply it on convex polytopes, what would not be possible based on the lesser general statement in [3], but which is essential in order to develope an algorithm for the computation of the EHZ-capacity of convex Lagrangian products.

Let us briefly give an overview of the structure of this paper: In Sect. 2, we recall useful results from [16]. In Sect. 3, we prove Theorem 1 by mainly stating three theorems, whose proofs we outsourced in Sects. 4, 5, and 6.

2 Preliminaries

We recall statements from [16] which will be used within the following proofs.

Proposition 1

(Proposition 3.4 in [16]) Let $K,T\subset \mathbb {R}^n$ be convex bodies. Let $q=(q_1,...,q_m)$ be a closed (K, T)-Minkowski billiard trajectory with closed dual billiard trajectory $p=(p_1,...,p_m)$ in T. Then, we have

$$\begin{aligned} \ell _T(q)=\ell _{-K}(p). \end{aligned}$$

Proposition 2

(Proposition 3.5 in [16]) Let $K,T\subset \mathbb {R}^n$ be convex bodies and T is additionally assumed to be strictly convex and smooth. Let $q=(q_1,...,q_m)$ be a closed (K, T)-Minkowski billiard trajectory with its closed dual billiard trajectory $p=(p_1,...,p_m)$ in T. Then, p is a closed $(T,-K)$-Minkowski billiard trajectory with

$$\begin{aligned} -q^{+1}:=(-q_2,...,-q_m,-q_1) \end{aligned}$$

as closed dual billiard trajectory on $-K$.

For the following proposition, we denote by F(K), $K\subset \mathbb {R}^n$ convex body, the set of all sets in $\mathbb {R}^n$ that cannot be translated into $\mathring{K}$.

Proposition 3

(Proposition 3.9 in [16]) Let $K,T\subset \mathbb {R}^n$ be convex bodies. Let $q=(q_1,...,q_m)$ be a closed (K, T)-Minkowski billiard trajectory with closed dual billiard trajectory $p=(p_1,...,p_m)$. Then, we have

$$\begin{aligned} q\in F(K)\; \text { and } \; p\in F(T). \end{aligned}$$

Theorem 2

( Theorem 3.12 in [16]) Let $K,T\subset \mathbb {R}^n$ be convex bodies, where T is additionally assumed to be strictly convex. Then, every $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory is an $\ell _T$-minimizing element of $F_{n+1}^{cp}(K)$, and, conversely, every $\ell _T$-minimizing element of $F_{n+1}^{cp}(K)$ can be translated in order to be an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory.

Especially, one has

$$\begin{aligned} \min _{q\in F^{cp}_{n+1}(K)}\ell _T(q) = \min _{q \in M_{n+1}(K,T)} \ell _T(q).\end{aligned}$$

(4)

3 Proof of Theorem 1

The proof of Theorem 1 relies on the following three theorems which we will prove in Sects. 4, 5, and 6, respectively.

Theorem 3

Let $K\subset \mathbb {R}^n$ be a convex polytope and $T\subset \mathbb {R}^n$ a strictly convex body. We consider $K\times T\subset \mathbb {R}^{2n}$ as convex Lagrangian product. Then, for every closed/action-minimizing closed characteristic x on $\partial (K\times T)$, there is a closed characteristic $\widetilde{x}=(\widetilde{x}_q,\widetilde{x}_p)$ on $\partial (K\times T)$ which is a closed polygonal curve and where $\widetilde{x}_q$ is a closed/an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory with $\widetilde{x}_p$ as its closed dual billiard trajectory on T and

$$\begin{aligned} \mathbb {A}(x)=\mathbb {A}(\widetilde{x})=\ell _T(\widetilde{x}_q). \end{aligned}$$

Conversely, for every closed/$\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory $q=(q_1,...,q_m)$ with closed dual billiard trajectory $p=(p_1,...,p_m)$ on T, $x=(q,p)$ (after a suitable parametrization of q and p) is a closed/an action-minimizing closed characteristic on $\partial (K\times T)$ with

$$\begin{aligned} \ell _T(q)=\mathbb {A}(x). \end{aligned}$$

Especially, one has

$$\begin{aligned} c_{EHZ}(K\times T) = \min _{q \text { cl.}\,(K,T)\text {-Mink.}\,\text {bill.}\,\text {traj.}} \ell _T(q). \end{aligned}$$

Theorem 4

Let $K,T\subset \mathbb {R}^n$ be convex bodies. Then, every $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory is an $\ell _T$-minimizing element of $F_{n+1}^{cp}(K)$, and, conversely, for every $\ell _T$-minimizing element of $F_{n+1}^{cp}(K)$, there is an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory with $\le n+1$ bouncing points and with the same $\ell _T$-length.

Especially, one has

$$\begin{aligned} \min _{q\in F^{cp}_{n+1}(K)}\ell _T(q) = \min _{q \in M_{n+1}(K,T)} \ell _T(q).\end{aligned}$$

(5)

We note that Theorem 4 is the generalization of (4) without requiring the strict convexity of T. So far, in contrast to Theorem 2, it is not clear whether the minimizers in (4) coincide (even not up to translation).

For the next theorem we introduce the Hausdorff-distance $d_H$ between two sets $U,V\subset \mathbb {R}^n$. It is given by

$$\begin{aligned} d_H(U,V)=\max \left\{ \max _{u\in U}\min _{v\in V}||u-v||,\max _{v\in V}\min _{u\in U}||u-v||\right\} . \end{aligned}$$

Theorem 5

• (i) If $T\subset \mathbb {R}^n$ is a strictly convex body and $(K_i)_{i\in \mathbb {N}}$ a sequence of convex bodies in $\mathbb {R}^n$ that $d_H$-converges to some convex body $K\subset \mathbb {R}^n$, then there is a strictly increasing sequence $(i_j)_{j\in \mathbb {N}}$ and a sequence $(q^{i_j})_{j\in \mathbb {N}}$ of $\ell _T$-minimizing closed $(K_{i_j},T)$-Minkowski billiard trajectories which $d_H$-converges to an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory.

• (ii) If $K\subset \mathbb {R}^n$ is a convex body and $(T_i)_{i\in \mathbb {N}}$ a sequence of strictly convex bodies in $\mathbb {R}^n$ that $d_H$-converges to some convex body $T\subset \mathbb {R}^n$, then there is a strictly increasing sequence $(i_j)_{j\in \mathbb {N}}$ and a sequence $(q^{i_j})_{j\in \mathbb {N}}$ of $\ell _{T_{i_j}}$-minimizing closed $(K,T_{i_j})$-Minkowski billiard trajectories which $d_H$-converges to an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory.

We come to the proof of Theorem 1:

Proof (Proof of Theorem 1)

Let $K,T\subset \mathbb {R}^n$ be convex bodies such that $K\times T\subset \mathbb {R}^{2n}$ is a convex Lagrangian product. We first prove

$$\begin{aligned} c_{EHZ}(K\times T) = \min _{q \in M_{n+1}(K,T)} \ell _T(q) = \min _{q\in F_{n+1}^{cp}(K)}\ell _T(q) . \end{aligned}$$

(6)

We can find a sequence of convex polytopes $(K_i)_{i\in \mathbb {N}}$ in $\mathbb {R}^n$ that $d_H$-converges to K for $i\rightarrow \infty$ and a sequence of strictly convex bodies $(T_j)_{j\in \mathbb {N}}$ in $\mathbb {R}^n$ that $d_H$-converges to T for $j\rightarrow \infty$. Applying Theorem 3, we conclude

$$\begin{aligned} c_{EHZ}(K_i\times T_j) = \min _{q \text { cl.}\,(K_i,T_j)\text {-Mink.}\,\text {bill.}\,\text {traj.}} \ell _{T_j}(q). \end{aligned}$$

Because of the $d_H$-continuity of $c_{EHZ}$ (see, e.g., [1, Theorem 4.1(v)]) and Theorem 5(i), for the limit $i\rightarrow \infty$, we get

$$\begin{aligned} c_{EHZ}(K\times T_j) = \min _{q \text { cl.}\,(K,T_j)\text {-Mink.}\,\text {bill.}\,\text {traj.}} \ell _{T_j}(q). \end{aligned}$$

Again using the $d_H$-continuity of $c_{EHZ}$ and this time Theorem 5(ii), for the limit $j\rightarrow \infty$, we get

$$\begin{aligned} c_{EHZ}(K\times T) = \min _{q \text { cl.}\,(K,T)\text {-Mink.}\,\text {bill.}\,\text {traj.}} \ell _{T}(q). \end{aligned}$$

By Theorem 4, this implies (6).

It remains to prove

$$\begin{aligned} \min _{q\in F_{n+1}^{cp}(K)}\ell _T(q) = \min _{p\in F_{n+1}^{cp}(T)}\ell _K(p). \end{aligned}$$

Let $(T_j)_{j\in \mathbb {N}}$ be a sequence of strictly convex and smooth bodies in $\mathbb {R}^n$ converging to T for $j\rightarrow \infty$. Then, for every $j\in \mathbb {N}$, one has

$$\begin{aligned} \min _{q\in F_{n+1}^{cp}(K)}\ell _{T_j}(q)&= \min _{q \text { cl.}\,(K,T_j)\text {-Mink.}\,\text {bill.}\,\text {traj.}} \ell _{T_j}(q)\\&= \min _{p \text { cl.}\,(T_j,-K)\text {-Mink.}\,\text {bill.}\,\text {traj.}} \ell _{-K}(q)\\&= \min _{p\in F_{n+1}^{cp}(T_j)}\ell _{-K}(q)\\&= \min _{p\in F_{n+1}^{cp}(T_j)}\ell _{K}(q), \end{aligned}$$

where the first and third equality follows from Theorem 4, the second from Propositions 1 and 2 (requires strict convexity and smoothness of $T_j$), and the last from the following consideration: one has the equivalence

$$\begin{aligned} p=(p_1,...,p_m)\in F_{n+1}^{cp}(T_j)\;\Leftrightarrow \; p^-=(p_m,...,p_1)\in F_{n+1}^{cp}(T_j),\end{aligned}$$

and therefore

$$\begin{aligned} \min _{p=(p_1,...,p_m)\in F_{n+1}^{cp}(T_j)}\ell _{-K}(p)=&\min _{p\in F_{n+1}^{cp}(T_j)}\ell _{K}(p^-=(p_m,...,p_1))\\ =&\min _{p^-\in F_{n+1}^{cp}(T_j)}\ell _K(p^-)\\ =&\min _{p\in F_{n+1}^{cp}(T_j)}\ell _K(p). \end{aligned}$$

Using (6), summarized, for every $j\in \mathbb {N}$, we can conclude

$$\begin{aligned} c_{EHZ}(K\times T_j)= \min _{q\in F_{n+1}^{cp}(K)}\ell _{T_j}(q) = \min _{p\in F_{n+1}^{cp}(T_j)}\ell _{K}(q) = c_{EHZ}(T_j\times K).\end{aligned}$$

Due to the $d_H$-continuity of $c_{EHZ}$ and the generality of (6), for $j\rightarrow \infty$, one has

$$\begin{aligned} \min _{q\in F_{n+1}^{cp}(K)}\ell _{T}(q) = c_{EHZ}(K\times T) = c_{EHZ}(T\times K) = \min _{p\in F_{n+1}^{cp}(T)}\ell _{K}(q). \end{aligned}$$

$\square$

We remark that the proof of Theorem 1 implies the following relationships:

$$\begin{aligned}{} & {} c_{EHZ}(K\times T) = c_{EHZ}(T\times K),\\{} & {} c_{EHZ}(K\times T)=c_{EHZ}(-K\times T)=c_{EHZ}(K\times -T)=c_{EHZ}(-K\times -T) \end{aligned}$$

for general convex bodies $K,T\subset \mathbb {R}^n$, and

$$\begin{aligned} c_{EHZ}(K\times T)= & {} \min _{q \in M_{n+1}(K,T)} \ell _{T}(q)=\min _{p \in M_{n+1}(T,K)} \ell _{K}(p),\\ c_{EHZ}(K\times T)= & {} \min _{q \in M_{n+1}(K,T)} \ell _{T}(q)=\min _{q \in M_{n+1}(-K,T)} \ell _{T}(q)\\= & {} \min _{q \in M_{n+1}(K,-T)} \ell _{-T}(q)=\min _{q \in M_{n+1}(-K,-T)} \ell _{-T}(q) \end{aligned}$$

when either T or K is additionally assumed to be strictly convex and smooth.

4 Proof of Theorem 3

Let $K\subset \mathbb {R}^n$ be a convex polytope and $T\subset \mathbb {R}^n$ a strictly convex body. We start by investigating properties of closed characteristics on the boundary of the Lagrangian product

$$\begin{aligned} K\times T\subseteq \mathbb {R}^n_q \times \mathbb {R}^n_p \end{aligned}$$

For this, we split $x\in \mathbb {R}^{2n}$ into q- and p-coordinates: $x=(x_q,x_p)$. Then, we observe

$$\begin{aligned} H_{K\times T}(x(t))=H_{K\times T}((x_q(t),x_p(t)))=\max \{H_K(x_q(t)),H_T(x_p(t))\}, \end{aligned}$$

what for

$$\begin{aligned} x(t)\in \partial (K\times T)\setminus (\partial K \times \partial T) \end{aligned}$$

(7)

means

$$\begin{aligned} H_{K\times T}(x(t))={\left\{ \begin{array}{ll}H_T(x_p(t)) &{} ,x(t)\in \mathring{K}\times \partial T,\\ H_K(x_q(t))&{}, x(t)\in \partial K\times \mathring{T},\end{array}\right. } \end{aligned}$$

(see Fig. 4). A straight forward calculation yields

$$\begin{aligned} \partial H_{K\times T}(x(t))={\left\{ \begin{array}{ll}(0,\partial H_T(x_p(t)))&{}, x(t)\in \mathring{K}\times \partial T, \\ (\partial H_K(x_q(t)),0) &{} , x(t)\in \partial K\times \mathring{T},\end{array}\right. } \end{aligned}$$

for the case (7) and

$$\begin{aligned} \partial H_{K\times T}(x(t))&\subset \{(\alpha \partial H_K(x_q(t)),\beta \partial H_T(x_p(t)))\vert (\alpha ,\beta )\ne (0,0), \alpha ,\beta \ge 0\}\\&=N_{K\times T}(x(t)) \end{aligned}$$

for the case $x(t)\in \partial K\times \partial T$. Because of

$$\begin{aligned} \dot{x}(t)\in J\partial H_{K\times T}(x(t))\; a.e., \end{aligned}$$

this yields almost everywhere

$$\begin{aligned} \dot{x}(t)\in {\left\{ \begin{array}{ll}(\partial H_T(x_p(t)),0) &{} , x(t)\in \mathring{K}\times \partial T, \\ (0,-\partial H_K(x_q(t))) &{} , x(t)\in \partial K \times \mathring{T}, \\ (\beta \partial H_T(x_p(t)),-\alpha \partial H_K(x_q(t))) &{} , x(t)\in \partial K \times \partial T, \end{array}\right. } \end{aligned}$$

(8)

for $(\alpha ,\beta )\ne (0,0)$ and $\alpha , \beta \ge 0$.

Fig. 4

Illustration of $K\times T\subset \mathbb {R}^n\times \mathbb {R}^n$ and $\partial H_{K\times T}$

We notice that in the case $x(t)\in \mathring{K}\times \partial T$, there is just moving $x_q$, while in the case $x(t)\in \partial K\times \mathring{T}$, there is just moving $x_p$. For the case $x(t)\in \partial K\times \partial T$, it is apriori not clear whether $x_q$ and $x_p$ are never moving at the same time. However, this fact is guaranteed by the strict convexity of T:

Proposition 4

We can reduce (8) to

$$\begin{aligned}{} & {} \dot{x}(t)\in {\left\{ \begin{array}{ll}(\partial H_{T}(x_p(t)),0) &{} , x(t)\in \mathring{K}\times \partial T, \\ (0,-\partial H_K(x_q(t))) &{} , x(t)\in \partial K \times \mathring{T}, \end{array}\right. }\quad a.e. \end{aligned}$$

(9a)

$$\begin{aligned}{} & {} \dot{x}(t)\in (\partial H_{T}(x_p(t)),0) \textit{ or } \dot{x}(t)\in (0,-\partial H_K(x_q(t))),\;\; x(t)\in \partial K \times \partial T,\quad a.e. \end{aligned}$$

(9b)

Proof

We assume

$$\begin{aligned} \dot{x}(t)=(\dot{x}_q(t),\dot{x}_p(t))\in (\beta \partial H_{T}(x_p(t)),-\alpha \partial H_K(x_q(t))) \end{aligned}$$

for

$$\begin{aligned} x(t)\in \partial K\times \partial T\; \forall t\in [a,b], \; a<b, \end{aligned}$$

and $\alpha ,\beta >0$.

We split the proof into two parts.

Supposing $x_q([a',b'])$, $a\le a'<b' \le b$, is a subset of the interior of a facet, i.e., an $(n-1)$-dimensional face, $K_{n-1}$ of K, then $N_K(x_q(t))$ is for every $t\in [a',b']$ one-dimensional, which implies because of

$$\begin{aligned} \dot{x}_p(t)\in -\alpha \partial H_K(x_q(t))\subset -N_K(x_q(t)) \end{aligned}$$

that $x_p([a',b'])$ is a subset of a one-dimensional straight line. However, together with $x_p([a',b'])\subset \partial T$ this is a contradiction to the strict convexity of T.

Fig. 5

Illustration of the idea behind the proof of Proposition  4 when $x_q([a',b'])$ is a subset of the interior of a j-face of K, $1\le j \le n-2$. We have $t_0\in [a',b']$ and clearly see $N_T(x_p(t_0))\cap (T_{n-j})^{\perp ,\mathbb {R}^n_p}=\{0\}$

Supposing $x_q([a',b'])$, $a\le a'<b'\le b$, is a subset of the interior of a j-face $K_j \subset \partial K$, $1\le j \le n-2$, then $N_K(x_q(t))$ is $(n-j)$-dimensional for every $t\in [a',b']$ (see Fig. 5). Considering

$$\begin{aligned} \dot{x}_p(t)\in -\alpha \partial H_K(x_q(t))\subset -N_K(x_q(t)), \end{aligned}$$

we conclude that $x_p([a',b'])$ is a subset of the intersection of an $(n-j)$-dimensional plane $T_{n-j}$ (orthogonal to $K_j$) and $\partial T$. Note that because of the strict convexity of T, $T_{n-j}$ necessarily has a nonempty intersection with the interior of T. From this, we conclude

$$\begin{aligned} N_{T}(x_p(t))\cap (T_{n-j})^{\perp ,\mathbb {R}^n_p}=\{0\} \quad \forall t\in [a',b'], \end{aligned}$$

(10)

where by $(T_{n-j})^{\perp ,\mathbb {R}^n_p}$ we denote the orthogonal complement to $T_{n-j}$ in $\mathbb {R}^n_p$.

Indeed, let $t\in [a',b']$. If

$$\begin{aligned} n\in N_{T}(x_p(t))\cap (T_{n-j})^{\perp ,\mathbb {R}^n_p}, \quad n\ne 0, \end{aligned}$$

then one has

$$\begin{aligned} n\in N_T(x_p(t)),\quad \text { i.e., }\langle n,z-x_p(t)\rangle < 0 \;\; \forall z\in \mathring{T}, \end{aligned}$$

(11)

and

$$\begin{aligned} n\in (T_{n-j})^{\perp ,\mathbb {R}^n_p},\quad \text { i.e., } \langle n,z-x_p(t)\rangle = 0 \; \;\forall z\in T_{n-j}. \end{aligned}$$

(12)

Since

$$\begin{aligned} \mathring{T}\cap T_{n-j} \ne \emptyset , \end{aligned}$$

there is a $z_0\in \mathring{T}\cap T_{n-j}$ which due to (11) implies

$$\begin{aligned} \langle n,z_0 -x_p(t)\rangle < 0 \end{aligned}$$

and due to (12)

$$\begin{aligned} \langle n,z_0 -x_p(t)\rangle =0, \end{aligned}$$

a contradiction. This implies (10).

Considering

$$\begin{aligned} \dot{x}_q(t)\in \beta \partial H_{T}(x_p(t))\subset N_{T}(x_p(t)), \end{aligned}$$

we get

$$\begin{aligned} \dot{x}_q([a',b'])\nsubseteq (T_{n-j})^{\perp ,\mathbb {R}^n_p},\end{aligned}$$

which ends up in a contradiction since by construction of $T_{n-j}$, we have

$$\begin{aligned} K_{j,0} \subseteq (T_{n-j})^{\perp ,\mathbb {R}^n_p}, \end{aligned}$$

where by $K_{j,0}$ we denote the in the origin translated $K_j$ (how exactly, is not relevant), and therefore

$$\begin{aligned} \dot{x}_q([a',b'])\subset (T_{n-j})^{\perp ,\mathbb {R}^n_p}. \end{aligned}$$

$\square$

Let x be a closed characteristic. We denote its changing points, i.e., the points where the movement of $x_q$, respectively of $x_p$, goes over to the movement of $x_p$, respectively of $x_q$, by

$$\begin{aligned} \dots \rightarrow (q_j,p_j) \rightarrow (q_{j+1},p_j) \rightarrow (q_{j+1},p_{j+1})\rightarrow (q_{j+2},p_{j+1}) \rightarrow \dots \end{aligned}$$

(13)

and conclude from (9) that they satisfy

$$\begin{aligned} {\left\{ \begin{array}{ll} q_{j+1}-q_j\in N_T(p_j)\\ p_{j+1}-p_j\in -N_K(q_{j+1})\end{array}\right. } \end{aligned}$$

for all $j\in \{1,...,m\}$. We compute their respective trajectory segments’ contributions to the action of x (denoted by $\mathbb {A}_{x'\rightarrow x''}$ for a trajectory segment from $x'$ to $x''$) as follows: Suppose, we have

$$\begin{aligned} x(a)=(q_{j},p_{j}),\;\; x(b)=(q_{j+1},p_j)\; \text { and } \; x(c)=(q_{j+1},p_{j+1}) \end{aligned}$$

for $a<b<c$, then

$$\begin{aligned} \mathbb {A}_{x(a)\rightarrow x(b)}(x)=\mathbb {A}_{(q_j,p_j)\rightarrow (q_{j+1},p_j)}(x)=&\int _a^b \langle x_p(t),\dot{x}_q(t)\rangle \;dt\\ =&\left\langle \int _a^b \dot{x}_q(t)\;dt,p_j\right\rangle \\ =&\langle x_q(b)-x_q(a),p_j\rangle =\langle q_{j+1}-q_j,p_j\rangle \end{aligned}$$

and

$$\begin{aligned} \mathbb {A}_{x(b)\rightarrow x(c)}(x)=\mathbb {A}_{(q_{j+1},p_j)\rightarrow (q_{j+1},p_{j+1})}(x)=\int _b^c \langle x_p(t),\dot{x}_q(t)\rangle \;dt =0. \end{aligned}$$

We note that the action of x only depends on the consecutive changing points in (13), no matter what happens between them. Therefore, it makes sense to think of the following equivalence relation on closed characteristics:

$$\begin{aligned} x \sim y :\Leftrightarrow \text { consecutive changing points of } x \text { and }y\text { coincide}. \end{aligned}$$

Representatives of the same equivalence class have the same action, i.e.,

$$\begin{aligned} \forall x',x''\in [x]_\sim : \mathbb {A}(x')=\mathbb {A}(x''). \end{aligned}$$

Then, by (9), there is a closed characteristic $\widetilde{x}=(\widetilde{x}_q,\widetilde{x}_p)$ in the equivalence class of x, which is a closed polygonal curve consisting of the straight line segments connecting the changing points in (13). Consequently, using

$$\begin{aligned} q_{j+1}-q_j\in N_T(p_j) \quad \forall j\in \{1,...,m\} \end{aligned}$$

and [16, Proposition 2.2], we have

$$\begin{aligned} \mathbb {A}(\widetilde{x})=\mathbb {A}(x)=\sum _{j=1}^m \langle q_{j+1}-q_j,p_j\rangle =\ell _T(x_q)=\ell _T(\widetilde{x}_q). \end{aligned}$$

$\widetilde{x}_q$ is a closed polygonal curve with vertices $q_1,...,q_m$ on $\partial K$. Without loss of generality, we can assume $q_{j+1}\ne q_j$ and $p_{j+1}\ne p_j$ for all $j\in \{1,...,m\}$.

Otherwise, if $q_{j+2}=q_{j+1}$, then the changing points

$$\begin{aligned} ...\rightarrow (q_j,p_j)\rightarrow (q_{j+1},p_j) \rightarrow (q_{j+1},p_{j+1})\rightarrow (q_{j+2},p_{j+1}) \rightarrow (q_{j+2},p_{j+2})\rightarrow ... \end{aligned}$$

(14)

can be replaced by

$$\begin{aligned} ...\rightarrow (q_j,p_j) \rightarrow (q_{j+2},p_j)\rightarrow (q_{j+2},p_{j+2})\rightarrow ... \end{aligned}$$

(15)

Indeed, because of

$$\begin{aligned} p_{j+1}-p_{j}\in -N_K(q_{j+1}) \; \text { and } \; p_{j+2}-p_{j+1}\in -N_K(q_{j+2}), \end{aligned}$$

we have

$$\begin{aligned} p_{j+2}-p_{j}\in N_T(q_{j+2}), \end{aligned}$$

and because of

$$\begin{aligned} q_{j+1}-q_j\in N_T(p_j), \end{aligned}$$

we have

$$\begin{aligned} q_{j+2}-q_j\in N_T(p_j). \end{aligned}$$

Therefore, the changing points in (15) are in the sense of (9). If $p_{j+1}=p_j$, then again, (14) can be replaced by (15) by similar reasoning. In both cases the lengths of the respective associated closed characteristics remain unchanged.

As consequence, without loss of generality, we can assume that $\widetilde{x}_q$ is a closed polygonal curve with vertices $q_1,...,q_m$ on $\partial K$, where $q_{j+1}\ne q_j$ and $q_j$ not contained in the line segment connecting $q_{j-1}$ and $q_{j+1}$ for all $j\in \{1,...,m\}$ (otherwise, if $q_j$ is contained in the line segment connecting $q_{j-1}$ and $q_{j+1}$, then $N_T(p_{j-1})=N_T(p_j)$, and by the strict convexity of T, $p_{j-1}=p_j$, but then the corresponding segment again can be removed), i.e., q is a closed polygonal curve in the sense of Footnote 1. Therefore, by the definition of Minkowski billiard trajectories, $\widetilde{x}_q$ is a closed (K, T)-Minkowski billiard trajectory with closed dual billiard trajectory $\widetilde{x}_p$ and with $\ell _T$-length equal to the action of x.

Summarized, we proved that for every closed characteristic x on $\partial (K\times T)$, there is a closed characteristic $\widetilde{x}=(\widetilde{x}_q,\widetilde{x}_p)$ on $\partial (K\times T)$ which is a closed polygonal curve and where $\widetilde{x}_q$ is a closed (K, T)-Minkowski billiard trajectory with $\widetilde{x}_p$ as closed dual billiard trajectory on T and

$$\begin{aligned} \mathbb {A}(x)=\mathbb {A}(\widetilde{x})=\ell _T(\widetilde{x}_q). \end{aligned}$$

And conversely, for every closed (K, T)-Minkowski billiard trajectory $q=(q_1,...,q_m)$ with closed dual billiard trajectory $p=(p_1,...,p_m)$ on T, $x=(q,p)$ (after a suitable parametrization of q and p) is a closed characteristic on $\partial (K\times T)$ with

$$\begin{aligned} \ell _T(q)=\mathbb {A}(x). \end{aligned}$$

Since these relations remain uneffected by minimizing the action/length, we have

$$\begin{aligned} c_{EHZ}(K\times T) = \min _{q \text { cl.}\,(K,T)\text {-Mink.}\,\text {bill.}\,\text {traj.}} \ell _T(q) \end{aligned}$$

and consequently proved Theorem 3.

5 Proof of Theorem 4

The structure of the proof of Theorem 4 is similar to the structure of the proof of Theorem 2.

Proof (Proof of Theorem 4)

It is sufficient to prove the following two points:

• (i) Every closed (K, T)-Minkowski billiard trajectory is either in $F_{n+1}^{cp}(K)$ or there is an $\ell _T$-shorter closed polygonal curve in $F_{n+1}^{cp}(K)$.

• (ii) For every $\ell _{T}$-minimizing element of $F_{n+1}^{cp}(K)$, there is a closed (K, T)-Minkowski billiard trajectory with $\le n+1$ bouncing points and the same $\ell _T$-length.

Ad (i): Let $q=(q_1,...,q_m)$ be a closed (K, T)-Minkowski billiard trajectory. From Proposition 3, we conclude $q\in F(K)$. For $m\le n+1$, we then have $q \in F_{n+1}^{cp}(K)$. If $m> n+1$, then, by [15, Lemma 2.1(i)], there is a selection

$$\begin{aligned} \{i_1,...,i_{n+1}\}\subset \{1,...,m\} \; \text { with } \; i_1< ... < i_{n+1} \end{aligned}$$

such that the closed polygonal curve

$$\begin{aligned} (q_{i_1},...,q_{i_{n+1}})\end{aligned}$$

is in $F_{n+1}^{cp}(K)$. One has

$$\begin{aligned} \ell _T((q_{i_1},...,q_{i_{n+1}})) \le \ell _T(q). \end{aligned}$$

Ad (ii): Let $q=(q_1,...,q_m)$ be an $\ell _T$-minimizing element of $F^{cp}_{n+1}(K)$. Further, let $(T_i)_{i\in \mathbb {N}}$ be a sequence of strictly convex bodies in $\mathbb {R}^n$ that $d_H$-converges to T. For all $i\in \mathbb {N}$, let

$$\begin{aligned} q^{i,m_i}=(q_1^{i,m_i},...,q_{m_i}^{i,m_i}) \end{aligned}$$

be an $\ell _{T_i}$-minimizing closed $(K,T_i)$-Minkowski billiard trajectory. Then, by Theorem 2, $q^{i,m_i}$ is an $\ell _{T_i}$-minimizing closed polygonal curve in $F_{n+1}^{cp}(K)$ for all $i\in \mathbb {N}$ (therefore $m_i\le n+1$ for all $i\in \mathbb {N}$). We conclude

$$\begin{aligned} q^{i,m_i}\in F_{n+1}^{cp,*_R}(K)=\left\{ q\in F_{n+1}^{cp}(K):q\subset B_R^n(0)\right\} \quad \forall i\in \mathbb {N}, \end{aligned}$$

where R is chosen sufficiently large. Since $(F_{n+1}^{cp,*_R}(K),d_H)$ is a compact metric subspace of the complete metric space $(P(\mathbb {R}^n),d_H)$ (see the proof of Theorem 2), via a standard compactness argument, we find a strictly increasing sequence $(i_j)_{j\in \mathbb {N}}$ and a closed polygonal curve $q^*\in F_{n+1}^{cp,*_R}(K)$ such that

$$\begin{aligned}{} & {} m_{i_j}\equiv :m\le n+1,\\{} & {} (q^{i_j,m_{i_j}})_{j\in \mathbb {N}} \;d_H\text {-converges to }q^*,\\{} & {} q^*=(q_1^*,...,q_{\widetilde{m}}^*)\; \text { with } \; \widetilde{m}\le m \le n+1. \end{aligned}$$

We show that $q^*$ is a closed (K, T)-Minkowski billiard trajectory. Without loss of generality, we assume

$$\begin{aligned} \lim _{j\rightarrow \infty } q_k^{i_j} \ne \lim _{j\rightarrow \infty } q_{k+1}^{i_j} \quad \forall k\in \{1,...,m\}. \end{aligned}$$

(16)

Otherwise, we neglect $q_k^{i_j}$ and continue with

$$\begin{aligned} (q_1^{i_j}, ...,q_{k-1}^{i_j},q_{k+1}^{i_j},...,q_m^{i_j}). \end{aligned}$$

We do exactly the same in the case $\lim _{j\rightarrow \infty }q_k^{i_j}$ is contained in the line segment connecting

$$\begin{aligned} \lim _{j\rightarrow \infty } q_{k-1}^{i_j}\; \text { and }\; \lim _{j\rightarrow \infty } q_{k+1}^{i_j}. \end{aligned}$$

These cases are responsible for possibly having $\widetilde{m}<m$. From now on, we can assume $\widetilde{m}=m$. Then, due to (16), we have that

$$\begin{aligned} \lim _{j\rightarrow \infty } \left( q_{k+1}^{i_j}-q_k^{i_j}\right) \ne 0, \end{aligned}$$

and because of the strict convexity of $T_{i_j}$ (for strictly convex body $\widetilde{T}$ one has that $p_i\ne p_j$ is equivalent to $N_{\widetilde{T}}(p_i)\cap N_{\widetilde{T}}(p_j)=\{0\}$), there is a unique $p_k^{i_j}\in \partial T_{i_j}$ with

$$\begin{aligned} q_{k+1}^{i_j}-q_k^{i_j} \in N_{T_{i_j}}(p_k^{i_j}). \end{aligned}$$

Then, since $q_{k+1}^{i_j}-q_k^{i_j}$ converges for $j\rightarrow \infty$, this is also true for $p_k^{i_j}$: we write

$$\begin{aligned} \lim _{j\rightarrow \infty } p_k^{i_j}=:p_k^*. \end{aligned}$$

This can be argued for every $k\in \{1,...,m\}$. Since

$$\begin{aligned} \lim _{j\rightarrow \infty }N_{T_{i_j}}(p_k^{i_j})\subseteq N_T(p_k^*) \; \text { and } \; \lim _{j\rightarrow \infty } N_K(q_k^{i_j})\subseteq N_K(q_k^*)\quad \forall k\in \{1,...,m\} \end{aligned}$$

by possibly going to a subsequence and by specifying the meaning of the limits by: a sequence of cones $(C_i)_{i\in \mathbb {N}}$ converges to some convex cone if the sequence

$$\begin{aligned} (C_i \cap B_1^n(0))_{i\in \mathbb {N}} \end{aligned}$$

$d_H$-converges to $C\cap B_1^n(0)$, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} q_{k+1}^*-q_k^ *\in N_T(p_k^*), \\ p_{k+1}^*-p_k^* \in - N_K(q_{j+1}^*). \end{array}\right. } \end{aligned}$$

Therefore, $q^*$ is a closed (K, T)-Minkowski billiard trajectory.

It remains to show that

$$\begin{aligned} \ell _T(q^*)=\ell _T(q). \end{aligned}$$

(17)

For that, we show that $q^*$ is an $\ell _T$-minimizing element in $F_{n+1}^{cp}(K)$. We assume by contradiction that there is a $\bar{q}$ in $F_{n+1}^{cp}(K)$ with

$$\begin{aligned} \ell _T(\bar{q})<\ell _T(q^*). \end{aligned}$$

(18)

Since for all $j\in \mathbb {N}$, $q^{i_j,m_{i_j}}$ is an $\ell _{T_{i_j}}$-minimizing element of $F_{n+1}^{cp}(K)$, it follows that

$$\begin{aligned} \ell _{T_{i_j}}(q^{i_j,m_{i_j}})\le \ell _{T_{i_j}}(\bar{q}) \quad \forall j\in \mathbb {N}. \end{aligned}$$

Using the $d_H$-convergence of $(T_i)_{i\in \mathbb {N}}$ to T and [16, Proposition 3.11(vi)], this implies

$$\begin{aligned} \ell _T(q^{i_j,m_{i_j}})\le \ell _T(\bar{q})\quad \forall j\in \mathbb {N}. \end{aligned}$$

Then, using [16, Proposition 3.11(v)], we obtain

$$\begin{aligned} \ell _T(q^*)\le \ell _T(\bar{q}), \end{aligned}$$

a contradiction to (18). Therefore, $q^*$ is an $\ell _T$-minimizing element of $F_{n+1}^{cp}(K)$. This implies (17). $\square$

So far, in the general case, it is not known whether there is an example in order to sharpen the statement of this theorem, i.e., whether every minimizer $\ell _T$-minimizing element of $F^{cp}_{n+1}(K)$ has a translate which is an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory.

6 Proof of Theorem 5

Proof (Proof of Theorem 5)

$\underline{\mathrm{Ad (i)}:}$ For all $i\in \mathbb {N}$, let $q^i$ be an $\ell _{T}$-minimizing closed $(K_i,T)$-Minkowski billiard trajectory. Then, by Theorem 2 (or Theorem 4), for all $i\in \mathbb {N}$, $q^i$ is an $\ell _T$-minimizing closed polygonal curve in $F_{n+1}^{cp}(K_i)$.

Since $(K_i)_{i\in \mathbb {N}}$ $d_H$-converges to K, for all $\varepsilon >0$, there is an $i_0=i_0(\varepsilon )\in \mathbb {N}$ such that

$$\begin{aligned} (1-\varepsilon )K \subset K_i \subset (1+\varepsilon )K \quad \forall i\ge i_0.\end{aligned}$$

This means by [16, Proposition 3.11(i)] (which also holds for proper inclusions) that

$$\begin{aligned} F_{n+1}^{cp}((1+\varepsilon )K)\subset F_{n+1}^{cp}(K_i) \subset F_{n+1}^{cp}((1-\varepsilon )K) \quad \forall i\ge i_0. \end{aligned}$$

(19)

By (19) and the fact that, for all $i\in \mathbb {N}$, $q^i$ is an $\ell _T$-minimizing element of $F_{n+1}^{cp}(K_i)$, for $\varepsilon >0$ and $i_0=i_0(\varepsilon )$ big enough, we have that

$$\begin{aligned} q^i \in F_{n+1}^{cp}((1-\varepsilon )K) \; \text { and } \; q^i \subset B_R^n(0) \quad \forall i\ge i_0, \end{aligned}$$

where by $B_R^n(0)$ we denote the n-dimensional ball in $\mathbb {R}^n$ of sufficiently large radius $R>0$ that contains K. Via a standard compactness argument (see the proof of Theorem 2), there is a strictly increasing sequence $(i_j)_{j\in \mathbb {N}}$ and a closed polygonal curve

$$\begin{aligned} q\in F_{n+1}^{cp}((1-\varepsilon )K) \quad \forall \varepsilon > 0 \end{aligned}$$

such that $(q^{i_j})_{j\in \mathbb {N}}$ $d_H$-converges to q and every $q^{i_j}$ has $m\le n+1$ vertices/bouncing points (we note that, in general, the $q^i$s can have a varying number of vertices/bouncing points).

We show that q is an $\ell _{T}$-minimizing element of $F_{n+1}^{cp}(K)$. Since the aforementioned is true for any $\varepsilon >0$, we have

$$\begin{aligned} q\in \bigcap _{\varepsilon >0} F_{n+1}^{cp}((1-\varepsilon )K)\subseteq F_{n+1}^{cp}(K), \end{aligned}$$

where the last inclusion follows from the fact that any closed polygonal curve with at most $n+1$ vertices that can be translated into $\mathring{K}$ can also be translated into $(1-\varepsilon )\mathring{K}$ for $\varepsilon >0$ small enough. Therefore, q is in $F_{n+1}^{cp}(K)$. It remains to show that q is $\ell _{T}$-minimizing. We assume by contradiction that there is a $\widetilde{q}\in F_{n+1}^{cp}(K)$ with

$$\begin{aligned} \ell _{T}(\widetilde{q})<\ell _{T}(q). \end{aligned}$$

We choose $\varepsilon >0$ such that

$$\begin{aligned} \ell _{T}((1+\varepsilon )\widetilde{q})<\ell _{T}(q). \end{aligned}$$

(20)

Then, by [16, Proposition 3.11(ii)],

$$\begin{aligned} (1+\varepsilon )\widetilde{q} \in (1+\varepsilon )F_{n+1}^{cp}(K)=F_{n+1}^{cp}((1+\varepsilon )K). \end{aligned}$$

From (19), it follows for j big enough that

$$\begin{aligned} (1+\varepsilon )\widetilde{q}\in F_{n+1}^{cp}(K_{i_j}), \end{aligned}$$

and hence

$$\begin{aligned}\ell _{T}((1+\varepsilon )\widetilde{q})\ge \ell _{T}(q^{i_j})\end{aligned}$$

since $q^{i_j}$ is an $\ell _T$-minimizing element of $F_{n+1}^{cp}(K_{i_j})$. Passing to the limit in j and using [16, Proposition 3.11(v)], we obtain

$$\begin{aligned} \ell _{T}((1+\varepsilon )\widetilde{q})\ge \ell _{T}(q), \end{aligned}$$

a contradiction to (20). Therefore, q is an $\ell _{T}$-minimizing element of $F_{n+1}^{cp}(K)$.

We show that q is an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory. Since $(q^{i_j})_{j\in \mathbb {N}}$ $d_H$-converges to q, under the assumption that q also has m vertices $q_1,...,q_m$ (satisfying $q_k\ne q_{k+1}$ and the condition that $q_k$ is not contained in the line segment connecting $q_{k-1}$ and $q_{k+1}$ for all $k\in \{1,...,m\}$; see Footnote 1), it follows that $(q_k^{i_j})_{j\in \mathbb {N}}$ converges to $q_k$ for all $k\in \{1,...,m\}$ (see again the aforementioned identification given in the proof of Theorem 2). Then, from the $d_H$-convergence of $(K_i)_{i\in \mathbb {N}}$ to K and $q_k^{i_j}\in \partial K_{i_j}$ for all $k\in \{1,...,m\}$ and all $j\in \mathbb {N}$, it follows that $q_k\in \partial K$ for all $k\in \{1,...,m\}$. By referring to Theorem 2 (T is strictly convex; here Theorem 4 would not be enough), q then satisfies all the conditions in order to be an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory. If q has less than m vertices, i.e., if

$$\begin{aligned} \lim _{j\rightarrow \infty } q_k^{i_j} = \lim _{j\rightarrow \infty } q_{k+1}^{i_j} \; \text { for a } \; k\in \{1,...,m\}, \end{aligned}$$

or $\lim _{j\rightarrow \infty } q_k^{i_j}$ is contained in the line segment connecting

$$\begin{aligned} \lim _{j\rightarrow \infty } q_{k-1}^{i_j}\; \text { and }\; \lim _{j\rightarrow \infty } q_{k+1}^{i_j}, \end{aligned}$$

then, without loss of generality, we can neglect the k-th vertex of $q^{i_j}$ for all $j\in \mathbb {N}$, but get the same result: all the vertices of q are on $\partial K$ and q satisfies all other conditions in order to be an $\ell _T$-minimizing closed (K, T)-Minkowski billiard trajectory.

$\underline{\mathrm{Ad (ii)}:}$ We can copy completely the proof of point (ii) within the proof of Theorem 4. $\square$