1 Introduction

As Covid-19 vaccines are still not widely available in many countries, home quarantine measures remain the most effective intervention tool for controlling the epidemic. Restrictions imposed by home quarantine policies on businesses and individuals help to decrease the number of social contacts and thus slow down the spread of the disease. These restrictions differed in their scale, forms and timings in the states and countries where they were implemented by the government and health authorities.

However, massive lock-downs are not a sustainable solution for economic, social and psychological reasons. The situation is complicated by the asymptomatic Covid-19 infection. The asymptomatic individuals can account for as many as 40–45% of infections [17] and can transmit the virus to others for an extended period of time.

Asymptomatic infection, the latent infectious phase of the disease and cases with mild symptoms can be detected by diagnostic tests. As such, massive diagnostic testing of the population and isolation of positively tested individuals can potentially offer an alternative to indiscriminate quarantining of large population groups [15]. The isolation strategy based on diagnostic screening was implemented by a number of organizations, business and government authorities. For example, major airlines such as American Airlines and Lufthansa added on-site pre-flight rapid testing facilities at a number of American and German airports. The Duke University comprehensive Covid-19 testing program received results from 16,146 tests administered to students and faculty from November 7–13, 2020. The Chinese city of Qingdao reported testing its entire population of nine million people for Covid-19 over a period of five days in October, 2020. Slovakia tested 3.6 million people—two thirds of its population—in two days on October 31–November 1, 2020 and repeated testing the same population in a week’s time in the first attempt of a large-scale blanket testing campaign in Europe. These massive testing efforts were assisted by new pulling technologies and the development of affordable rapid tests such as Abbott’s BinaxNOW.

The health and government authorities are concerned with keeping the number of active cases below the level dictated by the capacity of the health care system. Several recent studies have attempted to predict and analyze the effect of quarantine measures on the dynamics of the Covid-19 pandemic using compartmental models of mathematical epidemiology. A variant of the standard well mixed SEIR model

$$\begin{aligned} \begin{array}{l} \dot{S}= -\beta SI,\\ \dot{E}= \beta SI - \omega E,\\ \dot{I}=\omega E - \delta I,\\ \dot{R}=\delta I,\\ \end{array} \end{aligned}$$
(1)

was used to analyze the effect of social distancing and reducing the number of contacts [13]. Another implementation of the quarantine policy was studied in [19], where the authors adapted the SIR model assuming that all the infected individuals are isolated after the incubation period. Stochastic age-structured transmission models were applied to explore a range of intervention scenarios [9]. A model with a two-threshold switching prevention strategy predicted that flattening the curve can lead to periodic recurrence of the disease [7]. The authors of all the above mentioned studies conclude that the interventions are effective in reducing the infection peak; however, extreme interventions are likely to be required to contain the infection spread.

Amid the ongoing efforts of bringing the Covid-19 epidemic under control continues, it is important to explore different scenarios using a variety of models and modeling assumptions. In this paper, we are interested in estimating the potential of massive diagnostic testing measures for reducing the quarantining rate, which enforces a given constraint on the maximum of active cases. A few earlier studies addressed the role of testing in the trajectory of the epidemic. In particular, the discrete time adaptation of the SEIR model proposed in [4] suggests that the isolation based on testing interventions can make unnecessary costly lockdown measures. Two types of testing strategy have been introduced in [2], namely testing the whole population and testing just symptomatic cases and their contacts. They showed that both strategies lead to the 90 percent reduction of the total cases.

Several mathematical models for Covid-19 including modelling both of testing and quarantine have been appearing since the beginning of the pandemic. In [1] they build a detailed agent-based model of Covid-19 transmission in the Boston metropolitan area with susceptible, latent, asymptomatic, latent symptomatic, presymptomatic, infectious asymptomatic, infectious symptomatic, hospitalized, hospitalized in intensive care and recovered individuals. They found by numerical simulations that a period of strict social distancing followed by a robust level of testing, contact-tracing and household quarantine could keep the disease within the capacity of the healthcare system while enabling the reopening of economic activities. In [18] the authors analysed several strategies to replace the quarantine through rapid antigen testing. They assumed that all contacts are successfully identified and traced and, once traced, are subject to one of several quarantine-based strategies. At the time being, the number of publications is very high, so it is difficult to keep track of everything that is being published.

Below we propose a new compartmental model, which accounts for indiscriminate quarantine measures, targeted detection and isolation of infected individuals based on diagnostic testing. We compute the basic reproduction number \(R_0\) for this model and show that for \(R_0<1\) only one infection free equilibrium point exists, which is globally stable. For \(R_0>1\) endemic equilibrium occurs.

Similar model studying slightly different features was introduced recently in [3], where they exhibit a series of simulations and compare different levels of isolation and testing. They conclude, as expected, that isolation (social distancing) and testing among asymptomatic cases are fundamental actions to control the epidemic, and the stricter these measures are and the sooner they are implemented, the more effective they are in flattening the curve of infections. They assume that the isolation rate and testing rate are time dependent, which is the advantage of their model.

In order to better understand the mechanism of managing the epidemic, we aim to analyze the quantitative properties of our proposed model. Also contrary to other papers our model considers imperfect quarantine. We compute the trajectories of the infected and quarantined populations in the case when indiscriminate quarantining is applied and in the case when targeted quarantining is facilitated by diagnostic testing. We then evaluate the relative efficiency of the testing effort by matching the parameters of both scenarios to ensure that they produce the same infection peak. As the measure of the efficiency, the time-integral of the total quarantined population over the duration of the epidemic is used.

Based on the effective reproduction number we suggest a strategy to manage the epidemic. It consists in introducing the abrupt quarantine at the time when certain threshold is reached and releasing the quarantine abruptly again at a later time. Although during the second phase of the epidemic of Covid-19 such strategies were used in many countries - schools and other facilities were closed basically from day to day, not many papers attempt to model this complex problem mathematically. The most important question is to set the parameters of the quarantine i.e. its timing and size in such a way that the epidemic gets under control. We demonstrate that if this is chosen carefully further waves will not occur. An uncertain parameter in the model is the strictness of the restrictions which in reality is difficult to predict. Therefore the final effect of quarantining is strongly influenced also by how well people obey the imposed restrictions. Therefore any successful intervention strategy has to be accompanied by good public communication.

The paper is organized as follows: The compartmental model with asymptomatic groups is presented in the next section. We describe in details the flows between compartments. Then we derive equlibria and reproduction number of the proposed model.

The second section we end by an overview of the related epidemiological parameters. The values used in the numerical simulations are based on the average characteristics of Covid-19 that we distilled from the current literature.

The results are presented in Sect. 3. In the first part we concentrate on the quantitative properties of the model. We numerically analyze the effect of the imposed home quarantine on the dynamics of \(I_{sQ}\). In the second part we introduce an intervention strategy proposed to manage epidemic without occurrence of the next waves. We discuss the role of the main factors which are part of the intervention strategy.

2 The Model

2.1 Model Description

Several recent studies have reported that the coronavirus can be transmitted during the incubation period before the first symptoms develop. Moreover, a significant portion of individuals with Covid-19 lack symptoms [8]. These characteristics of Covid-19 together with the state imposed quarantine and testing motivate the following extension of the SEIR model:

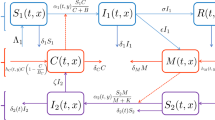
$$\begin{aligned} \begin{aligned}&\dot{S}= \mu -\beta SI_a - \beta (1-\rho ) S\left( I_{aQ}+ I_{sQ}\right) - \mu S,\\&\dot{S}_Q= -\beta (1-\rho ) S_QI_a -{ \beta }{(1-\rho )}^{2} S_Q\left( I_{aQ}+ I_{sQ}\right) -\mu S_Q,\\&\dot{E}= \beta SI_a +\beta (1-\rho ) S\left( I_{aQ}+I_{sQ}\right) - \omega E- \mu E,\\&\dot{E}_Q= \beta (1-\rho ) S_Q I_a +{ \beta }{(1-\rho )}^{2} S_Q\left( I_{aQ}+ I_{sQ}\right) - \omega E_Q -\mu E_Q ,\\&\dot{I}_a= k \omega E -\delta I_a-\psi I_a -\mu I_a,\\&\dot{I}_{aQ}= k \omega E_Q -\delta I_{aQ} -\psi I_{aQ}-\mu I_{aQ} ,\\&\dot{I}_{sQ}= (1-k) \omega \left( E+E_Q\right) + \psi \left( I_a+I_{aQ}\right) -\delta I_{sQ} -\mu I_{sQ} ,\\&\dot{R}= \delta \left( I_a+ I_{sQ}\right) -\mu R,\\&\dot{R}_Q = \delta I_{aQ}-\mu R_Q, \end{aligned} \end{aligned}$$
(2)

see Fig. 1. Here S denotes the density of susceptible individuals who are not quarantined and \(S_Q\) is the density of susceptible individuals at home quarantine. A similar labeling convention is adopted for other groups of individuals, where the subscript Q refers to the subpopulation at home quarantine. It is assumed that the exposed individuals labeled E and \(E_Q\) have been infected but are not infectious yet, and show negative test results if tested for the virus. The compartment \(I_{sQ}\) includes infectious individuals with symptoms and those infectious individuals without symptoms who tested positively for the virus (which corresponds to the published statistics such as the graphs provided by WHO [20]). It is therefore the compartment of detected active cases. The individuals from the compartment \(I_{sQ}\) are all quarantined. Infectious asymptomatic individuals labeled \(I_a\) and \(I_{aQ}\) show positive test results if tested for the virus, in which case they are transferred to the compartment labeled \(I_{sQ}\). That is, testing an asymptomatic infectious non-quarantined individual results in their quarantining. Upon recovery, the individuals from compartments \(I_a\) are recruited to the compartment R, and individuals from compartment \(I_{aQ}\) are recruited to the compartment \(R_Q\). Moreover we assume that there is no need to isolate those individuals who recovered from the infection, i.e. individuals from compartment \(I_{sQ}\) are recruited to the compartment R. Contact tracing per se is not included in the model but can be accounted for as a factor increasing the isolation rates. Two different types of tests are used to detect the presence of the virus during the illness and the presence of antibodies after the illness. For simplicity we do not consider tests for antibodies which detect that a person had Covid-19 in the past but now is healthy. Therefore we assume that one can impose home quarantine also on the individuals in compartment R. We exclude reinfection, although a few cases have been reported. The quarantined population is composed of the groups \(S_Q,E_Q,I_{aQ},I_{sQ}, R_Q\). We assume a constant total population size, and we scale its density to unity, hence the equation for the density of the recovered quarantined population \(R_Q=1-S-S_Q-E- E_Q-I_a-I_{aQ}-I_{sQ}-R\) is redundant.

Parameters \(\beta \), \(\omega \) and \(\delta \) have the same interpretation as for the SEIR model (1), i.e. \(\beta \) represents the transmission rate, \(\omega \) is the rate at which an exposed individual becomes infectious and \(\delta \) is the recovery rate. We cover a demographic effect through the parameter \(\mu \). The parameter \(\psi \) denotes the testing rate, i.e. the rate of detection and isolation of asymptomatic individuals. The fraction of individuals who do not develop symptoms when infected we represent by parameter k. Assuming \(I_a(0)=I_{aQ}(0)=I_{sQ}(0)=0\), the ratio of the symptomatic population to the asymptomatic population remains \((1-k):k\) at all positive times.

We propose to consider two types of home quarantine, namely abrupt and gradual quarantine. Abrupt quarantine at time \(t_{switch}\) can be simply described as one time movement from non-quarantine departments to the quarantined ones with rate \(\chi \). For simplicity we assume indiscriminate quarantining, i.e. the same rate \(\chi \) is applied on all non-quarantined departments. The exact time point \(t_{switch}\) is often set by the health authorities and its determination may depend on various factors, e.g. the number of infected people, lack of hospital beds, occurrence of more serious mutations, etc. In addition, we define initial abrupt quarantine as the abrupt quarantine imposed at the time \(t_{switch}=0\), i.e. exactly at time when the first cases appear. Initial abrupt quarantine was applied e.g. in Slovakia, in March 2020 - all schools have been closed right after the first confirmed case.

On the other hand, gradual quarantine is spread in time and again can depend on different factors such as the immediate number of infected people or positively tested people, available hospital beds, etc. In our model we assume that the total gradual quarantining rate is proportional to \(I_{sQ}\) and decreases with the increasing proportion of the total quarantined population. Assuming indiscriminate quarantining, the rate of quarantining from a particular compartment is proportional to the density of the population associated with this compartment. For example, the rate of quarantining from the S-compartment is set to \(\chi I_{sQ} (S+I_a+E+R) S/(S+I_a+E+R) = \chi I_{sQ} S\).

Fig. 1
figure 1

Compartmental diagram of model (2). Arrows show the flows (with the corresponding rate parameters) between the compartments. Red dashed arrows indicate the transfer induced either by abrupt or gradual quarantine. The dashed rectangle includes the quarantined populations

Full size image

Finally, the model (2) allows for the possibility of imperfect isolation with \(\rho \in [0, 1],\) representing the isolation effectiveness as in [11]. Let us note that the actual value of this parameter depends on how people behave, i.e. how they follow the imposed restrictions. Naturally, the value of \(\rho \) can strongly influence the epidemic development. So people themselves by their responsible behaviour can influence the situation, or eventually some effective state controlling tools can also play an important role.

2.2 Theoretical Background

First of all note that for interpretation reasons we are interested only in solutions whose all components are non-negative and less or equal then 1. The proposed model (2) exhibits a continuum of equilibrium states when \(\mu = 0,\) for which \(I_a = I_{sQ}=I_{aQ}= E_Q =E= 0\) and \(S+S_Q + R+R_Q =1.\)

For \( \mu \ne 0 \) the model has the infection-free equilibrium (1, 0, 0, 0, 0, 0, 0, 0, 0) and the endemic equilibrium:

$$\begin{aligned}&S = \frac{abc}{\beta \omega (k \rho c + (1-\rho )a)}, \nonumber \\&S_Q = 0,\nonumber \\&E = \frac{ \mu \left( \beta \omega ( k \rho c + (1-\rho ) a ) - abc\right) }{\beta \omega b ( k \rho c + (1-\rho )a)},\nonumber \\&E_Q =0,\nonumber \\&I_a = \frac{k \mu (\beta \omega ( k \rho c + (1-\rho ) a) - abc)}{\beta a b( k \rho c +(1-\rho ) a)},\nonumber \\&I_{aQ} = 0,\nonumber \\&I_{sQ} = \frac{\mu (c (1-k)+\psi )(\beta \omega (k \rho c + (1-\rho )a)-abc)}{\beta abc (k\rho c + (1-\rho )a)},\nonumber \\&R = \frac{ \delta (\beta \omega (k \rho c + (1- \rho ) a) - abc)}{\beta b (k \rho c + (1-\rho ) a)},\nonumber \\&R_Q = 0, \end{aligned}$$
(3)

where \(a =(\psi + \mu + \delta )\), \(b =(\mu + \omega )\) and \(c = (\delta + \mu )\).

The basic reproduction number \(R_0 \) is given by the expression

$$\begin{aligned} R_0 = \frac{\beta \omega ( k\rho (\delta +\mu ) +(\delta + \mu +\psi )(1-\rho ))}{(\delta + \mu )(\mu + \omega )(\delta + \mu + \psi )}. \end{aligned}$$
(4)

Let us note that all involved parameters are non-negative.

Theorem 1

If \(R_0<1\), the system (2) has only one infection free equilibrium. If \(R_0>1\), the system (2) has additionally an endemic equilibrium given by expressions (3).

Recall that we are interested in solutions in the region where all variables are bigger or equal than 0 and less than 1. The condition for the existence of the endemic equilibrium is

$$\begin{aligned} k \rho (\delta + \mu ) + ( 1 - \rho )(\mu + \psi + \delta )&> 0, \end{aligned}$$

which is always satisfied and

$$\begin{aligned} \frac{(\delta + \mu )(\mu + \omega )(\delta + \mu + \psi )}{\beta \omega ( k\rho (\delta +\mu ) +(\delta + \mu +\psi )(1-\rho ))} <1, \end{aligned}$$
(5)

which is equivalent to \(R_0>1\).

Lemma 1

\(R_0 \) is decreasing with increasing \(\psi \) and \(\rho \).

Proof

The statement follows from the direct differentiation of (4) by \(\psi \) and \(\rho \) resp.:

$$\begin{aligned} \frac{\partial R_0 }{\partial \psi } = \frac{ - (\mu + \omega )\beta \omega k\rho }{{\left( (\mu + \omega )(\delta + \mu + \psi )\right) }^2}<0. \end{aligned}$$

Similarly

$$\begin{aligned} \frac{\partial R_0 }{\partial \rho }=\frac{ \beta \omega k (\delta + \mu ) -\beta \omega (\delta + \mu + \psi ) }{(\delta + \mu )(\mu + \omega )(\delta + \mu + \psi )} <0\nonumber \end{aligned}$$

since \(k<1.\) \(\square \)

Theorem 2

If \(R_0<1\) the infection free equilibrium of the system (2) is globally stable.

Proof

Let us assume first \(\psi =0.\) In this case the eigenvalues at the infection free equilibrium can be easily computed and there are as follows: \(-\mu - \omega , \) \( -\delta - \mu ,\) (with multiplicity 2), \( -\mu ,\) (with multiplicity 4) and the last two eigenvalues are

$$\begin{aligned} \lambda= & {} \frac{-\delta - 2\mu - \omega - \sqrt{4 \beta k \omega \rho - 4 \beta \omega \rho + 4 \beta \omega + \delta ^2 - 2 \delta \omega + \omega ^2}}{2} \end{aligned}$$

and

$$\begin{aligned} \nu =\frac{-\delta - 2\mu - \omega + \sqrt{4 \beta k \omega \rho - 4 \beta \omega \rho + 4 \beta \omega + \delta ^2 - 2 \delta \omega + \omega ^2}}{2}. \end{aligned}$$

Let us note that the last two eigenvalues are always real since the positive sign of the discriminant \(4 \beta k \omega \rho - 4 \beta \omega \rho + 4 \beta \omega + \delta ^2 - 2 \delta \omega + \omega ^2\) is equivalent to the condition \(\frac{{(\delta - \omega )}^2}{4\beta \omega (1-k)}+ \frac{1}{1-k } \ge \rho \), which is always satisfied since \(\rho \le 1.\) Let us note that all eigenvalues except the last one, are always negative, \(\nu .\)

We show that \(\nu <0\) if \(R_0 <1\) and if \(R_0 >1\) then \(\nu >0.\) This follows easily if we realize that

$$\begin{aligned} \nu = \frac{-\delta - 2\mu - \omega + \sqrt{\left( \delta + 2\mu + \omega \right) ^2 + 4 (\mu + \omega )(\delta + \mu )\left( R_0 -1\right) }}{2}. \end{aligned}$$

For the general case where \(\psi \) is possibly non-zero, the eigenvalues are as follows: \(-\mu - \omega , \) \( -\delta - \mu ,\) \( -\mu ,\) (with multiplicity 4) and the last three eigenvalues are still possible to calculate, but the expressions are several lines long and difficult to handle. We can prove the statement by using Hurwitz criterion. The last three eigenvalues are solutions of the following cubic polynomial

$$\begin{aligned} {\lambda }^3 + A_2 {\lambda }^2 + A_1 {\lambda } + A_0 = 0, \end{aligned}$$

where

$$\begin{aligned} A_2= & {} 2 \delta + 3 \mu + \omega + \psi ,\\ A_1= & {} {\delta }^2 + 4 \delta \mu + 3 {\mu }^2 - \beta \omega + 2 \delta \omega + 2 \mu \omega + \delta \psi + 2 \mu \psi + \omega \psi + \beta \omega \rho - \beta k \omega \rho \end{aligned}$$

and

$$\begin{aligned} A_0= & {} {\delta }^2 \mu + 2 \delta {\mu }^2 + {\mu }^3 -\beta \delta \omega + {\delta }^2 \omega -\beta \omega \mu + 2 \delta \omega \mu + {\mu }^2 \omega + \delta \mu \psi +{\mu }^2\psi \\&- \beta \omega \psi + \delta \omega \psi +\mu \omega \psi + \beta \delta \omega \rho - \beta \delta k \omega \rho + \beta \mu \omega \rho - \beta k \mu \omega \rho + \beta \omega \psi \rho . \end{aligned}$$

We want to show that if \(R_0 <1, \) then \(A_1 A_2 - A_0 >0, \) which means by Hurwitz criterion that all the eigenvalues have negative real part and the statement follows. To show the later we rewrite \(A_1 A_2 - A_0\) as

$$\begin{aligned}&A_1 A_2 - A_0 = (a+b+c)(ab+ac+bc \\&\quad -\beta \omega (k \rho +(1-\rho ))) - abc + \beta \omega (\rho k c + (1-\rho ) a), \end{aligned}$$

where \(a = \psi +\mu +\delta , b = \mu +\omega , c = \delta + \mu \). Let us note that \(a>0\), \(b>0\) and \(c>0\).

Now \(R_0 <1\) is equivalent to the condition

$$\begin{aligned} \beta \omega \rho k c + \beta \omega (1-\rho ) a < abc. \end{aligned}$$

Therefore

$$\begin{aligned} \beta \omega \rho k < ab, \end{aligned}$$

which implies

$$\begin{aligned} (a+b)(\beta \omega \rho k) < (a+b)ab \end{aligned}$$

and

$$\begin{aligned} \beta \omega (1-\rho ) < bc, \end{aligned}$$

which implies

$$\begin{aligned} (b+c)(\beta \omega (1-\rho ) ) < (b+c) bc. \end{aligned}$$

This all together implies that \(A_1 A_2 - A_0 >0, \) and the statement for general \(\psi \) follows. \(\square \)

2.3 Setting Model Parameters

The values of the epidemiological parameters used in the numerical simulations presented below are based on the average characteristics of Covid-19 published so far.

One key parameter is the average duration of the infectious period. The period of infectiousness (or period of communicability) is defined as the time interval during which an infectious agent may be transferred directly or indirectly from an infected person to another person [10]. According to [16], Covid-19 can be transmitted by an infected individual before the symptoms develop. The average infectious period is the reciprocal of the parameter \(\delta \). The period of infectiousness is difficult to estimate directly. According to [16], the mean incubation period of Covid-19 is 6 days. In [5], the serial interval of Covid-19 was estimated as the weighted mean of the published parameters and described by the gamma distribution with the mean serial interval of 4.56 days (credible interval (2.54, 7.36)) and standard deviation 4.53 days (credible interval \((4.17-5.05)\)).

With a serial interval shorter than the average incubation period (\(4.56<6\)), we expect that a significant number of transmissions occur before the index case has symptoms. Following [9], the period of infectiousness is assumed to be 5.5 days, 2 days before and 3.5 days after symptom onset. This data translates into the values \(\delta =1/5.5,\) \(\omega =1/4 \) of our model parameters.

Another key parameter is the transmission rate \(\beta \), which can be expressed as the product of the average number of daily contacts which a susceptible individual has with infected individuals and the probability of transmission during each contact. The value of this parameter, which is not directly observable, is inferred from the estimation of the basic reproduction number \(R_0\).

The value of \(R_0\) for Covid-19 has been estimated within the range of \(2.24\le R_0\le 3.58\) [23]. Taking into account the theoretical relation between \(R_0\) and \(\beta \) (see (4)) and the setup of the other model parameters, we assume in our numerical analysis \(\beta =0.6.\)

The value of the parameter k, which measures the proportion of asymptomatic individuals among the infected population, is set to 0.5 in accordance with the estimate from [21]. According to [22] the average value of the parameter \(\mu \) (the birth/death rate) is set to 0.01/365.

The coefficient \((1-\rho )\in [0,1]\) measures the decrease in the transmission rate due to isolation. We assume that parameter \(\rho \) is a part of intervention strategy: its value can be determined according to current epidemiological situation and reflects the strength of the imposed quarantine restrictions. Values of \(\rho \) close to one mean that quarantined individuals are perfectly isolated and their ability to spread the disease is strongly limited. The exact value of \(\rho \) is not directly measurable. However, there are attempts to quantify the effectiveness of the government restrictions (see e.g. [12]). Such rankings can be considered as a basis for setting the values of the parameter \(\rho \).

The values of the parameter \(\psi \) will be specified for each particular simulation. In general we assume \(\psi \in [0,0.5].\) This restriction is due to the limited availability of tests and the limited number of tests that can be performed in one day. This assumption is not essential for the results interpretation and now-days with the increased availability of test, can be extended.

To summarize, if not explicitly stated otherwise, the values of the epidemiological parameters used in the simulations presented below are as follows: \(\beta =0.6\), \(\omega =1/4\), \(\delta =1/5.5\), \(\mu = 0.01/365 \) and \(k=0.5.\) Initial conditions are chosen in accordance with the real situation in the city where the population size N is approximately 500,000. All simulations of model (2) are initiated with \(E(0)=2/N\). We assume that initially all other individuals are susceptible. The initial division between S and \(S_Q\) compartment is specified for each analyzed case.

3 Results

The current epidemiological situation is raising many questions about the dynamics of the virus spread and the effectiveness of the imposed quarantine policies. The proposed model (2) aims to explore some plausible scenarios depending on the size of the initial quarantine, gradual quarantining rate, quarantine effectiveness and the testing rate.

Fig. 2
figure 2

Comparison of the graphs of \(I_{sQ}\) and \(I_a+I_{aQ}+I_{sQ}\) for model (1) and model (2). Parameter \(\psi =0\)

Full size image

We first compare the classical SEIR model (1) and model (2), see Fig. 2a. Model (2) reduces to (1) in the special case when \(k=0\), \(\rho =0\), \(\psi =0, \) \(\mu =0\). The grey curve in Fig. 2a depicts the time evolution of the infected population for this case. Let us note that the \(I_{sQ}\) compartment in model (2) fully corresponds to the I compartment in (1) under this parameters setup. Taking \(k=0.5\) with other parameters unchanged in model (2), we observe the decrease of the infected population by a half because half of the infected individuals don’t show symptoms: instead of being included in the \(I_{sQ}\) they are now logged in the compartment \(I_a\). Setting \(\rho =0.5\) leads to a slower infection spread due to quarantine.

Let us note that typical Covid-19 statistics such as graphs provided by WHO [20] record confirmed cases only. However, according to some sources including [21], the data suggest that up to 80% (we assume 50% in simulations) of infections can be mild or asymptomatic. Therefore, one can expect that the propagation of the disease by unregistered cases might play a significant role in its spread, possibly even more significant than the symptomatic cases because the latter are usually quarantined and therefore spread the virus less. It remains a controversial topic whether symptomatic and asymptomatic cases are equally infectious and in particular whether symptomatic and asymptomatic individuals produce the same numbers of antibodies, which would suggest that they spread the disease approximately equally. We assume equal transmission rates from symptomatic and asymptomatic individuals in our model (2) for simplicity. Figure 2 shows that the proportion of asymptomatic individuals in the population can have a significant impact on the height of the maximum of \(I_{sQ}\) (grey versus dotted and dashed dotted curves), i.e. the number of infected symptomatic individuals at the peak of the epidemic. As a result, countries with different proportions of symptomatic versus asymptomatic individuals (e.g. due to different age structure of the population or for other immunity reasons) might show different dynamics of the epidemic, although other conditions are similar. Introducing a reduction of the transmission due to quarantine by setting \(\rho =0.5\) lowers the infection peak and simultaneously prolongs the epidemic (dashed versus dotted curves).

3.1 Response of the Model to Variations of the Quarantine Size

The most effective way to slow down the spread of a disease which is not vaccine preventable, is probably to impose isolation and quarantine on the population or a selected subpopulation. We assume that symptomatic and positively testing individuals are isolated (either at a hospital when symptoms are severe, or at home). Further, the model assumes home quarantining of part of the untested population, including healthy and asymptomatic individuals who stay at home due to various state/business restrictions (such as school closures etc.). We assume that these interventions result in a decreased transmission rate.

First we analyzed the effect of the initial abrupt quarantine. Figure 3 shows how the number of infected symptomatic individuals depends on the initial quarantine size. As expected, the infection peak of \(I_{sQ}\) lowers with increasing \(S_Q(0)\) (\(S_{sQ}(0)+S_{aQ}(0)\), respectively), but simultaneously the duration of the epidemic increases.

Fig. 3
figure 3

Effect of the initial abrupt quarantine size on \(I_{sQ}\) and \(I_a+I_{aQ}+I_{sQ}\). Parameters \(\rho =0.5\) and \(\psi =0\)

Full size image

Another way to control the home quarantine size in model (2) is by using a positive isolation rate \(\chi \). Below this strategy is referred as the gradual quarantining. The setup allows \(\chi \) to depend on time or to be controlled by the phase variables such as \(I_{sQ}\) through a feedback loop but, for simplicity, we assume \(\chi \) to be constant.

Figure 4 compares the above two approaches to controlling the quarantine size in our model (2). The same infection peak and a similar profile of the function \(I_{sQ}(t)\) can be achieved either with nonzero \(\chi \) or with nonzero \(S_Q(0),\) see Fig. 4a. The total quarantined population is twice larger than \(I_{sQ}\) because equal proportions of symptomatic and asymptomatic individuals are assumed, see Fig. 4b. Figure 4c shows that the total quarantined population is initially smaller for the gradual quarantining strategy than for the abrupt quarantine strategy but eventually has to exceed the latter to ensure the same infection peak height. The peak appears earlier with gradual quarantining, and this effect becomes more pronounced with increasing quarantine size (dotted versus solid curve).

Fig. 4
figure 4

Comparison of the effect of initial abrupt and gradual quarantine on dynamics of a \(I_{sQ}\) population; b \(I_{a}+I_{aQ}+I_{sQ}\) population; and c total quarantined population. Parameters \(\rho =0.5\) and \(\psi =0\)

Full size image

3.2 Response of the Model to Variations of the Testing Rate

By testing we understand the detection and isolation of infectious asymptomatic individuals. We assume that symptomatic cases are confirmed as positive and isolated (quarantined), hence they all belong to the \(I_{sQ}\) compartment.

The parameter \(\psi \) can be interpreted as the rate of successful detection of infectious asymptomatic individuals. We assume that this rate is the same for all compartments in which testing can detect infectious individuals. Newly detected cases are recruited from the compartments \(I_a\) and \(I_{aQ}.\) Therefore the compartment \(I_{sQ}\) is interpreted as the compartment of confirmed active cases.

As our simulations show, the time interval from the advent of the epidemic to the infection peak and the total duration of the epidemic increase with the increasing testing rate \(\psi \), see Fig. 5. Further, a significant increase in the testing rate decreases the epidemic peak. However, for a relatively low testing rate, for instance if \(\psi = 0.1\), a small increase in the number of confirmed active cases is observed, compared to the case when \(\psi =0\) (dashed dotted curve versus the dotted curve in Fig. 5). Under low detection rate, the decrease of the spread of infection due to quarantining of positively tested asymptomatic individuals can be masked by the apparent increase of the \(I_{sQ}\) population due to newly detected cases. However, the total number of cases (i.e. \(I_{sQ} + I_{aQ} + I_a\)) always decreases with increasing testing rate, as Fig. 5b shows.

Fig. 5
figure 5

Effect of testing on dynamics of \(I_{sQ}\) and \(I_a+I_{aQ}+I_{sQ}\). Parameter \(\rho =0.5\)

Full size image

3.3 Indiscriminate Quarantining Versus Massive Testing

Due to economic and social reasons, it is clear that lockdowns applied in many countries cannot last for very long. Therefore there is a demand to find a more economically sustainable solution to replace massive home quarantine measures. One reasonable possibility seems to be effective testing. The grey curve in Fig. 6a shows the evolution of the infected population for model (2) with 13.5% of the total population quarantined at the initial moment and zero testing rate; the dashed curve corresponds to the situation where nobody stays in quarantine initially but of total population is screened daily for Covid-19 (more precisely, 10% of infected asymptomatic individuals are successfully detected daily). Under both setups the total infected population \(I_a+I_{aQ}+I_{sQ}\) follows approximately the same trajectory. However, comparing the dynamics of the quarantined population, we see that it is significantly smaller at all times when testing is used than in the case when indiscriminate quarantining is applied, see the dashed and grey curves in Fig. 6b. A similar observation can be made when instead of abrupt quarantining the gradual quarantining strategy with the parameter \(\chi \) is applied, see the black solid curves in Fig. 6a, b. Again, the quarantined population is significantly smaller when quarantining is based on testing than in the case when indiscriminate gradual quarantining is used, while the trajectories of the infected population are similar for both scenarios. Recall that the number of active symptomatic cases is proportional to the total infected population and equals \((1-k)(I_a+I_{aQ}+I_{sQ})\).

Fig. 6
figure 6

Indiscriminate quarantining versus quarantining based on testing. Parameter \(\rho =0.5\). a Dynamics of the total infected population, \(I_a+I_{aQ}+I_{sQ}\), for a selected testing rate \(\psi \) and the corresponding value of \(S_Q(0)\) and \(\chi \) resulting in the same height of the peak of \(I_a+I_{aQ}+I_{sQ}\). b Dynamics of the total quarantined population corresponding to the graphs on panel a; the same color coding is used. c For every point \((\psi _0, s_0)\) of the dotted curve, the testing rate \(\psi =\psi _0\) with zero indiscriminate quarantining (\(S_Q(0)=0\)) in the same peak of infection \(I_a+I_{aQ}+I_{sQ}\) as the initial quarantine \(S_Q(0)=s_0\) with zero testing (\(\psi = 0\)). For every point (\(\psi _0\), \(\chi _0\)) of the solid curve, the testing rate \(\psi =\psi _0\) with zero indiscriminate quarantining (\(S_Q(0)=0\)) results in the same peak of infection as the indiscriminate quarantining rate \(\chi =\chi _0\) with zero testing and zero initial quarantine (\(\psi =0\), \(S_Q(0)=0\)). d The ratio of the time-integral of the total quarantined population in the case of indiscriminate quarantining to the value of this integral in the case of quarantining based on testing under the constraint that the infection peak is the same for both scenarios. The dotted and solid curves show the dependence of this ratio on \(\psi \) and correspond to the curves of the same colors, respectively, on panel c

Full size image

Figure 6c, d presents similar results for a range of values of the testing rate. We compare the scenario with a positive testing rate \(\psi \) and zero initial quarantine size \(S_Q(0)=0\) to the scenarios with \(\psi =0\), \(S_Q(0)>0\) and with \(\psi =0\), \(\chi >0\), \(S_Q(0)=0\). The first scenario corresponds to quarantining based on testing, while the second and third scenarios correspond to indiscriminate abrupt and gradual quarantining, respectively. Given a \(\psi >0\) in the first scenario, the \(S_Q(0)>0\) and \(\chi >0\) in the second and third scenarios are selected in such a way as to ensure that the height of the infection peak in all the three scenarios is the same (as in Fig. 6a). This constraint defines \(S_Q(0)\) and \(\chi \) in the second and third scenarios, respectively, as functions of the testing rate \(\psi \) used in the first scenario, see the graphs in Fig. 6c. For each point of these graphs, we also compute the time-integral of the total quarantined population over the duration of the epidemic; the latter is technically defined as the the time interval \([0,t_e]\) where \(t_e\) is the moment after the infection peak when \(I_{sQ}(t_e)=0.1/N\). Figure 6d shows that the time-integral of the quarantined population is by an order of magnitude smaller when quarantining is based on massive testing than in the case when indiscriminate (abrupt or gradual) quarantining is applied. Moreover, the ratio of the value of this time-integral in the case of indiscriminate quarantining to its value in the case of quarantining based on testing increases with the increasing testing rate.

These observations indicate that effective testing might be a way to replace massive quarantine measures. Moreover, they may help to explain why some countries such as South Korea and Singapore, which implemented massive rapid free testing and an extremely good system of contact tracing, have been most successful in containing the first phase of Covid-19 outbreak.

3.4 Managing epidemic Using Abrupt Quarantine

As we have already mentioned quarantine can be considered as one the most effective prevention strategy especially in the case of a new infectious disease. In the previous sections we studied and compared the quantitative properties of the gradual and initial abrupt quarantine on epidemic dynamic. However, the pool of the available strategies is much larger as we could observe during the 2020–2021 period. The implemented strategies differed in many factors, especially in size, strenght and timing. However, the aim of any strategy is the same: to decrease the disease spread and to stop the epidemic.

In this section we extend our quantitative analysis and concentrate on the effect of the abrupt quarantine in general. In the initial phase of Covid-19 epidemic quarantine was introduced just few days after the first cases occurred. This was understandable, the disease had many unknown factors and this decision gained time to explore it more. However, in general to introduce the quarantine early may not be the best decision since relaxing the quarantine may bring other epidemic waves as we observed for Covid-19 in many countries during the fall 2020.

It is an interesting problem to determine the ideal timing of the introduction of the abrupt quarantine in our model. The second related question is the size of the imposed quarantine.

We first propose a simplified control strategy which aims to prevent the arrival of the next epidemic waves. Let’s assume that initially nobody is quarantined, i.e. \(S_Q(0)=E_Q(0)=I_a(0)=R_Q(0)=0\). Once the critical level \(I_{up}\) of the observed cases \(I_{sQ}\) is achieved, home quarantine is applied on \({\bar{\chi }}\) percentage of non-quarantined population (i.e. \(S_Q\)+\(E_Q\)+\(I_{aQ}\)+\(R_Q\)). Let us denote \(t_{switch}\) the time, when the threshold level \(I_{up}\) of \(I_{sQ}\) has been achieved for the first time. Assuming indiscriminate quarantining, the rate of quarantining from a particular compartment is proportional to the density of the population associated with this compartment.

The abrupt quarantine immediately decreases the number of non-quarantined population. We will use the following notation:

$$\begin{aligned} \begin{aligned} S^{new}\left( t_{switch}\right)&= S\left( t_{switch}\right) - \bar{\chi }S\left( t_{switch}\right) ,\\ S_Q^{new}\left( t_{switch}\right)&= S_Q\left( t_{switch}\right) + {\bar{\chi }} S\left( t_{switch}\right) ,\\ E^{new}\left( t_{switch}\right)&= E\left( t_{switch}\right) - \bar{\chi }E\left( t_{switch}\right) ,\\ E_Q^{new}\left( t_{switch}\right)&= E_Q\left( t_{switch}\right) + {\bar{\chi }} E\left( t_{switch}\right) ,\\ I_{a}^{new}\left( t_{switch}\right)&= I_a\left( t_{switch}\right) - {\bar{\chi }} I_a\left( t_{switch}\right) ,\\ I_{aQ}^{new}\left( t_{switch}\right)&= I_a\left( t_{switch}\right) + {\bar{\chi }} I_a\left( t_{switch}\right) ,\\ R^{new}\left( t_{switch}\right)&= R\left( t_{switch}\right) - \bar{\chi }R\left( t_{switch}\right) ,\\ R_Q^{new}\left( t_{switch}\right)&= R_Q\left( t_{switch}\right) + {\bar{\chi }} R\left( t_{switch}\right) . \end{aligned} \end{aligned}$$
(6)

Further disease transmission depends on the following three factors:

  1. 1.

    the level of the quarantine \({\bar{\chi }}\),

  2. 2.

    the strictness of the imposed quarantine \(\rho \),

  3. 3.

    the threshold at which the abrupt quarantine is imposed, \(I_{up}\).

Due to the complexity of the proposed Model (2), we study the dependence of the epidemics development on the parameters \(\chi \), \(\rho \) and \(I_{up}\) numerically. Different scenarios are depicted in Fig. 7. In Fig. 7a we study the effect of different sizes of abrupt quarantine for fixed parameters \(\rho =0.7\) and \(I_{up}=0.01\). If the quarantine is not sufficiently large (corresponding to \(\chi =0.2\), 0.3), the epidemic continues to spread. Figure 7b shows different scenarios for different levels of \(I_{up}\), keeping \(\rho \) and \({\bar{\chi }}\) fixed. If the value of \(I_{up}\) is set up too high, the restrictions have no effect on the epidemic. If this value is too low, the time of the epidemic is prolonged and second wave develops. Figure 7c shows different scenarios under different values of the parameter \(\rho ,\) measuring the quarantine efficiency, keeping \(I_{up} \) and \({\bar{\chi }} \) fixed. The higher the \(\rho ,\) the effect of the imposed restrictions is more effective. Figure 7 illustrates that choosing the right strategy is a complex problem. The governments can in practice directly influence the epidemic spread by choosing to impose the restrictions at the right time and they have to be strong enough to avoid second waves of epidemic. The situation also strongly depends on how people well behave, i.e. how they follow the imposed restrictions. This fact can be influenced by people themselves or by some effective control tools.

Fig. 7
figure 7

Number of \(I_{sQ}\) cases under different quarantine parameters. a \(\rho =0.7\), \(I_{up}=0.01\), \(\chi _{crit}=0.545\) b \(\rho =0.7\), \({\bar{\chi }}=0.4,\) c \({\bar{\chi }}=0.4\), \(I_{up}=0.01\). In all simulations \(\psi =0\)

Full size image

Based on the above observations we want to determine the best strategy how to handle the epidemic. Assuming that the parameters \(\rho \) and \(I_{up}\) are fixed, we propose to determine the value of the parameter \({\bar{\chi }} \) in such a way that the effective reproduction number (defined below) drops to 1 at the time when we impose abrupt quarantine and thus the spread of the disease will slow down.Footnote 1

Standard measure of the disease spread is the so-called effective reproduction number. For model (2) the effective reproduction number can be defined as:

$$\begin{aligned} R_{e} = R_0 \left( S+(1-\rho )S_Q\right) , \end{aligned}$$
(7)

where \(R_0\) is the basic reproduction number, see (4).

We determine the size of the abrupt quarantine in such a way that the effective reproduction number will become less then 1 at the time when quarantine is introduced, i.e.:

$$\begin{aligned} R_0 \left( S^{new}\left( t_{switch}\right) +(1-\rho )S^{new}_Q\left( t_{switch}\right) \right) < 1, \end{aligned}$$
(8)

which using (6) leads to the condition

$$\begin{aligned} {\bar{\chi }} > \frac{1}{\rho S\left( t_{switch}\right) }\left( S\left( t_{switch}\right) +(1-\rho )S_Q\left( t_{switch}\right) - \frac{1}{R_0 }\right) , \end{aligned}$$
(9)

which is equivalent to

$$\begin{aligned} {\bar{\chi }} > \frac{R_e(t_{switch}) - 1}{\rho R_0 S(t_{switch})}. \end{aligned}$$
(10)

Furthermore, if at time \(t_{switch}\) nobody is in home quarantine, i.e. \(S_Q(t_{switch})=0\), condition (10) reduces to:

$$\begin{aligned} {\bar{\chi }} > \frac{1}{\rho }\left( 1 - \frac{1}{R_0 S (t_{switch})} \right) . \end{aligned}$$
(11)

Let us note that the condition (11) for initially fully susceptible population, i.e. \(S=1\) and perfect home quarantine (\(\rho = 1\)) actually resembles the conditions for the threshold vaccination level needed to achieve the collective immunity (for more details see e.g. [6]).

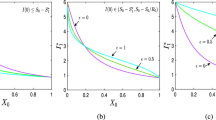
The values of \(S(t_{switch})\) and \(S_Q(t_{switch})\) depend on the threshold \(I_{up}\) and the parameter \(\rho \). We denote the critical level from condition (10) as \({\bar{\chi }}_{crit}\), i.e.:

$$\begin{aligned} {\bar{\chi }}_{crit}:= \frac{R_e\left( t_{switch}\right) - 1}{\rho R_0 S\left( t_{switch}\right) }. \end{aligned}$$

Due to the complexity of the proposed Model (2), we study the critical level of the abrupt quarantine \({\bar{\chi }}_{crit}\) as a function of the threshold level \(I_{up}\) for different values of the parameter \(\rho \) numerically. Our results are graphically depicted in Fig. 8. Let us note that the threshold level \(I_{up}\) determines directly the time at which the home quarantine is imposed. The higher level of \(I_{up}\) corresponds to the latter phase of the epidemic. In Fig. 8 the point when the particular curve crosses the \(I_{up}\)-axis corresponds to the level of the epidemic peak for a given value of the parameter \(\rho \). Naturally, closer to the peak, the lower proportion of the population needs to be quarantined in order to get \(R_e<1\). Further, observe that for small values of \(\rho \) it is impossible to reduce \(R_e\) below 1 in the early stages of epidemic (i.e. when \(I_{up}\) is small) since the parameter \({\bar{\chi }}\) cannot exceed 1. Finally, Fig. 8 illustrates the importance of the parameter \(\rho \) in the control of the disease spread: a more strict compliance of quarantine can substantially reduce the proportion of the population needed to impose to home quarantine in order to stop spreading the disease.

Fig. 8
figure 8

Critical level of the abrupt quarantine \(\bar{\chi }_{crit}\) as a function of threshold level \(I_{up}\) for different values of the parameter \(\rho \). Parameter \(\psi =0\)

Full size image

3.5 Relaxing the Quarantine Measures

Strict quarantine measures or possibly a total lock-down can get the epidemic under control but naturally lead to huge economic losses. The impact of the interruption of the economic/social activities is probably even stronger if the restrictions are imposed for longer time. The question of when it is safe to relax the quarantine restrictions? is answered quite inconsistently by different states and countries. The primary aim of this section is to demonstrate how the timing of different relaxation strategies can influence the development of the epidemic.

Similarly as for the question when to quarantine, strategy to relax home quarantine covers not only the decision when to relax. Equally important is to ask how much of the quarantine can be relaxed in order to avoid new infection waves.

Let us denote as \(I_{down}\) the relaxation threshold, \(t_{relax}\) the first time when \(I_{sQ}\) drops below this relaxation threshold \(I_{down}\) and \({\underline{\chi }}\) the proportion of quarantine which will be released at time \(t_{relax}\). We consider \(I_{down}<I_{up}\). Our strategy is as follows: Similarly as in the proposed quarantine strategy described in the previous section we assume that the decision to relax the quarantine depends on the number of detected active cases: Whenever \(I_{sQ}\) drops below relaxation threshold \(I_{down}\) certain portion of the quarantine, \({\underline{\chi }},\) is released. More formally, we model the relaxation of quarantine at time \(t_{relax}\) as one time movement of \({\underline{\chi }}\)-proportion of the quarantined population to non-quarantine departments:

$$\begin{aligned} \begin{aligned} S^{new}\left( t_{relax}\right)&= S\left( t_{relax}\right) + {\underline{\chi }} S_Q\left( t_{relax}\right) \\ S_Q^{new}\left( t_{relax}\right)&= S_Q\left( t_{relax}\right) - {\underline{\chi }} S_Q\left( t_{relax}\right) \\ E^{new}\left( t_{relax}\right)&= E\left( t_{relax}\right) + {\underline{\chi }} E_Q\left( t_{relax}\right) \\ E_Q^{new}\left( t_{relax}\right)&= E_Q\left( t_{relax}\right) - {\underline{\chi }} E_Q\left( t_{relax}\right) \\ I_{a}^{new}\left( t_{relax}\right)&= I_a\left( t_{relax}\right) + {\underline{\chi }} I_{aQ}\left( t_{relax}\right) \\ I_{aQ}^{new}\left( t_{relax}\right)&= I_a\left( t_{relax}\right) - {\underline{\chi }} I_{aQ}\left( t_{relax}\right) \\ R^{new}\left( t_{relax}\right)&= R\left( t_{relax}\right) + {\underline{\chi }} R_Q\left( t_{relax}\right) \\ R_Q^{new}\left( t_{relax}\right)&= R_Q\left( t_{relax}\right) - {\underline{\chi }} R_Q\left( t_{relax}\right) \\ \end{aligned} \end{aligned}$$
(12)

Here again, we assume that the population which leaves quarantine is uniformly distributed between departments. The important question is how to set the threshold \(I_{down}\) and the parameter \({\underline{\chi }}\) so the epidemic will be under control.

Ideally, after relaxing home quarantine we still want to ensure

$$\begin{aligned} R_{e}(t_{relax}) < 1, \end{aligned}$$

i.e.:

$$\begin{aligned} R_{e}\left( t_{relax}\right) = R_0 \left( S^{new}\left( t_{relax}\right) +(1-\rho )S^{new}_Q\left( t_{relax}\right) \right) < 1, \end{aligned}$$
(13)

which using (12) leads to the condition

$$\begin{aligned} {\underline{\chi }} < \frac{1}{\rho S_Q\left( t_{relax}\right) }\left( \frac{1}{R_0} - \left( S\left( t_{relax}\right) +(1-\rho )S_Q\left( t_{relax}\right) \right) \right) \end{aligned}$$
(14)

or equivalently

$$\begin{aligned} {\underline{\chi }} < \frac{1 - R_e(t_{relax})}{\rho R_0 S_Q\left( t_{relax}\right) }. \end{aligned}$$
(15)

Since \({\underline{\chi }}\in [0,1],\) condition (15) can be fulfilled only if \(R_{e}< 1\) at the time of relaxation. Let us denote \({\underline{\chi }}_{crit}\) the proportion of quarantine for which there is equality in (15), i.e.:

$$\begin{aligned} {\underline{\chi }}_{crit} := \frac{1 - R_e\left( t_{relax}\right) }{\rho R_0 S_Q\left( t_{relax}\right) }. \end{aligned}$$
(16)

Let us note that the values of \(S(t_{relax})\) and \(S_Q(t_{relax})\) depend on the threshold \(I_{down}\) and the parameter \(\rho \). Due to the complexity of the proposed model (2), we study the relation between the parameters \({\underline{\chi }}\), \(\rho \) and \(I_{down}\) and the epidemic development numerically. Our results are graphically depicted on Fig. 9.

Fig. 9
figure 9

Relaxation of quarantine. \({\underline{\chi }}_{crit}\) dependence on the threshold \(I_{down}\) for different values of \(\rho .\) a \(I_{up}=0.002\), b \(I_{up}=0.014\). In all simulations \(\psi =0\)

Full size image

Figure 9 illustrates how \({\underline{\chi }}_{crit}\) depends on the threshold \(I_{down}\) for different values of \(\rho .\) Since the results depend also on the parameter \(I_{up}\) we consider two situations. Figure 9a shows the epidemic development for \(I_{up}\)=0.002, i.e. for the case when the abrupt quarantine has been introduced relatively early. Figure 9b shows results for \(I_{up}=0.014\), i.e. for the case when the abrupt quarantine has been introduced later and thus closer to the epidemic peak. Let us note that the size of the originally imposed restrictions is different for each case with different \(\rho .\)

As we can observe, early introduction of the abrupt quarantine (small \(I_{up}\)) limits the possibilities to relax the quarantine without re-growing. Only for sufficiently low values of the relaxation threshold \(I_{down}\) a small proportion of quarantined population can be released (we assume that the effective reproduction number \(R_e\) stays below 1 after relaxation). This observation corresponds to what happened during spring 2020 e.g. in Slovakia: early quarantine implies that the size of the susceptible department stays almost unchanged. Without any other changes (e.g. vaccination) quarantine results only in postponing the epidemic: every relaxation of higher size can restart the epidemic.

In Fig. 9b the flexibility of the relaxation is much higher. However the price paid for the possibility of bigger size release due to later introduction of the abrupt quarantine is the higher epidemic peak/size. In both cases the critical value of \({\underline{\chi }}_{crit}\) decreases with the decline of the \(\rho \) value. It is important to notice that we assume that even after relaxation the strength of the remaining quarantine is still determined by the parameter \(\rho \). This means that to ensure \(R_e < 1\) for lower values of \(\rho \) larger portion of the population has to quarantined.

As our results indicate, the decision to relax quarantine restrictions should be taken very carefully and with respect to all above mentioned factors.

First let us analyze how the level of \(I_{down}\), i.e. the timing of the reopening, can influence further epidemic development. For this analysis we consider two situations which differ in the critical level \(I_{up}\). More precisely, we assume \(I_{up}=0.002\) and \(I_{up}=0.014\). In both cases at time \(t_{switch}\) when the \(I_{sQ}\) grows up to \(I_{up}\) for the first time, we impose the abrupt quarantine of size \({\bar{\chi }} = {\bar{\chi }}_{crit}\). We compare several release strategies which differ in the setup of the the critical levels of \(I_{down}\) (see Fig. 10). The level of \({\underline{\chi }}\) was determined for each set of parameters according to the relation (16), i.e. we set \({\underline{\chi }}={\underline{\chi }}_{crit}\). Figure 10 illustrates that under such careful reopening strategy, the exact timing does not play a significant role. However, it is important to notice here that for reopening which happens too early (i.e. \(I_{down}\) close to \(I_{up}\)) only insignificant proportion of the quarantined individuals can be released, otherwise the second wave of the disease outbreak cannot be avoided. On the other hand, when abrupt quarantine is introduced later, i.e. boundary \(I_{up}\) is higher, significantly higher proportion of the quarantined individuals can be released without the fear of the second wave (see Fig. 9b).

Fig. 10
figure 10

Relaxation of the abrupt quarantine. Parameter \(\rho =0.7\) and \(\psi \)=0. Level of relaxation \({\underline{\chi }}\) is determined according to (16), i.e. we set \({\underline{\chi }}={\underline{\chi }}_{crit}\). a \(I_{up}=0.002\), \({\bar{\chi }}={\bar{\chi }}_{crit}=0.61\), b \(I_{up}=0.014\), \(\bar{\chi }={\bar{\chi }}_{crit}=0.50\)

Full size image

Further, a cautionary reopening seems to be an important factor when making decisions to relax quarantine restrictions. Figure 11 shows the possible development of epidemic under different choices of the relaxation parameter \({\underline{\chi }}\). Naturally, for the relaxation level \({\underline{\chi }} > {\underline{\chi }}_{crit}\) further epidemic waves can appear. This effect is demonstrated in Fig. 11a, b.

Fig. 11
figure 11

Different relaxation levels \({\underline{\chi }}_{crit}\). Parameter \(\rho =0.7\) and \(\psi \)=0. a \(I_{up}=0.002\), \({\bar{\chi }}_{crit} =0.61\), \(I_{down}=I_{up}/2\). b \(I_{up}=0.01\), \({\bar{\chi }}_{crit}=0.54\), \(I_{down}=I_{up}/2\)

Full size image

Moreover, the \(I_{up}\) value (and thus the \(I_{down}\) value, since here we assume \(I_{down} = I_{up}/2\)) determines the length of the epidemic period regardless of the relaxation level \({\underline{\chi }}_{crit}\). In our illustrative example a shift from \(I_{up}=0.002\) to \( I_{up}=0.01\) shortens the epidemic period by approximately one half.

On the other side, longer period of the first wave with the low peak can be considered as the advantage of the early quarantine restrictions: this period can be used as a preparation for the second wave, as happened in many countries during the spring 2020 with the Covid-19 infection. Let us note that because of the economic/social reasons it is not possible to impose the quarantine forever, the second wave cannot be avoided without changing the size of the susceptible pool. Thus as our simulations demonstrate the price paid for the low first wave can be a huge and long-lasting second wave. This situation describes the epidemic development for instance in Slovakia, where during the first wave the peak of confirmed cases reached max. 1000 and lasted around 2.5 months, while in the second wave the peak rose over 58,000 and the critical situation lasted from October to April (for more details see [14]).

So far in our relaxation experiments we have considered \(\psi =0\). As we have showed in Sect. 3.3 quarantine can be replaced by effective testing. Therefore in our next experiment we analyze the role of testing in the relaxation strategy. For simplicity in this experiment we assume that testing with efficiency rate \(\psi >0\) is introduced starting at the time of relaxation. The effect of the testing rate on the critical relaxation level \({\underline{\chi }}_{crit}\) is graphically depicted in Fig. 12.

Fig. 12
figure 12

Replacing abrupt quarantine by testing introduces at the relaxation time determined by the critical boundary \(I_{down}\). Parameters \(\rho =0.7\) and \(I_{down}=I_{up}/2\)

Full size image

As expected, the increase in the effective testing rate results in the increase of the \({\underline{\chi }}_{crit}\), i.e. with the presence of testing a higher proportion of quarantine can be released without the appearance of the second wave. However, for the case of the early imposed quarantine (i.e. low \(I_{up}\)) even the effective testing (within the range of admissible values of \(\psi \)) does not permit to release the quarantine completely. As we can see \({\underline{\chi }}_{crit}=1\) can be achieved only for the \(I_{up}=0.014\) and \(\psi >0.25\). However, increasing availability of different kinds of tests (e.g. home self-tests) can increase the proportion of positively performed tests and thus decrease the need of quarantine.

As we have already mentioned, abrupt quarantine measures are determined by three main factors: size, strength and timing. In our experiments timing of the quarantine introduction and relaxation is presented by critical boundaries \(I_{up}\) and \(I_{down}\). Our last experiment illustrates that choosing these thresholds is not enough, part of a careful quarantine management must also be the size of the quarantine (assuming here \(\rho \) fixed). We present two illustrative examples. In both we consider a fixed long-time abrupt quarantine strategy determined by the parameters \(I_{up}\), \(I_{down}\), \(\bar{\chi }\), \({\underline{\chi }}\) and \(\rho \). By long term we understand that the strategy is applied repeatably whenever the value of \(I_{sQ}\) rises above the \(I_{up}\), resp. falls below \(I_{down}\) boundary.

Fig. 13
figure 13

Cycling quarantine. Parameters: \(\rho =0.7\) and \(\psi =0\). a \({\bar{\chi }}=0.9\), \({\underline{\chi }}=1\), \(I_{down}=I_{up}/2\). b \({\underline{\chi }}\)=1, \(I_{up}=0.002\), \(I_{down}=I_{up}/2\)

Full size image

Figure  13 demonstrates that if the parameters values of the quarantine measures are not chosen carefully, further epidemic waves might occur. Figure  13a compares the \(I_{sQ}\) dynamics under different setup of \(I_{up}\) values for fixed \(\rho \). We assume here that \(I_{down}\) = \(I_{up}/2\). For the illustrative purposes we set the value of the parameter \({\bar{\chi }}\) to 0.9, i.e. we introduce a large-scale quarantine. Further we assume \({\underline{\chi }}=1\), i.e. once \(I_{sQ}\) falls below the critical boundary \(I_{down}\), the quarantine measures are completely relaxed. As our results suggest the earlier introduction of quarantine (i.e. low \(I_{up}\) threshold) results in the repeating need of abrupt quarantine. On the other hand the later introduction of quarantine (i.e. higher \(I_{up}\) values) might result in high successive epidemic peaks. Thus finding of the reasonable compromise might be an interesting but complex optimization problem. We do not attempt to solve it here.

Figure 13b compares the \(I_{sQ}\) dynamics under different setup of the parameters \({\bar{\chi }}\) with fixed boundaries \(I_{up}\) and \(I_{down}\). We can observe that the \({\bar{\chi }} < \bar{\chi }_{crit}\) values prevent us from the need of the oscillating quarantine. But the price paid for this kind of strategy is a high epidemic peak. On the other hand, our simulations illustrate that the values \({\bar{\chi }} > \bar{\chi }_{crit}\) lead to similar oscillating \(I_{sQ}\) dynamics between the same thresholds. The switching between the thresholds is more frequent as the value of \({\bar{\chi }} \) increases, which is undesirable. Therefore to choose values above \(\bar{\chi }_{crit}\) in this case seems to be inefficient. Due to economic and social consequences of quarantine the relaxation value \(\bar{\chi }_{crit}\) is thus an important parameter of the intervention strategy.

4 Conclusions

Several issues involved in modeling the spread of an epidemic in a population were discussed. We presented a modified SEIR model, which accounts for symptomatic and asymptomatic individuals. In addition we introduced two intervention strategies: indiscriminate quarantining of part of the population and isolation of positively tested individuals.

We determined the reproduction number and calculated the equilibria of the model. The reproduction number depends on several parameters. Two of them are part of the intervention strategy, the testing rate and the level of quarantine measures. We have shown that the reproduction number decreases as any of these parameters increases.

In the numerical analysis we used average values of epidemiological parameters according to the current publications on Covid-19. We introduced two types of home quarantine, namely gradual and abrupt. We have shown that under gradual one larger proportion of population needs to stay in the home quarantine in order to achieve the similar epidemic development.

The course of the current pandemic was influenced not only by the initial lack of information about the new disease, but also by the lack of previous practical experiences with managing the epidemic on a global scale. The construction of theoretical models and subsequent numerical simulations helps to compensate for the lack of empirical observations and thus clarify the impact of the intervention strategies on the development of the epidemic. The aim of our work was to summarize the most important qualitative properties among the individual factors that affect the course of the disease.

The model predicts that dynamics of infection are similar for both intervention strategies. However, massive testing allows to control and contain the infection spread using a much lower isolation rate than in the case of indiscriminate quarantining. In particular, given a constraint that limits the maximal number of simultaneous active cases, the isolation rate decreases with the increasing testing rate. Further, we demonstrate that massive testing measures can help to decrease the size of the quarantine, which enforces the above constraint, by an order of magnitude and more.

In the last part of our work, we proposed a strategy that would avert the re-emergence of the epidemic even after the release of quarantine measures. Our aim was to demonstrate that the developments we have seen in several countries were not at all surprising. As an example, we mentioned Slovakia, where after early strict restrictions during the spring of 2020, which ensured the end of the first wave, a larger and much longer second wave arrived in the autumn of 2020. Our results show that the second wave, after the almost complete release of the measures we observed during the summer of 2020 in many European countries, was inevitable without available vaccination. Unfortunately, only a few wanted to admit it, so the measures usually came late. Although the presented model does not take into account all the details (e.g. the emergence of new mutations), we believe that our analysis provides a comprehensive overview of the basic quantitative observations that can help to manage the epidemic.

The next step in this research would be to build the optimization model and determine the optimal intervention strategy. In this work we provided a preliminary analysis and presented how the timing, size and the strength of the abrupt quarantine affects the epidemic development.