On the Lyapunov Exponents for a Class of Circle Diffeomorphisms Driven by Expanding Circle Endomorphisms

Abstract

We consider skew-product maps on $\mathbb {T}^2$ of the form $F(x,y)=(bx,x+g(y))$ where $g:\mathbb {T}\rightarrow \mathbb {T}$ is an orientation-preserving $C^2$-diffeomorphism and $b\ge 2$ is an integer. We show that the fibred (upper and lower) Lyapunov exponent of almost every point (x, y) is as close to $\int _\mathbb {T}\log (g'(\eta ))d\eta$ as we like, provided that b is large enough.

1 Introduction

In this paper we investigate the dynamics of circle diffeomorphisms which are driven by the strongly expanding map $x\mapsto bx ~(\text {mod } 1)$ on $\mathbb {T}=\mathbb {R}/\mathbb {Z}$, where the integer $b\gg 1$. More precisely, we consider skew-product maps $F:\mathbb {T}^2\rightarrow \mathbb {T}^2$ of the form

$$\begin{aligned} F(x,y)=(bx,x+g(y)) \end{aligned}$$

(1.1)

where $g:\mathbb {T}\rightarrow \mathbb {T}$ is an orientation-preserving $C^2$-diffeomorphism.¹

We are interested in the question of finding conditions on b and g for which F acts (for a.e. $(x,y)\in \mathbb {T}^2$) contracting in the fibre direction. Numerical experiments (see, e.g., the introduction in [6]) indicates that this many times seems to be the case. There are also rigorous results for certain classes of g [1, 6]. In the present paper we will derive very precise bounds for the contraction for general g, under the condition that the driving map $x\mapsto bx$ is chaotic enough (b sufficiently large). The contraction is measured by the (fibred) Lyapunov exponents, which are defined as follows. Given (x, y) we use the notation $(x_n,y_n)=F^n(x,y)$. Since $y_n=b^{n-1}x+g(y_{n-1})$ we have by the chain rule that

$$\begin{aligned} \frac{\partial y_n}{\partial y}=\prod _{j=0}^{n-1}g'(y_j). \end{aligned}$$

The upper and lower (fibred) Lyapunov exponent $L^\pm (x,y)$ of the point (x, y) are now defined by

$$\begin{aligned} \begin{aligned} L^+(x,y)&=\varlimsup _{n\rightarrow \infty }\frac{1}{n}\log \frac{\partial y_n}{\partial y}= \varlimsup _{n\rightarrow \infty } \frac{1}{n}\sum _{j=0}^{n-1}\log (g'(y_j)) \quad \text { and } \\ L^-(x,y)&=\varliminf _{n\rightarrow \infty }\frac{1}{n}\log \frac{\partial y_n}{\partial y}= \varliminf _{n\rightarrow \infty } \frac{1}{n}\sum _{j=0}^{n-1}\log (g'(y_j)). \end{aligned} \end{aligned}$$

(1.2)

Before stating our main result we introduce the following notation. If $w:\mathbb {T}\rightarrow \mathbb {R}$ we let $\Vert w\Vert$ denote the supremum norm, i.e., $\Vert w\Vert =\sup _{y\in \mathbb {T}}|w(y)|$. We also let

$$\begin{aligned} h(y)=\log (g'(y)). \end{aligned}$$

Theorem 1

For any $\beta >0$ there exists a $b_0=b_0(\beta ,\Vert h\Vert ,\Vert h'\Vert )\ge 2$ such that for all integers $b\ge b_0$ we have

$$\begin{aligned} \int _{\mathbb {T}}h(\eta )d\eta -\beta \le L^-(x,y)\le L^+(x,y)\le \int _{\mathbb {T}}h(\eta )d\eta +\beta \end{aligned}$$

for a.e. $(x,y)\in \mathbb {T}^2$.

As an immediate application of this theorem we have: Assume that $u:\mathbb {T}\rightarrow \mathbb {R}$ is a $C^2$-function and let $g_\varepsilon (y)=y+\varepsilon u(y)$. Since $\log (1+t)=t-t^2/2+O(t^3)$ and $\int _{\mathbb {T}}g'(\eta )~d\eta =0$ (because $g:\mathbb {T}\rightarrow \mathbb {R}$) we see that applying Theorem 1 with $g=g_\varepsilon$ and $\beta =\varepsilon ^3$, where $\varepsilon >0$ is small, we get

$$\begin{aligned} -\frac{\varepsilon ^2}{2}\int _{\mathbb {T}}u'(\eta )^2d\eta -C\varepsilon ^3\le L^-(x,y)\le L^+(x,y)\le -\frac{\varepsilon ^2}{2}\int _{\mathbb {T}}u'(\eta )^2d\eta +C\varepsilon ^3 \end{aligned}$$

for all large b. Thus, we have $L^\pm (x,y)\approx -\varepsilon ^2$ almost surely. Note that the smaller is $\varepsilon$ the larger we have to take b for this to hold. However, we would expect that the asymptotic is true for all small $\varepsilon$ for some fixed b. A similar asymptotic is indeed true in the closely related case of the Schrödinger cocyle with small potentials [4].

A heuristic argument for the latter type of results goes as follows (here we follow [7, Section II]). Let $F_\varepsilon (x,y)=(bx,x+y+\varepsilon u(y))$. As we saw above we have

$$\begin{aligned} \frac{1}{n}\log \frac{\partial y_n}{\partial y}=\frac{1}{n}\sum _{j=0}^{n-1}\log (1+\varepsilon u'(y_j))= \frac{1}{n}\sum _{j=0}^{n-1}(\varepsilon u'(y_j)-\varepsilon ^2u'(y_j)^2/2+O(\varepsilon ^3)). \end{aligned}$$

(1.3)

For the unperturbed map $F_0(x,y)=(bx,x+y)$ it is not difficult to verify that the iterates $y_j=\pi _2(F_0^j(x,y))$ are uniformly distributed in $\mathbb {T}$ for a.e.(x, y). Thus one could expect that the iterates $y_j=\pi _2(F_\varepsilon ^j(x,y))$ also are “close to” uniformly distributed for small $\varepsilon$ and thus that the right hand side of (1.3) would converge to (or at least to something very close to)

$$\begin{aligned} \varepsilon \int _{\mathbb {T}}u'(\eta )~d\eta -(\varepsilon ^2/2)\int _{\mathbb {T}}u'(\eta )^2~d\eta +O(\varepsilon ^3)=-(\varepsilon ^2/2)\int _{\mathbb {T}}u'(\eta )^2~d\eta +O(\varepsilon ^3) \end{aligned}$$

as $n\rightarrow \infty$.

This is the route we will take to prove Theorem 1. In fact, we will show that for fixed $g:\mathbb {T}\rightarrow \mathbb {T}$ and fixed scale (fine partition of $\mathbb {T}$), the iterates $(y_j)_{j=1}^\infty$ of a.e. point (x, y) are as close to uniformly distributed (relative the fixed scale) as we want, provided that b is large enough (see Proposition 2.1 below). It is thus possible to work with g which are not necessarily close to the identity when b is large.

The approach we use is close in spirit to the ones we use in [1, 2], which both are based on ideas from [8, 9] (especially the idea that strong expansion in the base, i.e., b large, is a powerful tool to get a good control on the statistics of typical orbits). However, the big difference, compared with the present situation, is that both [1, 2] deal with a situation where (most of) the fibre maps are far from a rigid rotation. In the present paper we can handle the intermediate region between “very close to rotation” and “far from rotation”.

One could expect that, in the case when $L^+(x,y)$ is almost surely negative, one has a ”global contraction” in the fibre, in the sense that $|F^n(x,y)-F^n(x,y')|\rightarrow 0$ as $n\rightarrow \infty$ for almost every $(x,y),(x,y')\in \mathbb {T}^2$. This is the situation in [1, 6], and also in [9] (via Oseledets’ theorem). In our analysis we only control the distribution of most orbits (up to a fixed scale) so we do not a priori get such a global contraction result. But we expect that this would be the typical case.

A very interesting problem, which appears in [7] (and which to the best of our knowledge still is open), would be to prove that a similar result to the ones above also hold true for the map $G(x,y)=(x+\omega ,x+y+\varepsilon g(y))$ where $\omega \in \mathbb {R}{\setminus } \mathbb {Q}$ and $\varepsilon$ is small. Numerical experiments indicate that this indeed could be true (see [7, Section II]). In [3] we investigate this type of maps when the fibre maps are far from the identity.

The rest of the paper is organized as follows. In Sect. 2 we prove Theorem 1 by applying Proposition 2.1 which contains the main estimates. This proposition is in turn proved in Sect. 3.

We end this introduction by remarking that the same method as we use to prove Theorem 1 can be used to handle other classes of forced circle maps $(x,y)\mapsto (bx, f_x(y))$. However, for simplicity and definiteness we have restricted our attention to maps of the form (1.1) which allows a very transparent analysis.

2 Proof of Theorem 1

In this section we prove Theorem 1. The key ingredient in the proof is Proposition 2.1 stated below. This proposition will be proved in the next section.

We shall use the following notation. If $\varphi :\mathbb {T}\rightarrow \mathbb {T}$ we denote by $\deg (\varphi )$ the degree of $\varphi$ (i.e., if $\Phi :\mathbb {R}\rightarrow \mathbb {R}$ is a lift of $\varphi$ then $\deg (\varphi )=\Phi (1)-\Phi (0)$).

Given an integer $m\ge 1$, let

$$\begin{aligned} J_k=J_k(m)=\left[ \frac{k-1}{m},\frac{k}{m}\right) \quad \text { for } 1\le k\le m. \end{aligned}$$

(2.1)

Then the intervals are pairwise disjoint and $\bigcup _{k=1}^mJ_k=\mathbb {T}$. Thus, $(J_k(m))_{k=1}^m$ is a partition of $\mathbb {T}$ into m intervals of equal length.

Proposition 2.1

Let $v:\mathbb {T}\rightarrow \mathbb {T}$ be a $C^1$-map of degree 1 and let $G(x,y)=(bx,x+v(y))$. Given $m\ge 2$ and $\delta >0$ there exists a $b_0=b_0(m,\delta ,\Vert v'\Vert )\ge 2$ such that the following holds for all $b\ge b_0$. For any $y_0\in \mathbb {T}$ there is a set $X_{y_0}\subset \mathbb {T}$ of full Lebesgue measure such that if we take $x_0\in X_{y_0}$ and let $y_n=\pi _2(G^n(x_0,y_0))$ and let

$$\begin{aligned} P_n(k)=\#\{j: 0\le j\le n-1, y_j\in J_k(m)\}, \end{aligned}$$

then $|P_n(k)/n -\frac{1}{m}|<\delta$ for all $1\le k \le m$ and all sufficiently large n.

Remark 1

Note that v need not be one-to-one.

From this proposition the statement in Theorem 1 easily follows. Let $h(y)=\log (g'(y))$ and let $M=\Vert h'\Vert$. Note that $M<\infty$ since g is an orientation-preserving circle diffeomorphism. Take $m\ge 1$ so large so that if $\delta =1/m^2$ then

$$\begin{aligned} \frac{M}{m}+m\delta \int _{\mathbb {T}}|h(\eta )|~d\eta <\beta . \end{aligned}$$

(2.2)

Now we apply Proposition 2.1 with m and $\delta$ as above. Let $b_0$ be as in the proposition and assume that $b\ge b_0$. Fix $y_0\in \mathbb {T}$ and assume that $x_0\in X_{y_0}$. Thus we know that $|P_n(k)/n-1/m|<\delta$ for all $1\le k\le m$ and all large n.

For any $1\le k\le m$ and any $t\in J_k$ we have, by applying the mean value theorem,

$$\begin{aligned} \left| \int _{J_k}h(y)dy-\frac{h(t)}{m}\right| \le \int _{J_k}|h(y)-h(t)|dy\le \frac{M}{m^2}. \end{aligned}$$

Hence we get

$$\begin{aligned} \left| \frac{1}{n}\sum _{j=0}^{n-1}h(y_j)-\frac{m}{n}\sum _{k=1}^mP_n(k)\int _{J_k}h(\eta )~d\eta \right| \le \frac{m}{n}\sum _{k=1}^mP_n(k)\frac{M}{m^2}=\frac{M}{m}. \end{aligned}$$

Moreover, provided that n is large enough we have

$$\begin{aligned} \begin{aligned} \left| \frac{m}{n}\sum _{k=1}^mP_n(k)\int _{J_k}h(\eta )~d\eta -\int _{\mathbb {T}}h(\eta )~d\eta \right|&= \left| m\sum _{k=1}^m\left( \frac{P_n(k)}{n}-\frac{1}{m}\right) \int _{J_k}h(\eta )~d\eta \right| \\&\quad \le m\delta \int _{\mathbb {T}}|h(\eta )|~d\eta . \end{aligned} \end{aligned}$$

By combining these two estimates, and recalling (2.2), we thus get

$$\begin{aligned} \left| \frac{1}{n}\sum _{j=0}^{n-1}h(y_j)-\int _{\mathbb {T}}h(\eta )~d\eta \right| \le \frac{M}{m}+m\delta \int _{\mathbb {T}}|h(\eta )|~d\eta <\beta \end{aligned}$$

for all large n. Recalling the definition of $L^\pm (x,y)$ in (1.2) finishes the proof.

3 Proof of Proposition 2.1

Let v and G be as in the statement of Proposition 2.1 and assume that $m\ge 1$ and $\delta >0$ are fixed. The integer $b\ge 2$ is assumed to be sufficiently large, depending on $m,\delta$ and $\Vert v'\Vert$.

Fix any $y_0\in \mathbb {T}$ (this is the $y_0$ in the statement of the proposition) and define the functions $\varphi _n:\mathbb {T}\rightarrow \mathbb {T}$ by

$$\begin{aligned} \varphi _n(x)=\pi _2(G^n(x,y_0)),\quad n\ge 0. \end{aligned}$$

Thus, we need to control the distribution of the iterates $\{\varphi _n(x)\}$ for fixed x.

Let J be one of the intervals $J_k(m)$ ($1\le k\le m$) defined in (2.1). We define the sets

$$\begin{aligned} A_n=\varphi _n^{-1}(J), \quad n\ge 1. \end{aligned}$$

(3.1)

As we will see below we have $|A_n|\approx 1/m$ for all n provided that b is sufficiently large. The strategy is to prove that “the events” $A_n$ are very close of being independent.

3.1 Geometry of the graphs of $\varphi _n$

From the definition we have $\varphi _0(x)=y_0$ and

$$\begin{aligned} \varphi _{n+1}(x)=b^nx+v(\varphi _n(x)) \text { for } n\ge 0. \end{aligned}$$

Since $\deg (v)=1$ we have $\deg (\varphi _{n+1})=b^n+\deg (\varphi _n)$. By using the fact that $\deg (\varphi _0)=0$ we therefore get

$$\begin{aligned} \deg (\varphi _{n+1})=\sum _{j=0}^nb^j=\frac{b^{n+1}-1}{b-1}. \end{aligned}$$

We also have

$$\begin{aligned} \varphi _{n+1}'(x)=b^n+v'(\varphi _n(x))\varphi _n'(x). \end{aligned}$$

Since $\varphi _1(x)=x+v(y_0)$, and hence $\varphi _1'(x)=1$, we get, by induction,

$$\begin{aligned} \varphi _{n+1}'(x)\le b^n+b^{n-1}\Vert v'\Vert +b^{n-2}\Vert v'\Vert ^2+\cdots +\Vert v'\Vert ^n \end{aligned}$$

and

$$\begin{aligned} \varphi _{n+1}'(x)\ge b^n-b^{n-1}\Vert v'\Vert -b^{n-2}\Vert v'\Vert ^2-\cdots -\Vert v'\Vert ^n. \end{aligned}$$

Thus, for any $\tau >0$ we have

$$\begin{aligned} \left| \frac{\varphi _{n+1}'(x)}{b^n}-1\right| <\tau , \end{aligned}$$

(3.2)

provided that b is large enough, depending on $\tau$ and $\Vert v'\Vert$.

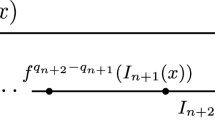
Since we, in particular, have $\varphi _n'(x)>0$ for each $x\in \mathbb {T}$ and for each $n\ge 1$ (for large b), it follows that for every $n\ge 1$ we can find $\deg (\varphi _n)$ pairwise disjoint intervals $I_n^j\subset \mathbb {T}$ such that $\bigcup _{j=1}^{\deg (\varphi _n)} I_n^j=\mathbb {T}$, $\varphi _n(I_n^j)=\mathbb {T}$, the restriction of $\varphi _n$ to $I_n^j$ is one-to-one, and $A_n\cap I_n^j$ is a single interval (recall the definition of $A_n$ in (3.1)).² Moreover, from (3.2) we get

$$\begin{aligned} \frac{1}{b^{n-1}(1+\tau )}\le |I_n^j|\le \frac{1}{b^{n-1}(1-\tau )} \text { for } j=1,2,\ldots , \deg (\varphi _n). \end{aligned}$$

(3.3)

Furthermore, since the length of the interval J is 1/m, we get, by using (3.2), the following bounds on the intervals $A_n\cap I_n^j$:

$$\begin{aligned} \frac{1}{mb^{n-1}(1+\tau )}\le |A_n\cap I_n^j|\le \frac{1}{mb^{n-1}(1-\tau )} \text { for } j=1,2,\ldots , \deg (\varphi _n). \end{aligned}$$

(3.4)

Thus, $|A_n|\approx 1/m$ for all n, and the approximations become better and better the larger is b.

3.2 Probability

We will now show that “the events” $A_n$ are very close of being independent and use this fact to prove the statement of Proposition 2.1. Below we shall use the following notation: If $r\in \mathbb {R}$ we denote the integer part of r by $\lfloor r\rfloor$.

We shall begin by stating an elementary intersection result. By using the above estimates of the intervals $I_n^j$ we get:

Lemma 3.1

Let $U\subset \mathbb {T}$ be an interval of length $\ell >0$. For each $n\ge 2$ we have that the interval J contains at least $\lfloor \ell b^{n-1}(1-\tau )\rfloor -2$ of the intervals $I_n^j$; and J intersects at most $\lfloor \ell b^{n-1}(1+\tau )\rfloor +2$ of the intervals $I_n^j$.

Proof

Since $(I_n^j)_{j=1}^{\deg (\varphi _n)}$ is a partition of $\mathbb {T}$, the result follows easily by using the estimates in (3.3). $\square$

Based on the estimates in the previous lemma we introduce the following integers:

$$\begin{aligned} N_1=\left\lfloor \frac{b(1-\tau )}{m(1+\tau )}\right\rfloor -2, \quad N_2=\left\lfloor \frac{b(1+\tau )}{m(1-\tau )}\right\rfloor +2 \end{aligned}$$

and

$$\begin{aligned} M_1=\left\lfloor b\left( \frac{1-\tau }{1+\tau }-\frac{1}{m}\right) \right\rfloor -4, \quad M_2=\left\lfloor b\left( \frac{1+\tau }{1-\tau }-\frac{1}{m}\right) \right\rfloor +4. \end{aligned}$$

Lemma 3.2

For all $n\ge 1$ the following holds for all $1\le j\le \deg (\varphi _n)$:

• (1) $A_n\cap I_n^j$ contains at least $N_1$ intervals $I_{n+1}^i$ and intersects at most $N_2$ intervals $I_{n+1}^i$.

• (2) $I_n^j{\setminus } A_n$ contains at least $M_1$ intervals $I_{n+1}^i$ and intersects at most $M_2$ intervals $I_{n+1}^i$.

Proof

(1) We know that $A_n\cap I_n^j$ is an interval which satisfies the length estimates (3.4). Applying Lemma 3.1 yields the results.

(2) The set $I_n^j{\setminus } A_n$ is either a single interval or consists of two disjoint intervals. By combining (3.3) and (3.4) we get the estimate

$$\begin{aligned} 1/(b^{n-1}(1+\tau ))-1/(mb^{n-1}(1-\tau ))\le |I_n^j{{\setminus }} A_n|\le 1/(b^{n-1}(1-\tau ))-1/(mb^{n-1}(1+\tau )). \end{aligned}$$

Assuming that $I_n^j{\setminus } A_n$ consists of two intervals (which is the worst case), and applying Lemma 3.1 to each interval, using the above estimate of the sum of the lengths, gives the statement. $\square$

Lemma 3.3

For any $n\ge 1$ the following holds. Let $C\subset \mathbb {T}$ be a set of the format $C=B_1\cap B_2\cap \cdots \cap B_n$, where $B_j=A_j$ for k ($0\le k\le n$) indices j and $B_j=\mathbb {T}{\setminus } A_j$ for $n-k$ indices j. Then C contains at least $N_1^kM_1^{n-k}$ of the intervals $I_{n+1}^i$, and C intersects at most $N_2^kM_2^{n-k}$ of the intervals $I_{n+1}^i$.

Proof

We use induction to prove the statement. When $n=1$ the statement follows directly from Lemma 3.2 since $I_1^1=\mathbb {T}$.

To prove the inductive step we do as follows. Assume that $n\ge 1$ and that $C\subset \mathbb {T}$ is a set that contains at least $N\ge 1$ of the intervals $I_{n+1}^i$, and C intersects at most $M\ge N$ of the intervals $I_{n+1}^i$. Then it follows from Lemma 3.2 that $C\cap A_{n+1}$ contains at least $NN_1$ of the intervals $I_{n+2}^j$ and intersects at most $MN_2$ of them; and $C\cap (\mathbb {T}{\setminus } A_{n+1})$ contains at least $NM_1$ of the intervals $I_{n+2}^j$ and intersects at most $MM_2$ of them. $\square$

For each $n\ge 1$ we now let

$$\begin{aligned} S_n(k)=\{x\in \mathbb {T}: x\in A_j \text { for exactly } k \text { indices } j, 1\le j\le n\}, \quad 0\le k\le n. \end{aligned}$$

Clearly the sets $S_n(k), 0\le k\le n$, are pairwise disjoint and $\bigcup _{k=0}^nS_n(k)=\mathbb {T}$. Moreover, by definition we have that if $x\in S_n(k)$, then $\#\{j:1\le j\le n \text { and } \varphi _j(x)\in J\}=k$. Thus, we need to prove that almost every $x\in \mathbb {T}$ belongs to $\bigcup _{k=(1/m-\delta )n+1}^{(1/m+\delta )n-1}S_n(k)$ for all large n.

Since there are $\left( {\begin{array}{c}n\\ k\end{array}}\right)$ possible ways to choose k different indices in $\{1,2,\ldots , n\}$, it follows from Lemma 3.3 and the estimates of $|I_{n+1}^i|$ in (3.3) that

$$\begin{aligned} \left( {\begin{array}{c}n\\ k\end{array}}\right) \frac{N_1^kM_1^{n-k}}{b^{n}(1+\tau )}\le |S_n(k)|\le \left( {\begin{array}{c}n\\ k\end{array}}\right) \frac{N_2^kM_2^{n-k}}{b^{n}(1-\tau )}. \end{aligned}$$

By letting $p=N_2/b$ and $q=1-M_2/b$ we can write the second part of the above inequalities as

$$\begin{aligned} |S_n(k)|\le \left( {\begin{array}{c}n\\ k\end{array}}\right) \frac{p^k(1-q)^{n-k}}{(1-\tau )}=\frac{1}{1-\tau }\left( {\begin{array}{c}n\\ k\end{array}}\right) (p/q)^kq^k(1-q)^{n-k}. \end{aligned}$$

(3.5)

Note that $p>q$ and that we can get p and q as close to 1/m as we like by choosing $\tau$ sufficiently small and taking b large. In particular, if we let $\delta '=\delta /2$ we have $p/q<\exp ((\delta ')^2)$ if b is sufficiently large.

Let

$$\begin{aligned} X_n=\bigcup _{k=(q-\delta ')n}^{(q+\delta ')n}S_n(k) \quad \text {and} \quad X=\bigcup _{i=1}^\infty \bigcap _{n=i}^\infty X_n. \end{aligned}$$

The set $X=X_{y_0}$ will be the set in the statement of Proposition 2.1. By the definition of X we have for each $x\in X$ that

$$\begin{aligned} 1/m-\delta<q-\delta '\le \frac{\#\{j:1\le j\le n \text { and } \varphi _j(x)\in J\}}{n}\le q+\delta '<1/m+\delta \end{aligned}$$

for all sufficiently large n. It thus remains to show that X has full measure.

Before estimating the measure of $\mathbb {T}{\setminus } X_n$ we first recall a few well-known facts about the binomial distribution. For fixed $0<t<1$, let

$$\begin{aligned} H_n(k)=\sum _{j=0}^k\left( {\begin{array}{c}n\\ j\end{array}}\right) t^j(1-t)^{n-j} \text { for all } n\ge 1. \end{aligned}$$

By Hoeffding’s inequality [5] we have the following tail bounds for $a>0$:

$$\begin{aligned} H_n((t-a)n)\le \exp (-2a^2n) \text { and } 1-H_n((t+a)n-1)\le \exp (-2a^2n). \end{aligned}$$

By combining this inequality with (3.5), and recalling that $p>q$, we get

$$\begin{aligned} \begin{aligned} \left| \bigcup _{k=0}^{(q-\delta ')n}S_n(k)\right|&\le \frac{(p/q)^{(q-\delta ')n}}{1-\tau }\sum _{k=0}^{(q-\delta ')n}\left( {\begin{array}{c}n\\ k\end{array}}\right) q^k(1-q)^{n-k}\\&\le \frac{(p/q)^{(q-\delta ')n}}{1-\tau } \exp (-2(\delta ')^2n)< 2(p/q)^{n}\exp (-2(\delta ')^2n); \end{aligned} \end{aligned}$$

and similarly

$$\begin{aligned} \left| \bigcup _{k=(q+\delta ')n}^{n}S_n(k)\right| \le \frac{(p/q)^n}{1-\tau } \exp (-2(\delta ')^2n)<2(p/q)^{n}\exp (-2(\delta ')^2n) \end{aligned}$$

Hence we have (since $p/q<\exp ((\delta ')^2)$)

$$\begin{aligned} |\mathbb {T}{\setminus } X_n|\le 4\exp (-(\delta ')^2n). \end{aligned}$$

It therefore follows from the Borel-Cantelli lemma that $|\mathbb {T}{\setminus } X|=0$, i.e. $|X|=1$. This finishes the proof of Proposition 2.1.