Skip to main content
SpringerLink
Log in

The Dynamics of a Predator–Prey Model with Diffusion and Indirect Prey-Taxis

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

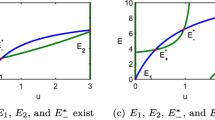
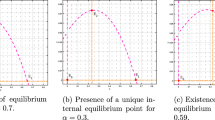
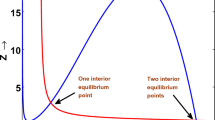
This paper concerns with a reaction–diffusion system modeling the population dynamics of the predator and prey, in which the predator moves toward the gradient of concentration of some chemical released by prey instead of moving directly toward the higher density of prey. The first objective is to investigate the global existence and boundedness of the unique classical solution. Then we study the asymptotic stabilities of nonnegative spatially homogeneous equilibria. Moreover, the convergence rates are also studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ainseba, B.E., Bendahmane, M., Noussair, A.: A reaction–diffusion system modeling predator-prey with prey-taxis. Nonlinear Anal. Real World Appl. 9, 2086–2105 (2008)

    MathSciNet  MATH  Google Scholar 

  2. Amann, H.: Dynamic theory of quasilinear parabolic equations. II. Reaction–diffusion systems. Differ. Integral Equ. 3(1), 13–75 (1990)

    MathSciNet  MATH  Google Scholar 

  3. Bellomo, N., Bellouquid, A., Tao, Y., Winkler, M.: Toward a mathematical theory of Keller–Segel models of pattern formation in biological tissues. Math. Models Methods Appl. Sci. 25, 1663–1763 (2015)

    MathSciNet  MATH  Google Scholar 

  4. Grünbaum, D.: Advection–diffusion equations for generalized tactic searching behaviours. J. Math. Biol. 38(2), 169–194 (1999)

    MathSciNet  MATH  Google Scholar 

  5. He, X., Zheng, S.: Global boundedness of solutions in a reaction–diffusion system of predator–prey model with prey-taxis. Appl. Math. Lett. 49, 73–77 (2015)

    MathSciNet  MATH  Google Scholar 

  6. Henry, D.: Geometric Theory of Semilinear Parabolic Equations. Springer, Berlin (1981)

    MATH  Google Scholar 

  7. Hoefler, C.D., Taylor, M., Jakob, E.M.: Chemosensory response to prey in Phidippus audax and Pardosa milvina. J. Arachnol. 30, 155–158 (2002)

    Google Scholar 

  8. Horstmann, D., Winkler, M.: Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 215(1), 52–107 (2005)

    MathSciNet  MATH  Google Scholar 

  9. Jin, H.Y., Wang, Z.A.: Global stability of prey-taxis systems. J. Differ. Equ. 262, 1257–1290 (2017)

    MathSciNet  MATH  Google Scholar 

  10. Kareiva, P., Odell, G.: Swarms of predators exhibit “preytaxis” if individual predators use area-restricted search. Am. Nat. 130, 233–270 (1987)

    Google Scholar 

  11. Ladyzenskaja, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasi-linear Equations of Parabolic Type. Academic Press, New York (1968)

    Google Scholar 

  12. Lee, J.M., Hillen, T., Lewis, M.A.: Continuous traveling waves for prey-taxis. Bull. Math. Biol. 70, 654–676 (2008)

    MathSciNet  MATH  Google Scholar 

  13. Lee, J.M., Hillen, T., Lewis, M.A.: Pattern formation in prey-taxis systems. J. Biol. Dyn. 3(6), 551–573 (2009)

    MathSciNet  MATH  Google Scholar 

  14. Lieberman, G.M.: Second Order Parabolic Differential Equations. World Scientific Publishing Co., Inc., River Edge (1996)

    MATH  Google Scholar 

  15. Sapoukhina, N., Tyutyunov, Y., Arditi, R.: The role of prey taxis in biological control: a spatial theoretical model. Am. Nat. 162, 61–76 (2003)

    Google Scholar 

  16. Tao, Y.S.: Global existence of classical solutions to a predator–prey model with nonlinear prey-taxis. Nonlinear Anal. Real World Appl. 11(3), 2056–2064 (2010)

    MathSciNet  MATH  Google Scholar 

  17. Tello, J.I., Wrzosek, D.: Predator–prey model with diffusion and indirect prey-taxis. Math. Models Methods Appl. Sci. 26(11), 2129–2162 (2016)

    MathSciNet  MATH  Google Scholar 

  18. Wang, J.P., Wang, M.X.: The diffusive Beddington-DeAngelis predator–prey model with nonlinear prey-taxis and free boundary. Math. Methods Appl. Sci. 41, 6741–6762 (2018)

    MathSciNet  MATH  Google Scholar 

  19. Wang, J.P., Wang, M.X.: Boundedness and global stability of the two-predator and one-prey models with nonlinear prey-taxis. Z. Angew. Math. Phys. 69(3), 63(1-24) (2018)

  20. Wang, M.X.: The diffusive logistic equation with a free boundary and sign-changing coefficient. J. Differ. Equ. 258, 1252–1266 (2015)

    MathSciNet  MATH  Google Scholar 

  21. Wang, M.X.: A diffusive logistic equation with a free boundary and sign-changing coefficient in time-periodic environment. J. Funct. Anal. 270(2), 483–508 (2016)

    MathSciNet  MATH  Google Scholar 

  22. Wang, M.X.: Note on the Lyapunov functional method. Appl. Math. Lett. 75, 102–107 (2018)

    MathSciNet  MATH  Google Scholar 

  23. Wang, M.X., Zhang, Y.: Dynamics for a diffusive prey–predator model with different free boundaries. J. Differ. Equ. 264, 3527–3558 (2018)

    MathSciNet  MATH  Google Scholar 

  24. Wang, Q., Song, Y., Shao, L.J.: Nonconstant positive steady states and pattern formation of 1D prey-taxis systems. J. Nonlinear Sci. 27, 71–97 (2017)

    MathSciNet  MATH  Google Scholar 

  25. Wang, X.L., Wang, W.D., Zhang, G.H.: Global bifurcation of solutions for a predator–prey model with prey-taxis. Math. Methods Appl. Sci. 38, 431–443 (2015)

    MathSciNet  MATH  Google Scholar 

  26. Winkler, M.: Aggregation vs. global diffusive behavior in the higher-dimensional Keller–Segel model. J. Differ. Equ. 248(12), 2889–2905 (2010)

    MathSciNet  MATH  Google Scholar 

  27. Wu, S.N., Shi, J.P., Wu, B.Y.: Global existence of solutions and uniform persistence of a diffusive predator–prey model with prey-taxis. J. Differ. Equ. 260, 5847–5874 (2016)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees for their helpful comments and suggestions.

Author information

Authors and Affiliations

  1. School of Mathematics, Harbin Institute of Technology, Harbin, 150001, People’s Republic of China

    Jianping Wang & Mingxin Wang

Authors
  1. Jianping Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mingxin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mingxin Wang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by NSFC Grant 11771110.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, J., Wang, M. The Dynamics of a Predator–Prey Model with Diffusion and Indirect Prey-Taxis. J Dyn Diff Equat 32, 1291–1310 (2020). https://doi.org/10.1007/s10884-019-09778-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-019-09778-7

Keywords

Mathematics Subject Classification

Search

Navigation