Sturm 3-Ball Global Attractors 2: Design of Thom–Smale Complexes

Abstract

This is the second of three papers on the geometric and combinatorial characterization of global Sturm attractors which consist of a single closed 3-ball. The underlying scalar PDE is parabolic,

$$\begin{aligned} u_t = u_{xx} + f(x,u,u_x)\,, \end{aligned}$$

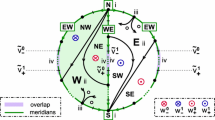
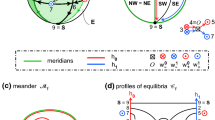
on the unit interval $0< x<1$ with Neumann boundary conditions. Equilibria are assumed to be hyperbolic. Geometrically, we study the resulting Thom–Smale dynamic complex with cells defined by the unstable manifolds of the equilibria. The Thom–Smale complex turns out to be a regular cell complex. Our geometric description is slightly more refined. It involves a bipolar orientation of the 1-skeleton, a hemisphere decomposition of the boundary 2-sphere by two polar meridians, and a meridian overlap of certain 2-cell faces in opposite hemispheres. The combinatorial description is in terms of the Sturm permutation, alias the meander properties, of the shooting curve for the equilibrium ODE boundary value problem. It involves the relative positioning of extreme 2-dimensionally unstable equilibria at the Neumann boundaries $x=0$ and $x=1$, respectively, and the overlapping reach of polar serpents in the shooting meander. In the first paper we showed the implications

$$\begin{aligned} \text {Sturm attractor}\quad \Longrightarrow \quad \text {Thom}{-}\text {Smale complex} \quad \Longrightarrow \quad \text {meander}\,. \end{aligned}$$

The present part 2 closes the cycle of equivalences by the implication

$$\begin{aligned} \text {meander} \quad \Longrightarrow \quad \text {Sturm attractor}\,. \end{aligned}$$

In particular this cycle allows us to construct a unique Sturm 3-ball attractor for any prescribed Thom–Smale complex which satisfies the geometric properties of the bipolar orientation and the hemisphere decomposition. Many explicit examples and illustrations will be discussed in part 3. The present 3-ball trilogy, however, is just another step towards a still elusive geometric and combinational characterization of all Sturm global attractors in arbitrary dimensions.

Appendix: Wolfrum’s Lemma

In this technical Appendix we comment on, and repair, a gap in the original proof of Wolfrum’s Lemma 5.2.

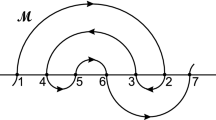
In [52, theorem 2.1] the lemma has first been formulated in the present form. The gap in the proof arises, formally, by an overinterpretation of realization results in [16] to provide templates for arbitrary sequences of saddle-node bifurcations. This is not quite what we had proved there. The relevant result is [16, lemma 3.1]. Already in the simplest case it is based, first, on a “short arc” nose retraction, via a saddle-node bifurcation. Second, the resulting nose in the meander $\mathcal {M}$ has to be retracted counterclockwise towards the lower, reduced, number of equilibria. See [16, fig. 3]. This brings the relevant Sturm shooting meanders $\mathcal {M}$ into canonical form, as specified in [16]. The counterclockwise retraction in the second step has not been addressed in [52].

In fact, the results in [16] do allow a nose removal by a saddle-node bifurcation which pushes its “short arc” of $\mathcal {M}$ nearly vertically through the horizontal axis. This addresses the first step, locally. Neither before, nor after, such a local sadlle-node bifurcation, however, would the resulting meander be in canonical form, globally.

Therefore it remains crucial to lift the clockwise restriction in the second step, towards canonical meanders. We use the global rigidity of Sturm attractors proved in [17]: global Sturm attractors $\mathcal {A}_f$ and $\mathcal {A}_g$ with identical Sturm permutations $\sigma _f = \sigma _g$ are $C^0$ orbit equivalent. In view of that global rigidity, the Sturm permutations on either side of the local saddle-node bifurcation can therefore be realized by shooting curves, again, which are canonical meanders. As a caveat we add that it is still unknown to us whether that second step can be achieved by a global parameter homotopy of Sturm nonlinearities f, within the PDE class (1.1). Instead, the rigidity proof in [17] used a discretization, and subsequent dimensional augmentation, to provide parameter homotopies in the potentially much wider ODE class of finite-dimensional Jacobi systems. At any rate, this remark remedies both gaps in the proof of [52, theorem 2.1].

The proof of Wolfrum’s lemma is independent of an earlier Conley index argument in [15] which led to a weaker result. See [52, remark 4.1]. Above we have indicated how arguments of [16, 17] enter, instead.