Skip to main content
SpringerLink
Log in

Extremal Trajectories and Maxwell Strata in Sub-Riemannian Problem on Group of Motions of Pseudo-Euclidean Plane

  • Published:
Journal of Dynamical and Control Systems Aims and scope Submit manuscript

Abstract

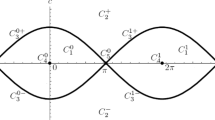
We consider the sub-Riemannian length minimization problem on the group of motions of pseudo-Euclidean plane that form the special hyperbolic group SH(2). The system comprises of left invariant vector fields with 2-dimensional linear control input and energy cost functional. We apply the Pontryagin maximum principle to obtain the extremal control input and the sub-Riemannian geodesics. A change of coordinates transforms the vertical subsystem of the normal Hamiltonian system into the mathematical pendulum. In suitable elliptic coordinates, the vertical and the horizontal subsystems are integrated such that the resulting extremal trajectories are parametrized by the Jacobi elliptic functions. Qualitative analysis reveals that the projections of normal extremal trajectories on the xy-plane have cusps and inflection points. The vertical subsystem being a generalized pendulum admits reflection symmetries that are used to obtain a characterization of the Maxwell strata.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Strichartz RS. Sub-Riemannian geometry. J Differ Geom. 1986;24(2):221–63.

    MATH  MathSciNet  Google Scholar 

  2. Montgomery R. A tour of sub-Riemannian geometries, their geodesics and applications. Number 91 in Mathematical Surveys and Monographs. American Mathematical Society; 2002.

  3. Agrachev AA, Barilari D, Boscain U. Introduction to Riemannian and sub-Riemannian geometry (from Hamiltonian viewpoint). Preprint SISSA; 2012.

  4. Gromov M. Carnot-Caratheodory spaces seen from within, volume 144 of sub-Riemannian geometry, progress in mathematics. Birkhäuser Basel; 1996.

  5. Vershik AM, Gershkovich VYa. Nonholonomic dynamical systems, geometry of distributions ad variational problems. Dynamical Systems - 7, Itogi Nauki i Tekhniki. Ser. Sovrem. Probl. Mat. Fund. Napr., 16, VINITI; 1987. p. 5–85.

  6. Brockett RW. Control theory and singular Riemannian geometry. New directions in applied mathematics; 1982. p. 11–27.

  7. Le Donne E. Lecture notes on sub-Riemannian geometry. Preprint; 2010.

  8. Monroy F, Anzaldo-Meneses A. Optimal control on the Heisenberg group. J Dyn Control Syst. 1999;5(4):473–99.

    Article  MATH  Google Scholar 

  9. Boscain U, Rossi F. Invariant Carnot-Caratheodory metrics on S 3, S O(3), S L(2) and Lens spaces. SIAM J Control Optim. 2008;47:1851–78.

    Article  MATH  MathSciNet  Google Scholar 

  10. Moiseev I, Sachkov YL. Maxwell strata in sub-Riemannian problem on the group of motions of a plane. ESAIM: COCV. 2010;16:380–99.

    Article  MATH  MathSciNet  Google Scholar 

  11. Sachkov YL. Conjugate and cut time in the sub-Riemannian problem on the group of motions of a plane. ESAIM: COCV. 2010;16:1018–39.

    Article  MATH  MathSciNet  Google Scholar 

  12. Sachkov YL. Cut locus and optimal synthesis in the sub-Riemannian problem on the group of motions of a plane. ESAIM: COCV. 2011;17:293–321.

    Article  MATH  MathSciNet  Google Scholar 

  13. Ardentov AA, Sachkov YuL. Extremal trajectories in a nilpotent sub-Riemannian problem on the Engel group. Sbornik: Math. 2011;202(11):1593–615.

    Article  MATH  MathSciNet  Google Scholar 

  14. Mazhitova AD. Sub-Riemannian geodesics on the three-dimensional solvable non-nilpotent Lie group SOLV −. J Dyn Control Syst. 2012:1–14.

  15. Sachkov YL. Discrete symmetries in the generalized Dido problem. Sbornik: Math. 2006;197(2):235–57.

    Article  MATH  MathSciNet  Google Scholar 

  16. Sachkov YL. The Maxwell set in the generalized Dido problem. Sbornik: Math. 2006;197(4):595–621.

    Article  MATH  MathSciNet  Google Scholar 

  17. Wong Yung-Chow. Euclidean n-planes in pseudo-Euclidean spaces and differential geometry of Cartan domains. Bull Am Math Soc. 1969;75(2):409–14.

    Article  MATH  Google Scholar 

  18. Vilenkin NJa. Special functions and theory of group representations (translations of mathematical monographs). American Mathematical Society, Revised edition; 1968.

  19. Thurston WP. Three-dimensional manifolds, Kleinian groups and hyperbolic geometry. Bull Am Math Soc (N.S.). 1982;6(3):357–81.

    Article  MATH  MathSciNet  Google Scholar 

  20. Agrachev A, Barilari D. Sub-Riemannian structures on 3D Lie groups. J Dyn Control Syst. 2012;18(1):21–44.

    Article  MATH  MathSciNet  Google Scholar 

  21. Agrachev AA, Sachkov YL. Control theory from the geometric viewpoint. Berlin: Springer; 2004.

    Book  MATH  Google Scholar 

  22. Sachkov YL. Control theory on Lie groups. J Math Sci. 2009;156(3):381–439.

    Article  MATH  MathSciNet  Google Scholar 

  23. Montgomery R. Isoholonomic problems and some applications. Commun Math Phys. 1990;128:565–92.

    Article  MATH  Google Scholar 

  24. Rashevsky PK. 1938. About connecting two points of complete nonholonomic space by admissible curve. Uch Zapiski Ped 83–94.

  25. Chow WL. Uber systeme von linearen partiellen dierentialgleichungen erster ordnung. Math Ann. 1940;117:98–105.

    Article  Google Scholar 

  26. Agrachev AA. Exponential mappings for contact sub-Riemannian structures. J Dyn Control Syst. 1996;2(3):321–58.

    Article  MATH  MathSciNet  Google Scholar 

  27. Whittaker ET, Watson GN. A course of modern analysis, an introduction to the general theory of infinite processes and of analytic functions; with an account of principal transcendental functions. Cambridge: Cambridge University Press; 1996.

    MATH  Google Scholar 

  28. Gradshteyn IS, Ryzhik IM. Table of integrals, series, and products. 7th ed. Amsterdam: Academic Press; 2007.

  29. Palais RS. A modern course on curves and surfaces. Virtual Math Museum; 2003.

  30. Catoni F, Boccaletti D, Cannata R, Catoni V, Nichelatti, Zampetti P. The mathematics of Mikowskian space-time with an introduction to commutative hypercomplex numbers. London: Springer; 2008.

  31. Sachkov YL. Maxwell strata in the Euler elastic problem. J Dyn Control Syst. 2008; 14(2):169–234.

    Article  MATH  MathSciNet  Google Scholar 

  32. Jacquet S. Regularity of sub-Riemannian distance and cut locus. Univ. Stud. Firenze, Florence, Italy 1999, 35; May 1999.

  33. Sachkov YL. Conjugate points in the Euler elastic problem. J Dyn Control Syst. 2008;14:409–39.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electronic Engineering, Muhammad Ali Jinnah University, Islamabad, Pakistan

    Yasir Awais Butt & Aamer Iqbal Bhatti

  2. Program Systems Institute, Pereslavl-Zalessky, Russia

    Yuri L. Sachkov

Authors
  1. Yasir Awais Butt
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuri L. Sachkov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aamer Iqbal Bhatti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yasir Awais Butt.

Additional information

Work of the second author is supported by Grant of the Russian Federation for the State Support of Researches (Agreement No 14.B25.31.0029).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Butt, Y.A., Sachkov, Y.L. & Bhatti, A.I. Extremal Trajectories and Maxwell Strata in Sub-Riemannian Problem on Group of Motions of Pseudo-Euclidean Plane. J Dyn Control Syst 20, 341–364 (2014). https://doi.org/10.1007/s10883-014-9239-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10883-014-9239-2

Keywords

Mathematics Subject Classifications (2010)

Search

Navigation