1 Introduction

In this work,Footnote 1 we concern ourselves with the problem of finding proper 3-colorings, or maximum order proper 3-colorable subgraphs, for geometric intersection graphs of line segments embedded in the plane under stringent length and directional constraints. More specically, we consider the following subclasses of these geometric intersection graphs:

Definition 1

Graph class “PURE-k-DIR” (Kratochvíl 1994; Kratochvíl and Matoušek 1994; Kratochvíl and Nešetřil 1990). A graph is in this class if and only if it admits a representation as an intersection graph of straight line segments lying in at most k directions in the plane, where all parallel line segments are disjoint.

Definition 2

Graph class “r-L-PURE-k-DIR”; generalizing graph classes discussed in (Cabello and Jejčič 2017; Chaplick et al. 2014; Otachi et al. 2007). A graph is in this class if and only if it admits a representation as an intersection graph of straight line segments lying in at most k directions in the plane, where all parallel line segments are disjoint, and where line segments can have at most r distinct lengths.

Definition 3

Graph class “UNIT-PURE-k-DIR”. A special case of the graph class r-L-PURE-k-DIR where \(r = 1\), and accordingly, all line segments must be of unit length.

Here, \(\forall \left( k,r\right) \in {\mathbb {N}}^{2}_{>0}\), it holds that r-L-PURE-k-DIR \(\subsetneq \) \(\left( r+1\right) \)-L-PURE-k-DIR \(\subsetneq \) PURE-k-DIR (Cabello and Jejčič 2017; Suk 2014). Furthermore, to see these classes as “limit” cases for increasingly constrained sets of intersection graphs, note that the graph classes “STRING” (see Ehrlich et al. 1976; Kratochvíl et al. 1986; Sinden 1966), “CONV” (see Kratochvíl 1991; Kratochvíl and Kuběna 1998; Roberts 1969; Steif 1985, “SEG” (see Ehrlich et al. 1976; Kratochvíl 1991, 1994; Kratochvíl and Matoušek 1994; Kratochvíl and Nešetřil 1990), and “k-DIR” (see Kratochvíl 1994; Kratochvíl and Matoušek 1994; Kratochvíl and Nešetřil 1990) correspond to intersection graphs of \({\mathbb {R}}^2\) embedded Jordan curves, convex objects, straight line segments, and straight line segments lying in at most k directions, respectively. We now remark that PURE-k-DIR \(\subsetneq \) SEG \(\subsetneq \) CONV \(\subsetneq \) STRING (Ehrlich et al. 1976; Kratochvíl and Matoušek 1994), that k-DIR \(\subsetneq \) \(\left( k+1\right) \)-DIR (Kratochvíl and Matoušek 1994), and that PURE-k-DIR \(\subsetneq \) PURE-\(\left( k+1\right) \)-DIR (Kratochvíl and Matoušek 1994).

Our motivation for this study is two-fold.

First, there has already been extensive work on characterizing the complexity of classically hard problems on geometric intersection graphs of “fat” objects in the plane (i.e., objects with bounded aspect ratios). While we cannot comprehensively review this literature in the current setting, to cite a well-known result, Clark et al. (1990) established that the maximum clique problem for intersection graphs of n unit disks—provided a polynomial sized intersection diagram (note that Breu and Kirkpatrick (1998) showed that the associated graph class recognition problem is NP-hard) – was solvable in \({\mathcal {O}}\left( n^{4.5}\right) \) time. In contrast, we can observe that the maximum clique problem is NP-hard in the case of geometric intersection graphs of general convex objects, even when provided polynomial sized intersection diagrams (Cabello et al. 2013; Kratochvíl and Kuběna 1998). Much more recently, letting \(l \in \Theta \left( n^{\alpha }\right) \) for some \(0 \le \alpha \le 1\), Biró et al. (2018) established that \(2^{\tilde{{\mathcal {O}}}\left( \sqrt{n \cdot l} \cdot \ln n \right) }\) time algorithms exist for proper l-coloring the intersection graphs of n “fat” objects, but at the same time, ruled out the existence of \(2^{o\left( \sqrt{n \cdot l}\right) }\) time algorithms for this problem under the Exponential Time Hypothesis (ETH) (see Section 2.5 for an elaboration on the ETH).

However, in contrast to this, much less appears to be known about the complexity of fundamental problems, notably proper k-coloring, on geometric intersection graphs of “thin” objects (i.e., objects with unbounded aspect ratios). This is particularly true when such objects (e.g., line segments) are subject to length, orientation, and “manner-of-intersection”-type constraints. Here, on one hand, we know for every \(k \ge 3\) that it is NP-hard to proper k-color SEG graphs (Ehrlich et al. 1976) (see also Eppstein (2009) for an alternative proof), to proper 3-color 2-DIR graphs with grid embeddings (see Deniz et al. (2018)), and to proper \(\left( k-1\right) \)-color PURE-k-DIR graphs for every \(k \ge 4\) (Angelini and Lozzo (2018)). Due to Biró et al. (2018), we also know that no \(2^{o\left( n\right) }\) algorithm can exist under the ETH for proper 6-coloring 2-DIR graphs. This latter result was also later strengthened by Bonnet and Rza̧\(\dot{\textrm{z}}\)ewski (2019) to establish various lower bounds under the ETH for proper k-coloring 2-DIR graphs as well as 3-DIR graphs with unit length segments. On the other hand, nothing appears to be known about the hardness of proper k-coloring PURE-k-DIR graphs under segment length constraints.

Second, we are motivated by the practical importance of finding minimum proper colorings for r-L-PURE-k-DIR geometric intersection graphs. Here, recall that in the traditional frequency assignment problem (see, e.g., Aardal et al. 2007; Eisenblätter et al. 2002; Hale 1980; de Werra and Gay 1994), one treats radio-emitters as the centerpoints of disks assigned radii based on their emission power. Next, one constructs a geometric intersection graph of these disks, where edges denote sources that are sufficiently proximal to interfere with one-another’s signals. The objective is then to assign a sparse set of at most k radio-frequency bands (colors) to each of the radio-emitters (vertices), such that the aforementioned geometric intersection graph is proper k-colored and we are guaranteed a minimum frequency separation (e.g., \(\approx 50 \ kHz\) in the model of de Werra and Gay (1994)) between any sufficiently proximal sources.

However, we argue that in realistic scenarios of the frequency assignment problem, one must take into account the existence of directional antennas (see, e.g., Balanis 2016; Dai et al. 2011). Such antennas are often used to relay a signal to one or more receivers at known locations, or to optimize energy efficiency by targeting emissions towards population centers (e.g., consider a coastal radio station). In this context, the radiation pattern for these antennas typically corresponds to a narrow cone with an intensity falling off according to the inverse square law, or in terms of the geographical area being covered, a convex geometric shape approximating a thin triangle or line segment.

For this study, in Sect. 3 we begin by first proving a number of results pertaining to finding minimum proper colorings of UNIT-PURE-4-DIR and 2-L-PURE-k-DIR graphs. In particular, we show that deciding the existence of a proper 3-coloring for graphs in the class UNIT-PURE-4-DIR, provided a polynomial sized unit segment intersection diagram witnessing graph class membership, is NP-complete (Theorem 1). Subsequently, we show that deciding the existence of a proper \(\left( k-1\right) \)-coloring for graphs in the class 2-L-PURE-k-DIR, provided a polynomial sized segment intersection diagram witnessing graph class membership, is NP-complete for each \(k \ge 4\) (Theorem 2).

More generally, we establish that the problem of proper 3-coloring a graph with m edges can be reduced in \({\mathcal {O}}\left( m^2\right) \) timeFootnote 2 to the problem of proper 3-coloring a graph in the class UNIT-PURE-4-DIR (Theorem 3). We remark that this latter result allows us to rule out the existence of a \(2^{o\left( \sqrt{n}\right) }\) time algorithm for proper 3-coloring order n UNIT-PURE-4-DIR graphs under the ETH (Corollary 1), and also allows for the efficient embedding of exceptionally hard 3-colorability instances (e.g., constructed via the method of Vlasie (1995) or Mizuno and Nishihara (2008)) in the class UNIT-PURE-4-DIR.

Next, in Sect. 4, we prove that counting proper 3-colorings of UNIT-PURE-4-DIR graphs is \(\#P\)-complete under many-one counting reductions (Theorem 4), and furthermore, that no \(2^{o\left( \sqrt{n}\right) }\) time algorithm can exist for counting proper 3-colorings of UNIT-PURE-4-DIR graphs under the Counting Exponential Time Hypothesis (#ETH) of Dell et al. (2014) (Corollary 2). In this context, we were also able to extend Theorem 4 to establish that counting proper \((k-1)\)-colorings of 2-L-PURE-k-DIR graphs is likewise \(\#P\)-complete under many-one counting reductions for every \(k \ge 4\) (Corollary 3).

Finally, in Sect. 5, we show that the problem of finding a maximum order proper 3-colorable induced subgraph of a UNIT-PURE-4-DIR graph, provided a polynomial size unit segment intersection diagram witnessing graph class membership, is NP-hard (Theorem 5).

2 Preliminaries

2.1 Graph theoretic notions and terminology

All graphs in this work should be considered to be simple (i.e., loop and multi-edge free), undirected, and unweighted. Concerning basic graph theoretic terminology, we will follow Bondy and Murty (1976), or where appropriate, Diestel (2017). Here, recall that a proper k-coloring of a graph is an assignment of at most k distinct colors (i.e., labels) to its vertices, such that no two adjacent vertices are assigned the same color. Accordingly, the proper k-coloring decision problem (respectively, function problem) is that of deciding the existence of (respectively, finding) a proper k-coloring of a given input graph. In this context, we can also define the maximum proper k-colorable induced subgraph problem as the problem of finding a maximum order induced subgraph of a graph which admits a proper k-coloring.

2.2 Orthogonal \({\mathbb {Z}}^2\) grid embeddings

In an orthogonal \({\mathbb {Z}}^2\) grid embedding \({\mathcal {Q}}\) of a graph G (which must have maximum degree \(\le 4\)), each vertex of G is placed at a unique coordinate \(\left( x_i,y_i\right) \) in a \({\mathbb {Z}}^2\) integer lattice, and each pair of adjacent vertices in G are connected in \({\mathcal {Q}}\) by a contiguous polyline of axis-parallel segments. In this context, adjacent polyline segments at \(\frac{\pi }{2}\) radian angles with one another are referred to as bends, no polylines are permitted to cross unless it is explicitly specified that this is allowed, and each grid point coordinate \(\left( x_i,y_i\right) \) is associated with a cell corresponding to a square area given by the coordinates \(\{\left( x_i - \frac{1}{2}, y_i - \frac{1}{2} \right) , \left( x_i + \frac{1}{2}, y_i - \frac{1}{2} \right) , \left( x_i + \frac{1}{2}, y_i + \frac{1}{2} \right) , \left( x_i - \frac{1}{2}, y_i + \frac{1}{2} \right) \}\). As an additional clarification, when we refer to an enlargement of an orthogonal \({\mathbb {Z}}^2\) grid embedding by some factor k, we mean that any line segment endpoint, at some coordinate \(\left( x_i,y_i\right) \) in the original embedding, is moved to the coordinate \(\left( k \cdot x_i, k \cdot y_i\right) \) in the factor of k enlarged embedding.

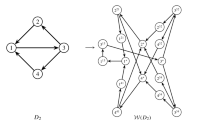
Here, to provide the reader visual intuition, in Fig. 1a we show the complete graph \(K_4\), and in Fig. 1b, we show an orthogonal \({\mathbb {Z}}^2\) grid embedding of this graph. For an example in which we permit polyline crossings, in Fig. 1c we show the complete graph \(K_5\), and in Fig. 1d, show an orthogonal \({\mathbb {Z}}^2\) grid embedding of this graph where a lone polyline crossing is indicated with a (gray diamond) polygon.

2.3 Segment intersection diagrams

An important notion in this work is the segment intersection diagram, which we define as follows:

Definition 4

Segment intersection diagram. An explicit embedding of line segments in \({\mathbb {R}}^2\) corresponding to a given geometric intersection graph, where the lengths and angles of all segments, as well as the number and manners of all segment-segment intersections, can be explicitly determined.

As a clarification, we will say that a given segment intersection diagram is a polynomial sized segment intersection diagram if it can be encoded using a number of bits polynomial in the size of its corresponding geometric intersection graph. In addition, we may refer to a segment intersection diagram as a unit segment intersection diagram in the special case where all embedded segments are of unit length.

2.4 Counting complexity

Recall that \(\#P\) Valiant (1979a, 1979b) is the class of integer counting problems asking for the number of witnesses for a given NP decision problem. To establish completeness for a problem in the class \(\#P\), it suffices to give either a Turing reduction or many-one counting reduction from a \(\#P\)-complete problem (e.g., \(\#3\)-SAT) to the problem of interest. Here, to reduce a problem \(\#f\) to a problem \(\#h\) via a many-one counting reduction, we require two polynomial time functions \({R}_{1}: {\Sigma }^{*} \rightarrow {\Sigma }^{*}\) and \({R}_{2}: {\mathbb {N}} \rightarrow {\mathbb {N}}\) satisfying the property that \(f(x)={R}_{2}(h({R}_{1} (x)))\). In this context, a parsimonious reduction is a special type of many-one counting reduction wherein \({R}_{2}\) is the identity function.

2.5 The exponential time hypothesis (ETH) & counting exponential time hypothesis (#ETH)

At a high level of abstraction, the Exponential Time Hypothesis (ETH) of Impagliazzo and Paturi (2001) is the unproven conjecture that k-SAT cannot be solved in subexponential time. A formal statement of the hypothesis is as follows:

Definition 5

Exponential Time Hypothesis (ETH) (Impagliazzo and Paturi 2001). Letting \(k \in {\mathbb {N}}_{>2}\), letting n and m be the number of variables and number of clauses in an instance of k-SAT, respectively, and letting \(s_k = inf\{\delta \, \ k\)-SAT can be solved in \(2^{\left( \delta \cdot n\right) } \cdot poly\left( m\right) \) time\(\}\), it holds that \(s_k > 0\).

In this context, the Strong Exponential Time Hypothesis (SETH) adds the assumption that \(s_{\infty } = 1\).

With regard to the Counting Exponential Time Hypothesis (#ETH) of Dell et al. (2014), letting \(\#k\)-SAT be the problem of counting the number of solutions for an instance of k-SAT, a formal statement of this hypothesis is as follows:

Definition 6

Counting Exponential Time Hypothesis (#ETH) (Dell et al. 2014). For a \(\#k\)-SAT instance with n variables and m clauses, where \(k \ge 3\), and letting \(s_k = inf\{\delta \, \ \#k\)-SAT can be solved in \(2^{\left( \delta \cdot n\right) } \cdot poly\left( m\right) \) time\(\}\), we have that \(s_k > 0\).

Here, the #ETH can be understood as a moderation of the ETH in the sense that it is only proposing it should take exponential time to count the number of witnesses for an instance of k-SAT for each \(k \ge 3\).

3 Finding proper colorings of r-L-PURE-k-DIR graphs

Fig. 1
figure 1

Example orthogonal \({\mathbb {Z}}^2\) grid embeddings of graphs, where larger (black) vertices and (highlighted black) edges indicate the vertices and polylines for the embeddings, respectively; a planar embedding of the complete graph \(K_4\); b orthogonal \({\mathbb {Z}}^2\) grid embedding of the complete graph \(K_4\); c non-planar embedding of the complete graph \(K_5\); d non-planar orthogonal \({\mathbb {Z}}^2\) grid embedding of the complete graph \(K_5\) with one crossing indicated by the (gray diamond) polygon

Full size image

Theorem 1

Deciding the existence of a proper 3-coloring for graphs in the class UNIT-PURE-4-DIR, provided a polynomial size unit segment intersection diagram witnessing graph class membership, is NP-complete.

Proof

Observe that the stated decision problem is in NP, as we are guaranteed that the input graph is in the class UNIT-PURE-4-DIR, and can verify a witness for proper 3-colorability in time linear in cardinality of the input graph’s edge set. To establish NP-hardness, we will proceed via reduction from the NP-complete problem of deciding the existence of a proper 3-coloring for a planar 4-regular graph (Dailey 1980). To begin, let G be an arbitrary planar 4-regular graph, and let \({\mathcal {Q}}\) be an orthogonal \({\mathbb {Z}}^2\) grid embedding of G enlarged by a factor of 2 (see Section 2.2 for an elaboration). Note that we can compute \({\mathcal {Q}}\) in polynomial time via network flow techniques (Biedl and Kant 1998; Cornelsen and Karrenbauer 2012; Papakostas and Tollis 1998; Tamassia 1987).

We will now use the embedding \({\mathcal {Q}}\) as a guide to generate a unit segment intersection diagram \({\mathcal {W}}\), which in turn will correspond to a UNIT-PURE-4-DIR graph that admits a proper 3-coloring if and only if G admits a proper 3-coloring. To do so, we will construct a unit segment intersection diagram, in each case corresponding to a UNIT-PURE-4-DIR graph, for every possible unit cell centered on a vertex in the embedding \({\mathcal {Q}}\). For visual intuition, we refer the reader to Fig. 2a–c, where we show examples of these unit cells drawn as (black dashed) boxes corresponding to vertices of degree 4, 3, and 2 in the embedding, respectively. Note that only the degree 4 and 2 cases will occur in this context, though we will cover the degree 3 case for completeness as it will arise in the later Theorem 3 proof argument.

To first treat cells in \({\mathcal {Q}}\) corresponding to vertices in G, we adopt the unit segment intersection diagram scheme shown in Fig. 2d through Fig. 2f, where all segments have one of at most four angle types, where the corresponding UNIT-PURE-4-DIR graphs are shown in Fig. 2g through Fig. 2i, respectively, and where these instances cover all possible cell types in \({\mathcal {Q}}\) up to rotation and reflection (due to our focus on proper 3-colorings we need not consider degree 1 vertices). Here, a simple caseology shows that, for any proper 3-coloring of the graphs in Fig. 2g through Fig. 2i, the vertices corresponding to segments \(\{w,x,y,z\}\) in Fig. 2d through Fig. 2f must be identically colored. In this context, we will refer to the color of unit segment intersection diagram placed on a cell as the color of the vertices corresponding to segments \(\{w,x,y,z\}\).

Fig. 2
figure 2

Scheme for substituting a vertex in an enlarged orthogonal \({\mathbb {Z}}^2\) grid embedding of a graph with a unit segment intersection diagram corresponding to a UNIT-PURE-4-DIR graph, where the (black dashed) box—with dimensions \(\left( \frac{3}{2} \times \frac{3}{2}\right) \)—indicates the placement of each diagram on a vertex in the embedding; (a,b,c) drawings of degree 4, degree 3, and degree 2 vertices in the embedding; (d,e,f) unit segment intersection diagrams for (a) through (c), where each segment is assigned a color according to a proper 3-coloration of its corresponding UNIT-PURE-4-DIR graph; (g,h,i) UNIT-PURE-4-DIR graphs corresponding to the unit segment intersection diagrams in (d) through (f), where each vertex is embedded at the midpoint of its respective segment

Full size image
Fig. 3
figure 3

Illustrative example of how the unit segment intersection diagrams from Fig. 2d–f can be placed on a contiguous region in an enlarged orthogonal \({\mathbb {Z}}^2\) grid embedding to copy color information—corresponding to vertex colors in any proper 3-coloring of the embedded graph—along polylines; (a) from left to right, drawings of degree 2, 3, and 2 vertices in the embedding, with the degree 2 vertices corresponding to points along polylines; (b) unit segment intersection diagram for (a), where each segment can be assigned a color according to a proper 3-coloration of its corresponding UNIT-PURE-4-DIR graph; (c) UNIT-PURE-4-DIR graph corresponding to the unit segment intersection diagram in (b), where each vertex is embedded at a coordinate corresponding to the midpoint of its respective segment

Full size image

To next treat cells corresponding to polylines, we need the ability to in certain cases copy the color of one unit segment intersection diagram placed on a cell to its neighbors, and in other cases, to require unit segment intersection diagrams placed on adjacent cells to have distinct colors. Concerning first color copying, we adopt the scheme shown in Fig. 3. Specifically, in Fig. 3a we show three adjacent cells in an example of \({\mathcal {Q}}\), where the left-most, central, and right-most vertices in the embedding have degrees 2, 3, and 2, respectively. In Fig. 3b we show how we can place unit segment intersection diagrams on these cells, in the process of constructing \({\mathcal {W}}\), in such a manner that the central and right-most diagrams are forced to have the same color. This is most evident by looking at the UNIT-PURE-4-DIR graphs corresponding to these diagrams in Fig. 3c. Concerning enforcement of distinct colorations for adjacent cells, we adopt the scheme shown in Fig. 4. Specifically, we can see in Fig. 4a, and its associated UNIT-PURE-4-DIR graph in Fig. 4b, how the unit segment intersection diagram placed in the central cell forces the cells to the left and right to have distinct colorations in any proper 3-coloring. We can also see in Fig. 4c, and its associated UNIT-PURE-4-DIR graph in Fig. 4d, how this scheme can be adopted to work for \(\frac{\pi }{2}\) radian bends in polylines.

Fig. 4
figure 4

Illustrative example of how the unit segment intersection diagrams from Fig. 2d–f can be placed on a contiguous region in an enlarged orthogonal \({\mathbb {Z}}^2\) grid embedding of a graph, while forcing vertices connected by polylines to have distinct colors in any proper 3-coloring; (a) unit segment intersection diagram encoding a degree 3 vertex, indicated by the left-hand-side (black dashed) box, and a degree 2 vertex, indicated by the right-hand-side (black dashed) box, where the diagram in the central (black dashed) box enforces the requirement that the diagrams to the left and right have distinct colorations for their outgoing polylines; (b) UNIT-PURE-4-DIR graph corresponding to the unit segment intersection diagram in (a), where each vertex is embedded at a coordinate corresponding to the midpoint of its respective segment; (c,d) variation on (a,b) for cases where polylines meet at an angle of \(\frac{\pi }{2}\) radians

Full size image

Putting everything together, using the scheme given in Fig. 2 to construct and place unit segment intersection diagrams on vertices in \({\mathcal {Q}}\), using the scheme in Fig. 3 to construct and place unit segment diagrams in all but one cell of each polyline, and using the scheme in Fig. 4 to construct and place unit segment diagrams in exactly one position on each polyline—which will always exist due to our enlarging the original grid embedding of G by a factor of 2—we will obtain unit segment intersection diagram \({\mathcal {W}}\) corresponding to a UNIT-PURE-4-DIR graph that admits a proper 3-coloring if and only if the original graph G admits a proper 3-coloring. As all of the steps used to construct this UNIT-PURE-4-DIR graph graph can be accomplished in polynomial time, this yields the current theorem. \(\square \)

Theorem 2

Deciding the existence of a proper \(\left( k-1\right) \)-coloring for graphs in the class 2-L-PURE-k-DIR, provided a polynomial size unit segment intersection diagram witnessing graph class membership, is NP-complete \(\forall k \ge 4\).

Proof

Let \({\mathcal {W}}\) be a unit segment intersection diagram with n lines, constructed from an orthogonal \({\mathbb {Z}}^2\) grid embedding as in the Theorem 1 proof argument, though in this context having segments embedded at angles of \(\{\frac{\pi }{8},\frac{3\pi }{8},\frac{5\pi }{8},\frac{7\pi }{8}\}\) with respect to the x-axis. Here, the case where \(k = 4\) is given by Theorem 1. To treat the cases where \(k \ge 5\), we proceed via the following steps:

  • (Step 1) We compute a convex hull \({\mathcal {C}}\) for the 2n endpoints of the n lines of \({\mathcal {W}}\) in \({\mathcal {O}}\left( n \cdot \ln n\right) \) time, via methods such as Graham’s scan (Graham 1972) or the algorithm of Kirkpatrick and Seidel (1986).

  • (Step 2) We use Shamos and Toussaint’s rotating calipers method (Shamos 1978; Toussaint 1983) to calculate a minimum axis-oriented bounding square \({\mathcal {B}}\) for \({\mathcal {C}}\) in \({\mathcal {O}}\left( n\right) \) time, then scale \({\mathcal {B}}\) and the enclosed line segments to ensure that it has unit side lengths. For an illustration, see the left-hand-side of Fig. 5 where we show an example of \({\mathcal {C}}\) as a polygon enclosed in a (black dashed) axis-aligned bounding square \({\mathcal {B}}\) specified by the vertices \(\{b1,b2,b3,b4\}\).

  • (Step 3) Letting (0, 0) be the coordinate for the bottom right-hand-side of \({\mathcal {B}}\), we construct three line segments of length \(tan^{-1}\left( \frac{\pi }{8}\right) + z + 1\) for some \(z \ge 1\) given by the vertex pairs \(\{\{l1.1,l1.2\},\{l2.1,l2.2\},\{l3.1,l3.2\}\}\), having angles of \(\{\frac{\pi }{8},\frac{3\pi }{8},\frac{5\pi }{8}\}\) with respect to the x-axis (as shown in Fig. 5), and with each having a midpoint at the coordinate \(\left( \frac{tan^{-1}\left( \frac{\pi }{8}\right) }{2} + z,\frac{1}{2}\right) \).

  • (Step 4) We draw at most n line segments of length \(tan^{-1}\left( \frac{\pi }{8}\right) + z + 1\), with z chosen to have the same value as in (Step 3), such that every line segment enclosed in \({\mathcal {B}}\) is intersected (though not at an endpoint) at least once, such that each added line segment passes through each of the line segments added in (Step 3), such that each of these line segments has an angle of 0 with respect to the x-axis, and such that each segment has endpoints on the vertical lines \(x = -1\) (i.e., corresponding to the left-hand-side of \({\mathcal {B}}\)) and \(x = tan^{-1}\left( \frac{\pi }{8}\right) + z\). In the Fig. 5 illustration of this construction, these thin horizontal line segments are depicted as longer than the segments added in (Step 3) for purely artistic reasons (i.e., this is not actually the case).

  • (Step 5) If \(k = 5\), we stop. Else, we iterate (Step 4) \(k-5\) additional times, each time choosing the same initial endpoints for the newly added line segments, then infinitesimally perturbing their angle by some distinct value for each iteration.

Fig. 5
figure 5

Illustration of the scheme used in the Theorem 2 proof argument to reduce the problem of deciding, for each \(k \ge 5\), the existence of a proper 3-coloring for a UNIT-PURE-4-DIR graph to the problem of deciding the existence of a proper \(\left( k-1\right) \)-coloring for a graph in the class 2-L-PURE-k-DIR

Full size image

Now let \({\mathcal {W}}'\) be the crossing diagram generated from \({\mathcal {W}}\) via (Step 1) through (Step 4), and let \(G'\) be its associated geometric intersection graph. Observe that \(G' \in \) 2-L-PURE-5-DIR due to the line segments of length \(tan^{-1}\left( \frac{\pi }{8}\right) + z + 1\) (for some \(z \ge 1\)) added in (Step 3) and (Step 4). Here, observe that \(G'\) will correspond to a modification of G, where letting \(V_G\) and \(V_{G'}\) be the vertex sets of G and \(G'\), respectively, all vertices \(v_i \in V_G\) are connected to at least one vertex \(h_i \in V_{G'} {\setminus } V_G\) (corresponding to one or more line segments added in (Step 4)), which is in turn connected to every vertex in the clique \(K_3\) (corresponding to the line segments added in (Step 3)). Accordingly, in any proper 4-coloring of \(G'\), each vertex \(h_i \in V_{G'} \setminus V_G\) must be assigned the same color, implying that G has a proper 3-coloring if and only if \(G'\) has a proper 4-coloring.

We can also observe that after \(k-5\) iterations of (Step 5), all vertices \(v_i \in V_G\) will be connected to every vertex in at least one clique of \(k-4\) vertices (all such cliques being themselves disjoint), each vertex of which will in turn be connected to every vertex in the clique \(K_3\). In this latter context, for any proper \(\left( k-1\right) \)-coloring of \(G'\), only the colors used for the \(K_3\) clique vertices will be available to color the original vertices of G, implying that G has a proper 3-coloring if and only if \(G'\) has a proper \(\left( k-1\right) \)-coloring. This yields the theorem. \(\square \)

Theorem 3

The problem of proper 3-coloring an arbitrary graph on m edges can be reduced in \({\mathcal {O}}\left( m^2\right) \) time to the problem of proper 3-coloring a UNIT-PURE-4-DIR graph.

Proof

Let G be an arbitrary graph with vertex set \(V_G\), edge set \(E_G\), and a set \(\Upsilon \subseteq V_G\) of vertices having degree \(\ge 5\). Replace every vertex \(v_i \in \Upsilon \) of degree \(d_f \ge 5\) with a cycle of length f, such that exactly one vertex in the cycle is adjacent to each distinct neighbor of \(v_i\), and assign a unique label to the vertices in each generated cycle. Let H be the graph resulting from this operation, let \(V_H\) be its vertex set, observe that the maximum degree of H will be \(\le 4\), and observe that \(|V_H| \in {\mathcal {O}}\left( |E_G|\right) \). As an example, if G is the wheel graph \(W_5\) with 6 vertices and 10 edges, H will be the 3-regular prism graph \(Y_5\) with 10 vertices and 15 edges.

Fig. 6
figure 6

Illustrations for the scheme used in the proof arguments for Theorem 3 and Theorem 4 to substitute a polyline crossing in a orthogonal \({\mathbb {Z}}^2\) grid embedding of a graph with a unit segment intersection diagram corresponding to a UNIT-PURE-4-DIR graph, where the (black dashed) box—with dimensions \(\left( \frac{9}{2} \times \frac{9}{2}\right) \)—indicates the placement of the diagram on a \(3 \times 3\) cell area centered on a polyline crossing (after deleting all existing segments in the area); (a) drawing of polyline crossing in a orthogonal \({\mathbb {Z}}^2\) grid embedding indicated with a (gray diamond) polygon; (b) unit segment intersection diagram substituted in place of the polyline crossing in (a), corresponding to a proper 3-coloring of its associated UNIT-PURE-4-DIR graph (forcing the segment pairs x and \(x'\) as well as y and \(y'\) to have the same coloration); (c) UNIT-PURE-4-DIR graph corresponding to the unit segment intersection diagram in (b), where each vertex is embedded at the midpoint of its respective segment; (d) instance of the UNIT-PURE-4-DIR graph shown in (c) where we illustrate the topology of the additional vertex (white colored vertex connected to adjacent vertices via dashed edges) added in the specific context of the Theorem 4 proof argument to ensure the same number of proper 3-colorations regardless of whether x and y have the same coloration

Full size image

Once H is constructed, we use the method of Papakostas and Tollis (1998) (see also the method of Biedl and Kant (1998)) to compute a factor of 2 enlarged orthogonal \({\mathbb {Z}}^2\) grid embedding \({\mathcal {Q}}\) of H, where we allow for polyline crossings, in \({\mathcal {O}}\left( |V_H|\right) \implies {\mathcal {O}}\left( |E_G|\right) \) time, and then create a new embedding \({\mathcal {Q}}'\) by further enlarging \({\mathcal {Q}}\) by a factor of 3. We subsequently follow the Theorem 1 proof argument to construct a unit segment intersection graph \({\mathcal {W}}\) corresponding to a UNIT-PURE-4-DIR graph from \({\mathcal {Q}}'\), with two exceptions: (1) we follow the scheme shown in Fig. 3 to ensure that the vertices in each uniquely labeled cycle in H are colored monochromatically; and (2) we replace polyline crossings (e.g., as illustrated in Fig. 1d or Fig. 6a) with the unit segment intersection diagram shown in Fig. 6b, where the aforementioned enlargement of \({\mathcal {Q}}\) by a factor of 3 ensures that this can be done without overlapping other diagrams.

Here, we can verify that the Fig. 6c UNIT-PURE-4-DIR graph corresponding to the Fig. 6b unit segment intersection diagram—which represents a minor modification of the standard “crossing gadget” used to establish the NP-completeness of the planar 3-coloring problem (see “pg. 88” of Garey and Johnson (1979)) will ensure that the vertices marked x and \(x'\) will have the same coloration and that the vertices marked y and \(y'\) will have the same coloration. Recasting the problem of enumerating proper 3-colorings as that of enumerating exact vertex covers, we can also use Knuth’s dancing links variant of his depth-first backtracking Algorithm X (Knuth 2000), e.g., as implemented in SageMath (W. A. Stein et al. (The SAGE Development Team) 2020), to confirm this fact by enumerating all 3072 proper 3-colorings of the Fig. 6c graph.

Putting everything together, as the vertices in each uniquely labeled cycle in H will be monochromatically colored, as the UNIT-PURE-4-DIR graph corresponding to the Fig. 6b unit segment intersection diagram can be used to address crossing polylines in \({\mathcal {Q}}'\), and as the method of Papakostas and Tollis (1998) to generate \({\mathcal {Q}}\) (and thus, \({\mathcal {Q}}'\)) is a linear time \({\mathcal {O}}\left( |E_G|\right) \) algorithm, we have a general method of reducing the problem of proper 3-coloring an arbitrary graph G to proper 3-coloring a UNIT-PURE-4-DIR graph with at most \({\mathcal {O}}\left( |E_G|^2\right) \) vertices. As this algorithm will take at most \({\mathcal {O}}\left( |E_G|^2\right) \) time, where the bound arises from the number of vertices in the constructed UNIT-PURE-4-DIR graph, this yields the theorem at hand. \(\square \)

Corollary 1

Unless the ETH is false, no \(2^{o\left( \sqrt{n}\right) }\) time algorithm can exist for proper 3-coloring an order n instance of a UNIT-PURE-4-DIR graph.

Proof

By a result of Cygan et al. (2016), under the ETH, we have that no \(2^{o\left( n\right) }\) time algorithm can exist for finding a proper 3-coloring of an arbitrary graph on n vertices having degree at most 4. Accordingly, as an order n graph of degree at most 4 can have at most 2n edges, and as Theorem 3 guarantees that an arbitrary graph on m edges can be reduced in \({\mathcal {O}}\left( m^2\right) \) time to the problem of proper 3-coloring a UNIT-PURE-4-DIR graph, unless the ETH is false, we have that no \(2^{o\left( \sqrt{n}\right) }\) time algorithm can exist for finding a proper 3-coloring of an order n UNIT-PURE-4-DIR graph. \(\square \)

4 Counting proper colorings of r-L-PURE-k-DIR graphs

Lemma 1

Not-All-Equal-3-SAT (\(\#\)NAE-3-SAT) is \(\#P\)-complete under linear time many-one counting reductions.

Proof

Letting \(l_i\), for \(1 \le i \le k\), be a positive or negative literal (i.e., where \(l_i\) encodes the value of a corresponding variable, \(var_i\), or its negation, \(\lnot \ var_i\)) we write \(f_{NAE} \left( l_1,\ldots ,l_k\right) \) to denote a clause for an instance of NAE-k-SAT. Now, letting \(l_{(i,j)}\) be an arbitrary positive or negative literal for any \(1 \le i \le n\) and \(1 \le j \le 4\), and letting x be an auxiliary positive literal, observe that an arbitrary 3-SAT formula of the form \(\phi = \left( l_{\left( 1,1\right) } \vee l_{\left( 1,2\right) } \vee l_{\left( 1,3\right) }\right) \wedge \ldots \wedge \left( l_{\left( n,1\right) } \vee l_{\left( n,2\right) } \vee l_{\left( n,3\right) } \right) \) can be reduced to an NAE-4-SAT formula of the form \(\phi ' = f_{NAE} \left( l_{\left( 1,1\right) }, l_{\left( 1,2\right) }, l_{\left( 1,3\right) }, x\right) \wedge \ldots \wedge f_{NAE} \left( l_{\left( n,1\right) }, l_{\left( n,2\right) }, l_{\left( n,3\right) }, x \right) \), where \(\phi '\) will have exactly twice the number of witnesses as \(\phi \). Finally, letting \(y_{\left( i,1\right) }\) and \(y_{\left( i,2\right) }\) be a pair of auxiliary positive literals for each \(1 \le i \le n\), observe that we can parsimoniously reduce any NAE-4-SAT formula to an NAE-3-SAT formula by simply replacing each clause of the form \(f_{NAE} \left( l_{\left( i,1\right) }, l_{\left( i,2\right) }, l_{\left( i,3\right) }, l_{\left( i,4\right) } \right) \) with the equivalent five clause expression \(f_{NAE} \left( l_{\left( i,1\right) },l_{\left( i,2\right) },y_{\left( i,1\right) }\right) \wedge f_{NAE} \left( l_{\left( i,1\right) },\lnot l_{\left( i,3\right) },y_{\left( i,1\right) } \right) \wedge f_{NAE} \left( \lnot l_{\left( i,1\right) },l_{\left( i,4\right) },\lnot y_{\left( i,1\right) } \right) \wedge f_{NAE} \left( l_{\left( i,3\right) },l_{\left( i,4\right) },y_{\left( i,2\right) } \right) \wedge f_{NAE} \left( y_{\left( i,1\right) },y_{\left( i,1\right) },y_{\left( i,2\right) } \right) \). Putting everything together, this gives a linear time many-one counting reduction from \(\#3\)-SAT to \(\#\)NAE-3-SAT, yielding the current lemma. \(\square \)

Theorem 4

Counting proper 3-colorings for graphs in the class UNIT-PURE-4-DIR, provided a polynomial size unit segment intersection diagram witnessing graph class membership, is \(\#P\)-complete under many-one counting reductions.

Proof

We will proceed by first carrying out a known linear time many-one counting reduction from an arbitrary instance of \(\#\)NAE-3-SAT with m clauses to the problem of counting proper 3-colorings of an arbitrary simple undirected graph G on \({\mathcal {O}}\left( m\right) \) edges. We will subsequently show that, with a suitable modification of original UNIT-PURE-4-DIR “crossing gadget” from Fig. 6, the approach given in the Theorem 3 proof argument for reducing the problem of proper 3-coloring G to the problem of proper 3-coloring a UNIT-PURE-4-DIR graph H will necessarily be an \({\mathcal {O}}\left( m^2\right) \) time many-one counting reduction.

For the initial reduction from \(\#\)NAE-3-SAT to the problem of counting proper 3-colorings of a simple undirected graph G, we adopt the approach of Dewdney (1982), which an analysis of Creignou and Hermann (1993) later established was a linear time many-one counting reduction. To begin, let \(l_i\), for \(1 \le i \le 3\), be a positive or negative literal (i.e., where \(l_i\) encodes the value of a corresponding variable, \(var_i\), or its negation, \(\lnot \ var_i\)), and let \(\phi _{NAE}\) be an arbitrary NAE-3-SAT formula of the form \(f_{NAE} \left( l_{\left( 1,1\right) }, l_{\left( 1,2\right) }, l_{\left( 1,3\right) }\right) \wedge \ldots \wedge f_{NAE} \left( l_{\left( n,1\right) }, l_{\left( n,2\right) }, l_{\left( n,3\right) }\right) \). Construct a graph G from \(\phi _{NAE}\), with m edges, by:

  • creating a cycle defined by the edge set \(\{var_{i} \leftrightarrow \lnot \ var_{i}, var_{i} \leftrightarrow v_q, \lnot \ var_{i} \leftrightarrow v_q\}\) for each variable of \(\phi _{NAE}\), with \(v_q\) as a common vertex;

  • for each clause \(f_{NAE} \left( l_{\left( i,1\right) }, l_{\left( i,2\right) }, l_{\left( i,3\right) }\right) \) of \(\phi _{NAE}\), where \(1 \le i \le n\), creating a cycle defined by the edge set \(\{s_{\left( i,1\right) } \leftrightarrow s_{\left( i,2\right) }, s_{\left( i,1\right) } \leftrightarrow s_{\left( i,3\right) }, s_{\left( i,2\right) } \leftrightarrow s_{\left( i,3\right) }\}\);

  • for each \(1 \le i \le n\) and \(1 \le j \le 3\), adding the edge \(\{s_{\left( i,j\right) } \leftrightarrow var_{i}\}\) (respectively, adding the edge \(\{s_{\left( i,j\right) } \leftrightarrow \lnot \ var_{i}\}\)) if \(l_{\left( i,j\right) }\) is a positive (respectively, negative) literal.

Here, Creignou and Hermann (1993) claimed that there would be \(3! \cdot 2^n\) instances of proper 3-colorings for G per witness for \(\phi _{NAE}\). However, noting that any witness for \(\phi _{NAE}\) will have a complementary witness where we invert all variable truth value assignments, this is an over count by a factor of 2, and in actuality there will be \(3 \cdot 2^n\) instances of proper 3-colorings of G per witness for \(\phi _{NAE}\).

We now follow along the lines of the reduction given in the Theorem 3 proof argument to convert G into a UNIT-PURE-4-DIR graph H in \({\mathcal {O}}\left( m^2\right) \) time, where we can recall that this construction also gives us an orthogonal \({\mathbb {Z}}^2\) grid embedding \({\mathcal {Q}}'\) (of a subdivision of G) that can be used to template the construction of H. However, we first need to modify the original UNIT-PURE-4-DIR “crossing gadget” from Fig. 6c to correct for the fact that, for a particular coloration of the vertices labeled x and y, there are exactly 512 proper 3-colorings that are possible if the coloration of x matches the coloration of y, and only 256 possible proper 3-colorings if the coloration of x is distinct from the coloration of y (giving the \(3 \cdot 512 + 3! \cdot 256 = 3072\) total “crossing gadget” proper 3-colorings enumerated in the Theorem 3 proof argument). In this context, it suffices to add the (white) vertex shown in Fig. 6d to the “crossing gadget”, which—as again verified using Knuth’s Algorithm X (Knuth (2000)), e.g., as implemented in SageMath (W. A. Stein et al. (The SAGE Development Team) (2020))—ensures that there are exactly 512 possible proper 3-colorings of the “crossing gadget” for any particular coloration of the vertices labeled x and y. We refer the reader to Fig. 14 in the Appendix for a modified version of the Fig. 6b unit segment intersection diagram having a new segment for the (white) vertex illustrated in Fig. 6d.

Moving forward, let \(C_1\) be the number of non-empty cells in \({\mathcal {Q}}'\) (i.e., containing either embedded vertices or non-crossing polylines) disjoint from any \(3 \times 3\) cell area centered on a polyline crossing, and let \(C_2\) be the number of polyline crossings in \({\mathcal {Q}}'\). Looking at the Fig. 2d–f UNIT-PURE-4-DIR subgraphs of H substituted in place of each cell type counted by \(C_1\), we can determine that each such cell will multiply the number of proper 3-colorings of G by a factor of 2. We can also determine that each instance of the modified UNIT-PURE-4-DIR “crossing gadget”, substituted in place of each \(3 \times 3\) cell block centered on a polyline crossing, will multiply the number of proper 3-colorings of G by a factor of 512. Accordingly, we have that H will have \(2^{C_1} \cdot 512^{C_2}\) proper 3-colorings per proper 3-coloring of G. As this is straightforwardly a many-one counting reduction from counting proper 3-colorings of G to counting proper 3-colorings of the UNIT-PURE-4-DIR graph H, we have established the current theorem. \(\square \)

Corollary 2

Unless the #ETH is false, no \(2^{o\left( \sqrt{n}\right) }\) time algorithm can exist for counting the number of 3-colorings of an order n instance of a UNIT-PURE-4-DIR graph.

Proof

Recall that Lemma 1 gives a linear time many-one counting reduction from \(\#3\)-SAT to \(\#\)NAE-3-SAT. Observe that the current corollary now follows from the fact that the Theorem 4 many-one counting reduction, specifically from \(\#\)NAE-3-SAT with n clauses to counting proper 3-colorings of a UNIT-PURE-4-DIR graph with \({\mathcal {O}}\left( n^2\right) \) vertices, will take at most \({\mathcal {O}}\left( n^2\right) \) time. \(\square \)

Corollary 3

Counting proper \(\left( k-1\right) \)-colorings for graphs in the class 2-L-PURE-k-DIR, provided a polynomial size unit segment intersection diagram witnessing graph class membership, is \(\#P\)-complete under many-one counting reductions \(\forall k \ge 4\).

Proof

In the case where \(k = 4\), the corollary follows from Theorem 4. In the case where \(k \ge 5\), we proceed by following exactly the construction given in the proof argument for Theorem 2, which reduces the problem of finding a proper 3-coloring of a UNIT-PURE-4-DIR graph to the problem of finding a problem \((k-1)\)-coloring of a 2-L-PURE-k-DIR graph. Here, letting G be an initial UNIT-PURE-4-DIR, and as noted in the final paragraph of the Theorem 2 proof argument, the result will be a graph \(G'\), wherein every vertex in G is connected to every vertex in at least one clique of \(k-4\) vertices, and all such cliques on \(k-4\) vertices are connected to every vertex in a common clique on 3 vertices (no vertex of which is adjacent to any vertex in G). Accordingly, letting \(\Psi \) be the number of proper 3-colorings for G, letting \(\Psi '\) be the number of proper \((k-1)\)-colorings for \(G'\), and letting M be the number of cliques on \(k-4\) vertices, adjacent to some vertex in G, generated via the Theorem 2 construction, it holds that \(\Psi ' = \left( 3!\right) \cdot {k-1 \atopwithdelims ()3} \cdot \left( \left( k-4\right) !\right) ^M\). This yields the current corollary for all cases where \(k \ge 4\). \(\square \)

5 Finding maximum order proper 3-colorable induced subgraphs for UNIT-PURE-4-DIR graphs

Theorem 5

Finding a maximum order proper 3-colorable induced subgraph of a UNIT-PURE-4-DIR graph, provided a polynomial size unit segment intersection diagram witnessing graph class membership, is NP-hard.

Proof

We proceed via reduction from the problem of finding a maximum proper 3-colorable induced subgraph of an arbitrary planar graph, or equivalently, determining the minimum number of vertices that must be deleted in an arbitrary planar graph to yield a proper 3-colorable graph. Here, observing that the property of a planar graph being proper 3-colorable is non-trivial, in the sense that infinitely many proper 3-colorable planar graphs exist, and hereditary, in the sense that any induced subgraph of a proper 3-colorable subgraph is also proper 3-colorable, by a metatheorem of Lewis and Yannakakis (1980) we have that this latter problem is NP-hard (see the author’s “Corollary 5”).

To begin, let G be an arbitrary planar graph with vertex set \(V_G\), edge set \(E_G\), and a set \(\Upsilon \subseteq V_G\) of vertices having degree \(\ge 5\). Akin to how we proceeded in the proof argument for Theorem 3, we replace every vertex \(v_i \in \Upsilon \) with a path (not a cycle as in the Theorem 3 proof argument) of length \(f_i\) vertices. More specifically, for a given vertex \(v_i \in \Upsilon \), exactly one vertex in the path is made adjacent to each distinct neighbor of \(v_i\), and we label the vertices in the path \(\{w_{\left( i,1\right) }, w_{\left( i,2\right) }, \ldots , w_{\left( i,f\right) }\}\), where \(w_{\left( i,1\right) }\) and \(w_{\left( i,f_i\right) }\) correspond to the path termini. Let H be the graph resulting from this operation, let \(V_H\) be its vertex set, observe that the maximum degree of H will be \(\le 4\), and observe that \(|V_H| \in {\mathcal {O}}\left( |E_G|\right) \). Here, we use the method of Papakostas and Tollis (1998) to compute a factor of 2 enlarged orthogonal \({\mathbb {Z}}^2\) grid embedding \({\mathcal {Q}}\) of H, where polyline crossings are forbidden, in \({\mathcal {O}}\left( |V_H|\right) \implies {\mathcal {O}}\left( |E_G|\right) \) time, and subsequently create a new embedding \({\mathcal {Q}}'\) by further enlarging \({\mathcal {Q}}\) by a factor of 3.

At a high level, our strategy will now be to construct a unit segment intersection diagram \({\mathcal {W}}\) by replacing the contents of various \(3 \times 3\) cell areas in \({\mathcal {Q}}'\) with copies of the \(\zeta _1\) and \(\zeta _2\) UNIT-PURE-4-DIR graph gadgets shown in Figs. 7 and 8, and otherwise following the method given in the Theorem 1 proof argument for replacing vertices and polyline segments in \({\mathcal {Q}}'\) with the unit segment intersection diagrams shown in Figs. 2 and 4. As a result, the UNIT-PURE-4-DIR graph \(H'\) associated with \({\mathcal {W}}\) will have the property that n vertices can be deleted in G to yield a proper 3-colorable induced subgraph if and only if n vertices can be deleted in \(H'\) to yield a proper 3-colorable subgraph.

In particular, we generate \({\mathcal {W}}\) from \({\mathcal {Q}}'\) via the following steps:

  • (Step 1) We substitute each \(3 \times 3\) cell area centered on a cell corresponding to a vertex \(w_{\left( i,1\right) }\), for \(i \in \left[ 1,|\Upsilon |\right] \), with the \(\zeta _1\) unit segment diagram shown in Fig. 7a (see Fig. 7b for the topology of its corresponding unit segment intersection graph).

  • (Step 2) We substitute each \(3 \times 3\) cell area centered on a cell corresponding to a vertex \(w_{\left( i,j\right) }\), for \(i \in \left[ 1,|\Upsilon |\right] \) and \(j \ne 1\), with the \(\zeta _2\) unit segment diagram shown in Fig. 8a (see Fig. 8b for the topology of its corresponding unit segment intersection graph).

  • (Step 3) We remove all polylines connecting cells \(c_a\) and \(c_b\) in \({\mathcal {Q}}'\) corresponding to a pair of vertices \(w_{\left( i,j\right) }\) and \(w_{\left( i,k\right) }\).

  • (Step 4) Allowing for rotations of each \(\zeta _1\) or \(\zeta _2\) unit segment diagram by increments of \(\frac{\pi }{2}\), or reflections of the diagrams across horizontal or vertical lines passing through their center:

    • (Step 4.1) for each \(i \in \left[ 1,|\Upsilon |\right] \), we draw polylines to connect the segments marked w and x for an instance of the \(\zeta _1\) gadget placed on a vertex \(w_{\left( i,1\right) }\), with the segments marked \(q_2\) and \(q_3\) for an instance of the \(\zeta _2\) gadget placed on a a vertex \(w_{\left( i,2\right) }\);

    • (Step 4.2) for each \(i \in \left[ 1,|\Upsilon |\right] \) and each \(j \in \left[ 2,f_i-1\right] \), we connect the segments marked \(q_3\) and \(q_4\) for an instance of the \(\zeta _2\) gadget placed on a vertex \(w_{\left( i,j\right) }\), with the segments marked \(q_2\) and \(q_3\) (in any order, e.g., \(q_3\) and \(q_2\)) for an instance of the \(\zeta _2\) gadget placed on a vertex \(w_{\left( i,j+1\right) }\);

    • (Step 4.3) for each polyline adjacent to a \(\zeta _1\) or \(\zeta _2\) gadget and remaining after (Step 3), we modify the polyline to connect it to the segment marked y or z in the case of a \(\zeta _1\) gadget, and the segment marked \(q_1\) in the case of a \(\zeta _2\) gadget.

  • (Step 5) For all remaining cells in \({\mathcal {Q}}'\) embedding vertices or polylines, we follow the construction given in the Theorem 1 proof argument to place the unit segment diagrams from Figs. 2 and 4 on these cells.

Here, in Fig. 9a we show a polyline connecting vertices (Solid squares) embedded on a pair of cells \(c_a\) and \(c_b\) in \({\mathcal {Q}}\), and in Fig. 9b we show how it is possible to substitute a pair of polylines in the enlarged embedding \({\mathcal {Q}}'\) to complete (Step 4.1) through (Step 4.3) for an appropriate placement of gadgets on \(c_a\) and \(c_b\). We can observe the following properties of the UNIT-PURE-4-DIR graphs corresponding to the \(\zeta _1\) and \(\zeta _2\) gadgets (see Fig. 7b and 8b, respectively):

  • (\(\zeta _1\) Gadget; Property 1) Vertices corresponding the w, x, y, and z segments must have the same coloration in any proper 3-coloring (of which there are 1536 for the gadget’s corresponding UNIT-PURE-4-DIR graph.

  • (\(\zeta _1\) Gadget; Property 2) Upon deletion of vertex indicated by an arrow in Fig. 7b, vertices corresponding to the w, x, y, and z segments can have arbitrary colorations in any proper 3-coloring (of which there are 49152) for the gadget’s corresponding UNIT-PURE-4-DIR graph.

  • (\(\zeta _2\) Gadget; Property 1) In any proper 3-coloring of the gadget’s corresponding UNIT-PURE-4-DIR graph (of which there are 208896), if the vertices corresponding to the segments \(q_2\) and \(q_3\) have the same coloration (24576 instances), then the vertices corresponding to the segments \(q_1\) through \(q_5\) have the same coloration; otherwise the vertex corresponding to the segment \(q_1\) may have an arbitrary coloration, and the vertices corresponding to the segments \(q_4\) and \(q_5\) can have distinct colorations.

Now, for each \(i \in \left[ 1,|\Upsilon |\right] \), let \(\Psi _i\) correspond to the subgraph of \(H'\)—where \(H'\) is again the UNIT-PURE-4-DIR graph associated with the unit segment intersection diagram \({\mathcal {W}}\) constructed via (Step 1) through (Step 5)—substituted in place of a given vertex \(v_i \in V_G\). Here, we have that (\(\zeta _1\) Gadget; Property 1) and (\(\zeta _2\) Gadget; Property 1) will initially ensure that, in any proper 3-coloring of \(H'\), every vertex in \(\Psi _i\) adjacent to a vertex not in \(\Psi _i\) will have the same coloration. This simulates an assignment of a single color to the vertex \(v_i \in V_G\) corresponding to \(\Psi _i\). However, (\(\zeta _1\) Gadget; Property 2) and (\(\zeta _2\) Gadget; Property 1) also guarantee that, with the deletion of a single vertex in \(\Psi _i\), there will be a cascade effect that allows vertices in \(\Psi _i\) adjacent to a vertices not in \(\Psi _i\) to have arbitrary colorations. This simulates the deletion of the vertex \(v_i \in V_G\) in the context of considering a proper 3-coloring of a subset of the vertices in \(V_G\).

Putting everything together, we have that n vertices can be deleted in G to yield a proper 3-colorable subgraph if and only if n vertices can be deleted in the UNIT-PURE-4-DIR graph \(H'\) to yield a proper 3-colorable subgraph. Accordingly, as G is an arbitrary planar graph, and as finding a minimum set of vertices to delete in a planar graph to yield a proper 3-colorable graph is NP-hard, this yields the theorem at hand. \(\square \)

Fig. 7
figure 7

Illustration of the scheme used in the Theorem 5 proof argument to substitute a vertex in a orthogonal \({\mathbb {Z}}^2\) grid embedding of a graph with a unit segment intersection diagram corresponding to the UNIT-PURE-4-DIR graph gadget \(\zeta _1\), where the (black dashed) box—with dimensions \(\left( \frac{9}{2} \times \frac{9}{2}\right) \)—indicates the placement of the diagram on a \(3 \times 3\) cell area centered on a vertex in the embedding (after deleting all existing segments in the area); (a) unit segment intersection diagram for the \(\zeta _1\) gadget (b) \(\zeta _1\) gadget, corresponding to the unit segment diagram from (a), where each vertex is embedded at the midpoint of its respective segment

Full size image
Fig. 8
figure 8

Illustration of the scheme used in the Theorem 5 proof argument to substitute a vertex in a orthogonal \({\mathbb {Z}}^2\) grid embedding of a graph with a unit segment intersection diagram corresponding to the UNIT-PURE-4-DIR graph gadget \(\zeta _2\), where the (black dashed) box—with dimensions \(\left( \frac{9}{2} \times \frac{9}{2}\right) \)—indicates the placement of the diagram on a \(3 \times 3\) cell area centered on a vertex in the embedding (after deleting all existing segments in the area); (a) unit segment intersection diagram for the \(\zeta _2\) gadget, where segments are colored in accordance with a proper 3-coloring of the corresponding UNIT-PURE-4-DIR graph; (b) proper 3-coloring of the \(\zeta _2\) gadget, corresponding to the coloring of the unit segments from (a), where each vertex is embedded at the midpoint of its respective segment

Full size image
Fig. 9
figure 9

Illustration of a scheme for connecting pairs of termini on \(\zeta _2\) UNIT-PURE-4-DIR graph gadgets from the Theorem 5 proof argument; (a) abstract illustration of a pair of embedded vertices (Solid squares) connected by a polyline in an orthogonal \({\mathbb {Z}}^2\) grid embedding; (b) an illustration of the scheme, after enlarging the embedding from (a) by a factor of 3, for placing an appropriate rotation or reflection of the \(\zeta _2\) gadgets (black dashed boxes) on the vertices (Solid squares), then tracing the polyline from (a) to connect two adjacent termini on one gadget with two adjacent termini on the other

Full size image

6 Concluding remarks

We very strongly suspect that deciding the existence of a proper \(\left( k-1\right) \)-coloring for graphs in the class UNIT-PURE-k-DIR, provided a polynomial size unit segment intersection diagram witnessing graph class membership, is NP-complete for each \(k \ge 4\), and leave this as an open problem. Here, we briefly remark that such a result may be interesting for at least the reason that unit segment intersection graphs are known to be \(\chi \)-bounded (see Suk (2014)), or in other words, to admit a proper coloring with a number of colors bounded by the size of their largest clique. Accordingly, such a result would connect proper k-colorings of SEG graphs and their subclasses to open problems concerning the complexity of finding maximum cliques and independent sets for these types of geometric intersection graphs (see Cabello et al. (2013); Kratochvíl and Nešetřil (1990)).