Introduction

Bio-molecules are inherently dynamic and populate a number of structurally different states. NMR spectroscopy is a unique tool to experimentally investigate these bio-molecular motions with atomic resolution. When the exchange rates between the different states are on the millisecond timescale Carr–Purcell–Meiboom–Gill (CPMG) and rotating-frame relaxation experiments at different effective magnetic fields can be exploited to record relaxation dispersion (RD) profiles. These profiles directly depend on thermodynamic (populations) and kinetic (rates) parameters of the exchange process and structural information (chemical shifts) of sparsely populated (invisible), short-lived excited states can be obtained. For proteins under 20 kDa, RD experiments can be recorded on protonated 15N-labeled samples, whereas deuteration and transverse relaxation optimized spectroscopy (TROSY; Pervushin et al. 1997) are required for larger systems. In very large complexes (> 80 kDa), methyl group labeling in a fully deuterated background combined with methyl TROSY based approaches (Tugarinov et al. 2003; Schütz and Sprangers 2019; Abramov et al. 2020) can be used to record 13C single quantum (SQ; Skrynnikov et al. 2001; Lundström et al. 2007; Rennella et al. 2016) and 13C multiple quantum (MQ; Korzhnev et al. 2004) as well as 1H SQ (Tugarinov and Kay 2007; Baldwin et al. 2010; Otten et al. 2010; Weininger et al. 2012), double quantum (DQ; Gopalan et al. 2018) and triple quantum (TQ; Gopalan et al. 2018) RD profiles.

Recently, fluorine (19F) NMR has regained attraction (Hellmich et al. 2009; Liu et al. 2012; Kim et al. 2013; Kitevski-Leblanc et al. 2013; Aramini et al. 2014; Hoang and Prosser 2014; Manglik et al. 2015; Matei and Gronenborn 2016; Lu et al. 2019; Huang et al. 2020). This spin is absent from virtually all biomolecules, however, 19F probes can be artificially introduced into proteins by incorporation of fluorinated amino acids (Crowley et al. 2012) or through post-translational modification with fluorine-containing tags (Brauer and Sykes 1986). These 19F labeling strategies provide a number of advantages. First, the resulting samples contain only a limited number of NMR probes and spectra can often be recorded in a simple 1 dimensional (1D) manner. Second, in most cases, fluorine-based experiments can be recorded in a fully protonated background and samples can thus originate from sources where deuteration or methyl group labeling is not easily achievable (e.g. mammalian expression systems). Third, 19F experiments can complement and verify information from deuterated systems, where structure, stability and dynamics can be altered due to the pervasive isotopic substitution (Korzhnev et al. 2005a, b). Fourth, 19F shares favorable characteristics with 1H with respect to RD experiments (Juen et al. 2016), including reduced sample heating on probe heads with inverse coil configuration, short pulses and an extended range of accessible effective field strengths. Finally, the 19F chemical shift dispersion is large, which can result in significant chemical shift differences between the ground state and excited states and thus RD profiles that have large amplitudes.

In the past, 19F RD CPMG experiments have been exploited to study dynamic protein interfaces (Aramini et al. 2014), dynamic dimer asymmetry (Kim et al. 2017), allostery (Manglik et al. 2015), ligand-bound states (Hoang and Prosser 2014), protein folding (Kitevski-Leblanc et al. 2013) and fold-switching (Liebau et al. 2020). In those experiments, a varying number of 180° pulses is applied within a fixed relaxation delay such that exchange induced line-broadening can be suppressed. Fitting of these RD profiles with analytical or numerical approaches provides insight into the exchange constant kex, the populations pA and pB as well as the absolute value of the chemical shift difference |Δω| between the two states. However, in many cases these data are not sufficient to unambiguously and accurately determine these parameters as significantly different exchange regimes can result in similar RD profiles. In those cases R1ρ experiments can be used to resolve these ambiguities. In R1ρ experiments the effective relaxation rate is measured in the rotating frame as a function of spin-lock field strengths (“on-resonance”) or as a function of spin-lock offsets (“off-resonance”). Compared to the CPMG approach, this has several advantages. First, R1ρ experiments can access higher frequencies and thus allow quantification of faster dynamics. Second, off-resonance experiments can provide not only the magnitude but also the sign of Δω. Third, the sampling of points in the frequency dimension is not restricted, as it is in CPMG experiments where only frequencies that correspond to an integer number of 180° pulses in the relaxation delay are possible. Motivated by these considerations, we developed a suite of one-dimensional CPMG, on-resonance R1ρ and off-resonance R1ρ pulse sequences for 19F nuclei. We validate the experiments on the unfolding transition of a cold shock protein, show that they yield consistent exchange parameters and extract thermodynamic information from a temperature series of RD datasets. Moreover, we demonstrate the applicability of 19F rotating frame relaxation to a fully protonated 360 kDa protein complex.

Materials and methods

Molecular biology

The protein coding sequence of cold shock protein from Thermotoga maritima (NCBI reference sequence WP_004082199.1, hereafter referred to as TmCsp, internal reference: 2093) was codon optimized with COOL (http://bioinfo.bti.a-star.edu.sg/COOL/), synthesized by Integrated DNA Technologies (Coralville, USA) and cloned into a pETGB-1a vector (kindly provided by Dr. Arie Geerlof, Helmholtz Zentrum München). The vector contains an N-terminal His6-GB1-tag followed by a tobacco etch virus protease (TEV protease) cleavage site constituted by the amino acid sequence ENLYFQGG. The final protein sequence therefore contains an additional GG at the N-terminus of the protein.

NMR sample preparation

Thermotoga maritima Csp

Plasmids were transformed into Escherichia coli BL21(DE3) CodonPlus-RIL cells (Stratagene) and grown in LB over night. Subsequently, M9 medium was inoculated with the LB culture and grown to an optical density OD600 of 1.0 at 37 °C. The medium was then supplemented with 50 mg/l 5-fluoroindole (Crowley et al. 2012) that was dissolved in DMSO at a 100 mg/ml stock concentration. 45–60 min later protein expression was induced by addition of 1 mM IPTG and the culture was shifted to 20 °C. Cells were harvested by centrifugation 12–18 h after induction. Cell pellets were resuspended in 10 mM Tris, pH 8.0, 10 mM imidazole, 1 mM EDTA, 1:1000 Triton X-100, 1 mg/l lysozyme and 0.2 U/ml DNaseI by vortexing for 30 min at 4 °C and then lysed by sonification. After addition of 5 mM MgCl2 and 5 µg/ml RNaseA the sample was incubated for 2 h at 37 °C. The cell debris was removed by centrifugation, the supernatant was additionally cleared with a 0.45 µm syringe filter and loaded onto a nickel–NTA gravity flow column that was pre-equilibrated with buffer A (10 mM Tris, 10 mM imidazole, pH 8.0). Subsequently, the column was washed with 20–30 column volumes of buffer A and the bound protein was eluted with 10 mM Tris, 300 mM imidazole, pH 8.0. The His6-GB1-tag was cleaved by addition of a His6-tagged TEV protease during dialysis for 12–18 h against 10 mM Tris, pH 8.0, 1 mM DTT at 20 °C. In order to separate the His-tagged proteins from the target protein, the dialyzed proteins were loaded on a nickel–NTA column pre-equilibrated with 10 mM Tris, pH 8.0, 10 mM imidazole. The column flow-through was dialyzed for 12–18 h against 10 mM NaHPO4, pH 6.8 and loaded onto a 5 ml Heparin HP HiTrap™ column. The protein was eluted with a salt gradient (0–500 mM NaCl in the presence of 1 mM EDTA) and the target fractions were combined and concentrated to a final volume of 1–1.5 ml. Finally, the protein was purified using a 16/600 Superdex S75 column in 50 mM Tris, pH 8.0, 100 mM NaCl, 1 mM EDTA. The target fractions were combined and concentrated with a simultaneous buffer exchange to 50 mM NaHPO4, pH 6.5, 20 mM NaCl, 0.2 mM EDTA, 1 mM DTT. The NMR sample was supplemented with 0.03% NaN3 and 5% D2O, the final protein concentration was 550 μM.

Thermoplasma acidophilum α7α7 complex

Plasmids were transformed into E. coli BL21(DE3) CodonPlus-RIL cells (Stratagene) and grown in LB over night. Fresh LB medium including antibiotics was inoculated from the overnight culture and grown to an optical density OD600 of 0.6–0.8 at 37 °C. The culture was shifted to 20 °C and protein expression induced with 0.5 mM IPTG for 12–18 h. Cell pellets were resuspended in 50 mM sodium phosphate, pH 7.4, 400 mM NaCl, 10 mM imidazole, 1 mM EDTA, 1:1000 Triton X-100, 1 mg/l lysozyme and 0.2 U/ml DNaseI by vortexing for 30 min at 4 °C and lysed by sonification. The cell debris was removed by centrifugation, the supernatant was additionally cleared with a 0.45 µm syringe filter and loaded on a nickel–NTA gravity flow column that was pre-equilibrated with buffer A2 (50 mM sodium phosphate, pH 7.4, 400 mM NaCl, 10 mM imidazole). In order to remove weakly bound contaminating proteins, the column was washed with 20–30 column volumes of buffer A2, after which the protein was eluted with 50 mM sodium phosphate, pH 7.4, 150 mM NaCl, 300 mM imidazole. The His6 tag was cleaved with His6-tagged TEV protease while dialyzing the elution against 50 mM sodium phosphate, pH 7.4, 150 mM NaCl, 1 mM DTT at 4 °C. The dialyzed sample was loaded on a second nickel–NTA column pre-equilibrated with buffer A2. The column flow-through was concentrated to 1 ml and finally purified using a 16/600 Superdex S200 column in 25 mM HEPES, pH 7.3, 125 mM NaCl, 1 mM DTT. The target fractions were combined and concentrated again to a volume of 0.5 ml. Bromotrifluoroacetone (Sigma-Aldrich) was added to a final concentration of 10 mM and incubated at 37 °C for 30′. The reaction was quenched with 20 mM DTT and the sample was purified over a PD 10 column pre-equilibrated with 25 mM HEPES, pH 7.3, 125 mM NaCl, 1 mM DTT. The NMR sample was supplemented with 0.03% NaN3 and 5% D2O, the final protein concentration was 1.3 mM (monomer concentration), corresponding to 93 µM α7α7 complex for the 18C mutant, and 0.75 mM (monomer concentration), corresponding to 54 µM α7α7 complex for the 35C mutant.

NMR spectroscopy

All NMR RD experiments were recorded on a 500 MHz Bruker NEO NMR spectrometer equipped with triple resonance TCI H/F–C–N–D nitrogen cooled probehead, where the proton coil was tuned and matched to the 19F resonance frequency (470 MHz). Data was acquired with 1024 points in the direct dimension and a relaxation delay of 1.5 s. The 1D spectra of TmCsp (Fig. 1) were recorded at 333 K, 343 K and 373 K on a Bruker 600 MHz spectrometer equipped with a TBI H–F–D probehead. Temperatures were calibrated using an ethylene glycol sample. Both the ethylene glycol sample as well as the sample of 5-fluoroindole dissolved in glycerol were locked using a capillary filled with D2O that was inserted into the 5 mm NMR tube. 19F spectra were referenced to TFA indirectly by measuring the absolute proton frequency of DSS and using a correction factor Ξ of 0.940866982 (Maurer and Kalbitzer 1996).

Fig. 1
figure 1

The folding-unfolding exchange of the TmCsp protein. a The chemical structure of 5-fluoro tryptophan (5FW; left) and a schematic presentation of the (un-) folding of TmCsp, which contains 5FW residues at positions 7 and 29 (Protein Data Bank, PDB ID 1G6P Kremer et al. 2001). b 19F spectra of TmCsp at 333 K, 343 K and 373 K with assignments for Trp7 and Trp29. The peak labeled with an asterisk results from a small impurity in the sample. This impurity resonates outside the displayed spectral window at the two lower temperatures

Full size image

The CPMG experiments for TmCsp were recorded with a relaxation delay of 40 ms and with 23 different CPMG frequencies of 50, 100, 150, 200, 250, 300, 350, 400, 450, 500, 600, 700, 800, 900, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500 and 5000 Hz.

The CPMG experiments for the α7α7 complex at 303 K, 313 K and 323 K were recorded with a relaxation delay of 8 ms and with 22 different CPMG frequencies of 125, 250, 375, 500, 625, 750 875, 1000, 1125, 1250, 1500, 1750, 2000, 2250, 2500, 2750, 3000, 3250, 3500, 4000, 4500 and 5000 Hz; the experiments at 293 K were recorded with a relaxation delay of 4 ms and with 20 different CPMG frequencies of 250, 500, 750, 1000, 1250, 1500, 1750, 2000, 2250, 2500, 2750, 3000, 3250, 3500, 3750, 4000, 4250, 4500, 4750 and 5000 Hz.

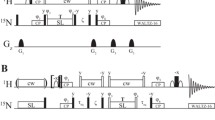
The fully extended phase cycle for the 19F CPMG including the aring-sequence (Fig. 2a) is φ1 = [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3], φ2 = [1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2], φ3 = [2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1], φ4 = [2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 3 1 3 1 3 1 3 1 3 1 3 1 3 1 3 1 1 3 1 3 1 3 1 3 1 3 1 3 1 3 1 3], φ5 = [0 0 2 2 1 1 3 3 0 0 2 2 1 1 3 3 2 2 0 0 3 3 1 1 2 2 0 0 3 3 1 1 1 1 3 3 2 2 0 0 1 1 3 3 2 2 0 0 3 3 1 1 0 0 2 2 3 3 1 1 0 0 2 2], φrec= [0 2 2 0 1 3 3 1 0 2 2 0 1 3 3 1 2 0 0 2 3 1 1 3 2 0 0 2 3 1 1 3 1 3 3 1 2 0 0 2 1 3 3 1 2 0 0 2 3 1 1 3 0 2 2 0 3 1 1 3 0 2 2 0], where [0, 1, 2, 3] corresponds to [x, y, − x, − y].

Fig. 2
figure 2

19F CPMG experiment. a Pulse sequence for recording 19F CPMG RD profiles. Narrow (wide) rectangles indicate 90° (180°) pulses, which are applied along the x-axis unless indicated otherwise. The phase cycle is φ1 = φrec = [x, x, − x, − x, y, y, − y, − y], φ2 = [y, − y, y, − y, x, − x, x, − x]. The number of CPMG pulses applied during the CPMG time TCPMG is given by 2n, where n is an integer. The maximum number nmax is chosen so that the highest applied frequency υCPMG = nmax/TCPMG is at or below 5 kHz. b CPMG relaxation dispersion profiles for W7 and W29 recorded at 344 K. The size of the error-bars correspond to 1 standard deviation

Full size image

The R1ρ on-resonance experiments for TmCsp were based on six different spin-lock times TSL (0, 4, 8, 16, 32 and 48 ms) and 28 different spin lock fields (351.05, 393.88, 441.94, 495.87, 556.37, 624.26, 700.43, 785.9, 881.79, 989.38, 1110.11, 1245.56, 1397.54, 1568.07, 1759.4, 1974.08, 2214.95, 2485.22, 2788.46, 3128.71, 3510.47, 3938.81, 4419.42, 4958.67, 5563.72, 6242.59, 7004.3, 7858.96 Hz). The 19F frequency carrier was centered on the respective peak maximum in the 1D 19F spectrum.

The R1ρ on-resonance experiments for the α7α7 complex were based on six different spin-lock times TSL (0, 2, 4, 8, 12 and 16 ms) and 31 different spin lock fields (103.54, 116.17, 130.35, 146.25, 164.10, 184.12, 206.591, 231.80, 260.08, 291.82, 327.42, 367.37, 412.20, 462.50, 518.93, 582.25, 653.29, 733.01, 822.45, 922.80, 1035.40, 1161.74, 1641.00, 2600.81, 3274.23, 4122.01, 5189.30, 5822.49, 6532.94, 7330.08, 8224.49 Hz). The 19F frequency carrier was centered on the respective peak maximum in the 1D 19F spectrum.

The R1ρ off-resonance experiments for TmCsp were based on six different spin-lock times TSL (0, 4, 8, 16, 32 and 48 ms), 71 different offsets frequencies (+ and − 0, 50, 100, 150, 200, 250, 300, 350, 400, 450, 500, 600, 700, 800, 900, 1000, 1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000, 2100, 2200, 2300, 2400, 2500, 2600, 2800, 3000, 3200 and 3400 Hz) and 4 different spinlock fields (100, 200, 300 and 400 Hz). The spin-lock is flanked by two hard pulses that transfer the magnetization to the spin-lock angle θ. θ is calculated from the spin-lock power and the spin-lock offset as θ = tan−1(ωSL/ΔΩ), after which the length of the θ-hard pulse is calculated from the 90° hard pulse phard as pθ = θ/90° * phard. The 19F frequency carrier was centered on the Trp7 peak maximum in the 1D 19F spectrum.

All relaxation dispersion datasets were recorded in triplicate in order to obtain the indicated error estimates.

Data processing/analysis/fitting

NMR experiments were processed with the NMRpipe software (Delaglio et al. 1995) and analyzed with in house written Python and Matlab scripts.

CPMG

Effective transverse relaxation rates were calculated as Reff2 = − ln(I/I0)/TCPMG, where I is the peak intensity, I0 is the reference intensity recorded without the CPMG element and TCPMG is the constant CPMG time. The CPMG profiles were numerically fitted (Korzhnev et al. 2004) to a two-state model using an in-house Matlab script. The transverse relaxation rates of the folded state and the unfolded state were assumed to be equal in the absence of exchange (R2,f = R2,u).

On-resonance R1ρ

R1ρ rates were extracted from an exponential fit of the resonance intensities in experiments with six different TSL times. R1ρ data was fitted with an in-house Matlab script using a numerical approach in which R1ρ is approximated as the least negative eigenvalue of the Bloch–McConnell evolution matrix (Trott and Palmer 2002).

Off-resonance R1ρ

R1ρ rates were extracted from an exponential fit of the resonance intensities in experiments with six different TSL times. The off-resonance R1ρ data was fitted with an in-house Matlab script using the Laguerre approximation as an analytical equation that is valid for off-resonance R1ρ data (Koss et al. 2017; Miloushev and Palmer 2005).

Monte Carlo simulations

Standard deviations and mean values of all datapoints were calculated using the experimental triplicates. In order to assess the uncertainties from the fitting, we performed a Monte Carlo Simulation with 100 fit iterations, where all data-points were varied in each iteration according to a Gaussian distribution.

Thermodynamic and kinetic analysis

Solutions for kex (= kF + kU) and pF from the CPMG fits at different temperatures were used to calculate the unfolding rate kU, the folding rate kF and the equilibrium constant Keq according to

$${p}_{U}=1-{p}_{F},$$
(1)
$${k}_{U}={p}_{U}\bullet {k}_{ex},$$
(2)
$${k}_{F}={p}_{F}\bullet {k}_{ex},$$
(3)
$${K}_{eq}={k}_{U}/{k}_{F}.$$
(4)

To obtain the thermodynamic parameters, first Keq was fit according to

$${K}_{eq}={e}^{-{\Delta }G/RT}={e}^{(T{\Delta }S-{\Delta }H)/RT}.$$
(5)

The values obtained for the change in entropy ΔS and in enthalpy ΔH were subsequently used as constraints

$${\Delta }S={{\Delta }S}^{\ddagger F\to U}+ {\varDelta S}^{\ddagger U\to F},$$
(6)
$$\varDelta H={\varDelta H}^{\ddagger F\to U}+ {\varDelta H}^{\ddagger U\to F}.$$
(7)

in the fit equations

$${k}_{U}=\frac{1}{\tau _{TPT}}{e}^{({T{\Delta }S}^{\ddagger F\to U}-{\varDelta H}^{\ddagger F\to U})/RT},$$
(8)
$${k}_{F}=\frac{1}{\tau _{TPT}}{e}^{({T\varDelta S}^{\ddagger U\to F}-{\varDelta H}^{\ddagger U\to F})/RT},$$
(9)

where τTPT is the transition path time, ΔS and ΔH are the differences in entropy and enthalpy between the folded and the unfolded state, \({\varDelta S}^{\ddagger F\to U}\)and \({\varDelta H}^{\ddagger F\to U}\) are the entropy and enthalpy differences between the folded state and the transition state and \({\varDelta S}^{\ddagger U\to F}\) and \({\varDelta H}^{\ddagger U\to F}\) are the entropy and enthalpy differences between the unfolded state and the transition state.

Results

Here we introduce a suite of one-dimensional 19F pulse sequences for the collection of CPMG, on-resonance R1ρ and off-resonance R1ρ data that only require a limited amount of experimental time. We use the cold shock protein from T. maritima (TmCsp) to highlight the applicability of these sequences to accurately determine exchange parameters in biomolecules. TmCsp is a small (7.5 kDa) thermostable protein that undergoes an unfolding transition with a melting temperature of Tm = 359 K (Schuler et al. 2002a, b). Two 19F probes were introduced into the protein by replacing the two natural tryptophan residues (W7 and W29) with 5-fluoro tryptophan (5FW; Fig. 1a; Supporting Information). Both the natural and the 5FW-labeled protein follow a two state unfolding transition (Perl et al. 1998; Wassenberg et al. 1999; Schuler et al. 2002a, b), which makes it a well-suited system to establish our 19F RD experiments.

The 19F NMR spectra of the protein show two sharp resonances at low (333 K) and high (373 K) temperatures corresponding to the fully folded (light blue) and fully unfolded (red) states (Fig. 1b). Based on these spectra, the chemical shift differences between the folded and thermally unfolded protein are 2.53 ppm (W7) and 0.33 ppm (W29) respectively. Of note, at temperatures above 373 K the resonances of the unfolded state (red) continue to shift towards lower ppm values. Based on this temperature dependence of the unfolded state chemical shift we can derive that the chemical shift differences at 333 K are 2.35 ppm (W7) and 0.48 ppm (W29). At 343 K (blue) extensive line broadening is observed, which arises from the exchange (kex = kF + kU) between the folded (F) and unfolded (U) states of the protein (Fig. 1a).

To quantify this exchange process we first recorded 19F CPMG RD profiles using the pulse sequence displayed in Fig. 2a (Supporting Information). This sequence contains two elements that we found to be particularly important for obtaining high quality data. First, we included a heat compensation block such that the sample is exposed to the same total RF power independent of the CPMG frequency. This is especially important when higher 19F CPMG frequencies (5 kHz) are used in combination with longer (> 20 ms) CPMG times. Second, when using a probehead where the 1H coil is de-tuned to record 19F spectra, we found broad baseline artifacts at the on-resonance 19F frequency that are due to suboptimal performance of the 1H RF coil for 19F experiments. These imperfections can be suppressed through the use of an “anti-ring” sequence (Gerothanassis 1987) that consists of three 90° pulses of different phases in combination with extensive phase cycling. We then used a sample that contains 5-fluoroindole in glycerol to show that the CPMG experiment results in flat RD profiles for a system that does not undergo chemical exchange (Fig. S1). Due to the high viscosity, the 19F T1 and T2 times are comparable to the 19F relaxation times in proteins making this a good testing system for biological samples.

Based on the above, we recorded CPMG RD profiles on TmCsp at 11.7 T (500 MHz 1H frequency) and 344 K, which is 15 K below the melting temperature of the protein. In total, we recorded a full dataset with 23 CPMG frequencies in approximately 40 min (64 scans, 1.5 s interscan delay), highlighting the efficiency of the 1D based 19F CPMG method. The 19F signals of the two 19F tryptophan residues show large dispersions, indicative of chemical exchange (Fig. 2b). A global numerical fit (solid line) according to a two-site exchange model (Supporting Information) gives an exchange rate of kex = 1966 ± 485 s−1, populations of pF = 95.2 ± 0.1%, pU = 4.8 ± 0.1% and chemical shift differences of |ΔωW7| = 2.46 ± 0.27 ppm and |ΔωW29| = 0.47 ± 0.05 ppm, where the errors in the extracted parameters are standard deviations calculated by Monte Carlo simulations based on three separately recorded datasets (Fig. S2). It is noteworthy that the determined chemical shift differences agree well with the values obtained from 1D spectra recorded at different temperatures (2.35 ppm and 0.48 ppm for W7 and W29 respectively; Fig. 1b), especially when considering that only two peaks at a single field strength are used to fit the exchange parameters. The relatively high accuracy of the extracted parameters can be explained based on the fact, that the values of |Δω| are significantly different for the two residues. The ratio between the kinetic parameter kex (1966 s−1) and the absolute value of |Δω|, which defines the exchange regime, effectively yields an intermediate exchange for W7 (|ΔωW7| = 2.44 ppm = 2π·1170 Hz), but is in fast exchange for W29 (|ΔωW29| = 0.46 ppm = 2π·216 Hz). Our data here show, that the exchange parameters can be reliably extracted from the CPMG dispersions alone. The associated standard deviations in the extracted parameters are nevertheless considerable (Fig. S2).

To complement the CPMG RD data and to be able to study systems that exchange on faster timescales we made use of a 19F on-resonance R1ρ pulse sequence (Fig. 3a and Supporting Information). We initially implemented the option to use adiabatic ramps with tanh/tan amplitude/phase modulation for the magnetization transfer to the transverse plane (Mulder et al. 1998). However, we found a transfer with hard pulses more convenient, as it is compatible with lower spin-lock powers, for which the adiabatic condition would otherwise be violated. As for the CPMG RD experiment, we observed significant baseline distortions in the spectra that result from acoustic ringing in the 1H/19F-coil at the 19F resonance frequency. These artifacts could be efficiently eliminated with an anti-ringing element. In addition, the pulse sequence includes a heating compensation for different spin-lock times TSL to ensure a constant RF power. We recorded separate datasets for W7 and W29 at 11.7 T and 344 K with the carrier frequency placed on-resonance (either at W7 or at W29), each with 28 spin-lock field strengths between 0.35 kHz and 7.9 kHz. Every datapoint corresponds to an R1ρ = R2 + Rex value that is obtained by fitting of an exponential decay recorded over six time points TSL. The total experimental time for 1 complete R1ρ dataset (32 scans, 1.5 s interscan delay) is around 2.3 h. To extract a reliable estimate of the error, we recorded three datasets for W7 and three datasets for W29. The data was simultaneously fitted using Trott’s and Palmer’s approach (2002) (solid line) and yields an exchange rate of kex = 2286 ± 268 s−1, populations of pF = 96.6 ± 0.4%, pU = 3.4 ± 0.4% and chemical shift differences of |ΔωW7| = 2.62 ± 0.18 ppm and |ΔωW29| = 0.51 ± 0.02 ppm. The extracted parameters agree well with the parameters that we extracted from the RD CPMG experiments (Fig. 2b) and with the chemical shift differences that we observe in the 1D NMR spectra (Fig. 1b).

Fig. 3
figure 3

19F on-resonance R1ρ experiment. a Pulse sequence for the 19F on-resonance R1ρ experiment. Narrow (wide) rectangles indicate 90° (180°) pulses, which are applied along the x-axis unless indicated otherwise. The phase cycle is φ1 = x, φ2 = [− x, x], φ3 = [x, x, − x, − x, y, y, − y, − y], φ4 = [y], φ5 = [− y], φrec = [x, − x, − x, x, y, − y, − y, y]. b On-resonance R1ρ relaxation dispersion profiles for W7 and W29. The size of the error-bars correspond to 1 standard deviation

Full size image

It is noteworthy, that higher spin-lock fields up to 20 kHz have been employed in proton R1ρ experiments on cryoprobes (Steiner et al. 2016), which accordingly expands the range of dynamics that can be studied with the presented fluorine R1ρ. On the other end, the lower limit of the spinlock field is dictated by the largest J-couplings present in the spin system (Zhao et al. 2014). In 5FW, the 3JHF coupling of ~ 9.9 Hz restricts the use of spin-lock to fields below 30 Hz (Zhao et al. 2014). This limitation is eluded by the use of a dual 1H–19F probehead where proton-fluor couplings can be decoupled and is also not applicable in fluorine labels where no vicinal protons are coupled to the 19F spin, as is the case in bromotrifluoroacetone (BTFA; see below). We note that in the CPMG experiment the 3JHF coupling leads to the interconversion of 19F in-phase and anti-phase magnetization during the periods 2τ between the refocusing pulses. Dependent on the CPMG frequency and on the difference of in-phase and anti-phase transverse relaxation rates, this can result in a distorted RD profile (Kay et al. 1992). This can be overcome by employing explicit relaxation–compensation, where in-phase and anti-phase contributions are averaged for all CPMG frequencies (Loria et al. 1999). However, in biological application of 19F NMR this problem is negligible for most practical purposes, as the anti-phase contributions only become relevant, when the periods 2τ between the refocusing pulses become longer than 1/4J. Even in the case of a strong three-bond H–F coupling of 10 Hz, this issue thus only arises for unusually long CPMG times (> 50 ms when 2 refocussing π pulses are used). Finally, it is worth mentioning that we here sampled six points of the exponential decay in order to rule out a non-exponential behavior of the spin-locked relaxation, that can arise due to inaccurate alignment of the magnetization with the spin lock field. The experimental time can be reduced at least by a factor of 3 when only a reference and a single timepoint are measured to determine the exponential decay for each spinlock field (Fig. S7), without a significant change in the values of the extracted parameters.

The CPMG and R1ρ RD experiments only yield the absolute value of the chemical shift difference between the two states (|Δωi|). 19F off-resonance R1ρ experiments (Fig. 4a and Supporting Information) on the other hand can be used to extract a full set of parameters (pF, kex, R2,i, Δωi) from measurements at a single B0 field in case of a two-state exchange process (Trott and Palmer 2002; Korzhnev et al. 2005a, b). In that experiment the effective field, which is defined by the vector sum of the spin-lock field ω1 and the spin-lock offset ωoffset, is now inclined by an angle θ. The magnetization is transferred from the ± z axis to an angle θ by hard pulses of the appropriate length, which allows to use very low spin-lock fields. Again, our pulse sequence included a heating compensation for the different spin lock lengths as well as an anti-ringing element. We recorded datasets for W7 at 11.7 T and 344 K at spin-lock fields of 100 Hz, 200 Hz, 300 Hz and 400 Hz and with 71 offsets in each experiment. The total experimental time for this complete dataset (16 scans, interscan delay 1.5 s) is 11.5 h. To estimate the error in the data, this dataset was recorded three times. Figure 4b shows the R1ρ data together with a global fit of all off-resonance datasets (solid line). A main peak corresponding to the observable resonance (F) is centered at zero offset, with a width determined by the spin lock power ω1. Exchange between the folded and the unfolded state leads to the appearance of a second peak that is centered around the resonance frequency of the excited, unfolded state (U). At 100 and 200 Hz, this peak gives rise to a distinct maximum; at higher spin-lock frequencies the resonances merge, but still add up to a clearly asymmetric profile that is indicative of the exchange process. The contribution of R2 + Rex can be extracted from the R1ρ data as R2 + Rex = (R1ρ – R1 * cos2θ)/sin2θ (Fig. 4c). The error in R2 + Rex rapidly increases with the spin-lock offset, because the contribution is scaled with the inverse of sin2θ. At the same time, the error at a given offset decreases when increasing the spin lock power, as is readily visible from the data between 100 and 400 Hz power. Based on a global fit of the complete off-resonance dataset, we extract an offset ΔωW7 of − 2π·1097 ± 84 Hz = − 2.33 ± 0.18 ppm, a ground state population of pF = 95.0 ± 0.2% and an exchange constant of kex = 1922 ± 137 s−1, which is close to the values obtained by the CPMG and on-resonance R1ρ RD experiments. We also observe that the single datasets at 100 Hz or 200 Hz can be used to obtain accurate exchange parameters. The 300 Hz data, and certainly the 400 Hz data, on the other hand fail to give well-defined results (Fig. S4), because a higher spin lock field increasingly overwrites off-resonance effects (Trott and Palmer 2002).

Fig. 4
figure 4

19F off-resonance R1ρ experiment. a Pulse sequence for the 19F off-resonance R1ρ experiment. Narrow rectangles indicate 90° pulses. The phase cycle is φ1 = x, φ2 = [− x, − x, x, x], φ3 = [x, x, x, x, − x, − x, − x, − x, y, y, y, y, − y, − y, − y, − y], φ4 = [y, − y], φ5 = [− y, y], φ6 = [x, − x], φ7 = [x], φ8 = [x, − x], φrec = [x, − x, − x, x, y, − y, − y, y]. The flip-angle of pulses that flank the spinlock block is θ, which ensures that the magnetization is aligned at the angle of the effective magnetic field. This angle depends on the offset and the spinlock power. The pulse pairs with phases φ7/φ8 are used to cycle the magnetization to ± z before the spin lock period and back to + z after the spin lock, which ensures that the rotating frame relaxation is symmetrically measured both above and below the transverse plane at all offsets. b R1ρ off-resonance relaxation dispersion profiles and c corresponding R2 + Rex contributions for W7 at spin-lock fields of 100 Hz, 200 Hz, 300 Hz and 400 Hz. Solid lines show the best fit to a two-state Laguerre approximation. The offsets of the folded (F) and the unfolded (U) state are indicated with dotted lines. Error bars show experimental uncertainty (1 standard deviation)

Full size image

In order to evaluate the consistency between the CPMG, the on-resonance R1ρ and the off-resonance R1ρ experiments, we used a global fit for all datasets (Figs. S5, S6). We expect that a global fit yields the most precise parameters, because the three experiments contain redundant information about the protein folding/unfolding transition. In the fit, we optimized the following parameters: kex, ΔωW7, ΔωW29, pF and R2. Because we observed small deviations on the order of 2 Hz in the R2 values from the CPMG and the R1ρ experiments we introduced two independent R2 variables: R2CPMG and R2R1ρ. Based on that, we obtained a ground state population of pF = 94.8 ± 0.1%, an exchange constant of kex = 1737 ± 54 s−1, and chemical shift differences of ΔωW7 = 2π·1086 ± 66 Hz  = −2.31 ± 0.14 ppm, |ΔωW29| =  2π·202 ± 5 Hz = 0.43 ± 0.01 ppm. These parameters are in agreement with the individually fitted datasets, but have a significantly increased precision (Fig. S5).

Temperature dependent RD measurements are well suited to extract thermodynamic parameters of chemical exchange processes (Mulder et al. 2001; Nikolova et al. 2011; Audin et al. 2013). Here, we measured 19F CPMG RD profiles at seven different temperatures between 328 and 343 K and determined the unfolding and folding rates (kU, kF) as well as equilibrium constants Keq = kU/kF (Fig. 5; Supporting Information). The temperature-profile of Keq between 335.5 and 343 K was subsequently fit to an Arrhenius model for Gibbs free energy ΔG = ΔH − TΔS = − RT ln Keq, from which we obtain ΔH = 43.9 ± 1.0 kcal/mol and TΔS = 40.6 ± 1.0 kcal/mol at 343 K, indicating an entropy–enthalpy compensation during TmCsp unfolding. Similarly, transition state theory can be used to obtain estimates of the enthalpic and entropic contributions to the energy barrier that separates the folded and the unfolded state. Because the traditional pre-exponential factor kBT/h in the Eyring equation is on the timescale of covalent bond vibrations and hence a suboptimal estimate for large-scale biomolecular dynamics (Moore 2012; Vallurupalli et al. 2016), we chose to estimate it as 1/τTPT, where τTPT is the transition path time. Based on MD simulations and single-molecule fluorescence studies that show that τTPT is similar even for proteins with vastly different folding rates (Shaw et al. 2010; Chung et al. 2012; Vallurupalli et al. 2016), we assumed τTPT to be 1 µs and obtained values of ΔH‡ = 45.8 ± 1.2 kcal/mol and TΔS‡ = 39.2 ± 1.2 kcal/mol at 343 K. We note that the value of the transition path time hardly effects the enthalpy of the transition state, but the entropic contribution is dependent on it and varies from 37.7 ± 1.1 kcal/mol for τTPT = 0.1 µs to 40.9 ± 1.3 kcal/mol for τTPT = 10 µs.

Fig. 5
figure 5

Kinetic and thermodynamic analysis of the TmCsp folding. a CPMG curves with a global fit, assuming a constant chemical shift difference between the folded and the unfolded state across all temperatures. b Temperature dependence of exchange rates and populations from 328 to 343 K. For comparison, the results from the experiments at 344 K are included. c Temperature dependence of ku, kf and Keq of 5FW-labeled TmCsp from 328 to 343 K. Note that only the data between 335.5 and 343 K was used to extract the thermodynamic parameters

Full size image

Based on these findings a higher temperature stabilizes the unfolded state (pU=1 − pF; Fig. 5b, lower panel; Fig. 5c, red curve; ΔGF→U decreases from 3.29 to 2.32 kcal/mol between 335.5 and 343 K) due to an entropic benefit. Likewise, but to a slightly lesser extent, a higher temperature reduces the free energy of the transition state. As a result, an increase in temperature results in a decreased energy barrier for the unfolding reaction (ΔG‡F→U decreases from 9.07 to 8.19 kcal/mol between 335.5 and 343 K), while the energy barrier for folding is slightly increased, (ΔG‡U→F changes from 5.78 to 5.87 kcal/mol between 335.5 and 343 K). This leads to the counterintuitive situation where the exchange rate (kex = kF + kU = exp(− ΔG/RT) that is dominated by kF) remains nearly constant with temperature (Fig. 5b, top panel), because ΔG‡U→F and T increase at approximately the same pace.

For high molecular weight systems, the R2 relaxation rates will be significantly higher than the rates that we observed for TmCsp. In those cases, the CPMG relaxation time has to be shortened to such an extent, that the lower relaxation dispersion frequencies can no longer be sampled, which will hamper the faithful examination of dynamics. This limitation can be resolved with R1ρ experiments that are able to sample arbitrary frequencies between a lower limit given by scalar couplings and an upper limit given by the probe head power limits. To illustrate this we applied 19F RD experiments to a 360 kDa double heptameric α7α7 complex (half proteasome) derived from the α7β7β7α7 20S proteasome of T. acidophilum (Fig. 6). The seven N-termini in each of the two α-rings have been shown to sample conformations in- and outside of the ring pore, thereby forming a functionally important dynamic gate (Sprangers and Kay 2007; Religa et al. 2010). We introduced single cysteine mutations at positions 18 and 35 of the α-subunit and labeled the purified half proteasome with BTFA to introduce a site specific 19F probe. The sample with a cysteine at position 35, that is remote from the pore, showed a modest relaxation rate of 122 Hz and a flat CPMG curve (Fig. S8). However, for the 18C-sample, we found that the single fluorine resonance at − 84 ppm shows strongly temperature dependent peak widths between 161 Hz (293 K) and 88 Hz (323 K). To monitor the gate dynamics, we collected CPMG (Fig. 6b) and R1ρ (Fig. 6c) datasets at 293 K, 303 K, 313 K and 323 K. The constant time in the CPMG experiment had to be restricted to 4 ms at 293 K which results in CPMG frequencies that are multiples of 250 Hz. In the rotating frame relaxation experiments, on the other hand, we recorded 8 different R1ρ rates below 250 Hz, which provides essential information on the exchange process. Of note, the trifluoroacetone moiety lacks vicinal protons that couple to the 19F spins and the largest scalar coupling present is a 4JFH coupling of around 1 Hz (Abraham et al. 1996) which eliminates the lower bound for the sampling of the frequencies. To extract exchange parameters, we simultaneously fitted the CPMG and R1ρ data at all temperatures with a two-state model, assuming that the Δω between the ground state and the excited state is independent of the experimental temperature. Based on that, we unexpectedly observe that higher temperatures result in significantly slower exchange rates and increased populations of the ground state (Fig. 6d). In line with this, an Eyring plot of the rate constants k1 and k−1 shows a linear decrease in ln(k) for both constants (Fig. 6e). These results arise from a negative entropy of the excited state (TΔS = − 10.1 ± 3.0 kcal/mol at 313 K) as well as the transition state (TΔS‡ = − 26.1 ± 4.8 kcal/mol at 313 K), which makes the excited state unfavorable at higher temperatures (Fig. 6f). Structurally, this behavior can be explained by a model where the N-terminal extensions are flexible in the open ground state and motionally restricted in the excited state where this region of the protein is located within the annulus pore (Fig. 6f).

Fig. 6
figure 6

19F Relaxation dispersion experiments of the 360 kDa α7α7 double heptamer. a Model of the double heptameric α7α7 complexes with 14 BTFA labeling sites at position 18C (purple) of each subunit. Position 35 that does not show exchange (Fig. S8) is indicated in cyan. The model of the complex is based on the structure of the 20S proteasome from T. acidophilum (PDB ID 1PMA). b CPMG experiments from 293 to 323 K. c On-resonance R1ρ experiments from 293 to 323 K. d Plot of exchange rates against temperatures as derived from the global fit of all RD data. e Logarithmic plot of kinetic rates against inverse temperature. f Schematic presentation of ΔG, ΔH and TΔS changes from the ground state GS to the excited state ES via a transition state TS

Full size image

Discussion and conclusions

Taken together, we here present a suite of one-dimensional 19F RD experiments, to study exchange processes in 19F-labeled proteins. The on-resonance and off-resonance R1ρ pulse sequences provide a number of important advantages over the complementary CPMG RD experiments. First, the rotating frame experiments can make use of very low spin lock fields, opening the possibility to obtain a full set of parameters at a single static magnetic field. The ability to sample arbitrary frequencies also allows study cases where the 19F signals experience fast relaxation and where CPMG experiments are restricted to higher frequencies due to the requirement for very short (2–3 ms) CPMG times (Manglik et al. 2015). In that light, it is also worth mentioning that short R1ρ sequences could be combined with recently introduced two-dimensional (2D) 19F–13C TROSY experiments, where destructive interferences between DD and CSA mechanisms in aromatic 19F–13C groups result in improved 13C line widths (Boeszoermenyi et al. 2019). Second, compared to CPMG RD experiments, the rotating frame approaches can expand the timescale of chemical exchange that is accessible to very fast (µs timescale) processes. Third, the off-resonance R1ρ experiments provide important information on the sign of the chemical shift differences, which provides direct information on the nature of the excited state.

We anticipate that fluorine NMR methods will become increasingly popular. Indeed, studies in the recent years have shown first examples of its applicability to challenging systems including GPCRs, where the possibilities for protein deuteration and methyl group labeling are limited due to the requirements of eukaryotic expression systems. Proteins from these sources can, however, be labeled with trifluoromethyl groups in a straightforward posttranscriptional manner at very low costs. The very short experimental times of the 19F based 1D experiments will further increase the applicability to systems that are not stable over time and where time intensive 13C, 15N or 1H based RD are not feasible. In the case of the TmCsp, the use of 19F RD approaches was motivated by enhanced amide-proton exchange rates at our experimental conditions, which resulted in very low quality 1H–15N based experiments. In general, 19F based experiment can thus be expected to outperform more traditional measurements at the elevated temperatures or at a higher pH. Finally, recent advances in labeling techniques have made RNA and DNA accessible for 19F NMR (Sochor et al. 2016; Nußbaumer et al. 2020; Baranowski et al. 2020), thereby further expanding the applicability of the presented methodologies. In summary, our approach will strengthen the use of 19F NMR to accurately quantify dynamic processes in a broad range of biological systems. This applicability of this strategy will benefit from the 19F capabilities of many modern NMR probe-heads.