Characterization microwave absorption from active carbon/BaSm_xFe_12−xO₁₉/polypyrrole composites analyzed with a more rigorous method

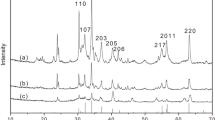
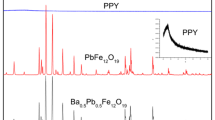
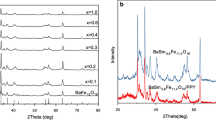
Abstract

There are problems with the conventional method of determining reflection loss for microwave absorption material. In particular, it is concluded that the ability of a material to absorb microwaves is related with sample thickness of the material. Based on this wrong conclusion, a model is then proposed on the quarter-wavelength’s sample thickness. However, it is shown in the present work that the conclusion together with the model is incorrect and that the associated experimental work needs therefore to be re-evaluated. In this work we evaluate our own experimental work on microwave absorption of a composite correctly and demonstrate the errors in the previous method. C/BaSm_xFe_12−xO₁₉ has been prepared by the hydrothermal method and C/BaSm_xFe_12−xO₁₉/PPY by in situ polymerization. The microwave absorption of the composites has then been characterized with an appropriate method. The maximum reflection loss was achieved at x = 0.2 consistently for both C/BaSm_xFe_12−xO₁₉ and C/BaSm_xFe_12−xO₁₉/PPY. The result shows that the components of active carbon, polypyrrole, and ferrite in the composites have a positive cooperating effect on microwave absorption. It is also clearly demonstrated that the result is independent of sample thickness.

Appendices

Appendices

There are many experimental reports published every year in which the theoretical background of the work is neglected and therefore needs to be re-evaluated [63, 64]. It can be argued that the research community is dependent more upon the state-of-the-art equipment and more interested in beautiful presentations than in fundamental theory and real understanding. Attractive often comes from mis- or incomplete understanding while real understanding usually comes from rudiments. Taking this into account, the Appendices provided here are included to encourage a keen interest in the rudiments of science for researchers in the field of microwave absorbing material.

The corrections made in this work demonstrated that there are theoretical background gaps between material researchers and physicians. It is a common practice to leave out the hardest elementary derivations in a presentation to achieve conciseness and clarity. However, this procedure, may give the impression that such understanding is not required by experimentalists and as a result theory is pushed further into the background. As shown in Appendix 4.3, the ability to conquer a problem or gain real understanding in research sometimes relies on the skills obtained from elementary scientific training. The derivations are detailed so that they should be easily followed by material researchers. An active attitude toward the rudiments of science is beneficial in solving scientific problems instead of only making attraction [65].

Appendix 1 The procession of magnetic moment in magnetic field

In classical physics the magnetic states of a material in microwave are related to procession of magnetic moment. The motion of a classical magnetic moment µ in a static magnetic field B₀ (=µH₀) is described by Eq. 8 [13].

$$\frac{{d{\mathbf{\mu }}}}{{dt}}=\gamma {\mathbf{\mu }} \times {{\mathbf{B}}_0}=\gamma {\mathbf{\mu }} \times {B_0}{\mathbf{k}}$$

(8)

γ is the gyromagnetic ratio. Mutually perpendicular unit vectors are indicated by i, j, k. If B is directed along the z axis with amplitude B₀ then

$$\left\{ \begin{aligned} {\mu _{xy}}(t)= & \mu _{{xy}}^{0}{e^{ - j\gamma {B_0}t}}= \mu _{{xy}}^{0}{e^{ - j{\omega _0}t}} \\ {\mu _z}(t)= & \mu _{z}^{0} \\ \end{aligned} \right.$$

(9)

µ_xy(0) and µ_z(0) are the initial values for the components of µ.

$${\mu _{xy}}={\mu _x}\mathbf{i}+{\mu _y}\mathbf{j}$$

(10)

Equations 9 and 10 illustrate the fact that the magnetic moment is processing around the magnetic field, or the z-axis. ω₀ can be either in (with respecte to negative charge) or opposite to (with respect to positive charge) the direction of k. If ω₀ is the counterclockwise rotation [3] with respect to the right-hand coordinate system

$${{\mathbf{\omega }}_0}= - \gamma {{\mathbf{B}}_0}= - {\omega _0}{\mathbf{k}}$$

(11)

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{\mu _x}(t)} \\ {{\mu _y}(t)} \\ {{\mu _z}(t)} \end{array}} \right)=\,& \left( {\begin{array}{*{20}{c}} {\cos ({\omega _0}t)}&{\sin ({\omega _0}t)}&0 \\ {\cos ({\omega _0}t+\frac{\pi }{2})}&{\sin ({\omega _0}t+\frac{\pi }{2})}&0 \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\mu _{x}^{0}} \\ {\mu _{y}^{0}} \\ {\mu _{z}^{0}} \end{array}} \right) \\ =\,& \left( {\begin{array}{*{20}{c}} {\cos ({\omega _0}t)}&{\sin ({\omega _0}t)}&0 \\ { - \sin ({\omega _0}t)}&{\cos ({\omega _0}t)}&0 \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\mu _{x}^{0}} \\ {\mu _{y}^{0}} \\ {\mu _{z}^{0}} \end{array}} \right) \\ \end{aligned}$$

(12)

Appendix 2 Relaxation after excitation

Relaxation after excitation is related to microwave consumption [13]. If there are only two energy levels with quantum spin number ± 1/2, then at time t

$$\begin{aligned} \frac{{d{n_1}(t)}}{{dt}}=\,& - {n_1}(t){P_{12}}+{n_2}(t){P_{21}} \\ =\,& - {n_1}(t)({P_{12}}+{P_{21}})+[{n_1}(t)+{n_2}(t)]{P_{21}} \\ = & - {n_1}(t)({P_{12}}+{P_{21}})+N{P_{21}} \\ \end{aligned}$$

(13)

$$\begin{aligned} \frac{{d{n_2}(t)}}{{dt}}=\,& {n_1}(t){P_{12}} - {n_2}(t){P_{21}} \\ =\,& N{P_{12}} - {n_2}(t)({P_{12}}+{P_{21}}) \\ \end{aligned}$$

(14)

$$\begin{aligned} \frac{{d{n_1}(t)}}{{dt}} - \frac{{d{n_2}(t)}}{{dt}}=\,& \frac{d}{{dt}}[{n_1}(t) - {n_2}(t)] \\ =\,& N({P_{21}} - {P_{12}}) - [{n_1}(t) - {n_2}(t)]({P_{12}}+{P_{21}}) \\ \end{aligned}$$

(15)

n₁ and n₂ are the number of magnetic moments in levels 1 and 2, respectively. P₁₂ and P₂₁ are the probabilities of upward and downward transitions, respectively. At thermodynamic equilibrium

$$\begin{aligned} N({P_{21}} - {P_{12}})= & (n_{1}^{0} - n_{2}^{0})({P_{12}}+{P_{21}}) \\ = & (n_{1}^{0} - n_{2}^{0})\left( {2\frac{{{P_{12}}+{P_{21}}}}{2}} \right)=\Delta {n^0}2\overline {P} \\ \end{aligned}$$

(16)

Inserting Eq. 16 into Eq. 15

$$\frac{{d[{n_1}(t) - {n_2}(t)]}}{{dt}}=\frac{{d[\Delta n(t)]}}{{dt}}= - 2\overline {P} \left[ {\Delta n(t) - \Delta {n^0}} \right]$$

(17)

In the magnetic field of B₀, the magnetization M is the resultant of N individual magnets processing around B₀ in unit volume and it is directed along the magnetic field, or the z axis at thermodynamic equilibrium. Transitions will occur when a linear magnetic field B₁ is applied perpendicular to the B₀ field. A linearly oscillating frequency is equivalent to two opposing circularly oscillating frequencies. The result is that M tilts away from the z-axis and processes around the axis as implied by Eqs. 37–39 and its component M_z(t) is proportional to the corresponding difference of population levels.

$$\frac{{d{M_z}}}{{dt}}= - 2\overline {P} \left[ {{M_z}(t) - M_{z}^{0}} \right]= - \frac{{{M_z}(t) - M_{z}^{0}}}{{{T_1}}}$$

(18)

T₁ is referred to as longitudinal or spin–lattice relaxation time. After excitation, M_z(t) = M_z(0) at t = 0.

$${M_z}(t)=M_{z}^{0} - \left[ {M_{z}^{0} - {M_z}(0)} \right]\exp \left( { - \frac{t}{{{T_1}}}} \right)$$

(19)

At thermodynamic equilibrium, the transverse component of the magnetization vector is equal to zero (M_⊥ = 0). With an excitation, a magnetization vector can be tilted away from z axis at a certain angle θ. In this case, there emerges a non-zero M_⊥ on the plane perpendicular to the magnetic field B₀ and the transverse or spin–spin relaxation time T₂ is not equal to T₁.

$$\frac{{d{M_ \bot }(t)}}{{dt}}= - \frac{{{M_ \bot }(t)}}{{{T_2}}}$$

(20)

$${M_ \bot }(t)={M_ \bot }(0)\exp \left( { - \frac{t}{{{T_2}}}} \right)$$

(21)

The terms relating to relaxation times contain information about the driven force and resistance to the oscillations of magnetic dipoles in microwaves.

Appendix 3 Absorption and dispersion signals

4.1 Appendix 3.1 Rotating frame of reference

Similar to Eq. 12, we obtain Eq. 22 for clockwise rotation if the exciting frequency is ω.

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{M_x}(t)} \\ {{M_y}(t)} \\ {{M_z}(t)} \end{array}} \right)=\,& \left( {\begin{array}{*{20}{c}} {\cos (\omega t)}&{ - \sin (\omega t)}&0 \\ {\cos \left( {\omega t - \frac{\pi }{2}} \right)}&{ - \sin \left( {\omega t - \frac{\pi }{2}} \right)}&0 \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{M_x}(0)} \\ {{M_y}(0)} \\ {{M_z}(0)} \end{array}} \right) \\ =\,& \left( {\begin{array}{*{20}{c}} {\cos (\omega t)}&{ - \sin (\omega t)}&0 \\ {\sin (\omega t)}&{\cos (\omega t)}&0 \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{M_x}(0)} \\ {{M_y}(0)} \\ {{M_z}(0)} \end{array}} \right) \\ \end{aligned}$$

(22)

Related to the induced M_x and M_y is the magnetic field B₁.

$${\mathbf{B}_1}={B_{1,x}}\mathbf{i}+{B_{1,y}}\mathbf{j}$$

(23)

If a rotating coordinate system is defined as

$$\left( {\begin{array}{*{20}{c}} {{\mathbf{i}}'} \\ {{\mathbf{j}}'} \\ {{\mathbf{k}}'} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {\cos (\omega t)}&{ - \sin (\omega t)}&0 \\ {\sin (\omega t)}&{\cos (\omega t)}&0 \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\mathbf{i}} \\ {\mathbf{j}} \\ {\mathbf{k}} \end{array}} \right)$$

(24)

i′, j′, k′ are unit vectors of the rotating system. i, j, k are unit vectors of the non-rotating coordinate system. The time derivatives of the unit directional vectors of rotating coordinate system can be expressed as Eq. 25 where ω = − ωk [3].

$$\left\{ {\begin{array}{l} {\frac{{d{\mathbf{i}}'}}{{dt}}={\mathbf{\omega }} \times {\mathbf{i}}'} \\ {\frac{{d{\mathbf{j}}'}}{{dt}}={\mathbf{\omega }} \times {\mathbf{j}}'} \\ {\frac{{d{\mathbf{k}}'}}{{dt}}={\mathbf{\omega }} \times {\mathbf{k}}'} \end{array}} \right.$$

(25)

Within the non-rotating coordinate system

$$\frac{{d\mathbf{M}(t)}}{{dt}}=\frac{{d{M_x}(t)}}{{dt}}\mathbf{i}+\frac{{d{M_y}(t)}}{{dt}}\mathbf{j}+\frac{{d{M_z}(t)}}{{dt}}\mathbf{k}$$

(26)

The rate of change of M(t) observed in the rotating coordinate system is denoted as $\frac{{\partial \mathbf{M}(t)}}{{\partial t}}$ and

$$\frac{{\partial \mathbf{M}(t)}}{{\partial t}} \ne \frac{{d\mathbf{M}(t)}}{{dt}}=\frac{{d{\mathbf{M}_{rot}}(t)}}{{dt}}$$

(27)

where within the rotating coordinate system

$$\frac{{\partial {{\mathbf{M}}_{rot}}(t)}}{{\partial t}}=\frac{{d{M_{x'}}(t)}}{{dt}}{\mathbf{i}}'+\frac{{d{M_{y'}}(t)}}{{dt}}{\mathbf{j}}'+\frac{{d{M_{z'}}(t)}}{{dt}}{\mathbf{k}}'$$

(28)

and from Eq. 25

$$\frac{{d{\mathbf{M}_{rot}}(t)}}{{dt}}=\frac{{\partial {\mathbf{M}_{rot}}(t)}}{{\partial t}}+\varvec{\upomega} \times {\mathbf{M}_{rot}}(t)$$

(29)

$$\begin{aligned} \frac{{\partial {\mathbf{M}_{rot}}(t)}}{{\partial t}}=\,& \frac{{d{\mathbf{M}_{rot}}(t)}}{{dt}} - \omega \times {\mathbf{M}_{rot}}(t) \\ =\,& \gamma {\mathbf{M}_{rot}}(t) \times ({B_{1,x'}}\mathbf{i}'+{B_{1,y'}}\mathbf{j}'+{B_0}\mathbf{k}')+{\mathbf{M}_{rot}}(t) \times \varvec{\upomega} \\ =\,& \gamma {\mathbf{M}_{rot}}(t) \times \left( {{\mathbf{B}_{rot}}+\frac{\omega }{\gamma }} \right)=\gamma {\mathbf{M}_{rot}}(t) \times {\mathbf{B}_{eff}} \\ \end{aligned}$$

(30)

From Eqs. 23 and 24 we obtain Eq. 31.

$$\left( {\begin{array}{*{20}{c}} {{B_{1,x'}}} \\ {{B_{1,y'}}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {\cos (\omega t)}&{ - \sin (\omega t)} \\ {\sin (\omega t)}&{\cos (\omega t)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{B_{1,x}}} \\ {{B_{1,y}}} \end{array}} \right)$$

(31)

Given that

$${{\mathbf{B}}_1}\left( t \right)={B_1}\cos (\omega t){\mathbf{i}} - {B_1}\sin (\omega t){\mathbf{j}}={B_{1,x}}{\mathbf{i}} - {B_{1,y}}{\mathbf{j}}$$

(32)

$$\left( {\begin{array}{*{20}{c}} {{B_{1,x'}}} \\ {{B_{1,y'}}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {\cos (\omega t)}&{ - \sin (\omega t)} \\ {\sin (\omega t)}&{\cos (\omega t)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{B_1}\cos (\omega t)} \\ { - {B_1}\sin (\omega t)} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {{B_1}} \\ 0 \end{array}} \right)$$

(33)

A linearly oscillating frequency is equivalent to two circularly oscillating frequencies.

4.2 Appendix 3.2 The Bloch equation

Summarizing from Eqs. 8, 18, and 20, the Bloch equations are obtained as Eqs. 34 and 35.

$$\frac{{d{\mathbf{M}}(t)}}{{dt}}=\gamma {\mathbf{{\rm M}}}(t) \times {\mathbf{B}} - \frac{{{M_x}(t){\mathbf{i}}+{M_y}(t){\mathbf{j}}}}{{{T_2}}} - \frac{{{M_z}(t) - M_{z}^{0}}}{{{T_1}}}{\mathbf{k}}$$

(34)

$$\frac{{\partial {{\mathbf{M}}_{rot}}(t)}}{{\partial t}}=\gamma {{\mathbf{M}}_{rot}}(t) \times {{\mathbf{B}}_{eff}} - \frac{{{M_{x'}}(t){\mathbf{i}}'+{M_{y'}}(t){\mathbf{j}}'}}{{{T_2}}} - \frac{{{M_{z'}}(t) - M_{z}^{0}}}{{{T_1}}}{\mathbf{k}}'$$

(35)

4.3 Appendix 3.3 Complex susceptibility

From Eqs. 32 and 34 we obtain Eqs. 36–39.

$$\mathbf{M}(t) \times \mathbf{B}=\left| {\begin{array}{*{20}{c}} \mathbf{i}&\mathbf{j}&\mathbf{k} \\ {{M_x}(t)}&{{M_y}(t)}&{{M_z}(t)} \\ {{B_1}\cos (\omega t)}&{ - {B_1}\sin (\omega t)}&{{B_0}} \end{array}} \right|$$

(36)

$$\frac{{d{M_x}(t)}}{{dt}}=\gamma {M_y}(t){B_0}+\gamma {M_z}(t){B_1}\sin (\omega t) - \frac{{{M_x}(t)}}{{{T_2}}}$$

(37)

$$\frac{{d{M_y}(t)}}{{dt}}= - \gamma {M_x}(t){B_0}+\gamma {M_z}(t){B_1}\cos (\omega t) - \frac{{{M_y}(t)}}{{{T_2}}}$$

(38)

$$\frac{{d{M_z}(t)}}{{dt}}= - \gamma {M_x}(t){B_1}\sin (\omega t) - \gamma {M_y}(t){B_1}\cos (\omega t) - \frac{{{M_z}(t) - M_{z}^{0}}}{{{T_1}}}$$

(39)

From Eqs. 22 and 24

$${M_{x'}}(t)={M_x}(t)\cos (\omega t) - {M_y}(t)\sin (\omega t)$$

(40)

$$\begin{aligned} {M_{y'}}(t) =\,& {M_x}(t)\cos \left( {\omega t \pm \frac{\pi }{2}} \right)+{M_y}(t)\sin \left( {\omega t \pm \frac{\pi }{2}} \right) \\ =\,& \pm \left[ {{M_x}(t)\sin (\omega t)+{M_y}(t)\cos (\omega t)} \right] \\ \end{aligned}$$

(41)

The negative sign in Eq. 41 is reasonable [13] because

$${M_{y'}}(t)=\frac{1}{{\gamma {B_0}}}\frac{{d{M_{x'}}(t)}}{{dt}}$$

(42)

In other words, M_x(t) = M_x′(t)exp(− t/T₂) and M_y(t) = M_y′(t)exp(− t/T₂) are solutions for Eqs. 37 and 38 after the excitation or when B₁ = 0. In fact, a solution for a differential equation multiplied by an arbitrary constant is still a solution to the equation. From Eqs. 25, 29, 37–41 we obtain Eqs. 43–45.

(43)

$$\begin{aligned} \frac{{d{M_{y'}}(t)}}{{dt}}=\,& \frac{{d{M_x}(t)}}{{dt}}\sin (\omega t)+\frac{{d{M_y}(t)}}{{dt}}\cos (\omega t) \\ + & \omega [{M_x}(t)\cos (\omega t) - {M_y}(t)\sin (\omega t)] \\ =\,& \left[ {\frac{{d{M_{y'}}(t)}}{{dt}}{\mathbf{j}}' - {\mathbf{\omega }} \times {M_{x'}}(t){\mathbf{i}}'} \right] \cdot {\mathbf{j}}' \\ =\,& \left[ {\gamma {M_y}(t){B_0}+\gamma {M_z}(t){B_{\text{1}}}\sin (\omega t) - \frac{{{M_x}(t)}}{{{T_2}}}} \right]\sin (\omega t) \\ + & \left[ { - \gamma {M_x}(t){B_0}+\gamma {M_z}(t){B_{\text{1}}}\cos (\omega t) - \frac{{{M_y}(t)}}{{{T_2}}}} \right]\cos (\omega t)+\omega {M_{x'}}(t) \\ =\,& (\omega - {\omega _0}){M_{x'}}(t) - \frac{{{M_{y'}}(t)}}{{{T_2}}}+\gamma {B_{\text{1}}}{M_z}(t) \\ \end{aligned}$$

(44)

$$\begin{aligned} \frac{{d{M_{z'}}(t)}}{{dt}}=\,& \frac{{d{M_z}(t)}}{{dt}} \\ =\,& \left[ {\frac{{d{M_{z'}}(t)}}{{dt}}\mathbf{k}' - \varvec{\upomega} \times {M_{x'}}(t)\mathbf{k}'} \right] \cdot \mathbf{k}' \\ =\,& \gamma {M_x}(t){B_y} - \gamma {M_y}(t){B_x} - \frac{{{M_z}(t) - M_{z}^{0}}}{{{T_1}}} \\ =\,& - \gamma {M_x}(t){B_1}\sin (\omega t) - \gamma {M_y}(t){B_1}\cos (\omega t) - \frac{{{M_z}(t) - M_{z}^{0}}}{{{T_1}}} \\ =\,& - \gamma {B_1}{M_{y'}}(t) - \frac{{{M_z}(t) - M_{z}^{0}}}{{{T_1}}} \\ \end{aligned}$$

(45)

M_x′(t) = M₀cos(ω − ω₀)exp(− t/T₂) and M_y′(t) = M₀sin(ω − ω₀)exp(− t/T₂) are solutions for Eqs. 43 and 44 when the excitation is finished or B₁ = 0. The solution to the differential equation concerning electric dipole given in Ref. [13] relates to the alternating electric field and the complex polarizability α is reproduced as Eq. 46.

$$\alpha =\frac{{{e^2}m(\omega _{0}^{2} - {\omega ^2})}}{{{m^2}{{(\omega _{0}^{2} - {\omega ^2})}^2}+4{{(\eta ')}^2}{\omega ^2}}} - j\frac{{2{e^2}\eta '\omega }}{{{m^2}{{(\omega _{0}^{2} - {\omega ^2})}^2}+4{{(\eta ')}^2}{\omega ^2}}}$$

(46)

η′ in Eq. 46 is the resistance to the movement of the electron and defined in Ref. [13] as η′ = mη. m and e are the mass and charge of an electron, respectively. Similarly, the general solution to Eqs. 43–45 relates magnetization to alternating magnetic field and the complex susceptibility is thus obtained. When the rate of change of frequency $\frac{{d\omega }}{{dt}}$ or the passage of time through the resonance region τ compared with the rate of spin–spin relaxation satisfies

$$\begin{array}{*{20}{l}} {\frac{{d\omega }}{{dt}}<<\frac{1}{{T_{2}^{2}}};}&{and}&{\tau>>{T_2}} \end{array}$$

(47)

The components of magnetization slowly change over time and all three of the time variables in Eqs. 43–45 are small and can be set equal to zero.

$$\left\{ {\begin{array}{*{20}{c}} { - \frac{1}{{{T_2}}}{M_{x'}}(t)+({\omega _0} - \omega ){M_{y'}}+0 \cdot {M_z}(t)=0} \\ {(\omega - {\omega _0}){M_{x'}}(t) - \frac{1}{{{T_2}}}{M_{y'}}(t)+\gamma {B_1}{M_z}(t)=0} \\ {0 \cdot {M_{x'}}(t) - \gamma {B_1}{M_{y'}}(t) - \frac{1}{{{T_1}}}{M_z}(t)= - \frac{{M_{z}^{0}}}{{{T_1}}}} \end{array}} \right.$$

(48)

The solution of Eq. 48 is

$$\left\{ {\begin{array}{*{20}{c}} {{M_{x'}}(t)=M_{z}^{0}\frac{{\gamma {B_1}T_{2}^{2}({\omega _0} - \omega )}}{{1+T_{2}^{2}{{({\omega _0} - \omega )}^2}+{\gamma ^2}B_{1}^{2}{T_1}{T_2}}}} \\ {{M_{y'}}(t)=M_{z}^{0}\frac{{\gamma {B_1}{T_2}}}{{1+T_{2}^{2}{{({\omega _0} - \omega )}^2}+{\gamma ^2}B_{1}^{2}{T_1}{T_2}}}} \\ {{M_z}(t)=M_{z}^{0}\frac{{1+T_{2}^{2}{{({\omega _0} - \omega )}^2}}}{{1+T_{2}^{2}{{({\omega _0} - \omega )}^2}+{\gamma ^2}B_{1}^{2}{T_1}{T_2}}}} \end{array}} \right.$$

(49)

The rotating field H₁ is a linearly polarized field along the x axis and represented by 2H₁cos(ωt). The response of nuclear moments to excitation with this radiation can be described by complex susceptibility χ similar to Eq. 46.

$$\chi =\chi ^{\prime} - {\text{j}}\chi ^{\prime\prime}$$

(50)

$${M_{x'}}(t)=(2{H_1})\chi '={\chi _0}{H_0}\frac{{\mu\gamma T_{2}^{2}({\omega _0} - \omega )}}{{2[1+T_{2}^{2}{{({\omega _0} - \omega )}^2}+{\gamma ^2}B_{1}^{2}{T_1}{T_2}]}}2{H_1}$$

(51)

$${M_{y'}}(t)=(2{H_1})\chi ^{\prime\prime}=\frac{{{\mu\chi _0}{\omega _0}{T_2}}}{{2[1+T_{2}^{2}{{({\omega _0} - \omega )}^2}+{\gamma ^2}B_{1}^{2}{T_1}{T_2}]}}2{H_1}$$

(52)

The real part of the susceptibility produces the positive or negative dispersion signal while the imaginary part of the susceptibility gives rise to the positive or negative absorption signal [66,67,68].

Appendix 4 Examples of absorptions from magnetic resonance

Absorption from non-resonance forced oscillation of dipole moment, related to the background of a resonance absorption spectrum, is weak and frequency insensitive [13]. There might be a peak with reflection loss R_M = − ∞ dB within very narrow frequency range when the microwave frequency is increased from a region where |ε_r| > |µ_r| to a region where |µ_r| > |ε_r|. The absorption from resonance is strong and narrow which can be easily missed in the data collection process when measured with a VNA [26]. Some examples of resonance absorption are presented with the NMR spectrum.

5.1 Appendix 4.1 The two-spin system AX

A single phased material is uniform and the microwave transmission-line theory can be applied [26]. However, the environments of a uniformed material may differ locally. The local resonance magnetic field H₀ experienced by two protons may resonate at different fields of H_A0 and H_X0, respectively, resulting in two absorption peaks at different positions. The two-spin system is denoted by AX when the environments of two protons A and X are completely different. If coupling between the two protons is ignored, there are only two resonance frequencies among four possible states as shown by Fig. 7a since the selection rule about the total spin quantum number for the system is ΔS_z = ± 1. The transitions of ΔS_z = 0 and ± 2 are forbidden.

Fig. 7

The states and the absorption peaks for a two-spin system AX. ν_A and ν_X are resonance frequencies for protons A and X, respectively, when the coupling constant J_AX is zero (a). (b) is for the case where the coupling constant is non-zero. α and β are spin wave functions with quantum number s_z of ±1/2, respectively

The energy of the four states of the AX system are given by Eqs. 53 and 54 [69].

$$\begin{aligned} {E_{{\alpha _A}{\alpha _X}}}=\,& \left( {\begin{array}{*{20}{c}} {{\alpha _A}}&{{\alpha _X}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\widehat {H}}&0 \\ 0&{\widehat {H}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\alpha _A}} \\ {{\alpha _X}} \end{array}} \right) \\ =\,& \left( {\begin{array}{*{20}{c}} {{\alpha _A}}&{{\alpha _X}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{1}{2}\gamma \hbar {H_{A0}}}&0 \\ 0&{\frac{1}{2}\gamma \hbar {H_{X0}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\alpha _A}} \\ {{\alpha _X}} \end{array}} \right) \\ =\,& \left( {\begin{array}{*{20}{c}} {{\alpha _A}}&{{\alpha _X}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{1}{2}h{\nu _A}}&0 \\ 0&{\frac{1}{2}h{\nu _X}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\alpha _A}} \\ {{\alpha _X}} \end{array}} \right) \\ =\,& \frac{h}{2}({\nu _A}+{\nu _X}) \\ \end{aligned}$$

(53)

and

$$\begin{aligned} {E_{{\alpha _A}{\beta _X}}} =\,& \frac{h}{2}({\nu _A} - {\nu _X}) \\ {E_{{\beta _A}{\alpha _X}}}=\,& - \frac{h}{2}({\nu _A} - {\nu _X}) \\ {E_{{\beta _A}{\beta _X}}} =\,& - \frac{h}{2}({\nu _A}+{\nu _X}) \\ \end{aligned}$$

(54)

$\widehat {H}$is the Hamiltonian operator. If proton A is affected by the magnetic field of the magnetic moment of X and vice versa, there will be coupling among the two protons. The energies of the states of α_Aα_X and β_Aβ_X are raised by J_AX/4 and those of β_Aα_X and α_Aβ_X are lowered by J_AX/4 as calculated by Eqs. 55 and 56 for the energy corrections from the coupling. The two absorption peaks originally at ν_A and ν_X are now split into four peaks as shown by Fig. 7b.

$$\begin{aligned} \Delta E_{{\alpha _{A} \alpha _{X} }} =\,& \;\left\langle {\alpha _{A} \alpha _{X} |J_{{AX}} \widehat{{s_{A} }}\widehat{{s_{X} }}|\alpha _{A} \alpha _{X} } \right\rangle \\ =\,& J_{{AX}} \left\langle {\alpha _{A} \alpha _{X} |\widehat{{s_{{x,A}} }}\widehat{{s_{{x,X}} }} + \widehat{{s_{{y,A}} }}\widehat{{s_{{y,X}} }} + \widehat{{s_{{z,A}} }}\widehat{{s_{{z,X}} }}|\alpha _{A} \alpha _{X} } \right\rangle \\ =\,& J_{{AX}} \left( {\frac{1}{4}\left\langle {\alpha _{A} \alpha _{X} |\beta _{A} \beta _{X} } \right\rangle - \frac{1}{4}\left\langle {\alpha _{A} \alpha _{X} |\beta _{A} \beta _{X} } \right\rangle + \frac{1}{4}\left\langle {\alpha _{A} \alpha _{X} |\alpha _{A} \alpha _{X} } \right\rangle } \right) \\ =\,& \frac{1}{4}J_{{AX}} \\ \end{aligned}$$

(55)

and

$$\begin{aligned} \Delta {E_{{\alpha _A}{\beta _X}}}=\,& - \frac{1}{4}{J_{AX}} \\ \Delta {E_{{\beta _A}{\alpha _X}}}=\,& - \frac{1}{4}{J_{AX}} \\ \Delta {E_{{\beta _A}{\beta _X}}}=\,& \frac{1}{4}{J_{AX}} \\ \end{aligned}$$

(56)

The behavior of the spin operators is demonstrated by Eqs. 57–59. The constant h/2π from the operations has been absorbed into the coupling constant.

$$\begin{gathered} \widehat {{{s_z}}}\alpha =\widehat {{{s_z}}}\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)=\frac{\hbar }{2}\alpha \hfill \\ \widehat {{{s_z}}}\beta =\widehat {{{s_z}}}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)= - \frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)= - \frac{\hbar }{2}\beta \hfill \\ \end{gathered}$$

(57)

$$\begin{gathered} \widehat {{{s_x}}}\alpha =\widehat {{{s_x}}}\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)=\frac{\hbar }{2}\beta \hfill \\ \widehat {{{s_x}}}\beta =\widehat {{{s_x}}}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)=\frac{\hbar }{2}\alpha \hfill \\ \end{gathered}$$

(58)

$$\begin{gathered} \widehat {{{s_y}}}\alpha =\widehat {{{s_y}}}\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 0&{ - j} \\ j&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)=\frac{\hbar }{2}j\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)=\frac{\hbar }{2}j\beta \hfill \\ \widehat {{{s_y}}}\beta =\widehat {{{s_y}}}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)=\frac{\hbar }{2}\left( {\begin{array}{*{20}{c}} 0&{ - j} \\ j&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)= - \frac{\hbar }{2}j\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)= - \frac{\hbar }{2}j\alpha \hfill \\ \end{gathered}$$

(59)

5.2 Appendix 4.2 The two-spin system AA

Another extreme is the AA spin system where the two protons are equivalent and thus the two states α_A1β_A2 and β_A1α_A2 must be combined as shown by Fig. 8 [70, 71].

Fig. 8

The states and the absorption peaks for a two-spin system AA. In (a) the coupling constant J_AA is zero while in (b) the coupling constant is non-zero

When the coupling from the two protons is ignored, the energies for the four states are

$$\begin{gathered} {E_{{\alpha _{A1}}{\alpha _{A2}}}}=\left( {\begin{array}{*{20}{c}} {{\alpha _{A1}}}&{{\alpha _{A2}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{1}{2}h{\nu _A}}&0 \\ 0&{\frac{1}{2}h{\nu _A}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\alpha _{A1}}} \\ {{\alpha _{A2}}} \end{array}} \right)=h{\nu _A} \hfill \\ {E_{({\alpha _{A1}}{\beta _{A2}}{+_{\beta A1}}{\alpha _{A2}})/\sqrt 2 }}=0 \hfill \\ {E_{({\alpha _{A1}}{\beta _{A2}}{ - _{\beta A1}}{\alpha _{A2}})/\sqrt 2 }}=0 \hfill \\ {E_{{\beta _{A1}}{\beta _{A2}}}}= - h{\nu _A} \hfill \\ \end{gathered}$$

(60)

The transitions are allowed only between wave functions of the same symmetry and forbidden between symmetric and antisymmetric wave functions. Although there are four spin states, only two transitions occur at the same position and the result is a singlet at ν_A as shown by Fig. 8a. The transition probability

$$\begin{gathered} \left\langle {\alpha _{{A1}} \alpha _{{A2}} |\widehat{{S_{ + } }}|(\alpha _{{A1}} \beta _{{A2}} + \beta _{{A1}} \alpha _{{A2}} ){\text{/}}\sqrt 2 } \right\rangle ^{2} \hfill \\ = \frac{1}{2}\left\langle {\alpha _{{A1}} \alpha _{{A2}} |\widehat{{s_{{ + ,A1}} }} + \widehat{{s_{{ + ,A2}} }}|(\alpha _{{A1}} \beta _{{A2}} + \beta _{{A1}} \alpha _{{A2}} )} \right\rangle ^{2} \hfill \\ = \frac{1}{2}\left\langle {\alpha _{{A1}} \alpha _{{A2}} |(\alpha _{{A1}} \alpha _{{A2}} + \alpha _{{A1}} \alpha _{{A2}} )} \right\rangle ^{2} = 2 \hfill \\ \end{gathered}$$

(61)

$$\begin{gathered} \left\langle {(\alpha _{{A1}} \beta _{{A2}} - \beta _{{A1}} \alpha _{{A2}} )/\sqrt 2 |\widehat{{S_{ + } }}|\beta _{{A1}} \beta _{{A2}} } \right\rangle ^{2} \hfill \\ = \frac{1}{2}\left\langle {(\alpha _{{A1}} \beta _{{A2}} - \beta _{{A1}} \alpha _{{A2}} )|(\alpha _{{A1}} \beta _{{A2}} + \beta _{{A1}} \alpha _{{A2}} )} \right\rangle ^{2} = 0 \hfill \\ \end{gathered}$$

(62)

where S₊ is the raising operator defined by

$$\begin{gathered} \widehat {{{s_+}}}|{s_z}\ge(\widehat {{{s_x}}}+j\widehat {{{s_y}}})|{s_z}\ge\sqrt {(s - {s_z})(s+{s_z}+1)} |{s_z}+1> \hfill \\ \widehat {{{s_+}}}\beta =\alpha \hfill \\ \widehat {{{s_+}}}\alpha =0 \hfill \\ \end{gathered}$$

(63)

When J_AA ≠ 0, the corrections for the energies of the four spin states are

$$\begin{aligned} \Delta E_{{(\alpha _{{A1}} \beta _{{A2}} + \beta _{{A1}} \alpha _{{A2}} )/\sqrt 2 }} =\,& \frac{1}{2}\left\langle {\alpha _{{A1}} \beta _{{A2}} + \beta _{{A1}} \alpha _{{A2}} |J_{{AA}} \widehat{{s_{{A1}} }}\widehat{{s_{{A2}} }}|\alpha _{{A1}} \beta _{{A2}} + \beta _{{A1}} \alpha _{{A2}} } \right\rangle \\ =\,& \frac{1}{2}J_{{AA}} \left\langle {\alpha _{{A1}} \beta _{{A2}} + \beta _{{A1}} \alpha _{{A2}} |\widehat{{s_{{x,A1}} }}\widehat{{s_{{x,A2}} }} + \widehat{{s_{{y,A1}} }}\widehat{{s_{{y,A2}} }} + \widehat{{s_{{z,A1}} }}\widehat{{s_{{z,A2}} }}|\alpha _{{A1}} \beta _{{A2}} + \beta _{{A1}} \alpha _{{A2}} } \right\rangle \\ =\,& \frac{1}{2}J_{{AA}} \left( {\frac{1}{2} + \frac{1}{2} - \frac{1}{2}} \right) = \frac{1}{4}J_{{AA}} \\ \end{aligned}$$

(64)

$$\begin{gathered} \Delta {E_{({\alpha _{A1}}{\beta _{A2}} - {\beta _{A1}}{\alpha _{A2}})/\sqrt 2 }}= - \frac{3}{4}{J_{AA}} \hfill \\ \Delta {E_{{\alpha _{A1}}{\alpha _{A2}}}}=\frac{1}{4}{J_{AA}} \hfill \\ \Delta {E_{{\beta _{A1}}{\beta _{A2}}}}=\frac{1}{4}{J_{AA}} \hfill \\ \end{gathered}$$

(65)

As shown by Fig. 8b, all the symmetric states are raised in energy by J_AA/4, and the asymmetric state is lowered by − 3J_AA/4. The transitions between symmetric and antisymmetric states are forbidden, and each symmetric state is perturbed by the same amount, the two transitions occur at the same position, and the result is a singlet at ν_A. There is no split among equivalent protons.

5.3 Appendix 4.3 The two-spin system AB

The most complex is that the two protons are similar in AB system. The combination of α_Aβ_B and β_Aα_B

$$\Phi ({\text{A}},{\text{B}})={c_1}{\alpha _A}{\beta _B}+{c_2}{\beta _A}{\alpha _B}$$

(66)

can be determined by Eq. 67 from Eqs. 54 and 56.

$$\left( {\begin{array}{*{20}{c}} {\frac{1}{2}({\nu _A} - {\nu _B}) - \frac{1}{4}{J_{AB}}}&{\frac{1}{2}{J_{AB}}} \\ {\frac{1}{2}{J_{AB}}}&{ - \frac{1}{2}({\nu _A} - {\nu _B}) - \frac{1}{4}{J_{AB}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{c_1}} \\ {{c_2}} \end{array}} \right)={E_{\alpha \beta }}\left( {\begin{array}{*{20}{c}} {{c_1}} \\ {{c_2}} \end{array}} \right)$$

(67)

$$\begin{gathered} {\left( {{E_{\alpha \beta }}+\frac{1}{4}{J_{AB}}} \right)^2}=\frac{1}{4}[{({\nu _A} - {\nu _B})^2}+J_{{AB}}^{2}] \hfill \\ {E_{\alpha \beta }}= \pm \frac{1}{2}\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} - \frac{1}{4}{J_{AB}} \hfill \\ \end{gathered}$$

(68)

while

$$\begin{gathered} {E_{\alpha \alpha }}=\frac{1}{2}({\nu _A}+{\nu _B})+\frac{1}{4}{J_{AB}} \hfill \\ {E_{\beta \beta }}= - \frac{1}{2}({\nu _A}+{\nu _B})+\frac{1}{4}{J_{AB}} \hfill \\ \end{gathered}$$

(69)

Figure 9a represents an AB system when the coupling constant J_AB = 0. As indicated by the dashed arrows, E_ββ = − (ν_A + ν_B)/2 and E_αβ⁺ = (ν_A − ν_B)/2. Thus, the transition from β_Aβ_B to α_Aβ_B⁺ occurs at ν_A. And similarly, the transition from β_Aβ_B to α_Aβ_B⁻ occurs at ν_B. Figures 7a and 9a are different representations of the same result. There are only two absorption peaks among the four states. Figure 9b is an intermediate representation. As indicated by the dashed arrows, the two states α_Aβ_B⁺ and α_Aβ_B⁻ are raised and lowered respectively in energy by D/2 from those shown by Fig. 9a. D is defined as

$$\frac{1}{2}D=\frac{1}{2}\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} - \frac{1}{2}({\nu _A} - {\nu _B})$$

(70)

and

$$({\nu _A} - {\nu _B})+D=\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}}$$

(71)

Fig. 9

The states and the absorption peaks for a two-spin system AB. aJ_AB = 0; b an intermediate representation; c a full representation

The changes in these two states only shift the absorption peaks and do not split them. Figure 9c is a full representation of Eqs. 68 and 69. It evolves from Fig. 9b indicated by the dashed arrows that the two middle states α_Aβ_B⁺ and α_Aβ_B⁻ are lowered in energy by J_AB/4 and the two outer states β_Aβ_B and α_Aα_B are raised in energy by J_AB/4, resulting four absorption peaks.

When ν_A − ν_B > > J_AB then $\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}}$ in Eq. 68 equals ν_A − ν_B and the AB spin system becomes the AX spin system. When ν_A = ν_B, the AB spin system becomes the AA spin system.

The transition probability

$$\begin{gathered} \left\langle {(c_{1}^{ + } \alpha _{A} \beta _{B} + c_{2}^{ + } \beta _{A} \alpha _{B} )|\widehat{{S_{ + } }}|\beta _{A} \beta _{B} } \right\rangle ^{2} \hfill \\ = \left\langle {(c_{1}^{ + } \alpha _{A} \beta _{B} + c_{2}^{ + } \beta _{A} \alpha _{B} )|\widehat{{s_{{ + ,A1}} }} + \widehat{{s_{{ + ,B}} }}|\beta _{A} \beta _{B} } \right\rangle ^{2} \hfill \\ = \left\langle {(c_{1}^{ + } \alpha _{A} \beta _{B} + c_{2}^{ + } \beta _{A} \alpha _{B} )|(\alpha _{A} \beta _{B} + \beta _{A} \alpha _{B} )} \right\rangle ^{2} \hfill \\ = (c_{1}^{ + } + c_{2}^{ + } )^{2} \hfill \\ \end{gathered}$$

(72)

$$\begin{gathered} \left\langle {\alpha _{A} \alpha _{B} |\widehat{{S_{ + } }}|(c_{1}^{ - } \alpha _{A} \beta _{B} + c_{2}^{ - } \beta _{A} \alpha _{B} )} \right\rangle ^{2} \hfill \\ = \left\langle {\alpha _{A} \alpha _{B} |(c_{1}^{ - } \alpha _{A} \alpha _{B} + c_{2}^{ - } \alpha _{A} \alpha _{B} )} \right\rangle ^{2} \hfill \\ = (c_{1}^{ - } + c_{2}^{ - } )^{2} \hfill \\ \end{gathered}$$

(73)

The coefficients of the combined functions can be obtained from Eqs. 67 and 68.

$$\left[ {\frac{1}{2}({\nu _A} - {\nu _B}) - \frac{1}{4}{J_{AB}} - {E_{\alpha \beta }}} \right]{c_1}+\frac{1}{2}{J_{AB}}{c_2}=0$$

(74)

$$\begin{aligned} \frac{{{c_2}}}{{{c_1}}}=\,& - \frac{{\left[ {\frac{1}{2}({\nu _A} - {\nu _B}) - \frac{1}{4}{J_{AB}} - {E_{\alpha \beta }}} \right]}}{{\frac{1}{2}{J_{AB}}}} \\ =\,& \frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B}) \pm \sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right] \\ \end{aligned}$$

(75)

The ratio of the intensities or transition probabilities are

$$\begin{aligned} \frac{{{{({c_{1,\alpha {\beta ^+}}}+{c_{2,\alpha {\beta ^+}}})}^2}}}{{{{({c_{1,\alpha {\beta ^ - }}}+{c_{2,\alpha {\beta ^ - }}})}^2}}}=\,& {\left( {\frac{{{c_{1,\alpha {\beta ^+}}}}}{{{c_{1,\alpha {\beta ^ - }}}}}} \right)^2}\frac{{{{\left( {1+\frac{{{c_{2,\alpha {\beta ^+}}}}}{{{c_{1,\alpha {\beta ^+}}}}}} \right)}^2}}}{{{{\left( {1+\frac{{{c_{2,\alpha {\beta ^ - }}}}}{{{c_{1,\alpha {\beta ^ - }}}}}} \right)}^2}}}={\left( {\frac{{{c_{1,\alpha {\beta ^+}}}}}{{{c_{2,\alpha {\beta ^+}}}}}} \right)^2}\frac{{{{\left( {1+\frac{{{c_{2,\alpha {\beta ^+}}}}}{{{c_{1,\alpha {\beta ^+}}}}}} \right)}^2}}}{{{{\left( {1+\frac{{{c_{2,\alpha {\beta ^ - }}}}}{{{c_{1,\alpha {\beta ^ - }}}}}} \right)}^2}}} \\ =\,& \frac{{{{\left\{ {1+\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}}}{{{{\left\{ {\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}{{\left\{ {1 - \frac{1}{{{J_{AB}}}}\left[ {({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}}} \\ =\,& \frac{{{{\left\{ {1+\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}}}{{{{\left\{ {\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right] - 1} \right\}}^2}}} \\ =\,& \frac{{{{\left\{ {1+\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}}}{{{{\left\{ {1 - \frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}}} \\ =\,& \frac{{{{\left( {1+\frac{{{c_{2,\alpha {\beta ^+}}}}}{{{c_{1,\alpha {\beta ^+}}}}}} \right)}^2}}}{{{{\left( {1 - \frac{{{c_{2,\alpha {\beta ^+}}}}}{{{c_{1,\alpha {\beta ^+}}}}}} \right)}^2}}}=\frac{{{{({c_{1,\alpha {\beta ^+}}}+{c_{2,\alpha {\beta ^+}}})}^2}}}{{{{({c_{1,\alpha {\beta ^+}}} - {c_{2,\alpha {\beta ^+}}})}^2}}}=\frac{{{{({c_{1,\alpha {\beta ^+}}}+{c_{2,\alpha {\beta ^+}}})}^2}}}{{{{({c_{2,\alpha {\beta ^+}}} - {c_{1,\alpha {\beta ^+}}})}^2}}} \\ =\,& \frac{{{{\left( {{c_{1,\alpha {\beta ^+}}}+{c_{2,\alpha {\beta ^+}}}} \right)}^2}}}{{{{\left( {{c_{1,\alpha {\beta ^ - }}}+{c_{2,\alpha {\beta ^ - }}}} \right)}^2}}} \\ \end{aligned}$$

(76)

$$\begin{aligned} \frac{{{{\left( {1+\frac{{{c_{2,\alpha {\beta ^+}}}}}{{{c_{1,\alpha {\beta ^+}}}}}} \right)}^2}}}{{{{\left( {1 - \frac{{{c_{2,\alpha {\beta ^+}}}}}{{{c_{1,\alpha {\beta ^+}}}}}} \right)}^2}}}=\,& \frac{{{{\left\{ {1+\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}}}{{{{\left\{ {1 - \frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}}} \\ =\,& \frac{{1+{{\left\{ {\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}+\frac{2}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]}}{{1+{{\left\{ {\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2} - \frac{2}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]}} \\ =\,& \frac{{2J_{{AB}}^{2}+2{{({\nu _A} - {\nu _B})}^2} - 2({\nu _A} - {\nu _B})\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} +2{J_{AB}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]}}{{2J_{{AB}}^{2}+2{{({\nu _A} - {\nu _B})}^2} - 2({\nu _A} - {\nu _B})\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} - 2{J_{AB}}\left[ { - ({\nu _A} - {\nu _B})+\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]}} \\ =\,& \,\frac{{{J_{AB}}[{J_{AB}} - ({\nu _A} - {\nu _B})]+{{({\nu _A} - {\nu _B})}^2} - \left[ {({\nu _A} - {\nu _B}) - {J_{AB}}]\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]}}{{{J_{AB}}[{J_{AB}}+({\nu _A} - {\nu _B})]+{{({\nu _A} - {\nu _B})}^2} - [({\nu _A} - {\nu _B})+{J_{AB}}]\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }} \\ =\,& \frac{{{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2} - J_{{AB}}^{2} - [({\nu _A} - {\nu _B}) - {J_{AB}}]\left[ {\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} +{J_{AB}}} \right]}}{{{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2} - J_{{AB}}^{2} - [({\nu _A} - {\nu _B})+{J_{AB}}]\left[ {\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} - {J_{AB}}} \right]}} \\ =\,& \frac{{\left[ {\left( {\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} - {J_{AB}}} \right) - ({\nu _A} - {\nu _B})+{J_{AB}}} \right]\left[ {\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} +{J_{AB}}} \right]}}{{\left[ {\left( {\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} +{J_{AB}}} \right) - ({\nu _A} - {\nu _B}) - {J_{AB}}} \right]\left[ {\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} - {J_{AB}}} \right]}} \\ =\,& \frac{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} +{J_{AB}}}}{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} - {J_{AB}}}}=\frac{{[({\nu _A} - {\nu _B})+D]+{J_{AB}}}}{{[({\nu _A} - {\nu _B})+D] - {J_{AB}}}} \\ \end{aligned}$$

(77)

[(ν_A − ν_B) + D] is defined by Eq. 71 and shown in Fig. 9c. Thus, the intensity ratio corresponds to the ratio of the distances between the outer and the inner absorption peaks [72]. The tough algebra in Eqs. 76 and 77 is considered to be elementary and is therefore often omitted for conciseness and clarity in presentations. However, to gain a real understanding, a rudimentary skill in algebra is vital.

The coefficients of the combined wave function in Eq. 66 can be calculated from Eqs. 74 and 78.

$$c_{1}^{2}+c_{2}^{2}=1$$

(78)

$$\frac{1}{{c_{1}^{2}}}=1+\frac{{c_{2}^{2}}}{{c_{1}^{2}}}=1+{\left\{ {\frac{1}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B}) \pm \sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}^2}$$

(79)

$$\begin{aligned} c_{1}^{2}=\,& \frac{{J_{{AB}}^{2}}}{{J_{{AB}}^{2}+{{\left\{ {\left[ { - ({\nu _A} - {\nu _B}) \pm \sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]} \right\}}^2}}} \\ =\,& \frac{{J_{{AB}}^{2}}}{{2J_{{AB}}^{2}+2{{({\nu _A} - {\nu _B})}^2} \mp 2({\nu _A} - {\nu _B})\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }} \\ =\,& \frac{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} \pm ({\nu _A} - {\nu _B})}}{{2\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }} \\ =\,& \frac{1}{2}(1 \pm \frac{{{\nu _A} - {\nu _B}}}{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }}) \\ \end{aligned}$$

(80)

Equation 81 is obtained from Eqs. 75 and 80.

$$\begin{aligned} {c_2}=\,& \frac{{{c_1}}}{{{J_{AB}}}}\left[ { - ({\nu _A} - {\nu _B}) \pm \sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right] \\ =\,& \sqrt {\frac{1}{2}\left( {1 \pm \frac{{{\nu _A} - {\nu _B}}}{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }}} \right)} \frac{{ - {J_{AB}}}}{{\left[ { - ({\nu _A} - {\nu _B}) \mp \sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} } \right]}} \\ =\,& \sqrt {\frac{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} \pm ({\nu _A} - {\nu _B})}}{{2\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }}} \frac{{{J_{AB}}}}{{\left[ { \pm \sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} +({\nu _A} - {\nu _B})} \right]}} \\ =\,& \pm \sqrt {\frac{{J_{{AB}}^{2}}}{{2\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} [\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} \pm ({\nu _A} - {\nu _B})]}}} \\ =\,& \pm \sqrt {\frac{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} \mp ({\nu _A} - {\nu _B})}}{{2\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }}} = \pm \sqrt {\frac{1}{2}\left( {1 \mp \frac{{{\nu _A} - {\nu _B}}}{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }}} \right)} \\ \end{aligned}$$

(81)

The same result as Eq. 77 can be obtained from Eqs. 80 and 81.

$$\begin{aligned} \frac{{{{({c_{1,\alpha {\beta ^+}}}+{c_{2,\alpha {\beta ^+}}})}^2}}}{{{{({c_{1,\alpha {\beta ^ - }}}+{c_{2,\alpha {\beta ^ - }}})}^2}}}=\,& \frac{{c_{{1,\alpha {\beta ^+}}}^{2}+c_{{2,\alpha {\beta ^+}}}^{2}+2{c_{1,\alpha {\beta ^+}}}{c_{2,\alpha {\beta ^+}}}}}{{c_{{1,\alpha {\beta ^ - }}}^{2}+c_{{2,\alpha {\beta ^ - }}}^{2}+2{c_{1,\alpha {\beta ^ - }}}{c_{2,\alpha {\beta ^ - }}}}} \\ =\,& \frac{{1+2{c_{1,\alpha {\beta ^+}}}{c_{2,\alpha {\beta ^+}}}}}{{1+2{c_{1,\alpha {\beta ^ - }}}{c_{2,\alpha {\beta ^ - }}}}}=\frac{{1+\frac{{{J_{AB}}}}{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }}}}{{1 - \frac{{{J_{AB}}}}{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }}}} \\ =\,& \frac{{\frac{{({\nu _3} - {\nu _1})+({\nu _4} - {\nu _3})}}{{{\nu _3} - {\nu _1}}}}}{{\frac{{({\nu _3} - {\nu _1}) - ({\nu _2} - {\nu _1})}}{{{\nu _3} - {\nu _1}}}}}=\frac{{{\nu _4} - {\nu _1}}}{{{\nu _3} - {\nu _2}}} \\ \end{aligned}$$

(82)

Reducing the strength of B₀ will reduce ν_A − ν_B while J_AB is not affected. When ν_A − ν_B = $\sqrt 3$J_AB, the distance between the inner absorption peaks is exactly J_AB so that a quartet results with intensities 1:3:3:1 similar to a single resonance split by three equivalent protons. As B₀ is further reduced so that ν_A approaches ν_B, the two inner absorption peaks approach each other, the outer peaks approach zero and the pattern becomes similar to a doublet with a small coupling constant. If ν_A = ν_B, the two inner peaks become one and the two out peaks have zero intensity. The two protons are thus chemically equivalent so that they have the same chemical shift and no splitting is observed. As shown from Fig. 9c Eq. 83 is implied by Eq. 71.

$$\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} =({\nu _A} - {\nu _B})+D={\nu _3} - {\nu _1}$$

(83)

From Eq. 83 we obtain Eq. 84. From Eq. 84 we obtain Eq. 85 which is implied by Fig. 10c for the relationship of ν_A − ν_B, ν₄ − ν₁, and ν₃ − ν₂.

Fig. 10

The graphical representation for the relationship between ν_A − ν_B, ν₄ − ν₁, and ν₃ − ν₂ as shown by Eq. 85

$$\begin{aligned} {({\nu _A} - {\nu _B})^2}=\,& {({\nu _3} - {\nu _1})^2} - J_{{AB}}^{2} \\ =\,& {({\nu _3} - {\nu _1})^2} - {({\nu _2} - {\nu _1})^2} \\ =\,& [({\nu _3} - {\nu _1})+({\nu _2} - {\nu _1})][({\nu _3} - {\nu _1}) - ({\nu _2} - {\nu _1})] \\ =\,& [({\nu _4} - {\nu _2})+({\nu _2} - {\nu _1})][({\nu _3} - {\nu _1}) - ({\nu _2} - {\nu _1})] \\ =\,& ({\nu _4} - {\nu _1})({\nu _3} - {\nu _2}) \\ \end{aligned}$$

(84)

$$\frac{{{\nu _4} - {\nu _1}}}{{{\nu _A} - {\nu _B}}}=\frac{{{\nu _A} - {\nu _B}}}{{{\nu _3} - {\nu _2}}}$$

(85)

Equation 87 can be obtained from Eqs. 78 and 86 [73].

$${\sin ^2}u+{\cos ^2}u=1$$

(86)

$$\begin{gathered} {c_{1,\alpha {\beta ^+}}}= - {c_{2,\alpha {\beta ^ - }}}=\sqrt {\frac{{1 - \cos 2u}}{2}} \hfill \\ {c_{2,\alpha {\beta ^+}}}={c_{1,\alpha {\beta ^ - }}}=\sqrt {\frac{{1+\cos 2u}}{2}} \hfill \\ \sin (2u)=2\sin u\cos u=\frac{{{J_{AB}}}}{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }} \hfill \\ \cos (2u)=\frac{{{\nu _A} - {\nu _B}}}{{\sqrt {{{({\nu _A} - {\nu _B})}^2}+J_{{AB}}^{2}} }} \hfill \\ \end{gathered}$$

(87)

Summary

Academic misconduct has been becoming a serious problem nowadays. Mistakes appeared in publications are also becoming more severe. The two are related because less and less attention is stressed on the rudiments of science in research community. The wrong method discussed in this work has been used by many researchers and the practice has lasted so long. There are so many works published with the method [4, 17, 21,22,23,24,25, 27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43] and such works still appear [52,53,54,55,56,57,58,59,60,61,62] after we first pointed out the problem in November 2017 [13]. Conclusions cannot be sensible if the method used to obtain them is wrong. “Some scientists wondered how a questionable line of research persisted for so long.” [64] One way to find mistakes promptly before or after their publications is encouraging a keen interest among researchers in fundamental principles instead of relying heavily on equipment.

Because less attention has been paid on the rudiments, the problem pointed out in this work is not unique. The environments of protons are vital for nuclear magnetic resonance as shown by Appendix 4. The environment of lattice node is also a basic concept used in the field of crystallography which is vital to material research [74]. However, there are problems about the issue in recent publications. By confusing the concepts of lattice node and Wyckoff site in crystal, it is misleadingly claimed that “it is obviously simply impossible to have different environments around two physically distinct but symmetrically equivalent atoms.” [75] In fact, the environments of two chiral positions connected by mirror or inverse operation are different. Diamond lattice [75] is a commonly used phrase [76,77,78,79,80,81,82] to distinguish different forms of cF lattice such as table salt, diamond, and spinel MgAl₂O₄. The phrase can be conveniently used for describing structures such as MgCu₂ [76] and MgAl₂O₄ where Mg occupies the points indicated in the “diamond lattice.” There are only 14 Bravais lattices. Thus, not every point in the cell of diamond lattice is a lattice node. In the unit cell of primitive diamond lattice there are two carbon atoms but they are represented by only one lattice node. Relative to translation operation, all the nodes (but not necessarily all the points or atoms) in a lattice have the same environment. The environments of the two carbon atoms in the primitive unit cell of diamond are different even though they are connected by symmetry operations. The same environment for all the lattice nodes in a lattice is an essential principle in the long-established Miller Indices. Failure to understand this has led to the redefinition [75, 83] of Miller indices [“In an I-centred cell, the Miller indices of this family of planes are (222), not (111)”], and in turn led to the absolutely wrong claims of unevenly distribution of lattice planes with the same Miller indices in a lattice [84] and different node densities within this family of planes [85].

Appendix 5 The comparison of s ₁₁ and R _M in microwave frequency from 10 to 18 GHz

The comparison between s₁₁ and R_M obtained at microwave frequencies 10–18 GHz is shown by Fig. 11.

Fig. 11

The comparison of s₁₁ obtained directly in the measurement with reflection loss R_M calculated from Eqs. 88 or 89 for NiSm_0.12Fe_1.88O₄, where permittivity, permeability, and s₁₁ were measured with Keysight Technologies 85055AR03-FG Airline Type N, 50 ohm replacement kit, and Z_l = Z_air = Z₀ = 377 ohm or Z_l = Z_apparatus = Z₀ = 50 ohm for the calculation of R_M

For planar transmission line

$$\begin{aligned} {Z_M}=\,& \sqrt {\frac{{{\mu _0}{\mu _{r,M}}}}{{{\varepsilon _0}{\varepsilon _{r,M}}}}} =\sqrt {\frac{{4\pi \times {{10}^{ - 7}}}}{{\frac{1}{{36\pi }} \times {{10}^{ - 9}}}}} \sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} =120\pi \sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} \\ R_M=\,& 20 \times {\log _{10}}\left| {\frac{{377 - 377\sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} }}{{377\sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} +377}}} \right|=20 \times {\log _{10}}\left| {\frac{{1 - \sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} }}{{\sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} +1}}} \right| \\ \end{aligned}$$

(88)

For coaxial sampler [13] with the inner and outer radii of a = 3 mm and b = 7 mm, respectively

$$\begin{gathered} {Z_M}=\sqrt {\frac{{{\mu _0}{\mu _{r,M}}}}{{{\varepsilon _0}{\varepsilon _{r,M}}}}} \frac{{\ln \frac{b}{a}}}{{2\pi }}=50\sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} \hfill \\R_M=20 \times {\log _{10}}\left| {\frac{{50 - 50\sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} }}{{50\sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} +50}}} \right|=20 \times {\log _{10}}\left| {\frac{{1 - \sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} }}{{\sqrt {\frac{{{\mu _{r,M}}}}{{{\varepsilon _{r,M}}}}} +1}}} \right| \hfill \\ \end{gathered}$$

(89)

Both Eqs. 88 and 89 do not involve sample thickness.