Introduction

Particle-reinforced metal matrix composites (PR-MMC) represent a class of advanced engineering materials that combine a metal matrix with reinforcing particles, significantly improving mechanical properties such as strength, stiffness, and wear resistance compared to their monolithic counterparts [1, 2]. These composites are finding extensive applications in various sectors, including aerospace, automotive, and electronics, where the demand for materials that contribute to weight reduction, energy efficiency, and improved performance is constantly increasing [3]. In such materials, key internal parameters such as particle size, volume fraction, and the processing technique used (e.g., casting, powder metallurgy, or hot isostatic pressing) critically influence properties and their subsequent service life [4, 5]. Controlling these parameters allows for optimization of the mechanical behavior, tailoring it to specific applications. Optimizing the microstructural and processing features along with the service loads not only contributes to the development of more sustainable materials but also aligns with global efforts toward environmental stewardship by minimizing waste and promoting efficient use of resources.

Building on the foundational understanding of particle-reinforced metal matrix composites (PR-MMCs), significant contributions by material scientists and researchers have clarified the relationship between microstructural features, the mechanical and damage properties of these composites. Through advanced experimental and characterization techniques, researchers have demonstrated how microstructural attributes, such as particle size [6], distribution [7], and matrix–particle interface quality [8, 9], directly influence mechanical behavior, including yield strength, ductility, and toughness. In addition, studies have extensively explored the impact of microstructural heterogeneity on damage initiation and progression mechanisms [10, 11], such as particle cracking [12], debonding [13], and nucleation of voids [14, 15], which critically affect the durability and fatigue life [16]. Yang et al. [17] investigated the SiCp/Al composites with different matrix strengths and particle sizes. They showed that PR-MMCs with relatively high strength or larger particle size would fracture because of a large amount of particle cracking and reduce the ultimate strength in comparison with that of the particle-free case. Here, the choice of the appropriate particle size and matrix is necessary for appropriate materials design. These insights have led to the development of models to predict material behavior with greater precision [18,19,20,21]. In the specific context of zirconia particle-reinforced TRIP steel metal matrix composites (MMCs), the concentration and distribution of reinforcing particles play an important role in dictating local deformation behaviors and the initiation and propagation of damage under mechanical stresses [22,23,24]. A higher concentration of zirconia particles tends to enhance overall strength and stiffness, due to the transfer of load from the steel matrix to the stiffer zirconia particles [25]. However, this comes at the cost of potential stress concentrations around the clusters of particles, leading to heterogeneous deformation and embrittlement [26]. Heterogeneity or a large gradient due to dramatic change can significantly influence the onset of microcracks, particularly in areas where particle distribution is uneven [27]. The interaction between the TRIP steel matrix and the brittle zirconia particles under load can lead to complex damage mechanisms, including particle fracture, interface debonding, and matrix tearing [10, 28, 29]. These phenomena are critical in determining toughness and its resistance to fractures and elongation. Despite the recognized importance of particle concentration and distribution in the affectation of these material properties, there has been a notable gap in the literature. Biermann et al. [30] conducted the compression and bending test on cylindrical rods and honeycomb samples for different zirconia content such as 0%, 5%, and 15%. The 5% zirconia content showed a higher compressive strength overall; however, 15% of the cases indicate initially increased before the 4% true compressive strain and further decreased the hardening rate compared to the zirconia-free case. Moreover, a macroscopically more brittle behavior in 15% zirconia content was investigated and attributed to the higher clustering degree as well as severe damage. Therefore, the least number of studies have been conducted systematically to quantitatively investigate the correlation between the concentration of zirconia particles, their distribution within the TRIP steel matrix, and the resulting impact on local deformation and damage mechanisms. This gap underscores the need for focused research to clarify these relationships.

In this work, the effect of the zirconia content on the local deformation and damage behavior has been quantitatively analyzed by sequentially increasing the zirconia content in the TRIP steel matrix. To fully understand the effect of zirconia content, zirconia-free material is chosen as reference case, and the zirconia-reinforced cases with and without the clustering effect for 10 % and 20 % reinforced composites at the microscale are analyzed. The zirconia content greater than 20% is assumed to contribute a qualitatively similar finding, except for the quantitative degree from the point of view of the particle distribution, damage evolution, and clustering degree. Therefore, in this work, the zirconia content greater than 20% is not considered. The preparation, testing, and data analysis of the experimental sample are presented in Sect. "Experiment" along with the methodology of digital image correlation, damage detection, and degree analysis. Global stress–strain results, local strain analysis with damage evolution, and the degree of change in clustering are discussed in Sect. "Results and discussion." All results are discussed in comparison with the published data in Sect. "Conclusions," and the study is concluded with reasonable outcomes and points of use. Adequate references are given in each section that refer to more details published in other studies that the readers are encouraged to read.

Experiment

Sample preparation and testing

In this study, a TRIP steel composite consisting of high-alloyed Cr–Mn–Ni cast steel (X3CrMnNi16-7-6) as a matrix with varying zirconia (Mg-PSZ) content is used as a strengthening material such as 0%, 10%, and 20% vol. The size of the reinforcement particle is in the range of 30–50 μm (d10 = 30 μm, d50 = 40 μm, d90 = 48 μm) across all specimens. Table 1 shows the chemical constitution of high-alloyed Cr–Mn–Ni steel and zirconia. Appropriate amounts of this steel and ceramic powder are mixed in a ball mill with a binder for more than 8 h, and compressed to form green compacts that are sintered in a vacuum electric furnace. The sintered plates are heat treated at 1330 K for 30 min under compressive load and then cooled to ambient temperature to further homogenize and densify the material. More details on material, process, and proprieties are published elsewhere [31,32,33]. This hot isostatic press (HIP) sintering technique has previously demonstrated the attainment of a remarkably uniform grain size and orientation in analogous materials, as evidenced in previous research [34]. It should be noted that the grain shape and texture are homogeneous and neutral during the hot isostatic press process, which results in uniform grain size and random orientation distribution.

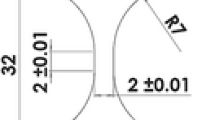
Table 1 Chemical composition of Cr–Mn–Ni medium-alloyed cast steel (X3CrMnNi16-7-6) and partially stabilized zirconia (in weight-%)
Full size table

Microtensile samples are machined perpendicular to the flat surfaces of the sintered disks. The samples are machined using water jetting cutting to prevent residual stress generation or surface twinning during production. To eliminate the influence of water jetting in surface irregularities on the sample, a grinding procedure is conducted on both planar surfaces employing emery papers ranging from 100 to 1200 grit sizes. Subsequently, metallographic polishing is performed using sandpapers and polishing pastes of a size from 46.2 to 1 μm, followed by the oxide polishing suspension (OPS) at the end. The microtensile sample geometry is developed with slight modification in DIN EN ISO 6892-1 [35]. Uniaxial tensile tests were carried out along the x direction, as shown in Fig. 1. The geometry of the current samples comprises the gauge length, fillet radius, width, total length, and thickness of the sample, which are 10, 5, 10, 42, and 1 mm, respectively. The surface of the polished samples is purposely not etched because it already contains high contrast because of the presence of ceramic particles.

Figure 1
figure 1

The diagram outlines the design of microspecimen of high-alloyed 16-7-6 CrMnNi austenitic steel composite-reinforced Mg-PSZ particles. Note that the geometry of the current samples in this work includes gauge length, fillet radius, width, total length, and thickness, which are 10, 5, 10, 42, and 1 mm, respectively.

Full size image

In situ tensile testing with data acquisition

The quasi-static in situ tensile tests are carried out using the Kammrath & Weiss test stage within the ZEISS Gemini 450 scanning electron microscope (SEM). Samples are tested to a true strain of 16% at a constant displacement rate of 5 μm/s or 0.001 strain/s. The test is interrupted after equal strain intervals to record secondary electron (SE) images in the middle of the microtensile samples, as indicated in Fig. 1 by the red box. It is important to note that the thickness of 1 mm serves to reduce the likelihood of stress and strain variations occurring along this direction. The initial SEM images of all three samples with different zirconia content are provided in Fig. 2. Please note that all the captured SEM images have 2048 × 1536 pixels resolution.

Figure 2
figure 2

SEM images with a 0%, b 10%, and c 20% zirconia content. Note that the white and gray colors indicated the Mg-PSZ particles and the high-alloyed 16-7-6 CrMnNi austenitic steel, respectively.

Full size image

To calculate the hardening behavior of each case, the initial step involves eliminating the vertical segment in the stress–strain curve attributed to the SEM image acquisition pause, as it could significantly influence slope calculations. An automatic detection method for vertical breaks is developed and used for data cleaning. The algorithm begins by locating the position of the local minimum, represented by a yellow solid line in Fig. 3a, which serves as the baseline. Subsequently, the critical distances dL and dR from the baseline indicate other points around the local maximum position, illustrated in purple and green dashed lines, respectively. Ultimately, removing these detected points from the flow curve results in a smooth flow curve as shown in Fig. 3b as an orange line. In this study, the distances dL and dR are adjusted to be 0.3% and 1.5% global strain, respectively.

Figure 3
figure 3

a Preprocessing step of eliminating the vertical segments due to breakdown when the SEM images were taken. b Comparison between the raw dataset and the modified dataset, shown in blue and orange colors, respectively. Note that the dL and dR indicated the left- and right-hand sides of the vertical segments as displayed by yellow solid lines to automatically detect and remove points within this range.

Full size image

Local strain measurement using DIC

The digital image correlation (DIC) technique for local strain measurement employs commercial software, VEDDAC, to derive two-dimensional, comprehensive displacement and von Mises strain data from a series of incremental images. This method, illustrated in Fig. 4, uses a digital image correction scheme that outlines the measurement points, reference, and analysis fields. Ceramic particles and the austenitic steel matrix are represented by white and gray, respectively. In VEDDAC, a correlation algorithm targets specific local image areas and measurement points within a simulated environment. The reference field, marked in purple and sized (n × n pixels) in the reference image (Fig. 4a), and the measuring field, colored blue and sized (m × m pixels) in the subsequent image (Fig. 4b), facilitate the correlation analysis. Before DIC strain measurements, the presence of adequate structural detail for gray value correlation analysis was verified in VEDDAC, eliminating the need for an artificially applied speckle pattern. To maintain higher resolution while maintaining computational efficiency [24], the measuring (m × m pixels) and the reference field (n × n pixels) are adjusted to 90 and 40 pixels across all datasets, respectively.

Figure 4
figure 4

The outline of the digital image correlation with a measuring points (black) and original reference field (purple) in the initial image, as well as b search reference field (red) and measurement field (blue) in the compared image, which continuously calculates the correlation coefficient to determine the final position and deformation along x and y. Note that the reference and measuring field are n × n pixels and m × m pixels, respectively.

Full size image

In the calculation of the correlation coefficient, the grayscale value for each pixel within the reference field (purple), as shown in Fig. 4a, is used as a baseline and further compared to that of the search field (red), as shown in Fig. 4b. Afterward, the coefficient field could be obtained, and the highest correlation value was regarded as the deformed position of that measurement point.

Image processing function

Damage detection

The quantitative assessment of the damaged region is conducted using MATLAB's image processing capabilities, structured into five sequential steps: threshold setting, filtering, defining free-hand regions of interest (ROI), applying a flood fill algorithm, and normalization. The step-by-step damage detection process is shown in Fig. 5. Initially, micrographs are analyzed using a grayscale threshold, with values set between 0 and 255. For this analysis, a threshold of 30 is selected, categorizing grayscale values below 30 as 0 (undamaged) and above 30 as 1 (damaged) as depicted in Fig. 5a. To address the errors of the pores in the matrix, the second step filters the image according to solidity, a measure of the area of a region relative to its convex hull, using the filterRegions function as displayed in Fig. 5b. A solidity range of 0–0.8 is chosen to exclude circular pores characterized by a solidity greater than 0.8.

Figure 5
figure 5

Damage detection by various steps: a threshold, b filtering, c free-hand regions of interest (ROI), and d flood fill, as an example from the 10% zirconia content at the final stage.

Full size image

Subsequently, any residual inaccuracies, such as arbitrary-shaped pores, are removed using the free-hand ROI tool, ensuring the comprehensive exclusion of non-damaged matrix pixels, as shown in Fig. 5c. The adjacent damaged regions near the ceramic particles are accurately identified with the flood fill technique, as outlined in Fig. 5d. It is noted that initial error detection may occur due to black coloring at interfaces, and therefore, by assuming that there is no damage in the initial state, this error is subtracted from the subsequent datasets. In the final normalization step, the count of damaged pixels is adjusted relative to the initial number of damaged pixels and the total pixel count of each image, improving the accuracy of the damage assessment.

Clustering degree analysis

A clustering-based image segmentation approach based on k-means is used to identify zirconia particles regardless of their shape and size [36]. In the k-means method, the image or input data are segmented into k clusters to minimize the sum of squared distances between each point and its closest center. Initially, k arbitrary centers are randomly chosen from the random dataset. After assigning each point to the closest center each center is recalculated to be center of mass of all points that are assigned to it. These center assignment and calculation step is repeated iteratively until the process stabilizes. In this study, the SEM image consists of two phases: zirconia particles (bright islands) and austenitic matrix (dark gray pool). Therefore, the number of clusters, k, is assumed to be 2. The investigation into the selection of k involved testing values of 2 and 3. It was concluded that setting k to 2 is more efficient in distinguishing zirconia clusters while maintaining higher accuracy. Figure 6 illustrates the detection for cases with 10% and 20% zirconia contents, respectively. After the k-means clustering process, due to shadows on the surface of the particle, it is necessary to identify solid particle geometry shown in Fig. 6 with a yellow overlay.

Figure 6
figure 6

Particle detection of a 10% and b 20% zirconia contents, which was already filtered for the error-detected pixel within the matrix and filled the holes due to the shadow on the surface of the ceramic particles. It should be noted that the grayscale contrast was enhanced to make it easier to find the phase boundary between the particle and the matrix.

Full size image

After the particles are detected successfully, the centroid of each particle can be calculated from the binarized image, as shown in Fig. 7a, indicated by red dots. On these detected centroids, Voronoi tessellation segmentation based on centroid positions is performed to generate the Voronoi cells (illustrated by green lines) as shown in Fig. 7b. The Voronoi cell for each particle can be further analyzed to investigate near-neighbor cells or particles and the clustering degree of particle distribution, as explained in the following section.

Figure 7
figure 7

a The centroid position calculated based on the particle detection results and marked by the red points, and b Voronoi tessellation distribution of each centroid for the 10% zirconia case. Note that white and black denote the particle and matrix.

Full size image

To improve the understanding of near-neighbor cell detection, nine arbitrary points (labeled in blue) are created with the distribution of Voronoi cells, as depicted in Fig. 8a. Additionally, identifying common nodes and edges is essential to define near-neighbor positions. Two points (from P1–P9) in the Voronoi diagram can be considered neighbors if they share an edge. Based on each pair of two common nodes, the shared edges (illustrated by red lines) for P5 can be sorted and specified, as shown in Fig. 8b. Finally, the cell for the P5 point is defined, as illustrated in Fig. 8c. It is important to note that the yellow and red patches represent the center and near-neighbor cells, respectively.

Figure 8
figure 8

a Illustrated Voronoi diagram featuring nine arbitrary points, b highlighted in red are the shared edges of neighboring cells around the P5 point, and c near-neighbor cells are depicted in red, with the target cell for the P5 point distinguished by a yellow face color. It is important to emphasize that the identification of near-neighbor cells for each point is accomplished by detecting shared edges.

Full size image

To quantify the degree of heterogeneity in the particle distribution, the coefficient of variance of the mean near-neighbor distance \({\text{COV}}_{{\text{d}}}\) is used. This coefficient is independent of the size and orientation. Following the creation of the Voronoi tessellation and the definition of near-neighbor positions, the mean particle spacing distance can be calculated for each particle assumed as the center, as illustrated in Fig. 8c. The nine particles yield nine mean near-neighbor spacing distances as in the previous example. Additionally, \(\sigma_{{\text{d}}}^{{}}\) and \(\mu_{{\text{d}}}\) denote the standard deviation and average of the mean near-neighbor spacing distances, respectively. The coefficient of variance of the mean distance can then be defined as follows:

$${\text{COV}}_{{\text{d}}} = \frac{{\sigma_{{\text{d}}}^{{}} }}{{\mu_{{\text{d}}} }}$$
(1)

In principle, the larger \({\text{COV}}_{{\text{d}}}\) values mean a more clustered distribution. It was validated that a value of 0.36 would represent a random particle distribution [37, 38]. Continuing from the analysis of the degree of clustering, Fig. 9 provides a visual representation of the Voronoi tessellation for TRIP steel samples with 10% and 20% zirconia contents. In these diagrams, the detected particles are highlighted with a yellow overlay, the centroids calculated from the binarized images are indicated in red, and the green lines delineate the boundaries of the Voronoi cells. The increase in zirconia content from (a) to (b) appears to influence the spatial distribution of the particles, which can be quantitatively assessed by the aforementioned coefficient of variance of the mean near-neighbor distance from 0.34 to 0.42. It shows that 10% of zirconia content is near random distribution; however, 20% of cases present a degree of clustering.

Figure 9
figure 9

The Voronoi diagrams of a 10% and b 20% zirconia contents. Note that particle detection, centroid, and Voronoi boundary were shown in yellow, red, and green colors.

Full size image

Results and discussion

Global behavior comparisons

The global results of the quasi-static in situ tensile tests are shown in Fig. 10. Solid lines denote the stress response of the material under tension, while dashed lines indicate the strain hardening rate—a measure of how the resistance to deformation increases with plastic deformation. The graph shows that the highest tensile strength and highest elongation are achieved in the TRIP steel sample without ceramic particles. Possibly, the phase transformation from austenite to martensite is dispersed throughout the material, preventing local necking, and thus promoting a uniform distribution of strain. Similar trends have been reported by other researchers [39,40,41,42] for metallic materials with increasing zirconia content. The strain hardening rate indicates that the Mg-PSZ-containing samples also exhibit the TRIP effect, although there appears to be a trade-off in mechanical properties. Due to the difference in mechanical attributes of the steel matrix and the ceramic particles the incorporation of the ceramic particles causes stress concentrators that could serve as crack initiation sites or hinder the transformation process, as has been previously reported [43, 44]. The difference essentially undermines the positive effects of the TRIP effect by causing early failure or limiting ductility. Therefore, it is observed that as the zirconia particle content in the material increases, this limits the ductility and hardening effect in the sample. Later on, during the discussion of the local results, it will be looked into more thoroughly.

Figure 10
figure 10

The stress–strain curves and work hardening curves for different zirconia cases, such as 0% (red), 10% (green), and 20% (blue), as denoted by the solid and dashed lines. Furthermore, the corresponding initial micrographs are shown on the upper side.

Full size image

Complementing the graphical data in Fig. 10, the key mechanical attributes are summarized in Table 2. The data show that the alloy without Mg-PSZ has the highest tensile strength (720 MPa) and elongation (76.4%), suggesting that it is the most ductile. As the Mg-PSZ content increases to 10% and then 20%, tensile strength and elongation decrease. Although a higher Mg-PSZ content seems to maintain or increase the yield stress, it negatively impacts the ductility and strength.

Table 2 Mechanical properties of different alloys as measured from tensile tests on miniature dog bone samples
Full size table

Local behavior comparisons

Figure 11 presents a visual comparison of local deformation patterns in TRIP steel samples with varying zirconia contents under different global strain conditions, as determined by DIC. In the images, three columns represent samples with different zirconia contents: 0%, 10%, and 20%. The rows correspond to the global strain levels experienced by the samples: ~ 1%, ~ 5%, and ~ 13%. The 0% zirconia sample shows an overall homogeneous strain distribution and higher strain levels. In this material, less local strain heterogeneity is found and is influenced by the local orientation of the grains. Generally, zirconia-free material shows that austenite grains can deform freely and grains with pronounced dislocation movement indicate the most deformation bands [45].

Figure 11
figure 11

The local strain field was calculated using the digital image correlation technique for different zirconia contents and global strain conditions.

Full size image

With increasing strain, localization increases probably due to the onset of austenite-to-martensite transformation in more favorably oriented grains, which further restricts the strain in certain areas, whereby significant high contrast in some other areas. This occurs due to the triaxiality of local stress [19, 46] as pointed out in previous work and affects the formation of local voids and damage behavior [47, 48]. Furthermore, previous studies [49, 50] have similarly shown strain localization within grains and grain boundaries, as well as strain-induced martensitic transformations with transformation-induced plasticity behavior (TRIP), which explains the possibility of strain localization. According to the TRIP effect, some studies show [51, 52] that the strain-induced phase transformation occurred at the intersection of the microshear band. In this paper, the reason for the strain localization would be the movement of dislocation within grains or around grains boundaries, the microshear bands, and TRIP effect in the zirconia-free case.

As the ceramic content increases to 10% and 20%, there is a noticeable emergence of local strain heterogeneity at very low strains (around 1%). This shows that zirconia particles affect the homogeneity of the deformation, possibly acting as stress concentrators. Specifically, in zirconia-reinforced material, grain deformation or dislocation slip in the matrix is suppressed overall by reinforcement material as examined experimentally by Al2O3 or Mg-PSZ particles [45], resulting in greater localization of stress in narrow localities, such as around particles and at the edges of voids induced by interfacial cracks. In addition, a physically stiffer inclusion such as reinforcements or precipitates represents a stronger effect than the effect of the Schmid factor on every single grain from the crystal plasticity analysis [53]. Herein, in principle, the stress or strain is significantly affected for zirconia-reinforced cases. However, as mentioned above, both zirconia-free and zirconia-reinforced materials qualitatively show the possibility of strain localization or heterogeneity. To further quantitatively investigate the heterogeneity behavior, the coefficient of the variance (COV) of local deformation is introduced and explained in detail later.

As global strain increases, the heterogeneity of local strain becomes more pronounced with different stress concentration sites that can act as critical locations for the initiation of microcracks or other damage features [54]. This suggests that higher local strain heterogeneities are likely to accelerate the initiation and propagation of damage in the material, as reported for other types of reinforced composites [55], so the trends are similar. For the 20% zirconia samples, the high local strain regions at 6% and 13% global strain are especially indicative of potential sites where microcracks are observed to initiate and coalesce (black regions), leading to macroscopic failure.

The local damage initiation is influenced by the material's microstructure; therefore, in samples with higher zirconia content, the increased heterogeneity leads to a greater likelihood of local damage initiation. Furthermore, the propagation of this damage is influenced by the interconnection of these high-strength regions. As seen in the 20% zirconia samples at high global strains, the connectivity of the high-stress regions can facilitate the formation of crack paths, which can lead to a reduction in the overall mechanical integrity and ductility of the material.

It is important to note that here only the effect of particle content on local deformation and damage is analyzed. However, the size, distribution, and morphology of the particles, as well as the stiffness of the metal matrix, the brittleness of the ceramic particles, and the ceramic/matrix interface, contribute to the overall damage mechanisms [56, 57]. The progressive localization of deformation into bands, oriented at 45° with respect to the loading direction, was observed in TRIP steels by Kim et al. [58] and Wang et al. [59], similar to the high-strain bands observed in all samples. Of course, the localization of the strain in composite samples is also influenced by the presence of brittle zirconia particles, as the strain can only be accommodated in the interlocked matrix regions.

Figure 12 presents a statistical representation of the deformation characteristics in TRIP steel samples with varying zirconia concentrations under progressive global stress. The average local strain, shown by black lines, reveals the mean local deformation experienced at the microscale, which increases in tandem with the applied global strain for all samples. The COV of local deformation, represented by blue lines, quantifies the heterogeneity at the strain level to make the comparison of strain in different materials. It is observed that the overall mean value of 20% zirconia content is the highest and 10% zirconia is the lowest. The reason for the highest average strain level in the 20% case is attributed to the higher clustering degree, calculated by 0.42. However, 10% zirconia-reinforced material indicates that the adequate addition of reinforced material with random distribution as calculated by 0.34 can reduce the overall strain level. In addition to the mean values, the dispersion degree of local deformation is more important for strain heterogeneity analysis. In general, standard deviation (SD) is used to assess the dispersion of a dataset. However, this measure is based on comparing datasets with the same mean values to investigate the effect of different standard deviations. The issue arises when datasets have different mean values, as they cannot be directly compared using SD alone as it is influenced by the mean. In such cases, the COV, which is the ratio of the standard deviation to the mean as explained in Eq. (1), is introduced to compare the dispersion degree of different datasets by normalizing for the mean. A higher COV indicates a higher dispersion within the dataset. Therefore, a higher COV value of local deformation represents stronger strain heterogeneity. It should be noted that there are two statistical applications of COV in the proposed work. One is the COV of the mean near-neighbor distance to investigate the degree of clustering. The other is the COV of the local deformation to determine the strain heterogeneity.

Figure 12
figure 12

Statistical analysis of the average local strain and the coefficient of variation of local deformation, as depicted by the black and blue lines on the left- and right-hand sides.

Full size image

From the COV analysis of local deformation, as shown in Fig. 12, it is evident that the overall trends at 10% and 20% indicate a more dispersed strain distribution and greater strain heterogeneity with increasing global strain conditions and quantitatively prove that the degree of strain heterogeneity is higher in the material with the highest zirconia content. With the highest strain heterogeneity, it implies that, due to the large parity in local deformation, the possibility of damage occurring is higher.

On the other hand, a noticeable peak in COV values starts in the initial stages (~ 1%) which is attributed to two reasons. The primary reason for this phenomenon is that the mean values at 10% and 20% zirconia contents are approximately 0.8 and 1 at the initial stage, respectively, which are relatively small compared to the mean value of 2.3 in the zirconia-free case. As a result, the COV becomes highly sensitive in the 10% and 20% cases because the denominator is close to zero. Additionally, the minor reason is that the SD (numerator) at 10% and 20% strain is significantly larger due to the increased dispersion in local deformation, which corresponds to similar results observed in Fig. 11. In contrast, the 0% strain case indicates a uniform distribution of local deformation, resulting in a smaller standard deviation. Therefore, sudden peaks in the COV values are attributed to these two factors: the mean values close to zero and the strain heterogeneity in the 10% and 20% cases compared to the zirconia-free case. It can be concluded that the higher clustering degree indicates a higher average of local deformation, strain heterogeneity degree, and severe damage behavior.

Apart from the physical meaning of COV of local deformation, the statistical meaning of COV can be explained so that the zirconia-reinforced material is larger and close to 100% at the initial stage for 20% and 10% zirconia contents, respectively, which means that the statistical distribution of the dataset is not the normal but rather skewed distribution. Here, to analyze the quantitative local deformation, the kernel distribution is introduced.

The local strain distribution data from the in situ test are plotted in 2D and the corresponding 3D coordinates in Fig. 13. These figures present kernel density estimates of local strain distributions for TRIP steel samples containing 0%, 10%, and 20% zirconia, denoted (a), (b), and (c), respectively. The subfigures labeled X.1 and X.3 display three-dimensional kernel density distributions that relate the frequency of observed local strains across different levels of global strain. These graphs provide an intuitive visual representation of the frequency with which certain local strains occur at each global strain level. Subfigures X.2 and X.4 present two-dimensional kernel density estimates plotted at comparative strain values, offering a flattened view for both full-scale (X.2) and zoomed small-scale (X.4) observations of the same data.

Figure 13
figure 13

Kernel distribution at (X.1 and X.3) full 3D and 2D, respectively, and (X.2 and X.4) magnified scales for 3D and 2D diagrams. It can be seen that X indicates a 0%, b 10%, and c 20% zirconia cases.

Full size image

In the 0% zirconia case (a), the full-scale two-dimensional density plot (a.2) demonstrates, at full scale, a peak shifting to the right with higher global strain, suggesting that local strains become more variable as deformation progresses. Figure 13a.3 reveals multiple peaks at lower global strains, which disperse as global strain increases, indicating initially low local strains that spread out with increasing deformation. Figure 13a.4 focuses on small-scale distributions, showing multiple peaks with similar densities at specific local strain percentages, which may indicate a uniform strain distribution compared to 10% and 20% cases.

For the 10% zirconia case (b), the three-dimensional plot (b.3) illustrates a dramatic change as global strain increases, suggesting higher heterogeneity in local strain at each global strain level compared to the 0% zirconia case. Figures (b.2) and (b.4) show a skewed distribution at varying local strains at the initial stage, as explained by COV of local deformation analysis, which indicates the mode and average value are close to zero and around 0.8, respectively. With increasing global strain, the kernel distribution gradually becomes the normal distribution as there are similar tendencies in COV values lower than 100%.

In the 20% zirconia case (c), the three-dimensional plot (c.3) shows the highest peak at low global strain, which quickly diminishes as global strain increases. This could imply that a concentration of high local deformations occurs early in the deformation process. The two-dimensional plots (c.2 and c.4) reveal very high frequencies at low local strains for smaller global strains and a distinctly skewed distribution compared to the 10% zirconia case, which decreases and becomes broader as the global strain increases, again indicating greater heterogeneity and potential for early onset of high local strains.

These observations suggest that with increasing zirconia content, there is a trend toward greater local strain distribution, potentially implying more irregular deformation and a higher likelihood of stress concentrations leading to damage initiation. This aligns with the earlier discussion on the effects of zirconia on the deformation behavior of TRIP steels.

Several researchers have pointed to this heterogeneity, such as Kim et al. [58] and Wang et al. [59], offering insights into microscopic strain partitioning effects. They suggested that this strain heterogeneity can be attributed to the heterogeneous distribution of mobile dislocations, and they proposed that even within a single phase, local mechanical responses can vary significantly due to microstructural features such as grain size and crystallographic texture.

Comparison of local damage

Figure 14 illustrates a comparison of the initiation and propagation in TRIP steel composites with 10% and 20% zirconia contents, using black and blue to distinguish between the two, respectively. When investigating the in situ tensile behavior of the test specimens, two main damage mechanisms could be identified. The first damage mechanism is the delamination of zirconia particles at the interface between steel and zirconia. The second is the breakage of zirconia particles. Small cracks form in the ceramic particles that then grow perpendicularly to the direction of stress.

Figure 14
figure 14

Comparison of qualitative and quantitative interfacial and particle damage of 10% and 20% zirconia as shown by black and blue colors, respectively.

Full size image

In the 10% zirconia samples, damage begins primarily at the zirconia–steel interface with delamination and to a lesser extent within the zirconia particles themselves via brittle crack formation. As strain increases, damage accumulation is gradual, as evidenced by the curve on the graph, which suggests a steady increase in damage pixels up to a maximum of 3.85%. This indicates that, while there is some interfacial and particle damage, it is relatively controlled and does not immediately lead to catastrophic failure. In contrast, the 20% zirconia samples show higher initial damage and a faster growth rate, leading to a maximum damage pixel percentage of 5.81%. This suggests that with a higher zirconia content, there is an increased likelihood of both interfacial delamination and particle breakage. Micrographs corroborate this, showing more extensive damage at equivalent strains compared to samples of 10% zirconia.

Again, this difference in damage behavior can be attributed to the increased volume of ceramic particles, which intensifies the stress concentration at the interfaces and within the particles, thus exacerbating the two main damage mechanisms. The steel matrix appears mostly intact in all samples, confirming that the predominant forms of damage are associated with the ceramic phases. These observations are consistent with previous findings that a higher ceramic content in composites is correlated with more defects during mechanical tests [12, 60,61,62]. To be more specific, Yang et al. [17] experimentally found that PR-MMCs with larger particle sizes tend to fracture due to significant particle cracking, resulting in a lower working hardening and ultimate strength compared to the case without particles. However, from a validated simulation analysis, Chiu et al. [23] found that the overall stress level decreased significantly due to traction-free zones around interfacial cracks, despite stress concentration at the crack tips, which implies a reduction in work hardening behavior during macro-deformation. From this, it was concluded that the addition of more zirconia reinforcement results in higher yield points but lower work hardening and decreased elongations. The increased yield strength is attributed to stiffer reinforcement. However, work hardening and elongation are significantly affected by the degree of clustering and damage behavior. In addition, a higher rate of damage from a large amount of zirconia likely reduces work hardening significantly during mechanical tests.

Conclusions

The work was carried out to investigate the deformation and damage behavior of TRIP steel with Mg-PSZ particles using an in situ SEM tensile test. The aim is to quantitatively characterize the contribution of the respective damage mechanism to the local failure of the composite material with increasing volume fraction of the reinforcement phase. Samples with different compositions of Mg-PSCs are tested, including non-reinforced TRIP steel without reinforcement (0%), 10%, and 20%. The DIC is conducted to observe the distribution and heterogeneity. Additionally, the clustering degree is analyzed step by step: k-mean for particle detection, centroid calculation for Voronoi tessellation, the algorithm for defining the near-neighbor cell, and finally the coefficient of variance of mean near-neighbor distance for quantifying the clustering degree. Moreover, damage detection and classification are introduced by image processing functions. The following conclusions are drawn:

  1. 1.

    From the averaged global results of the current study, it is concluded that adding more zirconia particles to the TRIP steel matrix increases the yield strength of the composite but significantly decreases the hardening and ductility, specifically under quasi-static tensile loading.

  2. 2.

    As the zirconia content is increased from 10 to 20%, the degree of clustering also increases, as evidenced by the coefficient of variance of the mean near-neighbor distance analysis from random (0.34) to clustered (0.42) situation.

  3. 3.

    Through in situ tensile testing with qualitative DIC analysis, the local strain heterogeneity in zirconia-reinforced material is higher than in zirconia-free materials. This is probably due to the stronger effect of a stiffer material than the Schmid factor for every single grain, as well as the TRIP effect.

  4. 4.

    From the quantitative DIC results, by analyzing the average, coefficient of variance, and 2D–3D kernel distribution of local deformation, it can be concluded that the higher clustering degree indicates a higher average of local deformation and strain heterogeneity degree. However, the lower average local strain compared to zirconia-free conditions could be obtained by the adequate addition of random distribution reinforcement material.

  5. 5.

    The sudden peaks in COV values at the initial stage (~ 1% global deformation) are attributed to two factors: the mean values close to zero and the strain heterogeneity in the 10% and 20% zircona-reinforced cases compared to the zirconia-free case.

  6. 6.

    From damage analysis, an increase in zirconia content from 10 to 20% significantly intensifies the rate and volume of damage, with the 20% zirconia compounds showing a higher initial damage level and a faster damage accumulation rate during tensile tests. Specifically, the 20% zirconia compounds exhibited a 5.81% damage pixel, compared to 3.85% in the 10% zirconia composites. This strong contrast underscores the influence of zirconia content on the mechanical integrity of TRIP steel composites.

The study suggests an appropriate improvement of 10% zirconia composite, suggesting the potential for increased life span and reliability in practical applications. This could facilitate scientists and engineers to improve their manufacturing and application decisions. Specifically, industries such as automotive, aerospace, and heavy machinery demand materials with exceptional toughness and durability.