Introduction

Frenkel theoretically showed in 1926 that a shear stress required for initiation of plastic deformation in an ideal infinite crystal is \({\uptau }_{{{\text{th}}}} = {G}/{2}\pi\), where \(G\) is the shear modulus [1]. This stress defines the theoretical shear strength, which is usually several orders of magnitude above the yield strength of real metals. A significant discrepancy between the yield strength of real and ideal crystalline materials is caused by lattice defects (primarily dislocations), which facilitate the onset of plasticity during deformation. Thus, the theoretical shear strength sets the upper bound on the mechanical strength of a solid.

A shear stress close to theoretical one can be reached by downscaling samples to submicrometer dimensions. The statistical theory of size effect gives the primary explanation, namely a presence of discontinuities, dislocations or flaws, is considerably less in a submicron sample than in bulk one. Typical examples are defect-free single crystal whiskers [2] with diameters 10–20 µm. According to estimates gained by bending tests [3], their theoretical shear strength varies from \({G}/{15}\) to \({{G}}/{10}\). Further examples are the micropillars fabricated by a focused ion beam [4, 5], which compressive yield strength on the nanoscale reaches a value of \({G}/{26}\). Recently, an ultra-high compressive strength of about \({G}/\text{8.3}\) was reported for Ni nanoparticles produced by solid-state dewetting [6]. Mechanical testing of materials on a microscale, such as nanoparticles, whiskers and thin films, is, however, rather a challenge due to specimen preparation and manipulation. Moreover, the above-mentioned techniques could be referred to rather plastic materials. Brittle materials require a particular consideration because they exhibit fractures before yielding.

An alternative approach in mechanical testing for nano- and microscales is to decrease locally deformed region on sample’s surface, while keeping sample’s size unchanged. This can be realized by nanoindentation—a very hard tip (indenter) is pressed into a sample, and dependence of load versus penetration depth is recorded at depths far below one μm with a displacement resolution of about 0.1 nm. The method is advantageous because it is simple and cheap as costly preparation of small samples is not needed. Noteworthy, a real pyramidal indenter is not ideally sharp. Its tip is close to spherical shape, which radius permanently increases and achieves a few hundred nanometers as a result of operation [7]. The plasticity under contact loading occurs, therefore, not immediately, rather at indenter’s displacements of several tens of nanometers. It makes the technique suitable for determination of the yield strength of nanostructures. Even brittle materials can be investigated with regard to plastic properties, since they experience elastic–plastic transition under nanoindentation [8].

It is established that the elastic–plastic transition in a nanocontact occurs either smoothly or sharply, that is accompanied by a sudden increase in penetration depth. The conventional smooth transitions from elastic to plastic behavior happen due to gliding and multiplication of already existing surface dislocations beneath the contact, when the size of contact region is substantially larger than the mean distance between dislocations [9]. On the contrary, the abrupt displacement bursts, also referred to as pop-ins, are observed if structural defects are almost negligible in stressed volume. Such situations can be achieved due to testing the well-annealed or etched crystals, since the nanoindentation technique can sample defect-free response volumes. The pop-ins are attributed to homo- or heterogeneous dislocation nucleation, or unlocking pinned dislocations [10, 11]. The theoretical shear strength can be evaluated from the pop-in events induced by the homogeneous nucleation of a dislocation loop beneath the indenter [12]. Consequently, experimental estimations of theoretical shear strength may be obtained even when testing big samples, including brittle materials [13,14,15].

The phenomenon of pop-in is well studied for fcc [16, 17], bcc [18] and hcp [19] metals, refractory materials (oxides [20, 21], borides [22, 23], nitrides [9, 24], carbides [25]), semiconductors [26] and ionic crystals [27]. However, the pop-in response of molecular single crystals remains poorly investigated [28]. The present contribution addresses this issue. More precisely, the focus is on the widely known C60 fullerite. Its C60 molecules closely resemble a soccer ball, forming a fcc crystal via weak van der Waals interactions [29]. To the best of the authors' knowledge, very few publications deal with the pop-in phenomena in this molecular crystal. The hardness of C60 fullerite thin films on mica and glass substrates was studied in [30]. Any pop-in event on the load–displacement curve was reported. On the contrary, a pop-in happened during nanoindentation of the epitaxial (111)-oriented fullerite films on mica substrates [31]. Recently, some pop-in and pop-out events were observed during nanoindentation of C60 nanowhiskers [32]. Nevertheless, the shear stresses at the pop-in formation were not determined.

The goal of this effort is twofold: to gain the experimental evidence of the pop-in in C60, and consequently, to obtain experimental estimate of theoretical shear strength of fullerite. The former is established by nanoindentation tests on (111) growth plane of C60 single crystal. Since the first pop-in indicates the elastic–plastic transition, the loading portion until the pop-in begins is used to be described in terms of the Hertzian elastic contact [33]. The theoretical shear strength is then estimated as the value of the maximum shear stress at the pop-in load [9]. The Hertzian analysis applies, however, to the contact of isotropic bodies, the condition, which is not fulfilled when considering the indentation of C60 single crystals. One possibility is to incorporate the Stroh formalism to approximate the stress fields in elastically anisotropic solids [34]. Alternatively, the stress state in the anisotropic solid being indented can be computed numerically. For example, the finite element (FE) method was applied for interpretation of basal slip in sapphire under indentation [35]. Following a similar concept, a FE model of elastic contact is developed in therein, taking into account both the fcc anisotropy of C60 and a true shape of indenter’s nose. The critical resolved shear stress is then computed for the octahedral slip systems \(\langle{01}\overline{1}\rangle\left\{ {{111}} \right\}\). These were earlier identified by X-ray topography of indents on C60 crystals [36]. Furthermore, the activation of the octahedral slip systems was determined by studying the pattern of slip traces, which were formed around the indents at loads exceeding 0.1–0.2 N [37, 38].

Experiment

C60 single crystal of 5 mm in size was grown in the Institute for Low Temperature Physics and Engineering, (Kharkiv city, Ukraine), by deposition from gaseous phase. The top and bottom surfaces of plane sample are the (111) crystallographic planes. Twelve nanoindentation tests were performed on Nano Indenter-II (Nano Instrument, Inc.) using Berkovich diamond pyramid. Its blunted tip is close to a spherical shape with a radius of 0.5 μm. The indentation was carried out at loading rate of 0.01 mN/s and under the peak load of 0.2 mN.

The well-established Oliver–Pharr method [39] was used for determination of hardness and effective Young’s modulus. The technique relies on contact stiffness, which is obtained as the slope of unloading branch at maximum indentation depth of load–displacement curve. Subsequently, the projected contact area can be computed from the value of the contact stiffness and linked to the hardness and Young’s modulus. Furthermore, the average contact pressure (which corresponds to Meyer's hardness) within the loading branch was determined according to [40]. For comparison, fcc single crystal of aluminum with 99.99% purity was also tested on the (111) crystallographic plane. The surface of the aluminum sample was prepared by spark erosion and subsequent electrolytic polishing to remove the damaged surface layer.

The Abaqus FE software, version 6.14-5, was used to model the elastic contact and to simulate the load–displacement curve until the first pop-in.

Results and discussion

Experimental observations

A typical load–displacement diagram recorded for the (111) face of the C60 sample is shown in Fig. 1a. Applying the method of Oliver and Pharr to the unloading branch yields for the Young’s modulus the value of 14 GPa and the hardness value of 0.3 GPa. The latter is somewhat higher than the values of microhardness 0.21–0.25 GPa obtained by [37] and 0.22 GPa reported by [41]. A comparison of hardness between C60 and some other molecular crystals is discussed in [29]. A significantly higher value of hardness 0.55 GPa was determined from the nanoindentation measurements of epitaxial fullerite films [31], which is probably caused by its photopolymerization [42] and/or nitrogen/oxygen saturation during sample storage and its preparation for testing [43]. Our tests were performed on fresh samples in order to omit the negative environmental impacts.

Figure 1
figure 1

a Load–displacement curve for a typical nanoindentation test on the (111) surface of C60 (full circles) and the respective average contact pressure (open circles) and b the initial elastic loading until the pop-in. The results of the FE simulations are indicated by the black curve for the indenter’s nose form \(y = 1.21 \cdot 10^{ - 4} r^{2.45}\) and the dashed curve for a spherical indenter with the radius of 684 nm

Full size image

The main feature of the loading curve is a sharp increase of contact depth by 9 nm (pop-in) at a load of 0.02 mN and time less than 0.17 s, see Fig. 1a. This pop-in was observed for eight imprints with the mean load of 0.019 mN and the relative standard deviation less than 7%. The averaged contact pressure (ACP) increases during loading until the pop-in occurrence, afterward ACP suddenly falls. As it was above said, this mechanical behavior may be attributed to the onset of elastic–plastic transition under the contact region. The transition from elastic deformation to subsequent plastic flow occurred smoothly, without any displacement jump, if fullerite samples had been previously saturated by hydrogen (at temperature 250 °C and pressure 30 atm during 900 h). The absence of the pop-in events is assumed to be owing to forcing interstitial impurities and dislocations in the surface layer. We invite a reader also to look into our recent paper [43] for the insight into the impact of gaseous interstitial impurities on mechanical characteristics of C60 single crystal. The influence of structural defects on the pop-in appearance indicates that the pop-in observed during nanoindentation of pure fullerite was likely caused by a homogeneous dislocation nucleation; keep in mind that a corresponding size of the contact region of about 110 nm was by two orders of magnitude less than the estimated average distance between dislocations [44].

Once a nucleation of the first dislocation loop and its multiplication occur, the stress relaxation takes place, and the ACP drop is observed. The post pop-in loading is accompanied by plastic deformation in the fullerite. ACP gradually decreases, approaching hardness value at indenter’s displacement of 150 nm. The highest value of ACP directly before the pop-in formation is referred to as a theoretical hardness, which is about 1.4 GPa for C60 fullerite. This is the hardness of an ideal defect-free fullerite, and it is about four times higher than that hardness of the fullerite.

One should note that there are other less recognizable discontinuities on the loading curve at displacements above 60 nm. Recent statistical analysis [45] of the pop-in events during nanoindentation of copper and iron clearly demonstrated that the second and subsequent pop-in magnitudes exhibited different statistics than the first pop-in magnitudes. The authors assumed the change in deformation mechanism from the dislocation nucleation resulting in the first pop-in event to a dislocation network evolution and dislocation avalanches causing the second and subsequent pop-ins.

Computation of stresses in the C60 single crystal under indentation

Two factors significantly affect on stresses in C60 sample experiencing the indentation load. First, a shape of indenter’s tip deviates at shallow penetration depths from that one of the idealized Berkovich indenter. A spherical approximation of tip form is widely used, which has the advantage that the respective Hertzian solution for the elastic contact can be eventually adopted. It predicts a well-known relation between a load and a mutual approach \(P \propto h^{1.5}\) for the initial elastic segment of the indentation curves [33]. The maximum shear stress can then be easily evaluated from the applied load and the estimated radius of the spherical tip [9]. An accurate analysis of indentation diagrams on various materials demonstrated, however, that the initial loading closely followed the power-law \(P \propto h^{1.41}\) at penetration depths of few tens of nanometers [7]. An exponent which is lower than 1.5 implies that indenter’s tip is effectively flatter than the idealized spherical surface. Note that the exponent approaches unity in the limiting case of indentation by a flat punch. The authors argued that nose’s shape changed from an almost flat one to a spherical one as the penetration depth increased from the initial contact and became close to the Berkovich pyramid at depths above 50 nm. The indentor’s tip can be therefore approximated by a solid of revolution deviating from a sphere at penetrations preceding the pop-in occurrence. The exponent of the revolving curve \(y \propto r^{d}\), where \({r}\) is the radial coordinate, is directly obtained from the exponent in the load–displacement curve as \(d = 1/(1.41 - 1) = 2.45\).

The second factor governing the mechanical response of C60 is its anisotropy. Zener’s anisotropy ratio \(A = 2c_{44} /\left( {c_{11} - c_{12} } \right)\) of this fcc single crystal is 2.16, which noticeably deviates from unity as a measure of isotropy. Nanoindentation tests and their FE simulations on another fcc crystal [46] demonstrated a pronounced orientational dependence of the pile-up patterns. The out-of-plane displacements around the indents manifested different discrete rotational symmetries on the surfaces of (001)-, (011)- and (111)-oriented single crystals. As conical indenters were used, these observations were explained in terms of the crystallographic anisotropy and single crystal plasticity. Hence, provided that the dislocation activity is restricted to the octahedral slip systems, the computation of the respective resolved shear stresses at the onset of plasticity is required. Therefore, the available analytical solutions for the elastic contact problems cannot be referred to the investigated problem.

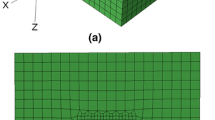
FE analyses are performed to simulate the indentation tests on the (111)-oriented C60 crystal. The model of indentation process was created in the Abaqus software, as presented in Fig. 2a. The calculations used elastic constants for C60 recently reported in [47]. An isotropic elastic response was assumed for diamond indenter and the elastic constants are summarized in Table 1. The indentation depth is controlled by a displacement of the marked top surface of indenter’s tip, which moves along the y-axis. The cylinder represents C60 single crystal. Its material coordinate system must be correctly oriented in the global coordinate system. Thus, the [111] direction is set in parallel to the y-axis in the global coordinate system in order to simulate the indentation on the (111) plane. For the sake of comparison, the indentation of a (001)-oriented sample is also simulated by setting the [001] direction parallel to the y-axis. The halves of the cylinder and indenter’s tip are modeled to reduce computational costs. The nodes in the cross-sectional symmetry xy-plane are precluded in the z-direction in order to satisfy the symmetry condition. Furthermore, the secondary orientation of the single crystal (rotation about the y-axis) is such that the (011) plane coincides with the cross-sectional plane. The nodes on the bottom surface of the sample are constrained along the indentation direction. The middle node in the bottom surface is constrained additionally in the x- and z-directions to avoid translation. The indentation load can be acquired by summing up the nodal reaction forces over the marked top plane of the indenter. The displacements fields in the sample were interpolated by quadrilateral elements C3D20. In order to quantify the mesh size refinement close to the contact region and the impact of the boundaries, the FE model was verified for a limiting case of spherical indentation into the isotropic medium. Its elastic constants were set to those of {111} planes of C60. The resulting deviation of the contact pressure from the Hertzian solution [33] was below 3%.

Figure 2
figure 2

a FE model of contact. b Tresca stress fields in MPa, as predicted by simulation of indentation experiments on the (001) and (111) planes of the fcc C60 single crystal. The displacement of \(u_{{\text{y}}} = - 12 {\text{ nm}}\) is applied on the top surface. The indenter’s nose shape follows \(y = 1.38 \cdot 10^{ - 4} r^{2.45}\). c The respective profiles of contact pressure along the x-axis (black curve) and for spherical indenter with the radius of 612 nm (dashed curve), which is depicted for comparison. The contact pressure is shown for indentation of the (111)-oriented sample. Note, the contact pressure is consistent with the ACP before the pop-in in Fig. 1a

Full size image
Table 1 Elastic constants, anisotropy ratio \(A\), shear modulus on {111} planes \(G\) and the theoretical shear strength \({\uptau }_{{{\text{th}}}}\) by Frenkel
Full size table

Nose of diamond indenter is modeled as an axial-symmetric body bounded by surface \(y = a \cdot r^{2.45}\), where \(r = \sqrt {x^{2} + z^{2} }\). The unknown parameter \(a\) is determined from the fit of the experimental elastic load–displacement curve preceding the pop-in, as shown in Fig. 1b. The obtained value for the parameter is \(a = 1.21 \cdot 10^{ - 4} {\text{nm}}^{ - 1.45}\). For comparison, another fit for a spherical indenter with the radius of 684 nm is also shown. Once the effective indenter’s shape is identified, the stress analysis is carried out for the displacement of 12 nm, at which the pop-in begins. The respective Tresca stresses are depicted in Fig. 2a and b, which demonstrate the strong impact of crystal orientation on stress distributions. As expected, the response of the (111)-oriented sample is stiffer than that of the (001) -oriented one. In order to quantify the effect of tip’s shape, a profile of contact pressure is compared in Fig. 2c with the contact pressure beneath the idealized spherical tip (keeping the other features of the FE model unchanged). The contact stress has two maxima and tends toward stress distribution under a flat punch [33]. Thus, the obtained contact pressure significantly differs from Hertz-like pressure beneath spherical indenter. In summary, change of indenter’s shape geometry to a power-law function with the exponent of 2.45 leads to a slightly better match of the load–displacement curve and considerable stress redistribution in the sample.

The critical resolved shear stress \(\tau_{{{\text{CRSS}}}}\) is obtained as the highest absolute value among the resolved shear stresses in twelve octahedral slip systems as the pop-in begins. The elastic response of an fcc single crystal was implemented as a user-defined material routine UMAT in order to compute the resolved shear stresses [48]. The value of \(\tau_{{{\text{CRSS}}}} = 0.33 {\text{ GPa}}\) is obtained from the simulation results at the respective indentation depth of \(12\,{\text{nm}}\). The critical resolved shear stress is about \(G/{11}\) of the shear modulus on {111} planes and about \(9\tau_{{{\text{th}}}} /16\) of the theoretical shear strength by Frenkel. These are obtained from the elastic stiffness coefficients [49] as \(G = 3{\text{c}}_{44} \left( {{\text{c}}_{11} - {\text{c}}_{12} } \right)/\left( {4{\text{c}}_{44} + {\text{c}}_{11} - {\text{c}}_{12} } \right)\) and \(\tau_{{{\text{th}}}} = G/2\pi\), respectively, see Table 1. As follows from [12], such high resolved shear stresses operating at the pop-in may indicate that the loss of lattice stability results from a homogeneous dislocation nucleation in bulk. On the contrary, heterogeneous nucleation of dislocations, as observed in micropillars, requires significantly lower resolved shear stresses. For instance, the critical shear stress for dislocation nucleation in a single crystal Mo-alloy was found to be \({G}/{8}\) from nanoindentations studies, while compression tests on the micropillars revealed a three times smaller value [12]. The evaluated \(\tau_{{{\text{CRSS}}}}\) is thus considered as the experimental estimate of the theoretical shear strength of C60 fullerite.

The molecular dynamics simulations of nanoindentation of pure Fe and Cu demonstrate that a vast multiplication of dislocations occurs during the first pop-in [45]. This results from the release of a large amount of elastic strain energy stored immediately before the pop-in. It is therefore assumed that the drop of ACP further evaluated as the ratio of the above-said theoretical hardness to the real one, characterizes the plastic strain accumulated right beneath the indenter. This ratio is depicted in Fig. 3a for various materials which were earlier tested in our laboratory. The results of nanoindentation of high-purity Al are shown for comparison in Fig. 3b. The hardness drop for C60 is slightly higher than that in sapphire, where the ideal hardness is only two times higher than the measured one. On the contrary, the values of the ideal and the measured hardness of Cu and Al differ by one order of magnitude. Note that the ACP drop correlates with the width of the first pop-in scaled by the contact radius at the pop-in formation. The ratio of the ideal to the real hardness and the pop-in width indicate the local material ductility, which is obviously much lower for C60 as compared to Al and Cu. Although these crystals have the same fcc lattice structure, the difference in the local ductility may be attributed to an unlikely cross-slip in C60 (due to formation of stacking faults [50]) and presumably higher Peierls stress [51] than that of Al and Cu.

Figure 3
figure 3

a Width of the first pop-in scaled by the contact radius at the pop-in start plotted against the ratio of the ideal hardness, that is ACP at the pop-in initiation, to the real hardness. The nanoindentation was performed on the (001) surface of W, Mo and MoIr solid solution, (111) surface of C60, Cu and Al single crystals and (0001) surface of Al2O3, ScB2 and Be single crystals. b Load–displacement and ACP curves for a typical nanoindentation test on the (111) surface of Al single crystal having purity of 99.99% (full circles) and the respective average contact pressure (open circles)

Full size image

Conclusions

The mechanical properties of (111)-oriented C60 single crystal were investigated by nanoindentation with Berkovich indenter. The pop-in event was observed on loading curve at the displacement of about 12 nm. The maximum resolved shear stress corresponding to the pop-in load reaches \({1}/{11}\) of the shear modulus on {111} planes. It is assumed that the first pop-in event is attributed to the homogeneous dislocation nucleation, and thus, the maximum resolved shear stress is close to the theoretical strength \(\tau_{{{\text{th}}}}\) of the defect-free fullerite. The underlying finite element analysis considers the anisotropic elastic response of the fullerite sample and approximates the realistic shape of indenter’s nose.