Room-temperature ferroelectricity, superparamagnetism and large magnetoelectricity of solid solution PbFe_1/2Ta_1/2O₃ with (PbMg_1/3Nb_2/3O₃)_0.7(PbTiO₃)_0.3

Abstract

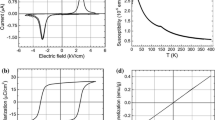
We report the properties of first synthesized ceramic samples of a perovskite solid solution (PbFe_1/2Ta_1/2O₃)_x[(PbMg_1/3Nb_2/3O₃)_0.7(PbTiO₃)_0.3]_1−x, x = 0.4, 0.5. The solution is a single-phase material contrary to broadly studied multiphase (magnetic/ferroelectric) composites. Both compounds are ferroelectrics with a diffuse phase transition. An increase in x value results in a decrease in phase transition diffuseness, and an increase in the remnant polarization. ²⁰⁷Pb NMR shows that iron ions are nonuniformly distributed over octahedral sites and tend to random occupation of these sites in the perovskite structure. In particular, the NMR data indicate a tendency to form regions with a higher concentration of iron in the perovskite structure. Magnetic measurements show the coexistence of superparamagnetic and paramagnetic phases in the samples. The paramagnetoelectric (PME) coefficients determined by a dynamic method at room temperature have values β ≈ 0.15 × 10⁻¹⁵ s A⁻¹ (x = 0.4) and 0.54 × 10⁻¹⁵ s A⁻¹ (x = 0.5) at low magnetic fields (± 300 Oe), which are three thousands times larger than that in most single-phase magnetoelectric materials. Our measurements show that the main contribution to the PME response is caused by the superparamagnetic phase. Because the ME response is proportional to dM²/dH, it can be amplified by many orders of magnitude for the multiferroics with the superparamagnetic phase due to a sharp change of magnetization with the field.

Appendix

Magnetization analysis

The solid solutions are materials with perovskite structure ABO₃. We may rewrite the chemical formula as (PFT)_x(PMN–PT)_1−x = PbFe_x/2Ta_x/2Mg_0.7(1−x)/3Nb_1.4(1−x)/3Ti_0.3(1−x)O₃. Magnetic ions Fe and nonmagnetic M = Ta, Mg, Nb, Ti occupy the sites of cubic sublattice B with the percentage given by the corresponding subscript in the formula. The Fe ions may be distributed randomly or form some kind of short- or long-range chemical order. Evidence for partial chemical ordering in the B sublattice of complex perovskites comes from experiments [54,55,56,57] and theory [20,21,22, 58, 59]. Our NMR studies (see above) confirm the nonuniform distribution of Fe in the B sublattice.

Magnetic measurements for (PFT)_x(PMN–PT)_1−x with x = 0.1, 0.2, 0.3 (Fig. 10) show that these samples are in the paramagnetic state in the studied temperature range. Thus, we omitted any additional investigations of these samples and focused our attention on samples with x = 0.4 and 0.5.

Figure 10

Magnetization dependence on magnetic field for solid solution (PFT)_x(PMN–PT)_1−x for x = 0.1 (a), 0.2 (b) and 0.3 (c) at different temperatures

We assume that a part of Fe³⁺ ions x_Fe < x/2 contribute to the paramagnetic response χ_p(T), another part, x_s= x/2 − x_Fe, participates in superparamagnetic response. The Curie constant

$$ C_{p} = N_{p} \frac{{\left( {g\mu_{B} } \right)^{2} S_{Fe} \left( {S_{Fe} + 1} \right)}}{{3k_{B} }} $$

gives the number N_p of Fe spins (per 1 g of the material) in the paramagnetic state; μ_B is Bohr magneton. Figure 8 shows that these numbers are very close for both samples N_p ≈ 2.8 × 10²⁰. Using the molar mass of the solid solution m_M(x), we find x_Fe = m_M(x)N_p/N_A ≈ 0.16 for both samples, N_A is the Avogadro number.

After that, we fit M(H) curves by the sum of paramagnetic and superparamagnetic contributions (cf. Eq.~(3) from Ref. [45]) given by Eq. (2).

We assume that the distribution of superspin moments is sharply peaked at the value μ_s(T) (i.e., all superspins are equal). Noting that L(x) → 1, for x → ∞, and $\left. {\frac{\partial L(x)}{\partial x}} \right|_{x = 0} = \frac{1}{3}$, we may obtain the superspin moment value, and the number of superspins

$$ \begin{aligned} \mu_{\text{s}} \left( T \right) & = \frac{{3k_{\text{B}} T}}{{M_{\text{s}} \left( {\infty ,T} \right)}}\left. {\frac{{\partial M_{\text{s}} \left( {H,T} \right)}}{\partial H}} \right|_{H = 0} \\ N_{\text{s}} & = \frac{{M_{\text{s}} \left( {\infty ,T} \right)}}{{\mu_{s} \left( T \right)}}, \\ \end{aligned} $$

(6)

from the slope of the superparamagnetic contribution to the isotherm curve at the origin $\left. {\frac{{\partial M_{s} \left( {H,T} \right)}}{\partial H}} \right|_{H = 0}$ = (7.5 ± 0.6) × 10⁻⁴ emu (g Oe)⁻¹ and saturated value of the superparamagnetic magnetization at large field M_s(∞,T) = 0.240 ± 0.003 emu g⁻¹, for T = 293 K. For the other isotherms, we find (assuming that N_s does not change with T)

$$ \mu_{\text{s}} \left( T \right) = \frac{{M_{\text{s}} \left( {\infty ,T} \right)}}{{N_{\text{s}} }}, $$

(7)

where M_s(∞,T) = 0.323 ± 0.003, 0.385 ± 0.003 emu g⁻¹, for T = 193 K, 120 K.

Equations (6), (7) allow to find the number N_s and the value μ_s(T) for our samples. The M(H) curves for 04PFT sample are well fitted by Eq. (2) with the parameter values, N_s = 6.3 × 10¹⁴, μ_s(T)/μ_B = 6.6 × 10⁴, 5.5 × 10⁴, 4.1 × 10⁴ for T = 120, 193, 293 K, respectively.

Assuming that the superspin moments display a mean-field like temperature dependence $\mu_{\text{s}} (T) = \mu_{\text{s}} (0)\sqrt {1 - T/T_{\text{c}} }$, we obtain μ_s(0)/μ_B ≈ 7.9 × 10⁴, T_c ≈ 400 K.

For x = 0.5, $\left. {\frac{{\partial M_{s} \left( {H,293} \right)}}{\partial H}} \right|_{H = 0}$ = 1.5 × 10⁻⁴ emu (g Oe)⁻¹, M_s(∞,T) = 0.089, 0.072, 0.058 emu g⁻¹ for T = 120, 193, 293 K, respectively. It gives N_s= 1.8 · 10¹⁴, μ_s(T)/μ_B= 4.8 × 10⁴, 4.3 × 10⁴, 3.5 × 10⁴ for T = 120, 193, 293 K, μ_s(0)/μ_B≈ 5.5 × 10⁴, T_c ≈ 490 K.

Let us consider the possibility to explain the superparamagnetism of our samples by magnetic impurity phases. In Refs. [50, 51], the hysteresis loops in PFT and solid solutions PFT–PbTiO₃ were supposed to be due to the presence of lead hexaferrite (magnetoplumbite) PbFe₁₂O₁₉. At room temperature, the saturation magnetization of the hexaferrite is ~ 50 emu g⁻¹ [60, 61], or 0.88μ_B per Fe spin. Thus, n_s12 = 4.7 × 10⁴ of Fe spins in a particle of PbFe₁₂O₁₉ would have a magnetic moment μ_s(T)/μ_B = 4.1 × 10⁴ at T = 293 K that would explain the superparamagnetism of 04PFT sample (see fourth row of Table 2). The size of the particle would be ~ 110 Å, because the volume of PbFe₁₂O₁₉ unit cell is 695 Å³ [62] and it contains 2 formula units, i.e., 24 Fe ions. Then the volume fraction of PbFe₁₂O₁₉ in our sample would be 0.7% and the mass fraction—0.48%; it can not be detected by XRD. But, as we have mentioned in the “Discussion” section, such a small fraction of the magnetic impurity phase can not produce appreciable ME response for two-phase composite material [53]. Also, against the presence of this impurity in our samples is the fact that the Curie temperature of bulk PbFe₁₂O₁₉ is 720 K [60, 63], which can be reduced in nanoparticles, but seems to be still much larger than T_c= 400–490 K found by us. If nonmagnetic ions substitute for Fe in the hexaferrite, the Curie temperature and the saturation magnetization are reduced dramatically [64,65,66,67]. In order to explain the superparamagnetism in our samples by such a diluted magnetoplumbite impurity, we would have to assume a larger fraction of the impurity phase, which is not observed by XRD.

In Ref. [52], the pyrochlore Pb₃FeTaO₇ impurity was supposed to be responsible for room-temperature hysteresis in PFT–PT solid solutions. Pb₃FeTaO₇ has 8 formula units in the cubic unit cell with a = 10.5 Å. The saturation magnetization at room temperature is ~ 2.7 emu g⁻¹. We obtain n_s,pyr = 8.8 · 10⁴ of Fe spins in a particle. The particle size is 233 Å, the volume fraction is ~ 7%, and the mass fraction is 9%. But our samples have no more than 2.4% of the pyrochlore admixture.

Therefore, neither PbFe₁₂O₁₉ nor Pb₃FeTaO₇ can be responsible for the magnetism and magnetoelectricity of the considered materials.

Magnetoelectric coupling

Within a phenomenological Landau–Ginzburg–Devonshire approach, linear and biquadratic ME couplings contribution to the system free energy are described by the terms μ_ijP_iM_j and ξ_ijklP_iP_jM_kM_l, respectively (P is polarization and M is magnetization, and μ_ij and ξ_ijkl are corresponding tensors of linear and biquadratic ME effects, respectively) [10, 19, 68]. In ceramics, the elements of the tensors are averaged and we are dealing with scalar LGD equations. If we start the description from the symmetric paraelectric paramagnetic phase, we should retain only biquadratic ME coupling

$$ F = F_{\text{P}} + F_{\text{M}} + F_{\text{ME}} , $$

(8)

$$ F_{\text{ME}} = \frac{{\xi_{\text{MP}} }}{2}M^{2} P^{2} , $$

(9)

where ξ_MP is the coupling parameter that is assumed to weakly depend on temperature. The terms F_P and F_M depend only on polarization and magnetization, respectively. For the second-order phase transitions they have the usual form in SI units system

$$ F_{\text{P}} = \frac{{\alpha_{\text{P}} }}{2}P^{2} + \frac{{\beta_{\text{P}} }}{4}P^{4} - {\text{PE}}, $$

(10)

$$ F_{\text{M}} = \frac{{\alpha_{\text{M}} }}{2}M^{2} + \frac{{\beta_{\text{M}} }}{4}M^{4} - \mu_{0} MH, $$

(11)

where only α_P,M have strong temperature dependence α ~ (T – T_C). For small external fields, we may write the solutions of Eq. (8) in the form

$$ P = P_{\text{s}} + \varepsilon_{0} \chi_{\text{E}} E, $$

(12)

$$ M = M_{\text{s}} + \chi_{\text{M}} H, $$

(13)

where P_s, M_s are spontaneous polarization and magnetization that become nonzero in the ordered phases; χ_E,M are dielectric and magnetic susceptibilities. Then ME coupling has the form

$$ F_{\text{ME}} = \frac{{\xi_{\text{MP}} }}{2}\left( {M_{\text{s}} + \chi_{\text{M}} H} \right)^{2} \left( {P_{\text{s}} + \varepsilon_{0} \chi_{E} E} \right)^{2} , $$

(14)

that allows us to express various magnetoelectric coefficients via ξ_MP

$$ \begin{aligned} \alpha \equiv - \frac{{\partial^{2} F}}{\partial E\partial H} = - 2\xi_{\text{MP}} M_{\text{s}} \chi_{\text{M}} P_{\text{s}} \varepsilon_{0} \chi_{\text{E}} , \\ \beta \equiv - \frac{{\partial^{3} F}}{{\partial E\left( {\partial H} \right)^{2} }} = - 2\xi_{\text{MP}} \left( {\chi_{\text{M}} } \right)^{2} P_{\text{s}} \varepsilon_{0} \chi_{\text{E}} , \\ \gamma \equiv - \frac{{\partial^{3} F}}{{\left( {\partial E} \right)^{2} \partial H}} = - 2\xi_{\text{MP}} M_{\text{s}} \chi_{\text{M}} \left( {\varepsilon_{0} \chi_{\text{E}} } \right)^{2} . \\ \end{aligned} $$

(15)

Due to the superparamagnetic contribution, the value of β will increase with temperature lowering according to the temperature dependence of magnetic susceptibility as [χ_M(T)]² ~ 1/T².

Using the value of β(T) obtained from experiments, we can estimate the biquadratic ME coefficient ξ_MP from the equation

$$ \xi_{MP} = - \frac{\beta \left( T \right)}{{2P_{s} \left( T \right)\varepsilon_{0} \chi_{E} \left( T \right)\left[ {\chi_{M} \left( T \right)} \right]^{2} }}. $$

(16)

We got ξ_MP ≈ –2.9 × 10⁻⁵ J m³ A⁻² C⁻² for the solid solution with x = 0.4 by substituting the room temperature values of parameters: β ≈ 0.15 × 10⁻¹⁵ s A⁻¹, the spontaneous electric polarization P_s≈3.0 μC cm⁻², susceptibilities dielectric χ_FE ≈2000, and magnetic (mass) χ_M ≈0.63 emu (g kOe)⁻¹. For x = 0.5, we have obtained ξ_MP≈ − 0.0014 J m³ A⁻² C⁻², using β ≈ 0.54 × 10⁻¹⁵ s A⁻¹, P_s≈ 4.4 μC cm⁻², χ_FE ≈2000, χ_M ≈0.142 emu (g kOe)⁻¹. All parameters were determined from the data of our experiments reported in previous sections.

Let us note that Eq. (11) is appropriate for the description of the paramagnetic phase in small fields where magnetization is proportional to H. For the description of the superparamagnetic phase at higher fields, we should consider another expression for the free energy part F_M

$$ F_{\text{M}} = - N_{\text{s}} T\ln Z, $$

(17)

where $Z = {{\sinh \left[ {\frac{{2\left( {S + 1} \right)\mu_{\text{s}} \left( T \right)H}}{{2Sk_{\text{B}} T}}} \right]} \mathord{\left/ {\vphantom {{\sinh \left[ {\frac{{2\left( {S + 1} \right)\mu_{\text{s}} \left( T \right)H}}{{2Sk_{\text{B}} T}}} \right]} {\sinh \left[ {\frac{{\mu_{\text{s}} \left( T \right)H}}{{2Sk_{\text{B}} T}}} \right]}}} \right. \kern-0pt} {\sinh \left[ {\frac{{\mu_{\text{s}} \left( T \right)H}}{{2Sk_{\text{B}} T}}} \right]}}$ is the partition function for an isolated spin S in the magnetic field H. For S ≫ 1 this gives $M_{\text{s}} \left( {H,T} \right) = - {{\partial F_{\text{M}} } \mathord{\left/ {\vphantom {{\partial F_{\text{M}} } {\partial H}}} \right. \kern-0pt} {\partial H}}$, Eq. (2). We will neglect the contribution from paramagnetic phase. Then instead of Eq. (14) we have

$$ F_{\text{ME}} = \frac{{\xi_{\text{MP}} }}{2}\left( {P_{\text{s}} + \varepsilon_{0} \chi_{\text{E}} E} \right)^{2} \left[ {M_{\text{s}} \left( H \right)} \right]^{2} $$

(18)

and

$$ \begin{aligned} P = - \frac{\partial F}{\partial E} = P_{\text{P}} + \Delta P_{\text{ME}} , \hfill \\ \Delta P_{\text{ME}} = - \xi_{\text{MP}} P_{\text{s}} \varepsilon_{0} \chi_{\text{E}} \left[ {M\left( H \right)} \right]^{2} \hfill \\ \end{aligned} $$

(19)

In the experiment, the ME effect is manifested as a polarization P_ac induced by a small ac magnetic field h_ac under application of dc field H_dc. With using collinear dc and ac magnetic fields H = H_dc + h_ac sin ωt, we obtain a generalization of Eq. (4)

$$ \begin{aligned} \Delta P_{ME} &= - \xi_{MP} P_{s} \varepsilon_{0} \chi_{E} \left[ {M\left( {H_{0} + h_{0} \sin\omega t} \right)} \right]^{2} \\ & = - \xi_{MP} P_{s} \varepsilon_{0} \chi_{E} \left[ {M\left( {H_{0} } \right)^{2} + 2M\left( {H_{0} } \right)\left. {\frac{\partial M\left( H \right)}{\partial H}} \right|_{{H = H_{0} }} h_{0} \sin\omega t} \right] \\ P_{ac} &= - \xi_{MP} P_{s} \varepsilon_{0} \chi_{E} 2M\left( {H_{0} } \right)\left. {\frac{\partial M\left( H \right)}{\partial H}} \right|_{{H = H_{0} }} h_{0} \sin\omega t. \\ \end{aligned} $$

(20)

Hence, the generalization of Eq. (5) shows that the amplitude of magnetoelectric current I_ME is proportional to dM²/dH (see inset in Fig. 9a).

The above consideration can only provide a qualitative agreement with the experiment. A more realistic theory should take into account at least a distribution of moment values.