1 Introduction

4D images refer to a series of 3D volumes acquired over time, for example, via dynamic X-ray computed tomography (CT). Such images may be used to study the evolution of 3D objects and have applications in e.g. medicine [1] and materials science [2,3,4]. To use 4D images in quantitative studies, we need segmentation methods that can detect and track objects over time. Additionally, some systems contain objects which merge or split as part of their time evolution, and such events are often of interest on their own [2, 5]. Therefore, a segmentation method should handle topological changes and still obtain an accurate result.

Furthermore, due to advancements in imaging technology [6, 7], 4D images can now be acquired with a very high spatial and temporal resolution, i.e., a voxel size \(\le 5\;\upmu \)m at hundreds of 3D volumes per second. This places high demands on the computational efficiency of segmentation methods.

In this paper, we address the problem of 4D segmentation via a simplifying assumption, which we demonstrate leads to a simple, elegant, and highly efficient segmentation method. We assume that objects only perform splits or merges during their evolution, but not both. While this assumption is slightly limiting, many interesting systems exhibit this behavior. For example, biological cells divide but do not merge, and bubbles in a foam merge but do not split. Furthermore, for such systems, enforcing that objects are only allowed split or merge can indeed be a benefit, as it exploits our prior knowledge of the system.

Fig. 1
figure 1

The principle of the 4D segmentation approach illustrated on a lower-dimensional 3D (2D+time) example. a Time series of 2D images, where two disks grow and merge. b 2D images are stacked to form a 3D (2D+time) volume. Here, the merging disks appear as a single simply connected component. c Segmentation given by sequentially detecting the disks in each 2D image. d Segmentation given by detecting the 2D boundary of the 3D connected component

Full size image

To illustrate our method, we initially describe it in 2D+time for simplicity. Consider the case in Fig. 1a where two solid blobs grow until they merge together to a single object. The scenario of splitting is identical, as we can transform one to the other by reversing time. We can think of the objects at time t as the intersection of a 3D connected component and an xy-plane at time t, as shown in Fig. 1b. To segment the objects, we could aim to segment the full 2D+time connected component. However, in 4D, this will require a large amount of memory. Instead, we could just represent the boundary by segmenting the object contours at every time, as in Fig. 1c. Yet, this still uses excessive memory and does not exploit our assumption of only splits or merges.

Our core observation is that if we assume solid objects only merge (or only split) the boundary of their 2D+time connected component is homeomorphic to a sphere. Thus, we can represent its boundary as a triangle mesh, \({\mathcal {M}}\), as shown in Fig. 1d. However, note that we do not have to close the mesh in the top (corresponding to time steps after the final image) which in practice means that the triangle mesh has n-disk topology rather than n-sphere topology. For 4D data, the mesh used for segmentation is a tetrahedral mesh embedded in 4D. Thus, we only have a single mesh whose cross sections represent the contours we seek. This is significantly less memory intensive than representing a segmentation for each time step.

We now proceed as follows. Given a sequence of input 2D images with merging objects, we segment the final image. This gives a contour which we fill in to produce a triangle mesh that represents the initial stage of \({\mathcal {M}}\). The surface mesh is now allowed to deform in 3D (i.e., 2D+time). Similar to classic active contours [8] or deformable surfaces [9, 10], this deformation is driven by an internal energy which keeps it smooth and external energy which attracts the mesh to object boundaries. When the computation stops, our spatiotemporal data has been segmented. We can obtain a segmentation at an arbitrary point in time, t, by intersecting \({\mathcal {M}}\) with a plane corresponding to that specific value of t. This results in a contour describing the boundary of the segmented object(s) at the given time.

The most significant benefit of our approach is that it allows us to precisely locate splits (or merges) in both time and space. Consider the mapping from a point \(p\in {\mathcal {M}}\) to time t(p). As shown in Fig. 1d, the points where splits occur correspond to saddle points of t(p) where the gradient is zero. Further, the center of the initial objects corresponds to the minima of t. In other words, by finding the singularities of t(p), as well as how they are connected, we can detect where specific objects split. This strategy also makes our approach robust to spurious self-intersections, since they do not affect the location of the singularities. In practice, we exploit this by computing the Reeb graph [11, 12] of \({\mathcal {M}}\) with respect to t(p) since the Reeb graph contains information both about the placement and connectivity between the singularities.

From a computational standpoint, our approach also offers considerable benefits. As we only store a boundary, we have a very compact description of the evolution of an object. Partly because storing the boundary inherently requires significantly less space. But also because a tetrahedron in 4D can span multiple time values, which exploits the coherence between two time-adjacent 3D volumes. This compactness also makes our method fast, which allows us to segment very large 4D images in only a few minutes. To make our method accessible, we publish a Python implementation at https://github.com/patmjen/4dsurf.

1.1 Related Work

Generally, existing methods for segmenting 4D images fall into two categories: mesh-based methods and voxel-based methods. Mesh-based methods are mainly used for tracking non-interacting objects over time. In [10, 13], a sequential approach is used where the fit in one 3D volume is used to improve the fit in the next. Here, one needs to establish a correspondence between segmentations in consecutive 3D volumes in order to obtain object tracking. When objects merge or split, this can be highly non-trivial, although some works have suggested approaches for handling this, e.g. [14, 15]. Others [16,17,18,19] use a more global approach where a separate mesh is placed in every 3D volume and then all meshes are fitted simultaneously. Common for these methods is that the mesh connectivity is kept fixed and only vertex positions are changed. This provides a natural correspondence between meshes and makes it easy to track the development of an object over time. However, it does not allow for the object to split or merge.

Voxel-based approaches on the other hand can easily handle topology changes. Here, authors have used methods ranging from level sets [5, 20], Markov random fields [21, 22], to deep learning [13, 23]. However, while voxel-based approaches are more flexible regarding the evolution of the object, they do not (directly) give access to a mesh-based representation, which can make postprocessing more challenging. Furthermore, small errors in the segmentation can have large effects on the resulting topology as two objects may merge prematurely. And finally, since modern 4D images have sizes measured in the tens of gigabytes (GB) to several terabytes (TB), segmenting 4D images with voxel-based methods quickly becomes unwieldy unless the data is severely downsampled.

2 Method

Deformable models are widely used in 2D and 3D segmentation in the form of curves and surfaces. In 4D segmentation, hypersurfaces that deform in space-time are rarely encountered, and existing approaches treat the time dimension differently than the space dimensions. In this section, we propose the methodology needed to generalize parametric deformable surfaces to 4D, providing a combined treatment of the deformation in space and time. We begin by introducing the continuous formulation of 4D deformable models and then detail how we discretize the problem. In the subsequent sections, we then detail each component of our 4D deformable model approach.

2.1 Continuous 4D Deformable Model

Given a 4D image, \( I: \Omega \subset {\mathbb {R}}^4 \rightarrow {\mathbb {R}} \), we aim to find a partition of the domain \( \Omega \) into two disjoint regions, \( \Omega _\textrm{in}\) and \( \Omega _\textrm{out}\), separated by a boundary \(\Gamma \). The region \(\Omega _\textrm{in}\) corresponds to the inside of the 4D connected component we wish to segment and \(\Omega _\textrm{out}\) to the outside. As \(\Gamma \) uniquely determines the regions \(\Omega _\textrm{in}\) and \(\Omega _\textrm{out}\) we formulate our problem as a search for a boundary, \(\Gamma ^*\), that minimizes the following energy functional

$$\begin{aligned} \Gamma ^* = \arg \min _\Gamma E_\textrm{ext}(\Gamma ) + E_\textrm{int}(\Gamma ). \end{aligned}$$
(1)

Here, \(E_\textrm{ext}\) is an external energy term that ensures that \(\Omega _\textrm{in}\) and \(\Omega _\textrm{out}\) correspond to the image regions we wish to segment and \(E_\textrm{int}\) is an internal energy that acts as a regularizer by encouraging the boundary \(\Gamma \) to remain smooth.

For \(E_\textrm{ext}\), we use the popular Chan-Vese energy [24], which assumes the image can be modeled as a piecewise constant function with value \(c_\textrm{in}\) in \(\Omega _\textrm{in}\) and \(c_\textrm{out}\) in \(\Omega _\textrm{out}\). It is given as

$$\begin{aligned} \begin{aligned} E_\textrm{ext}(\Gamma ) =&\int _{\Omega _\textrm{in}} (I - c_\textrm{in})^2\, \textrm{d}\Omega \, \\&+ \int _{\Omega _\textrm{out}} (I - c_\textrm{out})^2\, \textrm{d}\Omega . \end{aligned} \end{aligned}$$
(2)

Generally, \(c_\textrm{in}\) and \(c_\textrm{out}\) may be unknown values which are also optimized over. However, as that adds a significant computational cost, we assume in this paper that \(c_\textrm{in}\) and \(c_\textrm{out}\) are known a priori.

For \(E_\textrm{int}\), we use the Dirichlet energy

$$\begin{aligned} \begin{aligned} E_\textrm{int}(\Gamma ) = \gamma \int _\Gamma \left\Vert \nabla \Gamma ({\textbf {x}})\right\Vert _2^2 \textrm{d}{} {\textbf {x}}, \end{aligned} \end{aligned}$$
(3)

where \(\gamma \ge 0\) is a fixed parameter that controls the degree of regularization.

2.2 Discrete 4D Deformable Model

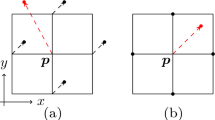
To find the optimal boundary, we use a discretized version of \( \Gamma \). Since \(\Gamma \) is the boundary between two 4D regions, it is a 3D hypersurface embedded in 4D [25]. We represent \( \Gamma \) with a tetrahedral mesh \({\mathcal {T}}\) with vertices \({\textbf {X}} \in {\mathbb {R}}^{V\times 4}\) where vertex positions \(\textbf{x}_i\) are given by four coordinates as shown in Fig. 2.

Fig. 2
figure 2

Single element of the tetrahedral mesh. Each vertex position, \(\textbf{x}_i\), has four coordinates: \(x_i\), \(y_i\), \(z_i\), and \(t_i\)

Full size image

Given an initial mesh \({\mathcal {T}}^{(0)}\), a solution to the discretized version of (1) can be found by gradient descent of the energy [8, 9]

$$\begin{aligned} \begin{aligned}&\nabla _{\textbf {X}} E_\textrm{ext}({\mathcal {T}}^{(i - 1)}) + \nabla _{\textbf {X}} E_\textrm{int}({\mathcal {T}}^{(i - 1)}) \\&\quad =-\frac{1}{\tau }({\textbf {X}}^{(i)} - {\textbf {X}}^{(i - 1)}), \end{aligned} \end{aligned}$$
(4)

where \(\tau \) is a step size. The gradient of the Dirichlet energy \(\nabla E_\textrm{int}(\Gamma )\) is given by the Laplacian \(\Delta \Gamma \) [26]. This gives the update equation

$$\begin{aligned} \left( {\textbf {I}} + \lambda {\textbf {L}} \right) {\textbf {X}}^{(i)} = {\textbf {X}}^{(i - 1)} - \tau \nabla E_\textrm{ext}({\mathcal {T}}^{(i - 1)}), \end{aligned}$$
(5)

where \({\textbf {L}}\) is a matrix approximating the Laplacian of \(\Gamma \), and \(\lambda = \tau \gamma \). We describe our initialization strategy in Sect. 2.3. As the mesh deforms from its initial configuration the tetrahedra will stretch, meaning the mesh will not be able to fit the image to sufficient detail. Therefore, we adaptively subdivide the mesh every \(n_\textrm{sub}\) iteration to prevent the mesh from becoming too coarse. We detail our subdivision strategy in Sect. 2.4.

For the external energy gradient in (5), it can be shown that the vertex displacements corresponding to \(\nabla E_\textrm{ext}({\mathcal {T}})\) are given by

$$\begin{aligned} \frac{\partial E_\textrm{ext}}{\partial {\textbf {x}}_i} = 2(c_\textrm{in} - c_\textrm{out})(I(\textbf{x}_i) - (c_\textrm{in} + c_\textrm{out})/2) \textbf{n}_i, \end{aligned}$$
(6)

where \({\textbf {n}}_i\) is the normal for vertex i [27]. As we adaptively subdivide the mesh during deformation, we want our normals to be robust to this. Therefore, we have developed an extension of angle-weighted normals to 4D, which we describe in Sect. 2.5.

For the Laplacian matrix, we use the scale-dependent Laplacian [28], in order to be robust to irregularly sized tetrahedra [26]. This computes the Laplacian at the i’th vertex as

$$\begin{aligned} L({\textbf {x}}_i) = \frac{1}{E}\sum _{j \in N(i)} \frac{{\textbf {x}}_j - {\textbf {x}}_i}{e_{ij}}, \quad E = \sum _{j \in N(i)} e_{ij}, \end{aligned}$$
(7)

where \(e_{ij} = \left\Vert {\textbf {x}}_j - {\textbf {x}}_i \right\Vert \) and N(i) are the neighbor vertices of vertex i. Since \({\textbf {L}}\) is sparse, we can solve the linear system in (5) efficiently using conjugate gradient iteration. However, constructing \({\textbf {L}}\) is relatively expensive, and we therefore only update it when we subdivide the mesh. While not strictly correct, we did not observe drawbacks with this strategy.

Finally, to extract the segmentation for a 3D volume at a given time, we compute a cross section of the fitted 4D mesh using the method detailed in Sect. 2.6.

2.3 Mesh Initialization

We assume objects only merge (similar to the example Fig. 1), since splitting can be viewed as merging in reverse. Thus, if the initial mesh is placed in the last 3D volume of the 4D image, it only needs to propagate backward in time. This makes a hyperdisk (i.e., a solid 3D ball) a good candidate for an initial mesh. The boundary of a hyperdisk forms a 2D surface, which we can represent with a triangle mesh.

This leads to the following initialization approach. First, fit a triangle mesh to the 2D object boundary in the last 3D volume. Since we only consider a single 3D volume here, we can ignore the time coordinate and treat it as a traditional 3D segmentation task. As a result, we can use an existing 3D method such as deformable surfaces [10], graph cut approaches [29, 30], or an isosurface [31] from a voxel segmentation to find the triangle mesh. We now let this triangle mesh be the boundary of the hyperdisk, and then tetrahedralize it using the TetGen tool by Si [32]. Finally, we add the time coordinate to the tetrahedron vertices, which results in the initial mesh. An illustration of the initialization approach for a lower-dimensional (2D+time) example is shown in Fig. 3.

Fig. 3
figure 3

The principle of initialization process illustrated on a 3D (2D+time) example. a First, the boundary of the object in a single image (volume in 4D) is located. b The interior of the boundary is triangulated (tetrahedralized in 4D), which gives the initial mesh. c The initial mesh is iteratively deformed to fit to the boundary of the connected component

Full size image

To avoid the mesh leaving the last 3D volume, we constrain the time coordinate of the tetrahedron vertices that correspond to the original triangle vertices to remain unchanged.

2.4 Adaptive 4D Mesh Subdivision

A considerable amount of research has been conducted on creating and subdividing tetrahedral meshes in 3D, and we want to leverage this. We will use an idea similar to that of coordinate charts from differential geometry [33], which are maps from manifolds to Euclidean space. In our case, we know the initial mesh is contained in a single 3D volume. After the mesh has been deformed in 4D, the initial mesh defines a natural mapping between 3D Euclidean space and the 4D mesh. For a point placed anywhere within the initial mesh, we can then use barycentric coordinates to find its corresponding position in 4D. See Fig. 4 for an illustration.

Fig. 4
figure 4

Illustration of the mapping from the coordinate mesh (left) to the deformed mesh (right). A point inserted in the highlighted face in the coordinate mesh can be mapped to its corresponding position in the deformed mesh using barycentric coordinates

Full size image

Specifically, we keep a copy of the initial mesh, \({\mathcal {T}}^{(0)}\), during deformation—henceforth referred to as the coordinate mesh, \({\mathcal {T}}^C\). To perform subdivision, we find all tetrahedra whose volume has grown larger than a threshold, s, and insert a new point at the barycenter of each tetrahedron. The volume of a tetrahedra with vertex positions \(\textbf{x}_1\), \(\textbf{x}_2\), \(\textbf{x}_3\), and \(\textbf{x}_4\) is given by [34, 35]

$$\begin{aligned} \textrm{vol}(\textbf{T}) = \frac{1}{6}\sqrt{G(\textbf{x}_2 - \textbf{x}_1, \textbf{x}_3 - \textbf{x}_1, \textbf{x}_4 - \textbf{x}_1)}, \end{aligned}$$
(8)

where G is the Gram determinant. Then, the original vertices of \({\mathcal {T}}^C\), along with the new points, are re-tetrahedralized with TetGen [32], which gives a new coordinate mesh. This is then re-mapped to 4D, after which the old coordinate and 4D mesh are thrown away.

While performing a full re-tetrahedralization is more expensive than updating the mesh, it has the benefits of resulting in a higher quality mesh, and is simple to implement with tools designed for 3D meshes.

2.5 Angle Weighted Normals in 4D

Analogous to surface meshes in 3D, vertex normals are defined as a weighted average of the adjacent tetrahedral face normals. These are in turn defined using a 4D analog of the cross product [36]; given 4D vectors \(\textbf{u}\), \(\textbf{v}\), and \(\textbf{w}\), we can find an orthogonal vector, \(\textbf{n} = (n_x, n_y, n_z, n_t)^\textrm{T}\), as

$$\begin{aligned} \begin{aligned} n_x&= \left|\begin{matrix} u_y &{} u_z &{} u_t \\ v_y &{} v_z &{} v_t \\ w_y &{} w_z &{} w_t \end{matrix}\right|,\hspace{5.0pt}n_y = \left|\begin{matrix} u_x &{} u_z &{} u_t \\ v_x &{} v_z &{} v_t \\ w_x &{} w_z &{} w_t \end{matrix}\right|,\\ n_z&= \left|\begin{matrix} u_x &{} u_y &{} u_t \\ v_x &{} v_y &{} v_t \\ w_x &{} w_y &{} w_t \end{matrix}\right|,\hspace{5.0pt}n_t = \left|\begin{matrix} u_x &{} u_y &{} u_z \\ v_x &{} v_y &{} v_z \\ w_x &{} w_y &{} w_z \end{matrix}\right|, \end{aligned} \end{aligned}$$
(9)

where \(|\cdot |\) is the determinant. For a tetrahedron with vertex positions \(\textbf{x}_1\), \(\textbf{x}_2\), \(\textbf{x}_3\), and \(\textbf{x}_4\), we form the vectors as \(\textbf{u} = \textbf{x}_2 - \textbf{x}_1\), \(\textbf{v} = \textbf{x}_3 - \textbf{x}_1\), and \(\textbf{w} = \textbf{x}_4 - \textbf{x}_1\).

Previous works have used simple averaging or weighted the normal of each tetrahedron by its volume [37]. However, as for triangle meshes [38], these weighting schemes are sensitive to re-tessellation of the mesh. In this work, we extend angle-weighted normals to four dimensions by weighting the contribution of each tetrahedron by the solid angle spanned by the tetrahedron at \({\textbf {v}}\). Assume, without loss of generality, that the mesh is scaled such that all edges are longer than 1. The solid angle, \(\omega \), is then given by the area of the spherical triangle formed by the intersection of the tetrahedron and a unit sphere, as illustrated in Fig. 5.

The area of the spherical triangle \(\omega \) is given by

$$\begin{aligned} \omega = \theta _1 + \theta _2 + \theta _3 - \pi , \end{aligned}$$
(10)

where \(\theta _1\), \(\theta _2\), and \(\theta _3\) are the dihedral angles of the tetrahedron edges connected to \({\textbf {v}}\) [39].

Fig. 5
figure 5

The solid angle \(\omega \) at vertex \({\textbf {v}}\) is the area of the spherical triangle given by the intersection of the tetrahedron and a unit sphere centered at \({\textbf {v}}\). \(\theta _1\), \(\theta _2\), and \(\theta _3\) denote the dihedral angles along the tetrahedron edges connected to v

Full size image

The normal at vertex i is then given by

$$\begin{aligned} {\textbf {n}}_i = \frac{\sum _{T \in {\mathcal {T}}_i} \omega _T {\textbf {n}}_T}{\left\Vert \sum _{T \in {\mathcal {T}}_i} \omega _T {\textbf {n}}_T\right\Vert }, \end{aligned}$$
(11)

where \({\mathcal {T}}_i\) are the incident tetrahedra for vertex i with normals \({\textbf {n}}_T\) and incident solid angles \(\omega _T\). The denominator ensures that the resulting normal is unit length. Similar to angle-weighted normals for triangle meshes, this weighting scheme is invariant to re-tessellation of the mesh.

As a proof, consider re-tesselating a tetrahedron meaning splitting it into multiple sub-tetrahedra where the original vertices remain in place and all new vertices are convex combinations of the original vertices. In this case, the face normals of the new tetrahedra will be equal to the original face normal. Furthermore, the solid angles of the sub-tetrahedra incident with \({\textbf {v}}\) will sum to the original solid angle \(\omega \). Therefore, the contribution of the incident sub-tetrahedra to the vertex normal of \({\textbf {v}}\) will be equal to the contribution of the original tetrahedron.

2.6 Cross sections of Tetrahedral Meshes in 4D

Computing a cross section is equivalent to finding the intersection with a hyperplane or extracting an isosurface. We use a simplified version of the marching tetrahedron method [40], which has been used previously for visualizing 4D tetrahedral meshes [36].

We assume without loss of generality that we compute the intersection with the xyz-hyperplane at \(t = 0\). If a tetrahedron intersects a hyperplane, the intersection will always be one of the eight cases illustrated in Fig. 6. The last three cases are problematic as the intersections are not surface elements. To avoid these, we perturb the time coordinate of all vertices which lie on the hyperplane by a small \(\varepsilon \ll 1\), which guarantees we will only encounter the first two cases.

Fig. 6
figure 6

All possible ways a tetrahedron in 4D may intersect a hyperplane. Black vertices are on the hyperplane (\( t = 0 \)), red vertices are ‘below’ (\( t < 0 \)), and blue vertices are ‘above’ (\( t > 0 \)). The intersection can be a a quadrilateral (which may be split into two triangles), b–e a triangle, (f) the entire tetrahedron, g a line, or h a point

Full size image

3 Results

To assess the performance of our method, we perform a series of numerical experiments, where we segment computer-generated 4D images with known ground truth. This allows a quantitative assessment and comparison with other methods. Next, we apply the method to a 4D dataset from dynamic X-ray CT. Here, a ground truth segmentation is not known, so we can only do a qualitative evaluation. Finally, we demonstrate how our method allows for tracking the evolution of splitting/merging objects through time by computing the Reeb graph [11, 12] of the fitted tetrahedral mesh.

3.1 Numerical experiments

We created an artificial 4D image containing five organic-looking blobs, shown in the top row of Fig. 8. As time progresses, the blobs move toward each other until they collide and merge to a new blob whose volume grows to equal the sum of the previous two blobs. Furthermore, as the blobs move, they rotate and deform to make the data more challenging to segment.

Fig. 7
figure 7

2D cross sections of the last 3D volume in the artificial 4D image for different values of the noise level \(\sigma \)

Full size image

The 4D image consists of 200 binary label volumes of size \(100 \times 100 \times 100\) voxels. Before segmenting, the intensity of the 4D image is transformed so the blobs have an intensity of 100 and the background an intensity of 200. After that, we add zero-mean Gaussian noise with standard deviations of 25 and 50 to create two additional 4D images. Figure 7 shows a cross section of the last 3D volume in each of the 4D images.

Fig. 8
figure 8

Segmentation results for the artificial 4D image using the proposed method. The rows show 3D renderings of (top to bottom): the data, segmentation for \(\sigma = 0\), segmentation for \(\sigma = 25\), and segmentation for \(\sigma = 50\). The segmentations have been overlaid on the data

Full size image

We segment the artificial images with the proposed method and compare with three other segmentation methods. These methods were chosen because they are well established and form the basis of many segmentation approaches [41].

  1. 1.

    Sequential 3D Markov Random Fields (MRFs). We segment each 3D image independently in sequence. The image segmentation is modeled as a graph minimum cut problem as detailed in [42]. Voxels are nodes in a graph and are connected to a special source and sink node. Each source/sink edge has a cost proportional to the background/foreground probability. Additionally, each node is connected to its six spatial neighbors with an edge whose cost controls the segmentation smoothness. We now seek a partition of the nodes into two disjoint sets by cutting edges of the graph until there is no path from the source to the sink node. The cost of the partition is the sum of the cut edges and we find the partition of minimum cost via the popular algorithm by Boykov and Kolmogorov (BK) [42].

  2. 2.

    4D Markov Random Fields (MRFs). We use the same construction as for 3D MRFs, but compute a single segmentation for the entire 4D images at once. As such, we also add edges between graph nodes and their temporal neighbors (in addition to their six spatial neighbors). Again, the segmentation is computed with BK algorithm [42]. We note that one could also use smaller overlapping temporal windows, instead of considering the entire 4D image, in order to reduce the computational costs. To be able to compare results with a global method, we chose not to do this.

  3. 3.

    Surface Detection via Graph Cut (GC). An initial mesh is placed at a user-defined location and deformed to fit the image contours, as detailed in [29, 30, 43]. New candidate positions for each mesh vertex are sampled equidistantly in a column along the outward vertex normals. These candidates are graph nodes connected to a special source and sink node. Each source/sink edge has an associated cost, computed as in [44], related to the probability of being inside/outside the deformed mesh. Nodes in neighboring column are connected with edges to enforce that vertex displacement varies by a maximum of \(\Delta \) steps to ensure a smooth surface. We then compute an optimal node partition into ‘inside’ and ‘outside’ with the BK algorithm [42] and move each vertex to the outermost ‘inside’ node in its column.

    The initial mesh is an 8-frequency subdivided icosahedron approximating a sphere. We process each volume sequentially and place a mesh at the centroid of each connected component of the ground truth label volume. Note that this represents a best-case scenario for this method, as it requires either a good pre-segmentation of the data or manual annotation at every time step. Furthermore, the sequential nature of this method means that we do not have any correspondence between segmentations in different 3D volumes as we do with our method. The correspondences would have to be established afterward which is non-trivial. We apply the graph cut method for two values of the max. difference parameter, \(\Delta \). A large value gives the method more freedom to fit elongated shapes, while a smaller value makes it more robust to noise.

For our method, we scale each spatial axis to \([-1, 1]\) and the time axis to \([-2, 2]\). We scale the time axis to ensure that the image features have roughly equal curvature. This allows us to maintain a more regular mesh during the deformation, which results in a better fit. We use the ground truth segmentation of the last volume to initialize as in Sect. 2.3. Furthermore, the max. tet. volume, s, starts at \(4\times \) the final value to perform a rough initial fit and is then set to the final value for the last 10 iterations to refine the fit.

Table 1 Parameters used to segment the artificial 4D images
Full size table

The parameters for all methods are shown in Table 1, and all experiments were performed with an AMD Ryzen 7 3700X processor. For the noiseless image, we only apply our method. The segmentation results for our method are shown in Fig. 8. Visually, the segmentations correspond well with the data, with some noise observable for \(\sigma = 50\).

Fig. 9
figure 9

Plots of mean and max. distance between cross sections of the fitted tetrahedral meshes and ground truth segmentation boundary. The gray regions signify times when merges are ongoing and the vertical dotted lines mark the beginning of a new merge

Full size image

To provide a quantitative measure of the quality of the segmentation, a ground truth segmentation boundary—stored as a surface mesh—was created for each 3D volume. These were then compared with cross sections of the tetrahedral mesh at the corresponding times. The comparison was done with the mean and maximum distance between the surface meshes as computed with the MESH tool by Aspert et al. [45]. The results are shown in Fig. 9.

The plots support what is seen in Fig. 8 as the mean distances remain small, i.e., below one voxel. There is a spike in the error at the end of the merges, since there is a slight discontinuity in the data when blobs merge. Thus, the temporal part of the chosen regularization introduces a larger error at these times. The same behavior occurs for the maximum distance, although the errors are larger since a single spurious vertex can significantly affect the value.

For the other methods, we also use the distance to the ground truth segmentation boundary. For the GC methods, this can be done directly. For the MRF methods, we extract an isosurface from each 3D label volume. The results are shown in Fig. 10. Additionally, we also compare the resource use of the methods. We measured runtime, peak memory use, and how much memory was needed to store the final segmentations. Table 2 shows the results along with the theoretical scaling of each measured value w.r.t. the image size. Our method performs as well as or better than the compared approaches while resulting in a more compact representation of the final segmentation.

Fig. 10
figure 10

Plots of the mean distance between the computed segmentation boundary for each method and ground truth segmentation boundary. The gray regions signify times when merges are ongoing and the vertical dotted lines mark the beginning of a new merge

Full size image
Table 2 Resource use for the segmentation approaches. The memory uses do not include the size of the image data (200 MB). The scaling w.r.t. the image size of each value is also shown. S represents the size of each 3D volume, and T is the number of 3D volumes in the 4D image
Full size table
Fig. 11
figure 11

Segmentation results for the 4D synchrotron X-ray CT data. The top row shows a 3D rendering of the 4D data at different times. The bottom row shows the segmentations overlaid on the data. Note that the last column shows an xyt-slice where the vertical axis represents time (bottom = \(t_0\) and top = \(t_{95}\))

Full size image

3.2 Application to Metal Foam

We now apply the method to a 4D synchrotron X-ray CT image. The dataset is a time series of foaming metal, where blowing agent powders have been mixed into a block of aluminum. As the aluminum sample is heated to its melting point the powders release gas, which causes bubbles to form. Over time, these bubbles expand and merge to form even larger bubbles. More details can be found in [2]. The data consists of 55 volumes of size \(888 \times 888 \times 600\) and uses 26 GB of memory. It is visualized in the top row of Fig. 11.

We initialize the mesh at the large bubble in the bottom of the last volume (see Fig. 11d). We again scale the spatial axes to \([-1, 1]\) and the temporal to \([-0.25, 0.25]\). The goal of the segmentation is to detect which bubbles merged together to form the final bubble. The parameters are shown in Table 3 and the segmentation itself took 5 min using an Intel Xeon Gold 6142 processor.

Table 3 Parameters used to segment the 4D synchrotron X-ray CT data. Please see Table 1 for more descriptive parameter names
Full size table

The result of the segmentation is shown in the bottom row of Fig. 11. The method has detected the merging of different bubbles. Furthermore, the 4D cross sections provide a good match with the data, even though the quality of the segmentation degrades somewhat the further we are from the initial mesh. Also, there are some minor errors in the last volumes where the tetrahedral mesh has moved into an adjacent bubble.

3.3 Tracking Evolving Topology

We now demonstrate how our method allows the quantification of splitting/merging by computing the Reeb graph [11, 12] of the fitted tetrahedral mesh. Reeb graphs are used to describe the evolution of level sets of a function defined on a manifold—in our case the time coordinate of our fitted tetrahedral mesh—making them ideal for detecting topological event such as splitting or merging [46]. As illustrated in Fig. 12, nodes are placed where topological changes occur such as local extrema and saddle points. If the level sets between two points form a connected component, the points are joined by an edge. As a result, the Reeb graph provides a compact description of the evolving topology of an object and also encodes when and where topological changes occur.

Fig. 12
figure 12

Illustration of the Reeb graph for a simple 2D+time example. The level sets are shown as black rings and the Reeb graph has nodes where the level sets change topology. The nodes are colored according to their time coordinate

Full size image

We use the Topology Toolkit [47, 48] to compute the Reeb graph for the (noiseless) segmentation of our 4D test image and the segmentation of the metal foam image. Prior to computation, we smooth the tetrahedral mesh with Laplacian smoothing and afterward we prune edges of the Reeb graph which are shorter than 10% of the mean edge length.

Fig. 13
figure 13

Reeb graphs for the artificial (top row) and metal foam (bottom row) images. Each column shows a 3D cross section of the fitted 4D tetrahedral mesh with the Reeb graph overlaid. The Reeb graph has been projected to 3D and its nodes are colored according to their time coordinate (scaled to be in \([-1, 1]\)) as in Fig. 12. The Reeb graph nodes corresponding to the merge in each subfigure have been highlighted with a black circle

Full size image

The results are shown in Fig. 13. For both segmentations, the Reeb graph provides a good description of where and how the objects merged together. Note especially how, even though a level set might have some slight self-intersections, e.g., in Fig. 13h, objects are not counted as having merged since the Reeb graph considers the full spatiotemporal structure.

4 Discussion

The method presented in this paper can segment merging or splitting objects in 4D. As demonstrated in Sect. 3.1, this can be achieved even in the presence of severe noise, although with a reduced quality. When objects are merging, our method also significantly outperformed the fixed-topology GC methods while being faster and using the same amount of memory. The MRF methods gave the most accurate segmentation, which is expected given that this is a binary segmentation problem with Gaussian noise. However, they used significantly more time and memory.

Furthermore, the time and memory benefits of our method will only improve as the image size increases, since the resource use of our method only depends on the complexity of the object to segment and not on the size of the input image. This is not the case for the compared methods. Finally, storing the segmentation as a tetrahedral mesh also results in an extremely compact description of the segmented objects—indeed, of the tested methods, ours provided the most compact segmentation. For the foaming aluminum data, which took up 26 GB of space, the resulting mesh only uses around 8.5 MB which is a reduction factor of more than 3,000.

Our method also offers increased robustness regarding quantifying the evolution of object topology. As we explicitly model the hypersurface boundary in 4D, splits/merges can be automatically detected as saddle points and do not need manual heuristics or collision detection like sequential methods. Furthermore, this also means that if some level sets intersect due to segmentation errors or imaging artifacts it is easily discarded as an error and not a merge/split—something which is not possible with sequential or 3D/4D voxel-based approaches. These benefits are unique to our object representation.

The main challenge with our method is how to maintain the mesh quality during deformation. With too high a regularization, the method cannot achieve a sufficient quality of fit due to over-smoothing. With too low, the tetrahedral mesh may start to self-intersect which results in a degenerate fit. Currently, finding the suitable balance between step size and regularization strength requires manual tuning. Promising avenues for addressing this are collision detection or displacing the vertices along non-intersecting search lines as in [49, 50]. However, as implementing these in a computationally efficient way is non-trivial, we relegate it to future work.

Furthermore, while Laplacian smoothing works well to regularize the spatial components of the fit, the spatiotemporal saddle points, that form at splits/merges (see Fig. 11e), are sensitive to over-smoothing. Additionally, for more complex image data (e.g. medical scans), an intensity-based deformation force may not be adequate. In these cases, performance may be improved by adapting approaches from [51,52,53,54] where the output of a neural network is used to guide the deformation of a contour in 2D images. Finally, our method does not attempt to detect if the topological assumptions are broken. As a result, fitting to image data where both splits and merges happen can result in degenerate fits.

5 Conclusion

We presented a method for simultaneously segmenting and tracking merging or splitting objects in 4D images. This was achieved by fitting a discretized hypersurface to the 3D boundary of the 4D simply connected component comprising the object of interest. Applications to artificial and real 4D images showed that the method was able to successfully segment, track, and quantify merging or splitting objects, even in the presence of noise. The method achieved comparable accuracy to existing methods with a resource use equal to or better than sequential 3D methods. Furthermore, our method only scales with object complexity and not image size making it suitable for the analysis of very large images.