Skip to main content
SpringerLink
Log in

Variational Methods for Normal Integration

  • Published:
Journal of Mathematical Imaging and Vision Aims and scope Submit manuscript

Abstract

The need for an efficient method of integration of a dense normal field is inspired by several computer vision tasks, such as shape-from-shading, photometric stereo, deflectometry. Inspired by edge-preserving methods from image processing, we study in this paper several variational approaches for normal integration, with a focus on non-rectangular domains, free boundary and depth discontinuities. We first introduce a new discretization for quadratic integration, which is designed to ensure both fast recovery and the ability to handle non-rectangular domains with a free boundary. Yet, with this solver, discontinuous surfaces can be handled only if the scene is first segmented into pieces without discontinuity. Hence, we then discuss several discontinuity-preserving strategies. Those inspired, respectively, by the Mumford–Shah segmentation method and by anisotropic diffusion, are shown to be the most effective for recovering discontinuities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Notes

  1. We consider only quadratic regularization terms: studying more robust ones (e.g., \(L^1\) norm) is left as perspective.

  2. Proof: by developing the terms inside the integral in (7), and integrating by parts, Theorem 6.2.5 in [3] applies with \(f:= -\nabla \cdot \mathbf {g}\) and \(g:= \mathbf {g} \cdot \varvec{\eta }\).

  3. Proof: by developing the terms inside the integral in (7) and integrating by parts, Theorem 6.2.2-(ii) in [3] applies with \(f:= -\nabla \cdot \mathbf {g} + \lambda z^0\) and \(g:= \mathbf {g} \cdot \varvec{\eta }\).

  4. This condition makes the matrix of the associated discrete problem strictly diagonally dominant, see Sect. 3.2.

  5. To ease the comparison between the variational and the discrete problems, we will use the same notation \(\varOmega \) for both the open set of \(\mathbb {R}^2\) and the discrete subset of the grid.

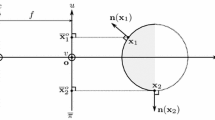
  6. In 3D-reconstruction applications such as photometric stereo [55], the assumption on the noise should rather be formulated on the images. This will be discussed in more details in Sect. 4.4.

  7. The assumptions of equal variance \(\sigma ^2\) for both components and of a diagonal covariance matrix are introduced only for consistency with the least-squares problem (7). They are discussed with more care in Sect. 4.4.

  8. The u-axis points “downward,” the v-axis points “to the right” and the z-axis points from the surface to the camera, see Fig. 1.

  9. \(\mathbf {A}\) and \(\mathbf {b}\) are purposely divided by two in order to ease the continuous interpretation of Sect. 3.3.

  10. In our experiments, the threshold of the stopping criterion is set to \(\epsilon = 10^{-4}\).

  11. In (25), the factor 5n is nothing else than the number of nonzero elements in \(\mathbf {A}\). Therefore, exploiting sparsity is not as “fruitless” as argued in [26] when it comes to solving large linear systems faster than using Gaussian elimination (complexity \(O(n^3)\)).

  12. As stated in [26], homogeneous Neumann boundary conditions of the type \(\nabla z \cdot {\varvec{\eta }} = 0\), used, e.g., in [1], should be avoided.

  13. This assumption is weaker than the homogeneous Neumann boundary condition \(\nabla z \cdot \varvec{\eta } = 0\) used by Agrawal et al. [1].

  14. Although (78) actually yields an isotropic diffusion model, since it “utilizes a scalar-valued diffusivity and not a diffusion tensor” [54].

References

  1. Agrawal, A., Raskar, R., Chellappa, R.: What is the range of surface reconstructions from a gradient field? In: Proceedings of the 9th European Conference on Computer Vision (vol. 1), Lecture Notes in Computer Science, vol. 3951, pp. 578–591. Graz (2006)

  2. Ambrosio, L., Tortorelli, V.M.: Approximation of functionals depending on jumps by elliptic functionals via \(\Gamma \)-convergence. Commun. Pure Appl. Math. 43, 999–1036 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  3. Attouch, H., Buttazzo, G., Michaille, G.: Variational Analysis in Sobolev and BV Spaces: Applications to PDEs and Optimization, 2nd edn. SIAM (2014)

  4. Aubert, G., Kornprobst, P. (eds.): Mathematical problems in image processing. In: Applied Mathematical Sciences, vol. 147, 2nd edn. Springer, Berlin (2006)

  5. Badri, H., Yahia, H., Aboutajdine, D.: Robust surface reconstruction via triple sparsity. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 2291–2298. Columbus (2014)

  6. Bähr, M., Breuß, M., Quéau, Y., Bouroujerdi, A.S., Durou, J.D.: Fast and accurate surface normal integration on non-rectangular domains. Comput. Vis. Media 3, 107–129 (2017)

    Article  Google Scholar 

  7. Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2(1), 183–202 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Belhachmi, B., Bucur, D., Burgeth, B., Weickert, J.: How to choose interpolation data in images. SIAM J. Appl. Math. 70(1), 333–352 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2011)

    Article  MATH  Google Scholar 

  10. Bredies, K., Holler, M.: A TGV-based framework for variational image decompression, zooming, and reconstruction. Part I: analytics. SIAM J. Imaging Sci. 8(4), 2814–2850 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  11. Catté, F., Lions, P.L., Morel, J.M., Coll, T.: Image selective smoothing and edge detection by nonlinear diffusion. SIAM J. Numer. Anal. 29(1), 182–193 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  12. Chambolle, A.: Image segmentation by variational methods: Mumford and Shah functional and the discrete approximation. SIAM J. Appl. Math. 55(3), 827–863 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  13. Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  14. Chan, T.F., Vese, L.A.: Active contours without edges. IEEE Trans. Image Process. 10(2), 266–277 (2001)

    Article  MATH  Google Scholar 

  15. Chang, J.Y., Lee, K.M., Lee, S.U.: Multiview normal field integration using level set methods. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Workshop on Beyond Multiview Geometry: Robust Estimation and Organization of Shapes from Multiple Cues. Minneapolis (2007)

  16. Charbonnier, P., Blanc-Féraud, L., Aubert, G., Barlaud, M.: Deterministic edge-preserving regularization in computed imaging. IEEE Trans. Image Process. 6(2), 298–311 (1997)

    Article  Google Scholar 

  17. Chen, S.S., Donoho, D.L., Saunders, M.A.: Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 20(1), 33–61 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  18. Du, Z., Robles-Kelly, A., Lu, F.: Robust surface reconstruction from gradient field using the L1 norm. In: Proceedings of the 9th Biennial Conference of the Australian Pattern Recognition Society on Digital Image Computing Techniques and Applications, pp. 203–209. Glenelg (2007)

  19. Durou, J.D., Aujol, J.F., Courteille, F.: Integration of a normal field in the presence of discontinuities. In: Proceedings of the 7th International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition, Lecture Notes in Computer Science, vol. 5681, pp. 261–273. Bonn (2009)

  20. Durou, J.D., Courteille, F.: Integration of a normal field without boundary condition. In: Proceedings of the 11th IEEE International Conference on Computer Vision, 1st Workshop on Photometric Analysis for Computer Vision. Rio de Janeiro (2007)

  21. Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Comput. Math. Appl. 2(1), 17–40 (1976)

    Article  MATH  Google Scholar 

  22. Geman, D., Reynolds, G.: Constrained restoration and recovery of discontinuities. IEEE Trans. Pattern Anal. Mach. Intell. 14(3), 367–383 (1992)

    Article  Google Scholar 

  23. Goldstein, T., O’Donoghue, B., Setzer, S., Baraniuk, R.: Fast alternating direction optimization methods. SIAM J. Imaging Sci. 7(3), 1588–1623 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  24. Goldstein, T., Osher, S.: The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2(2), 323–343 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  25. Haque, S.M., Chatterjee, A., Govindu, V.M.: High quality photometric reconstruction using a depth camera. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 2283–2290. Columbus (2014)

  26. Harker, M., O’Leary, P.: Regularized reconstruction of a surface from its measured gradient field. J. Math. Imaging Vis. 51(1), 46–70 (2015)

    Article  MATH  Google Scholar 

  27. Hayya, J., Armstrong, D., Gressis, N.: A note on the ratio of two normally distributed variables. Manag. Sci. 21(11), 1338–1341 (1975)

    Article  MATH  Google Scholar 

  28. Hoeltgen, L., Setzer, S., Weickert, J.: An optimal control approach to find sparse data for Laplace interpolation. In: Proceedings of the 9th International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition, Lecture Notes in Computer Science, vol. 8081, pp. 151–164. Lund (2013)

  29. Horn, B.K.P., Brooks, M.J.: The variational approach to shape from shading. Comput. Vis. Graph. Image Process. 33(2), 174–208 (1986)

    Article  MATH  Google Scholar 

  30. Horovitz, I., Kiryati, N.: Depth from gradient fields and control points: bias correction in photometric stereo. Image Vis. Comput. 22(9), 681–694 (2004)

    Article  Google Scholar 

  31. Ikehata, S., Wipf, D., Matsushita, Y., Aizawa, K.: Photometric stereo using sparse Bayesian regression for general diffuse surfaces. IEEE Trans. Pattern Anal. Mach. Intell. 36(9), 1816–1831 (2014)

    Article  Google Scholar 

  32. Kadambi, A., Taamazyan, V., Shi, B., Raskar, R.: Polarized 3D: high-quality depth sensing with polarization cues. In: Proceedings of the 15th IEEE International Conference on Computer Vision, pp. 3370–3378. Santiago (2015)

  33. Kimmel, R., Yavneh, I.: An algebraic multigrid approach for image analysis. SIAM J. Sci. Comput. 24(4), 1218–1231 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  34. Kornprobst, P., Aubert, G.: Image sequence analysis via partial differential equations. J. Math. Imaging Vis. 11(1), 5–26 (1999)

    Article  MathSciNet  Google Scholar 

  35. Koutis, I., Miller, G.L., Peng, R.: A nearly-m log n time solver for SDD linear systems. In: Proceedings of the IEEE Annual Symposium on Foundations of Computer Science, pp. 590–598. Palm Springs (2011)

  36. Lanza, A., Morigi, S., Sgallari, F.: Convex image denoising via non-convex regularization with parameter selection. J. Math. Imaging Vis. 56(2), 195–220 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  37. Mumford, D., Shah, J.: Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 42(5), 577–685 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  38. Nikolova, M.: Local strong homogeneity of a regularized estimator. SIAM J. Appl. Math. 61(2), 633–658 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  39. Noakes, L., Kozera, R.: Nonlinearities and noise reduction in 3-source photometric stereo. J. Math. Imaging Vis. 18(2), 119–127 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  40. Ochs, P., Brox, T., Pock, T.: iPiasco: inertial proximal algorithm for strongly convex optimization. J. Math. Imaging Vis. 53(2), 171–181 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  41. Ochs, P., Chen, Y., Brox, T., Pock, T.: iPiano: inertial proximal algorithm for nonconvex optimization. SIAM J. Imaging Sci. 7(2), 1388–1419 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  42. Or-el, R., Rosman, G., Wetzler, A., Kimmel, R., Bruckstein, A.M.: RGBD-Fusion: real-time high precision depth recovery. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5407–5416. Boston (2015)

  43. Pérez, P., Gangnet, M., Blake, A.: Poisson image editing. ACM Trans. Graph. 22(3), 313–318 (2003)

    Article  Google Scholar 

  44. Perona, P., Malik, J.: Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 12(7), 629–639 (1990)

    Article  Google Scholar 

  45. Peter, P., Hoffmann, S., Nedwed, F., Hoeltgen, L., Weickert, J.: Evaluating the true potential of diffusion-based inpainting in a compression context. Signal Process. Image Commun. 46, 40–53 (2016)

    Article  Google Scholar 

  46. Pock, T., Cremers, D., Bischof, H., Chambolle, A.: An algorithm for minimizing the Mumford–Shah functional. In: Proceedings of the 12th IEEE International Conference on Computer Vision, pp. 1133–1140. Kyoto (2009)

  47. Quéau, Y., Durou, J.D.: Edge-preserving integration of a normal field: weighted least squares, TV and L1 approaches. In: Proceedings of the 5th International Conference on Scale Space and Variational Methods in Computer Vision, Lecture Notes in Computer Science, vol. 9087, pp. 576–588. Lège Cap-Ferret (2015)

  48. Quéau, Y., Durou, J.D., Aujol, J.F.: Normal integration: a survey. J. Math. Imaging Vis. (2017). https://doi.org/10.1007/s10851-017-0773-x

  49. Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 60(1–4), 259–268 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  50. Saracchini, R.F.V., Stolfi, J., Leitão, H.C.G., Atkinson, G.A., Smith, M.L.: A robust multi-scale integration method to obtain the depth from gradient maps. Comput. Vis. Image Underst. 116(8), 882–895 (2012)

    Article  Google Scholar 

  51. Shefi, R., Teboulle, M.: Rate of convergence analysis of decomposition methods based on the proximal method of multipliers for convex minimization. SIAM J. Optim. 24(1), 269–297 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  52. Shi, B., Wu, Z., Mo, Z., Duan, D., Yeung, S.K., Tan, P.: A benchmark dataset and evaluation for non-Lambertian and uncalibrated photometric stereo. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas (2016)

  53. Simchony, T., Chellappa, R., Shao, M.: Direct analytical methods for solving Poisson equations in computer vision problems. IEEE Trans. Pattern Anal. Mach. Intell. 12(5), 435–446 (1990)

    Article  MATH  Google Scholar 

  54. Weickert, J.: Anisotropic Diffusion in Image Processing. Teubner, Stuttgart (1998)

    MATH  Google Scholar 

  55. Woodham, R.J.: Photometric method for determining surface orientation from multiple images. Opt. Eng. 19(1), 139–144 (1980)

    Article  Google Scholar 

Download references

Acknowledgements

We are grateful to the reviewers for the constructive discussion during the reviewing process.

Author information

Authors and Affiliations

  1. Technical University Munich, Garching, Germany

    Yvain Quéau

  2. IRIT, Université de Toulouse, Toulouse, France

    Jean-Denis Durou

  3. IMB, Université de Bordeaux, Talence, France

    Jean-François Aujol

  4. Institut Universitaire de France, Paris, France

    Jean-François Aujol

Authors
  1. Yvain Quéau
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jean-Denis Durou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jean-François Aujol
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yvain Quéau.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Quéau, Y., Durou, JD. & Aujol, JF. Variational Methods for Normal Integration. J Math Imaging Vis 60, 609–632 (2018). https://doi.org/10.1007/s10851-017-0777-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10851-017-0777-6

Keywords

Search

Navigation