Abstract
We give algebraic and geometric perspectives on our prior results toward the Putman–Wieland conjecture. This leads to interesting new constructions of families of “origami” curves whose Jacobians have high-dimensional isotrivial isogeny factors. We also explain how a hyperelliptic analogue of the Putman–Wieland conjecture fails, following work of Marković.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The goal of this paper is to expand on some of our recent results towards the Putman–Wieland conjecture. Our hope is that this somewhat leisurely exposition will serve as a useful entry point for geometric topologists hoping to use the Hodge-theoretic techniques developed in [17] to study mapping class groups. While many of the results of that paper are somewhat stronger than those explained here, our hope is that stripping away some of the technical aspects of the proofs therein will clarify the relevant arguments.
1.1 Review of the Putman–Wieland conjecture
We use \(\Sigma _{g,n}\) to denote an orientable topological surface of genus g with n punctures. Given a finite unramified H-cover of punctured topological surfaces  , there is an action of a finite index subgroup \(\Gamma \) of the mapping class group \({{\,\textrm{Mod}\,}}_{g,n+1}\) on \(H_1(\Sigma _{g'}, {\mathbb {C}})\), as we now explain. Explicitly, \(\textrm{Mod}_{g,n+1}\) acts on \(\pi _1(\Sigma _{g,n},x)\) for some basepoint x, and we can take \(\Gamma \) to be the stabilizer of the surjection\(\phi :\pi _1(\Sigma _{g,n},x) \twoheadrightarrow H\), where \(\phi \) corresponds to the cover
, there is an action of a finite index subgroup \(\Gamma \) of the mapping class group \({{\,\textrm{Mod}\,}}_{g,n+1}\) on \(H_1(\Sigma _{g'}, {\mathbb {C}})\), as we now explain. Explicitly, \(\textrm{Mod}_{g,n+1}\) acts on \(\pi _1(\Sigma _{g,n},x)\) for some basepoint x, and we can take \(\Gamma \) to be the stabilizer of the surjection\(\phi :\pi _1(\Sigma _{g,n},x) \twoheadrightarrow H\), where \(\phi \) corresponds to the cover  . Then, for
. Then, for  mapping to x, \(\Gamma \) acts on
mapping to x, \(\Gamma \) acts on  and hence on \(H_1(\Sigma _{g'},{\mathbb {C}})\).
and hence on \(H_1(\Sigma _{g'},{\mathbb {C}})\).
Conjecture 1.1
(Putman–Wieland, [24, Conjecture 1.2]) Fix \(g \geqslant 2\), \(n \geqslant 0\). For any unramified cover  , the vector space \(H_1(\Sigma _{g'}, {\mathbb {C}})\) has no non-zero vectors with finite orbit under the action of \(\Gamma \).
, the vector space \(H_1(\Sigma _{g'}, {\mathbb {C}})\) has no non-zero vectors with finite orbit under the action of \(\Gamma \).
Note that the Putman–Wieland conjecture is false when \(g=2\) (see [21] or Proposition 6.7 below). We state an equivalent version of the Putman–Wieland conjecture in Conjecture 2.3.
1.2 Our prior results toward the Putman–Wieland conjecture
One of the main results of [17] implies that  has no non-zero vectors with finite orbit when \(g^2 > \# \,H\). Here is the precise statement.
has no non-zero vectors with finite orbit when \(g^2 > \# \,H\). Here is the precise statement.
Theorem 1.2
([17, Theorem 1.4.1]) With notation as in Sect. 1.1, for any H cover  ,
,  has no finite orbits under the action of \(\Gamma \) whenever \(\#\, H < g^2\).
has no finite orbits under the action of \(\Gamma \) whenever \(\#\, H < g^2\).
This follows from Corollary 2.7 below, since any irrep of a finite group H has dimension at most \(\sqrt{\#\,H}\).
The proof of Corollary 2.7 given in [17] somewhat obscures what is going on for two reasons. First, there we opted to give an indirect proof which was shorter given our other results in that paper. Second, the proof was complicated due to the technical necessity of dealing with marked points. In Sect. 3, we give a more streamlined account of the idea, which we hope will be easier to digest. We also try to motivate the vector bundle methods described there with an alternative approach to proving Theorem 1.2 via elementary projective geometry in Sect. 4.
Remark 1.3
While Theorem 1.2 shows  contains no non-zero vectors with finite orbit when \(\#\,H < g^2\), the same is not true of
contains no non-zero vectors with finite orbit when \(\#\,H < g^2\), the same is not true of  , which is dual to
, which is dual to  by the universal coefficient theorem. The homology classes corresponding to loops around punctures have finite orbit under the mapping class group. This tells us that when
by the universal coefficient theorem. The homology classes corresponding to loops around punctures have finite orbit under the mapping class group. This tells us that when  ,
,  has an \(n'-1\) dimensional space of coinvariants under the action of a finite index subgroup of the mapping class group, but it has trivial invariants under the action of this subgroup. In particular, the \(\Gamma \)-action on
has an \(n'-1\) dimensional space of coinvariants under the action of a finite index subgroup of the mapping class group, but it has trivial invariants under the action of this subgroup. In particular, the \(\Gamma \)-action on  is not semisimple. We have opted to state most of our results in terms of homology rather than cohomology as the statements are a bit cleaner in this formulation.
is not semisimple. We have opted to state most of our results in terms of homology rather than cohomology as the statements are a bit cleaner in this formulation.
Remark 1.4
When the hypotheses of Theorem 1.2 are satisfied, it implies the corresponding case of Conjecture 1.1. Indeed, the action of \(\Gamma \) on  has as a natural subrepresentation its action on \(H^1(\Sigma _{g'}, \mathbb {C})\), which hence has no fixed vectors. This action is semisimple, hence the same is true for the dual representation on \(H_1(\Sigma _{g'}, \mathbb {C})\).
has as a natural subrepresentation its action on \(H^1(\Sigma _{g'}, \mathbb {C})\), which hence has no fixed vectors. This action is semisimple, hence the same is true for the dual representation on \(H_1(\Sigma _{g'}, \mathbb {C})\).
1.3 Motivation for the Putman–Wieland conjecture: Ivanov’s conjecture
Much of the original motivation for the Putman–Wieland conjecture was as an approach to proving Ivanov’s conjecture, which is a major open question in the study of mapping class groups. Ivanov’s conjecture states that \(\textrm{Mod}_{g,n}\) does not virtually surject onto \(\mathbb {Z}\) for \(g > 2\), \(n \geqslant 0\). See [14, Section 7] and [16, Problem 2.11.A].
As a historical note, it appears that Ivanov only posed this as a question, and not a conjecture. However, since then, many sources have referred to this question as Ivanov’s conjecture.
If we use \(\textrm{I}_{g,n}\) to denote the statement that Ivanov’s conjecture holds for (g, n) and \(\textrm{PW}_{g,n}\) to denote the statement that the Putman–Wieland conjecture holds for (g, n), then the relation between Ivanov’s conjecture and the Putman–Wieland conjecture is the following:
Theorem 1.5
([24, Theorem 1.3]) For \(g \geqslant 3\), \(n \geqslant 0\), \(\textrm{PW}_{g-1, n+1} \,{\implies }\, \textrm{I}_{g,n}\) and \(\textrm{I}_{g,n+1} \,{\implies }\, \textrm{PW}_{g,n}\).
Technically, [24, Theorem 1.3] states a slightly different version of Theorem 1.5. However, the above formulation is equivalent, see Remark 2.5. Therefore, a proof of the Putman–Wieland conjecture would also yield a proof of Ivanov’s conjecture in almost all cases, and vice-versa.
1.4 Motivation for the Putman–Wieland conjecture: big monodromy
Another source of motivation for the Putman–Wieland conjecture comes from a perspective on monodromy groups. Indeed, a typical slogan in much of algebraic geometry and number theory is:
Slogan 1.6
Monodromy groups should be as big as possible.
The Putman–Wieland conjecture [24] is implied by this philosophy. Indeed, if one strongly believes Slogan 1.6, one might imagine that the intersection form and H-action on the cover \(\Sigma _{g'}\) of Conjecture 1.1 are the only constraints on the (virtual) action of \(\textrm{Mod}_{g, 1}\), and so one might guess the image of the action of a finite index subgroup of \(\textrm{Mod}_{g,1}\) on \(H_1(\Sigma _{g'}, {\mathbb {C}})\) is via a finite-index subgroup of the centralizer of H in \(\textrm{Sp}_{2g}(\mathbb {Z})\). The Putman–Wieland conjecture merely predicts this action has no non-zero vectors with finite orbit. Even though the Putman–Wieland conjecture is substantially weaker than determining the monodromy, there are no pairs (g, n) with \(g \geqslant 2\) for which it is known to hold.
1.5 Counterexamples in low genus
For \(g\leqslant 1\), it turns out that the intersection form and the H-action are not the only constraints on the (virtual) action of \(\textrm{Mod}_{g,n+1}\) on  ; there are additional constraints arising from Hodge theory. That is, Slogan 1.6 is false, if naively interpreted. In Sect. 5 we give a number of new examples where the action of \(\textrm{Mod}_{g,n+1}\) factors through a smaller group than might be expected, for Hodge-theoretic reasons.
; there are additional constraints arising from Hodge theory. That is, Slogan 1.6 is false, if naively interpreted. In Sect. 5 we give a number of new examples where the action of \(\textrm{Mod}_{g,n+1}\) factors through a smaller group than might be expected, for Hodge-theoretic reasons.
For example, we give a number of new counterexamples to the Putman–Wieland conjecture with \(g = 1\), \(n =1\), arising from origami curves. These lead to interesting families of curves with high-dimensional fixed parts in their Jacobians in Examples 5.8–5.11. Most of our counterexamples are produced via a Hodge-theoretic criterion for the failure of Putman–Wieland, Proposition 5.4. These examples are the primary novelty of this paper. In particular, we give a sequence of families of “origami” curves whose Jacobians have isotrivial isogeny factors of arbitrarily large dimension in Example 5.10, and include a number of open questions in Sect. 5.2. In Sect. 6, we also discuss recent counterexamples of Marković for \(g=2\), which admit a routine generalization to the hyperelliptic setting in any genus. In Remark 6.12, we indicate how this hyperelliptic generalization demonstrates the sharpness of our methods for proving Theorem 1.2.
1.6 Overview
In Sect. 2 we recall our main results toward the Putman–Wieland conjecture. In Sect. 3, we sketch a streamlined version of our original proof, while in Sect. 4 we describe our original, more geometric approach to proving our results toward the Putman–Wieland conjecture. We discuss counterexamples to the Putman–Wieland conjecture in low genus in Sect. 5, and pose related questions in Sect. 5.2. We conclude with Sect. 6, giving an exposition of Marković’s genus 2 counterexample to the Putman–Wieland conjecture, based heavily on a theorem of Bogomolov–Tschinkel. We also explain a sense in which this generalizes to higher genus hyperelliptic curves.
1.7 Notation
Throughout, we work over the complex numbers, unless otherwise stated. For a pointed finite-type scheme or Deligne–Mumford stack (X, x) over \(\mathbb {C}\), we will use \(\pi _1(X, x)\) to denote the topological fundamental group of the associated complex-analytic space or analytic stack. We use Grothendieck conventions on projective space so that points of \({\mathbb {P}}V\) correspond to hyperplanes in V, as opposed to lines in V.
2 The Putman–Wieland conjecture
In this section we recall some notation related to the Putman–Wieland conjecture, as well as the main results toward it obtained in [17]. That paper proves some substantially more general results; we explain them here in the special case concerning the Putman–Wieland conjecture. Although we already stated the Putman–Wieland conjecture in Conjecture 1.1, it will be useful to have a slightly different version of it that also incorporates the covering group H. We next introduce notation to state this version precisely.
Notation 2.1
Let \(\Sigma _g\) be an oriented surface of genus \(g \geqslant 0\), and let \(\Sigma _{g,n}\) be the complement of \(n\geqslant 0\) disjoint points in \(\Sigma _g\), so that \(\Sigma _{g,n}\) is an oriented genus g surface with n punctures. We let \(\textrm{PMod}_{g,n}\) be the subgroup of the mapping class group of \(\Sigma _{g,n}\) fixing the punctures. Fix a basepoint \(v_0 \in \Sigma _{g,n}\), which we count as an additional puncture to obtain an action of \(\textrm{PMod}_{g,n+1}\) on \(\pi _1(\Sigma _{g,n},v_0)\). Suppose we are given a finite covering  . Let \(\Gamma \subset \textrm{PMod}_{g,n+1}\) denote the finite index subgroup preserving the covering h.
. Let \(\Gamma \subset \textrm{PMod}_{g,n+1}\) denote the finite index subgroup preserving the covering h.
We obtain an action of \(\Gamma \) on  . By filling in the punctures, we also obtain an action of \(\Gamma \) on
. By filling in the punctures, we also obtain an action of \(\Gamma \) on  , referred to in [24, pp. 80–81] as a higher Prym representation.
, referred to in [24, pp. 80–81] as a higher Prym representation.
In the case h is Galois with covering group H, we may view  as an H-representation. If \(\rho \) is an irreducible H-representation we let
as an H-representation. If \(\rho \) is an irreducible H-representation we let

denote the \(\rho \)-isotypic component. In this case, we obtain an action of \(\Gamma \) on the characteristic subrepresentation  .
.
Definition 2.2
Fix non-negative integers g and n and a finite covering  . Let \({{\,\textrm{PW}\,}}_{g,n}^H\) be the statement that for any Galois H-covering h and \(v \in V_h\) any non-zero vector, v has infinite orbit under \(\Gamma \).
. Let \({{\,\textrm{PW}\,}}_{g,n}^H\) be the statement that for any Galois H-covering h and \(v \in V_h\) any non-zero vector, v has infinite orbit under \(\Gamma \).
Conjecture 2.3
(Putman–Wieland, [24, Conjecture 1.2]) \({{\,\textrm{PW}\,}}_{g,n}^H\) holds for every group H with \(g \geqslant 2\), \(n \geqslant 0\).
Remark 2.4
It is known that the Putman–Wieland conjecture is not in general true for \(g=2\); see [21, Theorem 1.3] or Proposition 6.7 below.
Remark 2.5
We note that there are several differences between the original [24, Conjecture 1.2] and Conjecture 2.3, but the statements are equivalent, see also [17, Remark 6.1.4]. First, [24, Conjecture 1.2] is stated without a group H and with \({\mathbb {Q}}\) coefficients instead of \({\mathbb {C}}\) coefficients. Additionally, [24, Conjecture 1.2] keeps track of boundary components in addition to punctures, but it is enough to treat the case of only punctures by [17, Lemma 6.2.5].
We now recall the main result of [17] toward the Putman–Wieland conjecture.
Theorem 2.6
([17, Theorem 6.2.1]) With notation as in Notation 2.1, let \(\rho \) be an irreducible complex H-representation and let  be a finite-index subgroup. Then
be a finite-index subgroup. Then  has no non-zero \(\Gamma '\)-invariant subrepresentations of dimension strictly less than \(2g - 2\dim \rho \). The same holds for \(H_1(\Sigma _{g'},{\mathbb {C}})^\rho \) in place of
has no non-zero \(\Gamma '\)-invariant subrepresentations of dimension strictly less than \(2g - 2\dim \rho \). The same holds for \(H_1(\Sigma _{g'},{\mathbb {C}})^\rho \) in place of  .
.
Because the span of a fixed vector is a 1-dimensional subrepresentation, and \(1 < 2g -2 \dim \rho \) if and only if \(\dim \rho < g\), we get the following important corollary:
Corollary 2.7
([17, Corollary 6.2.3]) \({{\,\textrm{PW}\,}}_{g,n}^H\) holds for every group H such that every irreducible representation \(\rho \) of H has dimension \(\dim \rho < g\).
In particular, the hypotheses of Corollary 2.7 are satisfied if \(\#\,H<g^2\), implying Theorem 1.2.
3 The algebraic proof of Corollary 2.7
In this section, we outline the idea of the proof of Corollary 2.7, stripping away some of the additional technical complications from [17].
We restrict to the unramified case, as the ramified case is analogous, once one replaces usual vector bundles with parabolic vector bundles.
To start, given \(\phi :\pi _1(\Sigma _g)\twoheadrightarrow H\), we set up a parameter space of H-covers. We begin by finding a diagram

where \(\pi \) is a relative curve of genus g, \(\pi '\) is a relative curve of genus \(g'\), and f is an H-cover, such that the map  induced by \(\pi \) is dominant étale, and such that for
induced by \(\pi \) is dominant étale, and such that for  , the fiber \(f_m:X\rightarrow Y\) is a finite étale connected Galois H-cover corresponding to \(\phi \).
, the fiber \(f_m:X\rightarrow Y\) is a finite étale connected Galois H-cover corresponding to \(\phi \).
If \({{\,\textrm{PW}\,}}^H_{g,0}\) were false, there would be a non-zero vector \(v \in H_1(X, {\mathbb {Q}})\) fixed by a finite index-subgroup of  . After replacing
. After replacing  with a finite étale cover, we may thus assume v is in fact fixed by
with a finite étale cover, we may thus assume v is in fact fixed by  . This implies that the natural map
. This implies that the natural map  induced by the Gauss–Manin connection has non-zero kernel. Setting
induced by the Gauss–Manin connection has non-zero kernel. Setting  , Hodge theory gives a filtration
, Hodge theory gives a filtration

with quotient  . The theorem of the fixed part tells us that the kernel of the Gauss–Manin connection in fact arises from a sub-Hodge structure of \(R^1\pi '_*\mathbb {C}\), and hence meets
. The theorem of the fixed part tells us that the kernel of the Gauss–Manin connection in fact arises from a sub-Hodge structure of \(R^1\pi '_*\mathbb {C}\), and hence meets  non-trivially. This type of argument is spelled out in more detail in Lemma 6.10. The connection \(\nabla \), which is only a \({\mathbb {C}}\)-linear map, induces a
non-trivially. This type of argument is spelled out in more detail in Lemma 6.10. The connection \(\nabla \), which is only a \({\mathbb {C}}\)-linear map, induces a  -linear map
-linear map

which again has a non-trivial kernel, using the theorem of the fixed part.
We now relate the kernel of \(\overline{\nabla }\) to the vanishing of a particular map on cohomology. As above, fix a point  , whose fiber yields a finite étale cover \(f_m:X \rightarrow Y\). The map \(\overline{\nabla }_m\) may be identified as a map
, whose fiber yields a finite étale cover \(f_m:X \rightarrow Y\). The map \(\overline{\nabla }_m\) may be identified as a map

Using Serre duality and the identification \(H^0(X, \omega _{X}) \simeq H^0(Y, f_{m*} \omega _{X})\), this can be identified with the map

By assumption \(\theta \) has a non-zero kernel. Any non-zero element of the kernel yields a non-zero map \(f_{m*} \omega _{X} \rightarrow \omega _Y^{\otimes 2}\), inducing the zero map on global sections.
Finally, we use the vanishing of the above map on cohomology to produce a stable vector bundle of low rank and high slope on Y which is not generically globally generated, furnishing a contradiction. Given a representation \(\rho :\pi _1(Y)\rightarrow \textrm{GL}_r(\mathbb {C})\), we let \(\underline{\rho }\) be the associated local system on Y and set  . Note that if \(\rho \) has finite (or, indeed, unitary) image, then \(E^\rho \) is semistable of slope zero. We can identify
. Note that if \(\rho \) has finite (or, indeed, unitary) image, then \(E^\rho \) is semistable of slope zero. We can identify  , by viewing \(f_{m*} {\mathbb {C}}\) as a local system on Y induced by the the regular representation of H, and tensoring up with
, by viewing \(f_{m*} {\mathbb {C}}\) as a local system on Y induced by the the regular representation of H, and tensoring up with  . Hence by the projection formula,
. Hence by the projection formula,

As we have produced a non-zero map \(f_{m*} \omega _{X} \rightarrow \omega _Y^{\otimes 2}\), inducing the zero map on global sections, there must be some \(\rho \) and a non-zero map  which induces the 0 map on global sections. However,
which induces the 0 map on global sections. However,  is then a semistable vector bundle of slope \(2g-2\), all of whose global sections factor through the subbundle
is then a semistable vector bundle of slope \(2g-2\), all of whose global sections factor through the subbundle  . This will force U to have a very high-dimensional space of global sections relative to its rank.
. This will force U to have a very high-dimensional space of global sections relative to its rank.
We now explain why the condition that  leads to a contradiction. This is in tension with a version of Clifford’s theorem for vector bundles, which says that if U is a vector bundle which has a filtration by semistable bundles of slopes \(\geqslant 0\) and \(\leqslant 2g\), then \(h^0(Y, U) \leqslant \frac{\deg U}{2} + {{\,\textrm{rk}\,}}U\) [18, Lemma 6.2.1]. This idea is used to prove (without too much difficulty) the more precise [18, Proposition 6.3.1] which tells us that such a U can only exist when \(\dim \rho = {{\,\textrm{rk}\,}}E^\rho \geqslant g\). We now spell this proof out in the case
leads to a contradiction. This is in tension with a version of Clifford’s theorem for vector bundles, which says that if U is a vector bundle which has a filtration by semistable bundles of slopes \(\geqslant 0\) and \(\leqslant 2g\), then \(h^0(Y, U) \leqslant \frac{\deg U}{2} + {{\,\textrm{rk}\,}}U\) [18, Lemma 6.2.1]. This idea is used to prove (without too much difficulty) the more precise [18, Proposition 6.3.1] which tells us that such a U can only exist when \(\dim \rho = {{\,\textrm{rk}\,}}E^\rho \geqslant g\). We now spell this proof out in the case  . Note first that
. Note first that  by semistability of
by semistability of  and so
and so  . Riemann–Roch, Clifford’s theorem, and the above observation together yield
. Riemann–Roch, Clifford’s theorem, and the above observation together yield

Solving for  gives
gives  .
.
This verifies \({{\,\textrm{PW}\,}}_{g,0}^H\), since we assumed H was a group all of whose representations had rank less than g.
Remark 3.1
In fact the methods here can be used to prove a stronger statement, about families of curves that do not necessarily dominate  . Indeed, let
. Indeed, let

be as in (3.1), except we now assume that the map  has image of codimension \(\delta \); we assume
has image of codimension \(\delta \); we assume  is étale onto its image. Arguing as above, we find that
is étale onto its image. Arguing as above, we find that  has rank \(\delta \), and so replacing the use of [18, Proposition 6.3.1] with [18, Proposition 6.3.6], we obtain:
has rank \(\delta \), and so replacing the use of [18, Proposition 6.3.1] with [18, Proposition 6.3.6], we obtain:
Theorem 3.2
With notation as above, suppose \(\dim \rho <g-\delta \). Then the action of  on
on  has no non-zero finite orbits.
has no non-zero finite orbits.
Analogously to Theorem 1.2, one immediately obtains that for \(|H|<(g-\delta )^2\), the action of  on
on  has no non-zero vectors with finite orbit. Replacing usual vector bundles with parabolic vector bundles, one may prove an analogue of Theorem 3.2 for ramified covers.
has no non-zero vectors with finite orbit. Replacing usual vector bundles with parabolic vector bundles, one may prove an analogue of Theorem 3.2 for ramified covers.
4 A geometric approach to Theorem 2.6
While we were thinking about the Putman–Wieland conjecture, we first came up with a rather different argument for proving Theorem 2.6, which involves analyzing the geometry of the canonical map, and in particular the quadrics which contain the covering curve under its canonical map. We discovered that a certain degeneracy locus naturally appeared in the intersection of these quadrics, which yields a different method to produce the same non-generically globally generated vector bundles that are described in Sect. 3. It was only after we found this geometric approach that we were able to somewhat simplify the presentation via the algebraic argument described in Sect. 3. In this section, we aim to present our original, geometric approach. It is our hope that sharing this more geometric approach may shed some additional light on the problem, and may also be of use in related problems. Since we are only trying to convey the main idea, as in Sect. 3, we will assume \(n = 0\), i.e., the relevant cover \(X \rightarrow Y\) is étale.
The first steps in this geometric approach are the same as those described in Sect. 3. Namely, by studying the Gauss–Manin connection, we find that given a counterexample to Putman–Wieland, the natural map

has non-zero kernel. If \(X \rightarrow Y\) is an H-cover, we can decompose the above as H-representations, and there must be some irreducible H-representation \(\rho \) and a subrepresentation \(\rho \subset H^0(X, \omega _{X})\) in the kernel of \(\theta \). Let us now try to understand what this copy of \(\rho \) buys us in terms of the canonical map \(X \rightarrow {\mathbb {P}} H^0(X, \omega _X)\). Recall here we are using Grothendieck conventions, so points of \({\mathbb {P}} H^0(X, \omega _X)\) correspond to hyperplanes in \(H^0(X, \omega _X)\). By inspection of (3.2), the map

adjoint to \(\theta \) factors through \(\textrm{Sym}^2 H^0(X, \omega _X)\). Hence, restricting to  we obtain that the composition
we obtain that the composition

vanishes. Observe that \(H^0(Y, \omega _Y^{\otimes 2})\) carries the trivial H-representation, and hence \(\rho \) can only pair non-trivially under the above composition with \(H^0(X, \omega _X)^{\rho ^\vee }\), the \(\rho ^\vee \) isotypic part of \(H^0(X, \omega _X)\). Hence, the vanishing of (4.1) is equivalent to the vanishing of

where \(\alpha _1\) is the multiplication map, \(\alpha _2\) is the averaging map
and  . Indeed, viewing \({{\,\textrm{Sym}\,}}^2 H^0(X, \omega _X)\) as the space of quadrics on \(\mathbb {P}H^0(X, \omega _X)\), any element of the image of \(\alpha \) yields a quadric vanishing on the image of X under the canonical map.
. Indeed, viewing \({{\,\textrm{Sym}\,}}^2 H^0(X, \omega _X)\) as the space of quadrics on \(\mathbb {P}H^0(X, \omega _X)\), any element of the image of \(\alpha \) yields a quadric vanishing on the image of X under the canonical map.
Let us derive some consequences from this observation. To get a feeling for what is going on, we work out examples depending on the rank of \(\rho \), so as to motivate the general case. Suppose Y has genus g. By the Chevalley–Weil formula (see the original source [7] or the more expository [23, Theorem 2.1]), \(H^0(X, \omega _X)^{\rho ^\vee }\) is a direct sum of  many copies of \(\rho ^\vee \), and so has dimension
many copies of \(\rho ^\vee \), and so has dimension  .
.
4.1 Summary of the remainder of this section
We first see how to use the above observation to rule out 1-dimensional representations in Sect. 4.2. We use  . Following this, we will see how to use the above to produce a vector bundle
. Following this, we will see how to use the above to produce a vector bundle  which is not generically globally generated in the cases (\(r =2\), \(g=2\)) in Sect. 4.3, (\(r = 3\), \(g =2\)) in Sect. 4.4, and then the general case in Sect. 4.5. We stress that in these examples, we are not trying to prove or disprove the Putman–Wieland conjecture, but merely to indicate a geometric reason for why
which is not generically globally generated in the cases (\(r =2\), \(g=2\)) in Sect. 4.3, (\(r = 3\), \(g =2\)) in Sect. 4.4, and then the general case in Sect. 4.5. We stress that in these examples, we are not trying to prove or disprove the Putman–Wieland conjecture, but merely to indicate a geometric reason for why  is not generically globally generated. One can then argue as in Sect. 3 that any vector bundle which is not generically globally generated must have rank
is not generically globally generated. One can then argue as in Sect. 3 that any vector bundle which is not generically globally generated must have rank  using Clifford’s Theorem, and so this would lead to a proof of the Putman–Wieland conjecture in the case \(\dim \rho < g\). Again, there is a valid alternate argument given in Sect. 3 of why
using Clifford’s Theorem, and so this would lead to a proof of the Putman–Wieland conjecture in the case \(\dim \rho < g\). Again, there is a valid alternate argument given in Sect. 3 of why  fails to be generically globally generated. The point of this section is to give an alternate, more geometric explanation of that fact.
fails to be generically globally generated. The point of this section is to give an alternate, more geometric explanation of that fact.
4.2 The dimension of \(\rho \) is 1
We first indicate how to rule out the case that \(\rho \) has rank 1. The main idea is that the vanishing of (4.2) yields a quadric of rank 2 containing the image of X under the canonical map. Since rank 2 quadrics vanish on a union of two hyperplanes, this would force the image of X under the canonical map to be contained in a hyperplane, contradicting non-degeneracy of the canonical map. This conclusion is established in Remark 4.3.
Lemma 4.1
Let \(\alpha \) be as in (4.2). Any quadric in  has rank at most \(2\dim \rho \).
has rank at most \(2\dim \rho \).
Proof
Because the multiplication map is H-equivariant, any given map  , where the target has the trivial H-action, must factor through a map
, where the target has the trivial H-action, must factor through a map

for  an irreducible quotient representation isomorphic to the dual of \(\rho \). This in turn factors through
an irreducible quotient representation isomorphic to the dual of \(\rho \). This in turn factors through  , and so the resulting quadric has rank at most
, and so the resulting quadric has rank at most  .
.
The reason for the claimed factorization is that the given map factors through the quotient  where K is the subspace of \(H^0(X, \omega _X)^{\rho ^\vee }\) pairing to zero with \(\rho \); the quotient
where K is the subspace of \(H^0(X, \omega _X)^{\rho ^\vee }\) pairing to zero with \(\rho \); the quotient  is isomorphic as an H-representation to \(\rho ^\vee \).\(\square \)
is isomorphic as an H-representation to \(\rho ^\vee \).\(\square \)
Proposition 4.2
Suppose that the genus of Y is at least 2. Then there are no \(\rho \) of dimension 1 in the kernel of \(\overline{\nabla }_m\).
Proof
Any quadric of rank at most 2 is supported on a union of hyperplanes. Since the canonical map is always non-degenerate, its image cannot be contained in a hyperplane. Since X is smooth and connected, it also cannot be contained in the vanishing locus of a quadric of rank at most 2. But Lemma 4.1 implies that if a 1-dimensional representation was in the kernel of the \(\overline{\nabla }_m\), the image of the canonical map would be contained in such a quadric.\(\square \)
Remark 4.3
As in Sect. 3, Proposition 4.2 immediately implies if \(\Sigma _{g'}\rightarrow \Sigma _g\) is an H-cover, with \(g\geqslant 2\), and \(\rho :H\rightarrow \mathbb {C}^\times \) is one-dimensional, no non-zero vector in \(H^1(\Sigma _{g'}, \mathbb {C})^\rho \) has finite orbit under the (virtual) action of \(\textrm{Mod}_g\). One might say this verifies the “Putman–Wieland conjecture for 1-dimensional representations.” A related, but somewhat stronger statement is originally due to Looijenga [19].
4.3 The dimension of \(\rho \) is 2 and \(g = 2\)
To simplify matters somewhat, we will restrict to the case \(g = 2\), where all the main ideas are already present and we further assume that \(\rho \) is not self-dual. Though see Remark 4.4 for a remark on what happens in the self-dual case.
In the case \(\dim \rho = 2\), we have a \(2 (g-1)= 2\) dimensional space

by Chevalley–Weil, so  . We can consider the
. We can consider the  subspace of \(H^0(X, \omega _X)\) given by
subspace of \(H^0(X, \omega _X)\) given by  , where here \(\rho \) lies in the kernel of \(\theta \) from (3.2). From this, we get two quadrics \(Q_1\) and \(Q_2\) of rank 4 vanishing on the image of X under the projection of the canonical map to
, where here \(\rho \) lies in the kernel of \(\theta \) from (3.2). From this, we get two quadrics \(Q_1\) and \(Q_2\) of rank 4 vanishing on the image of X under the projection of the canonical map to  . Here, \(Q_1\) and \(Q_2\) are non-zero quadrics, corresponding to the universal quadrics expressing the incidence relation between \(\rho \) and the two copies of \(\rho ^\vee \).
. Here, \(Q_1\) and \(Q_2\) are non-zero quadrics, corresponding to the universal quadrics expressing the incidence relation between \(\rho \) and the two copies of \(\rho ^\vee \).
Remark 4.4
This crucially uses that \(\rho \) is not self-dual, as in the case \(\rho \) is symplectically self-dual, one of these quadrics may be identically the 0 quadric. What changes in the above is that \(\rho \) is already contained in \(H^0(X, \omega _X)^{\rho ^\vee }\), so  is not a subspace of \(H^0(X,\omega _X)\).
is not a subspace of \(H^0(X,\omega _X)\).
To see that one of the quadrics will be 0 in the symplectically self-dual case, we use the fact that there there is an isomorphism \(\rho \simeq \rho ^\vee \) inducing an injection  (using that we are in characteristic 0 to split the natural surjection) whose projection to \({{\,\textrm{Sym}\,}}^2 \rho \) vanishes. This induces the 0 quadric. When \(\rho \) is not self-dual, we always obtain two quadrics of rank 4. When \(\rho \) is symplectically self-dual, we obtain one quadric of rank 4, while when \(\rho \) is orthogonally self-dual, we obtain one quadric of rank 4 and one quadric of rank 3.
(using that we are in characteristic 0 to split the natural surjection) whose projection to \({{\,\textrm{Sym}\,}}^2 \rho \) vanishes. This induces the 0 quadric. When \(\rho \) is not self-dual, we always obtain two quadrics of rank 4. When \(\rho \) is symplectically self-dual, we obtain one quadric of rank 4, while when \(\rho \) is orthogonally self-dual, we obtain one quadric of rank 4 and one quadric of rank 3.
A picture of the variety V swept out by colored planes, which is a component of the variety \(Q_1 \cap Q_2\) cut out by certain quadrics containing the canonical image of X in the case that a 2-dimensional representation lies in the kernel of \(\theta \). Each colored plane corresponds to a point \(x \in {\mathbb {P}}\rho \) and is the span x together with the corresponding hyperplanes in each copy of \({\mathbb {P}}\rho ^\vee \) on which x vanishes
To make the situation even more concrete, continue supposing \(\dim \rho = 2\) and \(g = 2\), give \(\rho \) coordinates x, y, and give the two copies of \(\rho ^\vee \) dual coordinates u, v and s, t. Then, the two quadrics \(Q_1\) and \(Q_2\) can be concretely expressed as \(xu - yv = 0\) and \(xs - yt = 0\). The variety \(Q_1 \cap Q_2\) is a degree 4 variety which has two components: it is the union of the codimension 2 plane P given by \(x = y = 0 \) and the degree 3 variety V given by \(xu - yv = xs - yt = vs-tu=0\). Since the curve X is irreducible and non-degenerate, it cannot lie in the component P and so must be contained in V. We have now managed to produce a new equation containing X, \(vs - tu\), which is only a function of the variables in \(H^0(X, \omega _X)^{\rho ^\vee }\) and does not depend on the \(\rho \) component. Moreover, it is the degeneracy locus of the matrix
which already gives a hint as to where the failure of generic global generation of  may come from.
may come from.
There is yet another geometric perspective on the variety \(xu - yv = xs - yt = vs-tu=0\). Starting with a point [x, y] in \({\mathbb {P}} \rho \), we get corresponding hyperplanes in \({\mathbb {P}} \rho ^\vee \) at which [x, y] vanishes. In the case \(\dim \rho = 2\), this hyperplane has codimension 1 in the 1-dimensional \({\mathbb {P}} \rho ^\vee \), and hence corresponds to a point. The variety \(xu - yv = xs - yt = vs-tu=0\) expresses the incidence relation between these two; it parameterizes tuples (x, y, s, t, u, v) so that [x, y] vanishes on both [s, t] and [u, v]. We will next see a similar phenomenon when \(\dim \rho = 3\).
4.4 The dimension of \(\rho \) is 3 and \(g = 2\)
We next consider the case \(\dim \rho = 3\) and \(g = 2\). In this subsection, we will explain how to show  fails to be generically globally generated, which will not in general lead to a contradiction, but which motivates our arguments in Sect. 3, see Sect. 4.1. As in the dimension 2 case of Sect. 4.3, we obtain a variety cut out by three quadrics expressing the incidence between \(\rho \) and
fails to be generically globally generated, which will not in general lead to a contradiction, but which motivates our arguments in Sect. 3, see Sect. 4.1. As in the dimension 2 case of Sect. 4.3, we obtain a variety cut out by three quadrics expressing the incidence between \(\rho \) and  . Viewing this as a subvariety of
. Viewing this as a subvariety of  we find this degree 8, codimension 3 subvariety is the union of the codimension 3 plane \(\rho = 0\) and a certain degree 7 codimension 3 variety, which can be expressed as the closure V of the incidence variety
we find this degree 8, codimension 3 subvariety is the union of the codimension 3 plane \(\rho = 0\) and a certain degree 7 codimension 3 variety, which can be expressed as the closure V of the incidence variety

As in the previous case, the image of X is irreducible and non-degenerate, so cannot lie on the codimension 3 plane \(\rho = 0\), and hence lies in V.
A picture of the variety V swept out by colored planes, which is contained in the intersection of certain quadrics containing the canonical image of X when a 3-dimensional representation \(\rho \) lies in the kernel of \(\theta \). Each colored plane corresponds to a point \(x \in {\mathbb {P}}\rho \) and is the span x together with the corresponding hyperplanes in each copy of \({\mathbb {P}}\rho ^\vee \) on which x vanishes
Next, let us try to understand how the non-generically globally generated vector bundle appearing in Sect. 3 is related to this geometric setup. To find it, we project V away from  . Under this projection, we get that V projects to
. Under this projection, we get that V projects to

This can equivalently be expressed as
The map  is induced by a sub-linear system of \(\omega _X\). That is,
is induced by a sub-linear system of \(\omega _X\). That is,  pulls back to \(\omega _X\), or a subsystem thereof if \(\omega _X\) has basepoints in
pulls back to \(\omega _X\), or a subsystem thereof if \(\omega _X\) has basepoints in  . Therefore, the above map \(\iota \) is induced by a map of sheaves
. Therefore, the above map \(\iota \) is induced by a map of sheaves  . Since
. Since  , this also corresponds to a map
, this also corresponds to a map  or equivalently
or equivalently  . This is an H-equivariant map, and so descends to a map of vector bundles on Y.
. This is an H-equivariant map, and so descends to a map of vector bundles on Y.
Under the above translation, the condition defining W, that a, b, c are collinear, corresponds to the map \(\psi \) not having maximal rank. Here \(\rho \) denotes a trivial bundle of rank r on X with a specified H-action, and we use \(E^\rho \) to denote the corresponding descent to Y, which pulls back to \(\rho \) on X. Note that we can identify H-equivariant maps

Upon descending to Y, elements of this vector space correspond to elements of  . From this, the map \(\psi \) descends to a map of vector bundles on Y,
. From this, the map \(\psi \) descends to a map of vector bundles on Y,

Since the pullback \(\xi |_X\) factors through a proper sub-bundle of  , as was shown above, the same holds true of \(\xi \). Further, unwinding the definition of \(\xi \) shows it is none other than the natural evaluation map on global sections. This implies that
, as was shown above, the same holds true of \(\xi \). Further, unwinding the definition of \(\xi \) shows it is none other than the natural evaluation map on global sections. This implies that  is not generically globally generated.
is not generically globally generated.
We note that at this point we have not ruled out the possibility that Putman–Wieland fails in this \(r = 3\), \(g =2\) case because \(3 = r \geqslant g = 2\), see Sect. 4.1. All we have shown that  fails to be generically globally generated.
fails to be generically globally generated.
4.5 The general case
There are essentially no new ideas in generalizing the lack of global generation observed above beyond the \(\dim \rho = 3\), \(g = 2\) case. We consider only the case \(\rho \) is not self-dual, but the self-dual case can be handled similarly, with appropriate modifications. See Remark 4.4 for an example of this. We will explain how to show  fails to be generically globally generated. By combining this with the argument using Clifford’s Theorem for vector bundles in Sect. 3, we find that we must have \(\dim \rho \geqslant g\), see also Sect. 4.1.
fails to be generically globally generated. By combining this with the argument using Clifford’s Theorem for vector bundles in Sect. 3, we find that we must have \(\dim \rho \geqslant g\), see also Sect. 4.1.
Say \(\dim \rho = r\) and Y has genus g. By Chevalley–Weil, we obtain a variety cut out by \(r(g-1)\) quadrics expressing the incidence between \(\rho \) and  . As in Sect. 4.4, these quadrics cut out a reducible variety in
. As in Sect. 4.4, these quadrics cut out a reducible variety in , one of whose components is the plane \(\rho = 0\), with the other being the closure of the subvariety
, one of whose components is the plane \(\rho = 0\), with the other being the closure of the subvariety  . The canonical curve cannot lie in the plane, and thus lives in the latter subvariety. Projecting this subvariety away from \({\mathbb {P}} \rho \) gives a map from X to
. The canonical curve cannot lie in the plane, and thus lives in the latter subvariety. Projecting this subvariety away from \({\mathbb {P}} \rho \) gives a map from X to

As in the three dimensional case of Sect. 4.4, the map \(X \rightarrow {\mathbb {P}} H^0(X, \omega _X)^{\rho ^\vee }\) gives a map of vector bundles on X,  . The condition that X factors through W tells us this map of vector bundles drops rank. Letting \(E^\rho \) denote the descent of \(\rho \) to Y, the above map descends to Y and we obtain a map of vector bundles
. The condition that X factors through W tells us this map of vector bundles drops rank. Letting \(E^\rho \) denote the descent of \(\rho \) to Y, the above map descends to Y and we obtain a map of vector bundles  which again drops rank and corresponds to the natural evaluation map. Because this evaluation map drops rank,
which again drops rank and corresponds to the natural evaluation map. Because this evaluation map drops rank,  is not generically globally generated. By combining this with the argument using Clifford’s Theorem for vector bundles in Sect. 3, we find that we must have \(\dim \rho \geqslant g\), as described in Sect. 4.1.
is not generically globally generated. By combining this with the argument using Clifford’s Theorem for vector bundles in Sect. 3, we find that we must have \(\dim \rho \geqslant g\), as described in Sect. 4.1.
5 Examples
In this section, we give several counterexamples to the Putman–Wieland conjecture in low genus. Starting in Sect. 5.1, we give a method to produce genus 0 and 1 counterexamples to Putman–Wieland. We give a number of examples, showing that this realizes all the genus 0 cyclic counterexamples which McMullen found [22], as well as the “Eierlegende-Wollmilchsau” genus 1 counterexample in the original Putman–Wieland paper [24, Appendix A]. We also produce many new “origami” counterexamples in genus 1. In particular, Example 5.10 gives an infinite sequence of families of “origami" curves, whose Jacobians have isotrivial isogeny factors of arbitrarily large dimension. We conclude the section with a number of questions about creating families of curves whose Jacobians have isotrivial isogeny factors.
5.1 Genus 0 and 1 counterexamples
There are many cases where \({{\,\textrm{PW}\,}}_{0,n}\) and \({{\,\textrm{PW}\,}}_{1,n}\) fail to hold (see e.g. [22, Theorem 8.3] and [24, Appendix A]). From our point of view, these examples admit purely Hodge- and representation-theoretic explanations.
Let us now formally define what it means for a cover to give a counterexample to Putman–Wieland.
Definition 5.1
Suppose  is a finite covering of topological surfaces. Let \(\Gamma \subset \textrm{PMod}_{g,n+1}\) denote the finite index subgroup preserving h. The action of \(\Gamma \) on
is a finite covering of topological surfaces. Let \(\Gamma \subset \textrm{PMod}_{g,n+1}\) denote the finite index subgroup preserving h. The action of \(\Gamma \) on  induces an action on
induces an action on  which preserves the subspace spanned by homology classes of loops around punctures, and hence also induces an action on \(H_1(\Sigma _{g'}, {\mathbb {C}})\). We say h furnishes a counterexample to Putman–Wieland, if there is some non-zero \(v \in H_1(\Sigma _{g'}, {\mathbb {C}})\) with finite orbit under \(\Gamma \).
which preserves the subspace spanned by homology classes of loops around punctures, and hence also induces an action on \(H_1(\Sigma _{g'}, {\mathbb {C}})\). We say h furnishes a counterexample to Putman–Wieland, if there is some non-zero \(v \in H_1(\Sigma _{g'}, {\mathbb {C}})\) with finite orbit under \(\Gamma \).
Let Y be a compact Riemann surface of genus g with n marked points \(p_1, \ldots , p_n\). Upon identifying \(\pi _1(Y-\{p_1, \ldots , p_n\}) \simeq \pi _1(\Sigma _{g,n})\), let \(f:X \rightarrow Y\) be the covering of compact Riemann surfaces, ramified at most over \(p_1, \ldots , p_n\), corresponding to the topological cover h. If h furnishes a counterexample to Putman–Wieland, we also say \(f:X \rightarrow Y\) furnishes a counterexample to Putman–Wieland.
Remark 5.2
Even though the Putman–Wieland conjecture assumes \(g \geqslant 2\), we still say \(f:X \rightarrow Y\) furnishes a counterexample to Putman–Wieland when Y has genus \(g \leqslant 1\).
To state our criterion for producing counterexamples to Putman–Wieland, we set some notation to describe families of covers of curves.
Notation 5.3
We fix non-negative integers (g, n) so that \(n \geqslant 1\) if \(g = 1\) and \(n \geqslant 3\) if \(g = 0\), i.e., \(\Sigma _{g,n}\) is hyperbolic. Let  be a connected complex variety. A family of n-pointed curves of genus g over
be a connected complex variety. A family of n-pointed curves of genus g over  is a smooth proper morphism
is a smooth proper morphism  of relative dimension one, with geometrically connected genus g fibers, equipped with n sections
of relative dimension one, with geometrically connected genus g fibers, equipped with n sections  with disjoint images. Call such a family versal if the induced map
with disjoint images. Call such a family versal if the induced map  is dominant and étale. Here
is dominant and étale. Here  denotes the Deligne–Mumford moduli stack of n-pointed genus g smooth proper curves with geometrically connected fibers.
denotes the Deligne–Mumford moduli stack of n-pointed genus g smooth proper curves with geometrically connected fibers.
Recall that an irreducible representation \(\rho \) is symplectically self-dual if  , i.e., there is a non-zero map
, i.e., there is a non-zero map  .
.
Proposition 5.4
With notation as in Notation 5.3, let  be a point. Let
be a point. Let  ,
,  . Let \(V=H^1(X, \mathbb {Q})/H^1(Y, \mathbb {Q})\). Suppose that there exists an irreducible representation
. Let \(V=H^1(X, \mathbb {Q})/H^1(Y, \mathbb {Q})\). Suppose that there exists an irreducible representation
such that, letting \(V^\rho \) denote the \(\rho \)-isotypic piece of V,  with \(\rho _1, \ldots , \rho _s\) irreducible and pairwise distinct. Suppose that either:
with \(\rho _1, \ldots , \rho _s\) irreducible and pairwise distinct. Suppose that either:
-
(1)
the Hodge decomposition of
 is an isotypic decomposition, i.e. there is a subset \(S \subset \{1, \ldots , s\}\) so that
is an isotypic decomposition, i.e. there is a subset \(S \subset \{1, \ldots , s\}\) so that 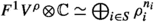 , or
, or -
(2)
for every i, \(\rho _i\) is symplectically self-dual, and \(\rho _i\) appears with multiplicity at most 1 in
 .
.
Then \(f:X \rightarrow Y\) furnishes a counterexample to Putman–Wieland.
Before proceeding with the proof, we comment on some restrictions on the representations that must be satisfied for the conditions to hold.
Remark 5.5
Note that in Proposition 5.4 (1), the representations \(\rho _i\) appearing in \(F^1 V^\rho \) must all be non-self dual. The reason for this is that, as  carries a Hodge structure, the quotient
carries a Hodge structure, the quotient  is dual to
is dual to  . However, if some \(\rho _i\) is self dual, it will appear in both the sub
. However, if some \(\rho _i\) is self dual, it will appear in both the sub  and the quotient
and the quotient  , and then the decomposition will not be isotypic.
, and then the decomposition will not be isotypic.
Remark 5.6
Note that by the Chevalley–Weil formula theorem [7, Theorem 2.1], as H-representations,  for \(\textrm{triv}\) the trivial representation, and \(\textrm{reg}\) the regular representation, where W is an auxiliary representation which is 0 if the cover is unramified, and is, in general, explicitly computable in terms of the ramification data of f. Therefore, conditions (1) and (2) of Proposition 5.4 each imply that \(g\leqslant 1\).
for \(\textrm{triv}\) the trivial representation, and \(\textrm{reg}\) the regular representation, where W is an auxiliary representation which is 0 if the cover is unramified, and is, in general, explicitly computable in terms of the ramification data of f. Therefore, conditions (1) and (2) of Proposition 5.4 each imply that \(g\leqslant 1\).
As pointed out by a referee, to verify the requirement \(g \leqslant 1\), one only needs the easier fact that the H-module \(H^1(X, \mathbb {Q})\) contains  . This is somewhat easier to prove than Chevalley–Weil by considering an H-equivariant triangulation of X, and can be verified with a proof analogous to that of [11, Proposition 1.1].
. This is somewhat easier to prove than Chevalley–Weil by considering an H-equivariant triangulation of X, and can be verified with a proof analogous to that of [11, Proposition 1.1].
Remark 5.7
Adding on to Remark 5.6, the Chevalley–Weil formula shows that for faithful representations we can only hope to apply Proposition 5.4 (2) to families where \(g = 1\), \(n = 1\), as if there is more than 1 marked point (and the H-representation is non-trivial at \(\geqslant 2\) points) or the genus is more than 1, any such representation will appear with multiplicity greater than 1.
Proof of Proposition 5.4
Let  be the \(\rho \)-isotypic part of
be the \(\rho \)-isotypic part of  . The connection on
. The connection on  induces a connection
induces a connection  . In turn, this induces a
. In turn, this induces a  -linear map
-linear map  . We claim that either of the conditions in the theorem statement imply that \(\overline{\nabla }\) is identically zero. By e.g. [15, (4.4.2)], this implies
. We claim that either of the conditions in the theorem statement imply that \(\overline{\nabla }\) is identically zero. By e.g. [15, (4.4.2)], this implies  has finite monodromy, and so \({{\,\textrm{PW}\,}}_{g,n}\) fails.
has finite monodromy, and so \({{\,\textrm{PW}\,}}_{g,n}\) fails.
We now verify \(\overline{\nabla }= 0\) in the two cases. Set  . In case (1), \(\overline{\nabla }\) is an H-equivariant map
. In case (1), \(\overline{\nabla }\) is an H-equivariant map

between H-representations with no irreducible subrepresentations in common, and therefore must vanish identically.
To verify (2), observe that an irreducible symplectically self-dual H-representation \(\pi \) satisfies \(({{\,\textrm{Sym}\,}}^2 \pi )^H= 0\). Indeed  is non-zero by assumption. By Schur’s lemma,
is non-zero by assumption. By Schur’s lemma,  has dimension exactly 1 (as \(\pi \) is self-dual). We then find
has dimension exactly 1 (as \(\pi \) is self-dual). We then find

and so  .
.
To check \(\overline{\nabla }\) vanishes, we can write it as a sum of maps

and show each \(\overline{\nabla }_i\) vanishes. If the multiplicity of \(\rho _i\) in  is 0, we have
is 0, we have  , and so \(\overline{\nabla }_i = 0\). Otherwise, \(\rho _i\) appears in
, and so \(\overline{\nabla }_i = 0\). Otherwise, \(\rho _i\) appears in  with multiplicity 1. For \(\alpha \) as in (4.1), since \(\rho _i\) appears with multiplicity 1 in \(H^0(X, \omega _X)\), \(\mathrm{{{\,\textrm{im}\,}}}\, \alpha \subset {{\,\textrm{Sym}\,}}^2\,H^0(X, \omega _X)^H\) factors through a copy of \({{\,\textrm{Sym}\,}}^2(\rho _1)^H = 0\). Hence \(\alpha \) vanishes, so \(\overline{\nabla }_i\) vanishes.\(\square \)
with multiplicity 1. For \(\alpha \) as in (4.1), since \(\rho _i\) appears with multiplicity 1 in \(H^0(X, \omega _X)\), \(\mathrm{{{\,\textrm{im}\,}}}\, \alpha \subset {{\,\textrm{Sym}\,}}^2\,H^0(X, \omega _X)^H\) factors through a copy of \({{\,\textrm{Sym}\,}}^2(\rho _1)^H = 0\). Hence \(\alpha \) vanishes, so \(\overline{\nabla }_i\) vanishes.\(\square \)
We now apply Proposition 5.4 to some examples. We first consider the “Eierlegende-Wollmilchsau” example discussed in the paper of Putman and Wieland where the Putman–Wieland conjecture was originally formulated.
Example 5.8
([24, Appendix A]) Let \(Q_8\) be the quaternion group (of order 8). Putman and Wieland describe in [24, Appendix A] a family of \(Q_8\) covers of genus one curves  , such that the vector space V of Proposition 5.4 is \(\mathbb {Q}\)-irreducible as a \(Q_8\)-representation, with \(F^1V_{\mathbb {C}}\) irreducible and symplectically self-dual. Hence Proposition 5.4 (2) applies.
, such that the vector space V of Proposition 5.4 is \(\mathbb {Q}\)-irreducible as a \(Q_8\)-representation, with \(F^1V_{\mathbb {C}}\) irreducible and symplectically self-dual. Hence Proposition 5.4 (2) applies.
Example 5.9
([22, Theorem 8.3]) The eight examples appearing in [22, Table 10] all satisfy Proposition 5.4 (1), by the displayed equation in the proof of [22, Theorem 8.3]. For example, this includes a family of \(\mathbb {Z}/4\mathbb {Z}\)-covers of \(\mathbb {P}^1\) which are totally ramified over four points. This family may be expressed in terms of equations as \(y^4 = x(x-1)(x-\lambda )\), for \(\lambda \in {\mathbb {A}}^1_\lambda - \{0, 1\}\) the parameter of the family.
We can also make new examples using Proposition 5.4.
Example 5.10
Let H be any non-abelian finite subgroup of \(\textrm{SL}_2({\mathbb {C}})\), with \(\rho :H\hookrightarrow \textrm{SL}_2({\mathbb {C}})\) the given embedding. Suppose H is generated by two elements, say \(\gamma \) and \(\delta \). Then we claim there is a cover with Galois group H, furnishing a counterexample to \({{\,\textrm{PW}\,}}_{1,1}\).
Indeed, since H is non-abelian and generated by two elements, any two generators of H cannot commute, so their commutator c is non-trivial. Moreover \(\rho \) is automatically irreducible, as H is non-abelian. Finally, note that \(\rho \) is symplectically self-dual, as the determinant yields a symplectic form preserved by \(\rho \). Since \(\rho \) is two-dimensional and semisimple, we obtain that \(\rho (c)\) has two eigenvalues which are inverse to each other and neither is equal to 1. Now, let Y be a once punctured genus 1 curve. Identify \(\pi _1(Y, y) \simeq F_2\), and let \(X \rightarrow Y\) be the cover associated to the representation \(F_2 \rightarrow H\) sending the first generator to \(\gamma \) and the second to \(\delta \). It follows from the Chevalley–Weil formula, as in [23, Theorem 2.1] that \(\rho \) appears with multiplicity 1 in \(H^0(X, \omega _X)\). Further, any Galois conjugate of \(\rho \) is also faithful, and by the same reasoning, it also appears with multiplicity 1 in \(H^0(X, \omega _X)\). Therefore, Proposition 5.4 (2) applies and \(f:X \rightarrow Y\) furnishes a counterexample to Putman–Wieland.
The non-abelian finite subgroups of \(\textrm{SL}_2({\mathbb {C}})\) are the dicyclic groups and three exceptional groups (the binary octahedral, binary icosahedral, and binary tetrahedral groups), see [25]. One can directly check that each such group is generated by two elements. Hence, for each such group, we can find a cover furnishing a counterexample to Putman–Wieland with \(g = 1\) and \(n = 1\).
The cover of \(\Sigma _{1,1}\) associated to an embedding of the order 4n dicyclic group \(\textrm{Dic}_n\) into \(\textrm{SL}_2({\mathbb {C}})\) as above has genus \(2n-1\). By analyzing the representation theory of dicyclic groups, one may verify the dimension of the fixed part is n if n is even and \(n-1\) if n is odd. In particular, the dimension of this fixed part tends to \(\infty \) as \(n \rightarrow \infty \).
Recall that a cover of a curve of genus one, branched over one point as in Example 5.10, is called an origami curve.
We can also make examples of representations of dimension more than 2. We expect there to be an unwieldy collection of these larger-dimensional examples, and it is an enjoyable exercise to look for them.
Example 5.11
Let H be the order 32 group given in terms of generators and relations by

As described at [12], the commutator subgroup of H is isomorphic to \(({\mathbb {Z}}/2{\mathbb {Z}})^2\). Since \(c^2 = a^{-1}\), this group is generated by b and c. One may directly verify that \(cbc^{-1}b^{-1}\) is not central. Let Y be a once punctured genus 1 curve. Upon identifying \(\pi _1(Y, y) \simeq F_2\), let \(X \rightarrow Y\) be the cover associated to the representation \(F_2 \rightarrow H\) sending the first generator to c and the second to b. There is a unique 4-dimensional symplectic representation \(\rho \) of H, and under this representation, the character \(\textrm{tr}\, \rho (cbc^{-1}b^{-1}) = 0\). Since \(cbc^{-1}b^{-1}\) has order 2, its eigenvalues are \(\pm 1\), and as they sum to 0, two must be 1 and two must be \(-1\). The Chevalley–Weil formula as in [23, Theorem 2.1] implies \(\rho \) appears with multiplicity 1 in \(H^0(X, \omega _X)\). Since \(\rho \) is the only symplectically self-dual representation of H, it has no non-isomorphic Galois conjugates so we conclude \(s = 1\) in Proposition 5.4. We therefore conclude by Proposition 5.4 (2) that \(f:X \rightarrow Y\) furnishes a counterexample to Putman–Wieland, where here \(g = 1\) and \(n = 1\).
5.2 Questions on families with large isotrivial isogeny factor
Examples 5.8–5.11 above seem interesting applications of Proposition 4.2, but they only scratch the surface. We were essentially able to characterize all 2-dimensional counterexamples to Putman–Wieland coming from Proposition 5.4 (2) in Example 5.10, while we gave only a single 4-dimensional counterexample in Example 5.11 via a non-systematic examination of 4-dimensional symplectic representations. Note such counterexamples can only occur when \(g = 1\) and \(n =1\), as remarked in Remark 5.7. We suspect there are infinitely many more counterexamples obtainable in this way, but do not have any systematic approach to searching for them.
Question 5.12
Other than the example in Example 5.11, are there more 4-dimensional counterexamples to Putman–Wieland obtainable via Proposition 5.4? Are there infinitely many such? Can one classify them?
Moreover, generalizing from 4-dimensional representations to higher dimensional representations, we ask the following.
Question 5.13
Can one obtain families of origami curves with isotrivial isogeny factor coming from Proposition 5.4 (2) via representations of arbitrarily large dimension? For each such dimension, are there infinitely many? Can one classify them?
In Example 5.10, we showed there are families of origami curves of arbitrarily large genus g, whose Jacobians have an isotrivial isogeny factor of dimension more than g/2.
Question 5.14
What is the supremum over all positive real numbers c so that, for arbitrarily large g, there is a non-isotrivial family of genus g curves whose Jacobians have an isotrivial isogeny factor of dimension at least cg? What about the analogous question for families of origami curves?
As mentioned above, by Example 5.10, \(c \geqslant 1/2\), and so \(1/2 \leqslant c \leqslant 1\).
Even deciding whether \(c < 1\) seems quite difficult, which leads to our next question. Möller showed in [20, Theorem 5.1] (using also [20, Corollary 3.3]), that for \(g \geqslant 6\), there are no families of genus g curves whose Jacobian has an isotrivial isogeny factor of dimension \(g - 1\). More recently, Aulicino and Norton showed moreover that no such curves exist when \(g = 5\) [1].
Question 5.15
For any fixed positive integer m, are there families of curves with an isotrivial isogeny factor of dimension \(g - m\) for arbitrarily large g?
As noted above, we find that the answer is “no” for \(m = 1\). If the answer to Question 5.15 is “yes" for any m, then \(c = 1\) in Question 5.14.
Finally, we note that many of the examples of isotrivial isogeny factors we found above were isotypic in the following sense: consider a family of curves  with a finite group H acting on
with a finite group H acting on  . For any \(b \in B\), the resulting H action on
. For any \(b \in B\), the resulting H action on  decomposes as a sum of \(\rho \)-isotypic components
decomposes as a sum of \(\rho \)-isotypic components  over H-irreps \(\rho \). We say the isotrivial isogeny factor of the Jacobian of
over H-irreps \(\rho \). We say the isotrivial isogeny factor of the Jacobian of  is isotypic if, for any \(b \in B\), the tangent space to the maximal isotrivial isogeny factor is identified with a direct sum of \(\rho \)-isotypic components of
is isotypic if, for any \(b \in B\), the tangent space to the maximal isotrivial isogeny factor is identified with a direct sum of \(\rho \)-isotypic components of  .
.
Question 5.16
Can one produce non-isotrivial families of curves  with an H action as above whose Jacobian has an isotypic isotrivial isogeny factor and so that the quotient
with an H action as above whose Jacobian has an isotypic isotrivial isogeny factor and so that the quotient  has genus at least 2? Can one produce such families where
has genus at least 2? Can one produce such families where  has arbitrarily large genus? Can one produce such families of curves with an isotypic isotrivial isogeny factor so that the base B has large dimension?
has arbitrarily large genus? Can one produce such families of curves with an isotypic isotrivial isogeny factor so that the base B has large dimension?
As a partial answer to the last question above, in a forthcoming paper, we will show it is impossible to have isotypic isotrivial isogeny factors whenever the quotient curve  has genus h and dominates
has genus h and dominates  if \(h \geqslant 3\). On the other hand, it would be quite interesting to find such an example when \(h = 2\). If such a family exists, it would give a counterexample to Putman–Wieland in genus 2.
if \(h \geqslant 3\). On the other hand, it would be quite interesting to find such an example when \(h = 2\). If such a family exists, it would give a counterexample to Putman–Wieland in genus 2.
6 Counterexamples for hyperelliptic curves
We now explain that the Putman–Wieland conjecture fails if we restrict our attention to the hyperelliptic mapping class group, following Marković [21]. In particular, this implies that the Putman–Wieland conjecture fails in genus 2.
Definition 6.1
Choose a hyperelliptic involution \(\iota \) acting on \(S_g\) and let the hyperelliptic mapping class group  denote the centralizer of \(\iota \) in \({{\,\textrm{Mod}\,}}_{g}\). Let \({{\,\textrm{HMod}\,}}_{g,n} \subset {{\,\textrm{Mod}\,}}_{g,n}\) denote the preimage of \({{\,\textrm{HMod}\,}}_g \subset {{\,\textrm{Mod}\,}}_g\) under the surjection \({{\,\textrm{Mod}\,}}_{g,n} \rightarrow {{\,\textrm{Mod}\,}}_g\).
denote the centralizer of \(\iota \) in \({{\,\textrm{Mod}\,}}_{g}\). Let \({{\,\textrm{HMod}\,}}_{g,n} \subset {{\,\textrm{Mod}\,}}_{g,n}\) denote the preimage of \({{\,\textrm{HMod}\,}}_g \subset {{\,\textrm{Mod}\,}}_g\) under the surjection \({{\,\textrm{Mod}\,}}_{g,n} \rightarrow {{\,\textrm{Mod}\,}}_g\).
Remark 6.2
Any two such hyperelliptic involutions \(\iota \in {{\,\textrm{Mod}\,}}_{g}\) are conjugate by [9, Proposition 7.15].
We next recall a foundational result on topology of the moduli stack of hyperelliptic curves. For a reference, we recommend the survey article [10, Proposition 1], and the reader may also consult [13, Theorem 2].
Lemma 6.3
Let \(g\geqslant 2\), \(n \geqslant 0\) and let  denote the closed substack parameterizing families of smooth proper hyperelliptic curves of genus g with geometrically connected fibers and n disjoint sections. Under the identification of \({{\,\textrm{Mod}\,}}(\Sigma _{g,n})\) with
denote the closed substack parameterizing families of smooth proper hyperelliptic curves of genus g with geometrically connected fibers and n disjoint sections. Under the identification of \({{\,\textrm{Mod}\,}}(\Sigma _{g,n})\) with  , one may recover \({{\,\textrm{HMod}\,}}_{g,n}\) as the image of
, one may recover \({{\,\textrm{HMod}\,}}_{g,n}\) as the image of  . Moreover
. Moreover  .
.
Remark 6.4
The hyperelliptic mapping class group is sometimes also called the symmetric mapping class group [9, Section 9.4].
Definition 6.5
In the setup of Definition 2.2, let \({{\,\textrm{HPW}\,}}_{g,n}\) be the statement that for every finite index characteristic subgroup \(K \subset \pi _1(\Sigma _{g,n}, v_0)\), there are no non-zero vectors  with finite orbit under the action of \({{\,\textrm{HMod}\,}}_{g,n+1}\).
with finite orbit under the action of \({{\,\textrm{HMod}\,}}_{g,n+1}\).
Problem 6.6
(Hyperelliptic Putman–Wieland problem, cf. [4, Problem 3.4]) Suppose \(g \geqslant 2\), \(n \geqslant 0\). Does \({{\,\textrm{HPW}\,}}_{g,n}\) hold?
The following result is essentially [21, Theorem 1.3] where the case \(g = 2\) is proven. We observe here that an analogous proof works for hyperelliptic curves in all genera. Recall we use  for the moduli stack of smooth hyperelliptic curves of genus g with n marked points, as in Lemma 6.3.
for the moduli stack of smooth hyperelliptic curves of genus g with n marked points, as in Lemma 6.3.
Proposition 6.7
Let \(g\geqslant 2\), \(n \geqslant 0\) be integers. There exists a finite étale map  , so that if
, so that if  is the corresponding relative curve over
is the corresponding relative curve over  , there is a finite étale cover
, there is a finite étale cover  of
of  of degree 36 such that:
of degree 36 such that:
-
(1)
the composite map
 has geometrically connected fibers,
has geometrically connected fibers, -
(2)
the relative Jacobian
 has an isotrivial isogeny factor.
has an isotrivial isogeny factor.
For  a geometric point, the finite index subgroup of the hyperelliptic mapping class group
a geometric point, the finite index subgroup of the hyperelliptic mapping class group  has a vector with finite orbit under its action on
has a vector with finite orbit under its action on  and so the answer to the hyperelliptic Putman–Wieland problem is negative for every \(g \geqslant 2,n \geqslant 0\). In particular, \({{\,\textrm{PW}\,}}_{2,n}\) is false for all \(n \geqslant 0\).
and so the answer to the hyperelliptic Putman–Wieland problem is negative for every \(g \geqslant 2,n \geqslant 0\). In particular, \({{\,\textrm{PW}\,}}_{2,n}\) is false for all \(n \geqslant 0\).
We will prove Proposition 6.7 below in Sect. 6.1. We will use the following result of Bogomolov–Tschinkel:
Theorem 6.8
([5, Proposition 3.8, Remark 3.10]) Let \(g\geqslant 2\) be an integer. Let \(C_0\) be the genus 2 curve defined by \(y^6=x(x-1)\) and \(E_0\) be the genus 1 curve defined by \(y^3=x(x-1)\). Let \(Z \in \{C_0, E_0\}\). There exists a finite étale cover  of
of  , and a finite étale cover
, and a finite étale cover  of
of  such that the composite map
such that the composite map  has geometrically connected fibers, and such that every fiber of \(\pi '_Z\) admits a non-constant map to the smooth projective curve Z. If \(Z = C_0\), the cover
has geometrically connected fibers, and such that every fiber of \(\pi '_Z\) admits a non-constant map to the smooth projective curve Z. If \(Z = C_0\), the cover  has degree 648 while if \(Z = E_0\) this map has degree 36. The non-constant map
has degree 648 while if \(Z = E_0\) this map has degree 36. The non-constant map  has degree 4.
has degree 4.
Proof
Strictly speaking, in [5, Proposition 3.8, Remark 3.10], it is only shown that a hyperelliptic curve C admits a finite étale cover X with a non-constant map to \(C_0\); however, their construction works in families, hence the statement. From their construction, the map is a composite of 5 maps of respective degrees 2, 9, 2, 9, and 2, so has degree  . (This was mistakenly claimed to be 72 in [5, Remark 3.10] but updated in a later version [6, Remark 3.10].) An intermediate step in the proof of [5, Proposition 3.8] shows that the hyperelliptic curve C admits a degree 36 finite étale cover X with a degree 4 non-constant map to \(E_0\). This cover \(X \rightarrow C\) is a composite of the first three maps of the above-mentioned 5 maps, which have degrees 2, 9, and 2. Hence, this cover has degree 36.\(\square \)
. (This was mistakenly claimed to be 72 in [5, Remark 3.10] but updated in a later version [6, Remark 3.10].) An intermediate step in the proof of [5, Proposition 3.8] shows that the hyperelliptic curve C admits a degree 36 finite étale cover X with a degree 4 non-constant map to \(E_0\). This cover \(X \rightarrow C\) is a composite of the first three maps of the above-mentioned 5 maps, which have degrees 2, 9, and 2. Hence, this cover has degree 36.\(\square \)
Remark 6.9
Note that there is a small typo in [5, Example 3.7], which claims that every hyperelliptic curve admits a non-constant map to an elliptic curve satisfying some extra conditions; this claim is evidently false. However, given a hyperelliptic curve C, one may construct a finite étale cover X of C mapping to an elliptic curve and satisfying the desired conditions as follows; such an X suffices for the rest of their argument to go through. Let \(f:C\rightarrow \mathbb {P}^1\) be the hyperelliptic double cover, which we may without loss of generality assume is branched over \(0,1,\infty \). Let \(\lambda \) be another branch point of f, and let \(E_\lambda \) be the elliptic curve defined by
Then any component X of the normalized fiber product  satisfies the desired properties.
satisfies the desired properties.
In order to prove Proposition 6.7, we will also use the following equivalences. This is a fairly standard Hodge-theoretic argument, the key input being the theorem of the fixed part.
Lemma 6.10
Suppose  is a scheme and we have a relative smooth proper curve
is a scheme and we have a relative smooth proper curve  with geometrically connected fibers. The following properties are equivalent:
with geometrically connected fibers. The following properties are equivalent:
-
(1)
For
 , the vector space
, the vector space 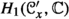 contains no non-zero vector with finite orbit under the action of
contains no non-zero vector with finite orbit under the action of  .
. -
(2)
The local system \(R^1 \pi '_* {\mathbb {C}}\) contains no sub-local system with finite monodromy.
-
(3)
The relative Jacobian
 has no isotrivial isogeny factor.
has no isotrivial isogeny factor.
The following properties are also equivalent:
- (1\('\)):
-
For
 , the vector space
, the vector space  contains no non-zero fixed vector under the action of
contains no non-zero fixed vector under the action of  .
. - (2\('\)):
-
The local system \(R^1 \pi '_* {\mathbb {C}}\) contains no trivial sub-local system.
- (3\('\)):
-
The relative Jacobian
 has no constant isogeny factor.
has no constant isogeny factor.
Proof
The equivalence of (1), (2), and (3) follow from that of (1\('\)), (2\('\)), and (3\('\)) by passing to a suitable connected finite étale cover of  upon which the vector with finite orbit in (1) becomes a fixed vector, the sub-local system with finite monodromy in (2) becomes trivial, and the isotrivial factor in (3) becomes trivial.
upon which the vector with finite orbit in (1) becomes a fixed vector, the sub-local system with finite monodromy in (2) becomes trivial, and the isotrivial factor in (3) becomes trivial.
It remains to verify the equivalence of (1\('\)), (2\('\)), and (3\('\)). Under the equivalence between \({\mathbb {C}}\) representations of  and local systems of \({\mathbb {C}}\) vector spaces on
and local systems of \({\mathbb {C}}\) vector spaces on  , a non-zero fixed vector in
, a non-zero fixed vector in  corresponds to a non-trivial sub-local system, which gives the equivalence between (1\('\)) and (2\('\)). Note here we are using Poincaré duality to identify
corresponds to a non-trivial sub-local system, which gives the equivalence between (1\('\)) and (2\('\)). Note here we are using Poincaré duality to identify  and
and  .
.
We next verify \((3')\) \(\Longrightarrow \) \((2')\). To this end, let  denote the structure map. A trivial isogeny factor
denote the structure map. A trivial isogeny factor  , gives a trivial sub-local system
, gives a trivial sub-local system  .
.
We conclude by demonstrating \((2')\) \(\Longrightarrow \) \((3')\). Suppose we begin with a trivial sub-local system of \({\mathbb {W}} \subset R^1 \phi _* {\mathbb {C}}\), the theorem of the fixed part [8, Corollaire 4.1.2] implies that \({\mathbb {W}}\) is also a variation of Hodge structure. Let \({\mathbb {W}}_{{\mathbb {Z}}} \subset {\mathbb {W}}\) denote the trivial \({\mathbb {Z}}\) local system on  for which
for which  . We can then recover the trivial isogeny factor as the quotient
. We can then recover the trivial isogeny factor as the quotient  . (On fibers, this corresponds to the fact that an abelian variety A can be written as the quotient \(H^0(A, \Omega _A)^\vee / H^1(A, {\mathbb {Z}})\).)\(\square \)
. (On fibers, this corresponds to the fact that an abelian variety A can be written as the quotient \(H^0(A, \Omega _A)^\vee / H^1(A, {\mathbb {Z}})\).)\(\square \)
6.1 Proof of Proposition 6.7
Let  ,
,  ,
,  be as defined in Theorem 6.8. As shown there, the cover
be as defined in Theorem 6.8. As shown there, the cover  has degree 36. The Jacobian of \(E_0\) is an isogeny factor of
has degree 36. The Jacobian of \(E_0\) is an isogeny factor of  .
.
Having produced a relative Jacobian with a constant isogeny factor, the equivalence of Lemma 6.10 (1) and Lemma 6.10 (3) together with the identification of  with \({{\,\textrm{HMod}\,}}_{g,n}\) from Lemma 6.3, implies the answer to Problem 6.6 is negative for every \(g \geqslant 2\), \(n \geqslant 0\).
with \({{\,\textrm{HMod}\,}}_{g,n}\) from Lemma 6.3, implies the answer to Problem 6.6 is negative for every \(g \geqslant 2\), \(n \geqslant 0\).
Finally, \({{\,\textrm{PW}\,}}_{2,n}\) fails because the natural map  is an isomorphism, and hence in genus 2 the hyperelliptic mapping class group is identified with the entire mapping class group by Lemma 6.3. \(\square \)
is an isomorphism, and hence in genus 2 the hyperelliptic mapping class group is identified with the entire mapping class group by Lemma 6.3. \(\square \)
Remark 6.11
Proposition 6.7 was originally claimed in [3]; unfortunately the proof there was incorrect (see [4, Remark 3.17]). We would like to thank Marco Boggi for his extremely helpful email correspondence regarding this issue, which was useful to our understanding of the Putman–Wieland conjecture. The reader may also consult [2, Corollary 6.11].
Remark 6.12
In some sense Proposition 6.7 shows that our proof of Corollary 2.7 and Theorem 3.2 is sharp. Indeed, Theorem 6.8 shows that for each g there exists a diagram

with \(\pi \) a relative curve of genus g, so that the induced map  dominates the hyperelliptic locus, and moreover such that f has degree bounded independently of g, yielding a counterexample to \({{\,\textrm{HPW}\,}}_{g,0}\). The hyperelliptic locus has codimension \(g-2\) in
dominates the hyperelliptic locus, and moreover such that f has degree bounded independently of g, yielding a counterexample to \({{\,\textrm{HPW}\,}}_{g,0}\). The hyperelliptic locus has codimension \(g-2\) in  , so this does not contradict Theorem 3.2; but that theorem shows that such an example is impossible with families of curves whose codimension \(\delta _g\) in
, so this does not contradict Theorem 3.2; but that theorem shows that such an example is impossible with families of curves whose codimension \(\delta _g\) in  grows such that \(g-\delta _g\rightarrow \infty \) with g.
grows such that \(g-\delta _g\rightarrow \infty \) with g.
References
Aulicino, D., Norton, C.: Shimura–Teichmüller curves in genus 5 (2019). arXiv:1904.01625v2
Boggi, M.: Notes on hyperelliptic mapping class groups (2021). arXiv:2110.13534v2
Boggi, M.: Retraction of: Linear representations of hyperelliptic mapping class groups. Michigan Math. J. 71(1), 221 (2022)
Boggi, M.: Linear representations of hyperelliptic mapping class groups (2022). arXiv:2110.13534v3
Bogomolov, F., Tschinkel, Yu.: On curve correspondences. In: Communications in Arithmetic Fundamental Groups (Kyoto, 1999/2001). Sūrikaisekikenkyūsho Kōkyūroku, vol. 1267, pp. 157–166. Research Institute for Mathematical Sciences, Kyoto (2002)
Bogomolov, F., Tschinkel, Yu.: On curve correspondences (2004). https://www.math.nyu.edu/~tschinke/papers/yuri/02genram/genram.pdf
Chevalley, C., Weil, A., Hecke, E.: Über das verhalten der integrale 1. gattung bei automorphismen des funktionenkörpers. Abh. Math. Sem. Univ. Hamburg 10(1), 358–361 (1934)
Deligne, P.: Théorie de Hodge. II. Inst. Hautes Études Sci. Publ. Math. 40, 5–57 (1971)
Farb, B., Margalit, D.: A Primer on Mapping Class Groups. Princeton Mathematical Series, vol. 49. Princeton University Press, Princeton (2012)
González Díez, G., Harvey, W.J.: Moduli of Riemann surfaces with symmetry. In: Harvey, W.J., Maclachlan, C. (eds.) Discrete Groups and Geometry (Birmingham, 1991). London Mathematical Society Lecture Note Series, vol. 173, pp. 75–93. Cambridge University Press, Cambridge (1992)
Grunewald, F., Larsen, M., Lubotzky, A., Malestein, J.: Arithmetic quotients of the mapping class group. Geom. Funct. Anal. 25(5), 1493–1542 (2015)
Group description c4.10d4. https://people.maths.bris.ac.uk/~matyd/GroupNames/1/C4.10D4.html. Accessed 9 Aug 2022
Harvey, W.J.: On branch loci in Teichmüller space. Trans. Amer. Math. Soc. 153, 387–399 (1971)
Ivanov, N.V.: Fifteen problems about the mapping class groups. In: Farb, B. (ed.) Problems on Mapping Class Groups and Related Topics. Proceedings of Symposia in Pure Mathematics, vol. 74, pp. 71–80. American Mathematical Society, Providence (2006)
Katz, N.M.: Algebraic solutions of differential equations (\(p\)-curvature and the Hodge filtration). Invent. Math. 18(1–2), 1–118 (1972)
Kirby, R.: Problems in low-dimensional topology. In: Kazez, W.H. (ed.) Geometric Topology (Athens, GA, 1993). AMS/IP Studies in Advanced Mathematics, vol. 2.2, pp. 35–473. American Mathematical Society, Providence (1997)
Landesman, A., Litt, D.: Canonical representations of surface groups (2022). arXiv:2205.15352v1
Landesman, A., Litt, D.: Geometric local systems on very general curves and isomonodromy (2022). arXiv:2202.00039v2
Looijenga, E.: Prym representations of mapping class groups. Geom. Dedicata 64(1), 69–83 (1997)
Möller, M.: Shimura and Teichmüller curves. J. Mod. Dyn. 5(1), 1–32 (2011)
Marković, V.: Unramified correspondences and virtual properties of mapping class groups. Bull. London Math. Soc. 54(6), 2324–2337 (2022)
McMullen, C.T.: Braid groups and Hodge theory. Math. Ann. 355(3), 893–946 (2013)
Naeff, R.: The Chevalley–Weil Formula. Master’s Thesis (2005)
Putman, A., Wieland, B.: Abelian quotients of subgroups of the mappings class group and higher Prym representations. J. London Math. Soc. 88(1), 79–96 (2013)
Symplectically self dual \(2\) dimensional representations. https://people.maths.bris.ac.uk/~matyd/GroupNames/R.html#dim2-. Accessed 9 August 2022
Acknowledgements
We would like to thank Paul Apisa, Marco Boggi, Simion Filip, Joe Harris, Eduard Looijenga, Eric Larson, Dan Margalit, Vladimir Marković, Carlos Matheus, Curtis McMullen, Andy Putman, Will Sawin, Ravi Vakil, Isabel Vogt, Melanie Matchett Wood and Alex Wright for helpful discussions related to this paper. We also thank an anonymous referee for many extremely helpful comments.
Funding
Open Access funding provided by the MIT Libraries.
Author information
Authors and Affiliations
Contributions
Both authors contributed significantly to the paper.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests that might be perceived to influence the results or discussion reported in this paper. The results and figures in this manuscript have not been published elsewhere, nor are they under consideration by another publisher.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Landesman was supported by the National Science Foundation under Award No. DMS-2102955. Litt was supported by NSF Grant DMS-2001196. This material is based upon work supported by the Swedish Research Council under Grant No. 2016-06596 while the authors were in residence at Institut Mittag-Leffler in Djursholm, Sweden during the fall of 2021.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Landesman, A., Litt, D. An introduction to the algebraic geometry of the Putman–Wieland conjecture. European Journal of Mathematics 9, 40 (2023). https://doi.org/10.1007/s40879-023-00637-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-023-00637-w






 is an isotypic decomposition, i.e. there is a subset
is an isotypic decomposition, i.e. there is a subset 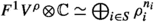 , or
, or .
. has geometrically connected fibers,
has geometrically connected fibers, has an isotrivial isogeny factor.
has an isotrivial isogeny factor. , the vector space
, the vector space 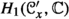 contains no non-zero vector with finite orbit under the action of
contains no non-zero vector with finite orbit under the action of  .
. has no isotrivial isogeny factor.
has no isotrivial isogeny factor. , the vector space
, the vector space  contains no non-zero fixed vector under the action of
contains no non-zero fixed vector under the action of  .
. has no constant isogeny factor.
has no constant isogeny factor.