Abstract
The reversibility, or Loschmidt paradox, is a thought experiment in which microscopic reversibility is exploited to generate an apparently spontaneous trajectory in which entropy decreases, thus violating the Second Law of Thermodynamics (SLT). To achieve this, the system is allowed to evolve from a low-entropy to a high-entropy configuration, at which point all velocities of its molecules are reversed, thus producing the desired effect. In this paper we focus on the velocity reversal step. Implementing this step requires the measurement of velocities and positions, which must be stored in a memory. Even in the case of a reversible measurement, the erasure of the stored information, necessary to reset the measuring device to its original state, has an entropy cost that offsets the entropy decrease during the reverse evolution of the system. This cost is sufficient to explain why the described procedure does not violate the SLT.
Similar content being viewed by others
1 Introduction
The purpose of this paper is to re-examine the reversibility paradox (RP), related to the Second Law of Thermodynamics (SLT), using modern developments in the physics of measurement and information. From this perspective we produce an account of the paradox that is sufficient to explain it: a step in the procedure of the paradox requires a measurement with an eventual entropy cost that offsets the entropy decrease one can achieve in a different step, thus avoiding a violation of the SLT.
The RP was formulated in the 1860s in the context of the infancy of kinetic theory. A complete, well-documented early history is presented in [1]. The initial formulation was made during discussions between Maxwell, Tait and Thompson (Lord Kelvin). It states that, if a system starts in a highly ordered state and one allows it to approach equilibrium, one can then simply at some point reverse the velocities of all its particles and thus produce a trajectory for which the entropy decreases, and therefore violate the SLT. The argument was independently formulated by Loschmidt in the 1870s and became known to Boltzmann. Brush [1] credits Loschmidt with motivating Boltzmann into formulating his H-theorem in terms of probabilities. It is precisely the velocity reversal step that this paper concentrates on.
In Sect. 2 we review some of the best-known resolutions of the RP. In Sect. 3 we look in more detail at the velocity reversal step, introduce elements from the modern theory of information and measurement, and recast the RP in such terms. All this results in a new understanding of the paradox. We discuss the findings in Sect. 4.
2 Previous Explanations of the Paradox
The point of the paradox is that one can construct processes that violate the SLT using an apparently simple reversal of velocities under the existence of reversible dynamics. This section describes previous explanations or resolutions of the paradox.
In the late 1800s it was argued that, since most available states in equilibrium have high entropy, encountering a configuration that evolved to a low-entropy state is statistically improbable [1]. More recent improbability argument address either the relatively small number of low-entropy initial conditions [2, 3] or the rarity of trajectories in which entropy decreases [4]. Note that such arguments do not explain the RP – they just make its implementation rather improbable. Similarly, we see sensitive dependence on initial conditions arguments as moot, since one can at least conceptually reverse velocities exactly. Even if not, a reversed trajectory in which entropy decreases should be feasible at least for short times, thus still violating the SLT.
A different current of thought is that microscopic reversibility and macroscopic irreversibility are not incompatible. Swendsen [5] has studied the case of free expansion of noninteracting particles, initially confined in a small volume, and with velocities following a Maxwell-Boltzmann distribution, into a large container with perfectly reflecting walls. He developed an exact solution for the 1D case, and showed that, while the dynamics is reversible, it mimics the irreversible approach to equilibrium one expects as the particles spread into the larger box. Lebowitz [6] has also stated that the paradox can be explained with three ingredients: a large separation of scales, the role of initial conditions, and probabilistic reasoning (not every state of a system evolves according to the SLT – only most of them).
Now, consider two scenarios. (1) A highly ordered macrostate is prepared (e.g., by non-adiabatic compression) and allowed to relax to a higher entropy state. Then the velocities are reversed, and the system comes back (close) to the initial microstate – not just macrostate. The velocity reversal step requires gaining a lot of knowledge about the system that we initially did not have. For the initial evolution we can at best offer a coarse-grained description, within which transitions from state to state are probabilistic. For the entire reversed evolution, we know “everything” about the system – not just its coarse-grained macroscopic configuration. (2) A highly ordered microstate is prepared, allowed to evolve to a state of higher entropy (as specified above); the velocities are reversed, and the system traces back its earlier evolution (close) to the initial microstate. This is allowed due to the reversibility of the system; in this case there is no paradox whatsoever. In scenario (1), however, a potential confusion arises due to the switch between the macro and a micro descriptions, which can be at the root of a misunderstanding of the paradox, as was pointed out almost 50 years ago [7]. In both cases I have included the specification “close to,” in order to accommodate the earlier point about sensitive dependence.
3 Measurement, Erasure, Information, and Entropy
The SLT is formulated for closed systems; it is time to look at the only step in the RP where the system is open to its environment: the velocity reversal step.
In order to determine the velocities and positions of the particle components of the system, measurements have to been made by some agent so that, for example, mirror-like barriers can be placed at the appropriate positions and angles so that the particles can indeed reverse their velocities. This has already been noticed by Zurek [8]. We will call this agent generically a “Laplace demon.” As part of the measurement process, a record is written in its memory.
The all-knowing demon (“une vaste intelligence”) proposed by Laplace in a different context [9] shares some features with the better-known Maxwell’s demon [10]. They both collect information about a system, store it in their memory, take subsequent actions that can presumably violate the SLT, and will either affect their environment during the measurement process, or need to have their memory reset at some point.
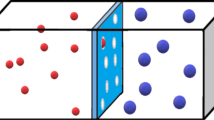
The Maxwell’s demon operates a trap between two containers so that it concentrates the faster particles in one of the containers. This creates a lower-entropy state that violates the SLT at no apparent cost. After 150 years of discussion in the literature, Bennett [11] proposed a solution for why the SLT is not violated after all. It invokes Landauer’s principle [12], which states that during irreversible operations such as memory erasure the entropy in non-information bearing degrees of freedom in the demon or its environment must increase. Landauer’s principle has been recently verified experimentally [13,14,15] in a variety of physical systems. This principle is an extension of an earlier discovery by Szilard [16, 17] that erasing a measurement has a thermodynamic cost, but which now has been extended to apply to irreversible measurements.
To elaborate on the above: following [11], a Maxwell’s demon can potentially perform either irreversible or reversible measurements. In the first case, the measurement of each bit of information will require the generation of at least k ln 2 of entropy, thus avoiding a violation of the SLT. A reversible measurement requires a standard state for the bits where the measurement will be recorded, so that no previous information is overwritten. Then, the irreversible step is not the measurement, but instead the erasure, or resetting of the memory to the standard state. This is where Landauer’s principle comes in.
Thus, in order to restore the demon (Maxwell’s or Laplace’s) to its original state after a reversible measurement, there is an entropy cost, which offsets the decrease in entropy in the system as it follows its reverse path. In the RP scenario, the SLT therefore, still holds. As an example, for N monatomic particles and 20 bits per coordinate, the required entropy increase is 120Nk ln 2. The decrease of entropy in the reverse trajectory is bounded from above by this number, and will usually be less, depending on the level of coarse-graining of the system used to calculate the entropy.
4 Discussion and Conclusions
The SLT is valid for closed systems. In this paper we have shown that in the standard formulation of the Reversibility Paradox, the system in question must interact, even if for a brief time, with a measuring device. There is an ensuing transfer of information that, either is irreversible, or in order to satisfy the constraints of the SLT of no changes in the environment, needs to be reset. The last step has an entropy cost that offsets the decrease of entropy resulting from the reversed trajectory. Thus, the SLT is not violated. The resolution of the paradox presented here closely mirrors that of the Maxwell’s demon offered by Bennett. While this explanation does not challenge the vast effort in going from microscopic to macroscopic descriptions of physical systems, it simply suggests that this machinery is not the way to explain the reversibility paradox.
To reinforce the argument, consider any ideal gas process in which the entropy of the gas decreases – for example, an isothermal compression. This decrease is legitimate, as long as there is an equal, or greater increase of entropy somewhere else (e.g., one, or multiple thermal reservoirs) so that the overall entropy of the closed system (gas + reservoir) does not decrease. The set-up of the RP is no different, although it contains an illusion. Our sight is directed to the forward and backwards “closed” evolution, while misdirecting us from the crucial interaction with the environment that protects the integrity of the SLT through a sequence of measurement, information storage, and erasure with an entropy increase through Landauer’s principle, if needed. None of this was known in the 1800s, but as was done with Maxwell’s demon 40 years ago, the complete story can now be told. The other two paradoxes from that time, Gibbs’ and the recurrence paradox, never involve opening the system to an external agent and hence their resolutions are totally different.
The final remark comes in the context that I have written this paper thinking about classical gases, which were familiar to scientists in the 1800s. By now, a real-life Maxwell’s demon has been implemented in a laser cooling experiment [18], in which ultracold atoms confined by magnetic traps are isolated with the use of carefully tuned laser beams. In this set-up, scattered photons, one per atom, carry information about the turning point and energy of each atom, thus constituting the memory. As these photons are absorbed far away from the set-up with possible re-emission of other photons uncorrelated with the original process, this information is lost and the entropy of the demon - contained in the radiation field - increases [19]. The demon here is an inert, physical device – but the point is that it is real – not just an idle object of speculation.
References
Brush, S.G.: The Kind of Motion We Call Heat. North-Holland, Amsterdam (1976)
Sklar, L.: Physics and Chance. Cambridge University Press, Cambridge (1993)
Holian, B.L., Hoover, W.G., Posch, H.A.: Resolution of the Loschmidt paradox: The origin of irreversible behavior in reversible atomistic dynamics. Phys. Rev. Lett. 59, 10–13 (1987)
Evans, D.J., Searles, D.J.: The fluctuation theorem. Adv. Phys. 51, 1529–1585 (2002)
Swendsen, R.H.: Explaining irreversibility. Am. J. Phys. 76, 643–648 (2008)
Lebowitz, J.L.: Microscopic origins of macroscopic irreversible behavior. Phys. A. 263, 516–527 (1999)
Rothstein, J.: Loschmidt’s and Zermelo’s paradoxes do not exist. Found. Phys. 4, 83–89 (1974)
Zurek, W.H.: Reversibility and stability of information processing systems. Phys. Rev. Lett. 53, 391–394 (1984)
De Laplace, P.S.: Philosophical Essay on Probabilities. Dover, New York (1951). Translated from the 1814 French original by Truscott, F. W., Emory, F. L
Leff, H.S., Rex, A.F. (eds.): Maxwell’s Demon. Princeton University Press, Princeton, USA (2014)
Bennett, C.H.: The thermodynamics of computation – a review. Int. J. Theor. Phys. 21, 905–940 (1982)
Landauer, R.: Reversibility and heat generation in the computing process. IBM J. Res. Develop. 5, 183–191 (1961)
Bérut, A., Arakelyan, A., Petrosyan, A., Ciliberto, S., Dillenschneider, R., Lutz, E.: Experimental verification of Landauer’s principle linking information and thermodynamics. Nature. 483, 187–189 (2012)
Jun, Y., Gavrilov, M., Bechhoeffer, J.: High-precision test of Landauer’s principle in a feedback trap. Phys. Rev. Lett. 113, 190601 (2014)
Hong, J., Lambson, B., Dhuey, S., Bokor, J.: Experimental test of Landauer’s principle in single-bit operations on nanomagnetic memory bits. Sci. Adv. 2, e1501492 (2016)
Szilard, L.: Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Zeit Phys. 53, 840–856 (1929)
Toyabe, S., Sagawa, T., Ueda, M., Muneyuki, E., Sano, M.: Information heat engine: Converting information to energy by feedback control. Nat. Phys. 6, 988–992 (2010)
Raizen, M.G.: Comprehensive control of atomic motion. Science. 324, 1403–1406 (2009)
Binder, P.-M.: Reflections on a wall of light. Science. 322, 1334–1335 (2008)
Acknowledgements
The author thanks Juan Manuel Pedraza, Samir Garzon, Ben Browning, Seneca Cox and Dallas Tada for conversations on this subject.
Funding
Publication charges were paid by the Reid Hoffman Foundation.
Author information
Authors and Affiliations
Contributions
P.M.B., as the only author, did all the work related to this manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Binder, P. The Reversibility Paradox: Role of the Velocity Reversal Step. Int J Theor Phys 62, 200 (2023). https://doi.org/10.1007/s10773-023-05458-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10773-023-05458-x