Effect of Time Dependent Coupling on the Dynamical Properties of the Nonlocal Correlation Between Two Three-Level Atoms

Abstract

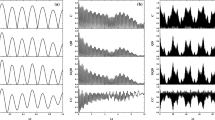
In this article, we present the analytical solution for the pair of entangled two three-level atoms in the cascade configuration with and without the atomic motion effect. The effects of time dependent coupling and photon multiplicity on the evolution of the nonlocal correlation between the two atoms are examined. It is shown that the amount of atom-atom entanglement increases for one photon transition when the atomic motion effect is considered. Also, the entanglement between the two atoms decreases by increasing the photons multiplicity when the time dependent coupling effect is ignored. Finally, the results explored very important phenomena such as entanglement sudden death and entanglement sudden birth.

Appendix A

In order to clarifying the derivations of (5) (i.e. the unitary operator) let us defined

$$ |1\rangle = \left(\begin{array}{lll} 1 \\ 0 \\ 0\end{array}\right) ,|2\rangle = \left(\begin{array}{lll} 0 \\ 1 \\ 0\end{array} \right)\text{ and\ \ }|3\rangle = \left(\begin{array}{lll} 0 \\ 0 \\ 1\end{array}\right) \text{.} $$

(24)

By product |1〉 column vector into row vector 〈1| we get the first matrix element

$$ S=|1\rangle \langle 1|= \left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right) \text{,} $$

(25)

as for as |i〉 〈j| = {.S _ii ifi = jS _ij ifi≠j, i, j = 1, 2, 3. Therefor, we can rewrite the total Hamiltonian in (1) as follows

$$\begin{array}{@{}rcl@{}} \hat{H}_{tot} &=&\omega_{F_{1}}\hat{a}^{\dagger }\hat{a}+\sum \limits_{j=1}^{3}{{\Omega}_{j}^{A}}S_{jj}^{A}+\omega_{F_{2}}\hat{b}^{\dagger } \hat{b}+\sum\limits_{j=1}^{3}{\omega_{j}^{B}}S_{jj}^{B} \\ &&+f\left(z_{1}\right) \left\{ {\lambda_{1}^{A}}\left(\hat{a}^{k}S_{12}^{A}+ \hat{a}^{\dagger k}S_{21}^{A}\right) +{\lambda_{2}^{A}}\left(\hat{a} ^{k}S_{23}^{A}+\hat{a}^{\dagger k}S_{32}^{A}\right) \right\} \\ &&+f\left(z_{2}\right) \left\{ {g_{1}^{B}}\left(\hat{b}^{k}S_{12}^{B}+\hat{b} ^{\dagger k}S_{21}^{B}\right) +{g_{2}^{B}}\left(\hat{b}^{k}S_{23}^{B}+\hat{b} ^{\dagger k}S_{32}^{B}\right) \right\} . \end{array} $$

(26)

In order to study the atoms A-B entanglement we must find the total wave function $|{\Psi }_{tot}\left (t\right ) \rangle$ and for more simplicity, we will calculate the unitary operator for the first atom A by using the Hamiltonian interaction as follows

$$\begin{array}{@{}rcl@{}} \hat{H}_{I}^{A} &=&{\lambda_{1}^{A}}\left(\hat{a}^{k}S_{12}^{A}+\hat{a} ^{\dagger k}S_{21}^{A}\right) +{\lambda_{2}^{A}}\left(\hat{a}^{k}S_{23}^{A}+ \hat{a}^{\dagger k}S_{32}^{A}\right) , \end{array} $$

(27)

$$\begin{array}{@{}rcl@{}} \hat{H}_{I}^{B} &=&{g_{1}^{B}}\left(\hat{b}^{k}S_{12}^{B}+\hat{b}^{\dagger k}S_{21}^{B}\right) +{g_{2}^{B}}\left(\hat{b}^{k}S_{23}^{B}+\hat{b}^{\dagger k}S_{32}^{B}\right) . \end{array} $$

(28)

where the normalization condition is satisfy $\left [ \hat {H}_{I}^{A},\hat {H}_{I}^{B}\right ] =0,$ i.e. $\hat {H}_{I}^{A}$ and $\hat {H}_{I}^{B}$ are commute. Thus, the time-dependence Schrödinger wave equation is [39]

$$\begin{array}{@{}rcl@{}} i\hbar \frac{dU_{1}(t)}{dt} &=&f\left(z_{1}\right) \hat{H}_{I}^{A}U_{1}(t), \text{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\left(\text{set }\hbar =1\right) \\ \ln U_{1}(t) &=&-i\gamma_{1}\left(t\right) \hat{H}_{I}^{A}+c\text{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\left(\text{put }c=0\right) \\ U_{1}(t) &=&e^{-i\gamma_{1}\left(t\right) \hat{H}_{I}^{A}}. \end{array} $$

(29)

This is unitary operator for the atom A, consider

$$ \hat{H}_{I}^{A}={\lambda_{1}^{A}}\left(\hat{a}^{k}S_{12}^{A}+\hat{a} ^{\dagger k}S_{21}^{A}\right) +{\lambda_{2}^{A}}\left(\hat{a}^{k}S_{23}^{A}+ \hat{a}^{\dagger k}S_{32}^{A}\right) =L, $$

(30)

hence

$$ L= \left(\begin{array}{ccc} 0 & \lambda_{1}\hat{a}^{k} & 0 \\ \lambda_{1}\hat{a}^{\dagger k} & 0 & \lambda_{2}\hat{a}^{k} \\ 0 & \lambda_{2}\hat{a}^{\dagger k} & 0 \end{array}\right) , $$

(31)

$$\begin{array}{@{}rcl@{}} L^{2} &=& \left(\begin{array}{ccc} (\lambda_{1})^{2}\hat{a}^{k}\hat{a}^{\dagger k} & 0 & \lambda_{1}\lambda_{2}\hat{a}^{2k} \\ 0 & (\lambda_{1})^{2}\hat{a}^{\dagger k}\hat{a}^{k}+(\lambda_{2})^{2}\hat{a }^{k}\hat{a}^{\dagger k} & 0 \\ \lambda_{1}\lambda_{2}\hat{a}^{\dagger 2k} & 0 & (\lambda_{2})^{2}\hat{a} ^{\dagger k}\hat{a}^{k} \end{array}\right) \\ &=& \left(\begin{array}{ccc} (\lambda_{1})^{2}\frac{\left(n_{1}+k\right) !}{n_{1}!} & 0 & \lambda_{1}\lambda_{2}\hat{a}^{2k} \\ 0 & \frac{(\lambda_{1}n_{1}!)^{2}+(\lambda_{2})^{2}\left(n_{1}+k\right) !\left(n_{1}-k\right) !}{n_{1}!\left(n_{1}-k\right) !} & 0 \\ \lambda_{1}\lambda_{2}\hat{a}^{\dagger 2k} & 0 & (\lambda_{2})^{2}\frac{ n_{1}!}{\left(n_{1}-k\right) !} \end{array}\right) \end{array} $$

(32)

$$ L^{3}= \left(\begin{array}{ccc} x_{1} & 0 & 0 \\ 0 & x_{2} & 0 \\ 0 & 0 & x_{3} \end{array}\right) \cdot L=DL, $$

(33)

where

$$\begin{array}{@{}rcl@{}} x_{1} &=&\left[ \frac{\left\{ \lambda_{1}\left(n_{1}+k\right) !\right\}^{2}+(\lambda_{2})^{2}n_{1}!\left(n_{1}+2k\right) !}{n_{1}!\left(n_{1}+k\right) !}\right] , \\ x_{2} &=&\left[ \frac{(\lambda_{1}n_{1}!)^{2}+(\lambda_{2})^{2}\left(n_{1}+k\right) !\left(n_{1}-k\right) !}{n_{1}!\left(n_{1}-k\right) !} \right] , \\ x_{3} &=&\left[ \frac{\left\{ \lambda_{1}\left(n_{1}-k\right) !\right\} ^{2}+(\lambda_{2})^{2}n_{1}!\left(n_{1}-2k\right) !}{\left(n_{1}-k\right) !\left(n_{1}-2k\right) !}\right] , \end{array} $$

(34)

and D is the diagonal matrix. Now, we can generalized the diagonal matrix as follows [39]

$$ L^{2j}=D^{j-1}L^{2}\text{\ \ for \ }j\geqslant 1\text{, }L^{2j+1}=D^{j}L \text{\ \ for \ }j\geqslant 0. $$

(35)

Now, we can rewrite $U_{1}\left (t\right )$ as follows

$$\begin{array}{@{}rcl@{}} U_{1}\left(t\right) &=&e^{-i\hat{H}_{I}^{A}}=e^{-iL\gamma_{1}\left(t\right) } \\ &=&\sum\limits_{j=0}^{\infty }\frac{\left(-iL\gamma_{1}\left(t\right) \right)^{2j}}{\left(2j\right) !}+\sum\limits_{j=0}^{\infty }\frac{\left(-iL\gamma_{1}\left(t\right) \right)^{2j+1}}{\left(2j+1\right) !} \\ &=&\sum\limits_{j=0}^{\infty }\left(-1\right)^{j}\frac{\left(L\gamma_{1}\left(t\right) \right)^{2j}}{\left(2j\right) !}-i\sum\limits_{j=0}^{\infty }\left(-1\right)^{j}\frac{\left(L\gamma_{1}\left(t\right) \right)^{2j+1}}{\left(2j+1\right) !} \\ &=&I+\frac{1}{D}\sum\limits_{j=1}^{\infty }\left(-1\right)^{j}\frac{\left(\gamma_{1}\left(t\right) \sqrt{D}\right)^{2j}}{\left(2j\right) !}L^{2}- \frac{i}{\sqrt{D}}\sum\limits_{j=0}^{\infty }\left(-1\right)^{j}\frac{ \left(\gamma_{1}\left(t\right) \sqrt{D}\right)^{2j+1}}{\left(2j+1\right) !}L \\ &=&I+\frac{1}{D}\left\{ -1+\cos \left(\gamma_{1}\left(t\right) \sqrt{D} \right) \right\} L^{2}-\frac{i}{\sqrt{D}}\sin \left(\gamma_{1}\left(t\right) \sqrt{D}\right) L, \end{array} $$

(36)

thus

$$\begin{array}{@{}rcl@{}} U_{1}\left(t\right) &=& \left(\begin{array}{ccc} u_{11} & u_{12} & u_{13} \\ u_{21} & u_{22} & u_{23} \\ u_{31} & u_{32} & u_{33} \end{array}\right) \\ &=& \left(\begin{array}{ccc} u_{11} & -i\lambda_{1}F_{n_{1}}\hat{a}^{k} & \lambda_{1}\lambda_{2}D_{n_{1}}\hat{a}^{2k} \\ -i\lambda_{1}S_{n_{1}}\hat{a}^{\dagger k} & C_{n_{1}} & -i\lambda_{2}S_{n_{1}}\hat{a}^{k} \\ \lambda_{1}\lambda_{2}Y_{n_{1}}\hat{a}^{\dagger 2k} & -i\lambda_{2}Z_{n_{1}}\hat{a}^{\dagger k} & r_{11} \end{array}\right) ,\end{array} $$

(37)