1 Introduction

1.1 Context

Whether private or public, healthcare service providers have an interest in planning facilities that are well-dimensioned to the demand for their services. A growing trend in systems with private healthcare providers is to encourage or induce the formation of hospital networks. Collaboration in networks could have various advantages. Some of those are the facilitation of collaborations that consolidate particular activities in order to achieve economies of scale and improve quality through specialisation, the dissemination of best practices, or increased capital investment strength Reames et al. (2019). Merging facilities is a commonly discussed topic in networks, raising the relevance of hospital location planning methodologies.

Planning capacity and evaluating the current use of capacity is challenging. Often, specific facilities are dimensioned based on the area that they are designed to service. In most systems with free choice of healthcare service providers, however, hospitals can compete for patients in areas without clearly circumscribed borders. Through the development of a reputation for operational efficiency, higher quality, better patient experience, superior pricing, or other competitive advantages, hospitals can attract patients away from competing facilities, even beyond their local operating area Noether (1988); Beukers et al. (2014). Thus, an approach where dimensioning is done by matching local expected demand with facilities does not sufficiently recognize the agency of hospitals, and their potential to grow.

In order to account for hospital agency, planning and evaluation models should integrate expected patient decision-making as driven by facility characteristics. Depending on the type of planning decision, models should aim to integrate those factors that are relevant within the timeframe in which the consequences of the decision play out. Facility location decisions will in most cases have an impact for decades. It is therefore meaningful to understand the transience of the factors used to evaluate particular locations. We can distinguish between describing patient choices for facilities as fully as possible, and describing patient choices in the context of those factors that are sufficiently stable over time to assume they are predominantly static over the economic life of the decision. At one extreme end, a model could be fitted that only includes distance decay, presuming that new hospital facilities start from an entirely level playing field. Accordingly, each hospital is equally competitive regardless of current size, accredited services, reputation, pricing, or other factors. Such an entirely geographical approach assumes full flexibility in other dimensions, aligning with a view of assumed regression to the norm of other relevant factors within the project lifetime. From a hospital director’s point of view, this type of model would inform on an optimal location assuming that all current competitive advantages and disadvantages are fleeting. Presumably though, such a bare-bones model will yield hospitals of various expected sizes. Since size itself is expected to affect attraction of a facility, either directly or as a proxy, an iterative process could be imagined in which resulting size differences are included in subsequent analysis rounds. On the other extreme end, a highly descriptive model could include many different factors that influence patients’ hospital choices. This model type would suffer from something like an inertia bias. Factors taken up in the model, such as the accredited services or number of affiliated specialists, might be volatile and subject to evolution over the economic life of location decisions. It could thus be argued that, in planning exercises, regression to the mean of these factors should be assumed, or that they should be left out of applied models, provided that their absence does not significantly bias the remaining model. Different project lifetimes or expectations concerning the change in input variable values can thus affect the variable set that should be included, or studying outcomes with different variables sets can align with different temporal perspectives on the project.

In this manner, though an important overlap exists between explaining behaviour and planning according to expected behaviour, the objectives could affect the applied model itself. In descriptive cases, most gravity-type models do not include many variables, often due to data availability constraints (De Beule et al. 2014). In general, size is the only variable aside from location-derived factors that is included, yielding a simple model such as described below (Bucklin 1971). The market share \(MS_{ij}\) of hospital j in block i is equal to the fraction of the utility of j perceived in block i out of the utility perceived of all alternative j in block i. The utility is related to a transformation of size \(S_{j}\), and decays over distance \(D_{ij}\). \(A_{ij}\) represents this decayed utility for a hospital facility j.

$$\begin{aligned} MS_{ij} = \dfrac{S_j^{\beta } D_{ij}^{-\alpha }}{\sum _{j}^{J}{A_{ij}}} \end{aligned}$$

If additional variables are added, they could take several forms. First, factors could have a symmetrical effect, in the sense that a value is related to a particular facility, and does not affect utility differently at diverse angles around the facility. Suitable examples are size, general reputation, or whether the facility was recently renovated. Asymmetrical factors could also be introduced. These are factors that can take different values for each combination of facility and region, for instance, boundary friction due to language borders, or reference rates by local general practitioners.

1.2 Relevant literature

Several model types have been used to estimate hospital admission rates in healthcare contexts, often depending on the type of objective or perspective taken. Broadly speaking, two types of perspectives are common. First, approaches that consider equal access from the patient’s point of view a primary objective. Second, approaches that consider dimensioning from the hospital’s viewpoint. In order to evaluate spatial accessibility and equity of accessibility, model types such as Floating Catchment Area (FCA) models (Zhang et al. 2021) and Kernel Density models (Spencer and Angeles 2007), cumulative opportunity models, nearest distance methods, such as Thiessen Polygons, and Huff-type models (Zhang et al. 2015) are common. Other models focus on patient choice rather than access. Fabbri and Robone (2010), for instance, analyze in and outflows from areas in the context of hospital and region characteristics. Others, such as Congdon (2000, 2001), describe the entirety of patient flows.

Fabbri and Robone (2010) focus on evaluating scale effects in the healthcare landscape, as opposed to other spatial factors in the distribution of healthcare resources. They use a Poisson Pseudo Maximum Likelihood approach to estimate the parameters, and find that technology availability and completeness, measured as the Theil index of the spread of technology within an area, yield the largest effects on patient inflows. The study reviews several diagnostic groups, and rather than modelling all admissions, it models the flows of patients that do not visit a facility in their Local Health Authority or area. They find that small and large area sizes are favourable determinants of the ability to attract inflows. Since their approach focuses on cross-border effects, it yields insight into drivers of hospital attraction, though it does not provide a model for general admissions estimation.

FCA methods generally calculate supply-to-demand metrics for particular areas. In a first step, a quantification of a supply node’s resources, such as the number of beds, is divided by the demand nodes’ need for resources, quantified with population numbers or pathology prevalence within the catchment area of the supply node. In a second step, the ratios per facility are summed up for all facilities within range for a demand node, which represents the resource accessibility of the demand node. Thus, it captures a measure of supply node utilization in the first step, and captures the supply options for a demand node in the second step. Some variants define the catchment area in more nuanced ways, with step functions over distance, or continuous decay functions reducing the weight of a supply node over a proximity metric. Some variants of these models add a third step in order to address demand overestimation problems. Demand overestimation problems for supply nodes occur since demand for a supply node in the first step is not affected by the presence of alternatives for the relevant demand nodes. In other words, it does not take into account the competitive interactions between, or realized choices for, facilities. Recently, adaptations of Floating Catchment Area models have been used to predict hospital admission patterns (Delamater et al. 2019; Bauer et al. 2020; Wang 2018).

Gravity-type models appear under various names in the literature, such as gravity models, Huff models, Multiplicative Competitive Interaction models, with minor differences in meaning. Huff showed the applicability of gravity models to trade areas, pioneering the use of such models in competitive location planning challenges (Huff 1964). Subsequently, many authors contributed to the further improvement of gravity-based methodologies and estimation methods. Nakanishi and Cooper linearized versions of gravity models, thereby increasing potential use of estimation procedures and estimator properties (Nakanishi and Cooper 1982). They refer to this type of model as a Multiplicative Competitive Interaction model. The essence of these types of models is that supply nodes exert an attraction over demand commensurate with their utility value, but that attraction decays over distance. The market share of a supply node is then the proportion of utility out of all the supply alternatives for a demand area, each supply alternative’s utility decayed according to its distance to the demand node. Various parameters can be used to quantify utility, though in practice, size is often used as the sole attraction variable due to data unavailability. Perception of utility is usually assumed to be homogeneous in a particular area, though some work has distinguished subgroups within areas and included their idiosyncrasies in one holistic model, such as Mao and Nekorchuk (2013). Advantages of gravity models are that they are intuitive, that they adopt widely use discrete choice utility theory, and they do not suffer from demand overestimation as two-step FCA-models do when applied to admissions estimation. An important disadvantage is that a lot of data is required, including data on competing nodes that is often not available.

The manner in which decay of utility occurs has been widely researched. In recent decades, exponential functions, log-logistic functions, or log-normal functions are used most commonly, as they are often shown to outcompete the power function (De Beule et al. 2014; de Mello-Sampayo 2014), which was the initial function type used by Huff and other early authors. Due to different reporting standards, it is hard to distill a prediction accuracy benchmark from the available literature for hospital facilities. In a study by Teow et al. (2018), the MAE (Mean Absolute Error) was found to be 24% of the mean of hospital admissions. Delamater et al. reported achieving a hospital visit prediction accuracy of 74%, meaning that the the choice of hospital for 74% of patients was predicted correctly. Bauer et al., using an FCA-model, reported that for about 30% of hospitals, the error of the predicted hospital admissions rate was lower than 15%. In retail context, a MAPE aggregated on destination level of 22.34% are reported by De Beule et al. (2014). In De Beule et al.’s replication of Orpana and Lampinen (2003), a MAPE of 26.78% is found.

Mao and Nekorchuk (2013) have integrated multiple travel modes into their FCA-model for hospital facility accessibility measurement. They divided the population into regions in proportion to those who use particular transport modes according to regional surveys. Similarly, Zhou et al. (2020), measured accessibility of healthcare facilities with different transportation modes. No admission rate prediction models in hospital facility context have made use of multiple transportation mode data as far as the authors could ascertain.

Only a subset of the literature in hospital facility planning is interested in estimating the number of admissions in a competitive context. At the root of this are diverging research objectives. First, measuring accessibility does not require it, nor do related models unambiguously suggest expected patient admissions. Second, hospitals in some healthcare systems do not compete for patients. Rather, policymakers plan which area a hospital serves. It therefore makes sense that not all of the literature and models in the domain report admissions estimation accuracy. For the limited number that does, the reported accuracy is measured in various ways, and hard to directly compare with each other. Our work focuses on providing models that improve on the accuracy of currently reported models in the context of competitive hospital systems. Accordingly, the accuracy of our models is analysed and reported varying three different components of the model. Concretely, distance decay specifications, the impact of different transportation modes, and different patient populations, i.e. daycare and inpatient admissions in different age groups, are compared.

1.3 Objectives

The central objective of this research is to improve the methods at the disposal of policymakers and hospital administrators to optimize hospital facility location decisions. Improving accuracy of models is a primary component of that. This research reviews improvements by examining three aspects of location planning with gravity models. First, this paper intends to improve the accuracy of admission estimates of hospital facilities by identifying the best modeling methods to capture geographical impedance. Second, this paper looks into the effects of accessibility by car and public transport on the choice of patients for particular hospitals. Third, the differences in geographical impedance for inpatient and daycare hospitalizations are compared, as well as differences between age groups.

2 Methodology

One of the primary points of investigation in this work is how proximity is best modelled in gravity models in the hospital context. Different proximity proxy variables are reviewed: network car travel time, great-circle distance, and a combination of both. Additionally, it is reviewed whether accessibility by public transport can create a competitive advantage for a hospital facility. All mass transit modes available in the considered region are taken into account. Differences in model estimates between inpatient and daycare facilities are reported, as well as between age groups.

2.1 Model description

2.1.1 Geographical impedance

A function is defined that represents the reduction of the utility of a hospital perceived by a patient, or geographical impendance, as proximity decreases. Proximity is a latent concept in the mind of an individual, conjectured to be a function of physical distance, travel time, experience, and other geographical characteristics that might inhibit or improve perceived access or closeness to a location. In this study, proximity to a hospital facility is calculated for the centerpoint of each sector, which is a granular spatial subdivision that generally corresponds in size to a small neighbourhood in urban or suburban environments.

Several approaches to modelling geographical impedance have been suggested in gravity-type models. Most prominently power functions, exponential functions, and log-logistic functions. Exponential and log-logistic functions have often been found to produce the best goodness of fit (De Beule et al. 2014; de Mello-Sampayo 2014). The models in this paper use an exponential function, prefering its parsimony and potential to be linearized over the log-logistic function. Additionally, different proxies for proximity are tested. First, great-circle distance \(D_{ij}\), second, network travel times by car based on maximum allowed segment speeds \(CTT_{ij}\), and third, a combination of the two \(DT_{ij}\), Table 1. Network travel times are calculated using the open source r5 engine (Byrd 2021). Any origin-destination combination for which no route is found is replaced by the expected car travel time assuming an average speed in terms of great-circle distance covered. Since transit coverage is incomplete to a significant degree and it is not expected to be the dominant transport mode, it is not used as a factor of proximity. Nonetheless, above or below-average transit accessibility is included as an asymetrical attraction factor, described in more detail in the subsection on attractors.

Table 1 Proxies of proximity used in the models
Full size table

A distinction is made between university hospitals and general hospitals. A multiplicative attraction variable \(UNI_{j}\) is added to the model which takes the value 1 for general hospitals and 2 for university hospitals. In conjunction, a separate distance decay parameter DU is applied to university hospital facilities rather than the decay parameter DF for the decay factor for regular facilities. University hospitals have an audience that only partially overlaps with that of general hospitals. For highly specialized care, patients are often referred to university hospitals. For more common procedures or pathologies, it is possible that patients are rather discouraged from visiting university hospitals. It is hypothesized that this behaviour could be modelled with a lower attraction for university hospitals generally, but combined with a lower distance decay of that utility. Ideally, if patients who could only have been treated in university hospitals could be empirically identified, a model would distinguish that subgroup of patients.

Introducing the distinction for university hospital facilities leads to the following model, with \(V_{ij}\) as the volume of patients from block i that choose hospital j, and \(P_{i}\) the number of patients that require care in block i. \(A_{ij}\) is the utility of alternative j perceived in block i.

$$V_{{ij}} = {\text{ }}\frac{{S_{j}^{\beta } UNI_{j}^{\eta } \times (isUni \times e^{{ - D_{{ij}} \times DU}} + (1 - isUni) \times e^{{ - D_{{ij}} \times DF}} )}}{{\sum\nolimits_{j}^{J} {A_{{ij}} } }} \times P_{i}$$

where\(V_{ij}\)= Volume of patients from block i that choose hospital j

2.1.2 Accessibility

Aside from size in terms of accredited beds \(S_{j}\), the basic attractor included in the model, two variables are introduced that are a measure of accessibility: relative car access speed \(DR_{ij}\) and relative public transport access speed \(TR_{ij}\). Both are measured by taking the average speed of travel on the network over the great-circle distance, divided by the mean of that metric for the relevant block i. The great-circle distance is used because it provides the shortest theoretical route across the planet’s surface between the origin and destination as a reference. These metrics are hypothesized to capture relative utility of accessibility by car and public transport modes.

2.2 Model estimation

In order to estimate the model, it is first linearized. A linearization of the standard Multiplicative Competitive Interaction Model is given by Nakanishi and Cooper (1982). An adaptation of this procedure is followed to linearize the MCI-model with exponential distance decay. Size \(S_j\) is the only attraction factor used in the following linearization for brevity. Other attraction factors are treated analogously.

$$\begin{aligned} V_{ij} = \dfrac{S_j^{\beta } e^{-D_{ij} \times DF}}{\sum _{j}^{J}{A_{j}}} \times V_i \end{aligned}$$
(1)

Take logarithm.

$$\begin{aligned} \log V_{ij}= \beta \log S_{j} - D_{ij} DF + \log V_i - \log (\sum _{j}^{J} S_j^{\beta } \exp (-D_{ij} \times DF)) \end{aligned}$$
(2)

Sum over j and divide by n = number of j’s.

$$\begin{aligned} \begin{aligned} \frac{1}{n} \sum _{j}^{J} \log V_{ij} =&\beta \frac{1}{n} \sum _{j}^{J} \log S_{j} - \frac{1}{n} \sum _{j=1}^{J} D_{ij} DF + \frac{1}{n} \sum _{j}^{J} \log V_i \\&- \frac{1}{n} \sum _{j}^{J} \log (\sum _{n=1}^{J} S_j^{\beta } \exp (-D_{ij} \times DF)) \end{aligned} \end{aligned}$$
(3)

The three last members can be simplified. They are respectively: the mean of \(D_{ij}\) over j, the mean of a constant \(log V_j\), and the mean of a constant \(\log (\sum _{j}^{J} S_j^{\beta } \exp (-D_{ij} \times DF))\). Additionally, for the members where a logarithm remains, the summation can be moved into the logarithm, yielding a multiplication.

$$\begin{aligned} \log \prod _{j}^{J} V_{ij}^{\frac{1}{n} }= \beta \log \prod _{j}^{J} S_{j}^{\frac{1}{n}} - \overline{D_{ij}} DF + \log V_i - \log (\sum _{n=1}^{J} S_j^{\beta } \exp (-D_{ij} \times DF)) \end{aligned}$$
(4)

With geometric mean \({\tilde{x}} = \prod _{j}^{J} x^{\frac{1}{n}}\).

$$\begin{aligned} \log \tilde{V_{ij}}= \beta \log \tilde{S_{j}} - \overline{D_{ij}} DF + \log V_i - \log (\sum _{n=1}^{J} S_j^{\beta } \exp (-D_{ij} \times DF)) \end{aligned}$$
(5)

The last member can be replaced based on equation (2), finally yielding

$$\begin{aligned} \log \frac{V_{ij}}{\tilde{V_{ij}}}= \beta \log \frac{S_j}{\tilde{S_{j}} } - DF\times (\overline{D_{ij}} - D_{ij}) \end{aligned}$$
(6)

The model, which is linear in the parameters, is then optimized using Non-Linear Least Squares (NLLS). The optimization is done in Python using the Scipy package.

2.3 Application context

The application in this paper is based on market share data of hospitals in Belgium. The data spans all Belgian hospitals for the year of 2018. The number of beds per campus and admissions per hospital are made available by the Federal Public Service for public health (Volksgezondheid 2021). Travel times are calculated with the R5 engine using OpenStreetMap data for the road network and open GTFS data dated 02-02-2021 for public transportation Transitfeeds (2021). The geographic area covered by the models is most of Flanders, Belgium, with the exception of the Brussels region and Antwerp. The former is not included due to expected language border effects. The latter is not included due to a data quality issue. The market share data is available on the hospital level, and not on the campus level. In response, for campuses that belong to multi-campus hospitals, expected campus market shares are derived from the consolidated hospital market shares. Regardless of location, a market share weighted according to the number of beds is allocated to the campus. The Antwerp region is dominated by one large multi-campus hospital, and is excluded because of this data quality issue. In Flanders, 8 082 blocks are within scope, and 73 hospital campuses. In total, 690 869 inpatient stays are included, and 902 197 daycare stays. Combinations of hospitals campus j and block i are excluded if their great-circle distance is larger than 50 kilometers. This is done to limit redundant computation for combinations of hospitals and locations where the empirical market shares are generally negligible.

3 Results

In this section, the results of the different models are discussed. First, variations on modelling proximity are described. Second, parameter values for different patient subgroups are elaborated on. Third, the overall accuracy of the model is reviewed.

3.1 Proximity modelling

3.1.1 Geographical impedance

In this section, the different ways of modelling geographical impedance are reviewed. Table 2 shows the performance of the model using different metrics for proximity. In all regions, the minimized Least Squares Error (LSE) is lowest when the great-circle distance \(D_{ij}\) is used as decay factor. Car travel time \(TTC_{ij}\) always yields the highest LSE, while the combination scores in between the two \(DT_{ij}\), with an exception for East-Flanders. The Mean Absolute Percentage Error does not follow this pattern entirely. Where the great-circle distance model MAPE is worse than one of the others, the difference is minor. Note that the model is not minimized on the MAPE error metric.

Table 2 Error metrics for basic models with various proximity quantifications. *Models without university-related factors, since the regions do not have university hospitals
Full size table

3.1.2 Accessibility attractors

The findings in the previous section indicate that the great-circle distance is the best metric for proximity in this context. Nonetheless, it is hypothesized that above-par accessibility improves the likelihood that a patient will choose a hospital facility. Accordingly, metrics of accessibility are included as multiplicative factors that determine perceived relative utility. Two factors are added: relative car accessibility \(DR_{ij}\) and relative transit accessibility \(TR_{ij}\). Table 3 shows the efficacy of models that include accessibility metrics. The optimized exponents \(\chi\) and \(\phi\) of the accessibility metrics are close to zero in most cases. The transit accessibility exponent \(\chi\) is zero in West-Flanders and the transit accessibility exponent is low, but positive. In East-Flanders, Limburg, and Flanders as a whole, both accessibility metrics yield mildly positive exponents.

Table 3 Fitted exponents of relative car and transit accessibility and related accuracy metrics for Flanders and subregions
Full size table

3.2 Subgroup comparisons

3.2.1 Age groups

In accordance with Jia et al. (2019), an increased distance decay effect is found in older age groups. The exponent of the size attractor \(\beta\) similarly increases along with size as shown in Table 4. For the youngest age group, children up to the age of 15, this might be related to the absence of dedicated pediatric facilities in some hospitals.

Table 4 Fitted distance decay and size parameters for model in Flanders per age group for inpatient hospitalization
Full size table

3.2.2 Hospital types

Table 5 Fitted distance decay parameters and MAPE for inpatient and daycare patient admissions
Full size table

In this section, differences in results between inpatient and daycare hospital types are examined. It is reviewed whether the fitted parameter that captures the degree of distance decay is higher for daycare hospitalizations. Table 5 does not indicate that a consistent difference exists in the distance decay parameter for inpatient and daycare hospitalizations. Though the fitted parameter is lower for daycare in Flanders as a whole, 0.1346 versus 0.1515 for inpatient care, this does not hold up for the subregions. In West-Flanders, fitted distance decay is lower for daycare hospitalizations than for inpatient hospitalizations.

3.3 Model accuracy

Table 6 shows the results of the best-fitting model for the different subregions of Flanders. The model fits the data better in rural areas, or areas where no competing hospitals are in close proximity to one another. The range of MAPE values is between 9.59% and 17.76%. For the entirety of Flanders excluding Antwerp and Brussels, the MAPE is 14.39%. The models for daycare admissions perform similarly, with the best performance in West-Flanders with a MAPE of 9.28% and the worst in East-Flanders with a MAPE of 24.99%. Using the great-circle distance as a distance decay parameter systematically outperforms the use of travel time, or combinations of both.

Table 6 Fitted inpatient admission model parameters and MAPE for Flanders and subregions
Full size table

4 Discussion

4.1 Modelling proximity and accessibility

The proxy of proximity that performs best is the great-circle distance. Several hypotheses could help explain this result. First, car travel time might not be an important factor in the perception of proximity to facilities for patients. Perhaps, due to infrequent exposure, patients do not even have a clear image of the relative travel times between options, but they do have a geographical sense of where a facility is positioned in space. Especially in cases where heavy traffic inverts the ranking of two destinations when considering distance versus travel time, it could require repeated exposure by a person to establish this aspect of proximity in his or her perception. While consumers might have a clear perception of travel times to destinations such as retail locations due to the frequency of their visits, the same might not be true for hospital facilities. It could also be that accessiblity is less important to patients, and that distance measures function as a proxy for general exposure to facilities themselves, rather than their accessibility.

Selective perception theory provides a framework for these types of explanations (Taylor et al. 2006). Selective perception theory proposes that not all information that people are exposed to is processed and retained equally. Selective perception is characterized as a four-part process of selective exposure, attention, comprehension, and retention. Pre-selection due to a lack of repeated exposure might be more strongly related to great-circle distance than to car travel times, since exposure in the broad sense comes through various channels, such as local news, word-of-mouth, or through doctors’ references.

Lastly, it might be the proximity of the referring doctor to hospital facilities that is most crucial. It is not self-evident which of variables considered in this research would be the best proxy for that type of proximity.

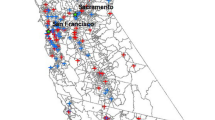
The models in which accessibility attractors are included do not provide strong evidence that either relative car or transit accessibility improve the likelihood that a patient will visit a particular facility. Since an active effort is made to connect all hospitals by public transport, a lower treshold of connection might be reached by most hospitals, removing any competitive advantages. This seems quite unlikely, however. Since relative accessibility is measured on the sector-level, it is improbable that each competing hospital could provide similar public transport accessibility to each sector. Alternatively, it is possible that proximity, as measured by the great-circle distance, is a proxy that works well to capture transit accessibility, so that relative transit accessibility does not provide any additional explanatory power. Lastly, the quantification of transit accessibility might interfere with other biases of the model. Relative driving accessibility (Fig. 1) and transit accessibility (Fig. 2) are usually highest from and between urban centers. Given this correlation, the specification of the model implies generally that a hospital’s perceived utility is higher for patients living in an urban area than for those living in rural areas. Given the expected underestimation of the distance decay parameter and that hospitals are primarily located in urban areas, it would be expected that absolute hospital patient numbers are mostly overestimated in surrounding urban cores, which implies an inverse relationship to the one expected by the accessibility quantification. A better quantification of relative accessibility would be the relative accessibility as compared to the mean of the accessibilities of other facilities for the sector, rather than the general mean.

Fig. 1
figure 1

Relative driving accessibility of campus in Lokeren. Accessibility is correlated with origin urbanization, which might interfere with biases of the model

Full size image
Fig. 2
figure 2

Relative transit accessibility of campus in Lokeren. Accessibility is correlated with origin urbanization, which might interfere with biases of the model

Full size image

4.2 Subgroups

In line with results by Jia et al. Jia et al. (2019), distance decay is found to be positively correlated with age. Older patients tend to travel less far to be hospitalized. This might be explained by a couple of reasons. First, older patients might attach a higher cost to travel, either because of increased perceived discomfort or fewer or different transportation modes at their disposal. Alternatively, a higher proportion of patients might be hospitalized through the emergency department, perhaps brought in by ambulance, with little choice or time to choose a hospital. For the youngest age group, children younger than 15, the lower distance decay might be due to the absence of dedicated pediatric wards at a subset of facilities, causing them to travel further than they would otherwise.

It was hypothesized that distance decay would be lower for inpatient hospitalizations than for daycare hospitalizations. Inpatient hospitalizations are expected to be more severe than daycare hospitalizations. Additionally, inpatient hospitalizations are longer, so the transportation costs should be relatively less important. Nonetheless, the fitted parameters do not show a consistent relationship between the type of hospitalization and distance decay.

4.3 Accuracy

The overall accuracy of the models is high, ranging from around 10% in rural areas to 17% in urban environments. This compares well to other work. Few other studies have reported error metrics that allow a direct comparison, though Teow et al. (2018) have reported a Mean Absolute Error of 24% of the mean of hospital admissions and Bauer et al. (2020) have reported achieving a percentage error of 15% or better for about 30% of the scoped hospitals. In retail models, which admittedly work at a more granular scale, De Beule et al. (2014) reported a MAPE of 22.34%. In this study, using the great-circle distance as the decay factor systematically yields better results than using car travel time, or combinations of car travel time and great-circle distance. In addition, models that include public transport accessibility metrics do not systematically perform better than those that do not. It is further observed that admission prediction accuracies are generally better in the 15–64 age group, and that prediction accuracy is not systematically higher in daycare or inpatient hospitalization types.

5 Conclusion

Variants of a linearized gravity model with an exponential decay function is proposed in this paper. The models show that achieving an admissions estimation accuracy of up to 9.59% on average is possible using the proposed gravity models. Using the great-circle as distance decay factor systematically outperforms the use of travel time or combinations of travel time and great-circle distance. It is also found that including public transport accessibility in the models did not improve their accuracy.

6 Summary and future work

This paper describes the main findings of an effort to build gravity-type models to describe patient choices in inpatient and daycare hospital facilities. It analyzes the distance decay effects as a function of car travel times and great-circle distance, and it offers a method for inclusion of university hospitals. Additionally, it reviews the impact of driving and transit accessibility on hospital attraction and reviews the differences in distance decay for patient age groups and hospitalization types.

An issue with using size in the model is the introduction of an endogenous element. Size in terms of beds is evidently a proxy for attraction-inducing factors, as well as a consequence of the number of admissions that were processed historically. When building a new hospital campus, the projected number of beds might not fairly capture the effect of the factors that size is a proxy for, as it presumably does for established campuses. For instance, size could be a proxy for exposure through word-of-mouth. More treatments mean more opportunities to be exposed to a treated person in your network. For a new hospital campus, this effect cannot be captured since size is, at the time of the analysis, an unrealized number and not yet a strong proxy for the number of treatments performed. A 2-Stage Least Squares (2SLS) (Terza et al. 2008) estimation approach might address this issue. Additionally, a model that makes recursive use of the size parameter might yield insight into the determinism of the location factor in hospital success.

A common issue in gravity models is a lack of complete data for all involved destinations. In this project as well, attractor variables were left out of the models due to unavailability for particular hospitals. A model with dummies might be able to handle the unavailability of data for a subset of hospitals, while using as much of the available data as possible.