Strong gravitational lensing by regular electrically charged black holes

Abstract

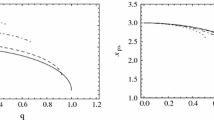
In nonlinear electrodynamics a photon does not follow null geodesics of background geometry, but moves along null geodesics of a corresponding effective geometry. Therefore, in the strong deflection limit, in order to study the gravitational lensing of the regular electrically charged black holes obtained by coupling general relativity to nonlinear electrodynamics, one should firstly obtain the corresponding effective geometry, which is a necessary and key step. I obtain the deflection angle of the photon in the strong deflection limit, and further calculate the angular position and magnification of relativistic images. It is found that, the electric charge has significant effect on the gravitational lensing of regular black holes. With the increase of the electric charge q, the angular position of the relativistic images $\theta _{\infty }$ and the relative magnification $\mathcal {R}_{m}$ as a function of q decrease, while the angular separation between the outermost relativistic image and the others $\mathcal {S}$ as a function of q increases. I also discuss the measurement of observables for the black hole at the center of our Galaxy in the cases of regular electrically charged black hole effective metrics.

Appendix A: Calculation of the deflection angle in the SDL

We define variable [16, 27]

$$\begin{aligned} z=1-\frac{x_{0}}{x}. \end{aligned}$$

(44)

The integral $I(x_{0})$ becomes

$$\begin{aligned} I(x_{0})=\int _{0}^{1}R(z,x_{0})f(z,x_{0}), \end{aligned}$$

(45)

where

$$\begin{aligned} R(z,x_{0})= & {} \frac{2x^{2}\sqrt{A(x)B(x)C_{0}}}{x_{0}C(x)}, \end{aligned}$$

(46)

$$\begin{aligned} f(z,x_{0})= & {} \frac{1}{\sqrt{A_{0}-A(x)\frac{C_{0}}{C(x)}}}. \end{aligned}$$

(47)

Here, it should be stressed that the functions without the subscript 0, A(x), B(x) and C(x) are evaluated at $x=\frac{x_{0}}{1-z}$. $R(z,x_{0})$ is regular for all values of z and $x_{0}$, while $f(z,x_{0})$ is divergent for $z\rightarrow 0$. In order to find the order of the divergence of (45), we expand the argument of the square root in $f(z,x_{0})$ to the second order in z:

$$\begin{aligned} f(z,x_{0})\sim f(z,x_{0})=\frac{1}{\sqrt{\zeta z+\chi z^{2}}}, \end{aligned}$$

(48)

where

$$\begin{aligned} \zeta= & {} \frac{x_{0}}{C_{0}}(A_{0}C'_{0}-A'_{0}C_{0}), \end{aligned}$$

(49)

$$\begin{aligned} \chi= & {} \frac{x_{0}}{2C^{2}_{0}}\bigg [(2C_{0}C'_{0}+x_{0}C_{0}C''_{0}-2x_{0}C'^{2}_{0})A_{0}\nonumber \\&+\,(2x_{0}C'_{0}-2C_{0})C_{0}A'_{0}-x_{0}C^{2}_{0}A''_{0}\bigg ]. \end{aligned}$$

(50)

(49) clearly shows that $\zeta$ vanishes at $x_{0}=x_{m}$, so $f(z,x_{0})\propto \frac{1}{z}$ and $I(x_{0})$ (and consequently the deflection angle $\alpha (x_{0})$) diverges logarithmically. Then, following Ref. [16], we split (45) into two pieces

$$\begin{aligned} I(x_{0})=I_{D}(x_{0})+I_{R}(x_{0}), \end{aligned}$$

(51)

where $I_{D}(x_{0})$ is divergent, while $I_{R}(x_{0})$ is regular. They are

$$\begin{aligned} I_{D}(x_{0})= & {} \int _{0}^{1}R(0,x_{m})f_{0}(z,x_{0})dz , \end{aligned}$$

(52)

$$\begin{aligned} I_{R}(x_{0})= & {} \int _{0}^{1}g(z,x_{0})dz, \end{aligned}$$

(53)

where

$$\begin{aligned} g(z,x_{0})=R(z,x_{0})f(z,x_{0})-R(0,x_{m})f_{0}(z,x_{0}). \end{aligned}$$

(54)

$I_{D}(x_{0})$ can be evaluated exactly as

$$\begin{aligned} I_{D}(x_{0})=R(0,x_{m})\frac{2}{\sqrt{\chi }}\log \frac{\sqrt{\chi }+\sqrt{\zeta +\chi }}{\sqrt{\zeta }}. \end{aligned}$$

(55)

We further expand $\zeta$ in powers of $(x_{0}-x_{m})$, getting

$$\begin{aligned} \zeta =\frac{2\chi _{m}}{x_{m}}(x_{0}-x_{m})+\mathcal {O}(x_{0}-x_{m})^{2}, \end{aligned}$$

(56)

where

$$\begin{aligned} \chi _{m}=\frac{x^{2}_{m}}{2C_{m}}(A_{m}C''_{m}-A''_{m}C_{m}). \end{aligned}$$

(57)

Substituting (56) and (57) into (55), we get

$$\begin{aligned} I_{D}(x_{0})=-a\log \bigg (\frac{x_{0}}{x_{m}}-1\bigg )+b_{D}+\mathcal {O}(x_{0}-x_{m}), \end{aligned}$$

(58)

where

$$\begin{aligned} a= & {} \frac{R(0,x_{m})}{\sqrt{\chi _{m}}}, \end{aligned}$$

(59)

$$\begin{aligned} b_{D}= & {} \frac{R(0,x_{m})}{\sqrt{\chi _{m}}}\log 2. \end{aligned}$$

(60)

We can also expand $g(z,x_{0})$ in powers of $(x_{0}-x_{m})$ to get

$$\begin{aligned} g(z,x_{0})=\sum _{n=0}^{\infty }\frac{1}{n!}(x_{0}-x_{m})^{n}\frac{\partial ^{n}g}{\partial x^{n}_{0}}\bigg |_{x_{0}=x_{m}}. \end{aligned}$$

(61)

Substituting (61) into (53), and just retaining the $n=0$ term, leads to

$$\begin{aligned} I_{R}(x_{0})=\int _{0}^{1}g(z,x_{m})dz+\mathcal {O}(x_{0}-x_{m}). \end{aligned}$$

(62)

Expanding (20), we get

$$\begin{aligned} u-u_{m}=c_{2}(x-x_{0})^{2}, \end{aligned}$$

(63)

where the coefficient $c_{2}$ is

$$\begin{aligned} c_{2}=\frac{C''_{m}A_{m}-C_{m}A''_{m}}{4\sqrt{A^{3}_{m}C_{m}}}=\frac{\chi _{m}}{2x^{2}_{m}}\sqrt{\frac{C_{m}}{A^{3}_{m}}}. \end{aligned}$$

(64)

Using (63), (64) and $\theta \approx \frac{u}{D_{OL}}$, we can finally express the deflection angle as a function of $\theta$ as

$$\begin{aligned} \alpha (\theta )=-\bar{a}\log \bigg (\frac{\theta D_{OL}}{u_{m}}-1\bigg )+\bar{b}+\mathcal {O}(u-u_{m}), \end{aligned}$$

(65)

where

$$\begin{aligned} \bar{a}= & {} \frac{R(0,x_{m})}{2\sqrt{\chi _{m}}} , \end{aligned}$$

(66)

$$\begin{aligned} \bar{b}= & {} -\pi +b_{R}+\bar{a}\log \frac{2\chi _{m}}{A_{m}}, \end{aligned}$$

(67)

where $b_{R}$ is defined as

$$\begin{aligned} b_{R}=I_{R}(x_{m})=\int _{0}^{1}g(z,x_{m})dz. \end{aligned}$$

(68)

[See (62)].