1 Introduction

During the last decades, extensive research, both theoretical and experimental, was carried out in order to investigate the different parameters affecting the cracking behaviour of fibre-reinforced concrete (FRC) structural elements.

Considering a FRC beam subjected to bending, several experimental studies suggest describing the flexural response, usually represented in terms of the applied load vs deflection diagram, by sub-dividing it into three different stages (Fig. 1). The structural behaviour starts with a linear ascending branch (Stage I), until the onset of the fracturing process. From this point onwards, the post-cracking regime (Stage II) takes place, which depends, among other parameters, on the fibre volume fraction, Vf. A deflection-softening or deflection-hardening behaviour can be observed, leading to the definition of the so-called minimum (or critical) fibre volume fraction, Vf,min, which is required to guarantee a stable post-cracking branch. The latter occurs when the maximum load experienced by the specimen, i.e., the load bearing capacity, is equal to or greater than the applied load at the onset of crack propagation. On the contrary, if the fibre volume content is not sufficiently high, i.e., Vf < Vf,min, this intermediate stage may not develop. Finally, the flexural response is described by a descending tail (Stage III) of the load vs deflection curve, which represents the fibre pull-out or rupture.

Fig. 1
figure 1

Typical experimental load vs deflection curves of FRC beams

Full size image

In this framework, different experimental investigations carried out so far indicate that the flexural performance of FRC specimens is affected by: (i) the fibre volume fraction, Vf (Almusallam et al. 2016; Barr et al. 2003; Barros and Sena Cruz 2001; Barros et al. 2005; Bencardino et al. 2010; Fantilli et al. 2016; Holschemacher et al. 2010; Mobasher et al. 2014; Naaman 2008; Soetens and Matthys 2014); (ii) the mechanical and geometrical properties of the reinforcing fibres (tensile strength, geometric profile, and aspect ratio) and of the cementitious matrix (Aydin 2013; Choi et al. 2019; Sahin and Koksal 2011; Yoo et al. 2015); (iii) the specimen size (Flàdr and Bily 2018; Jones et al. 2008; Paschalis and Lampropoulos 2015; Yoo et al. 2016).

In the latter case, recent experimental studies show a systematic decrease in the composite flexural strength—calculated with an elastic approach—by increasing the specimen size (Flàdr and Bily 2018; Paschalis and Lampropoulos 2015; Yoo et al. 2016). This geometric effect, which can be also related to the fibre distribution within the volume of the composite (Lo Monte and Ferrara 2020), can be quantitatively evaluated in the framework of Fracture Mechanics by using the Multi-fractal Scaling Law (MFSL) for initially uncracked specimens (Carpinteri 1994), or the Size Effect Law (SEL) for initially cracked specimens (Bažant 1984). These best-fitting laws were extensively discussed in the case of quasi-brittle materials.

The scale effects are also taken into account in the latest RILEM Recommendations (RILEM TC 162-TDF 2003) for the design of FRC structures, where the residual flexural stresses (evaluated at a specific crack mouth opening displacement, CMOD) are adjusted by a coefficient, which decreases with the increase in the specimen size.

In the present paper, size effects on the global post-cracking behaviour of FRC beams are investigated in the framework of Fracture Mechanics by means of the Updated Bridged Crack Model (UBCM). This model, originally proposed for steel-bar reinforced concrete elements (Carpinteri 1981, 1984a, b), has been adapted by some of the authors to the case of brittle-matrix fibrous composites subjected to bending (Bosco and Carpinteri 1995; Carpinteri and Massabò 1996, 1997a, b; Carpinteri and Puzzi 2007; Carpinteri and Accornero 2019, 2020). More recently, further applications of the model to the case of FRC beams have been discussed in Accornero et al. (2020, 2022a, b) and Rubino et al. (2021). In this work, the focus is on the scale-dependent post-cracking regimes predicted by the model, as a function of two dimensionless numbers, NP and Nw. Moreover, the critical value of the reinforcement brittleness number, NPC, allows for prediction of the minimum (critical) fibre volume fraction (Rubino et al. 2021), Vf,min, or, equivalently, the critical specimen size, hmin, required to guarantee a stable post-cracking response. In the following sections, the main features of the model will be recalled, and the related numerical predictions will be validated on the basis of experimental data reported in the scientific literature.

2 The Updated Bridged Crack Model (UBCM)

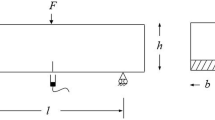
Considering a FRC beam element subjected to flexural loading, the model is able to describe the evolution of the fracturing process occurring in a notched rectangular cross-section where the damage is localized. The cross-section is characterized by the thickness, b, the depth, h, the initial edge crack depth, a0, and it is subjected to an external bending moment, M (Fig. 2).

Fig. 2
figure 2

Fibre-reinforced brittle-matrix beam model

Full size image

On the left of Fig. 3, a schematic of the notched cross-section subjected to bending is reported. Experimental evidences lead to identify the following four regions: (i) ligament in compression; (ii) uncracked ligament in tension; (iii) fibre bridging zone, in which the reinforcing fibres bridge the crack; (iv) stress-free crack zone—generally noticeable for large crack depths or very short fibres—where the bridging action of the fibres has vanished.

Fig. 3
figure 3

Critical cross-section of FRC beams with the stress distribution predicted by the UBCM

Full size image

These regions can be effectively interpreted in the UBCM. The model assumes the composite as a bi-phase material, in which the brittle matrix and the reinforcing fibres represent its primary and secondary phase, both contributing to the global toughness. The matrix is assumed to be linear elastic, being neglected other nonlinear contributions (nonlinear tensile and compression behaviours). In agreement with Linear Elastic Fracture Mechanics (LEFM), a singular stress distribution is predicted at the crack tip (see the right part of Fig. 3), and the matrix toughening contribution is defined by its fracture toughness, KIC.

On the other hand, the bridging mechanism of the secondary phase can be described by an appropriate cohesive softening constitutive law, which takes into account the progressive slippage of the fibre inside the matrix. The corresponding toughening contribution relates to the energy required to pull-out a single fibre and it is predominant if compared to that of the matrix.

In the framework of UBCM, the bridging action of the reinforcing fibres can be modelled by means of a discontinuous (discrete) formulation or a continuous one, which have been discussed in Carpinteri and Massabò (1997a). In the present investigation, the discontinuous version of the model is taken into account, for which the reinforcing fibres are considered as discrete entities. This assumption requires the following information: (i) the number of fibres in the critical cross-section under investigation; (ii) the position of the fibres; (iii) the bridging force of each fibre.

The total number of fibres in the cross-section, n, can be calculated as n = α Vfbh/Af, where Af is the cross-sectional area of the single fibre, and α the orientation factor. The coefficient α is defined as the ratio of the actual number of fibres in the critical section—obtained by investigating the specimen fracture surface—to the theoretical one (Robins et al. 2003).

Regarding the fibre position, they are considered evenly spaced in the ligament area, each one characterized by the corresponding level arm, hi, measured with respect to the bottom edge of the beam (see Fig. 2 and the right part of Fig. 3). The model disregards other factors that can affect the actual distribution of the fibres in the specimen volume, such as the casting procedure, wall effect, etc.

The m < n fibres crossing the actual crack are considered as active and their bridging action is taken into account by the closure forces, Fi, calculated as Fi = βi σs Af, in which σs is the nominal stress of the i-th reinforcing fibres adjusted by a coefficient βi. The latter is useful to define an equivalent stress acting in the fibre, which includes other phenomena as the “group effect” (the maximum pull-out force per fibre decreases as the number of fibres increases) and the “snubbing effect” (the maximum pull-out force changes due to the fibre orientation with respect to the applied load) (Li et al. 1990). The influence of these two parameters related to the fibre distribution, α and β, will be discussed later in the paper.

Under these assumptions, the singular crack-tip stress field is uniquely characterized by a global stress-intensity factor, KI:

$$ K_{{\text{I}}} = K_{{{\text{IM}}}} - \mathop \sum \limits_{i = 1}^{m} K_{{{\text{I}}i}} = \frac{M}{{bh^{3/2} }}Y_{{\text{M}}} - \frac{{\left\{ {Y_{{\text{F}}} } \right\}^{{\text{T}}} \left\{ F \right\}}}{{bh^{1/2} }}, $$
(1)

in which the contributions related to the applied bending moment, KIM, and to the i-th reinforcing fibre, KIi, appear. In agreement with the LEFM criterion, the crack propagation occurs when the stress-intensity factor, KI, reaches its critical value, KIC, i.e. the fracture toughness of the plain matrix (unreinforced material).

The bridging forces provided by the m active reinforcing layers can be calculated by means of a cohesive softening constitutive law, which takes into account the slippage mechanism of the fibres from the cementitious matrix. The latter is typically investigated by means of pull-out tests carried out on the single fibre. Namely, the pull-out response of a short fibre in a cementitious matrix depends on several factors, among which the fibre material (steel, polypropylene, natural, etc.), the fibre geometry (straight, crimped, twisted, with hooked ends, etc.), the orientation of the fibre with respect to the pull-out load, and the fibre embedment length (Abdallah et al. 2018).

In the following, the pull-out laws are defined for steel fibres characterized by straight or hooked-end profiles. In addition, the fibre is considered as aligned with respect to the applied load, and slippage is the main bridging mechanism. The fibre rupture, which usually occurs in the case of high orientation angle (Robins et al. 2002), or high-strength matrices coupled with low resistance fibres (Aydin 2013; Choi et al. 2019; Sahin and Koksal 2011; Yoo et al. 2015), is here excluded.

Under these assumptions, the pull-out response of a straight fibre is characterized by an initial ascending branch in which the bonding mechanism is due to the chemical adhesion between the fibre and the surrounding concrete. When the fibre is completely debonded and the pull-out strength is reached, the response is governed by the frictional mechanism, leading to a decrease in the slippage load until the fibre is entirely pulled-out from the matrix (Abdallah et al. 2018).

On the other hand, the pull-out response of an hooked-end steel fibre is characterized by an intermediate stage which reflects the mechanical interlocking of the fibre hooks. With respect to a straight fibre, this additional mechanism leads to an increase in the maximum pull-out load and to a variation in the shape of the constitutive law, which is now characterized by two horizontal plastic plateaux corresponding to the hook straightening (Alwan et al. 1999).

Therefore, two different constitutive laws have been implemented in UBCM (Fig. 4). In both cases, the constitutive law is defined by two parameters: (i) the slippage strength of the fibre, \({\sigma }_{\mathrm{s},\mathrm{max}}\), beyond which the fibre pull-out starts; (ii) the fibre embedment length, wc, beyond which the fibre bridging action is exhausted. The area subtended by the bridging laws represents the contribution of the reinforcing fibres to the global toughness of the composite.

Fig. 4
figure 4

Slippage law per unit embedded length: a straight fibre; b hooked-end fibre

Full size image

Considering the experimental investigation reported in the literature, a power-law (Fig. 5a; n = 0.5) seems appropriate to describe the pull-out behaviour of straight steel fibres. On the other hand, a piecewise function, indicated as f in Fig. 4b, has been recently suggested in the case of hooked-end steel fibres (Abdallah and Rees 2019). The analytical expressions of these constitutive laws can be found in Accornero et al. (2022a), in which the effectiveness of UBCM in reproducing the flexural response of FRC members is discussed.

Fig. 5
figure 5

Structural response of FRC beams (a0/h = 0.05) as a function of NP, and for different values of Nw: a Nw = 548; b Nw = 1370; c Nw = 2739. For each curve, the square marker indicates the first cracking moment, whereas the circle one indicates the ultimate moment

Full size image

Finally, a set of compatibility conditions is introduced to calculate the crack opening, wi, at each i-th active reinforcement level as a function of the applied bending moment, M, and of the m bridging forces, Fi. In matrix form:

$$ \left\{ w \right\} = \left\{ {\lambda_{{\text{M}}} } \right\}M - \left[ \lambda \right]\left\{ F \right\}, $$
(2)

where {w} is the crack opening vector, {λM} is the vector of the local compliances due to the bending moment, and [λ] is the matrix of the local compliances due to the bridging forces.

Summarizing, for a given crack depth, the problem relies in the determination of the 2m + 1 unknowns, i.e., the fracturing moment, MF, the profile of the crack opening displacements, {w}, and the corresponding distribution of bridging forces, {F}. The solution requires a numerical iterative procedure that leads to the complete evaluation of the stress-block diagram as schematically represented in Fig. 3.

At each loading step, i.e., for each crack length, the local rotation of the notched cross-section can be calculated as:

$$ \varphi = \lambda_{{{\text{MM}}}} M - \left\{ {\lambda_{{\text{M}}} } \right\}^{{\text{T}}} \left\{ F \right\}. $$
(3)

The corresponding deflection of the FRC element, δ, can be obtained by applying the superposition principle, according to which the total deflection takes into account both the inelastic contribution related to the fracturing process in the mid-span section (inelastic hinge) and that related to the elastic behaviour of the remaining part of the beam.

Under these assumptions, the UBCM is able to predict the FRC different post-cracking regimes ranging from softening to pseudo-hardening (Fig. 1) as a function of two scale-dependent dimensionless numbers, i.e., the reinforcement brittleness number, NP, and the pull-out brittleness number, Nw:

$$ N_{{\text{P}}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} F_{{{\text{P}},i}} }}{{K_{{{\text{IC}}}} bh^{1/2} }} = V_{{\text{f}}} \frac{{\alpha \overline{\beta }\sigma_{{{\text{s}},{\text{max}}}} }}{{K_{{{\text{IC}}}} }} h^{1/2} = V_{{\text{f}}} \frac{{\overline{\sigma }_{{{\text{s}},{\text{max}}}} }}{{K_{{{\text{IC}}}} }} h^{1/2} , $$
(4)
$$ N_{{\text{w}}} = \frac{{Ew_{{\text{c}}} }}{{K_{{{\text{IC}}}} h^{1/2} }}. $$
(5)

The reinforcement brittleness number, NP, represents the dimensionless maximum value of the bridging forces. It depends on the fibre volume fraction, Vf, on the maximum value of the generalized slippage strength of the fibre, \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\)—in which the parameters of fibre distribution, α and β are included—on the matrix fracture toughness, KIC, as well as on the beam depth, h. On the other hand, Nw depends on the matrix Young’s modulus, E, on the fibre embedment length, wc, on the matrix fracture toughness, KIC, and on the beam depth, h.

In Eq. (4), \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\), is obtained as the product between the orientation factor, α, the average value of the coefficients βi (it is different for each fibre), \(\overline{\beta }\), and the slippage strength of the fibre, \({\sigma }_{\mathrm{s},\mathrm{max}}\). In this sense, it is worth emphasizing that \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\) englobes the information related to the actual distribution and orientation of the fibres in the critical cross-section. As a consequence, the analysis of the FRC structural response does not require the determination of the single values α and \(\overline{\beta },\) but only of \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\), which can be identified on the basis of experimental flexural tests.

In addition, it is worth noting that the product between NP and Nw, which is equal to Vf \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\) wc E/KIC2, provides an information regarding the toughening contribution of the two constituent phases of the composite. As a matter of fact, it is proportional to the ratio between the toughening contribution provided by the reinforcing secondary phase, which is calculated as the area subtended by the bridging traction law (Fig. 4), and the fracture energy of the brittle concrete matrix, which is calculated as a function of KIC by means of the Irwin’s relationship. This product is used to thoroughly describe the post-cracking structural behaviours of brittle-matrix fibrous composites (Massabò 2008).

3 Numerical simulations

Let us consider a FRC cross-section characterized by a notch depth equal to 1/20 of the beam depth (a0/h = 0.05), and reinforced with hooked-end steel fibres (Fig. 4b). The critical cross-section is characterised by a discrete number of reinforcing layers, n = 100, which are considered to be evenly spaced in the ligament area and orthogonal with respect to the crack faces. In this sense, the coefficients α and βi have been assumed equal to 1. By means of the UBCM, the structural responses are plotted by varying the fibre volume fraction, Vf, and the fibre embedment length, wc, in order to highlight the influence of NP and Nw on the post-cracking behaviour of the FRC beams.

In Fig. 5a–c, three sets of numerical curves are represented, each of them referring to a constant value of Nw, whereas NP ranges from 0 (unreinforced material) to 2.

The three stages previously described (Fig. 1) can be clearly identified in each numerical curve. The elastic branch—valid until the first cracking moment (red square marker) is reached (\({\widetilde{M}}_{\mathrm{cr}}\)= 0.39 for a0/h = 0.05)—is the same for all the curves. When the crack starts propagating, the response is characterized by an intermediate stage (Stage II), in which the ultimate bending moment of the cross-section, \({\widetilde{M}}_{\mathrm{u}}\), is defined (circle markers). Depending on NP, the post-cracking response could be unstable, when the ultimate moment is smaller than the first cracking moment (see red, orange, yellow, and green curves), or stable, when the ultimate moment is greater than the first cracking moment (see cyan, blue, violet, and purple curves). This suggests to define the critical value of the reinforcement brittleness number, NPC (= 0.83 for a0/h = 0.05), which is required to guarantee a stable post-cracking response (ultimate bending moment equal to the first cracking moment) (Accornero et al. 2022). In all cases, a decrement in the load is observed in the final stage of the response (Stage III), which is governed by Nw. The latter, when sufficiently small (see Fig. 5a), provides the convergence of all the curves to a unique final softening branch.

Similar conclusions can be drawn in the case of the numerical simulations represented in Fig. 6a–c. In this case, each of the three families of curves corresponds to a constant value of NP, whereas Nw ranges from 274 to 2739. Consistent with the previous considerations, the stability of the post-cracking response in the Stage II—ranging from softening (Fig. 6a) to pseudo-hardening (Fig. 6c)—is defined by NP. Then, for a given value of NP, the numerical curves slip towards different final softening branches depending on the value of Nw, which has small influence on the ultimate bending moment, although it defines the rotational capacity at the cross-sectional level. The rotational capacity is intended as the difference between the local rotation occurring at the ultimate bending moment (circle marker) and the local rotation related to the first cracking moment (square marker).

Fig. 6
figure 6

Structural response of FRC beams (a0/h = 0.05) as a function of Nw, and for different values of NP: a NP = 0.50; b NP = 0.90; c NP = 1.30. For each curve, the square marker indicates the first cracking moment, whereas the circle one indicates the ultimate moment

Full size image

It is worth noting that these transitions in the flexural response hold even if a different value of the initial notch depth, a0/h, is assumed. This parameter affects the initial elastic branch of the response (Stage I), thus leading to a different value of the first cracking moment, \({\widetilde{M}}_{\mathrm{cr}}\). More precisely, a decrease in a0/h provides a nonlinear increase in \({\widetilde{M}}_{\mathrm{cr}}\), the latter tending to infinity for an unnotched specimen (LEFM). On the other hand, the initial notch depth has substantially no influence on the post-cracking regime—which is governed by NP in Stage II and Nw in Stage III, respectively—thus leading to the same value of the load bearing capacity, \({\widetilde{M}}_{\mathrm{u}}\). As a consequence, considering that the stability of the flexural response is defined by \({\widetilde{M}}_{\mathrm{cr}}\) and \({\widetilde{M}}_{\mathrm{u}}\), the numerical model predicts an increase in the critical value of the reinforcement brittleness number, NPC, with a decrease in the initial notch depth, a0/h. Further quantitative information regarding the influence of initial the notch depth on the critical value of the reinforcement brittleness number can be found in Accornero et al. (2022a).

Regarding size-scale effects, an increase in beam depth, h, provides an increase in NP and a decrease in Nw, consistently with Eqs. (4)–(5). Considering the numerical simulation shown above, it implies a larger stability in Stage II of the response, whereas a steeper pull-out tail (Stage III) is observed.

When the specimen size is very large, the fracture process zone—intended as the crack zone bridged by the reinforcing fibres (see Fig. 3)—becomes independent from the specimen geometry. By increasing the structural scale, the flexural response tends towards a LEFM limit condition, in which the toughening contribution of the concrete matrix and of the reinforcing fibres can be merged together by defining an equivalent fracture toughness of the composite. On the other hand, a further limit case can be observed when the specimen size is very small: the crack propagation process is mainly governed by the concrete matrix, whose nonlinearities cannot be neglected, thus making LEFM not suitable (Massabò 2008).

4 Experimental validation

In this section, UBCM is used to calibrate the model constitutive parameters on the basis of experimental results reported in the literature. After calibration, UBCM is used as a predictive tool in order to evaluate the influence of the specimen size on the stability of the FRC flexural response.

The experimental campaign under consideration was carried out by Jones et al. (2008), who investigated the flexural behaviour of FRC beams by means of four-point bending tests on unnotched FRC specimens characterized by a span of 500 mm, a thickness of 100 mm, and variable depths ranging from 50 to 100 mm (Fig. 7).

Fig. 7
figure 7

Test geometry adopted in Jones et al. (2008)

Full size image

The composite under investigation was made of a concrete matrix characterized by a 28-days cubic compression strength of 72 MPa, reinforced with hooked-end steel fibres of 30 mm in length, lf, aspect ratio λf = lf/df = 60, and tensile strength, fu = 1100 MPa. The experimental program included: (i) two fibre contents equal to 40 kg/m3 (Vf = 0.50%) and 80 kg/m3 (Vf = 1.00%); (ii) three different specimen depths as depicted in Fig. 7.

For each combination of fibre volume fraction and specimen size, three specimens were tested in four-point bending. Further information about the composition and the mechanical properties of the composite mixture can be found in Jones et al. (2008).

4.1 Identification procedure

The numerical modelling has been carried out by considering the reinforcing layers evenly spaced within the ligament area. Since no information regarding the fibre distribution are available from the considered experimental tests, the orientation factor, α, is assumed equal to one. The same assumption was applied for the coefficient βi. Nevertheless, these assumptions do not limit the application of the model because, as explained above, they are included in the equivalent slippage strength, \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\), which can be identified on the basis of the experimental curves. Then, the bridging law represented in Fig. 4b has been adopted for the analysis, since hooked-end steel fibres are used in the experimental investigation. Finally, a fictitious initial notch of depth a0/h = 0.05 has been used to model the initially smooth specimen. The influence of this choice on the obtained results will be discussed later in this section.

For each of the six specimen series, three experimental curves are averaged in order to obtain the corresponding load vs mid-span deflection diagram. Then, an identification procedure has been applied in order to identify the mechanical parameters of the matrix and of the reinforcing fibres, i.e., KIC, \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\), and wc, which cannot be known a priori. The matrix fracture toughness, KIC, is determined as the first parameter, being related to the first cracking moment of the FRC specimen. In other words, KIC is found by optimizing the difference between the first cracking moment experienced by the specimen and that predicted by the numerical model. On the other hand, the other two parameters, \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\) and wc, relate to the post-cracking behaviour of the composite, being directly related to the abovementioned dimensionless numbers, NP and Nw. In this case, \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\) and wc have been selected by taking into account two parameters: the maximum load, i.e., the load-bearing capacity of the specimen, and the area under the load vs deflection curve. For each pair of values (\({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\), wc), the comparison between a given experimental curve and the related numerical prediction permits the evaluation of the differences in terms of maximum load (ΔPmax) and of the area under the curve (ΔArea), as schematically shown in Fig. 8a.

Fig. 8
figure 8

a Schematic representation of ΔPmax and ΔArea; b multi-objective optimization following the Pareto’s procedure

Full size image

The problem consists in the optimization of multiple objectives by varying a set of multiple parameters. It can be addressed by applying the Pareto’s approach for the multi-objective optimization. Following this route, the objective functions are ΔPmax and ΔArea, which need to be minimized in order to find the best overlap between the experimental curve and the numerical prediction. On the other hand, the variable parameters are \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\) and wc, which must satisfy the following constraining conditions: \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\) must be greater than zero, whereas wc must be included between zero and half fibre length.

Within these boundary conditions, each pair of values (\({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\), wc) constitutes an acceptable solution, leading to the corresponding values of the two objective functions, ΔArea and ΔPmax. This solution can be represented by a point in the plane (ΔArea, ΔPmax) (Fig. 8a). A solution is said to be “Pareto efficient” if there is no variation able to produce improvements in one objective function, without deteriorating the other one. All the Pareto efficient solutions constitute the set of the Pareto’s front (marked black points in Fig. 8b). In this application, the best-fitting solution has been chosen among the points within the Pareto’s front as the one with the minimum distance from the origin (Fig. 8b).

Following this route, it is possible to obtain the set of three identifying parameters (KIC, \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\), wc) for each specimen series, which are summarized in Table 1. The corresponding results are represented in Fig. 9 where, for each specimen series, the experimental curve is depicted together with the corresponding numerical one.

Table 1 Mechanical parameters obtained by identification
Full size table
Fig. 9
figure 9

Identification of the experimental curves: a Vf = 0.50% (40 kg/m3); b Vf = 1.00% (80 kg/m3)

Full size image

Considering the identified parameters collected in Table 1, it is worth noting that, in the case of small specimens, the matrix fracture toughness, KIC, is found to be significantly smaller than that obtained in the other two cases (medium and large specimen). This result, which appears unexpected at first sight, finds a clear explanation in the framework of Fracture Mechanics. In fact, by reducing the specimen size, a transition from a crack propagation collapse, typical of LEFM, to a plastic flow collapse at the concrete ligament occurs. Consistently with the previous discussions, UBCM cannot capture this further transition, which actually requires a cohesive-crack modelling.

On the basis of these considerations, the results obtained in the case of the smallest specimens (h = 50 mm) have not been considered for the identification of the mechanical properties of the composite, which are now calculated by averaging the results obtained in the case of the medium and large specimens (see Table 2).

Table 2 Average mechanical parameters used to predict size effects
Full size table

4.2 Prediction of scale effects

When the mechanical properties of the composite are obtained, the UBCM can be used as a predictive tool, and the influence of the specimen size on the flexural response can be investigated by varying the beam depth, h, as the unique variable.

For each fibre volume fraction, numerical predictions were performed by varying solely the structural size in order to isolate the effect of the beam depth, h, and then they have been compared to the corresponding experimental curves. As shown in Fig. 10a and b, the model is able to fully capture the post-cracking response of the composite, which is ruled by NP and Nw (Table 3). It is worth noting that, in the case of Vf = 0.50% (40 kg/m3), NP increases from 0.70 to 0.81, but still remains lower than its critical value (NPC = 0.83 for a0/h = 0.05), leading to a global softening response. On the other hand, in the case of Vf = 1.00% (80 kg/m3), NP increases from 1.03 to 1.19, and in all cases is greater than NPC, consistently with the observed pseudo-hardening behaviour of the FRC specimens.

Fig. 10
figure 10

Prediction of the experimental curves: a Vf = 0.50% (40 kg/m3); b Vf = 1.00% (80 kg/m3)

Full size image
Table 3 Brittleness numbers NP and Nw
Full size table

In both cases, the prediction of the critical condition, i.e., the critical scale, hmin, corresponding to a stable post-cracking response, can be provided.

For Vf = 0.50% (40 kg/m3):

$$ h_{{{\text{min}}}} = \left[ {N_{{{\text{PC}}}} \left( {a_{0} /h} \right)\frac{{K_{{{\text{IC}}}} }}{{V_{{{\text{f}} }} \overline{\sigma }_{{{\text{s}},{\text{max}}}} }} } \right]^{2} = \left[ {0.83\frac{22}{{\left( {0.50\% } \right)355}} } \right]^{2} = 106\,{\text{mm}}. $$
(6)

For Vf = 1.00% (80 kg/m3):

$$ h_{{{\text{min}}}} = \left[ {N_{{{\text{PC}}}} \left( {a_{0} /h} \right)\frac{{K_{{{\text{IC}}}} }}{{V_{{{\text{f}} }} \overline{\sigma }_{{{\text{s}},{\text{max}}}} }} } \right]^{2} = \left[ {0.83\frac{24}{{\left( {1.00\% } \right)286.5}} } \right]^{2} = 48\,{\text{mm}}. $$
(7)

In the former case (Vf = 0.50%), the estimation of hmin is effective, whereas in the latter case (Vf = 1.00), hmin approaches the range in which LEFM was found not suitable. It implies that, when NPC is characterised by high fibre volume fractions and very small structural sizes, the definition of hmin requires further investigations.

It is worth noting that the value of hmin depends on the mechanical parameters of the composite and on the critical value of the reinforcement brittleness number, NPC, which in turn are affected by the choice of a0/h that is required to model a nominally unnotched specimen. In this work, it has been assumed a0 = 0.05 h.

As explained above, the initial crack depth mainly affects the value of the first cracking moment, whereas it has little influence on the post-cracking regime of the structural response. As a consequence, a0/h affects the identification of KIC, rather than that of the fibre constitutive parameters, \({\tilde{\sigma }}_{\mathrm{s},\mathrm{max}}\) and wc. The correct value of the first cracking moment can be captured by means of different combinations of a0/h and KIC: an increase in a0/h provides an increment in KIC. On the other hand, an increase in a0/h provides a decrease in NPC, as previously pointed out.

Therefore, different assumptions of a0/h lead to different values of KIC and NPC, although it can be shown that their product remains unchanged, leading to the same prediction in terms of critical structural size, hmin (see Eqs. 6, 7).

In conclusion, the key-point of the discussion is that, within the limit of applicability of LEFM, a consistent evaluation of the mechanical properties of the composite (by means of the identification procedure) leads to define the specimen size corresponding to the critical condition (NP = NPC). This is analogous to the determination of the minimum fibre volume fraction of the composite (Carpinteri and Accornero 2020), Vf,min, being both Vf and h involved in the reinforcement brittleness number, NP.

5 Conclusions

UBCM has been proposed as a Fracture Mechanics nonlinear approach to capture and interpret the scale effects in the structural behaviour of fibre-reinforced concrete beams in bending. Within the model assumptions, the post-cracking behaviour of the composite is governed by two dimensionless numbers, NP and Nw, which are both scale-dependent. In this respect, due to an increment in beam depth, h, a double brittle–ductile–brittle transition can be predicted. The critical value of the reinforcement brittleness number, NPC, permits description of the conditions required to guarantee a stable post-peak response, both in terms of minimum fibre volume fraction or, analogously, of minimum specimen depth. Numerical predictions are compared to experimental results related to flexural tests on FRC beams of different depths. In the first step, the experimental data have been used to identify the material mechanical properties. Once the mechanical properties of the composite have been implemented (average values), UBCM has proved its potential applicability in predicting the effect of the specimen size variation on the stability of the post-cracking regime. The model allows prediction of the critical size, hmin, for which a stable post-peak response is obtained, analogously to the case of the minimum fibre volume fraction, Vf,min.