1 Introduction

In recent years, demands on gear unit performance have increased steadily. Due to lightweight construction and the demands for a compact design, the required power density has increased significantly in some applications (Fuchs et al. 2021c). Furthermore, the very high cycle fatigue (VHCF) or even giga-cycle fatigue range is very significant for some components, for example in e-mobility, railway applications, wind power and power plant applications, due either to the high speed or long service life. To simultaneously fulfil the requirements of high-power density and long service life, case-hardened gears can additionally be shot-peened. However, in this case, crack initiation can shift from the surface to below the surface. The crack initiation usually occurs at a non-metallic inclusion and is combined with the formation of a fisheye (fisheye failure) (Bretl et al. 2013).

Recently published literature, e.g. Gao et al. (2019), Jiang et al. (2016), Krupp et al. (2014) and Wang et al. (2018), has considered crack initiation at non-metallic inclusions and has elaborated extensive fracture surface characteristics. However, to date it is not entirely clear why some fracture characteristics in tooth root fracture differ from those in standard specimens. Therefore, this paper uses an FEM simulation to simulate the stress state at the non-metallic inclusion in the tooth root fillet of a loaded gear. In particular, the simulation includes the influence of compressive residual stresses due to a shot peening process included in the simulation. Based on the simulation results and the fracture surface characteristics, a crack initiation and propagation analysis for tooth root fracture with crack initiation at a non-metallic inclusion is done. Subsequently, this analysis and the influence of residual stresses are compared with data from experimental investigations.

2 Overview of the state of scientific knowledge

2.1 Fisheye failure

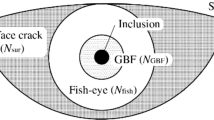
Crack initiation below the surface at a non-metallic inclusion is usually characterized by an optically brighter region in the surface area near the crack surface. This kind of fracture is referred to as a “fisheye” fracture in the literature, see Fig. 1. At the center of the fisheye is a non-metallic inclusion, which triggers the crack initiation. An area that appears darker is sometimes visible around the non-metallic inclusion (Shiozawa et al. 2010).

Fig. 1
figure 1

Schematic illustration of subsurface crack growth acc. to (Shiozawa et al. 2010)

Full size image

2.2 Numerical calculation of the stress condition

2.2.1 In the tooth root fillet of gears

The stress condition in the tooth root fillet is due to the application of a force at the tooth flank—a mixture of pressure, shear and significant bending stresses (Niemann and Winter 2003). Figure 2, shows a typical simulated stress condition in the tooth root fillet due to an application of force at the tooth flank. On the right side of the tooth, a stress maximum exists near the 30° tangent to the tooth root fillet. Furthermore, it can be seen that the greater the distance from the surface, the more the stresses decrease. However, in the simulation carried out by Stenico (2007) to generate a load profile for the latter model, only the stresses due to the external force were calculated. In the case of a case-hardened and shot-peened gear, further residual stresses need to be considered. In particular, a shot-peening process can induce high compressive residual stresses in the surface layer.

Fig. 2
figure 2

Typical stress condition in the tooth root fillet (image on the right) due to an application of force at the tooth flank (image on the left) (Stenico 2007)

Full size image

2.2.2 At a non-metallic inclusion in the steel matrix

In the literature, the stress condition at non-metallic inclusions under a specific uniaxial load is commonly determined by a simulation using a representative volume element (RVE), [c.f. (Ahmadian and Taghizadeh 2020; Qayyum et al. 2020; Ma et al. 2020)]. Usually a basic geometric shape, such as a circle (2D) or a sphere (3D), is used. However, the stress condition in the tooth root fillet differs from a uniaxial stress condition.

Furthermore, the morphology of the inclusion can have an influence: in the work of (Arreola-Herrera et al. 2018) the stress condition around real inclusion morphologies in 32CDV13 steels was determined using an RVE. They found that the real morphology of the NMI has a strong influence on the stress distribution. Regarding the residual stresses in the vicinity of a non-metallic inclusion due to heat treatments (Gu et al. 2019), confirmed that if the real morphology of a non-metallic inclusion is considered, then higher stresses are present in the surrounding steel matrix.

In Schäfer et al. (2019) a numerical model of a non-metallic inclusion situated in a martensitic high-strength steel was built. They investigated how the potential of a fatigue crack nucleation was influenced by different parameters affecting the non-metallic inclusion, such as defect size, defect shape, microstructural variability around the defect and residual stresses in the vicinity of oxide inclusions due to thermal heat treatments. It was found that all parameters do indeed have a great influence on fatigue crack nucleation.

However, most of the numerical investigations regarding crack initiation at non-metallic inclusions focus on uniaxial stressed specimens or the multiaxial pressure stress state in bearing rings (Al-Tameemi and Long 2020; Ma et al. 2020). In addition, macroscopic compressive residual stresses due to a case-hardening process and subsequent shot-peening in combination with multiaxial load stresses have yet to be considered in numerical simulations.

2.3 Theories for the crack initiation at non-metallic inclusions

Defects, for example non-metallic inclusions, cause stress step-ups in the material matrix. In Sakai et al. (2017a) the numerical estimated stress step-up at an aluminum oxide inclusion was 43.8% and at a manganese sulfide inclusion it was 32.6%. Sakai et al. stated that these are first indicative values, because the simulation model had still to be extended and modified. Tanaka and Mura (1982) investigated the crack initiation at non-metallic inclusions under shear stress. They identified three different types for the crack initiation:

  • Type A:Crack initiation from inclusions

  • Type B: Inclusion cracking by impinging slip bands

  • Type C: Slip band crack emanating from uncracked inclusion

In the case of type A, the crack initiates from a completely debonded inclusion and the inclusion can be treated like a void. Type B is based on the theory of Eshelby (1957). In type B, however, the size of the inclusion is assumed much smaller than the slip band zone in comparison to an inclusion of type A. Orowan loops are accumulated by the cyclic loading at the NMI. Hence, high stresses are induced at the NMI, which lead to crack initiation at the NMI. In the case of type C, the crack initiates at a slip band at the location of the highest stress concentration. Tanaka and Mura (1982) state that in steel alloys the crack is usually initiated at a slip-band crack emanating from a debonded inclusion. The resulting decreasing fatigue life is depending on the inclusion size, as well as its properties and the properties of the steel matrix, e.g. the grain size.

Wang et al. (2018) further develop the theory of Tanaka and Mura (1982). Thus, dislocations form in suitably oriented grains in the equatorial plane of the inclusion (plane perpendicular to the prevailing principal normal stress in which the inclusion lies), and are able to slide. Due to these dislocations, the bond between the matrix and the inclusion loosens and a higher stress is applied to the surrounding matrix. The resulting micro-vacuum between matrix and inclusion additionally facilitates the formation of further dislocations. The stress concentration, the micro-damage caused by sliding dislocations, and the resulting roughness pattern then initiate the crack. Similar findings are documented in Jiang et al. (2016). Gao et al. (2019) also consider the cause of crack initiation at non-metallic inclusions to be the formation of slip-bands inside grains. This theory also works for crack initiation without non-metallic inclusions, with crack initiation instead occurring at coarse microstructure (a coarse grain). An in-situ observation of the formation of such slip bands was carried out by Krupp et al. (2014). The theories have in common that the crack initiation inside the material is similar to the crack initiation at a technically smooth surface.

Another theory was developed by Nishijima and Kanazawa (1999). It is assumed that three shear-initiated independent cracks are formed that connect and form the origin of the fisheye. These stage I cracks are inclined in the direction of maximum shear stress. This can be seen in Fig. 3. Steps form in the direction of the main shear stresses. If the crack is long enough, the cracks move to stage II, in which they then grow increasingly concentric perpendicular to the axis of the maximum normal stress, thus forming the fracture lens.

Fig. 3
figure 3

Shear type cracks (number 1 to 3) around an inclusion (Nishijima and Kanazawa 1999)

Full size image

2.4 Theories on the formation of the darker-appearing area around non-metallic inclusions

A darker-appearing area is often visible around a non-metallic inclusion. In Fig. 1 it is marked as “darker area”. However, several different nomenclatures exist that are associated with different theories on how the darker area is formed:

  • ODA:Optically dark area acc. to Murakami (2019) and Murakami and Yamashita (2014)

  • GBF:Granular-bright facet acc. to Shiozawa et al. (2010)

  • FGA:Fine granular area acc. to Grad et al. (2012), Sakai (2009), Sakai et al. (2017c) and Shanyavskiy (2013)

  • RSA:Rough surface area acc. to Ochi et al. (2002)

The theories on the formation of a rough surface in the immediate vicinity of the non-metallic inclusion are summarized in the following. Firstly there is the theory of Murakami (2019) and Murakami and Yamashita (2014), in which hydrogen embrittlement and fatigue are mentioned as the cause for the formation of an “optically dark area” (ODA). Secondly, there is the theory of Shiozawa et al. (2006, 2010), in which the dispersive decohesion of carbides is mentioned as the reason for the formation of a “granular bright facet” (GBF). However, according to Wang et al. (2018), this theory is unlikely because rough surfaces around an inclusion also occur in non-carbide alloys, such as titanium alloys. Another theory is that of Shanyavskiy (2013), in which local volume rotation and the resulting grain refinement is given as the reason for the formation of a “fine granular area” (FGA). However, no further mention of this theory could be found in other, particularly more recent literature. Lastly, the theory of Sakai (2009) and Sakai et al. (2017b) also assumes an FGA that is formed by polygonization and then micro-detachments. These micro-detachments then combine to form a crack. This model was used, modified and further developed by Grad et al. (2012), Hong et al. (2016) and Wang et al. (2018). Grad et al. propose semi-continuous crack growth, in which grain refinement caused by dislocation sliding always occurs at the crack tip. This is also supported by Chai et al. (2015, 2016), who discussed the formation of nano-pores, a phenomenon that was also observed by Wang et al. meanwhile, take up the theory of Hong et al., who propose the “Numerous Cyclic Pressing” (NCP) model. Here, an FGA can only be formed with a loading ratio of R ≤ 0. Grain refinement takes place at the incipient crack by pressing the two surfaces together. Wang et al. also note that specimens with introduced compressive residual stresses also have a local negative stress ratio. Ochi et al.(2002) use the term “rough surface area” (RSA). However, no formation theory is associated with that term. In this paper, the nomenclature “FGA” acc. to Sakai is used.

Local plastic deformations in the form of slip bands and dislocations around the inclusion were observed on TEM images in Chai et al. (2015). This could be the preliminary stage of grain refinement described by Grad et al. (2012). Accurate observation is difficult because the processes all occur inside the material. However, a vacuum environment is often used as a comparative model (Spriestersbach et al. 2016). Regardless of the material, an FGA can be formed when both vacuum environment, repetitive contact of fracture surfaces, and long-term loading with over 107 cycles occur. In internal fractures in fatigue tests, these conditions are automatically met in the VHCF region (Li et al. 2016; Nakamura et al. 2010). According to Li et al. (2016), the size of the FGA depends on the material and the applied stress amplitude: if the latter increases, the size of the FGA decreases. Another influencing factor is the hardness, and the FGA also increases in size with increasing service life (Li et al. 2016). Common to all presented theories is that the formation of the FGA stops once a certain threshold for crack growth has been reached and a fisheye is formed.

2.5 Formation of the fisheye and crack propagation rate

According to Shiozawa and Lu (2002), compressive residual stresses at and near the surface, introduced by heat treatments or surface treatments, such as shot-peening, have no influence on the formation of the individual areas of the fisheye. However, the compressive residual stresses do influence the appearance of the fisheye. Thus, heat-treated, non-blasted specimens exhibit a circular, whereas heat-treated, shot-peened specimens exhibit an elliptical fisheye. This is because the internal crack is initially stopped by the high compressive residual stresses at the edge and instead propagates to areas of higher stress. Only when the crack is large enough, it generates such a high excess stress that it overcomes the area of the high compressive residual stresses. A schematic representation of the two forms of the fisheye is shown in Fig. 4.

Fig. 4
figure 4

Schematic representation for the formation of the fisheye a without and b with compressive residual stresses at and near the surface. From (Shiozawa and Lu 2002)

Full size image

In Stanzl-Tschegg (2017) the crack propagation rate was investigated for a martensitic high-strength steel (X20Cr13). It was found that inside the FGA the crack propagation rate is about 10–12 m/cycle. Inside the fisheye, until the surface is reached, the crack propagation rate increases from 10–11 m/cycle to 10–9 m/cycle. The propagation rate of 10–9 m/cycle is already considered to be part of the Paris regime. The threshold value of the stress intensity factor is calculated to be 5 MPa√m for crack growth of the FGA. This value is confirmed by Spriestersbach et al. (2017) for a high-strength bearing steel (100Cr6). Murakami et al. (1989) give an empirical formula (1) for calculation of the threshold value of the stress intensity factor for crack initiation at a non-metallic inclusion and to enable crack growth inside the FGA.

$$ {\Delta K}_{{{\text{th}},{\text{short}},{\text{ss}}}} = 2.77 \cdot 10^{ - 3} \cdot \left( {{\text{HV}} + 120} \right)\sqrt {area}^{1/3} $$
(1)

For the calculation, the local Vickers hardness HV (as a substitute for the material strength because the hardness can be obtained more easily) and the projected area of the non-metallic inclusion (“area”-parameter) are needed.

3 Summary of the state of scientific knowledge

Several numerical studies relating to the stress state at non-metallic inclusions especially in the context of bearings were found in literature. In addition, heat treatment induced residual stresses in the ultimate vicinity of the non-metallic inclusion were investigated. However, compressive residual stresses due to e.g. a shot-peening process and their effect on crack initiation at non-metallic inclusions have yet to be investigated.

The single crack propagation states for fisheye failures according to Richard and Sander (2012), Stanzl-Tschegg (2017), Stenico (2007), Tanaka and Mura (1982) and Wang et al. 2018) are:

  • Crack initiation at the non-metallic inclusion (NMI)

  • Formation of the dark area (nomenclature for example: “FGA”)

  • Crack propagation inside the fisheye

  • Crack propagation outside of the fisheye

  • Abrupt fast fracture until overload fracture occurs

As for crack initiation at a non-metallic inclusion, a mechanism similar to crack initiation at the surface is presented. Therefore, the formation of slip bands and micro-pores in suitably oriented former austenite grains play an important role. For the formation of a dark area in the vicinity of a non-metallic inclusion, multiple different theories exist. All theories (except Murakami) have in common that a finer microstructure is present in this area. Therefore, the initial former austenite grain size might also have an influence. Crack propagation inside and outside the fisheye occurs according to the Paris law until overload fracture occurs. Furthermore, the influence of the residual stresses on the shape of the fisheye is demonstrated and the crack propagation rates are explained.

4 Underlying database and geometry of the simulated gears

Extensive experimental investigations on case-hardened, shot-peened gears have already been carried out by Schurer (2016), Bretl (2010) and Stenico (2007) and in FVA project no. 293 IV (Fuchs et al. 2021d). Some of the experimental results and crack area characteristics have already been presented in Fuchs et al. (2019a). The foremost inclusion types in the investigated steels were manganese sulfides and aluminum oxides. Parts of the underlying experimental investigations at the FZG back-to-back test rigs and pulsator test rigs and the details of the test variants of Schurer (2016) and Fuchs et al. (2021d) were internationally published in Fuchs et al. (2019b) and Winkler et al. (2019). This paper builds on the results of a detailed fracture analysis of the experimental investigations of Schurer (2016) and Fuchs et al. (2021d), which were published in Fuchs et al. (2021a). The investigations were carried out using a scanning electron microscope (SEM) and an optical 3D measurement system (Alicona Imaging GmbH 2021). The size, distribution and density of the non-metallic inclusions present in the investigated materials were investigated previously. The results were already published in Fuchs et al. (2022). The experimental investigations were carried out on gears with a normal module of 1.5, 5 and 10 mm made out of steels with a higher degree of cleanliness (MnCr-, CrNiMo- and special alloyed). The number of investigated fisheye failures per alloy system is given in Table 1. For the simulation, gears with a normal module of 1.5 mm for the FZG back-to-back test rig were used. The main geometrical data of these gears are given in Table 2.

Table 1 Database of fisheye failures in this paper
Full size table
Table 2 Main geometrical data of the gears used for the simulation model
Full size table

5 Aim of the investigations

In Fuchs et al. (2021b) it was shown that fisheye failures in tooth root fillets have various characteristics. For example, at the non-metallic inclusion, as well as at the border of the fish-eye, a step can be detected, see Fig. 5.

Fig. 5
figure 5

a Step at the non-metallic inclusion in a fisheye (marked with a red arrow) (fracture surface diagonally in upper right corner) (not to scale) from Fuchs et al. (2021b) and b step at the border of the fisheye (red dashed line, marked by a red arrow) (not to scale)

Full size image

As stated in Fuchs et al. (2021b) investigations carried out in Murakami et al. (1999) and Sakai et al. (2017b) showed no step at the non-metallic inclusion. This is because the stress maxima are perpendicular to the stressed area, when an external uniaxial stress is applied, such as in tension–compression tests. According to Fuchs et al. (2021b) in rotating bending and tooth root bending tests performed on gears, the location of the stress maximum differs and shifts outside the perpendicular plane due to the multiaxial stress condition. Therefore, a shifting of the planes around the non-metallic inclusion, described by the angle α, could be determined (see Fig. 6). Furthermore, it was found that in a multiaxial stress condition, the non-metallic inclusion is not always located in the center of the fisheye, see Fig. 7. In addition, almost all fisheyes, in the case-hardened, shot-peened gears investigated, had an ellipsoidal shape.

Fig. 6
figure 6

Shifting of the planes around a non-metallic inclusion, described by the angle α from Fuchs et al. (2021b)

Full size image
Fig. 7
figure 7

Severely eccentric non-metallic inclusion (marked by a red arrow) in a fisheye (marked by a dashed red line) of a tooth root bending fracture in a gear from Fuchs et al. (2021b)

Full size image

The purpose of this paper is to explain the fracture surface characteristics as described in Fuchs et al. (2021a, 2021b) by means of a detailed 3D finite element simulation using the sub-modeling technique. In this context, not only the load stresses but also the residual stresses due to the case-hardening and a subsequent shot-peening process are incorporated within the simulation. Furthermore, a crack initiation and propagation analysis due to the multiaxial stress condition in tooth root bending tests in combination with the residual stresses is done. In addition, this analysis is subjected to a fractographic analysis of the experimental investigations. As residual stresses have a great influence on the load carrying capacity, they might also influence the crack initiation. Therefore, in a further step the calculation of the stress intensity factor ΔKth is reviewed under the prospect of the residual stresses.

6 Simulation model

The gear geometry as in the experimental investigations with a normal module of mn = 1.5 mm is used for the finite element simulation in ANSYS Workbench (for the geometrical data, see Table 2). To reduce the computational effort, the gear was reduced to a three-tooth model; see Fig. 8a. The hub of the wheel was set rigid and the load was applied at the hub of the pinion in form of a moment. The contact between one tooth of the wheel and one tooth of the pinion was modeled frictionless, as the amount of friction is neglectable for investigations regarding forces and stresses in the tooth root. For the detailed investigations, the sub-modeling technique was used in order to obtain more accurate results for an equal computational effort. The sub-model is placed in the tooth root area of the pinion in the middle of the model so that no edge effects occur; see Fig. 8b. The residual stresses were experimentally determined in discrete depths by X-ray diffractometry. After the modeling and the meshing, the nodes of the mesh were exported. The calculation of the residual stresses at each node was carried out in MATLAB. Therefore, the measured residual stresses were computed into a continuous curve and the residual stress at each node was determined from the distance of the node from the surface. The residual stresses at each node were then imported into ANSYS as external load data.

Fig. 8
figure 8

Three-tooth model (a), The embedded submodel into the three-tooth model of the pinion (marked by red arrow) (b) Sectional view of the tetragonal meshed submodel with refinements at the surface and the non-metallic inclusion. The Position of the non-metallic inclusion is shown with the red circle (c)

Full size image

The meshing of the sub-model was carried out with a tetrahedral mesh, with refinements at the surface and at the contact to the non-metallic inclusion. The non-metallic inclusion was modeled as a spherical Al2O3 with a diameter of 30 µm at a depth from the surface of 150 µm, because this is where most of the non-metallic inclusions were found during experimental investigations as previously published in Fuchs et al. (2021b). The contact between the matrix and the non-metallic inclusion was modeled as a joint contact. According to Alonso et al. (2017) in steels with a high cleanliness, the average distance between inclusions is usually greater than the corresponding inclusion size. Therefore, the different non-metallic inclusions do not have any cross influences on each other. Thus, it is not necessary to include more than one non-metallic inclusion into the sub-model. A sectional view of the meshed sub-model with the refinements and the position of the NMI is shown in Fig. 8c. The values of the calculated residual stresses are based on XRD-measurements carried out in Fuchs et al. (2021b, 2021d). The evaluation of the stresses takes place along a path normal to the surface through the non-metallic inclusion. The material data for the gear steel and the non-metallic inclusion (Al2O3) used in the simulation is given in Table 3.

Table 3 Material data used for the gear and the non-metallic inclusion (NMI) used in the simulation
Full size table

7 Results of the simulation

In the following, the results of the simulation are presented. First, Fig. 9 shows the main model. Here only the stress state due to the external load (not influenced by residual stresses and no NMI) is considered. In comparison to Fig. 2 (Stenico 2007) a similar stress state in the tooth root fillet is the result of the simulation. It is clearly apparent that the highest tensile stresses are located in the tooth root fillet of the pinion. It can also be seen that, as described in Stenico (2007), the stress due to the load is zero in the neighboring teeth. This means that, considering only the external load, the tooth root fillet is subjected to cyclic loading with only compression or tension (R = 0).

Fig. 9
figure 9

a Simulated stress state of the meshing gears and b A close up of the tooth root fillet of the pinion. Shown is the principal stress in MPa (no residual stresses and no NMI included)

Full size image

7.1 Results with consideration of residual stresses and their validation

First, a simulation of the sub-model was performed considering only residual stresses without an external load to verify the calculated residual stress state. Figure 10 compares the averaged measured residual stresses with the residual stresses calculated in the simulation. Except for the outermost surface layer (0–25 µm), there is good agreement between the two curves. The differences in the outermost surface layer are due to numerical errors during the simulation. However, since the residual stress state agrees very well at the depth of the non-metallic inclusion, the calculated residual stress profile is used in the following. However, the numerical error in the surface layer must be taken into consideration when interpreting the results.

Fig. 10
figure 10

Averaged, measured residual stresses compared with processed residual stresses within the simulation. Shown is the negative equivalent stress according to ‘von Mises’. Vertical lines indicate the position of the non-metallic inclusion as described in Sect. 5

Full size image

7.2 Simulated stress condition at the non-metallic inclusion

After verification of the residual stresses, a simulation was performed considering the load stresses in the tooth root caused by the torque and including the NMI. Figure 11 shows the results of the simulation with and without the additional consideration of the residual stresses.

Fig. 11
figure 11

Simulated stress condition at the surface and the non-metallic inclusion a without and b with consideration of the compressive residual stresses. Shown is the main principal stress in MPa

Full size image

It can be clearly seen that the stress on the material at the surface is significantly lower due to the residual stresses. The stresses near the non-metallic inclusion, on the other hand, are almost the same in both simulations. If the numerical error as described in Sect. 6.1 is taken into account, this effect tends to be even more noticeable. In addition, it becomes quite clear that the maximum stress acting on the material is not perpendicular to the main stress axis but almost parallel to it. Figure 12 compares the ‘von Mises’ stress in the simulated model with and without the residual stresses. This comparison is contrasted with a superposition of the simulated ‘von Mises’ stress without consideration of the residual stresses (no. 1 in Fig. 12) and the negative equivalent of the average of the measured residual stresses according to ‘von-Mises’.

Fig. 12
figure 12

Comparison of the stress according to ‘von Mises’ at the simulated model with and without residual stresses. Contrasted is a superposition of the stress in the simulated model without residual stresses and the negative equivalent of the measured residual stresses according to ‘von Mises’. The gray area indicates the depth over which the numerical error, as described in Sect. 6.1, occurs. Vertical lines indicate the position of the non-metallic inclusion as described in Sect. 5

Full size image

If residual stresses are considered, the maximum stress acting on the material is no longer at the surface, but at the non-metallic inclusion. This is the reason why crack initiation occurs at the non-metallic inclusion and not at the surface. It is also apparent that the residual stresses have a large impact on the stress state at or very close to the surface but less significant at the average depth of 150 µm of the non-metallic inclusions which was experimentally determined for the gears with a normal module of 1.5 mm in Fuchs et al. (2021b).

7.3 Stress condition at the non-metallic inclusion during cyclic loading

During cyclic loading of operating gears, such as in the FZG back-to-back test rig, the load on each tooth is cyclical and the stress state alternates between residual stresses acting on their own and the load stresses superimposed with the residual stresses. Therefore, these two states are simulated and compared with each other. The results are presented in Fig. 13.

Fig. 13
figure 13

Principal stress at the non-metallic inclusion a under external load and with consideration of the residual stresses and b without external load with just the residual stresses acting (Note: same colors do not correspond to the same stresses in a and b; qualitative comparison)

Full size image

In Fig. 13a, the axis connecting the two stress minima is exactly perpendicular to the 30°-tangent. The axis connecting the stress maxima is almost parallel to the 30°-tangent but is slightly offset towards the middle of the non-metallic inclusion. This is probably due to the higher stresses towards the surface. The location of the stress minima due to the residual stresses in Fig. 13b tends to be near the location of the maxima shown in Fig. 13a. Therefore, during cyclic loading, the stress ratio R is not zero but slightly negative. According to Wang et al. (2018) the formation of an ODA is more likely with a negative stress ratio then a stress ratio of zero. This is also confirmed by Deng et al. (2017), Grad et al. (2012), Hong et al. (2016) and Ritz et al. (2018). It can be concluded that the residual stresses may play an important role in forming an ODA in the case of the multiaxial stress state present in the tooth root fillet because there are no negative stresses induced by the external load in tooth root bending tests. This is one of the main differences in comparison to tension–compression or rotating bending tests.

8 Crack initiation and propagation analysis for fisheye failures in high-strength gears

In the following, a crack initiation and propagation analysis for fisheye failures in high-strength gears is performed. However, this paper does not establish any new crack theory, rather different theories found in the literature are linked and applied to the case of fisheye failures in the tooth root fillet of high-strength gears.

8.1 Crack initiation

According to the results of the simulation the maximum stress at the non-metallic inclusion is not perpendicular to the 30°-tangent, but approximately parallel to it. Below, the theories of Wang et al. (2018) and Nishijima and Kanazawa (1999) are used to describe crack initiation within the material. Thus, according to these theories, the crack is initiated due to the dislocations and sliding of crystal planes in a grain favorably oriented for crack initiation, in the zone of highest stress (cf. Fig. 14a). As there are two areas of maximum stress at the non-metallic inclusion, two crack initiations are possible. Due to the dimensions of the non-metallic inclusion, a step is automatically formed. This was also observed in Gao et al. (2019). After crack initiation, an FGA may be formed, especially because the compressive residual stresses cause a negative stress ratio during cyclic loading. Furthermore, the two cracks formed are redirected because their direction of growth is mainly controlled by normal stress above a certain crack size (Gao et al. 2019; Nishijima and Kanazawa 1999) (cf. Fig. 14b).

Fig. 14
figure 14

Schematic illustration of the a areas and axis of maximum stress and b positions and path of the initial cracks (views in axial direction)

Full size image

8.2 Crack propagation

Assuming the theory of Tanaka and Akiniwa (2002), the modified Paris Law for internal cracks applies and therefore stable crack growth prevails within the fisheye. According to the theory proposed in this work, the two incipient cracks initially propagate elliptically at their respective step heights until they have progressed to the point where they are outside the immediate effective range (range where the non-metallic inclusion affects the stress state in the matrix) of the non-metallic inclusion. In this process, the crack in the direction of the surface grows faster than the one in the material depth (stage Ia). This results from a higher stress in the region between the non-metallic inclusion and the surface. However, the faster growth of this crack only extends until the load stress minimum is reached in front of the surface. Here, the local stress may no longer be sufficient to open the crack further. In the material depth, the stress is now higher because there is already an internal material separation (internal crack) and the crack can grow further into the material (stage Ib). Due to the crack enlargement, the intensity factor for crack growth is further increased, so that a lower stress is sufficient for crack growth towards the surface. This interplay is repeated until the internal crack can overcome the stress minimum just below the surface. If the two individual cracks grow to such an extent that they join together, crack stage II is reached. Due to the crack initially growing faster towards the surface and in the axial direction, the step at the non-metallic inclusion can be slightly bent. The propagation of the two cracks and the formation of the fisheye is schematically illustrated in Fig. 15.

Fig. 15
figure 15

Schematic illustration of the crack propagation inside the fisheye from darker to lighter green and formation of the step at the non-metallic inclusion (NMI). On the left, the superposition of the simulated stress acc. to ‘von Mises’ and the averaged measured residual stresses (see Fig. 12) is given for reference. (view perpendicular to fracture surface)

Full size image

The stress minimum just below the surface is also the reason for the elliptical shape of the fisheye, because the stress is not only higher in the interior of the material than just below the surface, but also has a very high value at the level of the non-metallic inclusion in the axial direction. As a result, the crack propagates faster in the axial direction than perpendicular to it. This is in accordance with the findings in Shiozawa and Lu (2002).

When the fisheye reaches the surface, the crack can be treated like a surface crack for the fracture theory and the further service life calculation. At this point, the local stress in the material directly at the surface arising from the existing crack is so great that a fracture surface with unstable crack growth (stage III) forms there in the immediate vicinity of the fracture lens until a semi-elliptical surface crack has developed (fatigue fracture area I) (see Fig. 16a) A SEM-image of this matter can be seen in the next section in Fig. 21. It is also during this stage that the step at the far edge of the fisheye is formed. As shown in Fig. 5b and can be seen in Fig. 17, the step at the far edge of the fisheye is not only influenced by the step at the non-metallic inclusion, but also by the way the crack propagates from the surface into the depth of the material. An additional image of the step on the far edge of the fisheye can be seen in Fig. 18.

Fig. 16
figure 16

a Formation of the surface crack (stage III) after the fisheye has reached the surface. Areas at the surface correspond to the areas of highest local stress, where a fracture surface with unstable crack growth is formed. The arrows show the direction of crack propagation. b Propagation of the crack from the semi-elliptical surface crack across the entire tooth width, formation of the fatigue fracture region and overload fracture

Full size image
Fig. 17
figure 17

Schematic side view of the formation of the step at the far edge of the fisheye as well as the step at the non-metallic inclusion

Full size image
Fig. 18
figure 18

Fracture Surface with visible step at the far edge of the fish eye. False color representation (color scale on right extends from − 13 µm to + 5 µm). (running test: 20MnCr5, mn = 1.5 mm, 155 Nm, 37,300,000 cycles)

Full size image

After formation of the semi-elliptical surface crack, the crack propagates unstably in fatigue fracture area II across the entire width of the tooth (stage IV), until the remaining cross-section of the tooth can no longer bear the load and an overload fracture occurs (stage V) (see Fig. 16b).

9 Discussion and comparison with fractographic analysis

9.1 Crack initiation and step at the non-metallic inclusion

Theories on crack initiation at non-metallic inclusions have already been presented in the state of knowledge. In addition, the fracture theory presented in this paper draws upon these presented theories and links to them. The formation of slip bands and micro-pores as described by (Wang et al. 2018) is also visible at the fracture surfaces analyzed in this paper. Typical detected slipmarkings and micro-pores are shown in Fig. 19 (Fuchs et al. 2021b) performed an extensive in-depth analysis of fisheye fractures. It was shown that in many fisheye failures during tooth root bending tests a step at the non-metallic inclusion could be detected (see Fig. 19a). This contradicted findings in the literature Murakami et al. (1999) and Sakai et al. (2017b) where no step could be detected at crack-initiating non-metallic inclusions. The working theory derived from the extensive characterization was that, due to the unique multiaxial stress condition in rotating bending and tooth root bending tests the stress maximum differs in comparison to uniaxial loaded specimens (e.g. tension–compression tests) and a shifting of the fracture planes occurs (see Fig. 6). Fuchs et al. (2021b) With the numerical simulation performed in this paper, the working theory of Fuchs et al. (2021b) can be confirmed because it can be seen that the stress maxima are not perpendicular to the 30°-tangent but almost parallel to it. Therefore, it can be concluded that in all probabilities the step occurs because of two different cracks starting at the non-metallic inclusion with a shifting of the fracture planes due to the multiaxial stress condition in combination with residual stresses in the tooth root fillet.

Fig. 19
figure 19

Typical SEM observations of slipmarkings (circles) and micropores (arrows). In a) the step at the non-metallic inclusion is also clearly visible. (left: pulsator test, mn = 5 mm, 18CrNiMo7-6, 90 kN, 728,698 cycles/right: pulsator test, mn = 5 mm, 18CrNiMo7-6, 80 kN, 3,504,555 cycles)

Full size image

9.2 Eccentric inclusions

With the crack initiation and propagation analysis in Sect. 7, eccentric non-metallic inclusions as shown in Fuchs et al. (2021b) (Fig. 7) within the fisheye can be explained. If the non-metallic inclusion is situated in a greater depth, the stress towards the surface is higher than into the depth of the material. The deeper the non-metallic inclusion is situated the more the proportion of higher stress tends to be in the in the direction of the surface. Therefore, it is not possible for the second crack to propagate far into the material, as the stress might be too low. Thus, an asymmetric fisheye can be formed. In addition, if the non-metallic inclusion is situated very close to the surface the opposite is possible. As the stress very close to the surface is minimal due to the compressive residual stresses, the crack first propagates primarily into the depth of the material, as the stress is higher in this region.

9.3 Fisheye formation

As mentioned in the fracture theory, it is hypothesized that the fisheye is formed by two different cracks. In Fig. 20, a fracture surface is shown where two other non-metallic inclusions (marked in green) prevent the fisheye from being completely ellipsoidal. This example highlights the fisheye formation theory of high-strength gears.

Fig. 20
figure 20

Not ellipsoidal fisheye (circled in red) caused by two non-metallic inclusions (marked in green) other than the crack initiating NMI (pulsator test, mn = 1.5 mm, 20MnCr5, 5.0 kN, 363,627 cycles)

Full size image

Furthermore, in Fuchs et al. (2021b), unfinished fisheyes were found where the fisheye has formed but not reached the surface. These teeth were not responsible for the initial failure but broke due to a delay in detecting the initial breakage and stopping the test rig. These failures could be characterized by a clearly visible gap between the edge of the fisheye and the surface. This observation supports the theory that as soon as the completely formed fisheye reaches the surface, a surface crack is initiated.

9.4 Exemplary fracture analysis

Figure 21, shows a typical fracture surface of a tooth root fracture. Figure 21a shows a macro image of the whole fracture area, whereas Fig. 21b shows an SEM image of the fisheye. Below, the fracture surfaces Fig. 21c–g are explained.

Fig. 21
figure 21

a Macro image of a typical fracture surface due to a non-metallic inclusion in the tooth root, b SEM image (×90 magnification) of the fisheye with the non-metallic inclusion and SEM close-up images (×1500 magnification) of the different fracture areas: c inside the fisheye, d area between fisheye and surface, e fatigue fracture area I with stable crack growth, f fatigue fracture area II with unstable crack growth, g and overload fracture area. (pulsator test, mn = 5 mm, 18CrNiMo7-6, 80 kN, 10,151,290 cycles)

Full size image

The fracture surface is very smooth within the fisheye Fig. 21c. This might be caused by one of two different reasons: Firstly, the crack propagation is very slow, so that the crack can grow through grains but does not grow along the grain boundaries. Secondly, according to Shiozawa et al. (2006), minimal movements of the two fracture surfaces relative to each other take place under cyclic loading which causes an additional smoothing of the fracture surface. In the region between the fisheye and the surface, a comparatively coarse fracture structure is found Fig. 21d. The crack initiation and propagation analysis carried out in this paper, assumes that after the fisheye reaches the surface, the material stress is so great that unstable crack growth briefly occurs there. If this fracture pattern is compared with the two fracture patterns from the fatigue fracture region with stable Fig. 21e and unstable Fig. 21f crack growth, fracture portions are shown that can be assigned to both comparison patterns. The larger part, however, resembles the fracture pattern with unstable crack growth in the fatigue fracture region II. In comparison with fatigue fracture area I with stable crack growth Fig. 21e, significantly faster crack propagation must therefore take place in the fracture area Fig. 21d.

In fatigue fracture region I with stable crack growth, a relatively smooth surface is shown. If this fracture pattern is compared with that within the fisheye, it can be seen that apart from the smoothing of the surface within the fracture lens, there is not a very large difference. It can therefore be assumed that the crack propagation velocity in fatigue fracture region I is only one to two orders of magnitude higher than the crack propagation velocity within the fisheye. In the fracture region with unstable crack propagation, fatigue fracture region II, the crack propagates rapidly. Cleavage fractures occur here. The fracture surface is very rough and fissured. If the remaining component cross-section then becomes too small, overload fracture occurs. This can be seen in Fig. 21a where the fracture surface appears slightly darker in the lower half. This area is characterized by a very rough surface (see Fig. 21g). In Fig. 21a the clearly smoother area of fatigue fracture region I with stable crack propagation, which is semicircular in shape, can also be seen. In contrast, the transition from fatigue fracture area II to the overload fracture region is a straight line parallel to the axial direction.

10 Summary of the crack initiation and propagation analysis

The crack initiation and propagation analysis for fisheye fracture in the tooth root fillet of high-strength gears can be summarized as followed:

  • Crack initiation occurs within a favorably oriented grain along the axis of maximum stress (parallel to the 30°-tangent) within the zone of highest stresses. The crack initiation is induced by repeated sliding of the crystal planes and formation of dislocations within this grain acc. to Nishijima and Kanazawa (1999) and Wang et al. (2018).

  • The initial crack growth occurs in the direction of the axis of maximum stress in two locations at the non-metallic inclusion. The two incipient cracks are then deflected in the direction perpendicular to the 30°-tangent. In the process of microcrack growth, if present, the FGA is also formed.

  • After formation of the two internal cracks and possibly an FGA, the two incipient cracks grow to the material surface (stage Ia) and to the material depth (stage Ib) as well as in the axial direction. When the two internal cracks have grown sufficiently far, they join to form a step at the inclusion as well as the fisheye (stage II).

  • Once the fisheye reaches the surface, a semi-elliptical surface crack is formed with short-term unstable crack growth. A semi-elliptical surface crack is formed (stage III), which is called fatigue fracture area I. During this process, a step is also formed at the far surface edge of the fisheye.

  • Afterwards the unstable crack growth begins (stage IV) and forms the fatigue fracture area II. Stage V refers to the overload fracture, which occurs at the time when the residual cross-sectional area can no longer support the load and the static strength of the material is exceeded.

11 Threshold value of the stress intensity factor

In the following, the influence of the residual stresses on the threshold value of the stress intensity factor is discussed. In Eq. (1) the definition according to Murakami et al. (1989) has already been given. Here ΔKth depends on the two factors material strength and projected inclusion size (representing the geometry of NMI). The material strength is represented by the Vickers hardness because this parameter can be easily obtained. The size of the non-metallic inclusion is allowed for by the “area”-parameter which is the projected area of the non-metallic inclusion determined, e.g. using SEM analysis.

If Eq. (1) is applied to the experimental tests that this paper is based on, it is important to consider the local hardness at the non-metallic inclusion because this varies with the depth as a result of the case-hardening process. In Fig. 22a, ΔKth calculated according to Eq. (1) is shown. It is apparent that values of ΔKth are roughly scattered between six and ten. However, according to the presented literature, for a crack initiation at a non-metallic inclusion with formation of an FGA, a ΔKth value of five is more common and a value of ten is quasi-equivalent to the transition to crack growth according to the Paris law.

Fig. 22
figure 22

a Values of ΔKth according to Eq. (1) with the local Vickers hardness value at the depth of the inclusion, fisheye failures of three different gear sizes are considered; b Values of ΔKth according to Eq. (3) incorporating the effect of the residual stresses at the non-metallic inclusion (error bars indicate the scatter band of the hardness to material strength relationship (see Eq. 2), only fisheye failures of the gears with a normal module of 1.5 mm are considered

Full size image

The problem here is the representation of the material strength by the hardness. In this particular case as shown in the simulation results, considerable residual stresses remain at the non-metallic inclusion in the investigated gears. These residual stresses cannot be represented by the hardness value but they nevertheless slow down crack growth or even prevent crack initiation. Therefore, a decision was made to substitute the hardness parameter in Eq. (1) with the material strength. According to (Casagrande et al. 2011; Murakami et al. 1989) Eq. (2) describes the correlation between the fatigue strength and the Vickers hardness for steels. If Eq. (2) is inserted in Eqs. (1), (3) is obtained.

$$ {\upsigma }_{{\text{w}}} = 1,6 \cdot {\text{HV }} \pm 0,1 \cdot {\text{HV}} $$
(2)
$$ {\Delta }K_{th,short,ss,local} = 2,77 \cdot 10^{ - 3} \cdot \left( {\frac{{\sigma_{w} }}{1,6 \pm 0,1} + 120} \right)\sqrt {area}^{1/3} $$
(3)

The value of \({\sigma }_{w}\) is obtained from the superposition of the simulated stresses and the measured residual stresses for each material variant, which is then evaluated at the depth of the non-metallic inclusion. However, due to the high computing effort of the simulation model, only failed test points of the gears with the normal module of 1.5 mm of the database mentioned in Table 1 are considered. Figure 22 b shows the values of ΔKth according to Eq. (3) incorporating the residual stresses. The error bars indicate the scatter band of the hardness to material strength relationship (c.f. Eq. (2)). It can be seen that the values of ΔKth are mainly between four and six and thus correlate with the value in the literature. Furthermore, a trend towards smaller values of ΔKth with a higher number of cycles is visible. The scattering might be due to the multiple error possibilities of the different measured parameters.

It can be concluded, that residual stresses have a great influence on the crack initiation and therefore on the value of ΔKth. It is shown that when the residual stresses are significant, e.g. due to a shot peening process, the material strength used to calculate ΔKth cannot be substituted by the hardness parameter. Therefore, the actual stress state including the residual stresses at the depth of a non-metallic inclusion must be considered. The numerical approach presented here is one way of determining the actual stress state.

12 Summary and subsequent steps

New and different requirements for gears due to lightweight design, high power density and operation in the VHCF-range pose challenges for the tooth root and tooth flank load carrying capacity. One possibility for meeting the increased demands towards higher tooth root load carrying capacity is to apply a shot-peening process after case-hardening. However, especially in the VHCF-range, the crack initiation site can shift to a subsurface region and often leads to fisheye failures at a non-metallic inclusion. If these fisheye failures in the tooth root fillet of gears are compared with fisheyes in a standard specimen, a few differences in the crack area characteristics can be observed. The working theory was that the multiaxial stress state in combination with residual stresses due to the case-hardening and a subsequent shot peening process influenced the distinctive crack characteristics.

In this paper, a numerical simulation was performed in which not only load stresses but also compressive residual stresses were considered. A crack initiation and propagation analysis for fisheye failures in the tooth root fillet of gears was performed taking into consideration the numerical results and different fracture characteristics. Subsequently, further experimental results and fracture analyses were compared with fracture theory. Finally, the calculation of the ΔKth value was evaluated taking into consideration the influence of residual stresses.

The main findings in this paper are:

  • The results of the simulation show a shift of planes of the areas of maximum stress at the non-metallic inclusion if the compressive residual stresses are taken into consideration. Among other things, this is a possible explanation for the step at the non-metallic inclusion.

  • The presented crack initiation and propagation analysis for fisheye failures at non-metallic inclusions in the tooth root fillet of gears is based on the results and theories presented in previous papers and simply links these theories; we have not derived our own fracture theory.

  • The crack initiation and propagation analysis can be divided into six different stages:

    1. o

      crack initiation occurs at two different locations on the non-metallic inclusion which leads to the formation of a step;

    2. o

      formation of an FGA;

    3. o

      formation of the fisheye occurs through two independent cracks that unite to form a single crack;

    4. o

      when the surface is reached, the fisheye is considered to be a surface crack;

    5. o

      further crack growth initially occurs stable in fatigue fracture region I;

    6. o

      and then unstable crack growth occurs within fatigue fracture region II until overload fracture occurs.

  • If high compressive residual stresses are present in a component, it is recommended that Vickers hardness values should not be used as a parameter for the material strength when calculating the stress intensity factor ΔKth because the residual stresses are inadequately represented by this parameter. A calculation using the simulation-determined stress state instead, which takes into account the compressive residual stresses, provides results that fit very well to the values found in the literature for the fisheye failure mechanism.

In this paper and in literature referenced in it, it is assumed that the cracks at non-metallic inclusions are initiated in favorably orientated former austenite grains in the area of highest stress during cyclic loading. In addition, some theories in the referenced literature consider mechanisms inside grains or the grain size itself as very important factors in the formation and appearance of an FGA in the vicinity of a non-metallic inclusion. Therefore, in the future, investigations on case-hardened, shot-peened gears should be carried out in which the former austenite grain size is varied. This could provide more insight on how the crack initiation, propagation and formation of an FGA is dependent on the former austenite grain size. Furthermore, shot peening alters the dislocation density and leads to plastic deformation of the surface material. These influences should be considered for the crack propagation process in the future.