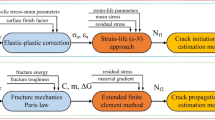
Abstract
One of the key challenges of epicyclic gearboxes in turbo gearbox applications is the high number of load cycles reached by the gearbox components. Standards such as ISO 6336 deliver design guidelines for bending strength up to a limiting number of NG = 3∙106 and AGMA up to 107 load cycles which is far less than the expected lifetime of turbo gearbox applications.
To design gears for geared turbofans safely and weight-optimized, the tooth root load capacity in the very high cycle fatigue (VHCF) range must be known as precisely as possible. Most VHCF SN-curve concepts show a continuously decreasing fatigue strength, so that a consideration of a constant fatigue strength level does not meet the material behavior. A life prediction model can be used to determine the specific load that can be carried for each number of load cycles.
In this paper, the nasgro crack growth equation is applied to gears to determine the tooth root life in the VHCF range. A lifetime for surface and sub-surface induced fractures is calculated, resulting in a stepped SN-curve. Most of the cycles until fracture occur during crack initiation and micro crack growth, while the macro crack is a small part of the total number of load cycles until tooth root fracture. The nasgro equation is able to represent micro and macro crack growth and is extended by further approaches to the threshold of crack initiation Kth, which also consider the characteristics of short and long crack growth. In addition, the tooth root stress depth curve (via FEM), the hardness depth curve, the residual stress depth curve and the defect distribution will be included in the life-time prediction as important influencing variables of the VHCF tooth root load capacity. The influence of the inputs is determined in an influence quantity analysis. In the future the lifetime prediction model is validated with rig tests up to the VHCF range.
Zusammenfassung
Eine der größten Herausforderungen von Planetengetrieben in Turbogetriebeanwendungen ist die hohe Anzahl von Lastzyklen, die die Getriebekomponenten erreichen. Normen wie ISO 6336 liefern Auslegungsrichtlinien für die Biegefestigkeit bis zu einer Grenzlastspielzahl von NG = 3∙106 und AGMA bis zu 107, was weit unter der erwarteten Lebensdauer von Turbogetriebeanwendungen liegt.
Um Zahnräder für Turbogetriebe sicher und gewichtsoptimiert auslegen zu können, muss die Zahnfußbelastbarkeit im Bereich der sehr hohen Zyklusermüdung (VHCF) möglichst genau bekannt sein. Die meisten VHCF-Wöhlerlinienkonzepte zeigen eine kontinuierlich abnehmende Dauerfestigkeit, so dass eine Betrachtung eines konstanten Dauerfestigkeitsniveaus dem Werkstoffverhalten nicht gerecht wird. Mit Hilfe eines Lebensdauervorhersagemodells kann die spezifische Belastung bestimmt werden, die für jede Anzahl von Lastspielen getragen werden kann.
In dieser Arbeit wird die NASGRO-Risswachstumsgleichung auf Zahnräder angewendet, um die Zahnfußlebensdauer im VHCF-Bereich zu bestimmen. Es wird eine Lebensdauer für oberflächen- und suboberflächeninduzierte Brüche berechnet, was zu einer stufenförmigen Wöhlerlinie führt. Die meisten Zyklen bis zum Bruch treten während der Rissinitiierung und des Mikrorisswachstums auf, während der Makroriss nur einen kleinen Teil der Gesamtanzahl der Lastzyklen bis zum Zahnfußbruch ausmacht. Die NASGRO-Gleichung ist in der Lage, das Wachstum von Mikro- und Makrorissen darzustellen und wird durch weitere Ansätze zum Schwellenwert der Rissinitiierung Kth erweitert, die auch die Eigenschaften von kurzem und langem Risswachstum berücksichtigen. Zusätzlich werden der Zahnfuß-Spannungstiefenverlauf (über FEM), der Härtetiefenverlauf, der Eigenspannungstiefenverlauf und die Fehlstellengröße als wichtige Einflussgrößen der VHCF-Zahnfußtragfähigkeit in die Lebensdauerprognose einbezogen. Der Einfluss der Inputs wird in einer Einflussgrößenanalyse ermittelt. In Zukunft wird das Lebensdauer-Vorhersagemodell mit Prüfstandsversuchen bis in den VHCF-Bereich validiert.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and motivation
Due to mandatory weight optimization in aviation, aerospace transmissions require a very high power density. On the one hand, this is achieved by high-purity materials produced in complex remelting processes. On the other hand, the roughness of the surfaces is optimized the residual compressive stresses close to the surface are applied by shot peening processes and a superfinishing process to optimize the roughness. The combination of high material purity and increased surface qualities can only be represented to a limited extent by standard-based approaches for tooth root load capacity calculation, since the optimization of the materials and surfaces leads to a shift of the damage origin below the surface [5, 14, 20]. Surface-induced cracks grow more slowly, so that they occur in the area of high load cycles. The initial location of these cracks are inclusions below the surface. In fracture mechanics, lifetime models exist which allow the calculation of the component lifetime by considering the crack growth rate. These models can also include the initial location of the crack by combining them with the murakami approaches and have been applied successfully to standard specimens [14]. A high-speed stress test rig was set up in a EU clean aviation project to investigate the tooth root load capacity up to the VHCF range. In order to be able to determine the lifetime of the cracked tooth root, calculation approaches are required which include all the main influencing variables such as the point of origin of the damage, the tooth-specific hardness depth profile and the residual stress curves and the defect sizes [13]. For this purpose, a lifetime prediction model for the tooth root was developed [13]. In order to have scope in the gear design, a good knowledge of the scatter and the influence of the scatter on the load capacity is of high importance. An influence quantity analysis of the lifetime prediction model should reveal the effects.
2 State of the art
In order to be able to analyze the lifetime prediction model for the tooth root, it is important to consider the main influencing variables on the tooth root load capacity at first [13]. In addition to the gear-specific influencing variables, parameters from fracture mechanics are also decisive for the lifetime prediction model. These are determined in the Compact Tension (CT) test.
2.1 Factors influencing the tooth root load carrying capacity
The greatest influence on the tooth root load capacity can be exerted by changing the macro-geometry. In addition to the macro-geometry and geometry of the tooth root fillet, material selection, material cleanliness, heat treatment, residual stresses and surface roughness have an influence on the tooth root load capacity.
2.1.1 Material selection and cleanliness
In terms of material, a distinction can be made between different types of material, which in turn can be produced in different degrees of cleanliness. According to ISO 6336, case-hardened alloy steels have a higher strength than quenched and tempered steels or nitriding steels and are therefore often used for gears. But there are also differences within the case-hardened steels. stenico investigated gears made of the case-hardened steels 16MnCr5, 20MnCr5 and 18CrNiMo7–6 up to a limiting load cycle number of Nlim = 6·106 on the pulsator and varied the heat treatment, module size and peening condition [20]. Regardless of the heat treatment type and blasting condition, the 18CrNiMo7–6 showed an increased tooth root load capacity compared to the 16MnCr5 and 20MnCr5 [20]. In addition to the chemical composition and heat treatment of the material, the degree of cleanliness also plays a role. Defects at and below the surface form stress peaks due to notch effects and residual stresses, which reduce the local load capacity at the defect compared to the base material and lead to sub-surface induced tooth root fractures. ISO 6336 and DIN 3990 distinguishes between the material grades ML, MQ and ME in ascending order of cleanliness, with the tooth root load capacity being greatest for the highest cleanliness ME. According to Kamjou, a higher material cleanliness leads to an increase in the tooth root and flank load capacity [8]. The cleanliness is increased by multiple remelting.
2.1.2 Manufacturing
In the manufacturing chain, there are various variables that influence the tooth root load capacity. In addition to the choice of material, the type of heat treatment also has an influence on the tooth root load capacity. The tooth root load capacity is increased for low-pressure carburized gears compared to gas carburized gears [20]. Another control variable is the austenitizing temperature. In the case of low-pressure carburizing, a 20% reduction in the tooth root nominal stress that can be sustained was shown by raising the austenitizing temperature from TA = 940 °C to TA = 1050 °C [20]. There is also a significant influence of the gas quenching intensity on the component strength, with the maximum intensity having the lowest strength [20]. For case hardening there are specifications for the optimum tooth root load capacity for case hardening depth and edge hardness of gear teeth. The case depth should be in the range of Eht550 = 0.1–0.25 mn, whereby the optimum is reached at about Eht550 = 0.15 mn. An increase in the surface hardness above 700 HV no longer leads to a significant increase in the tooth root load capacity [16].
The surface roughness is a decisive factor for the tooth root load capacity, with respect to surface-induced fractures. Roughness peaks act like notches, which lead to excessive stresses. To achieve good tooth root load capacity, the surface roughness should therefore be as low as possible [9]. The influence of roughness on the bending strength can be described by Eq. 1.
Lower roughness in the tooth root can be achieved by co-grinding the tooth root during hard finishing or by a superfinishing process usually connected to shot peening.
After heat treatment, residual stresses arise due to carbon diffusion into the component and the associated volume changes. In addition, peening processes are often carried out after hard finishing in order to introduce compressive residual stresses into the near-surface areas in a targeted manner, which counteract the tensile stresses in operation and thus increase the local load capacity in the near-surface area. stenico achieved an increase in the fatigue-resistant tooth root nominal stress of 38–50% for 18CrNiMo7–6 by shot peening the tooth root, depending on the component size, compared to the non-peened variant [20]. BRETL investigated the influence of shot peening up to the increased limiting load cycle number of Nlim = 108. In BRETL’s investigations, surface and sub-surface induced tooth root fractures occurred. The fatigue strength of the surface-induced tooth root fractures was increased by 25%, that of the sub-surface-induced tooth root fractures by 15% compared to the non-peened variant [1].
2.1.3 Operating conditions
For the operating conditions, the test temperature, load peaks due to shocks and the stress ratio are important influencing variables on the load capacity. Load peaks are rare in test rig operation and are therefore neglected.
A planetary gear, see Fig. 1, illustrates the different stress ratios of gears. The sun gear is under a purely smoldering tension load (R = 0), while the planet gear sees a fully reversed bending load (R = −1). Brinck showed a reduction of the tooth root load carrying capacity by 15% for spur gears under fully reversed bending load (R = −1) compared to pure pulsating load (R = 0), which corresponds to the reversed bending load factor YM = 0.85 [2]. For other stress ratios, there is a linear relationship between the reversed bending load factor YM and the stress ratio R, see Fig. 1 [17]. The findings are incorporated in the reversed bending load factor YM, ISO 6336 [17]. In DIN 3990, the reversed bending load factor for R = −1 is specified as YM = 0.75. Further investigations of the reversed bending load factor were carried out on the influences of series-sequence effects, the shear component and the helix angle [2].
Brinck carried out his investigations of the reversed bending load factor YM up to a limiting load cycle number of Nlim = 107. For the very high cycle fatigue (VHCF) range (up to Nlim = 108), Hong showed a deviation of about 7% from the ISO 6336 reversed bending load factor according to Brinck in the running test with the reversed bending load factor YM (R = −1) = 0.781 [2, 7]. Hong used a test speed of n = 4400 rpm which is low for the VHCF range [7].
Lisle describes a decrease in tooth root load capacity in pulsator testing for elevated test temperatures of 130 °C for the aerospace steels Lesco 53 (AMS6308), M50NiL (AMS6278), Ferrium QC64 (AMS6509), Ferrium QC61 (AMS6517), H11 (AMS 6487), and CSS-42L compared to room temperature [12]. Increasing the temperature changes the fracture mechanical properties, which affects the crack growth rate.
2.2 The compact tension test
In the compact tension test (CT test), the crack propagation curve, see Fig. 2, of a material can be determined. From the crack propagation curve, the fracture mechanics parameters, such as book toughness KIC, threshold value of the stress intensity Kth, the parameters of the paris straight lines m and C and the nasgro parameters p and q can be derived. For this purpose, the compact tension specimens are subjected to cyclic stress, as shown in Fig. 2 top left, with a defined crack initiation. The crack growth rate is determined either by strain measurement at the crack opening or by the electropotential method via change of the electric resistance [19]. By measuring the crack growth rate da/dN at different stress intensities, the slope of the paris degrees m and the axis distance C can be determined. The PARIS equation can then be used to calculate the crack growth rate, or the life to failure, for different specimen geometries. Forman extended the paris equation by various stress factors R and Newman by crack opening effects [4, 15]. The nasgro equation is an extension of the paris equation which accounts for microcrack growth and residual stress fracture and is therefore applicable to all three phases of crack growth. In its current form, the nasgro equation can only be used for homogeneous materials. Thus, a use for gears with hardening depth curve is not possible.
Compact Tension Test and the Calculation of the Crack Growth Rate [3]
3 Aim and approach
The aim of the report is to obtain more precise knowledge of the variables influencing the fracture-mechanical lifetime prediction for the tooth root with nasgro. The procedure is divided into three work packages. First, in WP 1, the main influencing variables of the lifetime prediction model are identified. This is followed by extensions to the lifetime prediction model, such as the differentiation between short- and long-crack growth in WP 2. Then, in WP 3, an analysis of the influencing variables on the lifetime of the tooth root is determined with the extended lifetime prediction model.
4 Lifetime prediction model for the tooth root
In the state of the art, the influencing variables on the tooth root load capacity have been described. In order to build up a lifetime prediction model for the tooth root that is as meaningful as possible, the main influencing variables should be integrated into the calculation, see Fig. 3. The fracture mechanics life model for the tooth root is divided into 3 basic steps.
-
1.
The local stress state is determined. For this purpose, the course of the tooth root stress over the material depth is first determined by an FEM simulation. The FE stresses are summed up with the residual stresses (measured values) to the local stress
-
2.
The crack initiation depth is calculated by comparing the local stress intensity factor, which results from the local stress state, with the local material strength, i.e. the threshold value of the crack initiation Kth
-
3.
The location and size of the initial crack is now known, so that the service life can be calculated via the crack growth rate
4.1 Step 1: Simulation of the local stress state
The simulation of the tooth root stress is performed with abaqus assuming a solid test gear body. It is assumed that the contact between test pinion and test gear, does not affect the opposite simultaneous contact. To represent the reversed bending load, the flank contacts of the planetary gears are examined one after another in the simulation model. To determine the cyclic amplitude of the stress ∆σFEM, the maximum of the tensile side and the minimum of the shear side are considered. The torques M1 = 1500 Nm, M2 = 1600 Nm, M3 = 1700 Nm are simulated. The main normal stress (Max Principal) is evaluated. This results in a stress curve for each element and each node as a function of the rolling angle, as shown in Fig. 4 on the left for a surface element. Each element or each interpolation along an element edge is assigned a unique depth. From this follows the evaluation of the maximum amplitudes of the stresses in the depth for the three considered torques in Fig. 4 right.
4.2 Step 2: Calculation of the crack initiation depth
In order to understand crack propagation in the tooth root, knowledge of the location and shape of the initial crack is necessary at first. In fracture mechanics, the stress is described by the stress intensity factor KI and the material strength by the threshold value of the stress intensity Kth. If cyclic loading is considered, the amplitude of stress intensity ∆K and the amplitude of threshold value ∆Kth are used. A crack occurs when the local stress intensity is exceeded by the local stress, i.e. the ratio K/Kth > 1.
On the stress side, the course of the local tooth root stress over the material depth including the residual stress state is considered for crack initiation. First, the main normal stress in the tooth root is simulated in ABAQUS with two tooth meshes under reversed bending load, see 4.1.
Measured values of the tangential residual stresses σES are added to the local depth-dependent stress σ(w) via the residual stress sensitivity Me as mean stress with the local main normal stress σFEM(w) with the depth steps w [18].
The residual stress sensitivity Me can be represented by the local fatigue strength σw(w) and the tensile strength Rm [18].
According to Murakami, the local fatigue strength σw(w) depends on the defect size √area and the hardening depth and is therefore depth-dependent [14]. For surface cracks, the maximum averaged roughness Rz is used instead of the defect size √area as the initial crack.
In fracture mechanics, the stress in the principal normal direction is given by the stress intensity KI. KI is composed of the crack length a and the applied stress σ(w). The initial crack length a0 is used for crack initiation. Murakami gives the stress intensity KI under reversed load (R = −1) for surface and sub-surface induced cracks [14]. The initial crack length a0 for sub-surface induced fractures corresponds to the projected diameter of the inclusion √area and for surface induced fractures to the averaged maximum roughness Rz.
In fracture mechanics, the material strength is represented by the threshold value of the stress intensity Kth. Material properties are included in the material strength. For sub-surface-induced damage, the defect size and the hardness depth profile on the material side, and for surface-induced damage, the surface hardness and roughness, are the main factors influencing the stressability. According to Murakami, ∆Kth can be specified for short cracks depending on the defect size √area and the local hardness HV [14].
To determine the crack initiation depth, the ratio ∆KI/∆Kth is formed under cyclic loading for each depth step. For ∆KI/∆Kth > 1, crack growth takes place. A different ∆KI is used for surface and sub-surface cracks, Eqs. 6 and 7.
4.3 Step 3: Crack growth and lifetime calculation
The crack growth rate da/dN can be represented by the nasgro equation. In order to determine the lifetime N, the crack growth rate is integrated over the crack length a. The crack growth rate da/dN can be used as an interval. Since a distinction is made between short and long crack growth, the limits of the interval are the initial crack length a0, the transition crack length a* and the fracture crack length afracture.
C, m, p and q are material parameters which are determined empirically from compact tension tests [11]. The fracture toughness KIC is also determined from CT tests.
For short and long crack growth, different threshold values of the stress intensity ∆Kth are used. Equation 7 according to Murakami is exclusively applicable for short cracks below the transition crack length a* [14]. Forman gives ∆Kth for long crack growth [4].
In the compact tension test, the threshold value of the stress intensity is determined experimentally for different hardness states and compared with the formulas. For the range −2 ≤ R ≤ 0, the crack opening function f according to Newman is shown in Eq. 11, which results from Eqs. 12 and 13 [15].
Here, the factor α is between 1 and 3. For the plane stress state, α takes the value α = 1 and for the plane strain state, it has the value α = 3 [15]. The ratio of the maximum stress to the yield stress is assigned a constant value of σmax/σF = 0.3 for most materials used for gears [18]. The range of stress intensity ∆KI is given according to Eqs. 6 and 7.
4.4 Main influencing variables of the lifetime model
The influencing variables of the life prediction model with constant gear geometry are the hardness depth profile, the residual stress depth profile, the roughness, the defect size and the fracture mechanical parameters. Therefore, the influence on the lifetime of these factors is determined. First, however, the real scatter of the influencing variables is determined in a comprehensive material characterization of test gears in order to define reasonable variation ranges.
5 Material characterization
In order to be able to define input variables for the lifetime models including scattering ranges, a complete characterization of the material and gear properties is necessary. This requires:
-
The hardening depth and residual stress profile perpendicular to the 30° tangent of the tooth root fillet.
-
The defect size
-
The surface roughness
-
The crack propagation curve including C, m, p, q, Kth and KIC
5.1 Fracture mechanical investigations
To determine the fracture mechanical parameters C, m, p, q, Kth and KIC, which describe the crack growth rate, compact tension tests are carried out according to ASTM E399. In order to be able to map the typical local measurement state over the depth (hardness, residual stresses), the CT specimens are manufactured and tested with 3 different hardness states (edge hardness, core hardness and medium level). When extracting the CT specimens, it is important that the incipient crack lies on the diameter of the tooth root fillet and that the orientation of the incipient crack corresponds to the direction of the tooth root fracture (perpendicular to the 30° tangent of the tooth root fillet). The specimen-extracting process is illustrated in Fig. 5 on the left. Hardness dependencies of the fracture mechanical parameters can then be determined via the 3 hardness states and formulaic relationships can be established.
Sample extraction, variants and determination of the crack propagation curve [19]
The crack growth rate is measured by the electropotential method [19]. Progressive crack growth reduces the cross-sectional area of the specimens and increases the electric resistance [19]. Thus, the change in crack length over time can be determined.
The determination of the total crack propagation curve is thereby carried out in 3 experiments. It starts with the KIC test, which represents the upper limit of the crack propagation curve (residual stress fracture). First, a fatigue crack is generated by cyclic loading. Subsequently, the specimen is loaded quasi-statically by successively increasing the force until brutal breakage occurs [19].
The crack propagation curve is determined according to ASTM E647 in 2 tests, see Fig. 5 right. Before the tests, a crack of about 1 mm length is again generated by cyclic loading. In test 1, the maximum and minimum forces are kept constant. As the crack length increases, the stress intensity at the crack tip also increases. Thus, the upper part of the crack propagation curve can be depicted. In test 2, the stress intensity is decreased as the crack length increases until the threshold stress intensity Kth is reached and the crack no longer propagates, allowing the lower part of the crack propagation curve to be mapped [19].
6 Influencing variable analysis on the tooth root lifetime prediction model
For the analysis of the influencing variables on the lifetime, a reference variant is first determined on the basis of the drawing specifications of the gears. The gear geometry has no public access. The fracture mechanics parameters are adopted according to Lewicki [10, 11].
First the fracture mechanics parameters C, m, p and q are varied. The variation range is selected according to the literature data for different steels. The effect of the fracture mechanical parameters on the lifetime of the tooth root is shown in Fig. 6.
As the number of load cycles increases, the stress at the tooth root that can be endured approaches a limit value, so that we speak of a stress that can be tolerated permanently (endurance strength).
The influences can be summarized as follows:
-
An increase in the pitch m leads to a flattening of the fatigue strength.
-
An increased p leads to a flattening of the fatigue strength, because the crack growth rate in phase I is slowed down to the micro-crack growth
-
An increase of fracture toughness KIC leads to a slower da/dN in high load area
-
An increased axial distance C leads to increased crack growth rate and shifts the SN-curve to a lower fatigue life
-
An increased q leads to an increase of the fatigue strength in the area of high loads, since the crack growth rate in phase III is slowed down to the residual stress fracture.
After the analysis of fracture mechanical parameters, the influence analysis of hardness, residual stresses, defect size and surface roughness is performed, which is shown in Fig. 7. The defect size of the aerospace steel is assumed to be 30 µm (±10 µm). Increasing the defect size to 40 µm decreases the local load capacity for sub-surface crack initiation by 4.6% because the defect size is directly incorporated into the local fatigue strength. Decreasing the defect size to 20 µm increases the bending strength by 7%. The percentage increases correspond to the increases in the load capacity with reduced defect size given in the state of the art [8]. In addition, the increase of the initial crack size results in a lower fatigue life. For surface cracks, increasing defect size results in lower fatigue strength, since the crack growth rate da/dN increases.
The surface hardness HV = 750 HV is taken from the manufacturing specifications of the gear teeth including their tolerance (±50 HV). With increased surface hardness of 800 HV, the local bending strength and also the local threshold value of the stress intensity Kth increase, so that on the one hand a higher fatigue strength can be achieved for surface and sub-surface (5.7%) and also the crack growth rate is minimally slowed down. For the decreased surface hardness of 650 HV, the bending strength lowers by 5.6%. ISO 336, on the other hand, does not give any increase in tooth root strength above 650 HV [17].
The residual stress depth curve is derived from references of similar modulus and same process chain. A reduction of the residual stresses by 50% shows a reduced permanent stress of the sub-surface, since the local stress at the critical defect increases and thus also to a small extent the crack growth rate. Finally, the surface roughness Rz is varied. In the basic variant, a superfinished tooth root with the specified roughness of Rz = 0.4 µm is assumed. This is compared with a purely generating-ground tooth root with the specified roughness Rz = 1.5 µm and an increased roughness of Rz = 3 µm. The roughness only influences surface-induced fractures. With increased roughness, the stress that can be permanently sustained (at the surface) decreases by 29%. Whereas for the surface-ground variant (Rz = 0.4 µm) the fatigue stress of the surface is above that of the sub-surface. At Rz = 3 µm no more sub-surface-induced fractures occur. Compared to the ISO 6336 (Eq. 1), the values deviate. ISO 6336 (Eq. 1) indicates a decrease in bending strength of 4 and 6%.
The influencing analysis shows that the accuracy in the determination of C and m is very important, since they have the greatest influence on the lifetime prediction. The influences resulting from the gear manufacturing, such as hardness or defect size, have such a small influence within the manufacturing and material tolerances compared to C and m that a good validation of the fracture mechanics parameters is of high importance.
7 Summary and outlook
Current material data for the design of the tooth root load capacity are based on tooth root load capacity investigations up to a limiting load cycle number of N = 107. In aviation, the planetary gears of a geared turbofan quickly reach load cycle numbers of N > 108. Tooth root fractures that occur in this load cycle number range usually occur at flaws below the surface. However, the standard calculation only represents surface-induced tooth root fractures. The lifetime factor exists in the standard calculation as a safeguard for higher numbers of load cycles. However, in order to better estimate the service life of gears with sub-surface induced damage and to save weight, fracture mechanics offers a possibility to determine the lifetime of specimens via the crack growth rate. In contrast to gears, standard specimens, e.g. from tensile tests, usually show a homogeneous hardness and no residual stress depth profile. Therefore, the nasgro fracture mechanics model was extended using Murakami approaches to account for fracture mechanics parameters that vary with depth.
Subsequently, the main influencing variables on the tooth root bending capacity were highlighted and an influence quantity analysis of the extended nasgro model for the tooth root load capacity was performed. The influence quantity analysis shows that for the calculation of the lifetime, the safeguarding of the fracture mechanical parameters is of high importance. In order to be able to transfer fracture-mechanical lifetime prediction models to gears with good accuracy, extensive investigations of the crack growth rate of case-hardened steels of different hardness states are carried out in the project in the future. This is followed by cyclic tensile tests on axial HCF specimens with homogeneous hardness.
In the variation of the gear-specific input variables, it is shown that all necessary influencing variables can be covered by the lifetime prediction model. Finally, in the future the tooth root load capacity is investigated in the running test with the highspeed back-to-back test rig, which serve to validate the lifetime prediction model.
References
Bretl N (2010) Einflüsse auf die Zahnfußtragfähigkeit einsatzgehärteter Zahnräder im Bereich hoher Lastspielzahlen (Dissertation. Institut für Maschinen- und Fahrzeugtechnik – Lehrstuhl für Maschinenelemente. Technische Universität München)
Brinck P (1989) Zahnfußtragfähigkeit oberflächengehärteter Stirnräder bei Lastrichtungsumkehr (Diss. Forschungsstelle für Zahnräder und Getriebebau (FZG) der TU München)
Cifuentes H, Lozano M, Holušová T, Medina F, Seitl S, Fernández-Canteli A (2017) Modified disk-shaped compact tension test for measuring concrete fracture properties. 11. https://doi.org/10.1007/s40069-017-0189-4
Forman R, Mettu S (1992) Behavior of surface and corner cracks subjected to tensile and bending loads in a Ti-6Al-4V alloy. In: Fracture mechanics. Twenty-second symposium, vol 1, pp 519–546
Höhn B‑R, Tobie T, Bretl N (eds) (2008) Späte Zahnfußbrüche. Zahnfußbruch mit Rissausgang unter der Oberfläche an einsatzgehärteten Zahnrädern
Hong I, Teaford Z, Kahraman A (2022) A comparison of gear tooth bending fatigue lives from single tooth bending and rotating gear tests. Forsch Ingenieurwes 86(3):259–271. https://doi.org/10.1007/s10010-021-00510-w
Hong IJ, Kahraman A, Anderson N (2021) An experimental evaluation of high-cycle gear tooth bending fatigue lives under fully reversed and fully released loading conditions with application to planetary gear sets. J Mech Des. https://doi.org/10.1115/1.4047687
Kamjou L, Ölund P, Claesson E, Fagerlund J, Wicks G, Wennmo M, Hansson H (2016) Innovative steel design and gear machining of advanced engineering steel. Gear Technol 33(8):82–87
Klocke F, Brecher C (2017) Zahnrad- und Getriebetechnik. Auslegung – Herstellung – Untersuchung – Simulation, 1st edn. Hanser, München
Lewicki G, Ballarini R (1997) Rim thickness effects on gear crack propagation life. Int J Fract 87:59–86
Lewicki G, Ballarini R (1996) Gear crack propagation investigations. NASA technical memorandum, vol 107147
Lisle TJ, Little CP, Aylott CJ, Shaw BA (2022) Bending fatigue strength of aerospace quality gear steels at ambient and elevated temperatures. Int J Fatigue 164:107125. https://doi.org/10.1016/j.ijfatigue.2022.107125
Loevenich J (2022) Test rig for tooth root load capacity investigations and material model in the area of very high cycle fatigue of geared turbofans. In: Towards sustainable aviation summit proceedings
Murakami Y (2002) Metal fatigue. Effects of small defects and nonmetallic inclusions, 1st edn. Elsevier, Amsterdam
Newman JC, Raju IS (1983) Stress-intensity factor equations for cracks in three-dimensional finite bodies, p I‑238-I-238-28 https://doi.org/10.1520/STP37074S
Niemann G, Winter H (2003) Getriebe allgemein, Zahnradgetriebe – Grundlagen, Stirnradgetriebe, 2nd edn. Maschinenelemente, vol 2. Springer, Berlin
Norm (2019) Calculation of load capacity of spur and helical gears. Part 3: calculation of tooth bending strength, 6336 Teil 3. ISO copyright office, Genf
Radaj D, Vormwald M (2007) Ermüdungsfestigkeit. Grundlagen für Ingenieure, 3rd edn. Springer, Berlin, Heidelberg
Richard HA, Sander M (2012) Ermüdungsrisse. Vieweg+Teubner, Wiesbaden
Stenico A (2007) Werkstoffmechanische Untersuchung zur Zahnfußtragfähigkeit einsatzgehärteter Zahnräder (Diss. Institut für Maschinen- und Fahrzeugtechnik. TU München)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
J. Lövenich, M. Zalfen, D. Mevissen, J. Brimmers and C. Brecher declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lövenich, J., Zalfen, M., Mevissen, D. et al. Crack growth based tooth root life prediction model—an influence quantity analysis. Forsch Ingenieurwes 87, 1057–1067 (2023). https://doi.org/10.1007/s10010-023-00704-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10010-023-00704-4