Analysis of the peel test for elastic-plastic film with combined kinematic and isotropic hardening

Abstract

The paper is dedicated to the mechanical analysis of peel tests for a ductile film on an elastic substrate. This test is widely adopted to access the interface fracture energy. In the literature, the analytical analysis of the peel test is often based on the bending model to quantify the work done by bending plasticity within the film. Isotropic hardening is only considered. In the present work, a new contribution is proposed where the ductile film has an elastic-plastic behavior with combined kinematic-isotropic hardening. A semi-analytical expression for the work done by bending plasticity is obtained in the general case and a closed-form expression is found when only kinematic hardening is present. The validation of the theoretical work is established via finite element simulations of $90^o$ peel test. Two model materials having the same uniaxial tensile response are considered: one presents isotropic hardening while the second only kinematic hardening. The comparison between them enables quantification of the role of kinematic hardening in the prediction of the interface fracture energy.

Appendices

Appendix A. Stress-strain response for plane strain loading/unloading

Fig. 8

Schematic longitudinal stress-strain response during tensile loading/unloading, under plane strain conditions. The evolution of the associated backstress component $X_{11}$ is also presented

The mechanical response of a material point subjected to a strain loading (up to $\varepsilon _{11}^{max}>0$) and reverse unloading (back to zero total strain), under plane strain conditions is presented next. This loading path is representative of the situation experienced by a material point during a peel test (with $z<0$). Stress $\varvec{\sigma }$, backstress $\varvec{X}$ and strain $\varvec{\varepsilon }$ tensors have the structure provided in Eq. (6). The longitudinal stress-strain evolution together with the longitudinal backstress are displayed in Fig. 8 with positive longitudinal strain $\varepsilon _{11}^{max}>0$. In the elastic domain, from Hooke’s law, under incompressibility condition, one has:

$$\begin{aligned} \sigma _{11}=\frac{4E}{3} \varepsilon _{11}. \end{aligned}$$

(24)

The elastic phase ends when $|\varepsilon _{11}|=\frac{\sqrt{3}\sigma _0}{2E}$. During plastic loading up to $\varepsilon _{11}^{max}$, the longitudinal backstress $X_{11}$ evolves according to Eq. (5). From the yield condition Eq. (3), the definition of the longitudinal stress components $\sigma _{11}$ is found. The expressions of $X_{11}$ and $\sigma _{11}$ are:

$$\begin{aligned} \begin{aligned}&X_{11}=\frac{C}{\sqrt{3}\gamma }(1-\exp (-\gamma p)\\&\sigma _{11}=2 X_{11}+\frac{2}{\sqrt{3}}(\sigma _0+Q(1-\exp (-bp))), \end{aligned} \end{aligned}$$

(25)

where the accumulated plastic strain during the first plastic loading phase is estimated as $p=\frac{2}{\sqrt{3}}|\varepsilon _{11}|-\frac{\sigma _0}{E}$.

For the elastic unloading, the following relationship holds:

$$\begin{aligned} \sigma _{11}-\sigma _{11}^{max}=\frac{4E}{3}(\varepsilon _{11}-\varepsilon _{11}^{max}), \end{aligned}$$

(26)

where $\sigma _{11}^{max}$ is the longitudinal stress at the total strain $\varepsilon _{11}^{max}$. The unloading stage is maintained until the reverse plastic loading stage starts. Let us denote $\varepsilon _{11}^{eu}$, the longitudinal strain when the elastic unloading ends. From the yield condition (3), one obtains:

$$\begin{aligned} \sqrt{3} |\frac{\sigma _{11}^{eu}}{2}-X_{11}^{max}| =\sigma _0+R(p^{max}), \end{aligned}$$

(27)

where $X_{11}^{max}$ designates the backstress component at $\varepsilon _{11}^{max}$ as no plastic strain is accumulated during elastic unloading. $p^{max}=\frac{2}{\sqrt{3}}|\varepsilon _{11}^{max}|-\frac{\sigma _0}{E}$ is the accumulated plastic strain at the end of the loading stage. From Eqs (26) and (27), the longitudinal strain $\varepsilon _{11}^{eu}$ is:

$$\begin{aligned} \varepsilon _{11}^{eu}=\varepsilon _{11}^{max}-\frac{\sqrt{3}}{E}(\sigma _0+Q(1-\exp (-b p^{max}))). \end{aligned}$$

(28)

During the reverse plastic loading stage, combining Eqs (3), (4) and (5), the backstress and Cauchy stress components are defined as follows:

$$\begin{aligned} \begin{aligned}&X_{11}=-\frac{C }{\sqrt{3}\gamma }+(\frac{C}{\sqrt{3} \gamma }+X_{11}^{max})\exp (-\gamma (p-p^{max})) \\&\sigma _{11}=2\left( X_{11}-\frac{\sigma _0}{\sqrt{3}}-\frac{Q}{\sqrt{3}}(1-\exp (-bp))\right) , \end{aligned} \end{aligned}$$

(29)

where the accumulated plastic strain during the reverse plastic loading phase is estimated as $p=p^{max}+\frac{2}{\sqrt{3}}|\varepsilon _{11}-\varepsilon _{11}^{eu}|$.

When the material point is subjected to loading/unloading with $\varepsilon _{11}^{max}<0$ (as for the part of the film with $z>0$), the above formula Eqs (25), (29) are still valid with adequate change of sign. Indeed, expressions for the elastic loading (24) and elastic unloading (26) are unchanged. Concerning the first plastic loading, Eq. (25) becomes:

$$\begin{aligned} \begin{aligned}&X_{11}=-\frac{C}{\sqrt{3}\gamma }(1-\exp (-\gamma p)) \\&\sigma _{11}=2 X_{11}-\frac{2}{\sqrt{3}}(\sigma _0+Q(1-\exp (-bp))). \end{aligned} \end{aligned}$$

(30)

The condition for reverse plastic loading (27) is still valid, leading to the following definition of $\varepsilon _{11}^{eu}$:

$$\begin{aligned} \varepsilon _{11}^{eu}=\varepsilon _{11}^{max}+\frac{\sqrt{3}}{E}(\sigma _0+Q(1-\exp (-b p^{max}))). \end{aligned}$$

(31)

Finally the expressions of the backstress and of the stress during the reverse plastic loading stage are:

$$\begin{aligned} \begin{aligned}&X_{11}{=}\frac{C}{\sqrt{3} \gamma }{-}\left( \frac{C}{\sqrt{3} \gamma }{-}X_{11}^{max}\right) \exp \left( -\gamma (p-p^{max})\right) \\&\sigma _{11}=2\left( X_{11}+\frac{\sigma _0}{\sqrt{3}}+\frac{Q}{\sqrt{3}}(1-\exp (-bp))\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(32)

Note that expressions for the accumated plastic strain p during the different phases are preserved.

The above expressions provide the expressions of the longitudinal stress and strain faced by the copper material during bending/reverse bending loading. They have been validated based on finite element calculations, Fig. 5.

Appendix B. Expression for the work done by bending plasticity

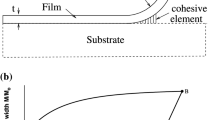
The present appendix provides the expression of the work done by bending plasticity $\varPsi$ by considering successsively the four stages (elasticity, plasticity, elastic unloading and reverse plastic loading) observed during peeling. From the elastic response of the film along path (OA), see Fig. 1b, one obtains based on Eq. (8):

$$\begin{aligned} \int _{0}^{K_e} MdK = \frac{\sigma _o^2 t}{6 E}. \end{aligned}$$

(33)

As the curvature $K_B$ is larger than $K_e$, one needs to evaluate the contribution to $\varPsi$ along (AB). The relationship between the moment M and the curvature K is given by Eq. (10). With the definition

$$\begin{aligned} F(-\frac{2 \gamma K}{\sqrt{3}}, \frac{t}{2}) = -\exp (-\frac{\gamma K t}{\sqrt{3}})\left( \frac{t\sqrt{3}}{4\gamma K}+\frac{3}{4 \gamma ^2 K^2}\right) , \end{aligned}$$

and with a change of variable $u=\frac{\gamma K t}{\sqrt{3}}$, one easily gets:

$$\begin{aligned}&\int _{K_e}^{K_B} F(-\frac{2 \gamma K}{\sqrt{3}}, \frac{t}{2}) dK =\frac{3}{4 \gamma ^2} \nonumber \\&\left[ G\left( -\frac{\gamma t}{\sqrt{3}}, K_B\right) - G\left( -\frac{\gamma t}{\sqrt{3}}, K_e\right) \right] , \end{aligned}$$

(34)

where $G(x,y) =\frac{\exp (xy)}{y}$. The work done by bending plasticity along the path (AB) is therefore:

$$\begin{aligned}&\int _{K_e}^{K_B} MdK = \frac{\alpha t^2}{2 \sqrt{3}}(K_B-K_e)\nonumber \\&+(\frac{\sigma _o}{\sqrt{3}}- \frac{\sqrt{3} \alpha }{2})\frac{\sigma _o^2}{E^2}(\frac{1}{K_e}-\frac{1}{K_B}) \nonumber \\&-\frac{\sqrt{3} B_1}{b^2}\left[ G\left( -\frac{b t}{\sqrt{3}}, K_B\right) - G\left( -\frac{b t}{\sqrt{3}}, K_e\right) \right] \nonumber \\&+\frac{\sqrt{3}B_1}{b}\exp (-\frac{b \sigma _o}{E}) (\frac{\sigma _o}{E}+\frac{1}{b})(\frac{1}{K_B} -\frac{1}{K_e})\nonumber \\&-\frac{\sqrt{3} B_2}{\gamma ^2}\left[ G\left( -\frac{\gamma t}{\sqrt{3}}, K_B\right) - G\left( -\frac{\gamma t}{\sqrt{3}}, K_e\right) \right] \nonumber \\&+\frac{\sqrt{3}B_2}{\gamma }\exp (-\frac{\gamma \sigma _o}{E}) (\frac{\sigma _o}{E}+\frac{1}{\gamma })(\frac{1}{K_B} -\frac{1}{K_e}). \end{aligned}$$

(35)

For the unloading path (BC), the contribution to $\varPsi$ is readily obtained:

$$\begin{aligned} \int _{K_B}^{K_B-K_B^*} M dK = - M_B K_B^* + \frac{E t^3}{18} (K_B^*)^2. \end{aligned}$$

(36)

For the reverse plastic loading phase (CD), no explicit expression can be found in the general case with combined isotropic and kinematic hardening. The expression of M given by Eq. (14) involves an integral term. In addition, the position of the elastic-plastic transition surface $h^{\prime }$ is defined implicitly via Eq. (13). Therefore, one obtains:

$$\begin{aligned}&\int _{K_B-K_B^*}^{0} M dK = \left[ \frac{8EK_Bh_B^3}{9} -\frac{2 \alpha }{\sqrt{3}}(h_B^2+\frac{t^2}{4}) \right. \nonumber \\&\left. + \frac{4 B_1}{\sqrt{3}} F(-\frac{2b K_B}{\sqrt{3}},h_B)+ \frac{4 B_2}{\sqrt{3}} F(-\frac{2\gamma K_B}{\sqrt{3}},h_B) \right] \nonumber \\&(K_B^*-K_B) + I, \end{aligned}$$

(37)

where the term I is defined by Eq. (19).

By adding Eqs. (33), (35), (36) and (37), the semi-analytical expression for the work done by bending plasticity $\varPsi$ given in Eq. (18) is obtained, for a material presenting combined kinematic and isotropic hardening.

Appendix C. Explicit relationship for kinematic hardening

For a material with kinematic hardening only, the coefficient responsible for isotropic hardening vanishes: $Q=0$ leading to $B_1=0$. It has already been mentioned that the curvature $K_B^*$ defined in Eq. (12) has a simple expression in that case: $K_B^*=2 K_e$. In addition, the elastic-plastic transition surface during reverse plastic loading $h^{\prime }$ has also an explicit relationship. From Eq. (13), one gets: $h^{\prime }=\frac{\sqrt{3}\sigma _0}{E(K_B-K)}$. Thus, it is possible to propose a closed-form expression for the integral term of Eq. (14). Therefore, an analytical expression of the bending moment is found, when reverse plastic loading takes place:

$$\begin{aligned}&M=\frac{\sigma _0^2}{E^2K_B^2}(\frac{\sigma _0}{\sqrt{3}}-\frac{\sqrt{3}\alpha }{2}) -\frac{\alpha t^2}{2\sqrt{3}}\nonumber \\&-\frac{4B_2}{\sqrt{3}} \exp (-\frac{\gamma \sigma _0}{E})(\frac{3\sigma _0}{4 E \gamma }+\frac{3}{4\gamma ^2})\frac{1}{K_B^2}\nonumber \\&+\left( \frac{4\sigma _0^2}{E^2}(\sqrt{3}\alpha -\frac{2\sigma _0}{\sqrt{3}})+\frac{8B_2}{\sqrt{3}}\exp (-\frac{\sigma _0 \gamma }{E})(\frac{3\sigma _0}{2 \gamma E}+\frac{3}{4 \gamma ^2})\right) \nonumber \\&\frac{1}{(K_B-K)^2}+\frac{ 4B_2}{\sqrt{3}}\left[ 2\exp (\frac{\sigma _0 \gamma }{E}) F(-\frac{2\gamma (K_B-K)}{\sqrt{3}},\frac{t}{2}) \right. \nonumber \\&\left. - \exp (2\frac{\sigma _0 \gamma }{E}) F(-\frac{2\gamma (2K_B-K)}{\sqrt{3}},\frac{t}{2}) \right] \nonumber \\&+ \frac{4 B_2}{\sqrt{3}}\left[ \frac{ \exp (2\frac{\sigma _0 \gamma }{E})}{(2K_B-K)^2} F(-\frac{\sqrt{3}\sigma _0}{E}\frac{ (2K_B-K)}{K_B-K},\frac{2\gamma }{\sqrt{3}}) \right. \nonumber \\&\left. - \frac{1}{K_B^2} F(-\frac{\sqrt{3}\sigma _0}{E}\frac{K_B}{K_B-K},\frac{2\gamma }{\sqrt{3}})\right] , \end{aligned}$$

(38)

where $\alpha =\sigma _0+\frac{C}{\gamma }$ for pure kinematic hardening.

From the explicit expressions of the moment curvature relationship along the whole loading path (OABCD), the work done by bending plasticity (or the work expenditure) per unit crack advance is evaluated in closed-form:

$$\begin{aligned} \varPsi= & {} \frac{\sigma _o^2 t}{6E}+\frac{\alpha t^2}{2 \sqrt{3}}(K_B-K_e) \nonumber \\&+(\frac{\sigma _o}{\sqrt{3}}- \frac{\sqrt{3} \alpha }{2})\frac{\sigma _o^2}{E^2}(\frac{1}{K_e}-\frac{1}{K_B}) \nonumber \\&-\frac{\sqrt{3} B_2}{\gamma ^2}\left[ G\left( -\frac{\gamma t}{\sqrt{3}}, K_B\right) - G\left( -\frac{\gamma t}{\sqrt{3}}, K_e\right) \right] \nonumber \\&+\frac{\sqrt{3}B_2}{\gamma }\exp (-\frac{\gamma \sigma _o}{E}) (\frac{\sigma _o}{E}+\frac{1}{\gamma })(\frac{1}{K_B} -\frac{1}{K_e}) \nonumber \\&-2M_B K_e+\frac{2E t^3}{9} K_e^2 \nonumber \\&+\left[ \frac{\sigma _0^2}{E^2K_B^2} (\frac{\sigma _o}{\sqrt{3}}- \frac{\sqrt{3} \alpha }{2})-\frac{\alpha t^2}{2 \sqrt{3}} \right. \nonumber \\&\left. + \frac{4 B_2}{\sqrt{3}} F(-\frac{2\gamma K_B}{\sqrt{3}},h_B) \right] (2K_e-K_B) \nonumber \\&+\left( \frac{4 \sigma _0^2}{ E^2}(\sqrt{3}\alpha -\frac{2 \sigma _0}{\sqrt{3}})+\frac{4\sqrt{3}C}{\gamma }(\frac{\sigma _0}{\gamma E}+\frac{1}{2\gamma ^2})\right) \nonumber \\&(\frac{1}{K_B}-\frac{1}{2K_e}) \nonumber \\&+\frac{\sqrt{3}B_2}{K_B \gamma ^2}\left( G(-2\frac{\gamma \sigma _0}{E}, \frac{K_B}{2K_e}) -G(-2\frac{\gamma \sigma _0}{E}, 1) \right) \nonumber \\&+\frac{2\sqrt{3}B_2}{\gamma ^2}\left( G(-\frac{\gamma t}{\sqrt{3}}, 2K_e)-G(-\frac{\gamma t}{\sqrt{3}}, K_B)\right) \exp (\frac{\gamma \sigma _0}{E})\nonumber \\&-\frac{\sqrt{3}B_2}{\gamma ^2} \left[ \left( G(-\frac{\gamma t}{\sqrt{3}}, K_B+2K_e)-G(-\frac{\gamma t}{\sqrt{3}}, 2K_B) \right) \right. \nonumber \\&\left. +\frac{1}{K_B}\left( G(-2 \frac{\gamma \sigma _0}{E}, \frac{K_B+2K_e}{2K_e}) -G(-2\frac{\gamma \sigma _0}{E}, 2) \right) \right] \nonumber \\&\exp (2\frac{\gamma \sigma _0}{E}), \end{aligned}$$

(39)

where as in Simlissi et al. (2019), one adopts the following definitions: $G(x,y)=\frac{\exp (xy)}{y}$ and $F(\delta , z)=\exp (\delta z)(\frac{z}{\delta }-\frac{1}{\delta ^2})$. The above equation (39) can be obtained from Eqs (18) and (20) (with $Q=0$ and $B_1=0$, no isotropic hardening). Note also that when $B_2=0$ (no kinematic hardening), the expression for an elastic-perfectly plastic material obtained by Kim and Aravas (1988) or Aravas et al. (1989) is retrieved.

Appendix D. Uncertainty for the estimate of the interface fracture energy

Let us consider that the film behavior accounts for kinematic hardening only (model material 1). Material parameters are listed in Table 1 with $\gamma =5$. After a numerical (or experimental) peel test, the force per unit width P and the curvature $K_B$ are measured. Based on Eqs (16) and (39), the interface fracture energy is estimated. It has been shown in the core of the paper that for a given set of parameters, a difference in $\varGamma$ value exists when data of the peel test are analyzed adopting either an isotropic or kinematic hardening. For parameters adopted in the paper, the difference may reach $40\%$ for a weak interface, see Fig. 7. The question addressed in the present appendix is to compare this difference generated by the adopted modeling route (isotropic versus kinematic) to the one induced by uncertainties on data. When $\varGamma ^{EF}=1055 N/m$, the numerical force is $P=1440 N/m$ and the curvature $K_B=5525 m^{-1}$. Knowing the force, curvature and material properties, the model predicts: $\varGamma ^{kin}=1042 N/m$ while the corresponding quantity for isotropic hardening is $\varGamma ^{iso}=879 N/m$. The choice of the hardening law to analyze peel test leads in that case to a 163N/m difference and an underestimation of $16\%$ when isotropic hardening is adopted instead of kinematic hardening as it should be. Next, we assume that all quantities are known with an uncertainty of $5\%$. For the considered case, the propagation of uncertainties leads to an estimate $\varGamma ^{kin}=1042~ \pm 158$ ($15\%$). In a second configuration, $\varGamma ^{EF}=264 N/m$ is imposed in the simulation. We obtain: $P= 582.5 N/m$ and $K_B= 4545 m^{-1}$. Depending on the hardening choice, the two estimated are: $\varGamma ^{kin}= 264 N/m$ and $\varGamma ^{iso}=148 N/m$. In that case, adopting an isotropic hardening instead of the correct kinematic law leads to an underestimation of $44\%$. The uncertainty on this value is in that case: $\varGamma ^{kin}= 264 ~\pm 97 N/m$ ($37\%$). From the two above configurations, it is seen that uncertainties on data or the selection of a salient modeling route for hardening lead to equivalent range on the $\varGamma$ value, when uncertainties on measurements is set to $5\%$. The force per unit width P, the film thickness t, and the maximum curvature $K_B$ are the parameters which contribute mostly to the global uncertainty, more than $60\%$ of it. Interestingly, these are also the parameters which can be measured with a higher degree of accuracy, see for instance (Girard et al. 2021) for the thickness measurement. Instead of adopting $5\%$ on these three data, $2\%$ uncertainty is enforced while keeping $5\%$ uncertainty for the other parameters. For the strong interface configuration, one obtains: $\varGamma ^{kin}=1042~\pm 76 N/m~(7.3\%)$ and for the weak intervafe, $\varGamma ^{kin}=264~\pm 49 N/m ~(18\%)$. In that case, the modeling issue generates more difference than the one provided by data uncertainty. Therefore, the role of the hardening law is of primary importance, as already mentioned by Wei and Hutchinson (1998). It is quantified in the present work. Finally, the present contribution may be used for the interpretation of tests when decohesion process takes place, e.g. for peel tests.