1 Introduction

Dynamic fracture mechanics is a well establish field of research with significant relevance in many areas of engineering (Baker 1960; Craggs 1960; Freund 1972; Itou 1978; Ravi-Chandar and Knauss 1984a, b; Freund 1990; Xu and Needleman 1994; Washabaugh and Knauss 1994; Gao 1996; Sharon et al. 1996; Willis and Movchan 1997; Morrissey and Rice 1998; Hauch et al. 1999; Broberg 1999; Aranson et al. 2000; Cramer et al. 2000; Belytschko et al. 2003; Cox et al. 2005; Gross and Seelig 2011). It has been generally accepted that in an elastic medium cracks can only grow and propagate at speeds below the speed of Rayleigh waves (Freund 1990; Xu and Needleman 1994; Washabaugh and Knauss 1994; Gao 1996; Sharon et al. 1996; Willis and Movchan 1997; Morrissey and Rice 1998; Hauch et al. 1999; Broberg 1999). Beyond this speed linear elastic solutions can be shown to lead to a vanishing energy release rate (at least in Mode I fracture) which is incompatible with the energy required to create the new crack surface. However, recent results both experimental and computational have shown crack propagation at significantly higher speeds both in the intersonic range and even beyond the speed of sound (Rosakis et al. 1999; Needleman 1999; Abraham and Gao 2000; Huang and Gao 2001; Gao et al. 2001; Rosakis 2002; Abraham et al. 2002; Guo et al. 2003; Buehler et al. 2003; Hao et al. 2004). Moreover, some of the published results exhibit features akin to shock waves of supersonic flow where solution discontinuities are seen to emerge from the crack tip as it travels along the material (Petersan et al. 2004; Willmott and Field 2006; Radi and Loret 2008; Bizzarri et al. 2010; Schubnel et al. 2011; Barras et al. 2018; Yue et al. 2019; Mai et al. 2020). No analytical models have been reported that predict such behaviour in linear elasticity. This paper will provide mathematical models with solutions that closely resemble some of these results. These are not inconsistent with existing analytical theories in so far as they are based on full transfer from strain into kinetic energy and therefore neglect the energy required to create the new surface.

Classical mathematical analysis of dynamic crack propagation has been based on the solution of the governing second order equation for the displacement field as a function of time and position (Freund 1972; Burridge 1973; Freund 1990; Andrews 1976; Freund 1979; Burgers and Freund 1980; Broberg 1989, 1994; Andrews 1994; Obrezanova and Willis 2003, 2008). Freund (1972) obtained a fundamental solution for Mode I type fracture in an infinite linear elastic domain by considering the solution of the second order equation for a half-plane in conjunction with cohesive type tractions on the fracture plane, leading to rupture velocities limited by the Rayleigh wave speed. Burridge (1973), using similar methods in the case of Mode II type fracture, showed that in the case of friction type forces (lacking cohesion), it is possible to obtain rupture velocities of the value of the dilatational wave velocity. Andrews (1976), resorting to a finite difference type method, reconciled Freund’s and Burridge’s solutions by considering a slip-weakening type model which combined friction and cohesion. This was further confirmed by Freund in Freund (1979), Burgers and Freund (1980) and Broberg in Broberg (1989) and Broberg (1994), the latter for the special case of a Mode II rupture velocity equal to \(\sqrt{2}\) the shear wave speed. Andrews in Andrews (1994) extended his previous work to the case of mixed-mode shear cracks, albeit this time employing analytic solutions and the boundary element method, obtaining similar conclusions, that is, mixed-mode ruptures can propagate faster than the Rayleigh speed. In Obrezanova and Willis (2003), Obrezanova and Willis (2008), the authors study the stability of intersonic shear cracks and provide stress fields in the vicinity of the crack, first in plane strain and subsequently in three dimensions.

Numerical methods and solutions enumerated above are appropriate for smooth solutions but side-step possible solutions where the first derivatives of the displacement field are discontinuous across moving surfaces. It is now well-accepted that this discontinuous type solutions exist and they exhibit complex Mach cone type profiles for velocities and strains/stresses. Indeed, numerous references have reported these type of solutions through either experiments or atomistic simulations (Abraham and Gao 2000; Gao et al. 2001; Rosakis 2002; Abraham et al. 2002; Buehler et al. 2003; Hao et al. 2004; Petersan et al. 2004; Schubnel et al. 2011; Yue et al. 2019; Abraham 2001). These are known as weak solutions and satisfy certain jump conditions across the moving discontinuities, known as shocks (Eringen and Suhubi 1975; Gurtin et al. 2010; Bonet et al. 2021). Motivated by improving numerical simulations, significant research has been recently devoted to re-expressing the fundamental equations of solid dynamics as a set of conservation laws for the linear momentum and the deformation (Lee et al. 2013, 2014; Aguirre et al. 2014; Bonet et al. 2015; Aguirre et al. 2015; Haider et al. 2017). These conservation laws lead to a system of first order differential equations for the velocity field and the deformation together with associated jump conditions across moving shocks. These equations are well known in the classical literature but typically only used as a step towards a final second order equation in terms of displacements. Using them directly allows for weak solutions to be obtained that could otherwise be by-passed. First order conservation laws with moving discontinuities are commonly used in the solution of fluid dynamic problems (LeVeque 1992; Toro 1999; Trangenstein 2009) where solution patterns incorporating Mach shock waves are frequently encountered.

The aim of the paper is to provide mathematical solutions of steady-state crack propagation in the context of linear elastic elastodynamics, where the governing equations are expressed as a set of first order linear hyperbolic conservation laws with accompanying jump conditions. The resulting solutions are two-dimensional extensions of well known so-called “local” solutions in one dimension (Bažant and Belytschko 1985). It is not the premise of the paper to claim that these solutions can provide an exact description of the physical reality as they are constrained by the conservative nature of linear elasticity; whereas, clearly, fracture is an inherently dissipative process. Energy losses through the creation of new crack surfaces and inelastic dissipative effects near the tip are ignored by the purely elastic solutions proposed. Instead, the aim of the paper is to show that Mach type of shock wave patterns as well as intersonic and supersonic crack propagation can be explained in linear elasticity under the assumption that surface energy is negligible in relation to the available strain energy in the material. This represents the opposite end of the energy balance spectrum to the classical Griffiths theory, where all the available strain energy is assumed to be used to create the new surfaces. It is clear that real physical phenomena will be found somewhere in between these two extremes. The contribution of this paper is therefore to suggest that fast crack propagation leading to shock wave formation is governed by the transfer of strain energy into kinetic energy rather than into surface energy. An additional intended contribution of the paper is to provide the outcome of the proposed solutions as initial and boundary conditions for computational models where dissipative effects can then be incorporated with relative simplicity. This will be the subject of future research.

The paper is organised as follows. As a way of motivation, Section 2 provides a mathematical description of the simple 1-D fracture of a bar in terms of first order differential equations describing the evolution of the velocity and strain with associated jump conditions in linear elasticity. This leads to a simple so-called “local” solution in which strain energy is transferred into kinetic energy in its entirety and the physical implications of this transfer are discussed. Section 3 extends the first order linear elastodynamics equations to 2-D in terms of velocity vector and displacement gradient. The speed of pressure (or dilatational) and shear (or distortional) shock waves are derived from the jump conditions and linear elasticity constitutive equations. Section 4 postulates a two-shock solution for supersonic crack propagation in mode I fracture and determines the constitutive conditions for this solution to exist. As in the 1-D model exact energy preservation is shown to hold through the transfer of elastic energy into kinetic energy. Section 5 examines supersonic mode II crack propagation and obtains very similar solutions to mode I, albeit with more severe restrictions in relation to the range of material properties for which the model is valid. Section 6 presents an intersonic solution where the pressure shock travels ahead of the crack tip and the shear shock. Section 7 provides some concluding remarks and recommendations for further work.

2 Motivation: the local one-dimensional fracture solution

In order to motivate the more complex two-dimensional solutions developed in the following sections, consider first the simplest possible fracture problem consisting of a one-dimensional bar under uniaxial tension as shown in Fig. 1. For simplicity, it will be assumed that the bar is initially at rest, linearly elastic and under the action of a constant external traction T as shown in the Figure.

Fig. 1
figure 1

Simple 1-D fracture model for a bar under uniaxial tension

Full size image

At time \(t=0\) fracture takes place at the centre of the bar and the resulting motion is governed by a set of first order hyperbolic equations given as,

$$\begin{aligned} \frac{{\partial (\rho v)}}{{\partial t}}&= \frac{{\partial \sigma }}{{\partial x}}; \end{aligned}$$
(1a)
$$\begin{aligned} \frac{{\partial \varepsilon }}{{\partial t}}&= \frac{{\partial v}}{{\partial x}}, \end{aligned}$$
(1b)

where \(\rho \) denotes the density, v(x, t) the velocity field, \(\sigma (\varepsilon )=E\varepsilon \) is the stress, \(\varepsilon (x,t)\) the strain field and E the Young’s modulus of elasticity. Note that the above set of equations represent a set of first order linear hyperbolic equations from which the standard second order wave equation for the displacement u(x, t) can be easily derived by noting that \(v=\partial u /\partial t\) and \(\varepsilon =\partial u/\partial x\). However, in order to establish weak solutions, that is solutions that contain discontinuities, it is preferable to consider the first order equations directly together with their associated jump conditions:

$$\begin{aligned} \rho c\llbracket v \rrbracket&= - \llbracket \sigma \rrbracket ; \end{aligned}$$
(2a)
$$\begin{aligned} c\llbracket \varepsilon \rrbracket&= - \llbracket v \rrbracket , \end{aligned}$$
(2b)

where the notation \(\llbracket a \rrbracket = a^ + - a^ - \) has been used to indicate the jump of a variable across a shock or discontinuity travelling at speed c along the bar. Noting that \(\llbracket \sigma \rrbracket = E\llbracket \varepsilon \rrbracket \) and substituting (2b) into (2a) gives the speed of propagation of a discontinuity as,

$$\begin{aligned} c = \sqrt{\frac{E}{\rho }}. \end{aligned}$$
(3)

Note that this corresponds to the speed of the sound wave in the bar which can be obtained considering smooth solutions of classical wave propagation theory.

Consider now the material fracturing at \(t=x=0\) as shown in Fig. 1. This creates an initial condition where the stress at the fracture point vanishes and two release waves travel in opposite directions along each half of the bar as shown in the Fig. 1. The above jump conditions can be applied between the values of the variables ahead and behind the shock in either the left or right halves of the broken bar to give,

$$\begin{aligned} \rho c(0 - v) = - (\sigma - 0), \end{aligned}$$
(4)

and therefore, an instantaneous release velocity at either side of the fracture point is generated at time \(t=0\) with a value given by,

$$\begin{aligned} v = \frac{\sigma }{{\rho c}}. \end{aligned}$$
(5)

This represents a complete transfer of elastic energy at the point of fracture into kinetic energy as shown by the simple identity,

$$\begin{aligned} K = \frac{1}{2}\rho v^2 = \frac{1}{2}\rho \left( {\frac{\sigma }{{\rho c}}} \right) ^2 = \frac{1}{2}\frac{{\sigma ^2 }}{{\rho c^2 }} = \frac{1}{{2E}}\sigma ^2 = \frac{1}{2}E\varepsilon ^2. \end{aligned}$$
(6)

Essentially, fracture is modelled in the above equations as a sudden removal of the equal and opposing internal traction forces acting on the section where fracture takes place. The above model, often referred to as the local solution (Bažant and Belytschko 1985), neglects the amount of energy required to generate the new surfaces at the point of fracture and therefore energy is exactly transferred from elastic to kinetic energy. From the point of view of hyperbolic differential equations, this results in a Riemann problem in each half of the broken bar with a simple analytical solution (LeVeque 1992; Toro 1999; Trangenstein 2009). The boundary fluxes at the point of fracture, namely stress and velocity, must be compatible with the jump conditions. In linear elasticity this compatibility leads to exact energy balance since the shock wave travels at the speed of sound. It is the end velocity given in equation (5) that would be responsible for a slender wire curling in a whipping like fashion as it snaps under tension or a rubber band snapping back after fracture. Note that from a mathematical point of view the problem is well posed in elastodynamics without the need to introduce dissipative or length effects, provided that the first order conservation equations and the jump conditions are used (Bažant and Belytschko 1985).

The energy balance in the solution described above represents the opposite end of the spectrum to the classical Griffiths theory where all the available strain energy is transferred to surface energy. Arguably, all brittle fracture process would occupy a point somewhere between these two extremes, where some of the strain energy is transferred into kinetic energy and some into surface energy and some dissipated as heat. Of course, if the aim is to assess the possible onset of crack growth in a metal sheet, it is prudent to consider the energy balance as stated in classical Griffiths theory, leading to a quasi-static fracture problem. Alternatively, modelling the curling motion of a snapping cable (Tjavaras et al. 1998) should be approached from the other end. For instance, a high strength steel cable would snap at a strain energy level in the order of magnitude of \(1\; \text {MJ}/\text {m}^3\), whereas the order of magnitude of the surface energy is \(1 \text {J}/\text {m}^2\). Hence, the energy required to generate the new surfaces is contained in a sliver of cable of thickness in the region of \(1 \mu \text {m}\), which is negligible in comparison to the length of the cable.

From a mathematical point of view, dissipative effects to account for the surface energy can be introduced in the above hyperbolic equations by including conductive fluxes proportional to the gradient of the variables. This can be done through a dependency of stress on the gradient of the velocity, leading to a visco-elastic model (Schreyer and Chen 1986; Simo and Ju 1987; Sluys and de Borst 1992; Etse and Willam 1999; Bažant and Jirásek 2002), or a dependency on the gradient of \(\varepsilon \) which results in a classical weakly non-local model (Bažant and Jirásek 2002; Belytschko and Lasry 1989; De Borst and Muehlhaus 1992; Fleck and Hutchinson 1993; De Borst 2001). From a computational point of view, many alternative methodologies have been derived, ranging from smeared crack theory (Pijaudier-Cabot and Bažant 1987; Jirásek and Zimmermann 1998), strong discontinuity approaches (Simo et al. 1993; Chen and Sulsky 1995), cohesive zone models (Barenblatt 1962; Falk et al. 2001; Camacho and Ortiz 1996), extended finite element methods (Moës and Belytschko 2002; Dolbow et al. 2001), configurational force methods (Miehe and Gürses 2007), phase field models (Miehe et al. 2010; Hesch and Weinberg 2014; Hesch et al. 2017) and others.

The sections that follow will essentially extend the above local solution to 2-dimensional mode I and mode II fracture configurations.

3 Linear elastodynamics in 2-D

The aim of this section is to review the equations of linear elasticity in the form of first order hyperbolic equations with associated jump conditions, so that conceptually similar solutions to the above one-dimensional model can be derived in the case of 2-dimensional isotropic elasticity.

3.1 First order hyperbolic governing equations

The general dynamic equilibrium in linear elasticity is established by the momentum conservation equation which in the absence of external body forces is given by Eringen and Suhubi (1975), Gurtin et al. (2010), Bonet et al. (2021),

$$\begin{aligned} \frac{\partial (\rho \varvec{v})}{\partial t} =\mathrm {div} \varvec{\sigma }, \end{aligned}$$
(7)

where \(\mathrm {div}\) indicates the divergence operator (the contraction of the gradient by the last index) and \(\varvec{\sigma }\) denotes the Cauchy stress tensor, which in linear elasticity can be related to the displacement gradient \(\varvec{G}=\varvec{\nabla }\varvec{u}\) via a symmetric fourth order elasticity tensor \(\varvec{\mathcal {C}}\) as,

$$\begin{aligned} \varvec{\sigma }=\varvec{\mathcal {C}}:\varvec{G};\qquad \varvec{\mathcal {C}}=\lambda \varvec{I} \otimes \varvec{I} +\mu \varvec{\mathcal {I}}+ \mu \tilde{\varvec{\mathcal {I}}}. \end{aligned}$$
(8)

In this expression \(\lambda ,\mu \) denote the Lamé coefficients, \(\varvec{I}\) the second order identity tensor, \(\varvec{\mathcal {I}}\) the fourth order identity tensor and \(\tilde{\varvec{\mathcal {I}}}\) the fourth order tensor that maps second order tensors to their transpose, that is \(\tilde{\varvec{\mathcal {I}}}: \varvec{G}=\varvec{G}^T\). Equation (8) is more commonly written in terms of the symmetric strain tensor \(\varvec{\varepsilon }=(\varvec{G}+\varvec{G}^T)/2\) rather than the displacement gradient \(\varvec{G}\) but the outcome will be the same when equation (8)\(_b\) is used as the constitutive relationship.

Note that plane stress can be obtained by simply replacing \(\lambda \) in equation (8)\(_b\) by its equivalent or effective value \(\bar{\lambda }\) defined as,

$$\begin{aligned} \bar{\lambda } = \frac{{2\mu \lambda }}{{\lambda + 2\mu }}. \end{aligned}$$
(9)

No distinction will be made in what follows between plane strain and plane stress on the understanding that \(\lambda \) is replaced by \(\bar{\lambda }\) for the latter.

A first order hyperbolic equation for the evolution of \(\varvec{G}\) similar to equation (1b) is given by,

$$\begin{aligned} \frac{\partial \varvec{G}}{\partial t}=\mathrm {div}(\varvec{v} \otimes \varvec{I}). \end{aligned}$$
(10)

This equation simply states that the rate of change of \(\varvec{G}\) is given by the gradient of the velocities. Equation (10) is the small strain counterpart of the evolution equation for the deformation gradient described in references (Bonet et al. 2021; Lee et al. 2013, 2014; Aguirre et al. 2014; Bonet et al. 2015; Aguirre et al. 2015; Haider et al. 2017).

Equations (7) and (10) represent a set of first order linear hyperbolic equations for which analytical solutions can be obtained under appropriate initial and boundary conditions. However, the type of solutions sought are weak solutions containing moving discontinuities, which require the formulation of the jump conditions associated to the conservation laws (7) and (10). These are derived in the following sections.

3.2 Jump conditions and wave speeds

Consider a shock in the solution, that is a discontinuity surface \(\Gamma \) with unit normal \(\varvec{n}\) travelling inside the solid with normal speed c as shown in Fig. 2. Variables ahead of the shock are denoted with a “+” sign, whereas the value of variables behind the shock is identified with the superscript “-”.

Fig. 2
figure 2

Shock or solution discontinuity travelling inside a 2-D solid

Full size image

In the presence of discontinuous solutions, the conservation equations (7) and (10) have associated jump conditions given, respectively, by Eringen and Suhubi (1975), Gurtin et al. (2010), Bonet et al. (2021), Bonet et al. (2015),

$$\begin{aligned} \rho c\llbracket {\varvec{v}} \rrbracket&= - \llbracket \varvec{\sigma } \rrbracket {\varvec{n}}; \end{aligned}$$
(11a)
$$\begin{aligned} c\llbracket {\varvec{G}} \rrbracket&= - \llbracket {\varvec{v}} \rrbracket \otimes {\varvec{n}}. \end{aligned}$$
(11b)

Using the constitutive relationship between the stress tensor and the displacement gradient given by equations (8) and substituting equation (11b) into equation (11a) gives, after simple algebra, an eigenvalue equation in terms of the acoustic tensor \(\varvec{A}\) as,

$$\begin{aligned} \rho c^2 \llbracket {\varvec{v}} \rrbracket = {\varvec{A}}\llbracket {\varvec{v}} \rrbracket ;\qquad \varvec{A} = (\lambda + \mu ) {\varvec{n}} \otimes {\varvec{n}} + \mu {\varvec{I}}. \end{aligned}$$
(12)

There are two solutions to this eigenproblem, corresponding to pressure shock waves (also known as dilatation or longitudinal) and shear waves (Eringen and Suhubi 1975; Gurtin et al. 2010; Bonet et al. 2021, 2015). In the first instance the jump in velocity is proportional to the normal vector and the shock travels at the speed of sound as,

$$\begin{aligned} \llbracket {\varvec{v}} \rrbracket = \Delta v_n \,{\varvec{n}};\qquad c_p = \sqrt{\frac{{\lambda + 2\mu }}{\rho }}. \end{aligned}$$
(13)

The second solution is obtained by taking velocity jumps parallel to the surface tangent \(\varvec{\nu }\) leading to shear shocks travelling at the speed of shear wave as,

$$\begin{aligned} \llbracket {\varvec{v}} \rrbracket = \Delta v_s \,\varvec{\nu };\qquad c_s = \sqrt{\frac{\mu }{\rho }}. \end{aligned}$$
(14)

The ratio between the pressure and shear shock speeds will be a useful material parameter in the derivations that follow and can be variously expressed in terms of the Lamé coefficients or Poisson’s ratio \(\nu \) as,

$$\begin{aligned}&{\text {Plane strain: }} \quad \frac{{c_p^{} }}{{c_s^{} }} = \sqrt{\frac{{\lambda + 2\mu }}{\mu }} = \sqrt{\frac{{2 - 2\nu }}{{1 - 2\nu }}}; \end{aligned}$$
(15a)
$$\begin{aligned}&{\text {Plane stress: }} \quad \frac{{c_p^{} }}{{c_s^{} }} = \sqrt{\frac{{\bar{\lambda } + 2\mu }}{\mu }} = \sqrt{\frac{2}{{1 - \nu }}}. \end{aligned}$$
(15b)

Note that in the incompressible limit this ratio tends to infinity in the case of plane strain but in plane stress the speed of the pressure wave cannot exceed twice the speed of the shear wave. In fact, in plane stress the pressure wave should be more correctly described as normal or longitudinal wave as it involves changes in the thickness and therefore transversal out of plane distortion.

4 Mode I crack propagation

This section describes a mathematical solution for a propagating crack under mode I fracture consisting of a pair of shock waves, a pressure and a shear wave, propagating from the crack tip.

4.1 The two-shock model

Consider the steady-state propagation of a crack under mode I conditions in an infinite 2-dimensional medium. Prior to the arrival of the crack the material is in a state of uniform stress given by a vertical traction \(\varvec{\sigma }=\sigma _{22}\varvec{e}_2 \otimes \varvec{e}_2\) as shown in Fig. 3.

Inspired by the one-dimensional model described in Sect. 2, a solution is postulated whereby two shock waves, a shear and a pressure wave, separate three regions of constant stress, strain and velocity as shown in Fig. 3, where due to symmetry only the upper half of the continuum is depicted. Notice that a similar Mach cone type solution was experimentally reported in Fig. 2 in Reference (Petersan et al. 2004) and in Figs. 4 and 5a in Reference (Yue et al. 2019). The regions I, II and III are formally defined as:

Fig. 3
figure 3

Propagation of a crack under mode I conditions accompanied by pressure and shear shocks (top half only)

Full size image

  • Region I: unfractured body, satisfying:

    $$\begin{aligned} \varvec{\sigma }^{(I)} = \sigma _{22}^{(I)} \,{\varvec{e}}_2 \otimes {\varvec{e}}_2 ;\qquad {\varvec{v}}^{(I)} = {\varvec{0}}. \end{aligned}$$
    (16)

  • Region II: transition region with stress, strain and velocity to be determined by the jump conditions;

  • Region III: unloaded region with stress tensor satisfying no traction on the crack surface:

    $$\begin{aligned} \varvec{\sigma }^{(III)} {\varvec{e}}_2 = {\varvec{0}}. \end{aligned}$$
    (17)

These three regions are separated by straight pressure and shear shocks originating from the crack tip and travelling at angles \(\alpha _p\) and \(\alpha _s\), respectively. At the crack tip, the intersection of the shear and pressure waves with the crack imply that the speed of the crack is related to the pressure and shear wave speeds as,

$$\begin{aligned} v_c = \frac{{c_p }}{{\sin \alpha _p }} = \frac{{c_s }}{{\sin \alpha _s }};\qquad \frac{{\sin \alpha _p }}{{\sin \alpha _s }} = \frac{{c_p }}{{c_s }}. \end{aligned}$$
(18)

Note that the existence of a solution as described above entails supersonic crack propagation as equation (18)\(_a\) implies that \(v_c \ge c_p \ge c_s\). Intersonic solutions can be found if the pressure shock wave is allowed to travel ahead of the crack tip. These solutions will be explored in a later section.

4.2 Velocity and stress relationships

The constant state of stresses and velocities in the three regions described above implies that the differential equations (7) and (10) are trivially satisfied. The key to determine the validity of the postulated solution is the satisfaction of the jump conditions at each shock wave and appropriate boundary conditions at the crack surface. Consider first the enforcement of the momentum jump condition (11a) at the pressure shock wave as,

$$\begin{aligned} \rho c_p \left( {{\varvec{v}}^{(I)} - {\varvec{v}}^{(II)} } \right) = - \left( {\varvec{\sigma }^{(I)} - \varvec{\sigma }^{(II)} } \right) {\varvec{n}}_p. \end{aligned}$$
(19)

Across the pressure shock the velocity jumps, and therefore the traction jumps, will be parallel to the normal vector \(\varvec{n}_p\) and can be expressed as,

$$\begin{aligned}&{\varvec{v}}^{(I)} - {\varvec{v}}^{(II)} = - {\varvec{v}}^{(II)} = \Delta v_n \,{\varvec{n}}_p ;\qquad \nonumber \\&\quad \left( {\varvec{\sigma }^{(I)} - \varvec{\sigma }^{(II)} } \right) {\varvec{n}}_p \mathrm{{ }} = \Delta t_n \,{\varvec{n}}_p, \end{aligned}$$
(20)

where the shock condition, equation (19), implies that the normal velocity and normal traction jumps, \(\Delta v_n\) and \(\Delta t_n\) respectively, are related as,

$$\begin{aligned} \Delta v_n = - \frac{{\Delta t_n }}{{\rho c_p }}. \end{aligned}$$
(21)

Consider next the enforcement of the displacement gradient jump condition (11b) across the pressure shock as,

$$\begin{aligned} c_p \left( {{\varvec{G}}^{(I)} - {\varvec{G}}^{(II)} } \right) = - \left( {{\varvec{v}}^{(I)} - {\varvec{v}}^{(II)} } \right) \otimes {\varvec{n}}_p. \end{aligned}$$
(22)

Substituting for the jump in velocity from equations (20)\(_a\) and (21), gives the displacement gradient in the intermediate region as,

$$\begin{aligned} {\varvec{G}}^{(I)} - {\varvec{G}}^{(II)} = \frac{{\Delta t_n }}{{\rho c_p^2 }}\,{\varvec{n}}_p \otimes {\varvec{n}}_p. \end{aligned}$$
(23)

Multiplying the above equation by the elasticity tensor gives the stress tensor at the intermediate region as,

$$\begin{aligned} \varvec{\sigma }^{(II)} = \varvec{\sigma }^{(I)} - \frac{{\Delta t_n }}{{\rho c_p^2 }}(\lambda {\varvec{I}} + 2\mu \,{\varvec{n}}_p \otimes {\varvec{n}}_p ). \end{aligned}$$
(24)

The same derivations can now be repeated across the shear shock where the velocity and traction jumps are parallel to the tangential unit vector as,

$$\begin{aligned} {\varvec{v}}^{(II)} - {\varvec{v}}^{(III)} = \Delta v_s \,\varvec{\nu }_s ;\qquad \left( {\varvec{\sigma }^{(II)} - \varvec{\sigma }^{(III)} } \right) {\varvec{n}}_s \mathrm{{ }} = \Delta \tau \,\varvec{\nu }_s. \end{aligned}$$
(25)

The jump condition now gives a relationship between the jump in tangential velocity and shear stress as,

$$\begin{aligned} \Delta v_s = - \frac{{\Delta \tau }}{{\rho c_s }}. \end{aligned}$$
(26)

The displacement gradient jump condition across the shear shock combined with the above relationship between jumps in tangential velocity and shear stress gives,

$$\begin{aligned} {\varvec{G}}^{(II)} - {\varvec{G}}^{(III)} = \frac{{\Delta \tau }}{{\rho c_s^2 }}\,\,\varvec{\nu }_s \otimes {\varvec{n}}_s. \end{aligned}$$
(27)

Finally, multiplying by the elasticity tensor and noting that \(\mu = \rho c_s^2 \) yields an expression for the stress tensor in region III as,

$$\begin{aligned} \varvec{\sigma }^{(III)} = \varvec{\sigma }^{(II)} - \Delta \tau ({\varvec{n}}_s \otimes \varvec{\nu }_s + \varvec{\nu }_s \otimes {\varvec{n}}_s ). \end{aligned}$$
(28)

Combining equations across both shocks enables direct relationships to be established between the velocity and stresses in region III and those in region I. For instance, using equations (20)\(_a\), (21), (25)\(_a\) and (26) and noting that the velocity in region I vanishes gives an expression for \({\varvec{v}}^{(III)}\) as,

$$\begin{aligned} {\varvec{v}}^{(III)} = \frac{{\Delta t_n }}{{\rho c_p }}{\varvec{n}}_p + \frac{{\Delta \tau }}{{\rho c_s }}\varvec{\nu }_s. \end{aligned}$$
(29)

Similarly, combining equations (24) and (28) gives the stress in region III as,

$$\begin{aligned} \varvec{\sigma }^{(III)}= & {} \varvec{\sigma }^{(I)} - \frac{{\Delta t_n }}{{\rho c_p^2 }}(\lambda {\varvec{I}} + 2\mu \,{\varvec{n}}_p \otimes {\varvec{n}}_p )\nonumber \\&- \Delta \tau ({\varvec{n}}_s \otimes \varvec{\nu }_s + \varvec{\nu }_s \otimes {\varvec{n}}_s ). \end{aligned}$$
(30)

Note that the displacement field \(\varvec{u}(x,y,t)\) in the proposed solution can be obtained by integrating in time the velocity field at any given point as the shock fronts go past. Since the velocity and gradient fields are constant in each region, the resulting displacement is inevitably linear in t, x and y. Therefore, the classical second order equation in \(\varvec{u}(x,y,t)\) is trivially satisfied. Essentially, weak solutions of the form proposed here require the use of the first order equations and their associated jump conditions and are missed by the second order classical wave equations.

4.3 General solution

In order to explore the existence of solutions in the form postulated in the sections above, the stress and velocity in region III need to satisfy appropriate boundary conditions on the crack surface. In particular, the traction on the crack surface must vanish, giving two scalar conditions as,

$$\begin{aligned} {\varvec{e}}_1 \cdot \varvec{\sigma }^{(III)} {\varvec{e}}_2 = 0; \qquad {\varvec{e}}_2 \cdot \varvec{\sigma }^{(III)} {\varvec{e}}_2 = 0. \end{aligned}$$
(31)

In order to derive a third condition, it is necessary to determine whether the crack propagates symmetrically or from a free surface as shown in Fig. 4. This section will consider only the symmetric case, in which case a third condition can be found by imposing that the velocity \({\varvec{v}}^{(III)}\) in region III should be vertical, that is,

$$\begin{aligned} {\varvec{v}}^{(III)} \cdot {\varvec{e}}_1 = 0. \end{aligned}$$
(32)
Fig. 4
figure 4

a Symmetric crack propagation and b propagation from a free surface

Full size image

Substituting for the stress and velocity in region III from equations (29) and (30) into equations (31) and (32) gives a set of three equations with three unknowns, namely \(\Delta t_n\), \(\Delta \tau \) and either the angle \(\alpha _p\) or \(\alpha _s\) since they are connected to the speed of crack propagation via equations (18). The resulting equations are nonlinear and trigonometric. Remarkably, however, simple solutions exist for a significant range of material properties. In order to show this, note first the following simple geometric relationships,

$$\begin{aligned} {\varvec{n}}_{p,s}&=\sin \alpha _{p,s} \,{\varvec{e}}_1 + \cos \alpha _{p,s} \,{\varvec{e}}_2; \end{aligned}$$
(33a)
$$\begin{aligned} \varvec{\nu }_{p,s}&= - \cos \alpha _{p,s} \,{\varvec{e}}_1 + \sin \alpha _{p,s} \,{\varvec{e}}_2. \end{aligned}$$
(33b)

Multiplying equation (29) by \(\varvec{e}_1\) and employing the above trigonometric relationships together with the crack propagation condition (18)\(_b\) gives, after simple algebra, a relationship between the jumps in shear stress and normal traction as,

$$\begin{aligned} \Delta \tau = \Delta t_n \tan \alpha _s. \end{aligned}$$
(34)

Enforcing condition (31)\(_a\) and noting again that \(\mu = \rho c_s^2 \), gives after simple trigonometric algebra,

$$\begin{aligned} c_s^2 \Delta t_n \sin 2\alpha _p = c_p^2 \Delta \tau \cos 2\alpha _s, \end{aligned}$$
(35)

which, when combined with condition (34) and taking into account the angle relationship provided by equation (18)\(_b\) gives a further geometric relationship between the angles of the shear and pressure shocks as,

$$\begin{aligned} \cos \alpha _p = \frac{{c_p }}{{2c_s }}\frac{{\cos 2\alpha _s }}{{\cos \alpha _s }}. \end{aligned}$$
(36)

Adding the square of this equation to the square of equation (18)\(_b\) and using the fundamental trigonometric relationship gives,

$$\begin{aligned} \begin{aligned} 1&= \cos ^2 \alpha _p + \sin ^2 \alpha _p \\&= \frac{{c_p^2 }}{{4c_s^2 }}\frac{{\cos ^2 2\alpha _s }}{{\cos ^2 \alpha _s }} + \frac{{c_p^2 }}{{c_s^2 }}\sin ^2 \alpha _s \\&= \frac{{c_p^2 }}{{4c_s^2 }}\left[ {\frac{{\cos ^2 2\alpha _s + 4\sin ^2 \alpha _s \cos ^2 \alpha _s }}{{\cos ^2 \alpha _s }}} \right] \\&= \frac{{c_p^2 }}{{4c_s^2 }} \frac{(\cos ^2 \alpha _s +\sin ^2 \alpha _s)^2}{\cos ^2 \alpha _s}\\&= \frac{{c_p^2 }}{{4c_s^2 }} \frac{1}{\cos ^2 \alpha _s}. \end{aligned} \end{aligned}$$
(37)

This leads to a simple equation for the shear shock angle as,

$$\begin{aligned} \cos \alpha _s = \frac{{c_p }}{{2c_s }} = \sqrt{\frac{{\lambda + 2\mu }}{{4\mu }}}, \end{aligned}$$
(38)

where only the positive solution has been considered as the negative value of the cosine leads to the geometrically obvious symmetric solution below the crack. The above equation for \(\alpha _s \) has a valid solution provided that \(c_p \le 2c_s \) or \(\lambda \le 2\mu \) , that is the speed of the pressure wave is not higher than twice the speed of the shear wave. For the case of plane stress, where \(\lambda \) should be replaced by \(\bar{\lambda }\) as given in equation (10), it is easy to show that this is the case for any value of the Poisson’s ratio in the physically meaningful range. For the plane strain case, valid solutions will only exist for Poisson’s ratios \(\nu \le {1/3}\). Beyond this value the solution postulated is no longer possible in isotropic linear elasticity.

Finally, combining equation (18)\(_b\) with equation (38) it is easy to show that the angle of the pressure shock is,

$$\begin{aligned} \alpha _p = 2\alpha _s, \end{aligned}$$
(39)

and the speed of the crack propagation is,

$$\begin{aligned} v_c = \frac{{c_s }}{{\sqrt{1 - \frac{{c_p^2 }}{{4c_s^2 }}} }}. \end{aligned}$$
(40)
Fig. 5
figure 5

a Crack speed propagation and b Shear and pressure shock angles

Full size image

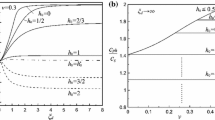
Figure 5a displays the crack speed propagation as a function of the Poisson’s ratio for both plane strain and plane stress scenarios, where physically meaningful solutions for the plane strain case are restricted to values of \(\nu \le 1/3\). Similarly, Fig. 5b displays the angle of the shear and pressure shocks as a function of the Poisson’s ratio.

4.4 The unloaded and transition regions

The solution derived in the section above enables the full evaluation of the stresses and velocity in region III. For this purpose, consider first equation (31)\(_b\), which after substitution for \(\varvec{\sigma }^{(III)}\) from equation (30) and for \(\Delta \tau \) from equation (34) gives,

$$\begin{aligned} \begin{aligned} 0&= {\varvec{e}}_2 \cdot \varvec{\sigma }^{(III)} {\varvec{e}}_2 \\&= \sigma _{22}^{(I)} - \Delta t_n \left( {\frac{{\lambda + 2\mu (1 - \sin ^2 \alpha _p )}}{{\rho c_p^2 }} + 2\tan \alpha _s \cos \alpha _s \sin \alpha _s } \right) \\&= \sigma _{22}^{(I)} - \Delta t_n \left( {1 - \frac{{2\mu \sin ^2 \alpha _p }}{{\rho c_p^2 }} + 2\sin ^2 \alpha _s } \right) \\&= \sigma _{22}^{(I)} - \Delta t_n \left( {1 - \frac{{2\mu \sin ^2 \alpha _s }}{{\rho c_s^2 }} + 2\sin ^2 \alpha _s } \right) \\&= \sigma _{22}^{(I)} - \Delta t_n, \end{aligned} \end{aligned}$$
(41)

leading to

$$\begin{aligned} \Delta t_n = \sigma _{22}^{(I)} ;\qquad \Delta \tau = \sigma _{22}^{(I)} \tan \alpha _s. \end{aligned}$$
(42)

These expressions can now be used to determine the complete velocity and stress fields in the unloaded and transition regions. For instance, the velocity in region III, which by construction will only have a vertical component, can be derived using equations (42) and the geometric relations (33) as,

$$\begin{aligned} \begin{aligned} {\varvec{v}}_{}^{(III)}&= \left( {\frac{{\sigma _{22}^{(I)} }}{{\rho c_p }}\cos \alpha _p + \frac{{\sigma _{22}^{(I)} \tan \alpha _s }}{{\rho c_s }}\sin \alpha _s } \right) {\varvec{e}}_2 \\&= \frac{{\sigma _{22}^{(I)} }}{{\rho c_p }}\left( {\cos \alpha _p + \frac{{c_p }}{{c_s }}\frac{{2c_s }}{{c_p }}\sin ^2 \alpha _s } \right) {\varvec{e}}_2 \\&= \frac{{\sigma _{22}^{(I)} }}{{\rho c_p }}\left( {\cos 2\alpha _s + 2\sin ^2 \alpha _s } \right) {\varvec{e}}_2 \\&= \frac{{\sigma _{22}^{(I)} }}{{\rho c_p }}{\varvec{e}}_2. \end{aligned} \end{aligned}$$
(43)

Note that this gives a velocity field identical to the one derived in the one-dimensional case in equation (5).

The state of stress in region III is by construction limited to a horizontal traction as,

$$\begin{aligned} \varvec{\sigma }^{(III)} = \sigma _{11}^{(III)} \,{\varvec{e}}_1 \otimes {\varvec{e}}_1, \end{aligned}$$
(44)

where the horizontal stress component \(\sigma _{11}^{(III)} \) emerges from equations (30), (33) and (34) after simple trigonometric algebra as,

$$\begin{aligned}&\sigma _{11}^{(III)} = {\varvec{e}}_1 \cdot \varvec{\sigma }^{(III)} {\varvec{e}}_1 \nonumber \\&\quad = - \sigma _{22}^{(I)} \left( {\frac{1}{{\rho c_p^2 }}(\lambda + 2\mu \sin ^2 \alpha _p ) - 2\tan \alpha _s \cos \alpha _s \sin \alpha _s } \right) \nonumber \\&\quad = - \frac{\sigma _{22}^{(I)}}{\rho c_p^2} \left( {\lambda + 2\mu \sin ^2 \alpha _p - 2\rho c_p^2\sin ^2 \alpha _s } \right) \nonumber \\&\quad = - \frac{\lambda }{{\lambda + 2\mu }}\sigma _{22}^{(I)}. \end{aligned}$$
(45)

The above expression can also be re-written in terms of the Poisson’s ratio for the plane strain and plane stress cases respectively as,

$$\begin{aligned} \sigma _{11}^{(III)} = - \frac{\nu }{{1 - \nu }}\sigma _{22}^{(I)} ;\qquad \bar{\sigma }_{11}^{(III)} = - \nu \,\sigma _{22}^{(I)}. \end{aligned}$$
(46)

Observe that by construction the above state of stress and velocity would be compatible with a crack propagating symmetrically in the left and right directions as shown in Fig. 4a. As the shear shock lines reach each other on the central symmetry axis reflections would take place into region II which would interact with the pressure shock in a complex manner as shown in Fig. 6. The analysis of this interaction and reflection is beyond the scope of the simple solution proposed here.

Fig. 6
figure 6

Propagation of a symmetric crack showing the shock reflections as dashed lines at the symmetry axis

Full size image

For completeness, it is useful to derive the velocity and stress fields in the transition region II. This is easily achieved using Eqs. (20)\(_a\), (21), (24) and (42) to give,

$$\begin{aligned} {\varvec{v}}^{(II)}= & {} \frac{{\sigma _{22}^{(I)} }}{{\rho c_p }}{\varvec{n}}_p ; \qquad \nonumber \\ \varvec{\sigma }^{(II)}= & {} \frac{{\sigma _{22}^{(I)} }}{{\rho c_p^2 }}\left[ {2\mu \left( {{\varvec{e}}_2 \otimes {\varvec{e}}_2 - {\varvec{n}}_p \otimes {\varvec{n}}_p } \right) - \lambda {\varvec{e}}_1 \otimes {\varvec{e}}_1 } \right] .\nonumber \\ \end{aligned}$$
(47)

The solution described above represents a mode I crack propagating symmetrically at speeds equal or higher than the speed of sounds in a manner consistent with the equations of linear isotropic elasticity. In the plane strain case, solutions in the simple form postulated here do not exist beyond \(\nu = {1/3}\) at which point the speed of propagation becomes infinite. The same effect takes place in plane stress at the incompressible limit \(\nu = {1/2}\). For a Poisson’s ratio different to zero, viable solutions where the horizontal stress in region III vanishes, which would correspond to cracks propagating from a free surface as shown in Fig. 4b have not yet been found with shocks emanating jointly from the crack tip, ie., in the supersonic range. However, intersonic solutions where the pressure shock moves away from the crack tip exist and will be described in Section 6.

4.5 Particular solutions

It is interesting to consider particular cases of the general solution derived above. For instance the case \(\nu =0\), or equivalently \(\lambda =0\), leads to an interesting particular solution where the angle of the shear shock is \(45^{\circ }\) and the pressure shock travels at \(90^{\circ }\) as shown in Fig. 7 (refer also to Fig. 5b). In this case the crack propagates at sonic speed (refer to Fig. 5a) and region III is fully unstressed. The pressure wave acting as a compressive shock wave first transforms the initial state of uniaxial vertical stress into a state of pure shear stress given as,

$$\begin{aligned} \varvec{\sigma }^{(II)} = \sigma _{22}^{(I)} ({\varvec{e}}_2 \otimes {\varvec{e}}_2 - {\varvec{e}}_1 \otimes {\varvec{e}}_1 ) = \sigma _{22}^{(I)} ({\varvec{n}}_s \otimes \varvec{\nu }_s + \varvec{\nu }_s \otimes {\varvec{n}}_s ). \end{aligned}$$
(48)

The shear shock then eliminates this state of shear stress and leaves the material fully unstressed in region III as shown in Fig. 7. The absence of horizontal stress in region III makes this solution valid for both the symmetric crack propagation case as well as for a crack propagating from a free surface.

Fig. 7
figure 7

Particular case \(\nu =0\)

Full size image

As a further example of a particular case obtained from the equations developed in the previous sections, consider the case where \(\lambda =\mu \) and therefore \(c_p/c_s=\sqrt{3}\). This corresponds to a Poisson’s ration of 0.25 in the case of plane strain or 1/3 in plane stress. The angles of the shear and pressure shock waves are \(30^{\circ }\) and \(60^{\circ }\) respectively and the crack propagates at a speed of,

$$\begin{aligned} v_c = \frac{{c_p }}{{\sin 60^{\circ } }} \simeq 1.155\,c_p . \end{aligned}$$
(49)

The state of stresses in regions III and II is given for this particular case as,

$$\begin{aligned} \varvec{\sigma }^{(III)} = - \frac{1}{3}\sigma _{22}^{(I)} \,{\varvec{e}}_1 \otimes {\varvec{e}}_1 ;\qquad \left[ {\varvec{\sigma }^{(II)} } \right] = - \frac{1}{6}\sigma _{22}^{(I)} \left[ {\begin{array}{*{20}c} 5 &{} {\sqrt{3} } \\ {\sqrt{3} } &{} 1 \\ \end{array}} \right] , \end{aligned}$$
(50)

where matrix notation has been used for simplicity in equation (50)\(_b\).

4.6 Energy balance

In the one-dimensional case presented in Sect. 2, it is clear that strain energy before fracture is converted into kinetic energy fully respecting energy conservation. It is also possible to show that this is the case in the proposed 2-D model, given that it has been developed using the equations of linear elastodynamics which do not incorporate any dissipative effects. In particular, it will be shown in this section that the elastic energy in region I is transformed into a smaller amount of strain energy in region III associated with the horizontal stress that emerges due to Poisson’s effect and the difference becomes kinetic energy in region III.

Consider the fixed control area shown in Fig. 8. It is simple to show that the energy flux across the boundaries of this region vanish so that the total energy inside remains constant. In order to show this, note first that energy flux per unit area (or length in the 2-D case) is given by,

$$\begin{aligned} {\mathcal {F}} = {\varvec{v}} \cdot \varvec{\sigma }{\varvec{n}}. \end{aligned}$$
(51)
Fig. 8
figure 8

Control volume for energy balance calculation

Full size image

The energy flow in region I is trivially zero as the velocity vector vanishes. In region III the energy flow across \(\Gamma _{(III)} \) also vanishes as the traction vector is horizontal whereas the velocity vector is vertical. Showing that the energy flow across the section of the control boundary in region II also vanishes requires a more detailed evaluation using equations (47) to give,

$$\begin{aligned} \begin{aligned} {\mathcal {F}}_{}^{(II)}&= {\varvec{v}}^{(II)} \cdot \varvec{\sigma }^{(II)} {\varvec{e}}_2 \\&= \frac{{\sigma _{22}^{(I)} }}{{\rho c_p }}{\varvec{n}}_p \cdot \frac{{\sigma _{22}^{(I)} }}{{\rho c_p^2 }}\left[ {2\mu \left( {{\varvec{e}}_2 - ({\varvec{n}}_p \cdot {\varvec{e}}_2 ){\varvec{n}}_p } \right) } \right] \\&= 0 . \end{aligned} \end{aligned}$$
(52)

Consequently, the energy in the control area must be conserved as the crack advances provided that there are no dissipative effects as the crack opens, which is the case in linear elastodynamics. It is easy to see that the area of region II inside the control volume remains constant as the crack progresses whereas the areas of regions I and III decrease and increase respectively in equal measure. Hence the energy per unit volume in regions I and III must coincide to ensure conservation of energy. In order to show that this is the case, note first that the strain energy is obtained in terms of the stress tensor and the 2-dimensional inverse elasticity tensor as,

$$\begin{aligned} {\mathcal {E}} = \frac{1}{2}\varvec{\sigma }:\varvec{\mathcal {C}}^{ - 1} :\varvec{\sigma };\qquad \varvec{\mathcal {C}}^{ - 1} = \frac{1}{{2\mu }}\varvec{\mathcal {I}} - \frac{\lambda }{{4\mu (\lambda + \mu )}}{\varvec{I}} \otimes {\varvec{I}}. \end{aligned}$$
(53)

Using this equation at regions I and II gives after simple algebra,

$$\begin{aligned} {\mathcal {E}}^{(I)}= & {} \frac{{\lambda + 2\mu }}{{8\mu (\lambda + \mu )}}\left( {\sigma _{22}^{(I)} } \right) ^2 ;\qquad \nonumber \\ {\mathcal {E}}^{(III)}= & {} \frac{{\lambda ^2 }}{{8\mu (\lambda + \mu )(\lambda + 2\mu )}}\left( {\sigma _{22}^{(I)} } \right) ^2. \end{aligned}$$
(54)

It is a simple exercise to show that the difference between these two energy expressions coincides with the kinetic energy per unit volume in region III as,

$$\begin{aligned} {\mathcal {K}}^{(III)}= & {} {\mathcal {E}}^{(I)} - {\mathcal {E}}^{(III)} = \frac{1}{{2(\lambda + 2\mu )}}\nonumber \\ \left( {\sigma _{22}^{(I)}} \right) ^2= & {} \frac{{\left( {\sigma _{22}^{(I)} } \right) ^2 }}{{2\rho c_p^2 }} = \frac{1}{2}\rho (v^{(III)})^2. \end{aligned}$$
(55)

Hence, in the proposed linear elastic solution strain energy is not dissipated or transformed into surface energy but exactly transformed into kinetic energy as the crack progresses. This represents the opposite end of the spectrum to the Griffiths energy balance where strain energy is transformed into surface energy.

5 Mode II crack propagation

The possibility of obtaining similar solutions to those derived above for the case of mode II fracture is discussed in this section. The unfractured stress field will be assumed to be a pure state of shear where the stress tensor is given as,

$$\begin{aligned} \varvec{\sigma }^{(I)} = \tau _{12}^{(I)} ({\varvec{e}}_1 \otimes {\varvec{e}}_2 + {\varvec{e}}_2 \otimes {\varvec{e}}_1 ). \end{aligned}$$
(56)

The release conditions in the fractured region III will now imply a horizontal velocity together with a vanishing traction vector at the crack surface. The resulting configuration is shown in Fig. 9 and leads to the following set of conditions,

$$\begin{aligned} {\varvec{e}}_2 \cdot \varvec{\sigma }^{(III)} {\varvec{e}}_2 = 0;\qquad {\varvec{e}}_1 \cdot \varvec{\sigma }^{(III)} {\varvec{e}}_2 = 0;\qquad {\varvec{v}}^{(III)} \cdot {\varvec{e}}_2 = 0. \end{aligned}$$
(57)

Note that in this case there is no vertical symmetry so the solution below the crack will need to be determined explicitly and independently but will need to satisfy appropriate skew-symmetry conditions.

Fig. 9
figure 9

Mode II crack propagation model

Full size image

Substituting for the velocity and stress fields into equations (57)\(_{a,c}\) from equations (29) and (30) gives, after simple trigonometric algebra and use of (33), a set of equations for the normal and shear stress jumps and the shock angles as,

$$\begin{aligned} \Delta t_n \cos \alpha _p + \Delta \tau \sin \alpha _p&= 0; \end{aligned}$$
(58a)
$$\begin{aligned} \Delta t_n \cos 2\alpha _s + \Delta \tau \sin 2\alpha _s&= 0. \end{aligned}$$
(58b)

These equations lead to a relationship between the shock angles as,

$$\begin{aligned} \tan 2\alpha _s = \tan \alpha _p, \end{aligned}$$
(59)

which in the \(0^{\circ }\) to \(360^{\circ }\) interval has the solutions,

$$\begin{aligned} 2\alpha _s^{(1)} = \alpha _p^{(1)} ;\qquad 2\alpha _s^{(2)} = \alpha _p^{(2)} + 180^{\circ } . \end{aligned}$$
(60)

Notice that similar angular relationships can be observed in Figs. 2 and 4 in Reference (Abraham and Gao 2000), Figs. 5 and 8 in Reference (Abraham 2001), Fig. 1 in Reference (Gao et al. 2001), Fig. 26 in Reference (Rosakis 2002), Fig. 4 in Abraham et al. (2002), Fig. 4b in Reference (Buehler et al. 2003) and Fig. 20c in Reference (Hao et al. 2004), where a Mach cone type solution is obtained using an atomistic simulation. In their case, for an equivalent Poisson’s ratio of \(\nu =0.3\), angles close to \(\alpha _s=30^\circ \) and \(\alpha _p=60^\circ \) are shown, which match those depicted in Fig. 5b. A similar Mach cone type solution can also be found in Fig. 8 in Reference (Schubnel et al. 2011). Combining these angle relationships with the crack propagation condition (18)\(_b\) gives the same angles as those obtained for mode I fracture plus a second solution which represents symmetric angles respect the horizontal axis as shown in Fig. 9. In particular,

$$\begin{aligned} \cos \alpha _s^{(1)}= & {} \frac{{c_p }}{{2c_s }}; \qquad \cos \alpha _p^{(1)} = \frac{{c_p^2 }}{{2c_s^2 }} - 1; \end{aligned}$$
(61)
$$\begin{aligned} \cos \alpha _s^{(2)}= & {} - \frac{{c_p }}{{2c_s }}; \qquad \cos \alpha _p^{(2)} = 1 - \frac{{c_p^2 }}{{2c_s^2 }}. \end{aligned}$$
(62)

In order to complete the solution, it is necessary to determine the normal and shear stress jump in terms of the shear stress in region I. This can be done by using condition (57)\(_b\), which after some algebra leads to,

$$\begin{aligned} \Delta \tau = - \tau _{12}^{(I)} ;\qquad \Delta t_n = \tau _{12}^{(I)} \tan \alpha _p^{}. \end{aligned}$$
(63)

Using these expressions, the values of the horizontal velocity and stress in the unloaded top and bottom regions emerge as,

$$\begin{aligned} {\varvec{v}}^{(III)}= & {} \pm v^{(III)} {\varvec{e}}_1 ;\qquad v^{(III)} = \frac{{\tau _{12}^{(I)} }}{{\rho c_p }}\frac{{\lambda + 2\mu }}{\lambda }; \end{aligned}$$
(64)
$$\begin{aligned} \varvec{\sigma }^{(III)}= & {} \pm \sigma _{11}^{(III)} {\varvec{e}}_1 \otimes {\varvec{e}}_1 ; \qquad \nonumber \\ \sigma _{11}^{(III)}= & {} 2\tau _{12}^{(I)} \frac{{\lambda + \mu }}{\lambda }\sqrt{\frac{{2\mu - \lambda }}{{2\mu + \lambda }}}, \end{aligned}$$
(65)

which can be re-written as,

$$\begin{aligned} v^{(III)}=\frac{{\tau _{12}^{(I)} }}{{\rho c_p }}\frac{1-\nu }{\nu };\qquad \sigma _{11}^{(III)}=\tau _{12}^{(I)}\frac{1}{\nu }\sqrt{\frac{1-3\nu }{1-\nu }}, \end{aligned}$$
(66)

for plane strain and

$$\begin{aligned} \bar{v}^{(III)}=\frac{{\tau _{12}^{(I)} }}{{\rho c_p }}\frac{1}{\nu };\qquad \bar{\sigma } _{11}^{(III)}=\tau _{12}^{(I)}\frac{1+\nu }{\nu }\sqrt{1-2\nu }, \end{aligned}$$
(67)

for plane stress, respectively.

Fig. 10
figure 10

a Velocity and b stress in unloaded region for Mode II fracture

Full size image

In both these Eqs. (64) and (65), the plus sign corresponds to the solution above the crack and the minus to the solution below the crack. Note that these equations become singular as \(\lambda \rightarrow 0\) which corresponds to \(\nu \rightarrow 0\) (refer to Eqs. (66), (67) and Fig. 10). In fact, well before reaching this value, the above state of stresses would imply a state of shear at \(45^{\circ }\) greater than the original shear in region I so the above solution has a limited range of physical validity. For completeness, the velocity and stress in the transition region II can be found by using Eqs. (20)\(_a\), (21), (24) and (63) to give

$$\begin{aligned} {\varvec{v}}^{(II)}= & {} \frac{{\tau _{12}^{(I)} \tan \alpha _p}}{{\rho c_p }}{\varvec{n}}_p ; \quad \nonumber \\ \varvec{\sigma }^{(II)}= & {} \tau _{12}^{(I)}\left[ \varvec{e}_1 \otimes \varvec{e}_2+\varvec{e}_2 \otimes \varvec{e}_1 -\tan \alpha _p \left( \varvec{n}_p \otimes \varvec{n}_p +\frac{\lambda }{\lambda +2\mu }\varvec{\nu }_p \otimes \varvec{\nu }_p\right) \right] .\nonumber \\ \end{aligned}$$
(68)

5.1 Energy balance

A similar energy balance to that presented in Sect. 4.6 can be established for mode II fracture. In this case, the energy balance equation is slightly more cumbersome as the energy flow is non-zero in a part of the boundary of the control volume. The energy flow in region I is zero as the velocity vector vanishes. In region II, the energy flow across \(\Gamma _{(II)}\) is also zero as

$$\begin{aligned} \begin{aligned} \mathcal {F}^{(II)}&=\varvec{v}^{(II)}\cdot \varvec{\sigma }^{(II)}\varvec{e}_2\\&=\frac{(\tau _{12}^{(I)})^2 \tan \alpha _p}{\rho c_p}(\varvec{e}_1 \cdot \varvec{n}_p - \tan \alpha _p \varvec{e}_2 \cdot \varvec{n}_p)\\&=\frac{(\tau _{12}^{(I)})^2 \tan \alpha _p}{\rho c_p}(\sin \alpha _p - \tan \alpha _p \cos \alpha _p)=0. \end{aligned} \end{aligned}$$
(69)

In region III, the energy flow is zero across the horizontal sides of \(\Gamma _{(III)}\) as the traction vector across them vanishes (i.e. \(\varvec{\sigma }^{(II)}\varvec{e}_2=\varvec{0}\)), reducing to

$$\begin{aligned} \mathcal {F}^{(III)}=-\varvec{v}^{(III)}\cdot \varvec{\sigma }^{(III)}\varvec{e}_1=-v^{(III)}\sigma ^{(III)}. \end{aligned}$$
(70)

As the area of region II inside the control volume remains constant as the crack progresses, the decrease of the area of region I is balanced by the increase of area of region III. Thus, referring to Fig. 11, the time rate of the energy in the control area must be equal to the energy flux as the crack advance, which can be expressed as

$$\begin{aligned} \mathcal {F}^{(III)} = v_c (\mathcal {E}^{(III)}+ \mathcal {K}^{(III)} - \mathcal {E}^{(I)}). \end{aligned}$$
(71)

It is straightforward to demonstrate that above energy balance equation is fulfilled for the stress and velocity states defined previously.

Fig. 11
figure 11

Control volume for energy balance calculation in Mode II

Full size image

6 Intersonic mode I solutions

The two shock model described above can be used to derive intersonic solutions by allowing the pressure shock to move ahead of a shear shock which is still attached to the crack tip. Similar intersonic shock distribution has been reported in Fig. 21 Reference (Rosakis 2002) and Fig. 4a in Reference (Buehler et al. 2003). This implies that the relationship between \(\alpha _p\) and \(\alpha _s\) given in Eq. (18)\(_a\) is no longer valid, leading to an additional unknown in the system of equations. The resulting configuration for mode I fracture is shown in Fig. 12 and generalizes the particular solution depicted in Fig. 7 to cases where the Poisson’s ratio is greater than zero. It will be shown below that the angles of the pressure and shear shocks will be \(90^{\circ }\) and \(45^{\circ }\) respectively as shown in the figure.

Fig. 12
figure 12

Intersonic mode I crack propagation model for symmetric case

Full size image

The additional equation required to solve the system in the absence of (18)\(_a\) can be obtained by noting that the symmetry condition along the horizontal axis implies that the shear stress in region II must vanish. With the help of Eq. (24), this gives the following condition for \(\alpha _p\) as,

$$\begin{aligned} \begin{aligned} 0&= \varvec{\sigma }^{(II)} :({\varvec{e}}_1 \otimes {\varvec{e}}_2 ) \\&= \varvec{\sigma }^{(I)} :({\varvec{e}}_1 \otimes {\varvec{e}}_2 ) - \frac{{\Delta t_n }}{{\rho c_p^2 }}\left[ {\lambda {\varvec{I}} + 2\mu ({\varvec{n}}_p \otimes {\varvec{n}}_p )} \right] :({\varvec{e}}_1 \otimes {\varvec{e}}_2 ) \\&= 0 - \mu \frac{{\Delta t_n }}{{\rho c_p^2 }}\sin 2\alpha _p \\&= \sin 2\alpha _p . \end{aligned} \end{aligned}$$
(72)

Equation (72) implies that \(\alpha _p=90^{\circ }\) as shown in Fig. 12. The angle of the shear shock can be derived by enforcing the same condition in region III to give,

$$\begin{aligned} \begin{aligned} 0&= \varvec{\sigma }^{(III)} :({\varvec{e}}_1 \otimes {\varvec{e}}_2 ) \\&= \varvec{\sigma }^{(II)} :({\varvec{e}}_1 \otimes {\varvec{e}}_2 ) - \Delta \tau \left[ {{\varvec{n}}_s \otimes \varvec{\nu }_s + \varvec{\nu }_s \otimes {\varvec{n}}_s } \right] :({\varvec{e}}_1 \otimes {\varvec{e}}_2 ) \\&= 0 - \Delta \tau \cos 2\alpha _s \\&= \cos 2\alpha _s . \end{aligned} \end{aligned}$$
(73)

Thus leading to \(\alpha _s=45^{\circ }\). The resulting crack propagation speed is therefore given by,

$$\begin{aligned} v_c = \sqrt{2} \,c_s \le c_p, \end{aligned}$$
(74)

which falls in the intersonic range except for the case where the Poisson’s ratio vanishes in which case the crack propagates at the speed of sound.

It is now possible to find solutions for both the symmetric propagation case, where \({\varvec{v}}^{(III)} \cdot {\varvec{e}}_1 = 0\), and the free surface case where \(\varvec{\sigma }^{(III)} = {\varvec{0}}\) . It is easy to show that in the former case the shear and normal stress jumps are related by,

$$\begin{aligned} \Delta \tau = \frac{{\sqrt{2} \,c_s }}{{c_p }}\Delta t_n, \end{aligned}$$
(75)

whereas in the latter the jumps are related by,

$$\begin{aligned} \Delta \tau = \Delta t_n . \end{aligned}$$
(76)

In both cases, the condition of vanishing vertical stress in region III, gives a relationship between \(\Delta \tau \), \(\Delta t_n\) and \(\sigma _{22}^{(I)}\) as,

$$\begin{aligned} \Delta \tau + \frac{\lambda }{{\lambda + 2\mu }}\Delta t_n = \sigma _{22}^{(I)} . \end{aligned}$$
(77)

This equation combined with either Eq. (75) for the symmetric case or Eq. (76) for the case where the crack propagates from a free surface will fully determine the states of stress and velocity in regions II and III. Specifically, for the symmetric case, these are

$$\begin{aligned} \varvec{v}^{(II)}&=\frac{\Delta t_n}{\rho c_p}\varvec{e}_1;\quad \nonumber \\ \varvec{\sigma }^{(II)}&=-\Delta t_n \varvec{e}_1 \otimes \varvec{e}_1 + \Delta \tau \varvec{e}_2 \otimes \varvec{e}_2; \end{aligned}$$
(78a)
$$\begin{aligned} \varvec{v}^{(III)}&=\frac{\Delta t_n}{\rho c_p}\varvec{e}_2;\quad \nonumber \\ \varvec{\sigma }^{(III)}&=(\Delta \tau - \Delta t_n) \varvec{e}_1 \otimes \varvec{e}_1, \end{aligned}$$
(78b)

and for the free surface case, these are

$$\begin{aligned} \varvec{v}^{(II)}&=\frac{\Delta t_n}{\rho c_p}\varvec{e}_1;\nonumber \\ \varvec{\sigma }^{(II)}&=-\Delta t_n \varvec{e}_1 \otimes \varvec{e}_1 + \Delta t_n \varvec{e}_2 \otimes \varvec{e}_2; \end{aligned}$$
(79a)
$$\begin{aligned} \varvec{v}^{(III)}&=\left( \frac{\Delta t_n}{\rho c_p}-\frac{\Delta \tau }{\sqrt{2}\rho c_s}\right) \varvec{e}_1 + \frac{\Delta \tau }{\sqrt{2}\rho c_s} \varvec{e}_2;\nonumber \\ \varvec{\sigma }^{(III)}&=\varvec{0}. \end{aligned}$$
(79b)

Regarding the energy balance, a similar analysis can be carried out to that presented in previous sections for supersonic modes I and II of fracture. In this case, it is easy to notice that the energy flow across the boundaries of the control volume is zero for the three regions I, II and III. However in this scenario, due to the intersonic nature of the fracture mode analysed, the area of region II is not preserved and the energy balance becomes

$$\begin{aligned}&-c_p \mathcal {E}^{(I)} +(c_p-\sqrt{2}c_s)(\mathcal {E}^{(II)}+\mathcal {K}^{(II)})+\sqrt{2}c_s(\mathcal {E}^{(III)}\nonumber \\&\quad +\mathcal {K}^{(III)})=0, \end{aligned}$$
(80)

which can be easily verified by substitution.

7 Conclusions

The paper has found novel local solutions to mode I and mode II fracture in isotropic linear elasticity that describe supersonic and intersonic crack propagation showing remarkable similarities to experimental and computational models previously reported in the literature (Gao et al. 2001; Rosakis 2002; Abraham et al. 2002; Guo et al. 2003; Buehler et al. 2003; Hao et al. 2004; Petersan et al. 2004; Willmott and Field 2006; Radi and Loret 2008; Bizzarri et al. 2010; Schubnel et al. 2011; Barras et al. 2018; Yue et al. 2019; Mai et al. 2020). Despite these results, no theoretical predictions describing Mach cone solutions had been reported in the literature before. In order to derive the solutions reported here, the equations of linear isotropic elastodynamics has been formulated in terms of first order hyperbolic equations for velocity and displacement gradients with their associated jump conditions rather than using the more common second order equation for the displacement field. The solutions obtained describe the steady state propagation of a crack in terms of pressure and shear waves emanating from the crack tip which separate states of constant velocity, strain and stress. In line with the linear elasticity model used, energy is exactly preserved and simply transformed from elastic energy before fracture into a combination of a smaller amount of elastic energy and kinetic energy. This neglects the energy required to create the new surfaces which dominates fracture mechanics in the Griffith theory model.

There are a number of physical limitations of the proposed mathematical solutions. First and foremost, the solutions developed are based on linear elasticity and therefore do not include any form of dissipative effects. This includes the absence of surface energy as the crack grows as explained above. In addition, the solutions consider only the steady state situation and provide stress fields that are uniform both ahead and behind the crack. It is obvious that just before the crack begins to grow a complex stress field with high concentrations around the tip will exist, as predicted by classical fracture models based on intensity factors. The transition between these two states is complex and beyond the scope of the analysis provided here. Finally, the state of stresses in the regions beyond the shocks can in some cases imply a state of stress more demanding than the original which would contradict the assumption of the crack propagating along the horizontal axis unless a prior weakness is assumed. In essence the paper has provided a set of very simple particular solutions that satisfy the linear elasticity equations of motion plus far field and crack surface boundary conditions under mode I and mode II fracture. It is likely that similar but more complex solutions with interacting or curved shock fronts will exist, or that through use of superposition techniques with homogenous solutions it will be possible to overcome some of the simplifying assumptions contained in the present work.

Regardless of the above physical shortcomings, the paper sheds light from an analytical point of view on the transfer of elastic to kinetic energy that takes place during brittle fracture. It provides a useful counterpoint to quasi-static fracture models where the strain energy is fully transformed into surface energy through the introduction of a length scale effect. It is likely that brittle fracture for most materials will include a component of kinetic energy transfer as well as a component of surface energy and dissipation. The balance between these different effects will be dictated by the problem configuration and physical considerations and obtained through experimental observations and computational models.

Given the growing number of experimental observations showing intersonic and supersonic crack growth with the presence of Mach type of shock waves very similar to those predicted by the theory above (refer to Abraham and Gao 2000; Gao et al. 2001; Rosakis 2002; Abraham et al. 2002; Buehler et al. 2003; Hao et al. 2004; Petersan et al. 2004; Schubnel et al. 2011; Yue et al. 2019; Abraham 2001), it is clear that high speed crack propagation in these regimes is governed by the transfer of strain energy into kinetic rather than into surface energy or dissipation.

The paper also provides a starting set of boundary and initial conditions for computational simulations where more complex material models and dissipative effects can be incorporated leading to more physically meaningful solutions. This will be explored in future work in the context of Smooth Particle Hydrodynamics (Lee et al. 2017, 2016, 2019; Ghavamian et al. 2021) discretization methodologies where the introduction of dissipative and/or length based effects to account for surface energy, hyperelasticity and inelastic effects will be possible.