Beam network model for fracture of materials with hierarchical microstructure

Abstract

We introduce a beam network model for hierarchically patterned materials. In these materials, load-parallel gaps intercept stress transmission in the load perpendicular direction in such a manner that damage is confined within hierarchically nested, load-carrying ‘modules’. We describe the morphological characteristics of such materials in terms of deterministically constructed, hierarchical beam network (DHBN) models and randomized variants thereof. We then use these models to analyse the process of damage accumulation (characterized by the locations and timings of beam breakages prior to global failures, and the concomitant avalanche statistics) and of global failure. We demonstrate that, irrespective of the degree of local disorder, failure of hierarchically (micro)structured materials is characterized by diffuse local damage nucleation which ultimately percolates on the network, but never by stress-driven propagation of a critical crack. Failure of non hierarchical reference networks, on the other hand, is characterized by the sequence of damage nucleation, crack formation and crack propagation. These differences are apparent at low and intermediate degrees of material disorder but disappear in very strongly disordered materials where the local failure strengths exhibit extreme scatter. We furthermore demonstrate that, independent of material disorder, the different modes of failure lead to significant differences in fracture surface morphology.

1 Introduction

Hierarchical materials consist of microstructural features which have themselves internal (micro)structures, forming self-similar repeating patterns at different scales. Such microstructures are ubiquitous in biological materials (Fratzl and Weinkamer 2007). Collagen, for instance, exhibits a hierarchical modular organization ranging from molecules over microfibrils and fibers to hierarchical fiber bundles. Other examples include the hierarchical structure of bone (Launey et al. 2010) and wood (Fratzl and Weinkamer 2007).

Hierarchical modular organization can serve multiple, even conflicting goals simultaneously: in addition to higher material strength, it ensures enhanced toughness over that of an assembly of isolated collagen molecules (Gautieri et al. 2011), and helps to efficiently distribute loads which improves structural resilience. Despite their hierarchical structure, all natural materials exhibit a certain degree of microstructural randomness and material heterogeneity. Several authors observed that hierarchical organization is a means of mitigating effects of localized flaws and of unreliability of the constituents at lowest structural level (see e.g. Sen and Buehler (2011)). Jiao et al. (2015) even argue that structural imperfections in hierarchical biomaterials may actually improve the mechanical properties.

The fracture mechanics of hierarchical materials in conjunction with recursive evaluation of their mechanical properties was investigated in a series of publications by Gao and co-workers (Gao 2006; Yao and Gao 2007). They demonstrated that hierarchical microstructures can mitigate against catastrophic propagation of a localized flaw driven by stress concentrations, ensuring enhanced damage tolerance.

The mathematical approach known as iterative homogenization (for overview see e.g. Lukkassen and Milton (2002)) has been employed to study linearized effective properties of hierarchical structures such as elasticity, wave propagation, or conductance. The reiterated homogenization method may be extended to account for internal length scales on different hierarchical levels by employing generalized continuum mechanics frameworks (Vernerey et al. 2007). Despite the intrinsic appeal of the method, however, evaluation of material’s effective properties based on sequential homogenization is somewhat problematic in the context of deformation and failure of strongly nonlinear materials, as these properties may be governed by localized flaws (e.g., a single critical crack) that may be difficult to capture in a homogenized framework.

Molecular simulations can model fracture of hierarchical materials on the lowest structural level. Multiscale modelling approaches may then use such simulations to parametrize mesoscale models describing the behavior at higher structural levels (see e.g. the work of Nova et al. (2010) on spider silk), or to encompass multiple structural levels into very large scale simulations (see e.g. the work of Gautieri et al. (2011) on collagen fibrils). However, since the computational cost increases exponentially with the number of hierarchical levels considered, such approaches are ultimately restricted to meso scales.

Hierarchical microstructures have also been addressed on a more conceptual level using simplified models which focus on the fundamental consequences of hierarchical organization rather than on material specific details. In so-called fiber bundle models where a material is envisaged as an array of load-carrying fibers (for a review, see Pradhan et al. (2010)). A fundamental model of this kind is the so-called equal load sharing fiber bundle model (ELS-FBM) where fibers fail according to some load-dependent criterion and, at each moment, the applied global load is equally shared by all still surviving fibers. Originally developed to investigate failure of disordered media, FBMs provide a framework for studying the interplay between local failure of microstructural elements and the concomitant load re-distribution. Hierarchical generalizations of such models were first proposed by Newman and Gabrielov (1991) and Newman et al. (1994). At order k of a hierarchical fiber bundle model (HFBM), $N_k$ fibers are assumed to share the load equally, and each of them is envisaged as an ELS fiber bundle of $N_{k-1}$ fibers. For the case $N_k = m \forall k$, exact results regarding the strength of such hierarchical structures were, for the case of elastic-brittle fiber behavior, given by Newman and Gabrielov (1991) and Newman et al. (1994). The latter work also considers time-dependent behavior where fibers fail at a rate that depends on the instantaneous fiber load. In recent times, the effective strength of more general hierarchical structures of elastic-brittle fibers was investigated by Pugno et al. (2012), while the statistics of avalanche precursors to failure in hierarchical elastic-brittle FBMs was studied by Biswas and Zaiser (2019). In all these studies, an important advantage of FBM approaches is their computational efficiency which allows to simulate systems with very many hierarchical levels and to study large ensembles of systems, thus ensuring statistical validity of the results. Self-similar ($N_k = const.$) and self-affine $(N_k \propto k^a)$ hierarchical FBM in addition allow for analytical investigation using the powerful tools of renormalization theory, see Newman et al. (1994).

By construction, ELS fiber bundle models—which represent mean-field models of collective phenomena in fracture—are devoid of spatial structure. In variants with local load sharing (LLS), fibers are embedded into a Euclidean space, and the load carried by a broken fiber is re-distributed on a finite neighborhood (e.g., on the nearest-neighbors) . In variants with variable interaction range (Hidalgo et al. 2002), finally, the amount of load re-distributed from a broken fiber onto another fiber depends on their Euclidean distance, typically according to a power law, which allows to interpolate— depending on the exponent—between the LLS and ELS limits (Hidalgo et al. 2002). Such models can be used to approximate stress re-distribution in specific geometries. However, crack-tip stress concentrations which play a crucial role in classical fracture mechanics are only captured in an approximate and phenomenological manner. As a consequence, important effects such as the transition from diffuse damage nucleation to critical crack growth are difficult to study in quantitative terms in fiber bundle frameworks. We therefore seek models which, while computationally efficient, can capture the key effects of stress concentrations and crack propagation. First steps into this direction were undertaken by Moretti et al. (2018) who used a so-called random fuse model (RFM) to study the effects of hierarchical structure on precursor activity in the run-up to failure, and on the mode of failure. Random fuse models consider the balance of scalar currents related to scalar voltages. The ensuing system of equations can be considered a scalar version of the equations of force balance in mechanics. Such models capture effects of load concentration at crack tips, i.e., the associated stress singularity and the long-range decay of the crack-tip stress field, and have been widely used in statistical studies of fracture of disordered media (Alava et al. 2006; Nukala et al. 2005). However, the fact that such equations use a mere scalar caricature of the conservation equations of linear and angular momentum, and of the constitutive equations of continuum mechanics which relate tensorial stresses to tensorial strains, makes it hard to quantitatively link RFM simulations to observations on real material systems: They essentially remain on the level of concept models.

To explicitly account for linear and angular momentum conservation within the framework of network models, it is necessary to resort to networks of beams (beam network model, BNM) connecting nodes and transmitting both forces and torques. Unlike the previously mentioned concept models, such models, which we consider here in the quasi-static (non-inertial) limit, can be quantitatively parametrized to capture the key features of fracture of real materials as a multi-scale process: The existence of local failure thresholds which reflect properties of the local material microstructure, the existence of an internal length above which the material can be described as a continuum, and the coupling of different material elements by long-range stress fields that emerge in response to local failure, and that are related to strains by tensorial constitutive relations such that general loadings and complex geometries, which in general lead to locally multi-axial stress states, can be adequately captured. At the same time, the models use a simplified description of local deformation and failure processes that abstracts from the bewildering detail of real material microstructures. Therefore BNM, while preserving the fundamental structure of continuum mechanics, achieve a degree of simplicity that makes them amenable to large-scale simulations and systematic studies over a wide range of system sizes, using ensembles of a size that allows for meaningful statistical predictions (Manzato et al. 2012).

Here we formulate for the first time a hierarchical version of a BNM. The beam network approach we use is similar to a non-hierarchical BNM used by Hosseini et al. (2020) for investigating disorder effects in non-hierarchical structures, whereas the geometrical construction of different network variants is the same as used by Moretti et al. (2018). We use this hierarchical BNM to explore how hierarchical organization affects the precursor activity in the run-up to failure and ultimately changes the mode of failure. The remainder of the paper is organized as follows: In Sect. 2 (method) we briefly introduce the BNM (technical details are given in the appendix), in Sect. 3 we show results of fracture simulations of this model and analyse the results in terms of fracture precursors, fracture/failure mode and fracture surface morphology, and in Sect. 4 we provide a general discussion of our results in the wider context of failure of disordered media.

2 The method: beam network model

We consider a two-dimensional BNM based on a 2D cubic lattice of interconnected beams which are clamped together at their intersections. The points where beams are mutually connected are referred to as nodes; a BNM of size L has L($L + 1$) nodes. $L = 2^n$ is referred to as the network size, it is taken to be a power of 2. At two opposite boundaries of the BNM (henceforth referred to as ‘top’ and ‘bottom’), all degrees of freedom (DOFs) are fixed through two rigid bars which are used to apply an axial displacement along one of the two cubic axes of the lattice structure (henceforth referred to as ‘vertical’ axis). Periodic boundary conditions are imposed in the load perpendicular (‘horizontal’) direction. Beams oriented along the loading axis are denoted as load-carrying (LC) beams, their number is $N_{\mathrm{LC}}$; a set of l vertically connected LC beams is denoted as a LC fiber of length l. Beams oriented in perpendicular direction are denoted as cross-link (CL) beams, their number is $N_{\mathrm{CL}}$; a set of l horizontally connected CL beams is denoted as a CL connector of length l. On the other hand, a set of l vertically adjacent sites where CL beams are missing or have failed is denoted as a gap of length l.

2.1 Construction of hierarchical and non hierarchical BNMs

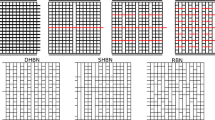
In order to construct a deterministic hierarchical beam network (DHBN), we start out from a full beam network, where $N_{\mathrm{CL}}= L(L-1)$ and $N_{\mathrm{LC}} = L^2 = 4^n$. From this starting point, a hierarchical structure is obtained by removing cross links such as to create gaps which recursively sub-divide the structure into load-carrying modules of decreasing order as illustrated in Fig. 1.

Fig. 1

Iterative ‘top-down’ construction of a hierarchical network (deterministic hierarchical beam network, DHBN): we start with full beam network; this is then divided by load-parallel cuts into four highest-level modules. These form two groups of two modules loaded in series, connected by a system spanning connector (the row of cross links shown in red); next, each of the four modules is again divided into four lower-level modules plus a module-spanning lateral connector, etc

This construction leads to a hierarchical pattern of modules separated by gaps, and of CL connectors connecting them. The overall structure has close similarities to the ‘hierarchical diamond lattice’ studied by Griffiths and Kaufman (1982) in the context of phase transitions in spin systems, and by Sornette (1989) and Roux et al. (1991) in the context of size scaling of breakdown strength. In the hierarchical DHBN pattern, the numbers of structural features such as CL connector lengths and gap lengths are connected to the respective lengths of these features by power laws. For instance, in a DHBN as illustrated above with n hierarchical levels, the number of CL connectors of length l is $N_{\mathrm{c}}(l) = 2^{(2n)}/(l+1)^2$ and the number of gaps of length l is $N_{\mathrm{g}}(l) = 2^{(2n-1)}/(l+1)^2$.

In addition to DHBN, we consider randomized variants as follows: (i) A random beam network (RBN) of size $L=2^n$ is constructed from the same number of $L^2$ LC links and $N_{\mathrm{CL}}$ cross-links as the corresponding DHBN, but the CL beams are distributed randomly over the possible CL sites, leading to an exponential gap length distribution; (ii) defining a row as a set of CL beams that share the same vertical position, and a column as a set of LC beams that share the same horizontal position, a shuffled hierarchical beam network (SHBN) is constructed by starting from a DHBN and first randomly reshuffling the columns and then the resulting rows. This results in a randomized structure which however preserves the power-law relationship between the numbers of connectors and gaps and their respective lengths (Moretti et al. 2018). For illustration, fiber bundle (FB), DHBN, RBN, and SHBN of size $L=16$ (order $n=4$) are shown in Fig. 2.

Fig. 2

Examples of deterministic and stochastic hierarchical beam networks with $n = 4$ hierarchical levels (DHBN, SHBN), and non hierarchical reference structures of the same size (fiber bundle, FB, and random beam network, RBN); loading is in all cases in tension along the vertical direction, all structures have the same number and length of load carrying fibers and RBN, DHBN and SHBN have equal numbers of lateral connectors; the dangling beams on the left and right boundary of the networks mutually connect, thus implementing periodic boundary conditions perpendicular to the loading direction

2.2 Material model

The constituents of the BNM are assumed to be straight, identical beams of unit modulus of elasticity, unit length and square cross section (cross-section area $A=1$), which are capable of resisting axial and shear forces as well as bending moments. There are three degrees of freedom (DOF) at each node including two translational DOF (node displacements u and v along the global x and y axes) and one rotational DOF (rotation angle $\theta$ about the global z axis). The beams are assumed to deform in a linearly elastic manner, their deformation is described using Timoshenko beam theory to relate the forces and moments acting on the beam endpoints to the corresponding displacements. This is done in a local coordinate system aligned with the beam axis where displacements (axial and shear displacements of the end nodes, rotations of the end nodes) are assembled into a local displacement vector $\tilde{\mathbf {u}}$ while axial and shear forces and moments acting on the end surfaces are assembled into a force vector $\tilde{\mathbf {F}}$ such that for all beams $\tilde{\mathbf {K}}\tilde{\mathbf {u}} = \tilde{\mathbf {F}}$. An explicit expression for the local stiffness matrix $\tilde{\mathbf {K}}$, which defines the elastic behavior of the beam, is given in the Appendix.

We consider quasi-static deformation, i.e., inertial forces are assumed negligible. Thus, the balance equations of linear and angular momentum reduce to the requirement that the sums of forces and moments acting on all beams connecting to each given node must be zero. This leads to a global equation of the type

$$\begin{aligned} \mathbf{K } . \mathbf{u } = 0 \end{aligned}$$

(1)

where $\mathbf{u }$ is the global displacement and force vector which comprises all nodal displacements and rotation angles, transformed to the global coordinate system. The matrix $\mathbf{K }$ depends in general on the individual beam orientations in the global coordinate system (see Appendix for explicit expressions) and thus on the nodal displacements, which makes the problem nonlinear even when the individual beam deformations are small. To keep the numerical effort manageable, we make the additional assumption that the beam orientations remain close to their values in the undeformed structure, such that the system of equations becomes linear. This assumption can be justified a posteriori for the boundary conditions and material parameters used in our simulations.

2.3 Failure criterion

The beams are assumed to behave in an elastic-brittle manner, i.e., they deform in a linearly elastic manner and then fail irreversibly once a stress-based criterion is met. In terms of nodal forces and moments this criterion reads for beam $_{ij}$ connecting nodes i and j

$$\begin{aligned} \sigma /t_{ij}= & {} 1,\nonumber \\ \sigma= & {} \sqrt{ \Big ( \dfrac{F_{i}n_i}{A}+\mathrm{max}(|M_{i}|,|M_{j}|)\dfrac{y_{\mathrm{max}}}{I} \Big ) ^ {2}+3 \Big ( \dfrac{Q_{i}}{A} \Big ) ^ {2} }\nonumber \\ \end{aligned}$$

(2)

where $n_i$ indicates the outward normal direction of the beam end surface connecting to node i, $F_i$ is the normal force which can be tensile ($F_i n_i > 0$) or compressive ($F_i n_i < 0$), $Q_i$ is the shear force, and $M_i$ is the moment acting on this surface. A derivation of Eq. (2) based on the Maximum Distortion Energy of Failure (von Mises) criterion is given in the Appendix. A simpler criterion often used in the literature (see e.g. Herrmann et al. (1989), Nukala et al. (2008)) is obtained by neglecting the shear force Q in this expression, however, this is inconsistent with a Timoshenko model for beam deformation and may seriously under-estimate the failure likelihood of lateral connector beams, which mainly transmit shear forces.

Mimicking material heterogeneity, beam failure thresholds $t_{ij}$ are randomly assigned based on a Weibull probability distribution function with probability density

$$\begin{aligned} p(t_{ij}) = \dfrac{\beta }{\eta } \Big ( \dfrac{t_{ij}}{\eta } \Big ) ^ {\beta - 1} \exp \left( -\Big ( \dfrac{t_{ij}}{\eta } \Big )^\beta \right) \end{aligned}$$

(3)

where $\beta > 0$ and $\eta > 0$ are the shape and scale parameters of the distribution, respectively. In this paper we adjust the scale parameter $\eta$ such as to have a fixed mean value $\langle t_{ij} \rangle = 1.0$ for the failure thresholds. The shape parameter $\beta$, on the other hand, is varied such as to implement different degrees of disorder, ranging from $\beta = 20$ (low disorder) over $\beta = 4$ and $\beta = 1.5$ to $\beta = 0.5$ (high disorder), thus covering the entire spectrum from very reliable to very unpredictable material behavior.

2.4 Simulation protocol

The BNM is loaded under conditions of displacement control, i.e., the external axial displacement is increased until the first beam breaks and then kept fixed while load is re-distributed which may trigger further failures (stress relaxation). This process is repeated iteratively in such a way that one beam is removed in every iteration, until loss of global connectivity indicates failure of the beam network.

To this end, at each iteration a unit vertical displacement is imposed on the nodes at the upper boundary of the network while the nodes at the lower boundary are fixed and periodic boundary conditions are imposed in the lateral direction (see Fig. 2). Displacements of all BNM nodes are calculated from Eq. (11) and then transformed into the beams’ local coordinate system, where the local loads on each beam are calculated using Eq. (6). The weakest element of the structure is identified as the beam with the highest $\sigma /t_{ij}$ ratio, $(\sigma /t_{ij})_{\mathrm{max}}$. Under the assumptions stated above (small global and local deformations) the beam forces and beam displacements are homogeneous functions of first degree of the applied boundary displacement. Thus, the global displacement $(\sigma /t_{\text {ji}})_{\mathrm{max}}^{-1}$ satisfies the failure criterion in Eq. (2) for the weakest beam which is then removed. However, due to the displacement-controlled deformation regime which does not allow for global relaxation, the actual imposed displacement is $\mathrm{max}((\sigma /t_{\text {ji}})_{\mathrm{max}}^{-1}, d)$ where d is the displacement of the previous step.

3 Results of fracture simulations

This section is concerned with the differences between materials with hierarchical and non-hierarchical microstructures in terms of nature and statistical signatures of the failure process. We first focus on qualitative differences in the damage growth patterns and stress–strain curves. Typical patterns of damage growth (damage pattern at increasing global displacement) are depicted in Fig. 3 for RBN and DHBN of size $L=1024$ where beam thresholds are Weibull distributed with shape parameters $\beta = 4.0$ and $\beta =0.5$.

Fig. 3

Typical stress distribution and damage growth patterns, from the system’s peak load (left) to global fracture (right), for different network variants of size $L = 1024$ and two different degrees of disorder (medium disorder, $\beta = 4$, high disorder, $\beta = 0.5$); a RBN, $\beta = 4.0$, b DHBN, $\beta = 4.0$, c RBN, $\beta = 0.5$, d DHBN, $\beta = 0.5$

In case of non-hierarchical materials at low to intermediate disorder as illustrated by the failure sequence of a RBN with $\beta = 4$ in Fig. 3a, fracture occurs by nucleation and propagation of a crack which becomes critical at the system’s peak load, and is then propagated by crack-tip stress concentrations until it spans the entire system. In hierarchical materials of the same disorder as illustrated in Fig. 3b, on the other hand, the hierarchically distributed gaps interrupt crack propagation on all scales, causing widely separated flaws which coalesce to form a super-rough crack profile. These differences are reduced in systems with very high disorder ($\beta = 0.5$), as illustrated in Fig. 3c and d, where crack nucleation is facilitated and crack propagation is impeded by the high disorder such that the effect of crack-tip stress concentrations is greatly diminished. As a consequence, one sees a transition to multiple crack nucleation-and-coalescence even in the non hierarchical system. Similar behavior is observed in many other systems in the limit of high disorder, from LLS fiber bundle models (Newman and Phoenix 2001; Phoenix and Newman 2009) to continuum models of plasticity and damage (Zaiser et al. 2013).

3.1 Stress–strain curves and damage patterns

Fracture surfaces and concomitant stress–strain curves are shown in Fig. 4 for different degrees of disorder, ranging from low disorder ($\beta = 20$, bottom row) to very high disorder ($\beta = 0.5$, top row). For low and intermediate disorder, the stress–strain curves of the non-hierarchical RBN network are of essentially brittle nature, with little pre-peak softening and an abrupt load drop to zero at the point of failure. This is expected when failure is governed by nucleation and propagation of a critical crack. The hierarchical networks, on the other hand, show a significant degree of both pre-peak and post-peak damage accumulation: failure does not occur immediately after the peak stress is reached but proceeds gradually by ongoing nucleation and coalescence of local flaws. This qualitative difference between hierarchical and non hierarchical networks disappears at the highest degree of disorder ($\beta = 0.5$) where the stress–strain curves of both hierarchical and non hierarchical samples show a gradual progression of failure.

Fig. 4

Typical behavior of different network variants under load, with $L = 1024$ and Weibull distributed beam thresholds with shape parameter $\beta$ where in subfigures a and b $\beta = 0.5$, c and d $\beta = 1.5$, e and f $\beta = 4$, g and h $\beta = 20$. Left column: crack shapes in a DHBN and a RBN; right column: stress–strain curves for DHBN, SHBN and RBN. All structures have the same initial stiffness. The label FB marks stress–strain curves for a ELS fiber bundle consisting of the same number and arrangement of load carrying links, hence same initial stiffness, which are also included for comparison (for $\beta = 0.5$ the FB stress–strain curve shows extremely low failure stress/strain as shown in the graph inset)

In the non-hierarchical structures the fracture profiles exhibit self-affine shapes as found in many experiments (for early investigations see e.g. Mandelbrot et al. 1984; Måløy et al. 1992) and also in many simulations of random fuse and random beam models (Hansen et al. 1991; Zapperi et al. 2005; Nukala et al. 2008)). The crack shapes in both DHBN and SHBN, by contrast, are qualitatively different and cannot be described as self-affine. In these networks the hierarchical structure with a power law distribution of vertical gaps imposes wide discontinuous jumps in the crack profile which are visually reminiscent of crack profiles encountered e.g. in bone (Moretti et al. 2018; Launey et al. 2010). The fracture surfaces of the hierarchical networks are super-rough with system-spanning discrete steps. This qualitative difference persists irrespective of the degree of disorder, though a gradual change is visible in the sense that, for high disorder, the large steps on the fracture surface in hierarchical network versions get less frequent, an observation which corresponds to a larger exponent of the power-law step size distribution analyzed in Sect. 3.3 below, while at the same time for very high disorder the roughness exponent of the self affine fracture surfaces of the non hierarchical systems increases, as also observed in other studies (see e.g. Hansen et al. (1991)).

3.2 Avalanches

As described in Sect. 2.3, the BNM are loaded in displacement control where the imposed global displacement is monotonically increased until at least one beam fails. In general, subsequent to failure of one beam, internal load re-distribution causes secondary failures, leading to an avalanche-like dynamics. The number of beam failures occurring at constant global displacement after primary beam failure has been caused by an external displacement increment is denoted as avalanche size s. As can be seen from Fig. 5, avalanche size distributions at low and intermediate disorder differ significantly between hierarchical and non hierarchical network variants. For non hierarchical networks, the avalanche distribution is composed of a power-law regime at small avalanche sizes where $p(s) \propto s^{-\alpha }$, plus an outlier which represents the avalanche associated with supercritical propagation of the final, system spanning crack. The power law regime is associated with diffuse damage accumulation prior to supercritical crack nucleation; it is more pronounced if the system is strongly disordered and disappears in highly ordered systems ($\beta = 20$) where there is only a single avalanche associated with abrupt failure. The avalanche exponent $\alpha$ of the initial power-law regime decreases with increasing disorder and for very large disorder falls below the asymptotic value $\alpha = 2.5$ characteristic of the mean-field (ELS) limit. In hierarchical networks, by contrast, the broad distribution of avalanche sizes can in general not be well described by a single power law. This behavior is reminiscent of hierarchical fuse networks as studied by Moretti et al. (2018) where it was shown that the pre-peak avalanche dynamics of such structures differs significantly from the mean field behavior represented by ELS fiber bundles. For details we refer the reader to Moretti et al. (2018). In the limit of high disorder ($\beta = 0.5$), the differences in avalanche statistics disappear as both non-hierarchical and hierarchical systems exhibit power-law statistics with an avalanche exponent $\alpha \approx 2.3$.

Fig. 5

Avalanche size distributions for different network variants of size $L = 512$. Each distribution is averaged over 6000 realizations. Beam strengths are Weibull distributed with shape parameters a $\beta = 0.5$, b $\beta = 1.5$, c $\beta = 4.0$ and d $\beta = 20.0$

3.3 Crack roughness

Fig. 6

Roughness plots (standard deviation $\sigma _l$ vs averaging length l) for different network variants of size $L = 512$. Each distribution is averaged over $N=6000$ realizations. Beam strengths are Weibull distributed with shape parameters a $\beta = 0.5$, b $\beta = 1.5$, c $\beta = 4.0$ and d $\beta = 20.0$

Fig. 7

Structure factors $C^m$ for different values of m and different network variants of size $L = 512$. Each curve is averaged over $N=6000$ realizations. Beam strengths are Weibull distributed with shape parameter $\beta$ where in subfigures a–c $\beta = 0.5$, d–f $\beta = 1.5$, g–i $\beta = 4.0$, j-l $\beta = 20$; left column shows $C^1$, middle column $C^2$, right column $C^4$

Typical fracture surface profiles of RBN and DHBN of size $L = 1024$ are shown in Fig. 4, left. To characterize the profiles, the BNM’s global coordinate system is used such that the x direction corresponds to the load perpendicular direction and y to the loading direction. The fracture surface profile can then be envisaged as a function y(x). To analyze the scale dependent morphology of this profile, we first determine the scale dependent roughness in terms of the scale dependent standard deviation

$$\begin{aligned} \sigma _l = \left\langle \langle (y(x) - \langle y(x)\rangle _l)^2 \rangle _l ^{1/2}\right\rangle _{L,N} \end{aligned}$$

(4)

where $\langle \dots \rangle _l$ denotes the average over a window of length l and $\langle \dots \rangle _{L,N}$ is the average over all windows contained in the sample cross section of length L, as well as over all samples in an ensemble of N simulations with different realizations of a given microstructure. Since the statistical properties of a self-affine profile y(x) are invariant under the scaling transformation $x \rightarrow \lambda x, y \rightarrow \lambda ^H y$ where H is the Hurst exponent, we expect for a self-affine fracture surface that $\sigma _l \propto l^H$.

For non hierarchical samples we consistently find self-affine scaling with a Hurst exponent $H \approx 0.65$ that does not depend strongly on the degree of material disorder(see Fig. 6a–d). This exponent compares well with observations on random fuse and random spring models in the published literature, see e.g. Hansen et al. (1991). In hierarchical networks, on the other hand, the absolute roughness of the fracture surfaces is much higher, and the same is true for the apparent Hurst exponent of the linear scaling regimes which is close to 0.9. This is in some sense expected since for hierarchical networks with an infinite number of hierarchical levels an asymptotic exponent of 1 follows trivially from the fact such networks are statistically invariant under the transition $x \rightarrow 2 x$, $y \rightarrow 2 y$ and the same must be true for the corresponding crack profiles. For finite networks as studied here, the apparent exponent is slightly less ($H \approx 0.9$) and scaling is limited to small l. The horizontal large-l asymptote corresponds to the value $\sigma _l = L/\sqrt{12}$ for the ELS FB model with fibers of length L, which is obtained by considering the y(x) values to be completely random variables equi-distributed on the interval [0...L] and uncorrelated among different fibers.

Fig. 8

Distribution of surface step heights for different network variants of size $L = 512$. Each distribution is averaged over 6000 realizations. Beam strengths are Weibull distributed with shape parameters a $\beta = 0.5$, b$\beta = 1.5$, c$\beta = 4.0$ and d $\beta = 20.0$

To analyze whether or not the apparent scaling regimes on the roughness plots represent true self-affine behavior, we perform a multi-scaling analysis. To this end, we denote as $\varDelta (x,l)$ the height difference $|y(x) - y(x+l)|$ between two points on a profile that are separated by a distance l. We then compute so-called structure factors of order m:

$$\begin{aligned} C^m(l) = \langle [\varDelta (x,l)]^m\rangle _{L,N}^{1/m}. \end{aligned}$$

(5)

For self affine profiles of Hurst exponent H, the self affine scaling invariance implies that $C^m(l) \propto l^H$ for all m. Thus, double-logarithmic plots of $C^m$ vs window size l scale linearly with m-independent slope H. Results of a multi-scaling analysis shown in Fig. 7 demonstrate that this requirement is approximately fulfilled for crack profiles in non-hierarchical RBN models.

In hierarchical networks, on the other hand, the scaling can not be described as self affine since the apparent Hurst exponent for different structure factors $C^m$ depends on the exponent m approximately like $H_m = 1/m$. This indicates that the increase of surface fluctuations with increasing scale may reflect the self-similar hierarchical architecture of the samples rather than dynamic correlations in crack growth. This idea is further borne out when we look at the statistics of fracture surface steps, which for hierarchical networks is strongly influenced by the power-law statistics of load-parallel gaps separating the different modules.

3.4 Statistics of surface steps

Statistics of step heights h (i.e., height differences between subsequent horizontal beams on the fracture surface) are plotted in Fig. 8 for different BNM variants. The non hierarchical RBN network exhibits exponential step height distributions. Hierarchical networks, on the other hand, are characterized by scale-free distributions $p(h)\propto h^{-K_h}$ of surface step heights h as shown in Fig. 8 for different degrees of threshold disorder, ranging from high disorder ($\beta = 0.5$), Fig. 8a, to low disorder ($\beta = 20$, Fig. 8d).

As such, a power-law scaling of step heights on surface profiles is not unexpected. For DHBN and SHBN structures as considered here, we find load-parallel gaps for which the gap height distribution in the 2D system is given by $p_{\mathrm{2D}}(h) \propto h^{-2}$. For a one-dimensional section perpendicular to the stress axis, we then expect that the intersecting gaps have a height distribution $p_{\mathrm{1D}}(h) \propto h^{-1}$. Assuming that, at each gap, the fracture surface is deflected to one of the gap endpoints (i.e., by an amount of the order of h) we then expect a ‘built-in’ step height distribution $p(h) \propto h^{-1}$. An exponent close to 1 is indeed what we find for highly reliable materials, where stochastic influences on damage accumulation are negligible. For unreliable materials, on the other hand, we still observe a power law statistics but now the exponent $K_h$ increases with increasing disorder (decreasing Weibull exponent) from 1.16 ($\beta = 20$) to 1.84 ($\beta = 1.5$ and $\beta = 0.5$). This indicates that, in the general case, the power law statistics of surface steps is an emergent phenomenon which is controlled by the interplay between structural morphology (built-in modular organization with power-law gap distribution), load re-distribution on the hierarchical network, and disorder.

4 Conclusions

We have analyzed the failure behavior of hierarchical beam networks, using non-hierarchical networks with the same elementary beam properties as a reference. The results indicate that hierarchical organization has a very significant influence on failure. Maybe the most conspicuous consequence of hierarchical organization resides in the fact that, irrespective of the degree of material disorder, hierarchically structured samples never fail by crack nucleation and propagation. The hierarchical modular organization thus proves efficient in containing damage which hardly ever propagates across modular boundaries: crack-tip stress concentrations, which ultimately lead to failure by supercritical crack propagation, are thus efficiently mitigated. Instead, failure occurs by the nucleation of damage in the hierarchically nested modules and subsequent coalescence of independently nucleated damage clusters. The overall failure behavior resembles in several respects the behavior of non hierarchical structures in the limit of extremely high disorder. This similarity concerns the asymptotic irrelevance of local stress concentrations, the avalanche statistics, and also the shape of the stress strain curves. At the same time, the distinctive super-rough morphology of the fracture surface, which is in characterized by power-law distributed discontinuities, represents a robust feature which irrespective of disorder distinguishes hierarchical structures from their non-hierarchical counterparts.

From a point of view of absolute strength, hierarchical organization is not inherently favorable. Our simulations indicate that hierarchical and non hierarchical samples consisting of the same number of beams with the same statistical properties on the beam level have comparable peak stresses: the more diffuse failure mode of hierarchical samples does not increase their maximum strength. In this respect our simulations, which use a more realistic load re-distribution scheme, confirm the results of Biswas and Zaiser (2019): Hierarchical organization into load carrying ‘modules’ impedes damage propagation across module boundaries, but at the same time damage accumulation within modules may be enhanced due to less efficient load re-distribution. The main benefit of hierarchical organization may thus not be enhancement of absolute strength, but rather toughening and mitigation against propagation of large flaws. An investigation of these issues, as well as a direct experimental validation of our findings, will be published separately.

Further investigation is also needed to establish the size dependent failure properties of hierarchical systems. In this respect, renormalization arguments as used by Sornette (1989), Roux et al. (1991), and Newman et al. (1994) may be exploited to establish the asymptotic behavior of hierarchical beam or fuse networks in the large-system limit, and complemented by analytical and numerical investigations to establish how this limit is approached. Again, a more profound investigation of these issues, and of the question to which extent large-system asymptotics explain the behavior of experimentally realizable metastructures which of necessity have only a rather limited number of hierarchical levels, will be a subject of further studies.

Appendix A: numerical implementation aspects

1.1 A.1 Governing equations of the beam model

The constituents of the BNM are assumed to be straight, identical beams of unit length, unit modulus of elasticity and square cross section which are capable of resisting axial and shear forces as well as bending moments. There are three degrees of freedom (DOF) at each node including two translational DOF (node displacements u and v along global axes x and y) and one rotational DOF (rotation angle $\theta$ about global z axis).

The beams are assumed to deform in a linearly elastic manner and to break irreversibly once a stress based criterion is met which we discuss below. Stresses and strains are evaluated using Timoshenko beam theory. We assume small beam deformations and introduce a local two-dimensional coordinate system for each beam where the $\tilde{x}$ axis is aligned with the beam axis, the $\tilde{y}$ axis points in perpendicular direction, and the origin is placed on the beam neutral axis. The corresponding displacements are denoted by $\tilde{u}$ and $\tilde{v}$. In this coordinate system, forces and end displacements are related by a matrix equation which can be written as $\tilde{\mathbf {K}} . \tilde{\mathbf {u}} =\tilde{\mathbf {F}}$ where the stiffness matrix $\tilde{\mathbf {K}}$, generalized displacement vector $\tilde{\mathbf {u}}$ and generalized force vector $\tilde{\mathbf {F}}$ are given by (Herrmann et al. 1989):

$$\begin{aligned} \begin{bmatrix} \gamma &{} &{} &{} &{} &{} \\ 0 &{} \zeta &{} &{} &{} SYM &{} \\ 0 &{} \lambda &{} \psi &{} &{} &{} \\ - \gamma &{} 0 &{} 0 &{} \gamma &{} &{} \\ 0 &{} - \zeta &{} - \lambda &{} 0 &{} \zeta &{} \\ 0 &{} \lambda &{} \xi &{} 0 &{} - \lambda &{} \psi \end{bmatrix} \begin{bmatrix} \tilde{u}_{i} \\ \tilde{v}_{i} \\ \theta _{i} \\ \tilde{u}_{j} \\ \tilde{v}_{j} \\ \theta _{j} \end{bmatrix} = \begin{bmatrix} \tilde{F}_{i} \\ \tilde{Q}_{i} \\ M_{i} \\ \tilde{F}_{j} \\ \tilde{Q}_{j} \\ M_{j} \end{bmatrix} \end{aligned}$$

(6)

where

$$\begin{aligned} \gamma = \dfrac{EA}{l}, \quad&\zeta = \dfrac{12EI_z}{l^{3}(1+\varPhi _y)},&\lambda = \dfrac{6EI_z}{l^{2}(1+\varPhi _y)},\nonumber \\&\psi = \dfrac{(4+\varPhi _y)EI_z}{l(1+\varPhi _y)},&\xi = \dfrac{(2-\varPhi _y)EI_z}{l(1+\varPhi _y)}. \end{aligned}$$

(7)

E is the modulus of elasticity, A is the beam cross-section area, l is the beam length, $I_z$ is the moment of inertia along the z axis, $\varPhi _y=\dfrac{12EI_z}{GAl^{2}}$ is the shear correction factor, and G is the shear modulus. Subscripts i and j refer to the two end nodes of the beam. The letters $\tilde{F}$, $\tilde{Q}$ and M in the force vector denote axial and shear forces and bending moments, respectively (Note that bending moments and rotation angles are identical in the local and global coordinate systems, so we have dropped the tildes on $M,\theta$). If $\varPhi _y=0$, shear strain is being neglected and Eq. (6) reduces to Euler–Bernoulli beam theory. However, such a simplification is not a suitable choice for a BNM because it presumes that the beam is so slender that each cross-section remains perpendicular to the neutral axis during deformation, which is not in accordance with our assumptions. Based on our preliminary simulations of BNMs of size $L=1024$, using Euler–Bernoulli instead of Timoshenko beam elements results in a significant underestimation of failure stress and fracture energy.

In order to obtain the equilibrium equations of the entire lattice, it is first required to transform $\tilde{\mathbf {K}}$ into a global coordinate system through:

$$\begin{aligned} {\mathbf {K}}_{ij} = {\mathbf {T}}^{T}_{ij}.\tilde{\mathbf {K}}\mathbf{T }_{ij} \end{aligned}$$

(8)

where ${\mathbf {K}}_{ij}$ represents the stiffness matrix of the beam connecting nodes i and j in the global coordinate system, and ${\mathbf {T}}^{T}_{ij}$ is the transpose of the transformation matrix ${\mathbf {T}}_{ij}$:

$$\begin{aligned} {\mathbf {T}}_{ij} = \begin{bmatrix} c_{ij} &{} s_{ij} &{} 0 &{} 0 &{} 0 &{} 0 \\ -s_{ij} &{} c_{ij} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} c_{ij} &{} s_{ij} &{} 0 \\ 0 &{} 0 &{} 0 &{} -s_{ij} &{} c_{ij} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$

(9)

where $c_{ij}$ and $s_{ij}$ represent $\cos$ and $\sin$ of the angle between the beam axis and the global x direction, respectively. Substitution of $\tilde{\mathbf {K}}$ and ${\mathbf {T}}_{ij}$ into Eq. (8) gives the stiffness matrix of beam ij in the global coordinate system:

$$\begin{aligned}&{\mathbf {K}}_{ij} =\nonumber \\&\begin{bmatrix} c^2_{ij} \gamma + s^2_{ij} \zeta &{} &{} &{} &{} &{} \\ s_{ij}c_{ij}(\gamma - \zeta ) &{} s^2_{ij} \gamma + c^2_{ij} \zeta &{} &{} &{} SYM &{} \\ -s_{ij} \lambda &{} c_{ij} \lambda &{} \psi &{} &{} &{} \\ -(c^2_{ij} \gamma + s^2_{ij} \zeta ) &{} s_{ij} c_{ij} (\zeta - \gamma ) &{} s_{ij} \lambda &{} c^2_{ij} \gamma + s^2_{ij} \zeta &{} &{} \\ s_{ij} c_{ij} (\zeta - \gamma ) &{} -(s^2_{ij} \gamma + c^2_{ij} \zeta ) &{} -c_{ij} \lambda &{} s_{ij} c_{ij} (\gamma - \zeta ) &{} s^2_{ij} \gamma + c^2_{ij} \zeta &{} \\ -s_{ij} \lambda &{} c_{ij} \lambda &{} \xi &{} s_{ij} \lambda &{} -c_{ij} \lambda &{} \psi \end{bmatrix}\nonumber \\ \end{aligned}$$

(10)

Then, the components of the beam stiffness matrices are assembled into the ${\mathbf {K}}$ matrix of the entire lattice by summing up the forces and moments of the beams which connect at each node. The resulting equilibrium equations of the lattice in the global coordinate system take the form

$$\begin{aligned} {\mathbf {K}} . {\mathbf {u}} = {\mathbf {F}} \end{aligned}$$

(11)

where ${\mathbf {u}}$ and ${\mathbf {F}}$ are the global displacement and force vectors, respectively.

1.2 A.2 Failure criterion

Beam failure occurs depending on a stress-based criterion. We use the Maximum Distortion Energy Theory of Failure (von Mises) criterion. For a 2D geometry with plane stress loading conditions, this criterion can be expressed as

$$\begin{aligned} \sigma =\sqrt{\sigma _{11}^{2}+3\sigma _{12}^{2}} = t, \end{aligned}$$

(12)

where $\sigma _{11}$ and $\sigma _{12}$ are axial and shear stress of the beam, respectively, and t is the equivalent stress at failure (beam failure threshold). Axial stress consists of tensile/compressive and bending components which are at the beam end surface with outward normal n given by

$$\begin{aligned} \sigma _{11}=\dfrac{F n}{A}+\dfrac{M \tilde{y}}{I}. \end{aligned}$$

(13)

where a force in direction of the outward normal of the beam end surface ($Fn >0$) yields a positive (tensile) stress contribution and a force in opposite direction a compressive stress contribution. Since the loads on each beam are only applied through the end nodes and the beam is in quasi-static equilibrium with small deformations, axial and shear forces form couples which lead to constant axial and shear stresses, i.e., for beam $_{ij}$ we have $F_i = - F_j, F_in_i = F_j n_j = \sigma _{11} A$ and $Q_i = - Q_j, Q_in_i = Q_j n_j = \sigma _{12} A$ . Because of the same reason, the bending moment varies linearly along the beam and therefore is maximum at one of the end nodes. We assume that beam failure initiates at the location of maximal tensile stress. Given that the bending moment is highest in the outer beam layer ($\tilde{y}=y_{max}$), maximum axial and shear stresses follow the relation:

$$\begin{aligned} \mathrm{max}(\sigma _{11})= & {} \dfrac{F_{i}n_i}{A}+\mathrm{max}(|M_{i}|,|M_{j}|)\dfrac{y_{\mathrm{max}}}{I}, \end{aligned}$$

(14)

$$\begin{aligned} \sigma _{12}= & {} \dfrac{Q_{i}}{A}. \end{aligned}$$

(15)

By substituting Eqs. (14) and (15) into Eq. (12), the failure criterion is given by

$$\begin{aligned}&\sigma /t = 1,\nonumber \\&\sigma = \sqrt{ \Big ( \dfrac{F_{i}n_i}{A}+\mathrm{max}(|M_{i}|,|M_{j}|)\dfrac{y_{\mathrm{max}}}{I} \Big ) ^ {2}+3 \Big ( \dfrac{Q_{i}}{A} \Big ) ^ {2} }\nonumber \\ \end{aligned}$$

(16)

A simpler criterion often used in the literature (see e.g. Herrmann et al. (1989), Nukala et al. (2008).) is obtained by neglecting the shear force Q in this expression, however, given that we consider Timoshenko rather than Euler–Bernoulli beams, it would be inconsistent to neglect shear stress effects which are of particular importance for failure of the lateral connector beams.

Mimicking material heterogeneity, beam failure thresholds t are randomly assigned based on a Weibull probability distribution function with probability density

$$\begin{aligned} p(t) = \dfrac{\beta }{\eta } \Big ( \dfrac{t}{\eta } \Big ) ^ {\beta - 1} \exp \left( -\Big ( \dfrac{t}{\eta } \Big )^\beta \right) . \end{aligned}$$

(17)

With $p(t) \ge 0 , t \ge 0 , \beta> 0 , \eta > 0$ where $\beta$ and $\eta$ are the shape and scale parameters of the distribution, respectively. For this distribution, the mean value of thresholds is

$$\begin{aligned} {\bar{t}} = \eta . \varGamma \Big ( \dfrac{1}{\beta } +1 \Big ) \end{aligned}$$

(18)

where $\varGamma$ is the gamma function. From Eq. (18), the scale parameter can be written as

$$\begin{aligned} \eta = \dfrac{{\bar{t}}}{\varGamma \Big ( \dfrac{1}{\beta } +1 \Big )} \end{aligned}$$

(19)

The variance of failure thresholds, on the other hand, is a function of the shape and scale parameters:

$$\begin{aligned} var(t)=\eta ^{2} \Big [\varGamma \Big ( \dfrac{2}{\beta } +1 \Big ) - \varGamma ^2 \Big ( \dfrac{1}{\beta } +1 \Big ) \Big ] \end{aligned}$$

(20)

Combining Eqs. (19) and (20) gives

$$\begin{aligned} var(t)= & {} \Big [\dfrac{{\bar{t}}}{\varGamma ( (1/\beta ) +1)} \Big ] ^{2} . \Big [\varGamma \Big ( \dfrac{2}{\beta } +1 \Big ) \nonumber \\&-\varGamma ^2 \Big ( \dfrac{1}{\beta } +1 \Big ) \Big ] \end{aligned}$$

(21)

Eq. (21) shows that for a given mean (average) threshold, the variance is a function of the shape parameter ($\beta$) only. In this paper we choose a fixed mean value of 1.0 for the failure threshold (measured in units of the elastic modulus). This ensures that strains are of typical order less than 0.1, warranting a small-strain approximation to the elastic problem on the beam level. However, under general loading conditions the problem is still geometrically non-linear since the beam angles, which depend on the global nodal displacements, are in general not close to their initial values even if the deformations of the individual beams are small. For the network sizes and loading mode considered here (axial loading of the networks along a statistical symmetry axis), but not in general, it is feasible to assume that the beam angles remain near their initial values. In this case, the behavior of materials with different mean threshold can be obtained by simple multiplication with the threshold ratio.