1 Introduction

Mathematical knowledge is typically perceived as a process leading to irrefutable truths through the application of classical logic. However, human reasoning does not always conform to the rigid rules of classical logic. Humans are prone to changing their perspectives and revising their conclusions when confronted with new information. Their knowledge can be incomplete and inconsistent, making it susceptible to being revised or retracted based on new evidence. The practice of mathematics is often a complex and dialectical process, characterized by obstacles and challenges that need to be overcome. Cognitive psychology studies, such as the work of Mercier and Sperber (2011), have highlighted the similarity between argumentation and human reasoning, showcasing how an argumentation-based approach can facilitate various forms of human reasoning, including dialogue, debate, validation, and proving-especially in incomplete and dynamically changing environments. This dynamic environment is often the case in mathematical proving, as the advance of mathematical knowledge has shown time and again. The objective of this research is to explore the concept of proof through the lens of argumentation, illustrating proof-events as dialogues among agents who employ arguments and counterarguments to establish the validity of a proposed proof.

The field of argumentation theory emerged in the 1990s with notable research contributions by Dung (1995), Vreeswijk (1997), and Pollock (1987, 1992), which remain relevant to this day. These theories have paved the way for expanding the application of argumentation beyond fixed problems to situations where modifications are required. As new information becomes available, the problem environment dynamically adjusts to accommodate the assimilation of this new knowledge into the proof process. In this paper, we aim to leverage and integrate these established approaches while also drawing insights from other notable works, such as Toulmin (1993) and Kakas & Michael (2016). By doing so, we provide an abstract and theoretical exploration of logical argumentation, primarily focusing on its application in the realm of mathematical proving.

The proposed “Argumentation-based Proof-Event Calculus” (APEC) integrates the concepts of proof-events and logic-based argumentation theories to provide a more comprehensive understanding of the cognitive processes involved in mathematical proofs. Our purpose is to introduce a model of mathematical discovery that illustrates the link between formal mathematics and their informal social context. The primary focus is on examining the argumentative process that unfolds during the proving activity. To achieve this, the concept of a proof-event, along with its temporal predicates, is combined with techniques and theories derived from the field of argumentation. This will facilitate the formalization of arguments relationships to describe cases of mathematical problems with contradictions and attacks. By merging these perspectives, we aim to enhance our understanding of the intricate nature of mathematical proofs and their associated reasoning processes.

Thus, the objectives of this study are:

  1. 1.

    To compare the structure of proof-events with arguments and expand the concept of a proof-event calculus by incorporating an argumentation-based framework. This involves examining the similarities and differences between proof-events and arguments and developing an enhanced understanding of their interplay within the context of mathematical proofs.

  2. 2.

    To establish an integrated framework called the Argumentation-based Proof-Event Calculus, which encompasses various types of argument moves, temporal predicates, and levels of argumentation. This framework provides a formalized structure to analyze and model the dynamics of arguments and their progression within the proving process.

  3. 3.

    To facilitate the modeling of argument schemes both internally and externally,Footnote 1 enabling a comprehensive representation of logical proving systems that encompass contradictions and attacks. By incorporating these elements, the framework can effectively capture the complexities and challenges that arise in mathematical proofs, enhancing our ability to describe and analyze the logical reasoning involved.

Given the context, the question of “why create a logic-based argumentative calculus” emerges. Logic-based systems for examining and assessing arguments have been broadly applied, generating various informal methods for argumentation-based reasoning (Arieli & Straber, 2015). The analytic framework of the calculus presented in this paper provides a tool to assess mathematical argumentation based on formal structure, argumentation sequences, and agents’ contributions, containing various categories of argumentation frameworks (Clark & Sampson, 2008). By creating a logic-based argumentative calculus, mathematical practitioners gain a valuable tool to analyze and assess mathematical argumentation in a more structured and in-depth manner.

Furthermore, another important point is that our approach encompasses a wider meta-methodological framework that goes beyond a specific context and can be applied to various proving procedures in science and everyday life. This framework incorporates both proofs and arguments and is rooted in the theory of proof-events. By adopting this framework, we aim to provide a flexible and versatile approach that can be employed in diverse domains where proving is essential, including scientific research, academic disciplines, and practical applications. This theory allows us to delve into the underlying structure of proving procedures, highlighting the logical connections, justifications, and explanations, but also the conflicts and impasses, that emerge throughout the process. With the ability to apply our approach to various contexts, we can analyze and comprehend the reasoning process in different fields and domains. Whether it's in mathematical proofs, scientific experiments, legal arguments, or even everyday problem-solving, our framework offers a unified methodology to explore and elucidate the intrinsic relationship between reasoning, arguments, and validation. By adopting this broader meta-methodological framework, we provide researchers, practitioners, and individuals with a powerful tool to enhance their understanding and analysis of proving procedures across a wide range of scientific and real-life contexts.

Considering the stated objectives, the paper is structured in six sections: Sect. 2 describes the theoretical background of proof-events and argumentation; Sect. 3 outlines the formalization of proof-events in terms of argumentation theories and illustrates the modeling of the multi-agent mathematical contributions at Fermat’s Last Theorem; Sect. 4 analyzes and interprets the findings; and Sect. 5 concludes with an overview of this paper.

2 Theoretical Background and Prerequisites

Discovery, reasoning, communication, and systematization are some of the key elements that proofs offer in mathematics (Villiers, 1990), but often proof is perceived mostly as a method for persuasion (Weber, 2010). The history of mathematical proofs has shown many cases where various agents (mathematicians or not) have added value with their attempts, assumptions, beliefs, proof steps or even false steps in the sequence of proof-events. Sienkiewicz (2019) supported the idea that some of our beliefs might be considered as knowledge, even when they are not, and that we lack the necessary reasons to establish them as such. In some instances, mathematical proofs evolved for many years until they reach the desired outcome, such as the famous Hilbert’s problems, Poincaré conjecture, Lobachevsky’s geometry, Riemann’s hypothesis, Fermat’s theorem, etc. Goguen (2001) suggested the broader concept of proof-event or proving, which is a social event that takes place in specific place and time and often involves public communication. The concept of a proof-event is designed to embrace any proving activity, including purported, faulty, vague, disputed, or incomplete proofs. Vandoulakis and Stefaneas (2015) describe proof-events as the activities of a multi-agent system incorporating the history of these activities to create sequences of proof-events in terms of “fluents”. Our purpose is to bridge the gap between formal and informal mathematical procedures by devising a modeling calculus that is closely related to the way that proving is actually done. The comparison between proof and argumentation is based on the perception that proofs (including incomplete or even false proofs, valid or invalid inference steps, ideas, etc.) can be regarded as a specific kind of argumentation in mathematics (Pedemonte, 2007).

Many researchers claim that the role of argumentation is central in mathematics, since most of their proving activity might be understood as kinds of argumentation (Aberdein, 2009; Hunter, 2020) and thus, various researchers (Aberdein, 2005; Aberdein & Dove, 2013; Banegas, 1998; Pedemonte, 2007, 2008) tried to show that the procedure by which mathematicians evaluate reasoning is similar to argumentation, by adapting Toulmin’s (1993) argumentation model to mathematical examples. In Toulmin’s model, an argument is constituted by six interrelated components: claim, data, warrant, backing, rebuttal, and qualifier. The first three elements are considered the substantial elements of applied arguments, whereas the last three are not always necessary. Lakatos’ “Proofs and Refutations” (1976) is also an enduring classic that highlights the role of dialogue between agents (a teacher and some students) at proof attempts along with the critiques of these attempts. The work of Pease et al. (2017) provides a way of formalizing social aspects of proofs by interpreting the informal logic of a Lakatos-based mathematical discovery through the lens of argumentative dialogue, an approach called “mixed-initiative collaborative proving”.

The studies conducted so far have emphasized the connection and continuity between reasoning in argumentation and proving. Our approach aims to clarify this inherent relationship by modeling the dialogues that occur between mathematicians when they provide justifications and explanations during the process of proving. Our objective is not to simply assign interpretations or descriptions to individual procedural steps. Instead, we strive to formally represent the entire practice of proving and its social interactions in the most comprehensive way possible. Additionally, our approach explicitly highlights the argument moves made by the mathematicians and the sequence of steps they follow. We consider not only the temporal aspects, using temporal predicates to represent the chronological order, but also the progressive nature of the argumentation process, represented by levels of argumentation. This progression continues until the outcome of the argument is ultimately either validated or invalidated. Our approach involves a broader meta-methodological framework, which incorporates both proofs and arguments through the theory of proof-events.

In the next subsections, a brief overview of proof-events calculus and argumentation theory is provided to gradually proceed in their integration and formalization.

2.1 A Brief Review of Proof-Events Calculus

Goguen (2001) presented the idea of “proof-event,” aimed to cover all exemplifications of proof as well as proof steps and computer proofs. From his perspective, the idea of proof-event is more comprehensive and less formal than that of purely mathematical logic, since it includes not only formal proof methods and steps, but also the intention to prove, its significant steps, and the complete structure of the proof, including conflict and other narrative devices.

Proof-events are not necessarily equivalent to mathematical truths, since a proof-event may refer to an incomplete proof, an outline of a proof, or even a proof-less expression of considerations referring to specific problem. The prover may experience an inspiration (or intention) in a particular mathematical problem and thus initiate a proof-event to communicate his/her experience (Stefaneas & Vandoulakis, 2015). Hence, agents involved in the process of proving act with intention and inspiration, and their attempt is goal-oriented. The goal of a prover might be to solve a particular problem and the goal of a subsequent interpreter of the proof attempt might be simply to aid in the clarification and understanding of the argumentation that had been suggested to this problem by the prover (Stefaneas & Vandoulakis, 2015). A sequence of proof-events, named “fluent,” is finalized when the agents involved in it conclude that they have perceived the proof and validated that a proof has been given, meaning that the proof is confirmed.

In “Proof-Events Calculus” (Stefaneas & Vandoulakis, 2015), certain temporal aspects of proof-events were modelled using the language of the calculus of events inspired by Kowalski’s “Event Calculus” (EC) (Kowalski & Sergot, 1985). The underlying ontology of proof-event calculus contains types of “proof-events”, “fluents”, and “time points.” Proof-event calculus has types of proof-events whose instantiations mark the time-dependent properties, a set of fluent constants that depict the various properties of the problem domain, and time points.

The definitions of proof-event and fluent, as described in Stefaneas and Vandoulakis (2015), are presented next:

Definition 2.1

(Proof-event) Proof-event e is a proof instance that takes place in space and time, it refers to a specific problem, and it is specified by certain conditions as predicates. A proof-event e has the following internal structure:

$$e = \left\langle { communicate\left( {Intention, Problem} \right), t } \right\rangle$$

which means that an intention (mathematical argument, assumption, idea, etc.) is linguistically articulated at time t for a time-independent problem.

Definition 2.2

(Fluent) Fluent f is a sequence of proof-events \(e\) evolving in time that refers to a specific problem. A fluent is a function that may be interpreted in a model as a set of time points \({t}_{n}, n= 1, 2,..,i,\) conventionally denoting the time when the communication output is available. Hence, fluents (alike proof-events) have “initial” and “terminal” points, i.e., they are extended spatially and temporally:

$$f = \left\{ {e_{1} , e_{2} , \ldots , e_{i} } \right\},{\text{where}}$$
$$e_{i} = \left\langle {communicate\left( {Intention_{i} , Problem} \right), t_{i} } \right\rangle ,$$
$${\text{for every}}\quad 1 \le i < n, t_{i} < t_{i + 1} , n \in N.$$

The fluent is subject to change over time, depending on the contribution and value of the individual proof-events. The temporal predicates for modeling this change are:

Happens(e,t): Proof-event e starts to happen at time t.

Initiates(e,f,t): The fluent f of e initiates at time t.

Clipped(e,f,t): The fluent f of e clipped at time t.

Terminates(e,f,t): The fluent f of e terminates at time t.

ActiveAt(e,f,t): The fluent f of e is active at time t.

Valid(e,f,t): The fluent f of e is valid at time t.

2.2 A Brief Review of Argumentation Theory

Argumentation can be conceived as a particular kind of language expressing syllogisms used in social interactions, in which beliefs are not only formulated but also supported in a dialectical environment of criticism, in which alternative opinions and counterarguments are expressed (Larrain et al., 2020). Logical argumentation is a logic-based approach for formalizing arguments and counterarguments expressed in terms of formal languages as well as entailment relations for drawing claim in the proving procedure (Hunter, 2007; Pollock, 1992; Prakken & Horty, 2012).

The definitions given below outline some of the fundamental concepts behind logical argumentation (Dung, 1995).

Definition 2.3

(Argumentation Framework) An argumentation framework is a pair \(AF =<Args, A>\), where Args is an enumerable set of elements that are called “arguments” and A is a binary relation on \(Args X Args\) whose instances are called “attacks.”

An argument has premises, warrant, and a claim. The method of inference by which a claim follows from a set of formulae is a deductive inference and is denoted by \({ \vdash }\). The definition of a deductive argument is given below.

Definition 2.4

(Argument) An argument is an ordered pair \(<\Phi ,\alpha >,\) where \(\Phi { \vdash }_{i}\) is the support, or premises, or assumptions of the argument, and \(\alpha\) is the claim or conclusion of the argument. The definition for a deductive argument only assumes that the premises entail the claim, i.e. \(\Phi { \vdash }_{i} \alpha\). For an argument \(A=<\Phi ,\alpha >,\) the function \(Support(A)\) returns \(\Phi\) and the function \(Claim(A)\) returns\(\alpha\).

Important benefits of arguments are the explicit representation of the claim (and of the information used to support it) as well as a consequence relation to connect simply and precisely the support and claim of the argument. What an argument does not provide is specific proof of the claim from the premises. There may be more than one way to prove the conclusion from the premises, but the argument does not determine which way is used (Aberdein, 2009).

The possible different kinds of arguments can either support a claim or attack it. Given a claim \(\alpha\) and an argument A, the possible arguments which provide support for \(\alpha\) (Haggith, 1996) include:

Equivalent an argument A for a claim which is equivalent to \(\alpha\).

Elaboration an argument A for an elaboration of \(\alpha\).

Given a claim \(\alpha\), an argument A, and a counterargument of the A, the possible arguments which oppose \(\alpha\) (Polock, 1992; Vreeswijk, 1997) include:

Rebutting a counterargument for a claim which attack the claim \(\alpha\) of the A.

Undermining a counterargument for a claim which attacks a premise of the A.

Undercutting a counterargument for a claim which attacks an inference rule of the A.

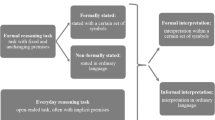
The next section outlines the formalization of proof-events based on argumentation, integrating features from both theories as illustrated in Fig. 1.

Fig. 1
figure 1

Proof-events and argumentation contributions in APEC

Full size image

3 Argumentation-Based Formalization of Proof-Event Calculus

In this section, we introduce the Argumentation-based Proof-Event Calculus (APEC), which serves as the model for our approach. A comparison of the basic elements of proof-events and argumentation theory shows similarities in the structure, the sequence, and the agents.

  1. (1)

    Arguments and proof-events have three common fundamental components: a set of premises for a task or problem (i.e., data in arguments and premises in proof-events), a method of reasoning (i.e., warrants in arguments and inference rules in proof-events), and a conclusion (i.e., claim in arguments and conclusion in proof-events).

  2. (2)

    The objective of proving emerges from the historical sequence of events, which can be sequences of proof-events (fluents) or sequences of arguments and counterarguments (Vandoulakis & Stefaneas, 2015). A sequence of proof-events is complete when the community involved in it concludes that they have understood the proof and agree that a proof has actually been given or that a proof is invalid, based on a suggested counterargument or counterexample.

  3. (3)

    Argumentation involves agents or groups of agents, enacting the roles of supporter and opponent of an argument (Kakas & Moraitis, 2003). Similarly, proof-events presuppose the existence of at least two types of agents: a prover, that is the agent that provides the proof; and an interpreter, that is the agent who checks the validity of the proof (Almpani & Stefaneas, 2017), encouraging its adoption as a framework for the development of multi-agent systems.

In a mathematical argument, as presented in our approach, there is typically a sender (the prover) and a receiver (the interpreter or audience) of an argument, where the prover formulates the proof, and the interpreter validates or examines it for potential errors or falsification. In the context of proving, the prover and the interpreter might be the same individual, i.e., the constructor of a proof. This means that the person who formulated the proof is also the one who evaluates and assesses their own reasoning and proving process. In such cases, the prover acts as both the sender and the receiver of the argument, engaging in a self-assessment of the work. However, in collaborative settings or when proofs are shared with the mathematical community, the receiver(s) can be other colleagues who study the proof independently. They act as external validators, carefully inspecting the proof for validity, correctness, and potential improvements. In this case, the prover becomes the sender, and their colleagues become the receivers of the argument. This two-fold process of mathematical proving, involving both the formulation of the proof and its subsequent validation.

This iterative process of self-assessment and external validation fosters a reliable mathematical proof, and it embodies the essence of the mathematical community's collective effort to uphold the highest standards of mathematical knowledge. Therefore, although a new proof is usually attributed to the prover of a problem, it may as well be the outcome of the communication with other agents and their previous experiences as they studied the problem (Trninic et al., 2018). During this communication, the steps that an individual agent wants to perform to accomplish a mathematical proof may interfere with the steps attempted or already performed by other agents. Take as example the Fermat Theorem (see Sect. 3.3) where mathematicians made attempts to prove it for more than three centuries and, lastly (in 1994, that is after 357 years), it was proved by mathematician Andrew Wiles. Indeed, Wiles’ proof has been the outcome of the creative efforts of mathematicians and their proofs which contained deficiencies and flaws, exposing that many of the creative breakthroughs relied on collaboration, communication, and social interaction (Trninic et al., 2018). This approach suggests a multi-agent system, enacting the roles of provers and interpreters, who generate sequences of proof-events with arguments and counterarguments. It builds upon and expands the sequent-based approach to logical argumentation described in (Almpani et al., 2017, 2019, 2023).

3.1 The Inner Structure of Argumentation-Based Proof-Events

The inner structure of APEC comprises its underlying components, argumentation-based proof-events and fluents, and their interconnections (Almpani, 2022).

Definition 3.1

(Argumentation-based proof-event) A proof-event \(e\) can be represented as a communicated argument \(<\Phi , c>\) Pollock, 1992) designated by the pair \(e<\Phi , c>\) as \(e = <communicate<\Phi , c>, w>,\) where Φ is the premise of the argument based on the available data, c is the claim that refers to the conclusion of a particular problem, and w are the inference rules ‘warrant’ which allow to be connected with c, so that:

  • \(\ \phi { \nvdash } \bot\)

  • \(\phi { \vdash } c\)

  • There is no Φ΄ \(\subset\) Φ such that \(\Phi { \vdash } c\)

Counterarguments are represented by the corresponding pair \({e}^{*}(\Psi , \beta ),\) where Ψ is the premises that the claim β of the counterargument is based.

Argumentation may require chains- or trees- of reasoning, where claims are used in the assumptions for obtaining further claims (Hunter, 2007), so that a proof-event could be an atomic argument or a sequence of arguments, i.e., a fluent.

Definition 3.2:

(Fluent) A fluent f is a formula of the form \({e}_{1},{e}_{2},\dots ,{e}_{n}\to e,n\in N\), where \({e}_{1}<{\phi }_{1}, {c}_{1}>{e}_{2}<{\phi }_{2}, {c}_{2}>,\dots , {e}_{n}<{\phi }_{n}, {c}_{n}>\) is a finite, possibly empty, sequence of arguments, where the conclusion of proof-event ei is the claim ci, i.e., \(concl({e}_{i}) \equiv {c}_{i}\), for some \({c}_{1},{c}_{2},\dots ,{c}_{n}\to c\) (Vreeswijk, 1997). Therefore, the meanings of the finite structural components of the argument (Toulmin, 1993)—which are abbreviated by corresponding prefixes- are defined for the notion of a fluent as below:

$$\begin{gathered} f = \left\{ {e_{1} , e_{2} , \ldots , e_{n} \to e,n \in N} \right\},{\text{where}} \hfill \\ e = \left\langle {communicate\left\langle {\Phi , c} \right\rangle , w} \right\rangle ,{\text{ and}} \hfill \\ Claim:concl\left( e \right) = concl\left( {e_{1} } \right) \cap concl\left( {e_{2} } \right) \cap ... \cap concl\left( {en} \right) \equiv c = c_{1} \cap c_{2} \cap ... \cap c_{n} \hfill \\ Data:prem\left( e \right) = prem\left( {e_{1} } \right) \cup prem\left( {e_{2} } \right) \cup ... \cup prem\left( {en} \right) \equiv \Phi 1 \cup \Phi 2 \cup ... \cup \Phi n \hfill \\ Warrant:inferrul\left( e \right) = inferrul\left( {e_{1} } \right) \cup inferrul\left( {e_{2} } \right) \cup ... \cup inferrul\left( {en} \right) \equiv w = w_{1} \cup w_{2} \cup ... \cup w_{n} \hfill \\ \end{gathered}$$

where claim c is the statement communicated by the speaker, data Φ are the premises of the claim, and the warrant w is the set of inference rules, which allows the premises to be connected to the claim. The aforementioned elements are frequently used to define consequence relations between the arguments and/or the counterarguments, e.g., Toulmin’s model.

Let’s see as an illustrative example a proof of the Pythagorean Theorem, according to which in a right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides, stated as a2 + b2 = c2.

The Pythagorean Theorem can be depicted as:

$$e_{Pythagorean} = \left\langle {communicate\left\langle {\Phi_{RigAngTriangle} , c_{Pythagorean} } \right\rangle , w_{Euclid} } \right\rangle$$

where:

\({e}_{Pythagorean}\) is the proof-event that refers to the proving procedure of Pythagorean theorem,

\({\Phi }_{RigAngTriangle}\) is the data that are used as premises, i.e., specific cases of right-angled triangles where the Pythagorean Theorem is valid,

\({c}_{Pythagorean}\) is the conclusion of the Pythagorean Theorem (i.e., a2 + b2 = c2), and.

\({w}_{Euclid}\) is the inference rules used in order to prove the conclusion of the theorem, which in our example is Euclid’s proof.

In the Fig. 2, the premise of this problem is the right-angled triangle ABC:

$$prem\left( {e_{Pythagorean} } \right) = prem\left( {ABC} \right).$$
Fig. 2
figure 2

Euclid’s proof of the Pythagorean theorem

Full size image

Euclid constructed squares BCED, ABFG, and ACKH from the sides of the right triangle ABC and sought to prove that the area of BCED was equal to the sum of the areas ABFG and ACKH. With APEC we can depict the steps included in this proof procedure. We want to show the claim that:

$$concl\left( {e_{Pythagorean} } \right) = concl\left( {e_{1} } \right) \cap concl\left( {e_{2} } \right),$$

where:

$$concl\left( {e_{1} } \right) \equiv c_{1} : Area_{ABFG} = Area_{BMLD}$$
$$concl\left( {e_{2} } \right) \equiv c_{2} : Area_{ACKH} = Area_{CELM}$$

The warrant for proving the concl(e1) includes the following steps:

$$inferrul\left( {e_{1} } \right) = inferrul\left( {e_{1a} } \right) \cap inferrul\left( {e_{1b} } \right) \cap inferrul\left( {e_{1c} } \right),$$

where:

\(inferrul\left( {e_{1a} } \right) : \Delta BCK = \Delta ACE\),

where the Greek letter ∆ symbolizes a triangle, thus we have that the triangle BCK equals the triangle ACE,

$$inferrul\left( {e_{1b} } \right): Area_{BCK} = \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} Area_{ACKH} ,$$

since ΔBCK and square ACKH share base CK, fall between parallel lines CK and BH, and line BH is a straight line. And in the same way,

$$inferrul\left( {e_{1c} } \right) : Area_{ACE} = \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} Area_{CELM}$$

Similar, we have the inferences rules for \({e}_{2}\):

$$inferrul\left( {e_{2} } \right) = inferrul\left( {e_{2a} } \right) \cap inferrul\left( {e_{2b} } \right) \cap inferrul\left( {e_{2c} } \right)$$

Combining the above proof-events, the warrant of Euclid’s proof is:

$$w_{Euclid} = inferrul\left( {e_{1} } \right){ } \cap inferrul\left( {e_{2} } \right).$$

The Pythagorean Theorem may have more known proofs than any other theorem: there are 370 proofs of the Theorem (Loomis, 1940), thus, there can be many different warrants except of \({w}_{Euclid}\) that lead to the same conclusion, to the same proof, e.g., geometric proofs (e.g., by Euclid), algebraic proofs (e.g., by James Abram Garfield), proofs by rearrangement, etc. Therefore, there can be different warrants leading to the same claim, since in mathematics there can be different inferences rules that lead to the same conclusion (proof), as in the example with the different proofs of the Pythagorean Theorem.

Moreover, theorems and proofs are typically established based on the initial premises and axioms of a particular mathematical system. If the underlying axioms change, the validity of the inference rules and the resulting conclusions can also change. A theorem might hold true in one specific context but may lose its validity when applied to another setting with different underlying axioms. Additionally, different mathematical systems and axiomatic foundations can lead to the development of distinct branches of mathematics, e.g., Euclidean Geometry and Non-Euclidean Geometry, where the parallel postulate of Euclid is replaced with alternative axioms, leading to the creation of hyperbolic and elliptic geometries. This highlights the importance of carefully defining in the inner structure of APEC the context and premises under which a proof is proven, as the applicability of different proof steps and inference rules may vary depending on these factors.

In the previous example, the internal structure of proof-events in a proof procedure was depicted. The next section presents how APEC can formalize the external relation of proof-events that communicate and simulate conflicts during a proof procedure.

3.2 The Outer Structure of Argumentation-Based Proof-Events

The outer structure of APEC encompasses its external interactions with the other agents (argument moves) and the chronological and progression sequence (temporal predicates and levels of argumentation).

3.2.1 Argument Moves

During a proof procedure, there can be various inference stages, such as attempts, impasses, confirmed or unconfirmed steps, false suggestions or implicit assumptions, intuitive ideas, intentions, etc. Arguments can then be specified as chains of reasoning leading to a conclusion with consideration of possible counterarguments at each step. With the explicit construction of the chain of reasoning a chain x0, x1,…, xn where the argument xi attacks the argument xi-1 for i > 0), various concepts of defeat can be conceptualized. When an agent has gained control of an argument, he/she must select which argument move to apply. Gordon (1991) referred to “argument moves” as analogs of three roles for legal cases. This term was also previously used by Rissland (1985), Asley and Aleven (1991), Pease et al (2013). In this work, the term “argument moves” is reserved for specific, active tactics or strategies that a prover can choose to support his claim. Five fundamental relations are used in this work that indicate links and conflicts at the sequence of proof-events. The possible argument moves, that are communicated during the proof-events sequences, can provide support equivalence, elaboration, or attack rebutting, undercutting, undermining to the claim.

3.2.1.1 Argument Moves that Support a Claim

A proof-event \({e}_{1}({\phi }_{1}, {c}_{1})\) is equivalent with a proof-event \({e}_{2}({\phi }_{2}, {c}_{2})\), whenever it has the same premises and the same conclusion, although they may have different warrants.

$$Equivalent\left( {e_{1} , e_{2} } \right):e_{1} \left( {\phi_{1} , c_{1} } \right) = e_{2} \left( {\phi_{2} , c_{2} } \right),$$

when \({\phi }_{1}={\phi }_{2}\), \({c}_{1}={c}_{2}\) and it might be \({w}_{1}\ne {w}_{2}\).

Equivalent proof-events can have different ways of proving. Thus, a proof-event \(e\left(\phi , c\right)\) can have a set of inference rules S which elaborate or embellish upon e, iff \(\Phi \cup S{ \vdash }c\). Thus,

$$Elaboration\left( {e, S} \right): inferrul\left( e \right) \cap inferrul\left( S \right) \to concl\left( e \right).$$

These moves are used for backing a claim and supporting a proof, therefore:

$$Support\left( {e, t} \right) \to Equivalent\left( {e, e^{\prime}} \right) \cup Elaboration\left( {e, S} \right).$$
3.2.1.2 Counterargument Moves that Attack a Claim

A counterargument communicated during the proof-event \({e}^{*}(\Psi , \beta )\) rebuts-attacks the conclusion of an argument communicated during the proof-event\(e\left(\phi , c\right)\), iff \({ \vdash }\beta \leftrightarrow \neg c\). Thus,

$$Rebutting\left( {e^{*} , e} \right): Rebut\left( {e^{*} , e} \right) \to \neg concl\left( e \right).$$

A counterargument communicated during the proof-event \({e}^{*}(\Psi , \beta )\) undermines-attacks some of the premises of the argument communicated during the proof-event\(e\left(\phi , c\right)\), iff \({ \vdash }\beta \leftrightarrow \neg \left( { \cap w_{i} } \right)\), for some \({w}_{1}, .., {w}_{n}\subset W\). Thus,

$$Undermining\left( {e^{*} , e} \right): Undermin\left( {e^{*} , e} \right) \to \neg prem\left( e \right).$$

A counterargument communicated during the proof-event \({e}^{*}(\Psi , \beta )\) undercuts-attacks some of the inference rules of the argument communicated during the proof-event\(e\left(\phi , c\right)\), iff \({ \vdash }\beta \leftrightarrow \neg \left( { \cap \phi_{i} } \right)\),or some \({\Phi }_{1}, .., {\phi }_{n}\subset \phi\). Thus,

$$Undercutting\left( {e^{*} , e} \right): Undercut\left( {e^{*} , e} \right) \to \neg inferrul\left( e \right).$$

A counterargument communicated with the proof-event \({e}^{*}(\Psi , \beta )\) attacks an argument communicated during the proof-event e \(\left(\phi , c\right)\), at time t, iff e* rebuts e or e* undercuts e or e* undermines e. Therefore:

$$Attack\left( {e^{*} , t} \right) \to Rebut\left( {e^{*} , e} \right) \cup Undercut\left( {e^{*} , e} \right) \cup Undermin\left( {e^{*} , e} \right)$$

3.2.2 Temporal Predicates

Even though proof-events can be regarded as taking place instantaneously, the EC is neutral with respect to whether events have duration or are instantaneous (Kowalski, 1992). Thus, for the duration of proof-events, the APEC uses the perspective of Reasoning about Actions and Change (RAC) which is about how fluents change when new information is acquired and how this view of the problem is affected by the observation of some events remaining active or terminated at a particular time (Hadjisoteriou & Kakas, 2015). RAC (Kakas & Miller, 1997) uses causal propositions of the form ‘A initiates F when C’ or ‘A terminates F when C’, which in this paper are represented in a more specific and detailed form through the arguments and counterarguments’ moves that initiate or terminate a fluent. In each case, the time point of action of a proof-event will be taken into consideration. In this work, the above-mentioned operators are combined with the basic temporal predicates from Stefaneas and Vandoulakis (2015):

$$Happens\left( {e, t} \right), Initiates\left( {e, f, t} \right), Terminates\left( {e, f, t} \right),$$
$$ActiveAt\left( {e, f, t} \right), Clipped\left( {e, f, t} \right).$$

The purpose of the use of the language of event calculus in describing proof-events is to express the progress of the sequences of proof-events in terms of fluents. Hence, they are formalized in the following relations.

\({\varvec{Happens}}\left( {e, t_{1} } \right)\), which means that a proof-event e occurs at time \(t_{1}\).

\({\varvec{Initiates}}\left( {e, f, t_{1} } \right):{\varvec{happens}}\left( {e, t_{1} } \right) \to \neg {\varvec{attack}}\left( {e , t_{1} } \right) \cup {\varvec{support}}\left( {e, t_{1} } \right),\) at time \(t_{1}\),

which means that, if a proof-event e occurs at time \({t}_{1}\), then there are no counterarguments e that attack the validity of the outcome of the proof-event and there is adequate support for our claim at the specific time t1.

$${\varvec{Clipped}}\left( {e_{1} , f,t_{2} } \right):\exists e_{1} , e_{1}^{*} , t_{1} ,t_{2} , t\left[ {{\varvec{Happens}}\left( {e, t_{1} } \right) \cap \left( {t_{1} \le t \le t_{2} } \right) \cap {\varvec{attack}}\left( {e_{1}^{*} , t} \right)} \right]$$
$$\cap \left[ {{\nexists }e_{2} \left( {{\varvec{Happens}}\left( {e_{2} , t_{2} } \right) \to \neg {\varvec{attack}}\left( {e_{1}^{*} , t} \right)} \right)} \right],\quad for\quad t_{1} \le {\text{t}} \le t_{2}$$

which means that a proof-event clips when there is a terminating proof-event e1 between t1 and t2 and there is no proof-event e2 that attacks the counterargument e*1 attacking the proof-event e1.

$${\varvec{Terminates}}\left( {e, f, t_{1} } \right): \exists e,e^{*} , t_{1} (\left[ {{\varvec{attack}}\left( {e^{*} , t_{1} } \right) \to \neg {\varvec{conc}}\left( e \right) \cup \neg {\varvec{prem}}\left( e \right) \cup \neg {\varvec{sent}}\left( e \right)} \right]$$
$$\cap \left[ {{\nexists }e_{2} , t_{2} \left( {{\varvec{Happens}}\left( {e_{2} , t_{2} } \right) \to \neg {\varvec{attack}}\left( {e^{*} , t_{1} } \right)} \right)} \right]),$$
$$with\; t_{1} < t_{2} ,$$

which means that a fluent terminates when there exists a counterargument attacking the sequence and there is no proof-event e2 that happens in time t2 (with t1 < t2), to defend the claim. In other words, the fluent ends when a valid counterargument is presented, and there is no subsequent evidence provided to uphold the initial assertion. The formula contains a conjunction between the two conditions, which means both conditions must be met for the fluent to terminate: (1) a counterargument exists that attacks the sequence; and (2) there is no proof-event e2 occurring at time t2 to defend the claim. If either condition is not satisfied, the fluent will not terminate. The termination of a sequence of proof-events may be caused by the indication of the falsity of the problem, or if there are counterarguments that attack the conclusion of the proof-event, or the undecidability of the problem, or there is a lack of adequate warrants to prove the desideratum, or there is an inefficiency of the required information (a lack of premises).

$${\varvec{ActiveAt}}\left( {e, f, t_{n + 1} } \right):{\varvec{Happens}}\left( {e_{n + 1} , t_{n + 1} } \right) \to \neg {\varvec{attack}}\left( {e_{n} , t_{n} } \right) \cup {\varvec{support}}\left( {e_{n} , t_{n} } \right),$$
$$for\; every\; n \in N,\quad t_{n + 1} ; t_{n}$$

which means that a fluent is active if there is an argument to support the claim for every counterargument attacking the claim. This means that for every counterargument\({e}^{*}<{\Psi }_{i},{\beta }_{\iota }>\),\(i = 1, ..., n\),\(n\in N\), there is a proof-event\({e}_{n+1}( {\Phi }_{n+1},{c}_{n+1})\), which \(Happens({e}_{n+1}, {t}_{n+1})\) and defeats the attack of the counterargument \({e}_{n}^{*}<{\Psi }_{n},{\beta }_{n}>,\) for tn+1 > tn.

A list with all the predicates that constitute the core syntax of APEC is depicted in Fig. 3.

Fig. 3
figure 3

APEC predicates

Full size image

From the above-mentioned, it is concluded that:

\({\mathbf{Happens}}\left( {e,t_{1} } \right) \cap {\mathbf{Initiates}}\left( {e,f,t_{1} } \right) \cap (t_{1} < t_{2} ) \cap \neg {\mathbf{attack}}\left( {e*,t_{2} } \right) \to {\mathbf{ActiveAt}}\left( {e,f,t_{2} } \right)\).which means that a fluent remains active at time t2, if a proof-event e has taken place at time t1, with t1 < t2 and has not been terminated at a time point between t1 and t2.

Consequently,

$$\forall i \le n\left[ {{\mathbf{ActiveAt}}\left( {e,f,t_{i} } \right) \cap \left( {t_{i} < t_{n} } \right) \cap \neg {\mathbf{Terminates}}\left( {e,f,t_{i} } \right)} \right] \to {\mathbf{Valid}}\left( {e,t_{n} } \right),$$
$$\mathrm{at\;time\;}{t}_{n}, i=1,.,n,n\upepsilon {\mathbb{N}}$$

which means that a fluent should be considered valid at time tn, if it is active and there is no counterargument to terminate it at time ti for every i = 1, …, n, \(n\in N\).

3.2.3 Levels of Argumentation

The argumentation framework is built in terms of logic programming rules expressing a priority relation among them (Kakas et al., 1992). To define the warranted premises that are justified by a set of arguments in the sequence, a mechanism is required which by recursion can examine the representation of the arguments. Kakas et al. (2019) presented three levels of arguments:

  • “Object level” arguments, represent the statement of a problem domain and the initial agents’ decisions or actions in the specific problem where the claim of an argument is an option or belief, and they can support even conflicting claims.

  • “First-level priority” arguments, which express justifications on the object-level arguments and supplement it with priority arguments to resolve possible conflicts and give a relative strength between arguments.

  • “Higher-order priority” arguments, which are used by the provers to deal with potential conflicts between priority arguments of the previous level until all conflicts are resolved.

The same levels can be applied to mathematical proofs to understand the history of proof-events, starting from the statement of a problem until its solution is validated or rejected, including all the attempts and failures (Vandoulakis & Stefaneas, 2015). The premise and the claim of the initial proof-events constitute the object-level arguments, which represent the problem domain and the initial beliefs or actions of provers. These argumentation-based proof-events involve options or beliefs that include unjustified statements and claims that have not yet been proven. Afterward, the subsequent proof-events establish the first-level priority arguments, providing support and valid justifications for the object-level arguments. The prover's strategy and preferences come into play as they select suitable proving methods and tools to address inaccuracies and conflicts during this process. The proof-events can be either terminated by counterarguments or continue to the higher-order priority arguments, forming stronger arguments. As proof-events continue from lower levels to higher, they constitute fluents.

The example below describes the possible steps and conflicts for the justification of a proof-event e through the levels of argumentation. In the object level arguments, it pertains to the claim and the initial representations of arguments.

$${\varvec{H}}{\varvec{a}}{\varvec{p}}{\varvec{p}}{\varvec{e}}{\varvec{n}}{\varvec{s}}({e}_{i},{t}_{i}),\boldsymbol{ }i=1,\dots .,m, m\epsilon {\mathbb{N}},{t}_{i}\le {t}_{m}<t$$
$$\forall {e}_{i}:[({\varvec{H}}{\varvec{a}}{\varvec{p}}{\varvec{p}}{\varvec{e}}{\varvec{n}}{\varvec{s}}({e}_{i},{t}_{i}))\to \neg {\varvec{a}}{\varvec{t}}{\varvec{t}}{\varvec{a}}{\varvec{c}}{\varvec{k}}({{\varvec{e}}}_{{\varvec{i}}}^{\boldsymbol{*}},{t}_{i})\cap ({t}_{i}\le {t}_{m})]\to {\varvec{I}}{\varvec{n}}{\varvec{i}}{\varvec{t}}{\varvec{i}}{\varvec{a}}{\varvec{t}}{\varvec{e}}{\varvec{s}}({e}_{i},{f}_{0},{t}_{m})$$

The proof-events that are not attacked constitute the fluent fo and continue to the first level priority arguments. The first-level priority arguments are presented as:

$${\varvec{Initiates}}\left( {e_{m + 1} ,f_{1} ,t_{m + 1} } \right),\varvec{ attacks}\left( {e_{m + 1}^{*} ,f_{1} ,t_{m + 1} } \right), i = 1, \ldots .,m_{1} ,{ }m_{1} {\mathbb{N}},t_{m + i} \le t_{{m + m_{1} }} < t,$$

For every iϵℕ that we have:

$$\exists e_{m + i} ,e_{m + i}^{*} ,t_{m + i} \left[ {{\varvec{attack}}\left( {e_{m + i}^{*} ,t_{m + i} } \right) \to \neg {\varvec{conc}}\left( {e_{m + i} } \right) \cup \neg {\varvec{prem}}\left( {e_{m + i} } \right)} \right] \cap$$
$$(t_{m + i} \le t_{{m + m_{1} }} < t) \cap [{\nexists }e_{m + i + 1} ,t_{m + i + 1} ({\varvec{Happens}}\left( {e_{m + i + 1} ,t_{m + i + 1} } \right) \to \neg {\varvec{attack}}\left( {e_{m + i}^{*} ,t_{m + i} } \right)\left] { \to {\varvec{Terminates}}\left( {e_{m + i} ,f_{1} ,t_{{m + m_{1} }} } \right)} \right]$$

so that the proof-events that have been attacked and could not resolve the conflict, terminate in this fluent. The rest of them remain active, so we have:

$$\mathbf{A}\mathbf{c}\mathbf{t}\mathbf{i}\mathbf{v}\mathbf{e}\mathbf{A}\mathbf{t}({e}_{m+j},{f}_{1},{t}_{m+{m}_{1}})\mathrm{for\; every\; }j\ne i, j\upepsilon {\mathbb{N}}$$

and they continue to the second-level priority arguments. The same pattern continues for n-level priority arguments and for n fluents fn that deal with potential conflicts between priority arguments of the previous level until either all conflicts are resolved, or the claim is proved invalid. Then, the final level follows:

In the higher-order priority arguments, if the proof-events fail to resolve all the conflicts, the claim cannot be proved, and it clips:

$${\varvec{Clipped}}\left( {t_{i} ,e,t_{n} } \right),\varvec{ }at\; the\; time\; t_{n} = t_{{m\left( {n - 1} \right) + mn}} \ge t_{i}$$

If the proof-events manage to deal with all the attacks and:

$$\exists {\text{j}},{ }j{\mathbb{N}}:\left[ {{\varvec{ActiveAt}}\left( {{\varvec{e}}_{{{\varvec{m}}\left( {{\varvec{n}} - 1} \right) + {\varvec{j}}}} ,f_{n} ,t_{n} } \right) \cap \neg {\varvec{Terminates}}\left( {e,f_{n} ,t_{n} } \right)} \right] \to {\varvec{Valid}}\left( {e,t_{n} } \right),at\; the\; time\; t_{n} = t_{{m\left( {n - 1} \right) + mn}} \ge t_{i} ,$$

then the claim is proved valid.

3.3 Implementing APEC in Mathematical Proving Endeavors: Insights from Fermat's Last Theorem

Fermat’s Last Theorem was formulated in 1637 by Pierre de Fermat, who stated that there are no three distinct positive integers a, b, and c, other than zero, that can satisfy the equation an + bn = cn, whenever n is an integer greater than two. The statement of the problem marks the starting-point of a proof-event. Even though Fermat claimed in the margin of his book “Arithmetica” to have proven this theorem, it actually took 358 years and numerous attempts undertaken by many famous mathematicians and amateurs to prove it until its final proof was given by Andrew Wiles in 1995. The statement of the problem marks the beginning of a sequence of proof-events that evolved in time for 358 years. This sequence of proof-events was evolving in time, as several “agents” (mathematicians and amateurs alike) were involved in various distinct proof-events that took place in various places and times in their attempts to solve the famous problem.

Some of the historical attempts (proof-events) of Fermat’s Last Theorem, which add in the validation of the final proof of the theorem, were selected to demonstrate how argumentation is involved in the search of a proof. In this section, we provide a concise depiction of this example by employing the APEC framework in Fermat’s Last Theorem and highlighting the argumentation-based proof-events, the temporal predicates and the levels of argumentation involved.

  • Object level arguments–Fermat’s Conjecture

In the object level arguments, there is Fermat’s conjecture as the initial proof-event \({e}_{Fermat}\)) and his claim that he had a prove for this conjecture, without any claim-counterargument (\({e}_{Fermat}\)) clearly opposes this conjecture:

$${\varvec{Happens}}\left( {e_{Fermat} ,t_{1637} } \right) \cap \neg {\varvec{attack}}\left( {e_{Fermat}^{*} ,t_{1637} } \right) \to {\varvec{Initiates}}\left( {e_{Fermat} ,f_{0} ,t_{1637} } \right)$$

  • First-level priority arguments—proofs for specific exponents

In the first-level priority arguments, there are proofs for specific exponent n of Fermat’s Last theorem from various mathematicians in different time points. For the exponent n = 3en=3), Leonhard Euler (eEuler) gave a proof in 1755, so we have: \({\varvec{H}}{\varvec{a}}{\varvec{p}}{\varvec{p}}{\varvec{e}}{\varvec{n}}{\varvec{s}}({{\varvec{e}}}_{{\varvec{E}}{\varvec{u}}{\varvec{l}}{\varvec{e}}{\varvec{r}}},{t}_{1755})\). Many other well-known mathematicians followed with equivalent proofs that support the validity of the proof for n = 3. Each prover used a different way (that is a different warrant) for proving the conclusion, so their proof-events are equivalent:

\({\varvec{Support}}\left( {e_{n = 3} ,t_{i} } \right) \to {\varvec{Equivalent}}\left( {e_{n = 3} ,e_{i} } \right),\) for i = 1,…,14.

with: i = 1:(eEuler,t1707), i = 2:(eKausler,t1802), i = 3:(eLegendre,t1823),

\(\user2{Happens}\left( {e_{{Euler}} ,t_{{1755}} } \right) \cap \user2{Initiates}\left( {e_{{n = 3}} ,f_{1} ,t_{{1755}} } \right) \cap \left[ {\neg \user2{attack}\left( {e_{{n = 3}}^{*} ,t_{i} } \right) \cup \user2{support}\left( {e_{{n = 3}} ,t_{i} } \right)} \right] \cap (t_{{1755}} < t_{i} ) \to \user2{ActiveAt}\left( {e_{{n = 3}} ,f_{1} ,t_{i} } \right)\)for t1755 < ti.

Similarly, for n = 5 and n = 7.

  • Second-level priority arguments–Sophie Germain

Germain tried unsuccessfully to prove Fermat's Last Theorem for all even exponents, which was proved by Guy Terjanian in 1977.

$${\varvec{Clipped}}\left( {t_{1776} ,e_{n = 2p} ,t_{1831} } \right):\exists e_{Germail} ,e_{Germail}^{*} ,t_{1} ,$$
$$\left[ {{\varvec{Happens}}\left( {e_{Germail} ,t_{1} } \right) \wedge \left( {t_{1776} \le t_{1} < t_{1831} } \right) \wedge {\varvec{attack}}\left( {e_{Germail}^{*} ,t} \right)} \right]$$
$$\left[ {{\nexists }e_{2} ,t_{2} \left( {{\varvec{Happens}} \left( {e_{2} ,t_{2} } \right) \to \neg {\varvec{attack}}\left( {e_{Germail}^{*} ,t} \right)} \right)} \right], for t_{1776} \le t < t_{1831}$$
$${\varvec{ActiveAt}}\left( {e_{n = 2p} ,f_{2} ,t_{1977} } \right): {\varvec{Happens}}\left( {e_{Terjanian} ,t_{1977} } \right) \to \neg {\varvec{attack}}\left( {e_{Terjanian}^{*} ,t_{1977} } \right)$$

  • Third-level priority arguments–Gabriel Lame

In 1847, Gabriel Lame’s proof failed because it claimed incorrectly that complex numbers can be factored into primes uniquely. This gap was indicated instantly by Joseph Liouville (eLiouville*).

$$\begin{aligned} & \exists ~e_{{Lame}} ,~e_{{Liouville}}^{*} ,t_{{1847}} \left[ {\varvec{attack}\left( {~e_{{Liouville}}^{*} ,t_{{1847}} } \right)~ \to \neg conc\left( {e_{{Lame}} } \right)} \right] \wedge (t_{{1847}} \le t_{1} < t_{2} )~ \\ & \wedge \left[ {{\nexists }e_{{Lame}} ,t_{2} \left( {\varvec{Happens}\left( {e_{{Lame}} ,t_{2} } \right) \to \neg \varvec{attack}\left( {~e_{{Liouville}}^{*} ,t_{{1847}} } \right)} \right)} \right] \to \varvec{Terminates}~\left( {e_{{Lame}} ,f_{1} ,t_{2} } \right) \\ \end{aligned}$$

  • Fourth-level priority arguments—Connection with elliptic curves

The Taniyama–Shimura-Weil (TSW) conjecture was proposed in 1955, and it wasn’t proved until 1994 when Andrew Wiles accomplished a partial proof of this conjecture.

$${\varvec{Initiates}}\left( {e_{TSW} ,f_{4} ,t_{1955} } \right):{\varvec{Happens}}\left( {e_{TSW} ,t_{1955} } \right) \to \neg {\varvec{attack}}\left( {e_{TSW}^{*} ,t_{1955} } \right) \vee {\varvec{support}}\left( {e_{TSW} ,t_{1955} } \right)$$
$${\varvec{ActiveAt}}\left( {e_{TSW} ,f_{4} ,t_{1994} } \right):\varvec{ Happens}\left( {e_{TSW} ,t_{2} } \right) \to \varvec{ }\neg {\varvec{attack}}\left( {e_{TSW}^{*} ,t_{1} } \right),$$
$$for\; t_{1955} \le t_{1} < t_{2} \le t_{1994}$$

  • Fifth-level priority arguments–Andrew Wiles

Andrew Wiles presented his work in June 1993, but it became evident that there was an incorrect critical point (eWiles) in the proving. Wiles tried for almost a year to resolve this point, firstly by himself and then with the contribution of Richard Taylor, but without success.

$${\varvec{Clipped}}\left( {t_{1993} ,e_{Wiles} ,t_{1994} } \right):$$
$$\begin{aligned} & \exists e_{{Wiles}} ,e_{{Wiles}}^{*} ,t_{{1,}} t_{2} [\varvec{Happens}\left( {e_{{Wiles}} ,t_{1} } \right) \cap (t_{{1993}} \le t_{1} < t_{{1994}} ) \\ & \cap \varvec{attack}\left( {e_{{Wiles}}^{*} ,t_{1} } \right)\left] { \cap \varvec{~}} \right[{\nexists }e_{2} ,t_{2} \left( {\varvec{Happens}\left( {e_{{Taylor}} ,t_{2} } \right) \to \neg \varvec{attack}\left( {e_{{Wiles}}^{*} ,t_{1} } \right)} \right)],\varvec{~}for~t_{{1993}} \le t_{2} < t_{{1994}} \\ \end{aligned}$$

Finally, in 1994, Wiles submitted two papers that combined the Kolyvagin–Flach approach and Iwasawa theory and that was the last step in proving Fermat’s Last Theorem:

$${\varvec{ActiveAt}}\left( {e_{Wiles} ,f_{5} ,t_{1994} } \right):{\varvec{Happens}}\left( {e_{Wiles} ,t_{1994} } \right) \to \neg {\varvec{attack}}\left( {e_{Wiles}^{*} ,t_{1994} } \right)$$
$$\varvec{ } \cap {\varvec{Elaboration}}\left( {e_{Wiles} ,S_{{Kolyvagin{-}Flach}} } \right) \cap {\varvec{Elaboration}}\left( {e_{Wiles} ,S_{Iwasawa} } \right)$$

  • Higher-order priority arguments–Fermat’s Last Theorem

The proof-event managed to deal with all the attacks, so:

\({\varvec{ActiveAt}}\left( {e_{Wiles} ,f_{n} ,t_{1994} } \right) \cap \neg {\varvec{Terminates}}\left( {e_{Fermat} ,f_{n} ,t_{1994} } \right)] \to {\varvec{Valid}}\;\left( {e_{Fermat} ,t_{1994} } \right)\) .

Thus, Fermat’s Last Theorem is proved by Wiles, with the contribution of the other agents that opened the way before him in this ages-long sequence of proof-events.

The presented example showcases how agents play a crucial role in the process of proving. The primary objective of proving is to persuade the broader community of the soundness and validity of one’s approach. The involvement of other agents is also instrumental in this procedure. Numerous individuals had to participate actively to achieve the initial objective of proving Fermat’s Last Theorem.

4 Discussion

The formalization of argumentation, initially proposed by Dung (1995), serves as a valuable foundation in which arguments and counterarguments are organized through a binary relation of attack, represented by a directed graph (Aberdein, 2009; Besnard & Hunter, 2014). In this work, we develop an argumentation-based formalization primarily based on the sequent-based approach (Modgil & Prakken, 2013), which incorporates the fundamental structure of Toulmin's model (1993) for representing arguments, along with Vreeswijk's perspective on defeasible reasoning (1997). Pollock's approach to logical argumentation (Pollock, 1987, 1992) also played a role in shaping our research direction. Although Pollock did not explicitly distinguish between arguments and defeat, his work presented one of the earliest non-monotonic logics that incorporated the notions of argument and defeat (Prakken & Horty, 2012). Pollock emphasized the importance of inductive reasoning, considering it as significant as deductive reasoning in both philosophy and Artificial Intelligence. He introduced defeasible reasoning, where arguments consist of chains of reasoning that can lead to a conclusion, but additional information has the potential to undermine or invalidate the entire chain of reasoning.

Our approach stands out as it utilizes argumentation theories to bridge the gap between formal proofs and the informal social interactions involved in the search for proof. Previous research by various scholars (Aberdein, 2009; Alcolea Banegas, 1998; Hunter, 2007; Pedemonte, 2008) has emphasized the significance of argumentation in mathematics, often by adapting argumentation models such as Toulmin's model (1958) and comparing them to the structural components of a proof. However, some criticism has been raised regarding the argument structure of Toulmin's model, as it may not fully account for the exchange of ideas among participants, leading to partial and ambiguous justifications (Pedemonte & Balacheff, 2016). In this paper, our objective is to expand the concept of arguments by incorporating the argument moves made by participants who either support or challenge an assumption. This extension is achieved within the broader framework of proof-events, which encompasses not only formally validated proofs but also informal reasoning processes involving trials, strategic choices, and the potential validation or rejection of parts of a proposed proof by the agents involved.

Other related studies that analyze original mathematical dialogues from the perspective of argumentation are: the so-called mixed-initiative collaborative proving in (Pease et al., 2017), a way of formalizing social aspects of proofs by interpreting the informal logic of a Lakatos-based mathematical discovery; the analysis of Minipolymath 3 by Alison Pease & Ursula Martin (2012); and c. the modelling of mathematical dialogues with the Inference Anchoring Theory + Content (IATC) framework by Corneli et al. (2018). The study by Pease and Martin (2012) employs a simple typology of comments, categorizing them as concepts, examples, conjectures, or proofs. While it provides a description of online collaborative mathematics, it is not primarily intended as a formal representation. The approach in Pease et al. (2017) utilizes various predicates to achieve formal clarity, but this can also make it complex and challenging to use. Similarly, the work by Corneli et al. (2018) employs descriptive predicates for procedural modeling, which can be subjectively interpreted in different ways (e.g., defining concepts like retract, helpful, beautiful, goal, strategy, etc.). In our paper we choose a different approach through the more general meta-methodological framework, which involves the theory of proof-events that incorporates both proofs and arguments. Unlike other approaches, we do not focus on tagging interpretations in the procedure steps but rather on capturing the overall process. Indeed, our approach aims to provide a comprehensive and formal depiction of the entire proving practice and its social interactions. We emphasize the explicit representation of argument moves implemented by the agents and the sequence of steps involved. This includes considering the temporal aspects using temporal predicates and the progressive nature of the argumentation process using levels of argumentation. The goal is to track the progression of arguments and ultimately determine their validation or invalidation. By highlighting these aspects, our approach offers a unique perspective on the dynamics of mathematical proving and the role of argumentation in it.

The BS belief system (Usó-Doménech et al., 2022) shares some common elements with APEC in the context of beliefs and reasoning. It involves the representation and organization of beliefs (which can be consider similar with arguments) in a systematic manner. The abstract level, denoted as BS, comprises two sets of elements: substantive beliefs and derived beliefs. Substantive beliefs represent the foundational truths of the system, which can function as axioms, while derived beliefs are formed from substantive beliefs and can constitute the theorems within the system (Nescolarde-Selva & Usó-Doménech, 2013). The BS belief system allows for dynamic changes in beliefs over time, with some beliefs gaining prominence and others evolving or disappearing, similar to the levels of argumentation, where proof-events are either terminated by counterarguments or continue to the higher levels, forming stronger arguments. This dynamic nature of both systems highlights the continuous evolution of either the ideas and statements held by individuals (beliefs) or the logical reasoning and justifications put forward to support those ideas (arguments). However, APEC emphasizes more on the collaborative nature of theorem proving, as various agents participate in constructing proof-events through argumentation, while BS belief systems are more centered on individual belief structures.

The educational aspects of argumentation and proof have been widely explored in various studies (Inglis et al., 2007; Knipping & Reid, 2019; Krummheuer, 2015; Pedemonte, 2007, 2008; Stylianides, 2007) as well as the students’ interaction in the classroom. While our model can certainly be implemented for educational purposes, in this paper, our focus is on modeling the collaborative discovery process within real mathematical communities. We aim to capture the dynamics and social interactions involved in the practice of mathematicians engaged in research work.

By studying the communication and collaboration between mathematicians, we can gain insights into the process of knowledge generation and the potential for significant results to emerge. Both arguments and counterarguments play an essential role in the process of proving, as they contribute equally in the building and the justification of a proving process. The warranted parts of the initial proof-events act as a groundwork for the next proof-events, while the counterarguments that signalize the faults in those unsuccessful proof-events pave the way for more elaborate proof-events and, in some cases, shift the interest of the mathematical community to new unexplored areas. As the example application to Fermat’s Last Theorem showed, incomplete proof-events may have added more or less to the proof of the Theorem, but the methods that were created with them led to major discoveries and to the creation of new fields in the era of Mathematics, like the foundation of modern algebra. In this case, it might be said that the discoveries that ensued turned out to be even more significant than the proving of the theorem itself and they might have not been made if it weren’t for the warranted proof-events and the counterarguments that emerged from the previous attempts of proving. Furthermore, such discovery events may have thrived through collaborative proving environments. Argumentation is more efficient in more interactive contexts, as they let counterarguments to be addressed and stronger arguments to surface. Thus, a mathematician is in a favored position if he wants to ask the assistance of some colleague to point out most of the possible counterarguments and resolve them in the final proof. By doing this, the proving process could be more convincing not only to those colleagues, but probably to the whole community.

Ultimately, our approach encompasses a broader meta-methodological framework, applicable to various proving procedures in science and everyday life. The theory of proof-events forms the basis of our approach, enabling us to comprehensively capture the interrelationship between proofs and arguments. By incorporating both proving and arguments, we are able to provide a more comprehensive understanding of the creativity and interactions within mathematical reasoning. By adopting this flexible and versatile framework, we aim to analyze and understand the reasoning process in diverse domains. With the ability to apply our approach to different contexts, we gain insights into reasoning practices across fields like mathematics, science, law, philosophy, and others. This framework provides researchers, practitioners, and individuals with a powerful tool to enhance their understanding and analysis of proving procedures in a wide range of scientific and real-life settings.

5 Conclusions

This paper presented the Argumentation-based Proof-Event Calculus (APEC), which extends the proof-events calculus with the integration of arguments and counterarguments. The combination of a theory based on proof-events and logic-based argumentation has the advantage of highlighting weak areas in a proof. Proof-events cannot be considered as infallible facts before their ultimate validation, enabling the exploration of flawed approaches and proofs to be found and resolved. Emphasis was placed on the connection between proof and human reasoning. A specially devised calculus is proposed here, defining argumentation-based proof-events, fluents, argument moves, and temporal predicates and these were analyzed in terms of levels of argumentation. The APEC system can represent the fundamental elements and sequence of steps (internal structure) in the evolution of mathematical practice, which is modelled in the form of logic-based interactions and conflicts that illustrate also the progress of proof (informal external procedures). At the final stage, proof may be accepted as completed, i.e., as a valid formal proof understood and recognised as true by all relevant agents. This approach enables us to examine more deeply the interplay between proof, human reasoning, cognitive processes, and creativity in the mathematicians’ practice.

The contribution of the presented work is that this calculus is formal, with wide applicability and particularly suited to express real-world mathematical proving. The main aim here was to create a new approach in which theories and techniques from the argumentation framework can be applied to bridge the gap between human reasoning and formal proving. Informal and social aspects play a significant role in real-life cognitive processes, and this prompts us to explore how they are reflected in the progress of mathematical proving. Our approach attempts to open new avenues to make proof-events more comprehensive by sketching on philosophical, social, and cognitive studies which highlight the importance of presenting the complete trip of a proof endeavor, alongside with the ultimate proof outcome. Thus, it provides the possibility to model the succession of mathematical ideas through conflicting arguments, unresolved moves, similarities, and contradictions in the context of multi-agent dialogues, social collaboration between provers and interpreters, controversies of previous accepted proofs, and so on.

Whereas arguments are considered as products of sociocultural construction, and the journey of a proof can be seen as a collaborative endeavor that brings together individuals with diverse backgrounds, perspectives, and interests, this calculus captures the ongoing interplay between formal and informal reasoning throughout each step of the journey. It serves as a link between the two hoops that connects the informal and social aspects during the process of knowledge discovery with the formal aspects of a logic-based calculus for proving. By employing abstract argumentation reasoning and semantics, this calculus introduces an additional dimension and plays a crucial role in establishing detailed and specific connections between the hoops. Its flexible framework enables us to analyze reasoning processes in diverse fields and it demonstrates the practicality of employing argumentation techniques in the realm of proving and thinking, not only in mathematics, but also in a wide range of scientific and real-life contexts.