Structure, Self-Similarity, and Fracture of Fiber-Reinforced Composites

We propose a theory for the relationship between structure and the self-similarity principle with initial damage and final fracture of composites. This relationship does not depend on the type of stress state, the dimensions of the composite, or the time scale. Based on the self-similarity principle, we have constructed the theoretical time-to-fracture distribution functions vs. the applied stress level, allowing us to estimate the lower limit corresponding to zero fracture probability. The distribution functions can be constructed without long-term testing. An estimate of the distribution of initial damage is obtained from the short-term strength distribution. As the critical parameter for the transition of the composite to final fracture, we take a critical measure of the stress tensor. At each instant of time, fracture is determined by a differential operator depending on the state of the system at that instant and the applied stress level. The theory is supported by experiments. The experiments were performed on model fiberglass-reinforced composites based on a phenol formaldehyde matrix under tension, compression, pure shear, and hydrostatic tension. The maximum testing time was ~ 20 000 hours. The theory is applicable to any systems with a partially ordered structure and satisfying the self-similarity principle (geophysical, social, economic, etc.).

Appendix

Estimating the upper and lower limit of the first integral in Eq. (10), we obtain respectively the lower $\left\langle {\overline{t}}_{\mathrm{f}}^{*}\right\rangle$ and upper estimate $\left\langle {\overline{t}}_{\mathrm{f}}^{*}\right\rangle$ for the time-to-fracture when testing at a constant rate w.

The lower estimate for the time-to-fracture is $\left\langle {\overline{t}}_{\mathrm{f}}^{*}\right\rangle$

$$ \left\langle {\overline{t}}_{\mathrm{f}}^{*}\right\rangle ={\overline{C}}^{m/\left(m+1\right)}{w}^{-m/\left(m+1\right)}\times {\left[1- \exp \left(-\frac{2{\left(m+1\right)}^2}{{\overline{C}}^{m/\left(m+1\right)}{w}^{-m/\left(m+1\right)}/{\overline{\varPi}}_{\mathrm{c}}+1}\right)\right]}^{1/\left(m+1\right)}<\left\langle {\overline{t}}_{\mathrm{f}}^{*}\right\rangle, $$

(A1)

If m >> 1, then the expression in square brackets in formula (A1) is practically equal to unity. From this we have $\left\langle {\overline{t}}_{\mathrm{f}}^{*}\right\rangle ={\overline{C}}^{m/\left(m+1\right)}{w}^{-m/\left(m+1\right)}$ , and the lower estimate of the strength for the composite ${\overline{\upsigma}}_{\mathrm{B}}$ according to (A1) will be equal to

$$ \begin{array}{l}{\overline{\upsigma}}_{\mathrm{B}}\ge \overline{w}\left\langle {\overline{t}}_{\mathrm{f}}^{*}\right\rangle ={\overline{C}}^{m/\left(m+1\right)}{w}^{1/\left(m+1\right)\Big)},\\ {}\begin{array}{cc}\hfill 0\le w<{w}_0,\hfill & \hfill {w}_0\approx \overline{C}\hfill \end{array}\end{array} $$

(A2)

Figure 6 shows the dependence of the relative short-term strength $\left\langle {\upsigma}_w\right\rangle /\left\langle {\upsigma}_{w_0}\right\rangle$ on the testing rate w according to Eq. (A2). We also show the experimental results on the same figure. Note the characteristic feature of this dependence: an abrupt change in the initial section and a weak variation at higher testing rates.

Fig. 6

Relative short-term tensile strength $\left\langle {\upsigma}_w\right\rangle /\left\langle {h}_{w_0}\right\rangle$ of model composites vs. testing rate w according to Eq. (A2): w ₀ =4/0 MPa/s; the experimental points refer to composites with different structures.

Analogously, from Eq. (10) in the case w ₀ < w < ∞, we obtain the upper estimate of the time-to-fracture $\left\langle {\overline{t}}_{\mathrm{f}}^{**}\right\rangle$.

$$ \left\langle {\overline{t}}_{\mathrm{f}}^{**}\right\rangle \approx \left\langle {\overline{t}}_{\mathrm{f}}^{*}\right\rangle {\left[1- \exp \left(-\frac{1{\left(m+1\right)}^2}{{\overline{C}}^{m/\left(m+1\right)}{w}^{1/\left(m+1\right)}/{\overline{\varPi}}_{\mathrm{c}}+1}\right)\right]}^{-1/\left(m+1\right)}{\left[\frac{{\left(m+1\right)}^2{\overline{\varPi}}_{\mathrm{c}}}{{\overline{\varPi}}_{\mathrm{c}}+w\left\langle {\overline{t}}_{\mathrm{f}}^{**}\right\rangle}\right]}^{1/\left(m+1\right)}, $$

and the estimate of the upper limit for the strength $\left\langle {\overline{\upsigma}}_{\mathrm{B},\infty}\right\rangle$ is

$$ \left\langle {\overline{\upsigma}}_{\mathrm{B},\infty}\right\rangle =w\left\langle {\overline{t}}_{\mathrm{f}}^{**}\right\rangle \cong \left\langle {\overline{\upsigma}}_{\mathrm{B}}\right\rangle {\left[1- \exp \left(-\frac{2{\left(m+1\right)}^2}{\left\langle {\overline{\upsigma}}_{\mathrm{B}}\right\rangle /{\overline{\varPi}}_{\mathrm{c}}+1}\right)\right]}^{-1/\left(m+1\right)}{\left[\frac{{\left(m+1\right)}^22}{2-\left\langle {h}_0\right\rangle}\right]}^{1/\left(m+1\right)} $$

(A3)

where $\left\langle {\overline{\upsigma}}_{\mathrm{B}}\right\rangle$ is the short-term strength in standard testing at the rate ${w}_0\approx \overline{C}$; 〈h ₀〉 is the average value of the initial degree of damage generated by the ensemble of clusters of the first type.

Note that as w → ∞ , the final degree of damage tends toward the initial degree of damage. Therefore, $w\left\langle {\overline{t}}_{\mathrm{f}}^{**}\right\rangle =\left\langle {\overline{\upsigma}}_{\mathrm{B},\infty}\right\rangle =\left(1-\left\langle {h}_0\right\rangle \right)\overline{\varPi}$. On the other hand, $\left\langle {\overline{\upsigma}}_{\mathrm{B}}\right\rangle$ is the average strength of clusters of the second type. The final extent of their undamaged regions, q _f =1 – h _f , is determined from solution of differential equation (13) and the relations $\left\langle {\overline{\upsigma}}_{\mathrm{B}}\right\rangle ={q}_c{\overline{\varPi}}_{\mathrm{c}}$ . Considering that $\left\langle {\overline{\upsigma}}_{\mathrm{B},\infty}\right\rangle \approx \left\langle {\overline{\upsigma}}_{\mathrm{B}}\right\rangle /{q}_{\mathrm{c}}$ , we obtain $\left\langle {\overline{\upsigma}}_{\mathrm{B}}\right\rangle =\left(1-\left\langle {h}_0\right\rangle \right){q}_{\mathrm{c}}{\overline{\varPi}}_{\mathrm{c}}$ . Let us write this relation in the form

$$ {\overline{\varPi}}_{\mathrm{c}}/\left\langle {\upsigma}_{\mathrm{B}}\right\rangle ={\left[\left(1-\left\langle {h}_0\right\rangle \right){q}_{\mathrm{c}}\right]}^{-1}. $$

(A4)

The final degree of damage h _f is approximately equal to the coefficient of variation v when 0 ≤ v ≤ 0.5. In this case, Eq. (A4) takes on the form

$$ {\overline{\varPi}}_{\mathrm{c}}/\left\langle {\overline{\upsigma}}_{\mathrm{B}}\right\rangle ={\left[\left(1-\left\langle {h}_0\right\rangle \right)\left(1-v\right)\upgamma \right]}^{-1}. $$

(A6)

From Eq. (A3), we find the equation relating the original structure of the composite, the self-similarity principle, and the final fracture

$$ {q}_{\mathrm{c}}{\left[1- \exp \left(-\frac{2{\left(m+1\right)}^2}{q_{\mathrm{c}}+1}\right)\right]}^{-1/\left(m+1\right)}=\left(1-\left\langle {h}_0\right\rangle \right){\left[\frac{1-\left\langle {h}_0\right\rangle /2}{{\left(m+1\right)}^2}\right]}^{-1/\left(m+1\right)}. $$

(A7)

Note that the expression containing the exponential in (A7) tends toward unity for m >> 1, and it can be simplified. As a result, we obtain:

$$ {q}_{\mathrm{c}}=\left(1-\left\langle {h}_0\right\rangle \right){\left[\frac{1-\left\langle {h}_0\right\rangle /2}{{\left(m+1\right)}^2}\right]}^{-1/\left(m+1\right)} $$

(A8)

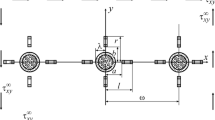
In order to estimate γ, we have the following relations [3, 12], determining the dimensions of the clusters l*, d* and the probability density for their angular distribution ρ(α)

$$ \uprho \left(\upalpha \right)=\frac{1}{1+{\left(l*/d*\right)}^{-1}}\left[ \cos \upalpha +{\left(l*/d*\right)}^{-1} \sin \upalpha \right], $$

(A9)

$$ \upgamma \kern0.5em = 1-\underset{\uppi /2-\varDelta \upalpha}{\overset{\uppi /2}{\int \uprho \left(\upalpha \right)d\upalpha \cong 1-\frac{1}{1+{\left(l*/d*\right)}^{-1}}\left[{\left(\varDelta \upalpha \right)}^2/2+{\left(l*/d*\right)}^{-1}\varDelta \upalpha \right].}} $$

(A10)

Here Δα is the maximum angle of deviation of the reinforcing element from the loading direction at which there is still a reinforcing effect (usually Δα ≤ π/9, d* ≅l[(Δα)²/2 + (l/d)^–1], and l* ≅ l[1 + (l/d)^–1(Δα)/2]. For l =10·10^–3 m and d =0.2·10^–3 m, from formulas (A9) and (A10) we will have l*/d* ≅5 and γ =0.891 ≅0.90.