Skip to main content

Advertisement

SpringerLink
Log in

Cooperative emission reduction behaviour of supply chain enterprises under cap-and-trade and government subsidies

  • Published:
Environment, Development and Sustainability Aims and scope Submit manuscript

Abstract

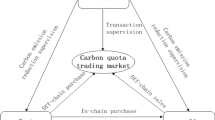
Carbon emissions have caused serious environmental pollution, carbon emission reduction (CER) is attracting widespread attention. Many enterprises have not been very effective in CER because of the high cost of CER. Government subsidies and the cooperation of enterprises play an important role in promoting CER. To identify the optimal cooperative emission reduction strategy under cap-and-trade (C&T) and government subsidies, this paper constructs three models to study the behavioural choice of suppliers and manufacturers. First, a static evolutionary game model is constructed between suppliers and manufacturers, and evolutionary stable strategies (ESSs) are discussed. Then, two dynamic mechanisms, dynamic subsidies and dynamic cooperation mechanisms, are constructed and the ESSs of these two models are discussed. Finally, a numerical simulation of the model is conducted to analyse the impact of government subsidies, shared CER cost, CER costs and carbon pricing on the behaviour of suppliers and manufacturers under the three mechanisms. The results show that higher government subsidies can encourage manufacturers to participate in CER activities. Carbon pricing has an incentive effect on the manufacturer’s emission reduction behaviour, while has a negative effect on suppliers to cooperate in the three mechanisms. A relatively small cost-sharing ratio is a way to promote upstream and downstream cooperation to reduce emissions. The dynamic cooperation mechanism can be more powerful to promote manufacturers to CER than the dynamic subsidy mechanism. The results provide a theoretical basis for the implementation of CER, governments can formulate reasonable subsidies and C&T policies to enterprises and promote cooperation among supply chain members. Suppliers and manufacturers can implement reasonable decisions to CER and achieve a win–win situation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Notes

  1. http://www.gov.cn/xinwen/2017-01/04/content_5156431.htm

  2. https://baijiahao.baidu.com/s?id=1683058028138925005&wfr=spider&for=pc

  3. https://www.sohu.com/a/477818949_117460

  4. http://ideacarbon.org/news_free/55330/

References

Download references

Acknowledgements

We sincerely thank the associate editor and two anonymous reviewers for their kind and helpful comments on this paper.

Funding

This work was supported by National Natural Science Foundation of China (71871002).

Author information

Authors and Affiliations

  1. School of E-Business and Logistics, Beijing Technology and Business University, Beijing, 100048, China

    Hongxia Sun, Kexin Wang & Xinjian Du

Authors
  1. Hongxia Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kexin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xinjian Du
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Conceptualization, funding acquisition, methodology, project administration and supervision were performed by HS. The first draft of the manuscript was written by KW, and all authors commented on previous versions of the manuscript. Investigation and validation were performed by XD. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Hongxia Sun.

Ethics declarations

Competing interests

The authors have no competing interests to declare that are relevant to the content of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Proof of Proposition 4

The stability analysis is shown in follows: See Tables 10 and

Table 11 The ESS of the system (S1) when \(\alpha_{2} < \delta_{1} < \alpha_{1}\)
Full size table

11

Proof of Proposition 6

See Tables

Table 12 The ESS of the system (S2) when \(\alpha_{2} < \alpha_{1} < \delta_{2}\)
Full size table

12 and

Table 13 The ESS of the system (S2) when \(\alpha_{2} < \delta_{2} < \alpha_{1}\)
Full size table

13

Proof of Corollary 1.

Since \(- \beta_{2} \Pi_{m} - H > 0\), \(\left( { - \beta_{2} \Pi_{m} + y_{1}^{*} V_{m} - H} \right) > 0\), \(\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} + \lambda C_{0} } \right] > 0\),

$$E_{1} - E_{0} = \frac{{ - P_{c} (G_{m} - E_{1} + E_{0} - G_{m} )}}{{P_{c} }} = \frac{ - \Delta E - \Delta C}{{P_{c} }} < 0,\; - \alpha_{2} \Pi_{S} C_{0} < 0$$

Hence \(\frac{{\partial x_{D} }}{\partial \lambda }{ = }\frac{{\left( {\beta_{2} \Pi_{m} + H} \right)C_{0} }}{{\left[ {\Pi_{m1} - \left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \lambda C_{0} } \right]^{2} }} < 0\), \(\frac{{\partial x_{D} }}{\partial V} = - \frac{1}{{\Pi_{m1} - \left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \lambda C_{0} }} < 0\),

$$\frac{{\partial x_{D} }}{{\partial P_{C} }} = \frac{{E_{1} - E_{0} }}{{\Pi_{m1} - \left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \lambda C_{0} }} < 0,\;\frac{{\partial y_{D} }}{\partial \lambda } = \frac{{ - \alpha_{2} \Pi_{S} C_{0} }}{{\left[ {\Pi_{s1} - \left( {1 + \alpha_{1} - \alpha_{2} } \right)\Pi_{s} - \lambda C_{0} } \right]^{2} }} < 0$$
$$\frac{{\partial y_{D} }}{{\partial C_{0} }} = \frac{{ - \alpha_{2} \lambda \Pi_{S} }}{{\left[ {\Pi_{s1} - \left( {1 + \alpha_{1} - \alpha_{2} } \right)\Pi_{s} - \lambda C_{0} } \right]^{2} }} < 0,$$
$$\frac{{\partial x_{1}^{*} }}{\partial \lambda } = \frac{{\frac{{ - \alpha_{2} \Pi_{S} C_{0} V_{m} }}{{\left[ {\Pi_{s1} - \left( {1 + \alpha_{1} - \alpha_{2} } \right)\Pi_{s} + \lambda C_{0} } \right]^{2} }}\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\prod_{m} - \Pi_{m1} + \lambda C_{0} } \right] - \left( { - \beta_{2} \Pi_{m} + y_{1}^{*} V_{m} - H} \right)C_{0} }}{{\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} + \lambda C_{0} } \right]^{2} }} < 0$$

\(\frac{{\partial x_{1}^{*} }}{\partial V} = \frac{y - 1}{{\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} + \lambda C_{0} }} < 0\), \(\frac{{\partial x_{1}^{*} }}{{\partial P_{C} }} = \frac{{E_{1} - E_{0} }}{{\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} + \lambda C_{0} }} < 0\), \(\frac{{\partial y_{1}^{*} }}{\partial \lambda } = \frac{{ - \alpha_{2} \Pi_{s} C_{0} }}{{\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} + \lambda C_{0} } \right]^{2} }} < 0\).

\(\frac{{\partial y_{1}^{*} }}{{\partial C_{0} }}{ = }\frac{{ - \alpha_{2} \lambda \Pi_{s} }}{{\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} + \lambda C_{0} } \right]^{2} }} < 0\),

\(\frac{{\partial x_{2}^{*} }}{\partial V}{ = } - \sqrt {\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} } \right]^{2} - 4\lambda C_{0} \left( {\beta_{2} \Pi_{m} + H} \right)} < 0\),

\(\frac{{\partial x_{2}^{*} }}{{\partial P_{C} }} = \left( {E_{0} - E_{1} } \right)\sqrt {\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} } \right]^{2} - 4\lambda C_{0} \left( {\beta_{2} \Pi_{m} + H} \right)} < 0\),

\(\frac{{\partial y_{2}^{*} }}{\partial \lambda } = \frac{{\alpha_{2} \Pi_{s} \left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} - \sqrt {\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \prod_{m1} } \right]^{2} - 4\lambda C_{0} \left( {\beta_{2} \Pi_{m} + H} \right)} } \right]}}{{2\lambda \left[ {\left( {1 + \alpha_{1} - \alpha_{2} } \right)\Pi_{s} - \Pi_{s1} - x_{D} \lambda C_{0} } \right]}} < 0\),

\(\frac{{\partial y_{2}^{*} }}{{\partial C_{0} }} = \frac{{\alpha_{2} \Pi_{s} \left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} - \sqrt {\left[ {\left( {1 + \beta_{1} - \beta_{2} } \right)\Pi_{m} - \Pi_{m1} } \right]^{2} - 4\lambda C_{0} \left( {\beta_{2} \Pi_{m} + H} \right)} } \right]}}{{2C_{0} \left[ {\left( {1 + \alpha_{1} - \alpha_{2} } \right)\Pi_{s} - \Pi_{s1} - x_{D} \lambda C_{0} } \right]}} < 0\).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, H., Wang, K. & Du, X. Cooperative emission reduction behaviour of supply chain enterprises under cap-and-trade and government subsidies. Environ Dev Sustain (2023). https://doi.org/10.1007/s10668-023-03980-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10668-023-03980-w

Keywords

Search

Navigation