Skip to main content
SpringerLink
Log in

An efficient hybrid method based on cubic B-spline and fourth-order compact finite difference for solving nonlinear advection–diffusion–reaction equations

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

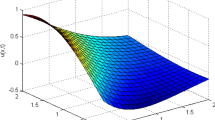
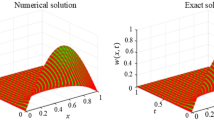
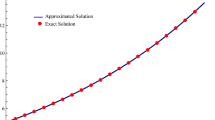
This paper proposes an efficient hybrid numerical method to obtain approximate solutions of nonlinear advection–diffusion–reaction (ADR) equations arising in real-world phenomena. The proposed method is based on finite differences for the approximation of time derivatives while a combination of cubic B-splines and a fourth-order compact finite difference scheme is used for spatial discretization with the help of the Crank–Nicolson method. Since desired accuracy and order of convergence cannot be reached using the traditional cubic B-spline method, to overcome this, the second-order derivatives are approximated using the unknowns and their first derivative approximations with the compact support. Thus, instead of expressing the second-order derivative in second-order accuracy, it is represented by the convergence of order four in the present method. The computed results revealed that this combined approach improves the accuracy of solutions of nonlinear ADR equations in comparison to up-to-date literature even using relatively larger step sizes. Besides, this method is seen to be capable of capturing the behavior of the models with very small viscosity values. The stability of the proposed method has been discussed by considering the matrix stability approach and it has been shown that the method is stable. In addition to the fact that the proposed method obtains sufficiently accurate solutions, another main superiority is its simplicity and applicability, which requires minimum computational effort.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Chen Z, Gumel AB, Mickens RE (2003) Nonstandard discretizations of the generalized Nagumo reaction–diffusion equation. Numer Methods Partial Differ Equ 19(3):363–379

    Article  MathSciNet  MATH  Google Scholar 

  2. Namjoo M, Zeinadini M, Zibaei S (2018) Nonstandard finite-difference scheme to approximate the generalized Burgers–Fisher equation. Math Methods Appl Sci 41(17):8212–8228

    Article  MathSciNet  MATH  Google Scholar 

  3. Chen Y, Zhang T (2019) A weak Galerkin finite element method for Burgers\(^{\prime }\) equation. J Comput Appl Math 348(1):103–119

    Article  MathSciNet  MATH  Google Scholar 

  4. Kumar S, Saha Ray S (2021) Numerical treatment for Burgers–Fisher and generalized Burgers–Fisher equations. Math Sci 15:21–28

    Article  MathSciNet  MATH  Google Scholar 

  5. Khater AH, Temsah RS, Hassan MM (2008) A Chebyshev spectral collocation method for solving Burgers\(^{\prime }\)-type equations. J Comput Appl Math 222(2):333–350

    Article  MathSciNet  MATH  Google Scholar 

  6. Hashim I, Noorani MSM, Al-Hadidi MRS (2006) Solving the generalized Burgers–Huxley equation using the Adomian decomposition method. Math Comput Model 43(11–12):1404–1411

    Article  MathSciNet  MATH  Google Scholar 

  7. Javidi M, Golbabai A (2009) A new domain decomposition algorithm for generalized Burger\(^{\prime }\)s–Huxley equation based on Chebyshev polynomials and preconditioning. Chaos Solitions Fractals 39(2):849–857

    Article  MathSciNet  MATH  Google Scholar 

  8. Duan Y, Kong L, Zhang R (2012) A lattice Boltzmann model for the generalized Burgers–Huxley equation. Phys A 391(3):625–632

    Article  Google Scholar 

  9. Seydaoglu M, Erdogan U, Ozis T (2016) Numerical solution of Burgers\(^{\prime }\) equation with high order splitting methods. J Comput Appl Math 291:410–421

    Article  MathSciNet  MATH  Google Scholar 

  10. Nascimento AA, Mariano FP, Silveria-Neto A, Padilla ELM (2014) A comparison of Fourier pseudospectral method and finite volume method used to solve the Burgers equation. J Braz Soc Mech Sci Eng 36(4):737–742

    Article  Google Scholar 

  11. Hammad DA, El-Azab MS (2015) 2N order compact finite difference scheme with collocation method for solving the generalized Burger\(^{\prime }\)s–Huxley and Burger\(^{\prime }\)s–Fisher equations. Appl Math Comput 258:296–311

    MathSciNet  MATH  Google Scholar 

  12. Lin J, Reutskiy SY (2018) An accurate meshless formulation for the simulation of linear and fully nonlinear advection diffusion reaction problems. Adv Eng Softw 126:127–146

    Article  Google Scholar 

  13. Malik SA, Qureshi IM, Amir M, Malik AN, Haq I (2015) Numerical solution to generalized Burgers–Fisher equation using exp-function method hybridized with heuristic computation. PLoS ONE 10(3):e0121728

    Article  Google Scholar 

  14. Wasim I, Abbas M, Amin M (2018) Hybrid B-spline collocation method for solving the generalized Burgers–Fisher and Burgers–Huxley equations. Math Probl Eng 2018:18

    Article  MathSciNet  MATH  Google Scholar 

  15. Prenter PM (1975) Splines and variational methods. Wiley, New York

    MATH  Google Scholar 

  16. Rubin SG, Graves RA (1975) Cubic spline approximation for problems in fluid mechanics. Nasa TR R-436, Washington

  17. Mat Zin S, Abd Majid A, Ismail AIM, Abbas, M (2014) Application of hybrid cubic B-spline collocation approach for solving a generalized nonlinear Klien–Gordon equation. Math Probl Eng Article ID 108560

  18. Mittal RC, Jain RK (2013) Numerical solution of non-linear Fisher\(^{\prime }\)s reaction–diffusion equation with modified cubic B-splines collocation method. Math Sci 7(1):6–18

    Article  Google Scholar 

  19. Mohammadi R (2012) Spline solution of the generalized Burgers–Fisher equation. Appl Anal 91(12):2189–2215

    Article  MathSciNet  MATH  Google Scholar 

  20. Mittal RC, Tripathi A (2015) Numerical solution of generalized Burgers–Fisher and generalized Burgers–Huxley equations using collocation of cubic B-Splines. Int J Comput Math 92(5):1053–1077

    Article  MathSciNet  MATH  Google Scholar 

  21. Rohila R, Mittal RC (2018) Numerical study of reaction diffusion Fisher\(^{\prime }\)s equation by fourth order cubic B-spline collocation method. Math Sci 12:79–89

    Article  MathSciNet  MATH  Google Scholar 

  22. Jiwari R, Alshomrani AS (2017) A new algorithm based on modified trigonometric cubic B-splines functions for nonlinear Burgers-type equations. Int J Numer Methods Heat Fluid Flow 27(8):1638–1661

    Article  Google Scholar 

  23. Jiwari R, Pandit S, Koksal ME (2019) A class of numerical algorithms based on cubic trigonometric B-spline functions for numerical simulation of nonlinear parabolic problems. Comput Appl Math 38:140

    Article  MathSciNet  MATH  Google Scholar 

  24. Tamsir M, Dhiman N, Chauhan A, Chauhan A (2021) Solution of parabolic PDEs by modified quintic B-spline Crank–Nicolson collocation method. Ains Shams Eng J 12(2):2073–2082

    Article  Google Scholar 

  25. Alinia N, Zarebnia M (2019) A numerical algorithm based on a new kind of tension B-spline function for solving Burgers–Huxley equation. Numer Algorithms 82:1121–1142

    Article  MathSciNet  MATH  Google Scholar 

  26. Singh A, Dahiya S, Singh PA (2020) A fourth-order B-spline collocation method for nonlinear Burgers–Fisher equation. Math Sci 14:75–85

    Article  MathSciNet  MATH  Google Scholar 

  27. Patel KS, Mehra M (2018) A numerical study of Asian option with high-order compact finite difference scheme. J Appl Math Comput 57:467–491

    Article  MathSciNet  MATH  Google Scholar 

  28. Dag I, Irk D, Saka B (2005) A numerical solution of the Burgers equation using cubic B-splines. Appl Math Comput 163:199–211

    MathSciNet  MATH  Google Scholar 

  29. Mittal RC, Arora G (2010) Efficient numerical solution of Fisher\(^{\prime }\)s equation by using B-spline method. Int J Comput Math 87(13):3039–3051

    Article  MathSciNet  MATH  Google Scholar 

  30. Cattani C, Kudreyko A (2008) Multiscale analysis of the Fisher equation, ICCSA Part I, vol 5072. Lecture Notes in Computer Science. Springer, Berlin pp 1171–1180

  31. Sharifi S, Rashidinia J (2019) Collocation method for convection–reaction–diffusion equations. J King Saud Univ-Sci 31(4):1115–1121

    Article  Google Scholar 

  32. Nazir T, Abbas M (2021) New cubic B-spline approximation technique for numerical solutions of coupled viscous Burgers equations. Eng Comput 38(1):83–106

    Article  Google Scholar 

  33. Huntul MJ, Tamsir M, Ahmadini AAH, Thottoli SR (2022) A novel collocation technique for parabolic partial differential equations. Ain Shams Eng J 13(1):101497

    Article  Google Scholar 

  34. Nair LC, Awasthi A (2019) Quintic trigonometric spline based numerical scheme for nonlinear modified Burgers’ equation. Numer Methods Partial Differ Equ 35:1269–1289

    Article  MathSciNet  MATH  Google Scholar 

  35. Tamsir M, Huntul MJ (2021) A numerical approach for solving Fisher’s reaction–diffusion equation via a new kind of spline functions. Ain Shams Eng J 12(3):3157–3165

    Article  Google Scholar 

  36. Dhiman N, Tamsir M (2018) A collocation technique based on modified form of trigonometric cubic B-spline basis functions for Fisher\(^{\prime }\)s reaction–diffusion equation. Multidiscip Model Mater Struct 14(5):923–939

    Article  Google Scholar 

  37. Kutluay S, Esen A (2004) A lumped Galerkin method for solving the Burgers equation. Int J Comput Math 81(11):1433–1444

    Article  MathSciNet  MATH  Google Scholar 

  38. Pandit S (2022) Local radial basis functions and scale-3 Haar wavelets operational matrices based numerical algorithms for generalized regularized long wave model. Wave Motion 109:102846

    Article  MathSciNet  MATH  Google Scholar 

  39. Appadu AR, Tijani YO (2022) 1D generalised Burgers–Huxley: proposed solutions revisited and numerical solution using FTCS and NSFD methods. Front Appl Math Stat 7:773733

    Article  Google Scholar 

  40. Rasoulizadeh MN, Avazzadeh Z, Nikan O (2022) Solitary wave propagation of the generalized Kuramoto–Sivashinsky equation in fragmented porous media. Int J Appl Comput Math 8:252

    Article  MathSciNet  MATH  Google Scholar 

  41. Singh BK, Gupta M (2021) A new efficient fourth order collocation scheme for solving Burgers equation. Appl Math Comput 399:126011

    MathSciNet  MATH  Google Scholar 

  42. Hepson OE, Yigit G, Allahviranloo T (2021) Numerical simulations of reaction–diffusion systems in biological and chemical mechanisms with quartic-trigonometric B-splines. Comput Appl Math 40:144

    Article  MathSciNet  MATH  Google Scholar 

  43. Hepson OE, Yigit G (2022) A numerical scheme for the wave simulations of the Kuromoto–Sivashinsky model via quartic-trigonometric tension B-spline. Wave Motion 114:103045

    Article  MATH  Google Scholar 

  44. Wang L, Li H, Meng Y (2021) Numerical solution of coupled Burgers’ equation using finite difference and sinc collocation method. Eng Lett 29(2):668–674

    Google Scholar 

  45. Hussain M, Haq S (2021) Numerical solutions of strongly non-linear generalized Burgers–Fisher equation via meshfree spectral technique. Int J Comput Math 98(9):1727–1748

    Article  MathSciNet  MATH  Google Scholar 

  46. Sharma KK, Singh P (2008) Hyperbolic partial differential-difference equation in the mathematical modeling of neuronal firing and its numerical solution. Appl Math Comput 201:229–238

    MathSciNet  MATH  Google Scholar 

  47. Verma AK, Kayenat S (2019) On the stability of Mickens type NSFD schemes for generalized Burgers Fisher equation. J Differ Appl 25(12):1706–1737

    Article  MathSciNet  MATH  Google Scholar 

  48. Jain MK (1983) Numerical solution of differential equations. Wiley, New York

    Google Scholar 

  49. Smith GD (1985) Numerical solution of partial differential equations: finite difference methods, 3rd edn. Oxford University Press, New York

    Google Scholar 

  50. Jiwari R, Kumar S, Mittal RC (2019) Meshfree algorithms based on radial basis functions for numerical simulation and to capture shocks behavior of Burgers type problems. Eng Comput 36(4):1142–1168

    Article  Google Scholar 

  51. Seydaoglu M (2018) An accurate approximation algorithm for Burgers equation in the presence of small viscosity. J Comput Appl Math 344:473–481

    Article  MathSciNet  MATH  Google Scholar 

  52. Tunc H, Sari M (2020) Simulations of nonlinear advection–diffusion models through various finite element techniques. Scientia Iranica B 27(6):2853–2870

    Google Scholar 

  53. Jiwari R (2015) A hybrid numerical scheme for the numerical solution of the Burgers equation. Comput Phys Commun 188:59–67

    Article  MathSciNet  MATH  Google Scholar 

  54. Verma AK, Rawani MK, Agarwal RP (2020) A high-order weakly L-stable time integration scheme with application to Burgers equation. Computation 8:72

    Article  Google Scholar 

  55. Erdogan U, Sari M, Kocak H (2019) Efficient numerical treatment of nonlinearities in the advection–diffusion–reaction equations. Int J Numer Methods Heat Fluid Flow 29(1):132–145

    Article  Google Scholar 

  56. Hussain M (2021) Hybrid radial basis function methods of lines for the numerical solution of viscous Burgers equation. Comput Appl Math 40(107):1–49

    MathSciNet  MATH  Google Scholar 

  57. Ismail HNA, Raslan K, Rabboh AAA (2004) Adomian decomposition method for Burger\(^{\prime }\)s–Huxley and Burger\(^{\prime }\)s–Fisher equations. Appl Math Comput 159(1):291–301

    MathSciNet  MATH  Google Scholar 

  58. Sari M, Gurarslan G, Dag I (2010) A compact finite difference method for the solution of the generalized Burgers–Fisher equation. Numer Methods Partial Differ Equ 26(1):125–134

    Article  MathSciNet  MATH  Google Scholar 

  59. Inan B, Bahadır AR (2015) Numerical solutions of the generalized Burgers–Huxley equation by implicit exponential finite difference method. J Appl Math Stat Inform 11:57–67

    Article  MathSciNet  MATH  Google Scholar 

  60. Wazwaz AM (2004) The tanh method for travelling wave solutions of nonlinear equations. Appl Math Comput 154(3):713–723

    MathSciNet  MATH  Google Scholar 

  61. Tamsir M, Huntul MJ (2021) A numerical approach for solving Fisher\(^{\prime }\)s reaction–diffusion equation via a new kind of spline functions. Ains Shams Eng J 12:3157–3165

    Article  Google Scholar 

  62. Arora G, Bhatia GS (2020) A meshfree numerical technique based on radial basis function pseudospectral method for Fisher\(^{\prime }\)s equation. Int J Nonlinear Sci Numer Simul 21(1):37–49

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

There are no funders to report for this submission.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Arts and Science, Tekirdag Namik Kemal University, Tekirdağ, Turkey

    Seda Gulen

Authors
  1. Seda Gulen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seda Gulen.

Ethics declarations

Conflict of interest

The authors declare that this work does not have any conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gulen, S. An efficient hybrid method based on cubic B-spline and fourth-order compact finite difference for solving nonlinear advection–diffusion–reaction equations. J Eng Math 138, 13 (2023). https://doi.org/10.1007/s10665-022-10249-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10665-022-10249-0

Keywords

Mathematics Subject Classification

Search

Navigation