Skip to main content
SpringerLink
Log in

RETRACTED ARTICLE: Thermodynamic effect in Darchy–Forchheimer nanofluid flow of a single-wall carbon nanotube/multi-wall carbon nanotube suspension due to a stretching/shrinking rotating disk: Buongiorno two-phase model

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

This article was retracted on 14 May 2024

This article has been updated

Abstract

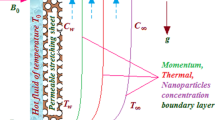
The present article gives an analysis of the impact of Darcy–Forchheimer flow and partial slip along with heat transfer in single-wall carbon nanotube/multi-wall carbon nanotube (SWCNT/MWCNT)-water nanofluid flow over a stretching/shrinking rotating disk. The study considers the heat transfer in nanofluids, using both static and dynamic models, namely the Xue and Buongiorno models, respectively. The effects of thermal radiation and viscous dissipation are considered. Nonlinear transformed coupled equations are solved computationally using a spectral quasilinearisation method. The numerical results show the impact of several physical parameters on radial and tangential velocity, temperature and nanoparticle concentration fields. The slip parameter accounts for a significant enhancement in the radial velocity and a decline in the tangential/azimuthal velocity. The presence of a porous medium has the effect of reducing the amplitude of velocity and momentum layer thickness for both SWCNTs-water and MWCNTs-water nanofluids. The present study indicates that the tangential velocity of SWCNT/MWCNT-water nanofluids diminishes due to the increment in slip parameter, while the radial velocity exhibits the reverse trends. The results also show that the involvement of a porous matrix gives rise to reduced velocity of SWCNT/MWCNT-water nanofluids. It is also observed that MWCNTs make a greater contribution in augmenting the heat transfer rate compared to SWCNT nanoparticles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

Change history

References

  1. Choi SUS (1995) Enhancing thermal conductivity of fluids with nanoparticles. ASME Fluids Eng Div 231:99–105

    Google Scholar 

  2. Xuan Y, Li Q (2003) Investigation on convective heat transfer and flow features of nanofluids. J Heat Transf 125:151–155

    Article  Google Scholar 

  3. Bhatti MM, Rashidi MM (2016) Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J Mol Liq 221:567–573

    Article  Google Scholar 

  4. Hayat T, Javed M, Imtiaz M, Alsaedi A (2017) Double stratification in the MHD flow of a nanofluid due to a rotating disk with variable thickness. Eur Phys J Plus 132:146–156

    Article  Google Scholar 

  5. Buongiorno J (2006) Convective transport in nanofluids. ASME J Heat Transf 128:240–250

    Article  Google Scholar 

  6. Tiwari RK, Das MK (2007) Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf 50:2002–2018

    Article  Google Scholar 

  7. Xue QZ (2005) Model for thermal conductivity of carbon nanotube-based composites. Physica B 368:302–307

    Article  Google Scholar 

  8. Ramasubramaniam R, Chen J, Liu H (2003) Homogeneous carbon nanotube/polymer composites for electrical applications. Appl Phys Lett 83:2928

    Article  Google Scholar 

  9. Ding Y, Alias H, Wen D, Williams RA (2006) Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids). Int J Heat Mass Transf 49:240–250

    Article  Google Scholar 

  10. Hayat T, Farooq M, Alsaedi A (2015) Homogeneous-heterogeneous reactions in the stagnation point flow of carbon nanotubes with Newtonian heating. AIP Adv 5:027130

    Article  Google Scholar 

  11. Khan WA, Khan ZH, Rahi M (2014) Fluid flow and heat transfer of carbon nanotubes along a flat plate with Navier slip boundary. Appl Nanosci 4:633–641

    Article  Google Scholar 

  12. Ellahi R, Hassan M, Zeeshan A (2015) Study of natural convection MHD nanofluid by means of single and multi walled carbon nanotubes suspended in a salt water solutions. IEEE Trans Nanotechnol 14:726–734

    Article  Google Scholar 

  13. Karimipour A, Taghipour A, Malvandi A (2016) Developing the laminar MHD forced convection flow of water/FMWNT carbon nanotubes in a microchannel imposed the uniform heat flux. J Magn Mater 419:420–428

    Article  Google Scholar 

  14. Imtiaz M, Hayat T, Alsaedi A, Ahmad B (2016) Convective flow of carbon nanotubes between rotating stretchable disks with thermal radiation effects. Int J Heat Mass Transf 101:948–957

    Article  Google Scholar 

  15. Saqib M, Khan I, Shafie S (2018) Natural convection channel flow of CMC-based CNTs nanofluid. Eur Phys J Plus 133:12

    Article  Google Scholar 

  16. Nasir S, Shah Z, Islam S, Bonyah E, Gul T (2019) Darcy Forchheimer nanofluid thin film flow of SWCNTs and heat transfer analysis over an unsteady stretching sheet. AIP Adv 9:015223

    Article  Google Scholar 

  17. Von Krmn T (1921) ber laminare und turbulente Reibung. Zeitschrift fur Angew Math Mech ZAMM 1:233–252

    Article  Google Scholar 

  18. Turkyilmazoglu M, Senel P (2013) Heat and mass transfer of the flow due to a rotating rough and porous disk. Int J Therm Sci 63:146–158

    Article  Google Scholar 

  19. Bdewadt UT (1940) Die Drehstrmungberfestem Grund. Zeitschrift Angew Math Mech 20:241–252

    Article  Google Scholar 

  20. Ariel PD (2002) On computation of MHD flow near a rotating disk. Zeitschrift fur Angew Math Mech ZAMM 82:235–246

    Article  MathSciNet  Google Scholar 

  21. Rashidi MM, Kavyani N, Abelman S (2014) Investigation of entropy generation in MHD and slip flow over rotating porous disk with variable properties. Int J Heat Mass Transf 70:892–917

    Article  Google Scholar 

  22. Miclavcic M, Wang CY (2004) The flow due to a rough rotating disk. Zeitschrift Angew Math Phys 54:1–12

    Google Scholar 

  23. Hayat T, Muhammad T, Shehzad SA, Alsaedi A (2017) On magnetohydrodynamic flow of nanofluid due to a rotating disk with slip effect: a numerical study. Comput Methods Appl Mech Eng 315:467–477

    Article  MathSciNet  Google Scholar 

  24. Attia HA (2009) Steady flow over a rotating disk in porous medium with heat transfer. Nonlinear Anal 14:21–26

    Article  Google Scholar 

  25. Bachok N, Ishak A, Pop I (2011) Flow and heat transfer over a porous rotating disk in a nanofluid. Physica B 406:1767–1772

    Article  Google Scholar 

  26. Turkyilmazoglu M (2012) MHD fluid flow and heat transfer due to a stretching rotating disk. Int J Therm Sci 51:195–201

    Article  Google Scholar 

  27. Hatami M, Sheikholeslami M, Gangi DD (2014) Laminar flow and heat transfer of nanofluids between contracting and rotating disks by least square method. Power Technol 253:769–779

    Article  Google Scholar 

  28. Sheikholeslami M, Hatami M, Ganji DD (2015) Numerical investigation of nanofluid spraying on an inclined rotating disk for cooling process. J Mol Liq 211:577–583

    Article  Google Scholar 

  29. Turkyilmazoglu M (2012) Three dimensional MHD stagnation flow due to a stretchable rotating disk. Int J Heat Mass Transf 55:6959–6965

    Article  Google Scholar 

  30. Turkyilmazoglu M (2014) Nanofluid flow and heat transfer due to a rotating disk. Comput Fluids 94:139–146

    Article  MathSciNet  Google Scholar 

  31. Mustafa M, Khan JA, Hayat T, Alsaedi A (2015) On Bödewadt flow and heat transfer of nanofluids over a stretching stationary disk. J Mol Liq 211:119–125

    Article  Google Scholar 

  32. Hassan M, Mohyud-Din ST, Ramzan M (2019) Study of heat transfer and entropy generation in ferrofluid under low oscillating magnetic field. Indian J Phys 93(6):749–758

    Article  Google Scholar 

  33. Kasaeian A, Azarian RD, Mahian O, Kolsi L, Chamkha AJ, Wongwises S, Pop I (2017) Nanofluid flow and heat transfer in porous media: a review of the latest developments. Int J Heat Mass Transf 107:778–791

    Article  Google Scholar 

  34. Das SK, Choi SUS, Yu W, Pradeep T (2007) Nanofluids: science and technology. Wiley, New Jersey

    Book  Google Scholar 

  35. Nield DA, Kuznetsov AV (2009) Thermal instability in a porous medium layer saturated by a nanofluid. Int J Heat Mass Transf 52:5796–5801

    Article  Google Scholar 

  36. Mahdi RA, Mohammed HA, Munisamy KM, Saeid NH (2015) Review of convection heat transfer and fluid flow in porous media with nanofluid. Renew Sustain Energy Rev 41:715–734

    Article  Google Scholar 

  37. Forchheimer P (1901) Wasserbewegung durch boden. Zeitschrift Ver D Ing 45:1782–1788

    Google Scholar 

  38. Muskat M (1946) The flow of homogeneous fluids through porous media. Edwards, Ann Arbor

    Google Scholar 

  39. Seddeek MA (2006) Influence of viscous dissipation and thermophoresis on Darcy–Forchheimer mixed convection in a fluid saturated porous media. J Colloid Interface Sci 293:137–142

    Article  Google Scholar 

  40. Shehzad SA, Abbasi FM, Hayat T, Alsaedi A (2016) Cattaneo-Christov heat flux model for Darcy-Forchheimer flow of an Oldroyd-B fluid with variable conductivity and non-linear convection. J Mol Liq 224:274–278

    Article  Google Scholar 

  41. Bakar SA, Arifin NM, Nazar R, Ali FM, Pop I (2016) Forced convection boundary layer stagnation-point flow in Darcy-Forchheimer porous medium past a shrinking sheet. Front Heat Mass Transf 7:38

    Google Scholar 

  42. Hayat T, Muhammad T, Al-Mezal S, Liao SJ (2016) Darcy-Forchheimer flow with variable thermal conductivity and Cattaneo-Christov heat flux. Int J Numer Methods Heat Fluid Flow 26:2355–2369

    Article  Google Scholar 

  43. Sheikholeslami M, Ghasemi A, Li Z, Shafee A, Saleem S (2018) Influence of CuO nanoparticles on heat transfer behavior of PCM in solidification process considering radiative source term. Int J Heat Mass Transf 126:1252–1264

    Article  Google Scholar 

  44. Mosayebidorcheh S, Hatami M (2017) Heat transfer analysis in carbon nanotube-water between rotating disks under thermal radiation conditions. J Mol Liq 240:258–267

    Article  Google Scholar 

  45. Nayak MK, Shaw S, Chamkha AJ (2019) 3D MHD free convective stretched flow of a radiative nanofluid insprired by variable magnetic field. Arab J Sci Eng 44:1269–1282

    Article  Google Scholar 

  46. Sheikholeslami M, Shehzad SA (2018) Simulation of water based nanofluid convective flow inside a porous enclosure via Non-equilibrium model. Int J Heat Mass Transf 120:1200–1212

    Article  Google Scholar 

  47. Nayak MK, Shaw S, Pandey VS, Chamkha AJ (2018) Combined effects of slip and convective boundary condition on MHD 3D stretched flow of nanofluid through porous media inspired by non-linear thermal radiation. Indian J Phys 92:1017–1028

    Article  Google Scholar 

  48. Nayak MK (2017) MHD 3D flow and heat transfer analysis of nanofluid by shrinking surface inspired by thermal radiation and viscous dissipation. Int J Mech Sci 125:185–193

    Article  Google Scholar 

  49. Akbar NS, Khan ZH, Nadeem S (2014) The combined effects of slip and convective boundary conditions on stagnation point flow of CNT suspended nanofluid over a stretching sheet. J Mol Liq 196:21–25

    Article  Google Scholar 

  50. Xue QZ (2005) Model for thermal conductivity of carbon nanotube-based composites. Physica B 368:302–307

    Article  Google Scholar 

  51. Bellman RE, Kalaba RE (1965) Quasilinearization and nonlinear boundary-value problems. Elsevier Publishing Company, New York

    Google Scholar 

  52. Motsa SS (2013) A new spectral local linearization method for nonlinear boundary layer flow problems. J Appl Math 2013:1–15 Article ID 423628

    MathSciNet  Google Scholar 

  53. Nayak MK, Mehmood R, Makinde OD, Mahian O, Chamkha AJ (2019) Magnetohydrodynamic flow and heat transfer impact on ZnO-SAE50 nanolubricant flow over an inclined rotating disk. J Cent South Univ 26:1146–1160

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Research Foundation of South Africa, the Durban University of Technology, and the University of KwaZulu-Natal, (Grant Number 116661). In addition, the authors are thankful to Amity University, Kolkata-700135, West Bengal, India for necessary support.

Author information

Authors and Affiliations

  1. Department of Physics, IHSE, Siksha O Anusandhan Deemed to be University, Bhubaneswar, Odisha, India

    M. K. Nayak

  2. Department of Mathematics, Amity University, Newtown, Kolkata, West Bengal, 700135, India

    S. Mondal

  3. Institute of Systems Science, Durban University of Technology, P O Box 1334, Durban, 4000, South Africa

    T. M. Agbaje & P. G. L. Leach

  4. School of Mathematics, Statistics and Computer Sciences, University of KwaZulu-Natal, Scottsville, Private Bag X01, Pietermaritzburg, 3209, South Africa

    T. M. Agbaje & P. Sibanda

Authors
  1. M. K. Nayak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. M. Agbaje
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Mondal
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. P. Sibanda
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. P. G. L. Leach
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Mondal.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This article has been retracted. Please see the retraction notice for more detail: https://doi.org/10.1007/s10665-024-10371-1

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nayak, M.K., Agbaje, T.M., Mondal, S. et al. RETRACTED ARTICLE: Thermodynamic effect in Darchy–Forchheimer nanofluid flow of a single-wall carbon nanotube/multi-wall carbon nanotube suspension due to a stretching/shrinking rotating disk: Buongiorno two-phase model. J Eng Math 120, 43–65 (2020). https://doi.org/10.1007/s10665-019-10031-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-019-10031-9

Keywords

Search

Navigation