Long run non-linearity in CO₂ emissions: the I(2) cointegration model and the environmental Kuznets curve

Abstract

I utilize the I(2) cointegration model to assess the empirical relevance of the environmental Kuznets curve for CO₂ emissions in the US between 1960 and 2014. This takes the non-linearity of CO₂ emissions into account by directly incorporating data that are integrated of order two, I(2). As a result, it enables an extensive dynamic analysis of the relationship between emissions and economic growth, as postulated by the environmental Kuznets curve both in the short, medium, and long run. The results indicate that the primary drivers behind the non-linear shape of US CO₂ emissions in the long run are an increase in emissions caused by energy use and a decrease caused by more trade and the utilization of less polluting energy sources. GDP only exhibits short run effects. Hence, I do not find evidence in favor of a long-run relationship between economic development and the concave shape of emissions, as suggested by the environmental Kuznets curve.

1 Introduction

One of the most widely used theoretical models on the relationship between economic activity and environmental effects such as greenhouse gas emissions or pollution, is the environmental Kuznets curve (EKC). The theory postulates a concave relationship between the two variables, where environmental degradation is increasing until a certain level of income is reached and then declines as the income level becomes higher. The theoretical framework of the EKC was first presented in the World Development Report 1992 (see World Bank 1992), based on research by Shafik (1994) and motivated by the relationship between inequality and the level of income in Kuznets (1955). Many studies have investigated the environmental Kuznets curve both theoretically and empirically since then; see e.g. Stern (2017) for a recent literature review.

The EKC suggests that $\hbox {CO}_2$ emissions should increase until a certain level of GDP per capita is reached, and then decline. This non-linearity and concave shape of $\hbox {CO}_2$ emissions over time is taken into account in empirical work on the EKC using different approaches. A common approach is to add a quadratic term for (real) GDP per capita as an explanatory variable in the model, which yields a polynomial relationship, but other approaches are also used. As pointed out by Stern (2017), a lot of the approaches in empirical work on the EKC are not statistically robust, and there is no consensus on the driver of the changes in emissions. However, there are recent works that use statistically robust methods in order to take non-linearity into account, see the next section for more information about the relevant work.

If I(2) trends are present in the standard cointegrated vector autoregressive (CVAR) model, there are some concerns that should be addressed (see Juselius (2006), p. 293). It is not possible to say anything about the number of I(2) trends in the short-run matrix of the vector error correction model (VECM), and the determination of the rank of the long-run matrix of the VECM may have poor small sample properties. The latter can be important in the investigation of the EKC because one often utilizes annual data and thereby has a relatively small sample size. Additionally, the cointegration relations cannot be interpreted in the same way as if only I(1) variables are used in the model, since these are not I(0) in the presence of I(2) trends but rather I(1). Hence, it is possible to estimate long-run relations in the presence of I(2) trends in the VECM, but the interpretation of the results is different, see Johansen (1995). By using the I(2) model, we are able to take this into account, and the estimated I(2) model will provide a rich dynamic analysis of the data, enabling us to analyze the relationship between economic activity and $\hbox {CO}_2$ emissions thoroughly. The non-linearity of $\hbox {CO}_2$ emissions may be investigated through an I(2) model if there are double unit roots, or “I(2)-ness”, in the data. Using this framework also enables estimating a system of non-linear variables, thus treating all variables as endogenous from the outset.

I am going to follow the empirical EKC literature on output, $\hbox {CO}_2$ emissions, energy consumption, and trade, by including and controlling for (the log of) all of them in the model and investigate the joint effects. Hence, I use the same per capita variables as e.g. in Halicioglu (2009), reducing the problem of omitted variable bias. This combines testing the EKC hypothesis with the nexus of investigating the relationship between economic growth and energy consumption, following Ang (2007, 2008); Soytas et al. (2007) and Soytas and Sari (2009). Including trade as an explanatory variable is also in line with the Hecksher-Ohlin trade theory (see Arrow et al. (1995) and Stern et al. (1996)), which suggest that developed countries will specialize in producing goods that are intensive in human capital as well as focusing on capital-intensive activities. This will result in pollution being reduced in developed countries and increased in developing countries, which specialize in producing labor and natural resource-intensive goods, due to trade. Hence, I test both the EKC hypothesis, the link between energy consumption and economic growth, and aspects related to the Hecksher-Ohlin trade theory such as the pollution haven hypothesis (see Cole (2004)) or carbon leakage (see Babiker (2005)). My contribution is thereby to investigate the EKC for $\hbox {CO}_2$ emissions using the I(2) model, allowing for a rich dynamic analysis of the link between economic activity and emissions. We also use other data sets and models as robustness and sensitivity analyses.

For the US, I find that $\hbox {CO}_2$ emissions show signs of being I(2). We may therefore use the I(2) model in order to take this into account, enabling the identification of common I(2) trends as the non-linear effects between the variables. I find that there is a non-linear relationship between the variables, but that the factors causing the non-linearity/concavity of $\hbox {CO}_2$ emissions in the long run seem to be related to trade and energy use and not GDP, suggesting that the pollution haven hypothesis or carbon leakage, along with changing energy sources, may have contributed to the concave shape of $\hbox {CO}_2$ emissions and the decline in emissions over the past years in the US.

The next section provides a brief motivation and literature review related to empirical research on the EKC. Section 3 presents the EKC model and the I(2) model as well as using simulated data to estimate the EKC model, Sect. 4 presents the data, estimates the unrestricted I(2) model and performs preliminary tests, while the next section shows the empirical results and analysis of the estimated I(2) model. The final section concludes. A description of the data sources, as well as robustness and sensitivity analyses, are in the Appendices.

2 Empirical assessment of the environmental Kuznets curve

By using cointegration analysis, both country specific analyzes (see e.g. Perman and Stern (2003), Halicioglu (2009) or Saboori et al. (2012)) and panel analyzes of multiple countries (see e.g. Apergis and Ozturk 2015 or Perman and Stern (2003)) have been carried out. Studies have utilized, among other methods, autoregressive distributed lag (ARDL) models (see e.g. Jalil and Mahmud 2009) and Granger non-causality tests such as those in Soytas et al. (2007) and Halicioglu (2009). Spatial effects have also been investigated (see e.g. Maddison 2006). However, as pointed out by Stern (2017), the econometric methods used for analyzing the EKC relationship are often not appropriate regarding the consideration of the properties of the data. For instance, Stern (2004) emphasizes that few econometric investigations of the EKC consider serial dependence or stochastic trends in time series, and that the empirical investigations of the EKC have been weak. For a more detailed overview, see Stern (2017) who provides a detailed recent literature review of work that assesses the empirical relevance of the EKC. See also Copeland and Taylor (2004) for a theoretical framework of the EKC.

Wagner (2008) accounts for non-linearity by replacing GDP by de-factored GDP, and Wagner (2015) extends the Fully modified OLS procedure to deal with this and estimates the EKC. See also Knorre et al. (2021) and Wagner et al. (2020) for newly developed procedures for monitoring polynomial regressions. Esteve and Tamarit (2012) and Sephton and Mann (2013) employ threshold cointegration to take the non-linear effects into account. Nonlinear cointegration is also taken into account in Sephton and Mann (2016) through the multivariate adaptive regression spline model, while Sephton (2020) and Sephton (2022) investigate mean reversion through non-linearity. Pata and Aydin (2022) utilize a wavelet unit root test in order to take non-linearity into account.

The concave behavior of $\hbox {CO}_2$ emissions can be taken into consideration by using a structural break, implying that there is one regime when $\hbox {CO}_2$ emissions are increasing and one when decreasing (or several breaks to account for multiple increases and decreases throughout the sample). See e.g. Campos et al. (1996) for using structural breaks in conjunction with cointegration, and Santos et al. (2008) and Johansen and Nielsen (2009) for impulse indicator saturation techniques to automate testing for the temporal location of these breaks. It is also possible to include multiple breaks (Castle et al. 2012). A recent modeling of UK $\hbox {CO}_2$ emissions using structural breaks has been carried out by Hendry (2020). A broken linear trend may then be a proxy for an omitted variable explaining changes in $\hbox {CO}_2$ emissions such as the composition of different types of manufacturing firms in the economy or activity in the agricultural sector in the country. Using structural breaks is in line with Narayan and Smyth (2008) who investigate how GDP depends on energy consumption by using the Westerlund (2006) cointegration test that allows the possibility of multiple structural breaks in panel regressions.

The choice between using an I(1) model with a structural break (or several structural breaks) or using the I(2) model to take non-linearity into account, is affected by whether we should have a deterministic or stochastic specification of the non-linearity. If there is no reason to expect a shift in the growth rate, the turning point of the EKC could be considered as the growth rate of emissions changing from positive to negative instead of being modeled by a deterministic shift. Furthermore, the EKC is a non-linear model, cf. the definition of non-linearity in Johansen (1997). The empirical model should thus also be non-linear in order to take this into account. A linear model with one or more shifts in the trend is not necessarily theoretically in line with the EKC model, even if it takes the non-linearity of the data into account empirically. $\hbox {CO}_2$ emissions, if found to be integrated of order two empirically and evolving according to an inverted u-shape, could show signs of a declining growth rate (first difference of its logarithm) rather than having a shift in the growth rate. This implies that the shift may be modeled stochastically, since it does not necessarily show a change in the behavior but only that the peak of $\hbox {CO}_2$ emissions has been reached and that the total emissions (per capita) is declining rather than increasing. Using the I(2) model also allows determining the number of common stochastic trends, such that we can analyze long run effects between variables in the model.

Variables that are expected to follow a linear stochastic trend and variables that are expected to have a concave shape may be I(1) and I(2), respectively. Furthermore, the results from a cointegration analysis between an I(1) and an I(2) variable without taking I(2)-ness into account may be misleading (see Juselius (2006) and the results in Appendix B2). By utilizing the I(2) model which will provide a rich dynamic analysis of the data, we can allow for I(2) variables directly in the model without using a structural break and thus have an empirical framework that is closer to non-linearity postulated by the EKC theory. This will provide information on the factors affecting emissions over the sample both in the long, medium and short run while taking non-linearity into account, in line with the EKC, while using a fully specified econometric framework.

Double unit roots are often not found in empirical literature. This is likely to be a result of using univariate unit root tests rather than multivariate tests, since univariate tests have been shown to have low power in detecting double unit root in many cases (Juselius 2014). Hence, multivariate tests such as the trace test for determining the rank performed in Sect. 4.3, should be the preferred method when testing for double unit roots (the presence of I(2)). This approach follows Juselius (1995), Bacchiocchi and Fanelli (2005), Johansen et al. (2010), Juselius and Assenmacher (2017), Hetland and Hetland (2017), Salazar (2017), Juselius and Stillwagon (2018) and Juselius and Dimelis (2019), who use the I(2) model and rely on multivariate tests. I will follow this literature and concentrate on the multivariate test. However, it is important to note that this multivariate test concerns the presence of double unit roots in the given system of variables, not just the data series for $\hbox {CO}_2$ emissions. Hence, the outcome of the test will be conditional on which variables that are included in the system. To address this, I also perform univariate tests in Appendix A2 and employ a bivariate system in Appendix B3, where only $\hbox {CO}_2$ emissions and GDP are considered. These alternatives also support the finding of double unit roots.

3 Theoretical framework and econometric approach

3.1 The EKC relationship

If we consider the EKC as an inverted U-shaped relationship between $\hbox {CO}_2$ emissions and GDP, the common representation is a polynomial equation (or one of higher order) such as

$$\begin{aligned} CO2_t = \beta _1 GDP_t + \beta _2 GDP_t^2 \text{, } \end{aligned}$$

(1)

where $CO2_t$ is emissions of $\hbox {CO}_2$ per capita, $GDP_t$ is GDP per capita and $GDP_t^2$ is squared GDP per capita in period t. We should expect $\beta _1>0$ since we are dealing with positive values for $CO2_t$ and $GDP_t$, and $\beta _2<0$ since the U shape should be inverted, allowing for a maximum value on the curve ($\beta _2$ should also be sufficiently small in relation to $\beta _1$, see Perman et al. (2011)). Control variables are also often added to (1) such as human capital, energy consumption, trade, fossil fuel consumption, investments, real capital, etc. in order to isolate the effect of GDP on environmental degradation. Micro foundations in order to explain the functional form of the EKC can be found e.g. in Andreoni and Levinson (2001).

A common empirical approach when investigating whether a long-run relationship exists between environmental pollution, such as $\hbox {CO}_2$ emissions, and economic activity, using cointegration, involves using $\hbox {CO}_2$ emissions per capita as the dependent variable and GDP per capita and squared GDP per capita as explanatory variables. Additional control variables, such as energy use per capita and international trade (relative to GDP), as motivated in the introduction and following Halicioglu (2009), are also often included. This approach allows testing the EKC hypothesis by assessing whether there is an inverted U shape between $\hbox {CO}_2$ emissions and economic growth while controlling for other effects. To test the presence of the EKC, one can then examine whether $\beta _1$>0 and $\beta _2<0$ in (1).

3.2 The I(2) model

If a variable is integrated of order two, I(2), it needs to be differenced twice in order to have a stationary representation, and the I(2) model may be used. For recent applications of the I(2) model, see e.g. Juselius and Stillwagon (2018) who investigate the relationship between interest rates, prices and the exchange rate for the UK and the US, Juselius and Assenmacher (2017) for Switzerland and the US, and Juselius (2017) for Germany and the US. Hetland and Hetland (2017) investigate the Danish housing market through the I(2) model, and the Greek crisis is analyzed in Juselius and Dimelis (2019). The presentation of the I(2) model below follows these papers closely. See also (Juselius (2006), ch. 17) and (Johansen 1995, ch. 9) for further details.

A VAR model with k lags

$$\begin{aligned} X_t = \Pi _1 X_{t-1} + \cdots \Pi _k X_{t-k} + \Phi D_t + \varepsilon _t \text{. } \end{aligned}$$

(2)

may be reformulated to a vector equilibrium correction model, such as

$$\begin{aligned} \Delta X_t = \Gamma _1 \Delta X_{t-1} +\cdots +\Gamma _{k-1}\Delta X_{t-k+1} + \alpha \tilde{\beta }^\prime \tilde{X}_{t-1}+\Phi D_t+\mu _0+\mu _1 t +\varepsilon _t \text{, } \end{aligned}$$

(3)

where for our purpose related to investigation the EKC, $X_t = [lco2_t, lgdp_t, lenergy_t, ltrade_t]^{\prime }$ where the variables in the vector $X_t$ is the natural logarithm of $\hbox {CO}_2$ emissions per capita, GDP per capita, energy use per capita and trade as share of GDP, respectively. Furthermore, $\tilde{\beta }^\prime =[\beta , \beta _0, \beta _1]$, $\tilde{X}_{t-1}=[X_{t-1}, 1, t]^\prime$, $\varepsilon _t \sim N_p(0,\Omega )$ (p is the number of variables in the information set) for $t=1,\ldots ,T$, and $X_{-1}, X_0$ is given. $D_t$ is a vector of dummy variables (if included), and $\mu _0$ and $\mu _1$ are constants. The trend is restricted to be in the cointegrating space in order to prevent quadratic trends (i.e. $\beta _1\ne 0$ and $\mu _1=0$). Below, we simplify the presentation by restricting the trend to be in $\beta ^\prime X_{t-1}$ and exempt from using the notation $\tilde{\beta }^\prime$.

We may also write (3) in acceleration rates, changes and levels, which for a lag of 2 (i.e. setting $k=2$ in (2) and (3)) yields

$$\begin{aligned} \Delta ^2X_t = \Pi X_{t-1} + \Gamma \Delta X_{t-1} +\Phi D_t + \mu _0 + \mu _1 t + \varepsilon _t \text{. } \end{aligned}$$

(4)

This provides the I(2) cointegrated vector autoregressive (CVAR) model formulated in acceleration rates, changes and levels.

By using the maximum likelihood parameterization suggested by Johansen (1997) on (4) we get

$$\begin{aligned} \Delta ^2X_t = \alpha (\beta ^\prime X_{t-1}+d^\prime \Delta X_{t-1})+\zeta \tau ^\prime \Delta X_{t-1}+\Phi D_t + \mu _0 + \mu _1 t + \varepsilon _t \text{. } \end{aligned}$$

(5)

Increasing the lag length to $k=3$, if empirically justified, results in adding the term $\Gamma _1 \Delta ^2 X_{t-1}$ with a negative sign to (4) and (5), where $\Gamma =-(I-\Gamma _1)$, providing a term for the short-run effects (see Johansen (1995)).

The hypothesis that there are unit roots in the data, i.e. that $X_t$ is I(1), is formulated as a reduced rank hypothesis on $\Pi =\alpha \beta ^\prime$, where $\alpha$ and $\beta$ are of dimension $p\times r$ where r is the rank of $\Pi$. As in the CVAR with variables that are at most I(1), the $\beta$ vector describes the long-run stationary relationships between the variables and the $\alpha$ vectors contain the adjustment parameters which describe how the system adjusts or error-corrects to a disequilibrium from $\beta ^\prime X_t$.

If $\Delta X_t\sim I(1)$, such that $X_t \sim I(2)$, this can be formulated by a linear transformation through a reduced rank hypothesis on $\Gamma$. This results in $\alpha _{\bot }^\prime \Gamma \beta _{\bot }=\xi \eta ^\prime$, where $\xi$ and $\eta$ are $(p-r)\times s_1$, and $\alpha _{\bot }$ and $\beta _{\bot }$ are the orthogonal complements of $\alpha$ and $\beta$, respectively (see Johansen 1992, 1995). As in the I(1) CVAR model, there are $(p-r)$ stochastic trends for the reduced rank r, and these are divided into $s_1$ trends of order I(1) and $s_2$ of order I(2). Hence, the I(1) reduced rank condition is associated with the levels of the variables, while the I(2) reduced rank condition is associated with the differenced variables, since the first difference is I(1) given the presence of I(2) in the levels. The trend, t, is restricted to be in the cointegrating relationship $\beta ^\prime X_{t-1}$, and the constant to be in $d^\prime \Delta X_{t-1}$ (often referred to as the multi-cointegrating relationship or dynamic equilibrium). As shown in Rahbek et al. (1999), we need a restricted linear trend in order to allow for linear trends in all linear combinations of $X_t$. The relation $\zeta {\tau }^\prime \Delta \tilde{X}_{t-1}$, where $\tau =[\beta ,\beta _{\bot 1}]$, describes the medium-run relations between the differences variables, and the cointegrating relations ${\tau }_{\bot ,1}X_t$ transforms the process from I(2) to I(1) by using the polynomial trends. It consists of r relations ${\beta }^\prime X_t$ and $s_1$ relations ${\beta }_{\bot ,1}X_t$.

As pointed out by Juselius and Assenmacher (2017), $\beta ^\prime X_t$ is generally I(1), and can be interpreted as an equilibrium error with pronounced persistence. The coefficients in the vectors $\alpha$ may then be interpreted as how the acceleration rates $\Delta ^2 X_t$ adjusts to the dynamic equilibrium relations $\beta ^\prime X_{t}+d^\prime \Delta X_{t}$, and d describes how the growth rates $\Delta X_t$ adjusts to the long-run equilibrium errors $\beta ^\prime X_t$. If $\alpha \ne 0$, d may be interpreted as a medium-run adjustment. For the variable $X_{i,t}$, (5) may be written in terms of the adjustment rates as

$$\begin{aligned} \Delta ^2 X_{i,t} = \cdots \sum ^r_{j=1}\alpha _{i,j} \sum ^p_{m=1}(\beta _{mj}X_{m,t-1}+d_{mj}\Delta X_{m,t-1})+ \sum ^r_{j=1}\zeta _{i,j} \sum ^p_{m=1}(\beta _{mj}\Delta X_{m,t-1})+\varepsilon _{i,t} \text{, } \end{aligned}$$

(6)

for $i=1,\ldots ,p$, where p is the number of variables in the vector $X_t$ and i is the ith variable. From this, we see that the signs of $\alpha$, $\beta$, and d determine whether the variable $X_{i,t}$ is error increasing or error correcting in the long run and in the medium run. If $\alpha _{ij} d_{mj}<0$ or/and $\alpha _{ij}\beta _{mj}<0$, the acceleration rate is error correcting to the changes $(\beta _j^\prime X_t+d^\prime _j \Delta X_t)$. Furthermore, if $d_{mj}\beta _{mj}>0$ (given $\alpha _{ij}\ne 0$), the change $\Delta X_{i,t}$ is error correcting to the levels $\beta ^\prime _j X_t$. Finally, if $\zeta _{i,j}\beta _{mj}<0$, then the acceleration rate $\Delta ^2 X_{i,t}$ is error correcting to $\beta ^\prime _j \Delta X_{t-1}$. In all other cases, the system is error increasing. Furthermore, error increasing behavior is offset by error correction elsewhere in the system if all the characteristic roots are inside or on the unit circle such that the system is stable. Hence, even though a variable may be error increasing in e.g. the medium run, this is offset by error correcting behavior in the long run or in another variable (see Juselius and Assenmacher (2017)). Even though cointegration measures co-movements and not causality, long-run adjustment may thus be assessed through the $\alpha$ coefficients in combination with $\beta ^\prime X_t$ and $\beta ^\prime X_t + d^\prime \Delta X_t$.

The moving average representation of the VAR model can, in a simplified manner, be given as

$$\begin{aligned} X_t = \tilde{\beta }_{\bot ,2}\alpha _{\bot ,2}^\prime \sum _{j=1}^{t}\sum _{i=1}^{j}(\varepsilon _i+\mu _0)+C_1\sum _{j=1}^{t}(\varepsilon _j+\mu _0)+C^*(L)(\varepsilon _t+\mu _0)+A+Bt \text{, } \end{aligned}$$

(7)

where $\alpha _{\bot ,2}^\prime$ gives information on the sources of exogenous shocks and $\tilde{\beta }_{\bot ,2}$ on how the I(2) trends $\alpha _{\bot ,2}^\prime \sum _{j=1}^{t}\sum _{i=1}^{j}\varepsilon _i$ loads into the variables in the system, $X_t$. This simplified representation is sufficient for the purpose of our analysis, as argued in Juselius and Stillwagon (2018). See (Juselius 2006, p. 313) for this simplification or Johansen (1992) for a more detailed description.

3.3 The I(2) model and the EKC relationship

Firstly, $\hbox {CO}_2$ may be I(2) and have a concave shape, following the non-linear relationship postulated by the EKC. We may then consider $\beta 'X_t$ as the long run relationship with highly persistent deviations from long-run static equilibrium errors. This highly persistent deviation may then be what is causing the concave shape of $\hbox {CO}_2$ emissions as suggested by the EKC, or it may also be in line with long-run deviations constituting an N-shape of $\hbox {CO}_2$ emissions (as found e.g. in Grossman and Krueger (1991)).

If we find that the rank is $r=1$, we have, from $\beta ^\prime X_t$, that the long-run relation between the log of CO2 emissions per capita, the log of GDP per capita, the log of energy use per capita and the log of net trade can be written as

$$\begin{aligned} lco2_t = \beta _1 lgdp_t + \beta _2 lenergy_t + \beta _4 ltrade_t + z_t \text{, } \end{aligned}$$

(8)

where $z_t$ is a residual integrated of order one. This is similar to the theoretical EKC relationship in (1) with control variables, except for not including the square of GDP in (8).¹ I also exempt from writing the constant term as it is not restricted to be in $\beta$, and I include a deterministic trend in the unrestricted $\beta ^\prime X_t$ to test for the presence of this. The I(2) model adds $d^\prime \Delta X_t$ in order to get a stationary relationship, which measures medium run changes in the variables. This can be thought of as a proxy for squared GDP in the EKC, such that the non-linearity may be accounted for through the I(2) model by $d^\prime X_t$ rather than by adding a quadratic term to the regression model. See, e.g., Juselius and Assenmacher (2017).

According to the EKC, the relationship between emissions and GDP depends on the level of GDP, where a quadratic term is added to explain the concave relationship. This is theoretically motivated as being a positive effect from GDP to emissions when a country’s GDP is low and it uses more emission-intensive resources in e.g. manufacturing, while the effect of GDP on emissions is smaller when GDP is high due to less use of emission-intensive factor inputs. Hence, technological advancements may cause this non-linear effect of GDP on emissions. GDP may therefore both be considered to error increase and error correct the system in the I(2) model, since deviations from a linear relationship such as in (8) is both increased and decreased by GDP. Error increasing factors will imply reinforcing effects, while error correcting factors adjust back to equilibrium. The non-linearity of the EKC can thus be considered the disequilibrium in (8), and should, according to the EKC, be a result of technological development which is explained through GDP. Hence, if technological improvements yield the shape of the EKC, then shocks to GDP should be relevant for $\hbox {CO}_2$ emissions. We should therefore observe that twice cumulated shocks to GDP will generate an I(2) trend that is concave and that these shocks feed into $\hbox {CO}_2$ emissions. This may be investigated through the moving average representation of the I(2) model as shown in (7).

The dynamic relation $\beta ^\prime X_t+d^\prime \Delta X_t$ (if $r=1$) will be given by

$$\begin{aligned}& lco2_t - \beta _1 lgdp_t - \beta _2 lenergy_t - \beta _4 ltrade_t \nonumber \\&\quad = d_0 \Delta lco2_t - d_1 \Delta lgdp_t - d_2 \Delta lenergy_t - d_4 \Delta ltrade_t + v_t \text{, } \end{aligned}$$

(9)

(also including a trend and a constant if applicable) where $v_t$ is stationary. Given a significant $\alpha$, this will show error correcting and increasing behavior in the medium run. This also shows how the non-stationary deviation from the equilibrium in the EKC without a quadratic term (i.e. the representation in (8)) can be explained through the estimated parameters and medium run error correction and increasing behavior. Hence, while the non-linearity and concave relationship in the EKC model is modeled through a polynomial relationship, the non-linearity in the I(2) model will be due to deviations from the estimated long-run equilibrium.

4 Data and empirical results

4.1 Data

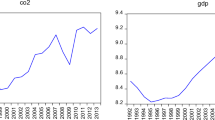
I use log of $\hbox {CO}_2$ emissions per capita, energy use per capita, GDP per capita and trade intensity (the sum of imports and exports as a share of GDP) in the empirical model. References to the data on GDP, $\hbox {CO}_2$ emissions, energy use and trade in the next sections thereby refers to the natural logarithm of these series. The data set covers the US in the period 1960-2014. Per capita $\hbox {CO}_2$ emissions are measured as emissions stemming from the burning of fossil fuels and the manufacture of cement, while per capita energy use is the use of primary energy before transformation to other end-use fuels, and includes energy from combustible renewable sources and waste.² For GDP, I use real GDP per capita, while trade intensity is measured as the sum of imports and exports as a percentage of GDP. The data are plotted in Fig. 1, and a description of the data sources can be found in Appendix A1. These over 50 years of data includes many changes in the US economy such as variation in its composition of industrial sectors. The sample starts with the consumer boom in the 1960 s, followed by the recessions and inflationary periods in the 70 s and 80 s (French and French 1997). Increased labor productivity in the second half of the 90 s, in particular due to information technology (Oliner and Sichel 2000) is also related, and the sample ends after the financial crisis.

Fig. 1

Plot of the natural logarithm of the US data series

As argued in e.g. Itkonen (2012) and Jaforullah and King (2017), using energy consumption as an explanatory variable for $\hbox {CO}_2$ emissions may lead to underestimation of the other explanatory variables and systematic volatility in the estimated coefficients. It may also cause misleading cointegration test results, and should thereby not be used when estimating the effects on $\hbox {CO}_2$ emissions. However, in this paper, our main concern is the unobserved shocks driving the stochastic trends of the system and not the estimated parameters, such that this should be of less importance here. Even though the data series for $\hbox {CO}_2$ emissions are constructed partially based on energy consumption, the difference between the shocks to the two variables may provide important information regarding whether changes in energy originates from changes in the use of renewable sources and thereby do not lead to an increase in $\hbox {CO}_2$ emissions. The estimated system for the US when excluding energy use also suggests that GDP may be excluded from the long run relation, such that the effect of GDP on $\hbox {CO}_2$ emissions does not seem to be underestimated when including energy use in the system. Excluding energy use also suggests no long run relationship between GDP and $\hbox {CO}_2$ emissions (see Appendix B3), indicating that including energy use in the model does not underestimate the effect between GDP and $\hbox {CO}_2$ emissions or the I(2) cointegration test results. Additionally, when using an error correction form such as in (3), (4) and (5), which contain our estimates, the multicollinearity effect is significantly reduced (see Juselius 2006, p. 60), such that using both energy use and $\hbox {CO}_2$ emissions in our model is less of a concern.

4.2 Unrestricted I(2) model

The results from the estimations I conduct here were obtained using CATS 3 for OxMetrics, see Doornik and Juselius (2017).³ I follow Rahbek et al. (1999) and restrict the constant term to be in $d'x_{t-1}$ and the deterministic trend to be in $\beta 'x_{t-1}$ in order to avoid quadratic trends as pointed out in Sect. 3.2. This enables us to separate between a quadratic trend and the presence of I(2) due to double unit roots.

I set the lag length of the unrestricted VAR to $k=3$, which is the most parsimonious well specified model without the need to include any step or indicator dummies. See Table 1 for the residual analysis which shows that the VAR(3) model is well specified. The tests of the residuals are described in Doornik and Juselius (2017).

Table 1 Misspecification tests for the unrestricted VAR(3) model

Information criteria and log-likelihood tests for lag reduction indicates that we should choose a lag length of one or two. However, the VARs with one or two lags are not correctly specified according to misspecification tests. This invalidates these test criteria since these tests are only valid under the assumption that the models are correctly specified (Juselius 2006). We need to add shift and impulse dummy variables to the VARs with one or two lags in order to make them well specified, so I instead proceed with a VAR with three lags in order to avoid the need to add dummy variables. This enables us to use a model which fully explains the system of variables in the sample period. An I(2) model with a lag length of three also provides estimates of short run effects which may be relevant to analyze.

Using impulse and step indicator saturation in Autometrics (see Doornik (2009)) provides a well specified VAR(1) model with a step shift dummy in 1973 and an impulse dummy in 1976. This step shift may take the non-linearity into account and be used in an I(1) cointegration model instead of using I(2) cointegration analysis as I utilize in this paper. Alternatively, the two approaches may be combined, following the framework in Kurita et al. (2011). However, I will use the I(2) model since this is in line with what the EKC suggests, and we are able to use a VAR(3) model that is well specified without the need to add deterministic terms.

4.3 Reduced rank and preliminary tests

Here, we use the I(2) trace test for the reduced rank hypothesis test of $\Gamma$ as the multivariate unit root test. This follows the literature utilizing the I(2) model as discussed in Sect. 2. The results are that a rank of $r=1$ and $s_2=2$ I(2) trends (i.e. the model H(1,1,2)) is accepted with a p-value of 0.208, as shown in Table 2 and highlighted in bold. The model H(1,0,3) may also be accepted with a p-value of 0.052, since we move from left to right row-wise in this procedure, but since the p-value is quite low we choose to interpret the results in favor of the H(1,1,2) model. This yields a rank of $r=1$, implying one polynomially cointegrating relation $\beta ^\prime \tilde{X}_t+d^\prime \Delta \tilde{X}_t$, and two relations $\beta _{\bot i}\Delta \tilde{X}_{t-1}$, $i=1,2$, which needs to be differenced in order to become stationary. A near unit root may be hard to distinguish from a unit root in a finite sample (see e.g. Granger and Swanson (1997)), suggesting that it is appropriate to use the I(2) model for modeling $\hbox {CO}_2$ emissions also when we find (near) I(2)-ness in the data.

I have also included univariate ADF tests of the variables in Appendix A2 in order to illustrate the behavior of double unit roots and motivate using the I(2) model. The results suggest that $\hbox {CO}_2$ emissions contains double unit roots, which is in line with the multivariate test used here.

Table 2 Rank test statistics (with p-values in brackets)

Tests for variable exclusion, weak exogeneity and I(1) tests are shown in Table 3. The tests for long-run weak exogeneity show that GDP may be weakly exogenous, observing a p-value of 0.40, such that GDP is not affected by the system being out of equilibrium. GDP may in addition be excluded from the long run relation $\beta$ and $\tau$, indicating that GDP is not relevant for the long-run polynomially cointegrating relation.

We may investigate whether a variable is I(1) or I(2) by testing for a unit vector in $\beta$ and $\tau$. As argued in (Juselius 2006, p. 297) and as shown by tests for I(2) trends in Juselius (2014), univariate tests of individual variables cannot (and should not) replace the multivariate I(1) or I(2) test procedures. The rank test here is therefore used as the appropriate multivariate test of double unit roots. From Table 3, we see that we reject the null hypothesis that the variable in question is at most I(1) for all variables. All of the variables may therefore considered to be (near) I(2) in our system. Even though theoretically justifying that all of the variables should be integrated of order two may not be appropriate, (near) I(2)-ness may be considered due to persistent deviations from I(1) behavior. As previously mentioned, the I(2) model is also appropriate to use in the case of (near) I(2)-ness (Frydman et al. 2010), such that the I(2) model is a suitable framework to estimate the EKC relationship given our data set. The estimated I(2) model is thus a suitable framework for taking the non-linearity and the concave shape of the EKC into account.

Table 3 Tests of restrictions (p-values in brackets)

5 Results

5.1 Long and medium run relations

Since whether the products of d, $\beta$ and $\alpha$ are positive or negative determines if variables in the system are error correcting or error increasing, c.f. (5) and (6), we need to assess the signs of these products from the estimated parameters. This is summarized in Table 4 where the significant parameters and the signs of their relevant products for interpreting the results are shown. Boldfaced font indicates that the variable in the corresponding column is error increasing, while an asterisk implies that there is no significant effect (given $|\text{ t-value }|<1.6$ following e.g. Juselius and Assenmacher (2017)). I also restrict $GDP_t$ to be excluded from $\beta$, which is accepted with a p-value of 0.15 according to the likelihood ratio test, c.f. Table 3. This provides an over-identified and more parsimonious model.

Table 4 Estimated polynomially cointegrating relations (t-values in brackets)

The estimated polynomially cointegrating relations show that energy use is error increasing (bold in Table 4) both in the long run and the medium run (interpreting coefficients in d as medium-run adjustment is conditional on $\alpha \ne 0$, as argued in Juselius and Assenmacher (2017)), while trade and $\hbox {CO}_2$ emissions are error correcting both in the long run and the medium run. This implies that energy consumption is a dominant trend follower in the long run, while $\hbox {CO}_2$ emissions and trade takes the burden of adjustment back to equilibrium. Hence, if variables are away from the long-run relationship, $\hbox {CO}_2$ emissions and trade will move back towards equilibrium (the equilibrium will here imply the long-run stationary relationship between the variables and the persistent $\beta ^\prime X_t$ in the medium run). The relationship between the variables in the system is pushed out of equilibrium mainly by use of primary energy. Hence, the increase in the I(2) trend has mainly been caused by use of primary energy, while the decrease in the trend is mainly a result of trade and less emission intensiveness. Even if d is significant for GDP, this cannot be interpreted as a medium run effect since $\alpha$ is insignificant for GDP.

The stationary dynamic long-run relation $\beta ^\prime X_t+d^\prime \Delta X_t$ then becomes

$$\begin{aligned} lco2_t&- \underset{(0.046)}{1.25}\ lenergy_t + \underset{(0.042)}{0.42}\ ltrade_t - \underset{(0.00086)}{0.0054}\ t \nonumber \\&+ \underset{(0.13)}{0.75}\ \Delta lco2_t+ \underset{(0.16)}{0.90} \Delta lenergy_t - \underset{(0.43)}{0.87}\ \Delta lgdp_t + \underset{(0.22)}{0.99}\ \Delta ltrade_t + \underset{(0.36)}{7.12} \end{aligned}$$

(10)

where standard errors are given in parentheses below the estimated coefficients.

While squared GDP may explain the non-linear relationship between GDP and emissions in the EKC theory, $d^\prime \Delta X_t$ will provide the factors that contribute to the non-linearity of $\hbox {CO}_2$ emissions estimated by the I(2) model. The other variables in $\beta ^\prime X_t$ may also be I(2).

$\hbox {CO}_2$ emissions and energy use enters with opposite signs in $\beta ^\prime X_t$, capturing energy intensity and a negative coefficient on excess energy use; $(lco2_t-lenergy_t)-0.25 lenergy_t$. Hence, energy intensity enters with a positive sign, while excess energy use enters negatively, and trade enters with a positive sign.

Rearranging the terms of $\beta ^\prime X_t$ in (10) yields

$$\begin{aligned} lco2_t = \underset{(0.046)}{1.25}\ lenergy_t - \underset{(0.042)}{0.42}\ ltrade_t + \underset{(0.00086)}{0.0054}\ t \end{aligned}$$

(11)

Hence, in the long run, energy use positively affects emissions, while trade has a negative effect on emissions. The coefficient on energy use is above unity, suggesting that a decrease in energy use is associated with an even larger decrease in $\hbox {CO}_2$ emissions. This suggests that declining energy use may lead to a larger emissions reduction, e.g., by also shifting to less emission intensive energy sources. Trade is negatively associated with emissions, suggesting that more trade is related to less emissions in the long run, in line with carbon leakage or the pollution haven hypothesis. The small but significant trend also suggest that there is something not included in the model associated positively with emissions in the long run, given that energy use and trade is unchanged.

However, we also need $d^\prime \Delta X_t$ in order to obtain a stationary relationship. As outlined in Sect. 3.3, this works as a proxy for squared GDP in the EKC model which is included to take non-linearity and a concave shape into account. From (10), we see that the non-linearity increases with growth in $\hbox {CO}_2$ emissions, energy use and trade, while it decreases with GDP growth.

5.2 Concavity and estimated I(2) trends

From the estimated common trends and their loadings shown in Table 5, we find that the first I(2) trend is generated from twice cumulated shocks to GDP, while the second I(2) trend is generated from twice cumulated shocks to energy use and $\hbox {CO}_2$ emissions. Furthermore, the first trend mostly loads into GDP, while the second trend loads into $\hbox {CO}_2$ emissions, energy use and trade with the same sign.

Table 5 Estimated common trends and their loadings

The EKC theory suggests that economic development is driving emissions through e.g. technological progress. Hence, we should expect shocks to GDP to provide the concave shape of $\hbox {CO}_2$ emissions. However, our results show that twice cumulated shocks to GDP mainly loads into GDP itself, while twice cumulated shocks to energy consumption and emissions loads into energy consumption, $\hbox {CO}_2$ emissions and trade. Hence, the two I(2) trends are not generated from the same source, and they do not load into the same variables. This indicates that the I(2)-ness of $\hbox {CO}_2$ emissions is not generated from shocks to GDP–as a proxy for productivity and technology – as suggested theoretically by the EKC. The two I(2) trends are shown in Fig. 2, where we see that they are shaped differently. Both may be considered to be concave, but the trend generated from shocks to GDP (due to e.g. technology development) does not feed into emissions and energy use and thus does not contribute to the concave shape of emissions. Hence, our results do not support the EKC theory of economic development causing the concave shape of $\hbox {CO}_2$ emissions.

Fig. 2

I(2) trends generated from twice cumulated shocks to GDP (I2trend1) and energy use and $\hbox {CO}_2$ emissions (I2trend2)

In the long run, the deviation from the stationary relationship $\beta 'x_t+d'\Delta x_t$ seems to be caused by energy use, while $\hbox {CO}_2$ emissions and trade have caused the system to move back to the stationary equilibrium in the long run. Furthermore, the I(2)-ness of $\hbox {CO}_2$ emissions seems not to be caused by GDP. This implies that the concave shape of $\hbox {CO}_2$ emissions that we observe in the data, cannot be explained by shocks to GDP. The I(2)-ness of $\hbox {CO}_2$ emissions seems to be a result of how energy consumption evolves. Additionally, the I(2)-ness of energy consumption does not seem to be caused by GDP either, such that there is no apparent link between economic growth, energy consumption and $\hbox {CO}_2$ emissions in the long or medium run.

The cointegrating relation $\beta 'x_t+d'\Delta x_t$ is hard to interpret in isolation as argued in Hetland and Hetland (2017). Even if we are able to connect the estimates of the I(2) model to the EKC, whether variables are error correcting or error increasing in the long run and medium run are more informative on how $\hbox {CO}_2$ emissions and the variables in our system are moving over time. We can investigate which factors that affected the non-linearity of the system and thereby how a potential EKC-relationship can be explained through the estimated I(2) model. The observed I(2)-ness in $\hbox {CO}_2$ emissions seems to be explained by the development in energy use, the choice of energy sources and trade. The I(2)-model is thereby a useful framework to analyze the long-run relationship between variables related to the EKC as it enables us to assess the factors causing this non-linear relationship in the long run.

5.3 Short run relations

The short run matrix is given in Table 6, where the estimated coefficients determining short run effects in the I(2) model are provided. This is only possible if we have a lag length of $k=3$ or more. Significant effects are shown in bold faced font.

Table 6 The short run matrix (t-values in brackets)

The short run parameters indicate that the acceleration rate of GDP and trade affects the acceleration rate of $\hbox {CO}_2$ emissions negatively in the short run. The acceleration rate of GDP is only affected by its own lag, while the acceleration rate of trade has a negative effect on the acceleration rate of energy use. Hence, $\hbox {CO}_2$ emissions may be affected by GDP in the short run, while trade affects both energy consumption and $\hbox {CO}_2$ emissions. We see that accelerated GDP growth leads to negative acceleration of $\hbox {CO}_2$ emissions (possibly due to improvements in technology making production less emission intensive) and that accelerated trade growth leads to negative acceleration of energy use and $\hbox {CO}_2$ emissions (possibly as a consequence of less domestic production of emission intensive goods). Hence, even though I do not find any long run effect from GDP on $\hbox {CO}_2$ emissions explaining the concave shape of $\hbox {CO}_2$ emissions over the long run in our sample, there may be an effect in the short run.

The short run coefficient of GDP on $\hbox {CO}_2$ emissions is negative, and this coefficient corresponds to the second derivative of GDP in the theoretical EKC relationship since it estimates the effect of acceleration rates. Hence, this relationship also indicates a concave relationship between GDP and $\hbox {CO}_2$ emissions.⁴ However, as our results from the estimated I(2) model indicate, the long run effect on $\hbox {CO}_2$ emissions and its non-linearity over the sample is not caused by GDP but rather by the long run movements in trade and emissions themselves through e.g. using different energy sources.

5.4 Robustness and sensitivity analysis

By using other data sets and other variable subsets and thereby model specifications, it is possible to assess the robustness and sensitivity of the I(2) model I have estimated.

I investigate the sensitivity of the results by using simulated data in Appendix B1, and by estimating the standard I(1) cointegration model on the US data in order to look for potential problems using (near) I(2) data in Appendix B2. I also estimate a bivariate model in Appendix B3 to investigate whether the results are sensitive to including both energy use and $\hbox {CO}_2$ emissions in the same system.

Additionally, I estimate the I(2) model for China and the UK in order to assess the robustness of the results when using other data sets in Appendix B4.

6 Conclusion

$\hbox {CO}_2$ emissions in the US can be explained by an inverted U-shape, as I find (near) I(2)-ness in the data, which may suggest concavity that is in line with an environmental Kuznets curve. However, it seems that the non-linearity is not attributed to economic development, as the stochastic I(2) trend driving $\hbox {CO}_2$ emissions is not generated by twice cumulated shocks to GDP. This implies that other factors than technology advancements and productivity improvements (typical examples of shocks to economic growth) contribute to the concave shape of $\hbox {CO}_2$ emissions.

In the long run, the relationship between $\hbox {CO}_2$ emissions and GDP growth per capita appears unrelated, while energy use and trade intensity seem to play significant roles. Thus, while the EKC may be observed empirically through the concave shape of $\hbox {CO}_2$ emissions relative to GDP, there are other factors causing $\hbox {CO}_2$ emissions to move from an increasing to a declining trend over time and thereby contributing to the concave EKC-shape. Therefore, relying solely on economic growth as a means to reduce emissions over time might not be effective.

Energy use is an important explanatory factor for the growth in the I(2) trends in the sample, whereas trade and $\hbox {CO}_2$ emissions have contributed to the decline in these trends. This suggests that using more renewable and less polluting energy sources, in addition to outsourcing pollution intensive industries, has played an important role in reducing US $\hbox {CO}_2$ emissions over the studied period. The initial rise in emissions at the beginning of our sample seems to be linked to increased use of primary energy in pollution and and energy-intensive manufacturing sectors.Future research could gain from considering trade dynamics and sector-specific pollution on a global scale to examine the EKC more comprehensively. Nevertheless, the relevance of the I(2) model for analyzing $\hbox {CO}_2$ emissions is demonstrated by the results here.

Appendices

Appendix A: Data and univariate unit root tests

1.1 A1. Data

Data on $\hbox {CO}_2$ emissions is measured in metric tons per capita, and are gathered from World Bank Open Data from a previous vintage of data from Carbon Dioxide Information Analysis Center, Environmental Sciences Division, Oak Ridge National Laboratory, Tennessee, United States, see Boden et al. (2017). However, the data set used measures $\hbox {CO}_2$ emissions in metric tons of $\hbox {CO}_2$ per capita, while the vintage data available on the websites use metric tons of carbon per capita. This implies that there is a difference of $\frac{44}{12}$ (the molecular weight of $\hbox {CO}_2$ divided by that of a carbon atom) between the data series, in addition to some minor differences, possibly due to rounding differences.

GDP per capita is measured in constant 2000 US $, and retrieved from Wold Bank Open Data using data ID NY.GDP.PCAP.KD, where the source is World Bank national accounts data, and OECD National Accounts data files. Energy use is measured as kg of oil equivalent per capita found in World Bank Open Data as data ID: EG.USE.PCAP.KG.OE, from IEA Statistics © OECD/IEA 2014 (iea.org/stats/index.asp), subject to iea.org/t &c/ termsandconditions. Data on trade measures trade intensity, i.e. the sum of imports and exports as a share of GDP. The trade data is from a previous vintage of World Bank national accounts data and OECD National Accounts data files going back to 1960. They are retrieved from World Bank Open Data, with the data ID NE.TRD.GNFS.ZS.

1.2 A2. Univariate unit root tests

In order to test for the order of integration in the variables, I perform augmented Dickey-Fuller tests for the log of each variable, as well its first difference and its second difference. This is done by estimating

$$\begin{aligned} \Delta y_t = \alpha +(\beta -1) y_{t-1}+\sum _{i=1}^s\gamma _i\Delta y_{t-1}+\mu t+\varepsilon _t \end{aligned}$$

for s lags and testing the null hypothesis of a unit root, $\beta =1$. Both a constant and a trend is included in order to account for the variable being stationary around a linear trend. To account for potential autocorrelation, I estimate using 0 to 4 lags of the first difference ($s=0$, $s=1$, $s=2$, $s=3$ and $s=4$), and select number of lags according to the Akaike information criterium (AIC).

The results form unit root tests are shown in Tables 7 and 8. The first column shows the variable name and the second column the number of lags of the first difference. The t-value for the ADF test is in the third column (critical values are $-$3.50 and $-$4.15 at the 5% and 1% significance level, respectively), with asterisks indicating significance for rejecting the null hypothesis of a unit root at the 1%, 5% and 10% significance level for three, two and one asterisk, respectively and thereby suggest stationarity. The next two columns show the estimated coefficient on $y_{t-1}$ and the standard error of the equation, respectively. The abbreviation “l.l.” represents “longest lag” such that “l.l. t.val” and “l.l. p-val” shows the t-value and the p-value of the longest lag of $\gamma _s$. AIC denotes the Akaike information criterion (where the lowest which indicates the preferred lag length is in bold) and F-prob the p-value of the F-tests on all lags dropped up to that point. See Hendry and Doornik (2001) for further details.

From the results shown in Tables 7 and 8, we see that we are able to reject the null hypothesis of a unit root for the level and the first difference of the log of $\hbox {CO}_2$ emissions but reject the null of a unit root for the second difference of $\hbox {CO}_2$ emissions. This suggests that the log of $\hbox {CO}_2$ emissions per capita is I(2). The ADF tests for the other variables suggest that they are all I(1), since we reject the null hypothesis of a unit root for the first difference of these.

Table 7 Augmented Dickey Fuller tests, $\hbox {CO}_2$ emissions and energy use

Table 8 Augmented Dickey Fuller tests, GDP and trade

I have also performed the ADF-GLS test, the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test and tested for fractional integration, but these tests show no consensus on the order of integration of $\hbox {CO}_2$ emissions. The ADF test suggests that log CO2 emissions per capita is I(2), while ADF-GLS only suggests this at a 8.1% significance level or higher. The KPSS tests suggests that it is I(1), and fractional integration tests are inconclusive. Hence, the main focus in this paper is to use the multivariate unit root test, following Juselius (2014) and the literature utilizing the I(2) model.

Appendix B: Robustness and sensitivity analysis

1.1 B1. Simulated data

In order to illustrate how the EKC is related to I(2)-ness, I simulate time series variables in line with the EKC model shown in Sect. 3.1 and I(1) explanatory variables which may be the case when using GDP. I use a data generating process (DGP) in line with the EKC where the DGP for the dependent variable consists of an explanatory variable integrated of order one and its square. I use

$$\begin{aligned} Y_t = b_0 + b_1 X_t + b_2 X_t^2 \text{, } \end{aligned}$$

as the DGP where $X_t$ is a random walk with drift, $X_t=X_0+t+v_t$ where t is a linear trend and $v_t\sim N(0,\sigma ^2)$. This provides a variable with a linear trend which is of relevance also in the case of a near-unit root since this also needs to be analyzed using non-stationary methods, cf. Granger and Swanson (1997). It is also illustrative for a stochastic trend with a unit root. I set $b_0=100,000$, $b_1=500$ and $b_2=-10$, providing the case where $\beta _1>0$ and $\beta _2<0$, c.f. (1), as well as $\beta _2$ being sufficiently small in absolute value compared to $\beta _1$ as required to provide the EKC theoretically (Perman et al. 2011). In addition, use $T=55$ in line with the size of the data set in the empirical analysis in this paper. The simulated variables are shown in Fig. 3, and they are drawn using the default seed of the random number generator, ’ranseed(-1)’, in OxMetrics.

Fig. 3

Simulated series, levels and first differences

As seen in Fig. 3, the non-stationary variable $X_t$ seems to be I(0) in first differences, while its square and $Y_t$ seems to be non-stationary in first differences. However, as shown in Fig. 4, the second differences of $X_t^2$ and $Y_t$ looks stationary, motivating that the I(2) model may be appropriate to use when analyzing the EKC. Additionally, if the data are “near I(2)”, the I(2) model is still appropriate to use, see e.g. Frydman et al. (2010). The same applies as for near I(2) as for near I(1) or near-unit root as in the I(1) case illustrated above: A near-unit root (near I(1)) should be analyzed using non-stationary, I(1), methods (Granger and Swanson 1997). Hence, even if the variable is not theoretically integrated of order two, it may empirically be hard to distinguish from a double unit root (I(2)) such that we should use the I(2) model.

Fig. 4

Simulated series, second differences

I also perform an I(2) rank test on the simulated series Y and X, shown in Table 9. This suggests a rank of $r=1$ (one stationary multi-cointegrating relationship) and $s_2=1$ common I(2) trend, such that the simulated data from our DGP contains I(2)-ness, making the I(2) model relevant for the EKC.

Table 9 Rank test statistics (with p-values in brackets)

1.2 B2. Estimating the I(1) model (and looking for indications of I(2))

I estimate the standard cointegrated VAR model for our four variables, i.e. estimating (3) using a lag length of $k=3$, and show rank tests in Table 10. The table contains the maximum eigenvalue, trace test statistics with critical values and p-values, and $\rho _{un}^{max}$ which is the modulus of the largest unrestricted root.

Table 10 I(1) Rank analysis

The trace test seems to suggest a rank of $r=1$, but when using Bartlett-corrected (marked with an asterisk) values, the conclusion based on p-values is a rank of $r=0$. This large deviation when using Bartlett-corrected values or not is a sign of I(2) variables in the system (Johansen 1997; Juselius 2006). The large unrestricted root for chosen rank ($r=1$) is also a sign of I(2) variables. Additionally, we see from the graphical presentation of the cointegrating relationship and the cointegrating relationship adjusted for first differences in the upper and lower panel of Fig. 5, respectively, that the former seems to follow a trend while the latter looks stationary. This is also a sign of I(2)-ness in the data, since the cointegrating relationship needs to be corrected for first differences in order to become stationary (Johansen 1997; Juselius 2006).

Fig. 5

The cointegrating relationship for $r=1$

1.3 B3. I(2) model for the US: $\hbox {CO}_2$ emissions and GDP

In order to assess whether including energy use and trade may mitigate the role of GDP for $\hbox {CO}_2$ emissions in our estimated model, I estimate a bivariate I(2) model using only $\hbox {CO}_2$ emissions and GDP. I also add squared GDP in order to investigate whether I(2)-ness in $\hbox {CO}_2$ emissions may be explained by a model formulated non-linearly by GDP (i.e. with a potential I(2) variable of squared GDP).

We thus have two VAR models, one with only GDP and $\hbox {CO}_2$ emissions, and one which also includes squared GDP. I then carry out I(2) rank tests for these models in order to see whether they can be used further to assess inference between GDP and $\hbox {CO}_2$ emissions. The results are shown in Tables 11 and 12.

Table 11 Rank test statistics model with $\hbox {CO}_2$ and GDP (with p-values in brackets)

Table 12 Rank test statistics model with $\hbox {CO}_2$, GDP, and GDP squared (with p-values in brackets)

The rank tests suggest that there is no multi-cointegration between $\hbox {CO}_2$ emissions and GDP. This is in line with our findings in the I(2) model that also included energy use and trade, since we were able to exclude GDP from the long run relationship. Hence, $r=0$ for both models as shown in boldfaced font in Tables 11 and 12, suggesting no long-run relationship between $\hbox {CO}_2$ emissions and GDP for our sample. This suggests that including energy use in our model does not seem to underestimate the effect of GDP.

1.4 B4. The UK and China

In order to do a comparative analysis, I also estimate the I(2) model for the UK and China, using the same variables as for the US from the World Bank data set. The data for the UK are shown in Fig. 6, and the data for China in Fig. 7. We then get a well specified VAR(3) model for the UK and a well specified VAR(2) model for China, where the sample contains annual data 1960–2014 for the UK and 1971–2014 for China. The VAR(2) model for China has moderate ARCH effects, but the rank test should be robust to this as argued in Rahbek et al. (2002), such that this is not a substantial problem in the case of the I(2) analysis here – see Doornik and Juselius (2017).

Fig. 6

Plot of the natural logarithm of the UK data series

Fig. 7

Plot of the natural logarithm of the China data series

Both the data from the UK and China show signs of I(2)-ness, yielding a rank of $(r,s_1,s_2)=(1,1,2)$ for the UK and $(r,s_1,s_2)=(1,0,3)$ for China, according to the rank tests shown in Table 13. As for the US, there is one polynomially cointegrating relationship, $r=1$ both for the UK and China. The rank test finds 2 separate I(2) trends for the UK (as we found for the US) and 3 for China.

Table 13 Rank test for the UK an China (p-values in brackets)

Table 14 Estimated polynomially cointegrating relations – UK and China (t-values in brackets)

The equilibrium error-increasing and error-correcting behavior in the model is different for the UK and China than for the US as we see in Table 14. $\hbox {CO}_2$ emissions is the main dominant trend follower in the UK, while trade and energy consumption have taken the main burden of adjustment in the long run. This indicates that the deviation from the long-run stationary relationship $\beta 'x_t+d'\Delta x_t$ is mainly caused by $\hbox {CO}_2$ emissions, while the return to equilibrium is a consequence of trade and energy use in the UK. Hence, the I(2)-ness of $\hbox {CO}_2$ emissions seems to be caused by an increase in emissions e.g. as a result of increased use of fossil fuels, while the decrease is mainly caused by energy use and trade. This is contrary to the US, where the increase seems to be caused by higher total energy use while the decrease was caused by $\hbox {CO}_2$ emissions and trade. Hence, the emissions reduction in the US is mainly caused by less use of emission intensive energy sources, while in UK it is mainly caused by reduced use of primary energy. This is in line with the findings in Le Quéré et al. (2019) who investigate the drivers behind $\hbox {CO}_2$ emissions reduction in 18 different countries and argues that the main driver behind reduction in $\hbox {CO}_2$ emissions in the US was a shift from coal to renewable and less polluting energy sources, while the main driver in the UK was a decrease in energy use. A decrease in primary energy use may also be caused by increased energy efficiency. I also find that trade plays an important role in emissions reduction both in Great Britain and the US, indicating that outsourcing of production may have caused the decline in emissions.

I also consider the error-increasing and error-decreasing behavior for China. In the long run, energy consumption seems to be the main error-increasing variable, while the main error-decreasing variable is trade. Hence, use of primary energy is also important for the I(2)-ness of $\hbox {CO}_2$ emissions the China, while trade has taken the burden of adjustment back to equilibrium.

The cointegrating relation $\beta 'X_t + d'\Delta X_t$ for the UK can then be written as

$$\begin{aligned} lco2_t + \underset{(0.41)}{1.88}\ lgdp_t-\underset{(0.27)}{1.32} lenergy_t- \underset{(0.009)}{0.033}\ t-\underset{(0.65)}{2.00}\Delta lco2_t-\underset{(1.3)}{4.1}\ \Delta ltrade_t -\underset{(2.73)}{9.37} \end{aligned}$$

or rearranged as

$$\begin{aligned} lco2_t =&\, - \underset{(0.41)}{1.88}\ lgdp_t+\underset{(0.27)}{1.32} lenergy_t+ \underset{(0.009)}{0.033}\ t \nonumber \\&+\underset{(0.65)}{2.00}\Delta lco2_t+\underset{(1.3)}{4.1}\ \Delta ltrade_t +\underset{(2.73)}{9.37} \end{aligned}$$

(12)

Further, we get the following cointegrating relation $\beta 'X_t + d'\Delta X_t$ for China:

$$\begin{aligned} lco2_t&- \underset{(0.36)}{0.90}\ lgdp_t- \underset{(0.26)}{1.1} lenergy_t-\underset{(0.11)}{0.69}\ ltrade+ \underset{(0.029)}{0.087} t\\&-\underset{(1.03)}{2.14}\Delta lco2_t+\underset{(2.19)}{5.76}\Delta lenergy_t - \underset{(1.16)}{6.55}\ \Delta ltrade_t + \underset{(2.05)}{13.3} \end{aligned}$$

or rearranged as

$$\begin{aligned} lco2_t =&\,\underset{(0.36)}{0.90}\ lgdp_t+ \underset{(0.26)}{1.1} lenergy_t+\underset{(0.11)}{0.69}\ ltrade- \underset{(0.029)}{0.087} t \nonumber \\&+\underset{(1.03)}{2.14}\Delta lco2_t-\underset{(2.19)}{5.76}\Delta lenergy_t + \underset{(1.16)}{6.55}\ \Delta ltrade_t - \underset{(2.05)}{13.3} \end{aligned}$$

(13)

The main difference between the UK and to China, is that the level of GDP has a negative effect on $\hbox {CO}_2$ emissions in the UK while it is positive in China. This may reflect that over the long run, while GDP is increasing in both countries, emissions are increasing in China while it is decreasing in the UK. Trade also seems to be associated with more emissions in China over the long run, while no such effect is found in the UK. I also found a negative effect between trade and emissions in the long run for the US. This may indicate signs of the pollution haven hypothesis or carbon leakage between the US and China. The non-linearity of the estimated system is affected by emissions and trade in the UK, while also energy use contributes in China.

Table 15 Estimated common trends and their loadings

For the UK, the first I(2) trend is generated from twice cumulated shocks to GDP and $\hbox {CO}_2$ emissions (the latter to a smaller degree), while the second I(2) trend is generated from twice cumulated shocks to energy consumption less $\hbox {CO}_2$ emissions and trade (to a smaller degree), as shown in Table 15. The first trend mainly loads into trade and $\hbox {CO}_2$ emissions with the same sign, while the second trend mainly loads into energy consumption and to a smaller degree into emissions (same sign) and trade (opposite sign). Twice cumulated shocks to GDP, which may be interpreted as technology or productivity shocks, is partially generating the I(2)-shape of $\hbox {CO}_2$ emissions for the UK, as opposed to what we found for the US. Hence, our findings for the UK are more in line with the EKC theory since it suggests that GDP shocks such as technological changes have contributed to the evolvement of emissions over the sample. This corresponds to the finding that the emissions reduction in the UK is caused by energy use which may be a result of the economic structure of the UK, as opposed to what we found for the US, where switching to less polluting energy sources was important. The former may be more in line with the EKC theory since it can be a result of the changing industrial structure of the country.

The estimated common trends and their loadings for China comprises of three ($s_2=3$) I(2) trends. These are generated by, respectively, $\hbox {CO}_2$ emissions, GDP and energy together with trade. The first trend mainly feeds into $\hbox {CO}_2$ emissions, while the second into GDP and trade (with opposite signs). The third trend mainly feeds into GDP and energy with opposite signs. Hence, shocks to GDP do not seem to contribute to the I(2)-shape of $\hbox {CO}_2$ emissions for China, as we also found for the US. These differences support the view that the EKC may not be appropriate to use for individual countries, as argued e.g. in Copeland and Taylor (2004).