Abstract
The difference between the differential geometric concept of an isometry between two given surfaces as purely mathematical objects and the kinematical concept of an isometric deformation of a single unstretchable material surface as a physical object is discussed. We clarify some misunderstandings that have been promoted in recent works concerning the mechanics of unstretchable material surfaces and we discuss this issue within the context of two specific examples. A revealing distinction between isometries and isometric deformations in two space dimensions is reviewed, and the use of rectifying developable surfaces to characterize the isometric deformation of rectangular material strips is analyzed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
From a kinematical perspective, a material surface is considered to be unstretchable as a physical two dimensional object if the intrinsic length between each pair of its material points cannot be changed during any deformation. Intuitively, the material surface can bend and twist, but its material filaments can never extend or contract. The constraint that models this intense kinematical idealization must affirm that no surfacial strain can be developed in any possible deformation, and it must allow for the existence of suitable constraint reactions in any deformation process. Because the operative internal constraint characterizes a physical restriction for a material surface, it is necessary to express it in terms of the material points of that surface. So, if  represents the reference configuration of an unstretchable two dimensional material surface whose points are denoted as \(\boldsymbol{x}\in {\mathcal {D}}\), and \({\mathcal {D}}\) is deformed (smoothly) to a configuration
represents the reference configuration of an unstretchable two dimensional material surface whose points are denoted as \(\boldsymbol{x}\in {\mathcal {D}}\), and \({\mathcal {D}}\) is deformed (smoothly) to a configuration  whose points \(\boldsymbol{y}\in {\mathcal {S}}\) are given by \(\boldsymbol{y}= \tilde{\boldsymbol{y}}(\boldsymbol{x})\), then the deformation \(\tilde{\boldsymbol{y}}\) must satisfy the constraint
whose points \(\boldsymbol{y}\in {\mathcal {S}}\) are given by \(\boldsymbol{y}= \tilde{\boldsymbol{y}}(\boldsymbol{x})\), then the deformation \(\tilde{\boldsymbol{y}}\) must satisfy the constraint

where \({\mathcal {D}}^{\text{tan}}\) is the tangent space of \({\mathcal {D}}\) at \(\boldsymbol{x}\in {\mathcal {D}}\), and ‘ ’ denotes the surface gradient on \({\mathcal {D}}\). The deformation from \({\mathcal {D}}\) to \({\mathcal {S}}\) that satisfies (1) is said to be an ‘isometric deformation’.
’ denotes the surface gradient on \({\mathcal {D}}\). The deformation from \({\mathcal {D}}\) to \({\mathcal {S}}\) that satisfies (1) is said to be an ‘isometric deformation’.
The literature abounds with papers aimed at studying deformations of unstretchable ribbon-like material surfaces, but which incorrectly identify the concepts of ‘developability’ and ‘isometry’ from differential geometry with the concepts of ‘unstretchability’ and ‘isometric deformation’ from the kinematics of continuous material surfaces. This is understandable because even within the differential geometry community there are differences in the usage and meaning of ‘isometry’ and ‘isometric’. Specifically, do Carmo [1, p. 219] uses the expression that ‘two surfaces are (locally) isometric’ to mean the same thing as Kreyszig’s [2] notion of ‘an isometry between two surfaces’, as embodied in what he refers to as his ‘criterion for isometry’ of Theorem 51.1 and in the language of his Sect. 52. In this case, it is clear that both authors have two a priori given primitive surfaces in mind. On the other hand, do Carmo’s notion of an ‘isometry’ is equivalent to Kreyszig’s notion of an ‘isometric mapping’, both commonly referred to as an ‘isometric deformation’ in the kinematics of material surfaces, and, here, it is clear that both authors are considering the mapping of a single a priori given primitive surface to its deformed image. Unfortunately, it is the common use of the word isometry in the settings of both differential geometry and the kinematics of material surfaces that contributes to the basis for a misunderstanding — along with the seemingly casual acceptance that there is no distinction between its meaning in these two different contexts. The misunderstanding is compounded by the occasional use of the conjoining construction ‘isometric deformation’ in differential geometry texts (see, for example, Pressley [3, p. 132]), where it is mentioned within the subject of ‘isometry’ but is not clearly distinguished as a particular kind of mapping of a given fixed surface configuration, whose geometrical elements (i.e., points, curves, and areas) are once and for all assigned material identity, to another surface configuration which preserves the length of every material curve.
An early work by Jellett [4] is often cited in connection with the mechanics of unstretchable material surfaces. However, the ideas of a reference configuration \({\mathcal {D}}\) of a material surface and a finite isometric deformation of that reference to a surface \({\mathcal {S}}\) are absent from his work. Although Jellett [4] correctly concludes that any deformational variation of a given unstretchable surface must leave the Gaussian curvature pointwise unchanged and he studies the ramifications of fixing the shape of a curve on a given unstretchable surface and subjecting the surface to an unstretchable variation, his work neither recognizes nor clarifies the distinction that we seek to address here.
Subsequent to Jellett’s [4] contribution, studies of the mechanics of unstretchable material surfaces have mostly dealt with situations in which the material reference configuration \({\mathcal {D}}\) is flat and rectangular and have operated under the presumption that the targeted configuration \({\mathcal {S}}\) of any isometric deformation of \({\mathcal {D}}\) can be parametrized as a portion of a rectifying developable surface with its domain of definition being \({\mathcal {D}}\). With reference to the distinction between ‘isometry’ and ‘isometric deformation’ that we employ throughout this work, which follows that of Kreyszig [2], this presumption exaggerates the importance of conditions that characterize an ‘isometry between surfaces’ \({\mathcal {D}}\) and \({\mathcal {S}}\) over those that characterize an ‘isometric deformation’ of \({\mathcal {D}}\) into \({\mathcal {S}}\).
Having recognized that any (smooth) deformation of an unstretchable rectangular material strip must have the shape of a developable surface, Sadowsky [6, 7] formulated a variational problem for determining the equilibrium shape of a rectangular strip of paper twisted and bent without stretching into a Möbius band as a minimizer of its bending energy. However, his formulation involves a dimension reduction argument predicated on the assumption that the deformation of the material strip, written parametrically in terms of two coordinates, to the band produces a configuration that is given in terms of those coordinates by a rectifying developable mapping, the strip being its domain of definition. Because there is no stated restriction that the ends of the material strip must correspond to rulings as a necessary condition to prevent stretching, the corresponding class of deformations differs from the set of all possible (smooth) deformed configurations of an unstretchable rectangular strip. Consequently, there is no reason to believe that a minimizer belonging to that class would constitute a possible deformed configuration of the unstretchable rectangular strip and, worse still, a genuine local or global minimizer over the set of all possible deformed configurations of the strip might not admit a parametrization of the rectifying developable type based on the rectangular reference material strip as its domain of definition and, thus, might be overlooked.
Although Sadowsky [6, 7] restricted attention to strips with infinitesimally small width-to-length ratios, Wunderlich [8, 9] reconsidered the dimensional reduction of Sadowsky for material strips with finite length-to-width ratios but continued the practice of allowing only deformed surfaces which are represented by rectifying developable parametrizations defined on the strip. While it is true that the isometrically deformed configuration of a given material reference strip must be associated with a portion of a rectifying developable surface, the deformed ends of the material strip need not be rulings. In particular, if the reference material strip is rectangular, then a rectifying developable parametrization of the isometrically deformed material configuration based on the rectangular reference strip as its domain of definition is highly restrictive, and cannot, for example, include the isometric deformation onto the surface of a right circular cone, though such a deformation is clearly possible. As a consequence, the Wunderlich dimensionally reduced functional does not provide a correct measure of the bending energy of an open ribbon unless its short edges are rulings, meaning that only certain boundary conditions can be considered on those edges. In particular, any boundary condition which involves bending one of the short edges cannot be accommodated. While Wunderlich’s dimensional reduction of the bending energy is correct for closed, unknotted ribbons without self intersection, independent of their orientation, as Seguin, Chen and Fried [5] have explained, the variational problem associated with minimum bending energy for such a ribbon must be carried out over an appropriate collection of competitors that differs from the class of rectifying developables, that class being the collection of isometric deformations \(\tilde{\boldsymbol{y}}\) defined on the reference region \({\mathcal {D}}\). This can be achieved by introducing suitable Lagrange multipliers to account for the constraint of unstretchability. The main oversight in the Wunderlich [8, 9] approach is that no reference configuration for an undistorted material surface is introduced so as to locate and distinguish the particles of the ribbon that is deformed and thereby properly track the deformation of the ribbon. Wunderlich’s [8, 9] approach to formulating a dimensionally reduced variational problem for determining the shape of a developable half-twist Möbius band is purely spatial.
Related contributions focused on the differential geometric features of Möbius bands as isometric immersions and embeddings in  have been published by Schwarz [10, 11], Randrup and Røgen [12], Chicone and Kalton [13], Sabitov [14], Kurono and Umehara [15], Solvesnov [16], and Naokawa [17]. Although the immersions and embeddings considered in the cited works are flat in the sense that their Gaussian curvatures vanish pointwise and, therefore, may qualify as isometric deformations of a rectangular flat strip, the points of
have been published by Schwarz [10, 11], Randrup and Røgen [12], Chicone and Kalton [13], Sabitov [14], Kurono and Umehara [15], Solvesnov [16], and Naokawa [17]. Although the immersions and embeddings considered in the cited works are flat in the sense that their Gaussian curvatures vanish pointwise and, therefore, may qualify as isometric deformations of a rectangular flat strip, the points of  that define them are not assigned with material identity and therefore they are not correlated with an isometric deformation of any a priori given rectangular flat material reference strip. To identify the shape of an isometric flattening, by severing and deformation, of any such immersion or embedding as the reference configuration of any single unstretchable material surface would therefore be misleading. Indeed, there is no unique way of isometrically flattening a developable Möbius band (or, for that matter, even the seemingly trivial alternative embodied by a right circular cylindrical ring) into a planar region. A developable Möbius band of uniform width can be severed along any of its rulings and isometrically flattened to produce a family of equilateral trapezoids, only one of which is rectangular. Moreover, such a band can be severed along paths that are not rectilinear, leading to a multitude of other flat shapes. A developable Möbius band can thus be thought of as the result of joining two opposing edges of a continuous equivalence class of flat reference shapes. Each such reference shape arises from an isometric flattening of a developable surface and thus, from a differential geometric perspective, forms an isometry with any other viable reference shape. The deformation from any reference shape to another cannot, however, be an isometric deformation. Each reference shape is consequently a reference configuration of a distinct unstretchable material surface. If a Möbius band is to be viewed as a material object constructed by smoothly joining the short edges of an unstretchable material strip with a flat rectangular reference configuration, this degeneracy reveals the compulsory importance of establishing a reference configuration which defines the location of all its material points, and which is used to maintain the identity of those points when the material strip is isometrically deformed.
that define them are not assigned with material identity and therefore they are not correlated with an isometric deformation of any a priori given rectangular flat material reference strip. To identify the shape of an isometric flattening, by severing and deformation, of any such immersion or embedding as the reference configuration of any single unstretchable material surface would therefore be misleading. Indeed, there is no unique way of isometrically flattening a developable Möbius band (or, for that matter, even the seemingly trivial alternative embodied by a right circular cylindrical ring) into a planar region. A developable Möbius band of uniform width can be severed along any of its rulings and isometrically flattened to produce a family of equilateral trapezoids, only one of which is rectangular. Moreover, such a band can be severed along paths that are not rectilinear, leading to a multitude of other flat shapes. A developable Möbius band can thus be thought of as the result of joining two opposing edges of a continuous equivalence class of flat reference shapes. Each such reference shape arises from an isometric flattening of a developable surface and thus, from a differential geometric perspective, forms an isometry with any other viable reference shape. The deformation from any reference shape to another cannot, however, be an isometric deformation. Each reference shape is consequently a reference configuration of a distinct unstretchable material surface. If a Möbius band is to be viewed as a material object constructed by smoothly joining the short edges of an unstretchable material strip with a flat rectangular reference configuration, this degeneracy reveals the compulsory importance of establishing a reference configuration which defines the location of all its material points, and which is used to maintain the identity of those points when the material strip is isometrically deformed.
It is largely the prevailing confusion in the literature that motivated us to prepare the present work concerning the conditions that characterize an isometry between given surfaces interpreted as purely mathematical objects and an isometric deformation of a given material surface interpreted as a single physical object, and, in particular, the consequential omission of a clear description of the deformation of an unstretchable material surface from its reference to any of its possible isometrically deformed configurations.
From a fundamental theorem in differential geometry, it is known that a (smooth) surface is developable if and only if the Gaussian curvature of the surface vanishes pointwise. From another fundamental theorem in differential geometry, it is also known that surfaces that form an isometry relation must have the same Gaussian curvature at corresponding coordinate pairs, along with the corollary that if the Gaussian curvature of different surfaces has the same constant value then the surfaces form an isometry relation. As a consequence, surfaces that are developable form an isometry relation with one another. An understanding of the differential geometric definition of an isometry relation between surfaces is inescapably crucial to making any sense out of the connections drawn in these last three sentences. Moreover, the critical difference between the notion of an isometry relation between surfaces as understood in differential geometry and the notion of isometrically deforming a single surface as understood kinematically will emerge only with such an understanding.
In Sect. 2, we discuss the concept of an isometry relation between surfaces in differential geometry, and its relationship to the possible isometric deformation of a given material surface. In Sect. 3, we consider the example of a half-catenoidal reference configuration \({\mathcal {D}}\). In addition to an isometric deformation \(\hat{\boldsymbol{y}}\) of \({\mathcal {D}}\) to a configuration \({\mathcal {S}}\) of right half-helicoidal form, we present a non-isometric deformation \(\bar{\boldsymbol{y}}\) of \({\mathcal {D}}\) to a configuration \(\bar{{\mathcal {S}}}\) with the same right-half helicoidal form as \({\mathcal {S}}\). The purpose of this example is to emphasize that the deformation may or may not be an isometric deformation even though the two surfaces form a mutual isometry relation. A figure shows that although \(\bar{{\mathcal {S}}}\) occupies the same right-half helicoidal surface as \({\mathcal {S}}\), the deformation \(\bar{\boldsymbol{y}}\) subjects every material curve on \({\mathcal {D}}\) to stretching and/or contraction. In Sect. 4, we discuss the distinction between the concepts of an ‘isometry relation between surfaces’ and an ‘isometric deformation’ of a given surface. Illustrative examples are provided in Sect. 5. In the example of Sect. 5.1, we briefly review a well-known observation concerning an isometry relation and an isometric deformation. The message of Sect. 5.2 is more substantial. Here, we consider an example from the literature whose goal is to determine the isometrically deformed shape of a Möbius band by minimizing the Wunderlich [8, 9] functional over the class of rectifying developable surfaces. Our purpose is to discuss certain major deficiencies in this approach — deficiencies that arise because no fundamental attention is given to the unstretchable material constraint of the strip and to the definition of a flat, rectangular or otherwise, fixed material reference configuration. Since the minimizing Möbius band is assumed a priori to have a rectifying developable form represented in terms of two parameters not connected to any particular fixed reference state, a definitive description of how the parameters relate to the material points of the strip and to its deformation from a fixed reference configuration becomes problematic. This brings into question how the two parameters are to serve as a coordinate cover for locating the material points of a fixed material reference strip, a question that was not sufficiently addressed in the published accounts of this example. We emphasize that minimizing the Wunderlich [8, 9] functional over the set of rectifying developable Möbius bands of fixed length and width in an effort to determine the configuration that results from the isometric deformation of a fixed, rectangular or otherwise, material strip is inadequately formulated because the set of admissible configurations does not take into account the material constraint of unstretchability. A discussion of why this variational problem and its proposed minimization strategy is incompatible with the constraint of unstretchability is given. It is noted that if the constraint is compromised, as has been the case, the variational problem leads to a purely geometrical problem in the differential geometry of rectifying developable Möbius bands that stands apart from the mechanical problem of interest. Finally, we briefly explain why any study based in mechanics of the isometric deformation of a given rectangular reference strip into a rectifying developable surface has limited physical application.
2 Isometry of Surfaces
In differential geometry a (smooth) two dimensional surface, a portion of which we denote as \({\mathcal {A}}\), is considered to be a compact two dimensional Riemannian manifold endowed with a Riemannian metric. As is common, the elements \(x\) of \({\mathcal {A}}\) may be parametrized by coordinates \((u^{1}, u^{2})\), in which case each element \(x\in {\mathcal {A}}\) is equivalent to a pair  , and it is well-known that the surface to which \({\mathcal {A}}\) belongs may be embedded in three dimensional Euclidean point space
, and it is well-known that the surface to which \({\mathcal {A}}\) belongs may be embedded in three dimensional Euclidean point space  . In this case, \({\mathcal {A}}\) may be represented by points
. In this case, \({\mathcal {A}}\) may be represented by points  , and its corresponding Riemannian metric coefficients are given by
, and its corresponding Riemannian metric coefficients are given by
Similarly, let us suppose that the elements \(y\) of a second surface, a portion of which we denote as ℬ, are parameterized by the coordinate pairs  , and that the embedding of the surface to which ℬ belongs into
, and that the embedding of the surface to which ℬ belongs into  has the representation
has the representation  . Corresponding to this embedding of ℬ, the Riemannian metric coefficients are given by
. Corresponding to this embedding of ℬ, the Riemannian metric coefficients are given by
A clear differential geometric definition of isometry between two given smooth surfaces is given by Kreyszig [2, p. 161]. In the present context, a given surface \({\mathcal {A}}\) whose elements \(x\) are parametrized by coordinates  and another given surface ℬ whose elements \(y\) are parametrized by coordinates
and another given surface ℬ whose elements \(y\) are parametrized by coordinates  are said to form an isometry relation if there exists a single coordinate parametrization
are said to form an isometry relation if there exists a single coordinate parametrization  for the elements \(x\in {\mathcal {A}}\) and \(y\in {\mathcal {B}}\) such that \(g_{ij}=h_{ij}\). Thus, if all elements \(x\in {\mathcal {A}}\) and \(y\in {\mathcal {B}}\) of two surfaces are parametrized by the same coordinate pairs and the metric coefficients of these parametrizations are equal then those surfaces are related by an isometry. While this provision guarantees that distances in the two surfaces may be measured by the same Riemannian metric coefficients, it does not suffice to ensure that a material surface, defined by the location of its material particles
for the elements \(x\in {\mathcal {A}}\) and \(y\in {\mathcal {B}}\) such that \(g_{ij}=h_{ij}\). Thus, if all elements \(x\in {\mathcal {A}}\) and \(y\in {\mathcal {B}}\) of two surfaces are parametrized by the same coordinate pairs and the metric coefficients of these parametrizations are equal then those surfaces are related by an isometry. While this provision guarantees that distances in the two surfaces may be measured by the same Riemannian metric coefficients, it does not suffice to ensure that a material surface, defined by the location of its material particles  in a given fixed reference configuration \({\mathcal {D}}\), and its deformed image \({\mathcal {S}}\), defined by the mapping
in a given fixed reference configuration \({\mathcal {D}}\), and its deformed image \({\mathcal {S}}\), defined by the mapping  , both of which are exact copies of, respectively, two surfaces \({\mathcal {A}}\) and ℬ that form an isometry relation, must be connected through an isometric deformation. It is true, though, that because of the isometry relation, there is an isometric deformation of \({\mathcal {D}}\) onto ℬ, as the following proposition shows.
, both of which are exact copies of, respectively, two surfaces \({\mathcal {A}}\) and ℬ that form an isometry relation, must be connected through an isometric deformation. It is true, though, that because of the isometry relation, there is an isometric deformation of \({\mathcal {D}}\) onto ℬ, as the following proposition shows.
Proposition 1
Let \({\mathcal {A}}\) and ℬ be surfaces whose elements \(x\in {\mathcal {A}}\) and \(y\in {\mathcal {B}}\) share a coordinate parametrization \((z^{1},z^{2})\) over some subset \(\varPi \) of  , so that they have representations in terms of points
, so that they have representations in terms of points  and
and  of the respective forms
of the respective forms
and
Suppose, also, that the parametrizations \(\hat{\boldsymbol{x}}\) and \(\bar{\boldsymbol{y}}\) satisfy
on \(\varPi \). Let  be the reference configuration of a material surface that is an exact copy of \({\mathcal {A}}\), so that \({\mathcal {D}}={\mathcal {A}}\) and that \(\boldsymbol{x}\in {\mathcal {D}}\) denotes the location of a material point. Then, there exists an isometric deformation
be the reference configuration of a material surface that is an exact copy of \({\mathcal {A}}\), so that \({\mathcal {D}}={\mathcal {A}}\) and that \(\boldsymbol{x}\in {\mathcal {D}}\) denotes the location of a material point. Then, there exists an isometric deformation  , such that \({\mathcal {S}}:= \tilde{\boldsymbol{y}}({\mathcal {D}})\) is an exact copy of ℬ.
, such that \({\mathcal {S}}:= \tilde{\boldsymbol{y}}({\mathcal {D}})\) is an exact copy of ℬ.
Proof
By the requirements for a parametrization of a surface, there exists a one-to-one correspondence between the material points \(\boldsymbol{x}\in {\mathcal {D}}\) and the parameter pairs \((z^{1},z^{2})\in \varPi \). This implies that there exist  and
and  , such that
, such that
Applying the surface gradient to both sides of (7) then yields

where  is the surface gradient of \(\tilde{z}^{i}\) and \(\boldsymbol{I}\) is the identity tensor in the tangent space \({\mathcal {D}}^{\text{tan}}\) of \({\mathcal {D}}\). Thus, it follows that
is the surface gradient of \(\tilde{z}^{i}\) and \(\boldsymbol{I}\) is the identity tensor in the tangent space \({\mathcal {D}}^{\text{tan}}\) of \({\mathcal {D}}\). Thus, it follows that

Now, define a deformation  of the material surface \({\mathcal {D}}\) by
of the material surface \({\mathcal {D}}\) by
Under \(\tilde{\boldsymbol{y}}\), \({\mathcal {D}}\) is deformed into a configuration \({\mathcal {S}}:=\tilde{\boldsymbol{y}}({\mathcal {D}})\) that is an exact copy of ℬ, and an arbitrary material filament \(\text{d}\boldsymbol{x}\) deforms to \(\text{d}\boldsymbol{y}\), which, in accordance to (9), is given by

It then follows from (6), (8), and (10) that

which shows that \(\tilde{\boldsymbol{y}}\) is an isometric deformation. □
To illustrate the meaning of the differential geometric interpretation of an isometry relation between surfaces and how such a relation differs from the isometric deformation of a given material surface, let \(\{\boldsymbol{\imath }_{1},\boldsymbol{\imath }_{2}, \boldsymbol{\imath }_{3}\}\) denote a positively oriented basis for  , and consider two surfaces, well-studied in differential geometry, given as follows:
, and consider two surfaces, well-studied in differential geometry, given as follows:
-
(i)
\({\mathcal {A}}\) is the half-catenoid whose representation in
 is given by $$ \left . \textstyle\begin{array}{c} \displaystyle \boldsymbol{x}= \hat{\boldsymbol{x}}(r,\theta ) := r \cos \theta \,\boldsymbol{\imath }_{1} + r\sin \theta \, \boldsymbol{\imath }_{2} + a\operatorname{arccosh}\Big(\frac{r}{a}\Big) \boldsymbol{\imath }_{3}, \cr r\in [a, \sqrt{2}a],\quad \theta \in [0, 2\pi ), \end{array}\displaystyle \right \} $$(11)
is given by $$ \left . \textstyle\begin{array}{c} \displaystyle \boldsymbol{x}= \hat{\boldsymbol{x}}(r,\theta ) := r \cos \theta \,\boldsymbol{\imath }_{1} + r\sin \theta \, \boldsymbol{\imath }_{2} + a\operatorname{arccosh}\Big(\frac{r}{a}\Big) \boldsymbol{\imath }_{3}, \cr r\in [a, \sqrt{2}a],\quad \theta \in [0, 2\pi ), \end{array}\displaystyle \right \} $$(11)wherein we have taken the coordinate parameters \((u^{1}, u^{2})\) noted in (2) to be the standard polar coordinates \((r,\theta )\) with polar axis \(\boldsymbol{\imath }_{3}\) and \(a>0\) is a fixed measure of length. In this case, the Riemannian metric coefficients of \({\mathcal {A}}\) are given by
$$ g_{11} = \frac{r^{2}}{r^{2} - a^{2}}, \qquad g_{12} = 0, \qquad g_{22} =r^{2}. $$(12) -
(ii)
ℬ is the right half-helicoid whose representation in
 is given by $$ \left . \textstyle\begin{array}{c} \boldsymbol{y}= \bar{\boldsymbol{y}}(v^{1}, v^{2}) := v^{1}\cos v^{2} \boldsymbol{\imath }_{1} + v^{1}\sin v^{2}\boldsymbol{\imath }_{2} + av^{2} \boldsymbol{\imath }_{3}, \cr v^{1}\in [0,a],\quad v^{2}\in [0, 2\pi ), \end{array}\displaystyle \right \} $$(13)
is given by $$ \left . \textstyle\begin{array}{c} \boldsymbol{y}= \bar{\boldsymbol{y}}(v^{1}, v^{2}) := v^{1}\cos v^{2} \boldsymbol{\imath }_{1} + v^{1}\sin v^{2}\boldsymbol{\imath }_{2} + av^{2} \boldsymbol{\imath }_{3}, \cr v^{1}\in [0,a],\quad v^{2}\in [0, 2\pi ), \end{array}\displaystyle \right \} $$(13)and whose Riemannian metric coefficients, according to (3), are
$$ h_{11} = 1, \qquad h_{12} = 0, \qquad h_{22} = (v^{1})^{2} + a^{2}. $$(14)
The coordinate parametrization \((v^{1}, v^{2})\) in the representation (13) of surface ℬ is not the same as the coordinate parametrization \((u^{1}, u^{2}) := (r,\theta )\) in the representation (11) of surface \({\mathcal {A}}\). Thus, to determine if the two surfaces \({\mathcal {A}}\) and ℬ form a mutual isometry relation, we must be able to reparametrize and cover the right half-helicoid ℬ in terms of \((r,\theta )\), the same coordinates involved in the representation (11) of the surface \({\mathcal {A}}\), such that the Riemannian metric coefficients of \({\mathcal {A}}\) are equal to those of ℬ. This is accomplished by the smooth one-to-one change of variables
with the consequence, from (13), that the reparametrized representation of ℬ in terms of \((r,\theta )\) is given by
because it readily follows, using (3), that under this reparametrization the Riemannian metric coefficients of ℬ are given by
exactly as in (12). With the reparametrization (15) of ℬ, \(g_{ij}=h_{ij}\) and the surfaces \({\mathcal {A}}\) and ℬ, from the differential geometric point of view, form a mutual isometry relation. Consequently, under this reparametrization the Gaussian curvatures of the two surfaces are equal at corresponding elements. It is well known, however, that the right half-helicoidal surface ℬ is ruled but not developable — as can be confirmed by computing the Gaussian curvature of ℬ from either (13) and the metric coefficients (14) or (16) alone; in either case, the Gaussian curvature of ℬ can be expressed in terms as \(-a^{2}/r^{4}\), which indicates that the tangent plane to ℬ along a ruling is not fixed (as must be so for a developable surface) but, instead, varies with \(r\).
3 Isometry Versus Isometric Deformation
An isometry in the differential geometry of surfaces is a special relation that exists between two given surface forms. In Sect. 2 we concentrated on the isometry relation between surfaces \({\mathcal {A}}\) and ℬ of (11) and (13), respectively. In the kinematics of material surfaces, the reference configuration  of a material surface is given with its material points denoted as \(\boldsymbol{x}\in {\mathcal {D}}\), and the surface is deformed into another configuration
of a material surface is given with its material points denoted as \(\boldsymbol{x}\in {\mathcal {D}}\), and the surface is deformed into another configuration  whose points are denoted as \(\boldsymbol{y}\in {\mathcal {S}}\) such that
whose points are denoted as \(\boldsymbol{y}\in {\mathcal {S}}\) such that  . Only the reference configuration \({\mathcal {D}}\) of a single material surface is given, and the deformation of the material points of that given surface is the object of interest. For example, let us suppose that we identify the elements \(x\) of the half-catenoidal surface \({\mathcal {A}}\), as parametrized by \((r,\theta )\) in (11), with the material points \(\boldsymbol{x}\in {\mathcal {D}}\); that is, suppose that
. Only the reference configuration \({\mathcal {D}}\) of a single material surface is given, and the deformation of the material points of that given surface is the object of interest. For example, let us suppose that we identify the elements \(x\) of the half-catenoidal surface \({\mathcal {A}}\), as parametrized by \((r,\theta )\) in (11), with the material points \(\boldsymbol{x}\in {\mathcal {D}}\); that is, suppose that
In doing this, we have identified the reference configuration \({\mathcal {D}}\) of a material surface with the image of the surface \({\mathcal {A}}\) as it is embedded in  , and the reference configuration \({\mathcal {D}}\) of this material surface has the form of the half-catenoidal surface \({\mathcal {A}}\) of (11). This is illustrated in Fig. 1(a).
, and the reference configuration \({\mathcal {D}}\) of this material surface has the form of the half-catenoidal surface \({\mathcal {A}}\) of (11). This is illustrated in Fig. 1(a).
(a): The surface \({\mathcal {A}}\), of (11), occupied by the half-catenoidal reference configuration \({\mathcal {D}}\) determined by (18). The material curve \({\mathcal {C}}\) on \({\mathcal {D}}\), defined in (25), is shown in black and the material curve on \({\mathcal {D}}\) corresponding to setting \(\theta =\pi \) in (18) is shown in white. (b): The right half-helicoidal surface ℬ, of (13), occupied by the deformed configuration \({\mathcal {S}}\) determined by the isometric deformation \(\hat{\boldsymbol{y}}\) defined in (19). The deformed images of \({\mathcal {C}}\) and the material curve corresponding to setting \(\theta =\pi \) in (18) are shown in black and white, respectively. (c-d): The right half-helicoidal surface ℬ, of (13), occupied by the deformed configuration \(\bar{{\mathcal {S}}}\) of \({\mathcal {D}}\) determined by the non-isometric deformation \(\bar{\boldsymbol{y}}\) defined in (20). The color bar ranges between the minimum and maximum values, \(E_{rr}(a)\approx -0.50\) and \(E_{rr}(\sqrt{2}a)\approx 0.96\), of the radial strain \(E_{rr}\) on \([a,\sqrt{2}a]\). Since \(E_{\theta \theta}\) satisfies \(-0.07\lesssim E_{\theta \theta}\le 0\) on \([a,\sqrt{2}a]\), the variations of color in (d) are not as obvious as those in (c). The deformed images of \({\mathcal {C}}\) and the material curve corresponding to setting \(\theta =\pi \) in (18) are again shown in black and white, respectively. Consistent with the observation that \(\bar{\boldsymbol{y}}\) subjects \({\mathcal {C}}\) to a uniform azimuthal contraction, its position in (c–d) is markedly shifted toward the axis of ℬ of (13) relative to its position as shown in (b) for the configuration \({\mathcal {S}}\) determined by the isometric deformation \(\hat{\boldsymbol{y}}\)
Now, suppose that the material surface is deformed from its half-catenoidal reference configuration \({\mathcal {D}}\), given in (18), to the right half-helicoidal deformed configuration  , via the deformation
, via the deformation  , where in parametric form
, where in parametric form
We emphasize that (19) represents the deformed configuration \({\mathcal {S}}\) of the material surface \({\mathcal {D}}\), and that the parameters \((r,\theta )\) in (19) are not associated with the reparametrization of any given surface, but, rather, define the location of the material points  of the reference configuration \({\mathcal {D}}\) through (18), and the location
of the reference configuration \({\mathcal {D}}\) through (18), and the location  of the corresponding material points of the deformed surface \({\mathcal {S}}\) through (19). However, by comparison with (16), we see that the form of \({\mathcal {S}}\) is an exact copy of the right half-helicoidal surface ℬ of (13). This is illustrated in Fig. 1(b). Thus, (18) and (19) represent the deformation of a half-catenoidal surface into a right half-helicoidal surface. Moreover, since
of the corresponding material points of the deformed surface \({\mathcal {S}}\) through (19). However, by comparison with (16), we see that the form of \({\mathcal {S}}\) is an exact copy of the right half-helicoidal surface ℬ of (13). This is illustrated in Fig. 1(b). Thus, (18) and (19) represent the deformation of a half-catenoidal surface into a right half-helicoidal surface. Moreover, since
for (18) and (19), \(\hat{\boldsymbol{y}}\) is an isometric deformation of a material surface with reference configuration \({\mathcal {D}}\) (an exact copy of the form of \({\mathcal {A}}\)) into the configuration \({\mathcal {S}}\) (an exact copy of the form of ℬ), and we confirm the notion expressed in Proposition 2 that for two surfaces that satisfy an isometry relation there is an isometric deformation of one of the surfaces, considered as the reference configuration of a material surface, onto the form of the other.
Now, suppose that the half-catenoidal reference configuration \({\mathcal {D}}\), given in (18), is subject to the deformation  , where in parametric form
, where in parametric form
By setting \(v^{1}=(r-a)/(\sqrt{2}-1)\) and \(v^{2}=\theta \), we see that, like \({\mathcal {S}}\), the form of the surface \(\bar{{\mathcal {S}}}\) defined in (21) represents an exact copy of the right half-helicoidal surface ℬ as defined in (13). However, while the two surfaces \({\mathcal {A}}\) of (11) and ℬ of (13) form an isometry relation from the differential geometry point of view, the deformation of \({\mathcal {D}}\) (an exact copy of the form of \({\mathcal {A}}\)) to \(\bar{{\mathcal {S}}}\) (an exact copy of the form of ℬ) is not an isometric deformation.
The parameters \((r,\theta )\) in (18) and (21) implicitly define the deformation \(\boldsymbol{x}\mapsto \boldsymbol{y}\) of the half-catenoidal configuration \({\mathcal {D}}\) to the right half-helicoidal configuration \(\bar{{\mathcal {S}}}\). However, because
for (18) and (21), we see that (1) does not hold and, thus, that \(\bar{\boldsymbol{y}}\) is not an isometric deformation. Even though surfaces \({\mathcal {A}}\) of (11) and ℬ of (13) form an isometry relation, it is therefore evident that there are many non-isometric deformations of the half-catenoidal reference configuration \({\mathcal {D}}\) to an exact copy of the form of the right half-helicoidal surface ℬ, all differing by surfacial stretching and, thus, having identical distributions of Gaussian curvature.
The distinction between the deformed configurations (19) and (21), whose surfaces \({\mathcal {S}}\) and \(\bar{{\mathcal {S}}}\) form an isometry relation, can be illustrated with recourse to the Green–Saint Venant strain tensor \(\boldsymbol{E}\) for each deformation, \(\hat{\boldsymbol{y}}\) or \(\bar{\boldsymbol{y}}\), of the reference configuration \({\mathcal {D}}\) defined through (18). For the isometric deformation from (18) to (19), \(\boldsymbol{E}\equiv \mathbf{0}\). In contrast, for the deformation from (18) to (21), \(\boldsymbol{E}\) is given by
where the radial and azimuthal \(E_{rr}\) and \(E_{\theta \theta}\) components of strain are defined by
Let \({\mathcal {C}}\) be the circular material curve defined by

By (24): \(E_{rr}\) increases monotonically on \([a,\sqrt{2}a]\) and satisfies \(E_{rr}(r)=0\) at \(r=a/\sqrt{2(\sqrt{2}-1)}\); \(E_{\theta \theta}\) is negative on \((a,\sqrt{2}a)\) and satisfies \(E_{\theta \theta}(r)=0\) on \({\mathcal {C}}\) at \(r=a\) and \(r=\sqrt{2}a\). Since \(E_{rr}=0\) and \(E_{\theta \theta}\approx -0.06\) on \({\mathcal {C}}\), then \({\mathcal {C}}\) is subjected to a pure azimuthal contraction. Hence, even though the deformation \(\bar{\boldsymbol{y}}\) defined in (21) takes the reference configuration \({\mathcal {D}}\) to the right half-helicoidal configuration \(\bar{{\mathcal {S}}}\), it subjects every material curve on \({\mathcal {D}}\) to extension and/or contraction. More specifically, the deformation \(\bar{\boldsymbol{y}}\) subjects any open, connected part of the reference configuration \({\mathcal {D}}\) that is strictly below \({\mathcal {C}}\) to radial and azimuthal contraction and any open, connected part of \({\mathcal {D}}\) that is strictly above \({\mathcal {C}}\) to radial extension and azimuthal contraction. These effects are illustrated in Fig. 1, where the surface \({\mathcal {A}}\) of (11) corresponding to the half-catenoidal reference configuration \({\mathcal {D}}\) in Fig. 1 is accompanied by three images, in Figs. 1(b–d), of the right half-helicoidal surface ℬ of (13). Figure 1(b) shows the configuration \({\mathcal {S}}\) obtained from the isometric deformation from (18) to (19), for which \(\boldsymbol{E}\equiv \mathbf{0}\). Figures 1(c–d) show the configuration \(\bar{{\mathcal {S}}}\) obtained from the deformation from (18) to (21), for which \(\boldsymbol{E} \ne\mathbf{0}\). Here, the color coding for \(E_{rr}\) in Fig. 1(c) and for \(E_{r\theta}\) in Fig. 1d) derives from (24).
4 Discussion
Within the subject of differential geometry, it is well known that surfaces that form a mutual isometry relation have the same Gaussian curvature at corresponding points, that corresponding curves on such surfaces have the same geodesic curvature at corresponding points, and that a surface that forms a mutual isometry with a subset of a plane is developable. From a physical perspective, within the subject of kinematics, a reference configuration \({\mathcal {D}}\) of a material surface may be considered to be an identification between the surface elements \(x\in {\mathcal {A}}\) and the points  . In addition, a (smooth) deformation of \({\mathcal {D}}\) to the deformed configuration \({\mathcal {S}}\) is a mapping
. In addition, a (smooth) deformation of \({\mathcal {D}}\) to the deformed configuration \({\mathcal {S}}\) is a mapping  . Such a mapping is an isometric deformation if the length of any curve in \({\mathcal {D}}\) and the length of the corresponding curve in \({\mathcal {S}}\) under the deformation are equal; clearly this may be expressed as in (1). What makes things somewhat confusing in the case of two dimensions is that because of the properties of embeddings, the Riemannian manifold which is used to define \({\mathcal {A}}\) can be embedded in
. Such a mapping is an isometric deformation if the length of any curve in \({\mathcal {D}}\) and the length of the corresponding curve in \({\mathcal {S}}\) under the deformation are equal; clearly this may be expressed as in (1). What makes things somewhat confusing in the case of two dimensions is that because of the properties of embeddings, the Riemannian manifold which is used to define \({\mathcal {A}}\) can be embedded in  and, also, the configurations of a two-dimensional material surface which undergoes deformation are embedded in
and, also, the configurations of a two-dimensional material surface which undergoes deformation are embedded in  . Thus, unless special care is taken to distinguish the differential geometric notion of an isometry between two surfaces considered as purely mathematical objects from the kinematical notion of an isometric deformation of a single material surface considered as a physical object, the distinction may easily be missed. In particular, while it is necessary that under an isometric (smooth) deformation of
. Thus, unless special care is taken to distinguish the differential geometric notion of an isometry between two surfaces considered as purely mathematical objects from the kinematical notion of an isometric deformation of a single material surface considered as a physical object, the distinction may easily be missed. In particular, while it is necessary that under an isometric (smooth) deformation of  to
to  the Gaussian curvature at \(\boldsymbol{x}\in {\mathcal {D}}\) and the Gaussian curvature induced by the deformation at \(\boldsymbol{y}\in {\mathcal {S}}\) be equal, the equality of Gaussian curvatures between two given surfaces does not guarantee that the deformation of one onto the other is isometric — the possibility that the two surfaces are related only by a mutual isometry cannot generally be dismissed.
the Gaussian curvature at \(\boldsymbol{x}\in {\mathcal {D}}\) and the Gaussian curvature induced by the deformation at \(\boldsymbol{y}\in {\mathcal {S}}\) be equal, the equality of Gaussian curvatures between two given surfaces does not guarantee that the deformation of one onto the other is isometric — the possibility that the two surfaces are related only by a mutual isometry cannot generally be dismissed.
In the above descriptions, within the overall context of the kinematics of material surfaces, it is perhaps useful to distinguish the notion of a ‘body’ as a (smooth) two-dimensional Riemannian manifold, namely a surface with Riemannian metric structure whose elements happen to be material points, from the notion of ‘configuration’ which is used to characterize the placement image of a body, namely a positioning of a material surface in  so as to describe its state of deformation. In the present setting, we have used the noun ‘isometry’, or ‘isometry relation’, in the differential geometric sense, which is where the notion of a ‘body’ resides, and we have used the conjunction ‘isometric deformation’ of the adjective ‘isometric’ and the noun ‘deformation’ in the kinematical sense, which is where the notion of ‘configuration’ resides.
so as to describe its state of deformation. In the present setting, we have used the noun ‘isometry’, or ‘isometry relation’, in the differential geometric sense, which is where the notion of a ‘body’ resides, and we have used the conjunction ‘isometric deformation’ of the adjective ‘isometric’ and the noun ‘deformation’ in the kinematical sense, which is where the notion of ‘configuration’ resides.
5 Examples and Discussion
5.1 Deformation of a Surface and an Isometry Relation
According to the elements of differential geometry as presented in do Carmo [1] and Kreyszig [2], any two planar surfaces in  form a mutual isometry relation. While these two surfaces, considered as material surfaces, may be deformed into one another with an appropriate in-plane shear and area dilatation field, if the surfaces are unstretchable the deformation must be isometric and, in
form a mutual isometry relation. While these two surfaces, considered as material surfaces, may be deformed into one another with an appropriate in-plane shear and area dilatation field, if the surfaces are unstretchable the deformation must be isometric and, in  , the surfaces must be exact copies of one another.Footnote 1 More generally, any deformation of a material surface embedded in
, the surfaces must be exact copies of one another.Footnote 1 More generally, any deformation of a material surface embedded in  with a curved reference shape into the same shape in a way that alters the intrinsic distances between its interior material points forms an isometry relation with its deformed image from a differential geometric perspective but is not an isometric deformation from the perspective of the kinematics of material surfaces. For example, \({\mathcal {S}}\) and \(\bar{{\mathcal {S}}}\) defined respectively by (19) and (21) describe the same right half-helicoidal surface ℬ but involve different arrangements of the material points of the referential half-catenoid \({\mathcal {D}}\) of (18), as is plainly evident from Fig. 1. As another example, a material surface in a configuration that coincides with some portion of the surface of a right circular cone can be internally stretched by a non-isometric deformation into another configuration while coinciding with the same portion of the conical surface, in which case the two configurations form an isometry relation but one is not the isometric deformation of the other.
with a curved reference shape into the same shape in a way that alters the intrinsic distances between its interior material points forms an isometry relation with its deformed image from a differential geometric perspective but is not an isometric deformation from the perspective of the kinematics of material surfaces. For example, \({\mathcal {S}}\) and \(\bar{{\mathcal {S}}}\) defined respectively by (19) and (21) describe the same right half-helicoidal surface ℬ but involve different arrangements of the material points of the referential half-catenoid \({\mathcal {D}}\) of (18), as is plainly evident from Fig. 1. As another example, a material surface in a configuration that coincides with some portion of the surface of a right circular cone can be internally stretched by a non-isometric deformation into another configuration while coinciding with the same portion of the conical surface, in which case the two configurations form an isometry relation but one is not the isometric deformation of the other.
5.2 Rectifying Developables and Isometric Deformations of Flat Material Strips
There are examples in the mechanics literature where the distinction between the isometric deformation of a reference material surface into its deformed image and a mutual isometry relation between the two surfaces are not identified and properly distinguished. To illustrate the importance of this circumstance, we consider the classical variational problem posed, but not solved, by Sadowsky [6] and Wunderlich [8, 9] of determining the shape of the deformed surface  of a \(180^{\circ}\) twist Möbius band as formed by the isometric deformation of a given flat, undistorted and unstretchable rectangular material strip of length \(L\) and width \(2w\). A strategy for solving this classical problem that has been advanced in the literature is based on minimizing the Wunderlich [8, 9] functional over the set of smooth rectifying developable Möbius bands \({\mathcal {S}}\), each of which is parametrized by
of a \(180^{\circ}\) twist Möbius band as formed by the isometric deformation of a given flat, undistorted and unstretchable rectangular material strip of length \(L\) and width \(2w\). A strategy for solving this classical problem that has been advanced in the literature is based on minimizing the Wunderlich [8, 9] functional over the set of smooth rectifying developable Möbius bands \({\mathcal {S}}\), each of which is parametrized by
for fixed \(L\) and \(w\). In (26), \(\boldsymbol{r}\) is the midline directrix, and \(\boldsymbol{t}\), \(\boldsymbol{b}\), \(\kappa \), and \(\tau \) are the corresponding unit tangent, unit binormal, curvature, and torsion. Of course, \(\boldsymbol{t}:=\boldsymbol{r}^{\prime}\), \(\boldsymbol{b}:=\boldsymbol{t}\times \boldsymbol{p}\), \(\kappa :=|\boldsymbol{t}^{\prime}|\), and \(\tau :=\boldsymbol{t}\cdot (\boldsymbol{p}\times \boldsymbol{p}^{ \prime})\), where the normal to the directrix is given by \(\boldsymbol{p}:=\boldsymbol{t}^{\prime}/\kappa \), and the Frenet–Serret equations hold: \(\boldsymbol{t}^{\prime }= \kappa \boldsymbol{p}\), \(\boldsymbol{p}^{ \prime }= -\kappa \boldsymbol{t}+ \tau \boldsymbol{b}\), \(\boldsymbol{b}^{ \prime }= - \tau \boldsymbol{p}\). The elements \(y\in {\mathcal {S}}\) are denoted by the parameter pair \(y :=(s, t)\), and  are points which define the form of \({\mathcal {S}}\) as being a portion of a rectifying developable surface. The parametrized lines \(s=\text{constant}\) are the generators \(\boldsymbol{g}\) of \({\mathcal {S}}\) which intersect the midline directrix \(\boldsymbol{r}\) at each \(s\in [0,L]\) and which are given by \(\boldsymbol{g}(s,t):=t[\boldsymbol{b}(s)+\eta (s)\boldsymbol{t}(s)]\) for \(t\in [-w,w]\); they form an angle \(\beta =\arctan (1/\eta )\) with the positive tangent direction. The shape of the surface \({\mathcal {S}}\) is thus completely determined by its midline directrix \(\boldsymbol{r}\), which is smooth and satisfies \(\boldsymbol{r}(0)=\boldsymbol{r}(L)\) with smooth connection at its closure point. To assure closure with a \(180^{\circ}\) twist, \(\boldsymbol{t}(L)=\boldsymbol{t}(0)\) and \(\boldsymbol{b}(L)=-\boldsymbol{b}(0)\). For \({\mathcal {S}}\) to be smooth, it is thus necessary that \(\boldsymbol{g}(L,t)=-\boldsymbol{g}(0,t)\) for \(t\in [-w,w]\) and, consequently, that \(\eta (L)=-\eta (0)\). According to (3), the Riemannian metric coefficients associated with \({\mathcal {S}}\) are given by
are points which define the form of \({\mathcal {S}}\) as being a portion of a rectifying developable surface. The parametrized lines \(s=\text{constant}\) are the generators \(\boldsymbol{g}\) of \({\mathcal {S}}\) which intersect the midline directrix \(\boldsymbol{r}\) at each \(s\in [0,L]\) and which are given by \(\boldsymbol{g}(s,t):=t[\boldsymbol{b}(s)+\eta (s)\boldsymbol{t}(s)]\) for \(t\in [-w,w]\); they form an angle \(\beta =\arctan (1/\eta )\) with the positive tangent direction. The shape of the surface \({\mathcal {S}}\) is thus completely determined by its midline directrix \(\boldsymbol{r}\), which is smooth and satisfies \(\boldsymbol{r}(0)=\boldsymbol{r}(L)\) with smooth connection at its closure point. To assure closure with a \(180^{\circ}\) twist, \(\boldsymbol{t}(L)=\boldsymbol{t}(0)\) and \(\boldsymbol{b}(L)=-\boldsymbol{b}(0)\). For \({\mathcal {S}}\) to be smooth, it is thus necessary that \(\boldsymbol{g}(L,t)=-\boldsymbol{g}(0,t)\) for \(t\in [-w,w]\) and, consequently, that \(\eta (L)=-\eta (0)\). According to (3), the Riemannian metric coefficients associated with \({\mathcal {S}}\) are given by
Unfortunately, the problem as stated with its proposed minimization strategy is a purely geometrical one that stands apart from the mechanical problem of interest. It provides a way of finding an optimal mutual isometry relation between a rectangular region of length \(L\) and width \(2w\) and a \(180^{\circ}\) twist Möbius band, among all rectifying developable Möbius bands of the form (26), but not an optimal isometric deformation from a given unstretchable rectangular material strip to a \(180^{\circ}\) twist Möbius band. Justification for this observation will be presented below.
A noticably missing element in the purely geometrical problem formulated above is the essential introduction of a fixed, undistorted reference configuration ℛ for the unstretchable rectangular material strip relative to which all deformations of the strip into a \(180^{\circ}\) twist Möbius band of the rectifying developable form (26) are to be measured. To rectify this omission, we unambiguously, and once and for all, identify the fixed material points \(\boldsymbol{z}\) of ℛ through
This is done modulo an essential uniquely defined relationship between the parameter pairs \((s, t)\) in (26) and the parameter pairs \((z_{1}, z_{2})\) in (28), a relationship which we now discuss.
Since \({\mathcal {S}}\) is a rectifying developable surface, it can be severed along the generator \(\boldsymbol{g}(0,t)\), \(t\in [-w,w]\), through its closure point and isometrically rolled out onto a plane. This shows that the corresponding subset of the plane and \({\mathcal {S}}\) satisfy a mutual isometry relation. Thus, due to the earlier stated Proposition, there is an isometric mapping of \({\mathcal {S}}\) into a planar strip \({\mathcal {D}}\) of midline length \(L\) and width \(2w\) and it is given by the parametrization

where \(\{\boldsymbol{\imath }_{1},\boldsymbol{\imath }_{2}\}\) denotes an orthonormal basis in the plane of \({\mathcal {D}}\).Footnote 2 Here, the elements \(x\in {\mathcal {D}}\) are denoted by the parameter pair \(x :=(s, t)\), and  are points which define the form of \({\mathcal {D}}\) as being a portion of a planar surface. According to (2), the Riemannian metric coefficients \(g_{ij}\) associated with \({\mathcal {D}}\) satisfy \(g_{ij} = h_{ij}\) in (27). The isometric mapping
are points which define the form of \({\mathcal {D}}\) as being a portion of a planar surface. According to (2), the Riemannian metric coefficients \(g_{ij}\) associated with \({\mathcal {D}}\) satisfy \(g_{ij} = h_{ij}\) in (27). The isometric mapping  is defined implicitly via the parameter pair \((s,t)\), together with the assignment that the single closure point \(\boldsymbol{r}(0)=\boldsymbol{r}(L)\) of the midline directrix in \({\mathcal {S}}\) corresponds to the two points \(\boldsymbol{x}(0, 0):=\boldsymbol{o}\) and \(\boldsymbol{x}(L,0)=L\boldsymbol{\imath }_{1}\) in \({\mathcal {D}}\). The ends of the strip \({\mathcal {D}}\) in (29) are thus given, respectively, by \(t\eta (0)\boldsymbol{\imath }_{1}+t\boldsymbol{\imath }_{2}\) and \((L+t\eta (L))\boldsymbol{\imath }_{1}+t\boldsymbol{\imath }_{2}\) for \(t\in [-w,w]\), where \(\eta (L)=-\eta (0)\), which has the consequence that \({\mathcal {D}}\) has the shape of an isosceles trapezoid, being rectangular only if \(\eta (L)=-\eta (0)=0\), which, for definiteness, we shall assume unless noted otherwise. With this assumption, the shape of the planar strip \({\mathcal {D}}\) is a rectangle of length \(L\) and width \(2w\), and so the points \(\boldsymbol{x}\in {\mathcal {D}}\) may be identified uniquely with the material points \(\boldsymbol{z}\in {\mathcal {R}}\) by enforcing the invertible relation
is defined implicitly via the parameter pair \((s,t)\), together with the assignment that the single closure point \(\boldsymbol{r}(0)=\boldsymbol{r}(L)\) of the midline directrix in \({\mathcal {S}}\) corresponds to the two points \(\boldsymbol{x}(0, 0):=\boldsymbol{o}\) and \(\boldsymbol{x}(L,0)=L\boldsymbol{\imath }_{1}\) in \({\mathcal {D}}\). The ends of the strip \({\mathcal {D}}\) in (29) are thus given, respectively, by \(t\eta (0)\boldsymbol{\imath }_{1}+t\boldsymbol{\imath }_{2}\) and \((L+t\eta (L))\boldsymbol{\imath }_{1}+t\boldsymbol{\imath }_{2}\) for \(t\in [-w,w]\), where \(\eta (L)=-\eta (0)\), which has the consequence that \({\mathcal {D}}\) has the shape of an isosceles trapezoid, being rectangular only if \(\eta (L)=-\eta (0)=0\), which, for definiteness, we shall assume unless noted otherwise. With this assumption, the shape of the planar strip \({\mathcal {D}}\) is a rectangle of length \(L\) and width \(2w\), and so the points \(\boldsymbol{x}\in {\mathcal {D}}\) may be identified uniquely with the material points \(\boldsymbol{z}\in {\mathcal {R}}\) by enforcing the invertible relation
between \((z_{1}, z_{2})\) in (28) and \((s, t)\) in (29). Based upon this observation, it is true that the rectifying developable Möbius band \({\mathcal {S}}\) of (26) is the isometric deformation of the particular undistorted material rectangular reference configuration ℛ of (28) in which the material points \(\boldsymbol{z}\) are identified in terms of the pair \((s, t)\) by (30). It is important to observe, however, that the location of each material point in this now specially structured configuration ℛ depends upon the particular Möbius band \({\mathcal {S}}\) because of the presence of the function \(\eta \) in (30). Although the deformation of each specially structured reference configuration ℛ to its particular corresponding \({\mathcal {S}}\) is isometric, this only confirms that each rectifying developable Möbius band \({\mathcal {S}}\) of the form (26) has an isometry relation with the planar rectangular strip of shape \({\mathcal {D}}\) with length \(L\) and width \(2w\). The minimization strategy of the proposed purely geometrical problem is based on the admissible set of all (smooth) rectifying developable Möbius bands parametrized as in (26) and this requires the involvement of a different set of material points \(\boldsymbol{z}\in {\mathcal {R}}\) for each choice \({\mathcal {S}}\) because of the presence of \(\eta \) in the linking relation (30). For an unstretchable material the specially structured reference configuration ℛ required by (30) does not serve to identify one fixed set of material points in a rectangular reference configuration relative to which the deformation of all rectifying developable Möbius bands \({\mathcal {S}}\) parametrized as in (26) is determined. With the exception of one Möbius band, all others in the minimization strategy of the proposed purely geometrical problem do not qualify as an isometric deformation from a single fixed rectangular material reference configuration. However, because all are developable and all can be rolled out to cover the same rectangular overall shape as does ℛ then all of the Möbius bands in the variational scheme form a mutual isometry relation with one another. However, it is worth emphasizing that all, with the exception of one, are not isometric deformations from the same fixed rectangular material reference configuration ℛ as was introduced in (28).
To explain further, suppose that
represents the form of the Möbius band \({\mathcal {S}}^{*}\) that is determined from the minimization strategy of the proposed purely geometrical problem among all competing rectifying developable Möbius bands \({\mathcal {S}}\) as parameterized in (26). Then, since \({\mathcal {S}}^{*}\) is in the set of all admissible \({\mathcal {S}}\) that are considered, we know that \(\eta ^{*}(0) = \eta ^{*}(L) = 0\) and, analogous to (29), that there is an isometric mapping of \({\mathcal {S}}^{*}\) into a planar rectangular strip \({\mathcal {D}}^{*}\) of midline length \(L\) and width \(2w\) and it is given by the parametrization

Moreover, based upon the hypothesis (31), the points \(\boldsymbol{x}^{*} \in {\mathcal {D}}^{*}\), \({\mathcal {D}}^{*}\) being fixed, may be identified uniquely with the material points \(\boldsymbol{z}\in {\mathcal {R}}\) via
by enforcing the invertible relationFootnote 3
between \((z_{1}, z_{2})\) in (28) and \((s, t)\). Thus, it follows that the deformation of the material points \(\boldsymbol{z}\in {\mathcal {R}}\mapsto \boldsymbol{y}\in {\mathcal {S}}\) may be considered to be the composition of the deformation of the material points \(\boldsymbol{z}\in {\mathcal {R}}\mapsto \boldsymbol{x}\in {\mathcal {D}}\) followed by the isometric mapping of the points \(\boldsymbol{x}\in {\mathcal {D}}\mapsto \boldsymbol{y}\in {\mathcal {S}}\), as noted above in relation to (29) and (26). Clearly, from (29) and (33), the deformation of the material points \(\boldsymbol{z}\in {\mathcal {R}}\mapsto \boldsymbol{x}\in {\mathcal {D}}\) may be written as
where \((s, t)\) is determined in terms of \(\boldsymbol{z}\) through (33) and (34). Because \(\eta (L) = -\eta (0) = \eta ^{*}(L) = -\eta ^{*}(0) = 0\), this deformation corresponds to an internal shear of the undistorted fixed rectangular material reference configuration ℛ.
Granted that the minimization strategy of the proposed purely geometrical problem determines a rectifying developable Möbius band \({\mathcal {S}}^{*}\) and a related flat reference configuration \({\mathcal {D}}^{*}\) such that \({\mathcal {S}}^{*}\) is the isometric deformation of \({\mathcal {D}}^{*}\). However, the admissible set of Möbius bands in the variational scheme is based upon the class of rectifying developable forms and this class includes non-isometric deformations. Thus, the proposed purely geometrical problem is related to the differential geometry of rectifying developable surfaces and does not apply to the mechanics of unstretchable material surfaces. It identifies the Wunderlich [8, 9] functional, which is based in mechanics and determines the bending energy for rectifying developable surfaces, as a convenient dimensionally reduced functional to minimize within the class of rectifying developable surfaces in order to determine an optimal rectifying developable Möbius band of given length \(L\) and width \(2w\). The constraint that the admissible surfaces must be unstretchable material surfaces is not accounted for in this scheme.
If a specific flat rectangular configuration is chosen as the undistorted and unstretchable material strip into which, by an isometric deformation, a Möbius band is to be formed by smoothly connecting its two short ends together after a \(180^{\circ}\) twist, and the band is considered to be a closed unknotted ribbon without self contact, then the Wunderlich [8, 9] functional is a correct dimensional reduction for accurately representing the bending energy and for formulating an appropriate minimization problem to determine its equilibrium form. However, to determine the optimal form the functional cannot be extremized over the class of rectifying developable surfaces as parametrized in (26). One acceptable approach, as Seguin, Chen and Fried [5] have noted, is to extremize an augmented functional that incorporates the constraints that ensure that the deformation is isometric through the introduction of suitable reactions in the form of Lagrange multiplier fields defined on the midline of the band. Of course, the appropriate conditions of smoothness at the connection of the two ends must be stated when defining the class of admissible variations that are used for determining the governing Euler–Lagrange equations — equations which ultimately will provide the field of generators. The minimization strategy of the proposed purely geometrical problem does not mention such concern about preserving the isometric deformation property of the ribbon as well as these constraints.
As a final observation, we note that the set of rectifying developable surfaces parametrized as in (26) is not a sufficiently rich set of surfaces to consider for the purpose of determining an energy minimizing isometric deformation of an unstretchable rectangular material strip. In particular, we demonstrated herein that the classical variational problem of determining the shape of an unstretchable Möbius band within that class of competitors is incompatible with the constraint that the reference rectangular material strip is unstretchable. More generally, other mechanics based studies have noted limited applicability when using a rectifying developable parameterization (26) to represent the isometrically deformed configuration of a given rectangular material strip. For example, if the deformed configuration lies on the surface of a right circular cylinder, then following this usage the strip must be wrapped onto the cylinder so that two of its parallel edges are coincident with the generators of the cylinder. However, a helical wrapping onto the surface of the cylinder is also isometric. Even more exclusive is the observation of Chen, Fosdick and Fried [19, §4.3] that if the deformed surface of a given unstretchable rectangular material strip is supposed to lie on the surface of a right circular cone then it cannot be described using the rectifying developable parameterization (26). However, such a deformation exists and it is isometric.
References
do Carmo, M.P.: Differential Geometry of Curves and Surfaces. Prentice-Hall, Inc., Englewood Cliffs, New Jersey (1976)
Kreyszig, E.: Introduction to Differential Geometry and Riemannian Geometry. Mathematical Expositions, vol. 16. University of Toronto Press, Toronto (1968). Reprinted, 1975
Pressley, A.: Elementary Differential Geometry. Springer Undergraduate Series. Springer, London (2010)
Jellett, J.H.: On the properties of inextensible surfaces. Trans. R. Ir. Acad. 22, 343–377 (1849)
Seguin, B., Chen, Y.-C., Fried, E.: Closed unstretchable knotless ribbons and the Wunderlich functional. Int. J. Nonlinear Sci. 30, 2577–2611 (2020)
Sadowsky, M.: Ein elementarer Beweis für die Existenz eines abwickelbaren Möbiusschen Bandes und die Zurückführung des geometrischen Problems auf ein Variationsproblem. Sitzungsber. Preuss. Akad. Wiss., Phys.-Math. Kl. 22, 412–415 (1930)
Hinz, D.F., Fried, E.: Translation of Michael Sadowsky’s paper “An elementary proof for the existence of a developable Möbius band and the attribution of the geometric problem to a variational problem”. J. Elast. 119, 3–6 (2015)
Wunderlich, W.: Über ein abwickelbares Möbiusband. Monatshefte Math. 66, 276–289 (1962)
Todres, R.E.: Translation of W. Wunderlich’s “On a developable Möbius band”. J. Elast. 119, 23–34 (2015)
Schwarz, G.: A pretender to the title “canonical Moebius strip”. Pac. J. Math. 143, 195–200 (1990)
Schwarz, G.E.: The dark side of the Moebius strip. Am. Math. Mon. 97, 890–897 (1990)
Randrup, T., Røgen, P.: Sides of the Möbius strip. Arch. Math. 66, 511–521 (1996)
Chicone, C., Kalton, K.: Flat embeddings of the Möbius strip in \(R^{3}\). Commun. Appl. Nonlinear Anal. 9, 31–50 (2002)
Sabitov, I.K.: Isometric immersions and embeddings of a flat Möbius strip in Euclidean spaces. Izv. Math. 71, 1049–1078 (2007)
Kurono, Y., Umehara, M.: Flat Möbius strips of given isotopy type in \(\boldsymbol{R}^{3}\) whose midlines are geodesics or lines of curvature. Geom. Dedic. 134, 109–130 (2008)
Slovesnov, A.V.: Möbius strips with flat metrics. Mosc. Univ. Math. Bull. 64, 183–186 (2009)
Naokawa, K.: Extrinsically flat Möbius strips on given knots in 3-dimensional space forms. Tohoku Math. J. 63, 341–356 (2013)
Chen, Y.-C., Fried, E.: Möbius bands, unstretchable material sheets and developable surfaces. Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 472, 20160459 (2016)
Chen, Y.-C., Fosdick, R., Fried, E.: Issues concerning isometric deformations of planar regions to curved surfaces. J. Elast. 132, 1–42 (2018)
Acknowledgements
We thank Vikash Chaurasia for his help preparing Fig. 1. We also thank two anonymous reviewers for their constructive suggestions. The work of Eliot Fried was supported by the Okinawa Institute of Science and Technology Graduate University with subsidy funding from the Cabinet Office, Government of Japan. Yi-chao Chen thanks the Okinawa Institute of Science and Technology for hospitality and generous support during a sabbatical and subsequent visits.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to all aspects of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Dedicated to Millard Beatty with affection and in appreciation for his meticulous and far-reaching contributions to mechanics and to the advancement of nonlinear elasticity
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, Yc., Fosdick, R. & Fried, E. Isometries Between Given Surfaces and the Isometric Deformation of a Single Unstretchable Material Surface. J Elast 151, 159–175 (2022). https://doi.org/10.1007/s10659-022-09909-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-022-09909-0
Keywords
- Inextensible surface
- Inextensional surface
- Two-dimensional Riemannian manifold
- Embedding
- Developable surface
- Rectifying developable
- Internal constraint




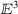 is given by
is given by 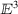 is given by
is given by 