Axonal Buckling Following Stretch Injury

Abstract

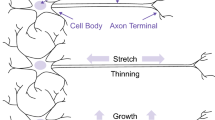
Diffuse brain injury is caused by rapid rotation of the head, and causes strain injury to tissue throughout the brain. Following strain injury, axons exhibit delayed recovery, showing regional buckling behavior immediately after stretch and returning to their original appearance over an extended period of time. This axonal buckling is hypothesized to occur as a result of localized stretching within the axon: Rapid strain causes mechanical damage to microtubules, increasing the effective length of axons. This damage is repaired gradually returning the axon to its initial length.

Here, we test the hypothesis that localized stretching is a possible explanation for the regional buckling behavior. An elongated region of axon is modeled as an Euler beam on an elastic foundation, where the foundation represents the surrounding brain tissue, which consists of glial cells and extracellular matrix. After stretch the elastic foundation returns immediately to its pre-stretch length, while the axon is initially elongated and returns to its original length over a longer period of time. The model exhibits solutions similar to those observed experimentally in post-stretch axons, with undulations that have a similar wavelength and amplitude.

Appendices

Appendix A: Solutions to the Model for $\lambda^{2} \leq4\beta$

This appendix shows that there are no non-trivial solutions to the system of (9)–(13) unless $\lambda^{2}>4\beta$.

1.1 A.1 $\lambda^{2}=4\beta$

Initially, we consider the case $\lambda^{2}=4\beta$. Note that since $\beta$ is positive constant, this implies that $\lambda$ is non-zero and so the general solution to (9) is

$$ w=A\cos(k x) + Bx\cos(k x) + C\sin(k x) + Dx\sin(k x), $$

(26)

where $k=\lambda/2$. By assumption, the beam is clamped at the boundaries, so that the appropriate boundary conditions are those of (13). Applying the boundary condition $w(\pm 1)=0$ and adding and subtracting the equations obtained gives:

$$\begin{aligned} & A\cos(k)+D\sin(k)=0, \end{aligned}$$

(27)

$$\begin{aligned} & B\cos(k)+C\sin(k)=0, \end{aligned}$$

(28)

while proceeding similarly with the boundary condition $w'(\pm1)=0$ we find another pair of equations:

$$\begin{aligned} & (D-Ak)\sin(k)+Dk\cos k =0, \end{aligned}$$

(29)

$$\begin{aligned} & (Ck+B)\cos(k)-Bk\sin k =0. \end{aligned}$$

(30)

Solving (27) and (29) gives that either $A=D=0$ or the dispersion relation $\sin k\cos k - k=0$ is satisfied. Graphically it can be shown that the only solution to this dispersion relation is $k=0$, which is inconsistent with $k=\lambda/2=\sqrt{\beta}>0$. We therefore conclude that $A=D=0$. Similarly, solving (28) and (30) gives that either $B=C=0$ or $\sin k\cos k + k=0$; the only solution to this equation is again $k=0$ and so $B=C=0$. As a result, no non-trivial solution exists that satisfies the clamped boundary conditions with $\lambda^{2}=4\beta$.

1.2 A.2 $\lambda^{2}<4\beta$

In the case $\lambda^{2}<4\beta$ the general solution to (9) is given by:

$$\begin{aligned} w =&A\cos(r x)\sinh(\rho x) + B\cos(r x) \cosh(\rho x) \\ &{}+ C\sin(r x) \sinh(\rho x) + D\sin(r x) \sinh(\rho x), \end{aligned}$$

(31)

where $k=\pm r \pm i \rho$ are the four solutions of the auxiliary equation $k^{4}-\lambda k^{2} + \beta=0$. Applying the boundary conditions at $w(\pm1)$ and adding and subtracting the results gives:

$$\begin{aligned} & A\cos r \sinh\rho+D\sin r \cosh\rho=0, \end{aligned}$$

(32)

$$\begin{aligned} & B\cos r \cosh\rho+C\sin r\sinh\rho=0. \end{aligned}$$

(33)

Similarly imposing $w'(\pm1)=0$ and manipulating we find another pair of equations:

$$\begin{aligned} & 0= A(-r \sin r \sinh\rho+ \rho\cos r \cosh\rho)+ D(r \cos r \cosh \rho+ \rho\sin r \sinh\rho), \end{aligned}$$

(34)

$$\begin{aligned} & 0=B(-r \sin r \cosh\rho+ \rho\cos r \sinh\rho) + C (r \cos r \sin \rho+ \rho\sin r \cosh\rho). \end{aligned}$$

(35)

Solving (32) and (34) we obtain that either $A=D$ or the dispersion relationship $\cos r \sin r/r=\sinh\rho\cosh\rho/ \rho$ holds. Graphically it can be shown that the only solution to the dispersion relation is $\rho=r=0$, contradicting our assumption that the root of the auxiliary equation is complex. Similarly solving (33) and (35) gives that either $B=C$ or $r$ and $\rho$ satisfy $\cos r \sin r/r=-\sinh\rho\cosh\rho/ \rho$, which also has no non-trivial solutions. We therefore conclude that no non-trivial solutions exist that satisfy the clamped boundary conditions when $\lambda^{2}<4\beta$.

Appendix B: Second Moment of Area for a Circular Arrangement of Microtubules

An upper bound, for the bending stiffness of an axon can be estimated by considering the constituent parts within the axon. Microtubules are the stiffest component of the cytoskeleton [35], and so we consider a structure consisting only of microtubules, whose Young’s modulus and radius have been extensively characterized [2, 19]. It is assumed that microtubules are arranged in a circular pattern located close to the perimeter of the axon, as shown in Fig. 7(a). This assumption of arranging the microtubules around the outermost boundary of the axon and neglecting sliding between axons gives an upper bound for stiffness. If $E_{m}$ is the Young’s modulus of microtubules and $I_{m}$ is the second moment of area for the arrangement of microtubules, then $B=E_{m} I_{m}$. For an arrangement of $N$ microtubules, each with radius $r_{m}$, and arranged at a radius $R$ from the centre of an axon, the second moment of area can be shown to be $\pi r_{m}^{2} R^{2} N/2$.

Fig. 7

(a) Cross section of an axon, showing the microtubules (arrow). $\mbox{Axon radius}=0.5~\upmu \mbox{m}$. Image taken from [44] with kind permission from Doug Smith. (b) Diagram illustrating the arrangement of $N=12$ microtubules which are used to calculate the second moment of area of an axon

The second moment of area for an arrangement of $N$ microtubules each with radius $r_{m}$ and positioned in a circular arrangement at a distance $R$ from the centre of an axon, as illustrated in Fig. 7(b) is given by $\pi r_{m}^{2} R^{2} N/2$. First consider the moment of area $I$ of a single microtubule, with centre located at distance $a_{j}$ from the vertical axis. The second moment of area is given by,

$$\begin{aligned} I(a_{j}) =& \int_{D} z^{2} ~\mathrm {d}z ~\mathrm {d}y = \int_{-r_{m}}^{r_{m}} \int_{a-\sqrt {r_{m}^{2}-y^{2}}}^{a+\sqrt{r_{m}^{2}-y^{2}}} z^{2} ~\mathrm {d}z ~\mathrm {d}y, \\ =& \frac{1}{3} \int_{-r_{m}}^{r_{m}} \Bigl(a+\sqrt{r_{m}^{2}-y^{2}} \Bigr)^{3} -\Bigl(a-\sqrt {r_{m}^{2}-y^{2}} \Bigr)^{3} ~\mathrm {d}y, \\ =&\frac{1}{3} \int_{-r_{m}}^{r_{m}} 8\sqrt {r_{m}^{2}-y^{2}}^{3}+6 \bigl(a^{2}-\bigl(r_{m}^{2}-y^{2}\bigr) \bigr) \Bigl(\sqrt{r_{m}^{2}-y^{2}}\Bigr) ~\mathrm {d}y. \end{aligned}$$

Parameterizing $y$ by $r_{m} \sin\theta$ for $\theta\in[-\pi/2, \pi /2]$. Then the integral simplifies to,

$$\begin{aligned} I(a_{j}) =\frac{1}{3}& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} 8r_{m}^{4} \cos^{4} \theta+ 6 \bigl(a^{2}-r_{m}^{2} \cos^{2} \theta\bigr) ~\mathrm {d}\theta, \\ =&\frac{2}{3} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} 2 r_{m}^{4} \biggl( \frac {3}{8}+ \frac{1}{2} \cos2\theta+ \frac{1}{8} \cos4\theta \biggr) + 3a_{j}^{2}r_{m}^{2}(1+ \cos\theta) ~\mathrm {d}\theta, \\ =&\pi r_{m}^{2} \biggl(\frac{r_{m}^{2}}{4} + a_{j}^{2} \biggr). \end{aligned}$$

Now considering a circular arrangement of $N$ microtubules, evenly spaced at radius $R$ from the centre of the axon. The distance from the vertical axis of each microtubules is given by $a_{j}=R \sin\theta_{j}$ where $\theta_{j}=\alpha+\frac{2\pi(j-1)}{N}$. The second moment of area of the collection is given by:

$$\begin{aligned} I =&\sum_{j=i}^{N} I(a_{j}) = \sum_{j=i}^{N} \pi r_{m}^{2} \biggl(\frac{r_{m}^{2} }{4}+(R \sin\theta_{j})^{2} \biggr), \\ =&\frac{N\pi r_{m}^{4}}{4} + \pi r_{m}^{2} R^{2} \sum _{j=i}^{N} \sin^{2} \biggl( \alpha+ (j-1) \frac{2 \pi}{N} \biggr). \end{aligned}$$

Finally it remains to evaluate the sum, it can be shown that for all $N>2$ and all $\alpha$ the sum in the equation above is $N/2$

$$\begin{aligned} \sum_{j=i}^{N} \sin^{2} \biggl( \alpha+ (j-1) \frac{2 \pi}{N} \biggr) =& \sum_{j=0}^{N-1} \biggl( \frac{1}{2i} \biggr)^{2} \bigl( e^{(\alpha+\frac {2\pi j}{N})i} - e^{-(\alpha+\frac{2\pi j}{N})i} \bigr) \\ =& \frac{N}{2} -\frac{1}{4} \Biggl( e^{2\alpha i}\sum _{j=0}^{N-1} e^{\frac{4 \pi i}{N}j} + e^{-2\alpha i}\sum _{j=0}^{N-1} e^{-\frac{4 \pi i}{N}j} \Biggr) \\ =& \frac{N}{2} -\frac{1}{4} \biggl( e^{2\alpha i} \biggl( \frac{1-e^{4 \pi i}}{1-e^{4\pi i/N}} \biggr) + e^{-2\alpha i} \biggl( \frac{1-e^{-4 \pi i}}{1-e^{-4\pi i/N}} \biggr) \biggr). \end{aligned}$$

The numerators $1-e^{\pm4 \pi i}$ are always equal to zero, and the denominator $1-e^{\pm4\pi i/N}$ is non zero unless $N=1$ or 2. Thus for $N>2$,

$$\begin{aligned} I =&\frac{N\pi r_{m}^{4}}{4} + \pi r_{m}^{2} R^{2} \frac{N}{2}=\frac{\pi r_{m}^{2} N}{2} \biggl(\frac{ r_{m}^{2} }{2} + R^{2} \biggr) \approx \frac{\pi r_{m}^{2}R^{2}N}{2}, \end{aligned}$$

where an approximation is made since the radius of a microtubule $r_{m}\ll R$ — the radius at which the microtubules are arranged within the axon $R$.

The typical diameter of a microtubule $r_{m}\approx25~\mbox{nm}$ [2] and, as previously, we take the radius of an axon $r_{0}\approx0.5~\upmu \mbox{m}$. It is assumed that the microtubules are arranged close to the edge of the axon so that $R=0.4~\upmu \mbox{m}$, and we assume that there are $N=12$ microtubules in a cross section. This number varies between axons but, as the bending stiffness varies only linearly with $N$, variations in $N$ will not have a great effect. Taking $E_{m}\approx1.2~\mbox{GPa}$ [19] we have,

$$ B=E_{m}I_{m}=E_{m} \times\frac{\pi r_{m}^{2} R^{2} N}{2} \approx6 \times 10^{-19}~\mbox{Nm}^{2}. $$

(36)

The cytoskeleton also consists of neurofilaments and microfilaments. Their overall contribution to the bending stiffness of axons are not fully understood.