Drift velocity in sediment-laden downward jets

Abstract

The drift velocity, defined as the velocity of individual phase relative to the water–sediment mixture, is a key variable in two-phase mixture model. In this paper, a relation for the drift velocity in sediment-laden jets, expressed as a power series of the nozzle Stokes number, was derived by using the perturbation approach. It shows that except the gravity and turbulent diffusion, effects of particle inertia, inter-phase interaction, and other forces contained in the first-order particle inertial corrections also play significant roles in sediment-laden jet flows. Based on the relation for the drift velocity, the velocity and concentration distribution were obtained from the similarity solutions for sediment-laden jets. The calculated concentration and velocity profiles agree well with the experimental observations in literature. Furthermore, analysis on the sediment diffusion coefficient shows that the fluid turbulence is not the only driving force for the sediment diffusion in sediment-laden jets; the effect of particle turbulence on the behavior of sediment-laden jets is also significant with the increasing of particle inertia.

1 Introduction

Turbulent jet, as a common phenomenon found in fluid engineering and a representative topic in fluid mechanics, has attracted considerable attention and received extensive investigation in the past several decades [1, 12, 18, 25, 34]. Previously reported focus is not only centered on single-phase jet flows but also on multi-phase jet flows which can be observed in a number of circumstances both in natural and engineering circumstances. For instance, sediment-laden jets, as a typical of two-phase jets, have been of great interest in fluvial hydraulics, not only because there still remain numerous unsolved problems in this field, but also because there are a wide variety engineering applications, such as dredging and deepening of canals, and desilting of reservoirs, in which both solid grains and fluids are sprayed out of nozzles to develop intensive and concentrated flows against deposited materials on channel bed. In this case, a better understanding of turbulent sediment-laden jets is helpful to improve the efficiency of devices used in dredging. Moreover, because turbulent jets as a typical boundary layer flows involve intensive momentum transfer between sprayed fluids and ambient fluids, and thus two-phase jets are usually adopted as a representative flow pattern to investigate the underlying mechanisms with respect to inter-phase interactions and momentum transfer in sheared two-phase boundary layers. Therefore, studies on sediment-laden jets are of importance in both practical applications and theoretical studies.

A number of experimental investigations upon sediment-laden jets have been conducted [2, 12, 18, 21, 22, 24, 31]. In the early stage of these studies, Singamsetti [31] observed the axial velocity distribution of sediment-laden downward jets, and found that the axial velocity followed a self-similar Gaussian distribution based on the dimensional analysis in the zone of established flow. Because the observation was made on water–sediment mixtures with the assumption that the sediment and fluid velocities were identical, and thus his result cannot reveal the difference between the solid and liquid phase. Subsequently, Parthasarathy and Faeth [24] carried out a series of experiments, in which the velocities for solid and liquid phase and the sediment concentration for solid phase were measured by using a Laser Doppler Anemometer (LDA). Their work were widely cited in theoretical studies on sediment-laden jets for it gives comprehensive view of the two-phase jets. With the rapid development of the measuring instrument for two-phase flows, more and more experiments on sediment-laden jets were conducted and reported. For example, Muste et al. [22] observed the sediment and water velocity in sediment-laden jets with Laser-Doppler Velocimetry (DLDV) and Particle Tracking Velocimetry (PTV); Jiang et al. [18] used an instantaneous whole-field velocimetry tool, Particle Image Velocimetry (PIV) to measure the mean and fluctuation velocity for fluid and sediment in sediment-laden downward jets.

It should be noticed that the aforementioned studies were conducted in the condition of low concentrations, which permits the assumption that fluids and particles have no significant interactions to be acceptable [37]. That those studies had to be limited to low sediment concentrations is due largely to the difficulty in measuring the velocity and concentration for sediment-laden jets with traditional measurement techniques such as PIV in high sediment load jet flows. This also has been a limitation for theoretical studies of sediment-laden jets under high concentrations. This difficulty has been partially solved recently. Hall et al. [12] developed a novel optical probe to measure concentration and velocity of particles simultaneously with initial sand concentration by volume as high as 0.124, which provides valuable observational data for the study of sediment-laden jets under high concentrations.

In addition to experimental studies, much effort has been made to theoretical descriptions of sediment-laden jets. However, because of the complexity arising from inter-phase interactions occurred in sediment-laden jets, a large part of theoretical studies have to be conducted under simplified circumstances. For instance, Al Taweel and Landau [1], Shuen et al. [27], Shuen et al. [28], Shuen et al. [29], and Sun and Faeth [32] suggested $k - \varepsilon$ models for sediment-laden jets with at least one of the approximations as (1) ignoring the relative velocity between the two phase; (2) ignoring the interactions between sediment and turbulence; (3) or adopting a stochastic approach to consider the effects of the relative velocity and the sediment-turbulence interactions. The assumptions make their results meet difficulty in reflecting the effect of the dynamics of two-phase flow on sediment-laden jets. For instance, it is well known that the effect of inter-phase interaction on velocity distributions for individual phase due to velocity difference between two phases is significant for sediment-laden flows [10, 11, 41]; neglecting relative velocity between two phases can lead to lose important information about two-phase jets.

As to the theoretical approaches in the studies regarding two-phase jets, it can be found that there are several different theories adopted in the previous investigations. Sediment-laden jets, as well as sediment-laden flows in rivers and channels, are typical two-phase flows, so that theories and methods developed in the realm of the two-phase fluid dynamics can be employed with minor adaptions. For instance, numerous achievements on the transport of suspended sediment in turbulent open channel flows were reported by means of theories and approach developed in two-phase flows dynamics [10, 11, 13, 14, 16, 33, 40, 41]. As to sediment-laden jets, Jiang et al. [18] analyzed the features of sediment-laden jets based on two-phase conservation equations. In his work, the governing equation for solid phase contains effects of various terms including body force, turbulence stress and inter-phase interaction. Furthermore, by considering dilute two-phase jets, the sediment velocity along the central axis was assumed to differ from that of the fluid phase by the settling velocity of sediment particles when turbulence stress and inter-phase interaction on particles is ignored. Subsequently, Jiang et al. [18] argued that this assumption was still approximately valid to extend to the whole jet field. This implies that the effects of particle turbulent stress and inter-phase interaction were not considered in his study. Actually, similar assumption was widely adopted in the study of sediment transport in turbulent open channel flows, which leads to the traditional convection–diffusion equation for suspended load and resulting in the Rouse equation for sediment concentration profiles. It is a widely accepted conclusion that the Rouse equation can give correct concentration profile of suspended sediment only under the circumstances of low particle inertia and concentration so that particle–particle and particle–fluid interactions can be neglected (see Greimann and Holly [10], Zhang and Prosperetti [38], Zhong et al. [40], Keetels et al. [20]). Similar problem occurs to sediment-laden jet flows. It shows that, with the increasing of the particle size and solid concentration, particle–particle and inter-phase interaction, play significant roles in the flow fields of sediment-laden jet. Based on the previous study by Elghobashi [8], when the volume fraction of particles is larger than 10⁻⁶, the interaction between the particle and the flow turbulence cannot be one-way coupling, which means that the properties of particles has a significant effect on flow turbulence. Therefore, how to establish a proper model considering the effects of all the mechanisms on motions of sediment-laden jets is the key step for the theoretical studies.

To take into account the inter-phase and particle–particle interactions, in the study conducted by Zhong et al. [41], a relationship for the drift velocity, which is defined as the velocity difference between the individual phase and the sediment–water mixture, was obtained with the perturbation approach. The expressions for the drift velocity for solid phase shows that the motion of the sediment was affected by several key factors including gravity, turbulent diffusion, inter-phase interaction, and particle inertia. Applications of two-phase mixture equations closed by the drift velocity shows that concentration and velocity distributions in open-channel flows are in good agreement with experimental observations. Based on the above-mentioned, the previous theoretical studies on sediment-laden jet flows has not considered the effect of velocity difference between individual phases (Jiang et al. [17]), because how to determine the relation for the relative velocity for sediment-laden jets considering the effect of inter-phase interaction theoretically is still an open issue.

In this paper, we intend to derive the drift velocity for sediment-laden jets with the similar approach based on the two-fluid equations for two-phase flows. Considering the similarities of the velocity and concentration profiles in sediment-laden round jets, theoretical expressions for the velocity and concentration distribution were obtained, which can account for the effects on sediment-laden jets due to inter-phase interactions and particle inertia. Satisfactory agreements between calculated results and experimental observations were obtained. Moreover, based on the calculated concentration distributions, the contributions of two different factors, i.e., fluid turbulence and particle turbulence which largely depends on the effect of particle inertia to the sediment diffusion coefficient were analyzed. It shows that the particle turbulence plays a crucial part in sediment diffusion in jet flows when the Stokes number (particle inertia) is large enough.

The paper is structured as follows. Following the Introduction, the constitutive relation for the drift velocity for sediment-laden jets is derived based on two-fluid equations for solid/liquid two-phase flows in Sect. 2. The concentration and velocity distribution are obtained by the similarity solutions to the mass and momentum conservation equations for sediment-laden jets in Sect. 3. Closures for equations are presented in Sect. 4. Comparisons with experimental observations by Parthasarathy and Faeth [24] and Hall et al. [12] are subsequently presented. Finally, a discussion about the effect of particle inertia on sediment diffusion and the velocity distributions for sediment-laden jets is given. We hope this study can not only deepen the understanding of underlying mechanism of sediment-laden jets, but also become the basic foundation of practical applications including dredging and deepening of canals, desalting of reservoirs, and sewage purification, etc.

2 Drift velocity for sediment-laden downward jets

The two-fluid equations for solid/liquid phase flows are widely applied to investigate sediment-laden flows. As typical incompressible solid/liquid two phase flows, sediment-laden flows can be described by the governing equations consisting of the ensemble-averaged mass and momentum conservation equations, which are given as follows [6, 9, 13, 14]

$$\frac{{\partial \bar{\alpha }_{k} \rho_{k}^{{}} }}{\partial t} + \frac{{\partial \bar{\alpha }_{k} \rho_{k}^{{}} \langle u_{ki}^{{}} \rangle }}{{\partial x_{i} }} = 0,$$

(1)

$$\bar{\alpha }_{k} \rho_{k}^{{}} \frac{{D_{k} \langle u_{ki}^{{}} \rangle }}{Dt} = \bar{\alpha }_{k} \rho_{k}^{{}} b_{i} - \bar{\alpha }_{k} \frac{\partial \langle p\rangle }{{\partial x_{i} }} + \frac{{\partial \bar{\alpha }_{k} \langle T_{kij}^{{}} \rangle }}{{\partial x_{j} }} + \overline{f}_{ki} ,$$

(2)

where the Cartesian tensor and the summation convention with respect to repeated indices $i$ and $j$ are used; the coordinate system and time are denoted, respectively, by $x_{i}$ ($i$ = 1, 2, or 3) and $t$; the subscript $k$ is used exclusively to denote the fluid phase with $k = f$, and to denote the dispersed phase with $k = p$; $\bar{\alpha }_{k}$ = volumetric fraction of phase-$k$, which satisfies $\bar{\alpha }_{f} + \bar{\alpha }_{p} = 1$; $\langle u_{ki}^{{}} \rangle$ = velocity of phase-$k$; $\rho_{k}$ = material density of phase-$k$; $p$ = pressure; $\langle T_{kij}^{{}} \rangle { = }\langle T_{kij}^{v} \rangle + \langle T_{kij}^{t} \rangle$ is stress tensor of phase-$k$, of which $\langle T_{kij}^{v} \rangle$ is the viscous stress and $\langle T_{kij}^{t} \rangle$ is the turbulent stress including both the small-scale and larger-scale Reynolds stresses; $b_{i}$ = body force; $\overline{f}_{ki}$ = momentum transfer between phases, which satisfies $\overline{f}_{fi} + \overline{f}_{pi} = 0$; and ${{D_{k} } \mathord{\left/ {\vphantom {{D_{k} } {Dt}}} \right. \kern-0pt} {Dt}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0pt} {\partial t}} + \langle u_{kj}^{{}} \rangle {\partial \mathord{\left/ {\vphantom {\partial {\partial x_{j} }}} \right. \kern-0pt} {\partial x_{j} }}$ is material derivative with respect to the phase-$k$. In the above equations, the variables with an over-bar “–” denote the ensemble-averaged mean values, and the variables enclosed by a pair of brackets “$\langle \rangle$” stand for the concentration-weighted mean values, which used the concept of an indicator function, defined as follows [6, 9, 10, 38, 42]:

$$\left\{ {\begin{array}{*{20}l} {I_{\alpha } = 1,} \hfill & {{\text{If phase }}\alpha {\text{ is present}}} \hfill \\ {I_{\alpha } = 0,} \hfill & {{\text{otherwise}} .} \hfill \\ \end{array} } \right.$$

(3)

The function $I_{\alpha }$ = discontinuous function at the interface between phases. Thus the volumetric fraction of phase-$p$ is $\bar{\alpha }_{p} = \overline{I}_{\alpha }$. The concentration-weighted average of a quantity s is defined as

$$\langle s\rangle = \frac{{\overline{{I_{\alpha } s}} }}{{\bar{\alpha }_{p} }}.$$

(4)

The inter-phase interaction corresponding to solid phase adopts the following relation reported by Zhong et al. [41]:

$$\overline{f}_{pi} = \frac{{\bar{\alpha }_{p} \rho_{p} \left( {\langle u_{fi} \rangle - \langle u_{pi} \rangle } \right)}}{{\langle \tau_{p} \rangle }} - \frac{{D_{ij} \rho_{p} }}{{\bar{\alpha }_{f} \langle \tau_{p} \rangle }}\frac{{\partial \bar{\alpha }_{p} }}{{\partial x_{j} }} + \overline{M}_{pi} ,$$

(5)

where $\overline{M}_{pi}$ = summation of external forces on sediment additional to drag; $D_{ij}$ = diffusion coefficient tensor; $\langle \tau_{p} \rangle$ = particle relaxation time in turbulent flows, which is expressed as

$$\langle \tau_{p} \rangle { = }\frac{{\rho_{p} D^{2} \left( {1 - \bar{\alpha }_{p} } \right)^{n} }}{{18\nu_{f} \rho_{f} C_{f} }},$$

(6)

where $D$ is the diameter of sediment particles; $\nu_{f}$ is the viscosity of fluid; $C_{f}$ is the drag correction coefficient; The term $(1 - \bar{\alpha }_{p} )^{n}$ is introduced to account for the influence from the particle cloud [26] and $n = 1.7$ is used in this paper [10, 41]. However, because information regarding the drag coefficient is lacking in turbulent flows of high concentration, the approximation for $\langle \tau_{p} \rangle$ is used [10]:

$$\langle \tau_{p} \rangle = \frac{{\rho_{p} \omega \left( {1 - \bar{\alpha }_{p} } \right)^{n} }}{{g\left( {\rho_{p} - \rho_{f} } \right)}} ,$$

(7)

where $\omega$ is the particle fall velocity. The inter-phase interaction expressed by Eq. (5) contains a term associated with turbulence diffusion, which is proved being of significance in the process of sediment suspension by turbulence [10, 11, 13, 41].

For a round jet, it is reasonable to adopt the axisymmetric coordinate system with $z$ denoting the axial direction (i.e. $x_{3}$ in Eqs. (1) and (2)) and $r$ denoting the radial direction (i.e. $x_{1}$ in Eqs. (1) and (2)) (Fig. 1).

Fig. 1

Configuration of a downward sediment-laden jet

Let $x_{3} = z$ and $k = p$ in Eq. (2) with the inter-phase interaction determined by Eq. (5), we had that

$$\begin{aligned} \bar{\alpha }_{p} \rho_{p} \frac{{D\langle u_{pz} \rangle }}{Dt} & = - \bar{\alpha }_{p} \frac{\partial \langle p\rangle }{\partial z} + \bar{\alpha }_{p} \rho_{p} g + \frac{{\partial \left( {\bar{\alpha }_{p} \langle T_{pzz} \rangle } \right)}}{\partial z} + \frac{1}{r}\frac{{\partial \left( {r\bar{\alpha }_{p} \langle T_{pzr} \rangle } \right)}}{\partial r} \\ & \quad + \frac{{\bar{\alpha }_{p} \rho_{p} \left( {\langle u_{fz} \rangle - \langle u_{pz} \rangle } \right)}}{{\langle \tau_{p} \rangle }} - \frac{{D_{zz} \rho_{p} }}{{\bar{\alpha }_{f} \langle \tau_{p} \rangle }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} - \frac{{D_{zr} \rho_{p} }}{{r\bar{\alpha }_{f} \langle \tau_{p} \rangle }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r} + \overline{M}_{pz} . \\ \end{aligned}$$

(8)

As in the study of Zhong et al. [41], by introducing the drift velocity defined as the velocities of the individual phases relative to the velocity of sediment–water mixture, the solid and liquid velocity are expressed as follows

$$\langle u_{pz} \rangle = \langle V_{pz} \rangle + U_{vz} ,$$

(9)

and

$$\langle u_{fz} \rangle = \langle V_{fz} \rangle + U_{vz} , ,$$

(10)

respectively, where $\langle V_{pz} \rangle$ and $\langle V_{fz} \rangle$ are the drift velocity of the solid and liquid phase, respectively; $U_{vz} = \bar{\alpha }_{f} \langle u_{fz} \rangle + \bar{\alpha }_{p} \langle u_{pz} \rangle$ is the velocity of water–sediment mixture with respect to the concentration average. The relation between the mass-weighted velocity of the mixture $U_{mz} = \bar{\alpha }_{f} \rho_{f} \langle u_{fz} \rangle + \bar{\alpha }_{p} \rho_{p} \langle u_{pz} \rangle$ and the concentration-averaged velocity is

$$U_{vz} {\text{ = U}}_{mz} - \bar{\alpha }_{p} \frac{{\rho_{p} - \rho_{f} }}{{\rho_{m} }}\langle V_{pz} \rangle ,$$

(11)

where $\rho_{m} = \bar{\alpha }_{f} \rho_{f} + \bar{\alpha }_{p} \rho_{p}$. The reason for using the concentration-averaged velocities of the mixture is that volumetric fluxes are more useful for kinematic analyses than the mass-weighted velocities for two-phase flow system [16]. Substituting Eqs. (9) and (10) into Eq. (8) yields

$$\begin{aligned} & \frac{{\left( {\langle V_{{pz}} \rangle - \langle V_{{fz}} \rangle } \right)}}{{\langle \tau _{p} \rangle }} + \frac{{D\left( {\langle V_{{pz}} \rangle + U_{{vz}} } \right)}}{{Dt}} \\ & \quad = - \frac{1}{{\rho _{p} }}\frac{{\partial \langle p\rangle }}{{\partial z}} + g + \frac{1}{{\bar{\alpha }_{p} \rho _{p} }}\frac{{\partial \left( {\bar{\alpha }_{p} \langle T_{{pzz}} \rangle } \right)}}{{\partial z}} + \frac{1}{{r\bar{\alpha }_{p} \rho _{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} \langle T_{{pzr}} \rangle } \right)}}{{\partial r}} \\ & \quad \quad - \frac{{D_{{zz}} }}{{\bar{\alpha }_{p} \bar{\alpha }_{f} \langle \tau _{p} \rangle }}\frac{{\partial \bar{\alpha }_{p} }}{{\partial z}} - \frac{{D_{{zr}} }}{{r\bar{\alpha }_{p} \bar{\alpha }_{f} \langle \tau _{p} \rangle }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{{\partial r}} + \frac{1}{{\bar{\alpha }_{p} \rho _{p} }}\bar{M}_{{pz}} \\ \end{aligned}$$

(12)

Considering

$$\begin{aligned} \bar{\alpha }_{f} \langle V_{fz} \rangle + \bar{\alpha }_{p} \langle V_{pz} \rangle =\, & \bar{\alpha }_{f} \left( {\langle u_{fz} \rangle - U_{vz} } \right) + \bar{\alpha }_{p} \left( {\langle u_{pz} \rangle - U_{vz} } \right) \\ =\, & \underbrace {{\left( {\bar{\alpha }_{f} \langle u_{fz} \rangle + \bar{\alpha }_{p} \langle u_{pz} \rangle } \right)}}_{{ = U_{vz} }} - \underbrace {{\left( {\bar{\alpha }_{f} + \bar{\alpha }_{p} } \right)}}_{ = 1}U_{vz} \\ = & U_{vz} - U_{vz} \\ =\, & 0 \\ \end{aligned} .$$

(13)

Equation (12) can be written as follows:

$$\begin{aligned} & \langle V_{pz} \rangle + \bar{\alpha }_{f} \langle \tau_{p} \rangle \frac{{D\left( {\langle V_{pz} \rangle + U_{vz} } \right)}}{Dt} \\& \quad = \bar{\alpha }_{f} \langle \tau_{p} \rangle g - \frac{{D_{zz} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} - \frac{{D_{zr} }}{{r\bar{\alpha }_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r} \\& \qquad + \frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ { - \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{\partial \langle p\rangle }{\partial z} + \frac{1}{{\rho_{p} }}\frac{{\partial \left( {\bar{\alpha }_{p} \langle T_{pzz} \rangle } \right)}}{\partial z} + \frac{1}{{r\rho_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} \langle T_{pzr} \rangle } \right)}}{\partial r} + \frac{1}{{\rho_{p} }}\overline{M}_{pz} } \right]\langle \tau_{p} \rangle \\ \end{aligned} .$$

(14)

Equation (14) can be solved asymptotically, because the term multiplied by $\langle \tau_{p} \rangle$ is of a small magnitude in comparison with others on the right hand side of Eq. (14) [41]. For this purpose, we introduced the reference length scale $L$, velocity scale $U$, and viscosity scale $\varGamma$ to non-dimensionlize Eq. (14) in order to analyze the relative importance of each term within it. The variables in Eq. (14) can be non-dimensionlized as follows:

$$t^{0} = t\frac{U}{L},x_{i}^{0} = \frac{{x_{i} }}{L},\langle u_{pi}^{0} \rangle = \frac{{\langle u_{pi}^{{}} \rangle }}{U},\langle p_{{}}^{0} \rangle = \frac{\langle p\rangle }{{\rho_{p} U^{2} }},\langle T_{pij}^{0} \rangle = \frac{{L\langle T_{pij}^{{}} \rangle }}{{\rho_{p} \varGamma U}},\overline{M}_{pi}^{0} = \frac{{\overline{M}_{pi}^{{}} L}}{{\rho_{p} U^{2} }}.$$

(15)

Using these non-dimensionlized variables, Eq. (14) is rewritten in the following form:

$$\begin{aligned} & \langle V_{pz}^{0} \rangle + \bar{\alpha }_{f} \frac{{\langle \tau_{p} \rangle U}}{L}\frac{{D\left( {\langle V_{pz}^{0} \rangle + U_{vz}^{0} } \right)}}{{Dt^{0} }} \\ &\quad = \bar{\alpha }_{f} \frac{{\langle \tau_{p} \rangle U}}{L}\frac{gL}{{U^{2} }} - \frac{{D_{zz}^{0} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{{\partial z^{0} }} - \frac{{D_{zr}^{0} }}{{r^{0} \bar{\alpha }_{p} }}\frac{{\partial \left( {r^{0} \bar{\alpha }_{p} } \right)}}{{\partial r^{0} }} \\ & \quad \quad { + }\frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ { - \bar{\alpha }_{p} \frac{{\partial \langle p^{0} \rangle }}{{\partial z^{0} }} + \frac{1}{\text{Re}}\frac{{\partial \left( {\bar{\alpha }_{p} \langle T_{pzz}^{0} \rangle } \right)}}{{\partial z^{0} }} + \frac{1}{{r^{0} \text{Re} }}\frac{{\partial \left( {r^{0} \bar{\alpha }_{p} \langle T_{pzr}^{0} \rangle } \right)}}{{\partial r^{0} }} + \overline{M}_{pz}^{0} } \right]\frac{{\langle \tau_{p} \rangle U}}{L}, \\ \end{aligned}$$

(16)

where $\text{Re} = {{UL} \mathord{\left/ {\vphantom {{UL} \varGamma }} \right. \kern-0pt} \varGamma }$. If we denote $St_{b} = {{\langle \tau_{p} \rangle U} \mathord{\left/ {\vphantom {{\langle \tau_{p} \rangle U} L}} \right. \kern-0pt} L}$ as the bulk Stokes number and $Fr = {U \mathord{\left/ {\vphantom {U {\sqrt {gL} }}} \right. \kern-0pt} {\sqrt {gL} }}$ as the Froude number, we can write Eq. (16) as follows:

$$\begin{aligned} & \langle V_{{pz}}^{0} \rangle + \bar{\alpha }_{f} St_{b} \frac{{D\left( {\langle V_{{pz}}^{0} \rangle + U_{{vz}}^{0} } \right)}}{{Dt^{0} }} \\ &\quad = \bar{\alpha }_{f} \omega ^{0} - \frac{{D_{{zz}}^{0} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{{\partial z^{0} }} - \frac{{D_{{zr}}^{0} }}{{r^{0} \bar{\alpha }_{p} }}\frac{{\partial \left( {r^{0} \bar{\alpha }_{p} } \right)}}{{\partial r^{0} }} \\ &\quad \quad {\text{ + }}\frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ { - \bar{\alpha }_{p} \frac{{\partial \langle p^{0} \rangle }}{{\partial z^{0} }} + \frac{1}{{\text{Re} }}\frac{{\partial \left( {\bar{\alpha }_{p} \langle T_{{pzz}}^{0} \rangle } \right)}}{{\partial z^{0} }} + \frac{1}{{r^{0} \text{Re} }}\frac{{\partial \left( {r^{0} \bar{\alpha }_{p} \langle T_{{pzr}}^{0} \rangle } \right)}}{{\partial r^{0} }} + \overline{M} _{{pz}}^{0} } \right]St_{b} \\ \end{aligned}$$

(17)

where $\omega^{0} = {{St_{b} } \mathord{\left/ {\vphantom {{St_{b} } {Fr^{2} }}} \right. \kern-0pt} {Fr^{2} }} = g{{\langle \tau_{p} \rangle } \mathord{\left/ {\vphantom {{\langle \tau_{p} \rangle } U}} \right. \kern-0pt} U}$.

The bulk Stokes number is usually a small value having the magnitude of 10⁻² (see Table 1 in a following section); therefore, the term multiplied by the bulk Stokes number as a small perturbation on the drift of sediment particles, as enable us to use perturbation techniques to find an asymptotic solution to Eq. (17). Similar approach has been adopted to explore the particle distributions in dilute two-phase flows by Druzhinin [7] and dispersion of sediment in turbulent open channel flows by Zhong et al. [41]. Here by expanding the drift velocity of the solid phase as a power series in terms of the bulk Stokes number, we had that:

$$\langle V_{pz}^{0} \rangle { = }\sum\limits_{l = 0}^{l = \infty } {\langle V_{Dz}^{0\left( l \right)} \rangle } St_{b}^{l} .$$

(18)

Substituting Eqs. (18) into (17), following the general procedure of the perturbation approach [7], we obtained the first two coefficients for the power series as

$$\langle V_{Dz}^{0\left( 0 \right)} \rangle = \bar{\alpha }_{f} \omega^{0} - \frac{{D_{zz}^{0} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{{\partial z^{0} }} - \frac{{D_{zr}^{0} }}{{r^{0} \bar{\alpha }_{p} }}\frac{{\partial \left( {r^{0} \bar{\alpha }_{p} } \right)}}{{\partial r^{0} }},$$

(19)

and

$$\langle V_{Dz}^{0\left( 1 \right)} \rangle = \frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ \begin{aligned} - \bar{\alpha }_{p} \frac{{D\left( {\langle V_{Dz}^{0\left( 0 \right)} \rangle + U_{vz}^{0} } \right)}}{{Dt^{0} }} - \bar{\alpha }_{p} \frac{{\partial \langle p^{0} \rangle }}{{\partial z^{0} }} \hfill \\ & + \frac{1}{\text{Re}}\frac{{\partial \left( {\bar{\alpha }_{p} \langle T_{pzz}^{0} \rangle } \right)}}{{\partial z^{0} }} + \frac{1}{{r^{0} \text{Re} }}\frac{{\partial \left( {r^{0} \bar{\alpha }_{p} \langle T_{pzr}^{0} \rangle } \right)}}{{\partial r^{0} }} + \overline{M}_{pz}^{0} \hfill \\ \end{aligned} \right].$$

(20)

Thus, we had an asymptotic expression for the velocity of the solid phase in terms of the bulk Stokes number

$$\begin{aligned} \langle u_{pz}^{0} \rangle & = U_{vz}^{0} + \bar{\alpha }_{f} \omega^{0} - \frac{{D_{zz}^{0} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{{\partial z^{0} }} - \frac{{D_{zr}^{0} }}{{r^{0} \bar{\alpha }_{p} }}\frac{{\partial \left( {r^{0} \bar{\alpha }_{p} } \right)}}{{\partial r^{0} }} \\ & \quad + \frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ \begin{aligned} - \bar{\alpha }_{p} \frac{{D\left( {\langle V_{Dz}^{0\left( 0 \right)} \rangle + U_{vz}^{0} } \right)}}{{Dt^{0} }} - \bar{\alpha }_{p} \frac{{\partial \langle p^{0} \rangle }}{{\partial z^{0} }} \hfill \\ & + \frac{1}{\text{Re}}\frac{{\partial \left( {\bar{\alpha }_{p} \langle T_{pzz}^{0} \rangle } \right)}}{{\partial z^{0} }} + \frac{1}{{r^{0} \text{Re} }}\frac{{\partial \left( {r^{0} \bar{\alpha }_{p} \langle T_{pzr}^{0} \rangle } \right)}}{{\partial r^{0} }} + \overline{M}_{pz}^{0} \hfill \\ \end{aligned} \right]St_{b} + O\left( {St_{b}^{2} } \right). \\ \end{aligned}$$

(21)

For convenience, the Eq. (21) is written in the dimensional form with the terms with the order higher than $O\left( {St_{b}^{2} } \right)$ neglected as follows:

$$\begin{aligned} \langle u_{pz}^{{}} \rangle & = U_{vz}^{{}} + \bar{\alpha }_{f} \omega - \frac{{D_{zz}^{{}} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} - \frac{{D_{zr}^{{}} }}{{r\bar{\alpha }_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r} \\ & \quad + \frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ \begin{aligned} - \bar{\alpha }_{p} \frac{{D\left( {\langle V_{Dz}^{\left( 0 \right)} \rangle + U_{vz}^{{}} } \right)}}{Dt} - \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{\partial \langle p\rangle }{\partial z} \hfill \\ + \frac{1}{{\rho_{p} }}\frac{{\partial \left( {\bar{\alpha }_{p} \langle T_{pzz}^{{}} \rangle } \right)}}{\partial z} + \frac{1}{{r\rho_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} \langle T_{pzr}^{{}} \rangle } \right)}}{\partial r} + \frac{1}{{\rho_{p} }}\overline{M}_{pz}^{{}} \hfill \\ \end{aligned} \right]\langle \tau_{p}^{{}} \rangle . \\ \end{aligned}$$

(22)

Equation (22) can be further written as

$$\begin{aligned} \langle u_{pz}^{{}} \rangle & = U_{vz}^{{}} + \bar{\alpha }_{f} \omega - \frac{{D_{zz}^{{}} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} - \frac{{D_{zr}^{{}} }}{{r\bar{\alpha }_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r} \\ & \quad + \frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ \begin{aligned} - \bar{\alpha }_{p} \frac{{D\left( {\langle V_{Dz}^{\left( 0 \right)} \rangle + U_{vz}^{{}} } \right)}}{Dt} - \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{\partial \langle p\rangle }{\partial z} + \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{{\partial \langle T_{pzz}^{{}} \rangle }}{\partial z}{ + }\frac{{\langle T_{pzz}^{{}} \rangle }}{{\rho_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} \hfill \\ + \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{{\partial \langle T_{pzr}^{{}} \rangle }}{\partial r}{ + }\frac{{\langle T_{pzr}^{{}} \rangle }}{{r\rho_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r} + \frac{1}{{\rho_{p} }}\overline{M}_{pz}^{{}} \hfill \\ \end{aligned} \right]\langle \tau_{p}^{{}} \rangle . \\ \end{aligned}$$

(23)

After the gradient of solid concentration is separated out, the solid velocity in the axial direction is written as

$$\begin{aligned} \langle u_{pz}^{{}} \rangle & = U_{vz}^{{}} + \bar{\alpha }_{f} \omega - \frac{{D_{pzz}^{{}} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} - \frac{{D_{pzr}^{{}} }}{{r\bar{\alpha }_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r} \\ & \quad + \frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ \begin{aligned} - \bar{\alpha }_{p} \frac{{D\left( {\langle V_{Dz}^{\left( 0 \right)} \rangle + U_{vz}^{{}} } \right)}}{Dt} - \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{\partial \langle p\rangle }{\partial z} \hfill \\ + \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{{\partial \langle T_{pzz}^{{}} \rangle }}{\partial z} + \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{{\partial \langle T_{pzr}^{{}} \rangle }}{\partial r} + \frac{1}{{\rho_{p} }}\overline{M}_{pz}^{{}} \hfill \\ \end{aligned} \right]\langle \tau_{p}^{{}} \rangle , \\ \end{aligned}$$

(24)

where the sediment diffusion coefficients are, respectively

$$D_{pzz} = D_{zz} - \frac{{\bar{\alpha }_{f} }}{{\rho_{p} }}\langle T_{pzz}^{{}} \rangle \langle \tau_{p}^{{}} \rangle ,$$

(25)

and

$$D_{pzr} = D_{zr} - \frac{{\bar{\alpha }_{f} }}{{\rho_{p} }}\langle T_{pzr}^{{}} \rangle \langle \tau_{p}^{{}} \rangle ,$$

(26)

As to the pressure gradient, it is assumed

$$\frac{\partial \langle p\rangle }{\partial z}{ = }\rho_{f} g\left( {1 + \beta \left( z \right)} \right),$$

(27)

where $\beta \left( z \right)$ is introduced to account for the effect of dynamic pressure gradient on the gradient of pressure in the axial direction. Because of the lack of information about the dynamic pressure gradient, for the sake of simplicity, we ignore the effect of dynamic pressure (i.e. $\beta \left( z \right){ = }0$) in this paper. Therefore, the pressure gradient is assumed as the $\rho_{f} g$ [18]. Consequently, Eq. (24) is reduced to

$$\begin{aligned} \langle u_{pz}^{{}} \rangle & = U_{vz}^{{}} + \bar{\alpha }_{f} \omega_{s} - \frac{{D_{pzz}^{{}} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} - \frac{{D_{pzr}^{{}} }}{{r\bar{\alpha }_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r} \\ & \quad + \frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ { - \bar{\alpha }_{p} \frac{{D\left( {\langle V_{Dz}^{\left( 0 \right)} \rangle + U_{vz}^{{}} } \right)}}{Dt} + \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{{\partial \langle T_{pzz}^{{}} \rangle }}{\partial z} + \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{{\partial \langle T_{pzr}^{{}} \rangle }}{\partial r} + \frac{1}{{\rho_{p} }}\overline{M}_{pz}^{{}} } \right]\langle \tau_{p}^{{}} \rangle , \\ \end{aligned}$$

(28)

where $\omega_{s} = \left( {1 - {{\rho_{f} } \mathord{\left/ {\vphantom {{\rho_{f} } {\rho_{p} }}} \right. \kern-0pt} {\rho_{p} }}} \right)\omega$ is the terminal settling velocity of a single particle in still water. When we consider fully developed sediment-laden jets, the term ${{D\left( {\langle V_{Dz}^{\left( 0 \right)} \rangle + U_{vz}^{{}} } \right)} \mathord{\left/ {\vphantom {{D\left( {\langle V_{Dz}^{\left( 0 \right)} \rangle + U_{vz}^{{}} } \right)} {Dt}}} \right. \kern-0pt} {Dt}}$ can be ignored. As to the force $\overline{M}_{pz}^{{}}$, it usually is the lift force [41]. Because lift on sediment particle is nonsignificant in comparison with other forces, for the sake of simplicity, the lift force is not considered, and thus $\overline{M}_{pz}^{{}} =0$ is assumed in this paper. Consequently, Eq. (28) reduces to

$$\begin{aligned} \langle u_{pz}^{{}} \rangle & = U_{vz}^{{}} + \bar{\alpha }_{f} \omega_{s} - \frac{{D_{pzz}^{{}} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} - \frac{{D_{pzr}^{{}} }}{{r\bar{\alpha }_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r} \\ & \quad + \frac{{\bar{\alpha }_{f} }}{{\bar{\alpha }_{p} }}\left[ {\frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{{\partial \langle T_{pzz}^{{}} \rangle }}{\partial z} + \frac{{\bar{\alpha }_{p} }}{{\rho_{p} }}\frac{{\partial \langle T_{pzr}^{{}} \rangle }}{\partial r}} \right]\langle \tau_{p}^{{}} \rangle . \\ \end{aligned}$$

(29)

Equation (29) shows that the drift velocity contains a number of effects including gravitational acceleration, turbulent diffusion, and inertia effects. Based on Eq. (29), it can be known that when the particle concentration is low enough and particle inertia is small, which means that $\bar{\alpha }_{p} \approx 0,\,\bar{\alpha }_{f} \approx 1$, and $U_{vz} \approx \langle u_{fz}^{{}} \rangle$, and thus Eq. (29) is reduced to

$$\langle u_{pz}^{{}} \rangle = \langle u_{fz}^{{}} \rangle + \omega_{s} - \frac{{D_{pzz}^{{}} }}{{\bar{\alpha }_{p} }}\frac{{\partial \bar{\alpha }_{p} }}{\partial z} - \frac{{D_{pzr}^{{}} }}{{r\bar{\alpha }_{p} }}\frac{{\partial \left( {r\bar{\alpha }_{p} } \right)}}{\partial r}.$$

(30)

If we use the similar method proposed by Jiang et al. [18] to estimate the last two terms of Eq. (30), it is found that the order of these two terms is much smaller than the settling velocity $\omega_{s}$; therefore, these two terms can be neglected and Eq. (30) can be further reduced to

$$\langle u_{pz}^{{}} \rangle = \langle u_{fz}^{{}} \rangle + \omega_{s} ,$$

(31)

which is consistent with the result reported by Jiang et al. [18]. However, with the increasing of the concentration and particle inertia, the effect of particle inertia term has to be considered.

3 Similarity solutions for sediment-laden jets

The particle concentration is involved in the expression of the velocity for the solid phase (Eq. (29)). In order to obtain the expression for the velocity and concentration distribution, respectively, the relation between these two variables must be determined in advance. For sediment-laden jets, considering the similarity solutions of the velocity and concentration [15], we assumed that

$$\frac{{\bar{\alpha }_{p} }}{{\bar{\alpha }_{pm} }} = \left( {\frac{{\langle u_{pz}^{{}} \rangle }}{{\langle u_{pzm}^{{}} \rangle }}} \right)^{Sc} ,$$

(32)

where $\bar{\alpha }_{pm}$ and $\langle u_{pzm}^{{}} \rangle$ are, respectively, the concentration and velocity along the centerline of the jet of interest; $Sc$ is the Schmidt number, defined as the ratio of the eddy viscosity coefficient of flows to the sediment diffusion coefficient. It is well known that the cross-sectional profiles of normalized concentration and mean velocity are self-similar in the zone of established flow [12, 15, 34], therefore, in this paper, the similarity solution of the concentration is given by

$$\frac{{\bar{\alpha }_{p} }}{{\bar{\alpha }_{pm} }} = f\left( \eta \right),$$

(33)

where $\eta ={r \mathord{\left/ {\vphantom {r z}} \right. \kern-0pt} z}$, defined as the ratio of the radial length $r$ to the axial length $z$, is a dimensionless length scale. Thus, the gradient of the concentration in the axial and transverse directions are, respectively, expressed as

$$\frac{{\partial \bar{\alpha }_{p} }}{\partial z} = - \frac{{\bar{\alpha }_{pm} \eta f^{\prime } }}{z} + f\frac{{\partial \bar{\alpha }_{pm} }}{\partial z},$$

(34)

and

$$\frac{{\partial \bar{\alpha }_{p} }}{\partial r} = \frac{{\bar{\alpha }_{pm} f^{\prime } }}{z},$$

(35)

where prime the superscript “$\prime$” denotes ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial \eta }}} \right. \kern-0pt} {\partial \eta }}$. Based on the Eq. (24), the corresponding velocity distribution for solid phase is expressed as

$$\frac{{\langle u_{pz}^{{}} \rangle }}{{\langle u_{pzm}^{{}} \rangle }} = f^{{{1 \mathord{\left/ {\vphantom {1 {Sc}}} \right. \kern-0pt} {Sc}}}} .$$

(36)

Substitution of Eqs. (33)–(36) into Eq. (29) leads to

$$\begin{aligned} \langle u_{pzm}^{{}} \rangle f^{{{1 \mathord{\left/ {\vphantom {1 {Sc}}} \right. \kern-0pt} {Sc}}}} & =U_{vz}^{{}} + \bar{\alpha }_{f} \omega_{s} - \frac{{D_{pzz}^{{}} }}{{\bar{\alpha }_{pm} f}}\left( { - \frac{{\bar{\alpha }_{pm} \eta f^{\prime } }}{z} + f\frac{{\partial \bar{\alpha }_{pm} }}{\partial z}} \right) \\ & \quad - \frac{{D_{pzr}^{{}} }}{{\bar{\alpha }_{pm} f}}\left( {\frac{{\bar{\alpha }_{pm} f^{\prime } }}{z} + \frac{{\bar{\alpha }_{pm} f}}{\eta z}} \right) + \frac{{\bar{\alpha }_{f} }}{{\rho_{p} }}\left[ { - \frac{\eta }{z}\frac{{\partial \langle T_{pzz}^{{}} \rangle }}{\partial \eta } + \frac{1}{z}\frac{{\partial \langle T_{pzr}^{{}} \rangle }}{\partial \eta }} \right]\langle \tau_{p}^{{}} \rangle . \\ \end{aligned}$$

(37)

So far as the Schmidt number, it is defined as the ratio of the eddy viscosity coefficient to the sediment diffusion coefficient and expressed as

$$Sc = \frac{{\nu_{f}^{t} }}{{D_{pzz} }} = \frac{{\nu_{f}^{t} }}{{D_{zz} - \frac{{\bar{\alpha }_{f} }}{{\rho_{p} }}\langle T_{pzz}^{{}} \rangle \langle \tau_{p}^{{}} \rangle }}.$$

(38)

Considering the velocity of the water–sediment mixture is

$$\begin{aligned} U_{vz} =\, & \bar{\alpha }_{f} \langle u_{fz}^{{}} \rangle + \bar{\alpha }_{p} \langle u_{pz}^{{}} \rangle \\ = \,& \left( {1 - \bar{\alpha }_{p} } \right)\langle u_{fz}^{{}} \rangle + \bar{\alpha }_{p} \langle u_{pz}^{{}} \rangle \\ =\, & \left( {1 - \bar{\alpha }_{pm} f} \right)\langle u_{fz}^{{}} \rangle + \bar{\alpha }_{pm} \langle u_{pzm}^{{}} \rangle f^{1 + 1/Sc} . \\ \end{aligned}$$

(39)

Consequently, Eq. (37) is rewritten as

$$\begin{aligned} \langle u_{pzm}^{{}} \rangle f^{{{1 \mathord{\left/ {\vphantom {1 {Sc}}} \right. \kern-0pt} {Sc}}}} & =\left( {1 - \bar{\alpha }_{pm} f} \right)\langle u_{fz}^{{}} \rangle + \bar{\alpha }_{pm} \langle u_{pzm}^{{}} \rangle f^{1 + 1/Sc} + \left( {1 - \bar{\alpha }_{pm} f} \right)\omega_{s} \\ & \quad - \frac{{D_{pzz}^{{}} }}{{\bar{\alpha }_{pm} f}}\left( { - \frac{{\bar{\alpha }_{pm} \eta f^{\prime } }}{z} + f\frac{{\partial \bar{\alpha }_{pm} }}{\partial z}} \right) - \frac{{D_{pzr}^{{}} }}{{\bar{\alpha }_{pm} f}}\left( {\frac{{\bar{\alpha }_{pm} f^{\prime } }}{z} + \frac{{\bar{\alpha }_{pm} f}}{\eta z}} \right) \\ & \quad + \frac{{\bar{\alpha }_{f} }}{{\rho_{p} }}\left[ { - \frac{\eta }{z}\frac{{\partial \langle T_{pzz}^{{}} \rangle }}{\partial \eta } + \frac{1}{z}\frac{{\partial \langle T_{pzr}^{{}} \rangle }}{\partial \eta }} \right]\langle \tau_{p}^{{}} \rangle . \\ \end{aligned}$$

(40)

4 Closures

Several parameters in the present model must be determined in advance before calculating the concentration and velocity distributions of sediment-laden jets. For the fluid phase, in order to determine the fluid velocity $\langle u_{fz}^{{}} \rangle$, the closure for the mean axial velocity $\langle u_{fzm}^{{}} \rangle$ needs to be given; in addition, the eddy viscosity of fluid phase $\nu_{f}^{t}$, which is involved in the diffusion coefficient $D_{pij}$, also needs to be given. For the solid phase, the mean concentration along the jet centerline $\bar{\alpha }_{pm}$ and the diffusion coefficients of sediment should be firstly determined; in order to determine the stress tensor for solid phase $\langle T_{pzz}^{{}} \rangle$ and $\langle T_{pzr}^{{}} \rangle$, closure for the particle turbulence also needs to be given. It should be pointed out that no matter for the fluid and solid phase, turbulent models are involved in the closures. Instead of invoking complicated turbulent models for two-phase flows [3], as has been adopted by Johansen [19], Greimann and Holly [10], and Zhong et al. [41], empirical or semi-theoretical relations are used in this paper for the purpose of turbulence closure. Details are presented in the following subsections.

4.1 Closures for the fluid phase

The empirical relation for the fluid velocity based on experimental observations in previous studies [18, 23, 34, 35] is given as

$$\langle u_{fz}^{{}} \rangle = \langle u_{fzm}^{{}} \rangle \exp \left[ { - k_{cw} \eta^{2} } \right],$$

(41)

where $k_{cw}$ is a coefficient; the mean axial velocity $\langle u_{fzm}^{{}} \rangle$ is related to that of the solid phase by an empirical relation as follows based on the experiments by Parthasarathy and Faeth [24]

$$\frac{{\langle u_{fzm}^{{}} \rangle }}{{u_{0} }} = k_{ccw} \frac{{\langle u_{pzm}^{{}} \rangle }}{{u_{p0} }},$$

(42)

where $k_{ccw}$ is a coefficient. The mean axial velocity of solid phase $\langle u_{pzm}^{{}} \rangle$ will be given in the following subsection.

The eddy viscosity coefficient of fluid phase was determined by Jiang et al. [18]

$$\nu_{f}^{t} = l\sqrt {\overline{{u_{fzm}^{\prime } u_{fzm}^{\prime } }} } = l\sqrt {\overline{{u_{fz}^{\prime } u_{fz}^{\prime } }} } \left| {_{{{r \mathord{\left/ {\vphantom {r {z = 0}}} \right. \kern-0pt} {z = 0}}}} } \right.,$$

(43)

where $l$ is the mixing length given by

$$l = k^{\prime } z,$$

(44)

where $k^{\prime }$ is a proportional coefficient, Jiang et al. [18] suggested an empirical value of $k^{\prime }$ = 0.017. However, we found in this study that the predicted concentration and velocity profiles for sediment-laden jets are in good agreement with experimental data conducted by Pathasarathy and Faeth [24], and Hall et al. [12] when it is modified to 0.1. As to the turbulence intensity of the fluid phase, the empirical relation based on experimental data is given as [18, 34]

$$\sqrt {\overline{{u_{fz}^{\prime } u_{fz}^{\prime } }} } { = }B_{0} \langle u_{fzm}^{{}} \rangle \left\{ {\exp \left[ { - k_{fcg} \left( {\eta - \eta_{0} } \right)^{{}} } \right] + \exp \left[ { - k_{fcg} \left( {\eta + \eta_{0} } \right)^{2} } \right]} \right\}.$$

(45)

4.2 Closures for the solid phase

The mean axial velocity and concentration for the solid phase along the jet centerline have respectively the following relations suggested by [12] based on the experimental observations:

$$\bar{\alpha }_{pm} = \frac{{k_{pcm} \bar{\alpha }_{p0} }}{{\left[ {{z \mathord{\left/ {\vphantom {z {\left( {D \cdot Fr_{0}^{2/5} } \right)}}} \right. \kern-0pt} {\left( {D \cdot Fr_{0}^{2/5} } \right)}}} \right]^{m} }},$$

(46)

and

$$\langle u_{pzm}^{{}} \rangle = \frac{1}{{Fr_{0} }}\frac{{k_{pcw} u_{pz0} }}{{\left[ {{z \mathord{\left/ {\vphantom {z {\left( {D \cdot Fr_{0} } \right)}}} \right. \kern-0pt} {\left( {D \cdot Fr_{0} } \right)}}} \right]^{n} }},$$

(47)

where $Fr_{0} = {{u_{0} } \mathord{\left/ {\vphantom {{u_{0} } {\left( {gD\left( {\rho_{p} - \rho_{f} } \right)/\rho_{f} } \right)^{0.5} }}} \right. \kern-0pt} {\left( {gD\left( {\rho_{p} - \rho_{f} } \right)/\rho_{f} } \right)^{0.5} }}$; $u_{pz0} = u_{0} + \omega_{s}$; $u_{0}$ is the discharge fluid velocity; $k_{pcm}$ and $k_{pcw}$ are coefficients; the exponent $m$ and $n$ are empirical parameters calibrated based upon experimental data. The diffusion coefficient $D_{ij}$ is determined by [5]

$$D_{ij} = \overline{{u_{fi}^{\prime } u_{pj}^{\prime } }} \langle \tau_{fp,j} \rangle .$$

(48)

As has adopted by Greimann and Holly [10], the correlation of fluctuation velocity of fluid phase and particle phase is approximated by the covariance of the fluctuation velocities of fluid phase [10], i.e.

$$\overline{{u_{fi}^{\prime } u_{pj}^{\prime } }} \approx \overline{{u_{fi}^{\prime } u_{fj}^{\prime } }} .$$

(49)

Thus, the diffusion coefficient is written as

$$D_{ij} = \overline{{u_{fi}^{\prime } u_{fj}^{\prime } }} \langle \tau_{fp,j} \rangle .$$

(50)

For the turbulent sediment-laden jets, there are no generally recognized theoretical expressions for time-scale of the eddy-particle interaction. By analogy with the results in turbulent open channel flows [10, 41], the axial and radial time-scale of eddy particle are, respectively, given as

$$\langle \tau_{fp,z} \rangle = {{\kappa \gamma_{c} \nu_{f}^{t} } \mathord{\left/ {\vphantom {{\kappa \gamma_{c} \nu_{f}^{t} } {\overline{{u_{fz}^{\prime } u_{fz}^{\prime } }} }}} \right. \kern-0pt} {\overline{{u_{fz}^{\prime } u_{fz}^{\prime } }} }},$$

(51)

$$\langle \tau_{fp,r} \rangle = {{c\gamma_{c} \nu_{f}^{t} } \mathord{\left/ {\vphantom {{c\gamma_{c} \nu_{f}^{t} } {\overline{{u_{fz}^{\prime } u_{fr}^{\prime } }} }}} \right. \kern-0pt} {\overline{{u_{fz}^{\prime } u_{fr}^{\prime } }} }}.$$

(52)

Consequently, the diffusion coefficients are rewritten as, respectively,

$$D_{zz} = \kappa \gamma_{c} \nu_{f}^{t} ,$$

(53)

and

$$D_{zr} = c\gamma_{c} \nu_{f}^{t} .$$

(54)

where $\kappa$, $c$ are proportional coefficients and are calibrated by experiments; $\gamma_{c}$ is the coefficient to take into account the crossing trajectory and continuity effects, which is given by Csanady [4]

$$\gamma_{c} { = }\left[ {1{ + }\left( {C_{\beta } \beta_{c} \sqrt {\frac{{\langle u_{ri} \rangle \langle u_{ri} \rangle }}{{\frac{2}{3}k_{f} }}} } \right)^{2} } \right]^{ - 0.5} ,$$

(55)

of which $\langle u_{ri} \rangle$ = relative velocity between sediment and water; $\beta_{c}$ = ratio of the Lagrangian time scale to the eddy-turn over time scale, having a value of 0.67 [30]. The parameter $C_{\beta }$ is used to account for the non-isotropic nature of diffusion in shearing flows: $C_{\beta } = 1$ for diffusion parallel to the stream and $C_{\beta } = 2$ for diffusion perpendicular to the stream [4, 10, 41].

The stress tensor for solid phase $\langle T_{pij} \rangle$ were determined as following relations [18]:

$$\langle T_{pzz} \rangle = - \rho_{p} \overline{{u_{pz}^{\prime } u_{pz}^{\prime } }} ,$$

(56)

$$\langle T_{pzr} \rangle = - \rho_{p} \overline{{u_{pz}^{\prime } u_{pr}^{\prime } }} .$$

(57)

With respect to the particle turbulence closures in dilute sediment-laden jets, it is found that they are similar to that of the fluid phase based on the experiments conducted by Parthasarathy and Feath [24] and Jiang et al. [18]; thus, the particle turbulence are given as the following forms:

$$\sqrt {\overline{{u_{pz}^{\prime } u_{pz}^{\prime } }} } =B_{0} \langle u_{pzm}^{{}} \rangle \left\{ {\exp \left[ { - k_{pcg} \left( {\eta - \eta_{0} } \right)^{2} } \right] + \exp \left[ { - k_{pcg} \left( {\eta + \eta_{0} } \right)^{2} } \right]} \right\},$$

(58)

$$\overline{{u_{pz}^{\prime } u_{pr}^{\prime } }} = BG^{\prime } \langle u_{pzm}^{{}} \rangle^{2} \eta \exp \left[ { - k_{{pw^{\prime } u^{\prime } }} \eta^{2} } \right].$$

(59)

where $B$ is a coefficient; $G^{\prime }$ is the radial function; $k_{{pw^{\prime } u^{\prime } }}$ is a proportional parameter values of all the coefficients are list in Table 1.

5 Comparisons with experiments

For verification, experiments conducted by Parthasarathy and Faeth [24] and Hall et al. [12] were selected to test the present formulation. Parthasarathy and Faeth [24] conducted their experiments in a windowed test tank (410 × 530 × 910 mm high) with a injector (5.08 mm dia, 350 mm long); Hall et al. [12] conducted their experiments in a rectangular glass tank (1.25 m wide, 2.50 m long, and 1.20 m deep) with a metal cone (0.50 m in upper diameter, 0.20 m in lower diameter, and 0.50 m in height). The details of flow and sediment characteristics of those experimental observations and parameters for theoretical calculations are summarized in Table 1. It should be pointed out that the nozzle Stokes number was introduced to denote the non-demensionalized particle relaxation time, which is expressed as

$$St_{b} = \frac{{\langle \tau_{p} \rangle }}{{\langle \tau_{f} \rangle }},$$

(60)

where $\langle \tau_{f} \rangle { = }{L \mathord{\left/ {\vphantom {L U}} \right. \kern-0pt} U}$. Usually, the width of the jet expansion $b$ and the initial velocity $u_{0}$ were selected as the length scale $L$ and the velocity scale $U$, respectively, and thus, $\langle \tau_{f} \rangle$ was regarded as the convective time scale of the sediment-laden jet flow. In the preceding section we have assumed that the nozzle Stokes number $St_{b} \ll 1$ to obtain an asymptotic solution for the drift velocity. Because the width of the jet expansion $b$ is proportional to the distance $z$ [36], in order to make sure that the nozzle Stokes number satisfies $St_{b} \ll 1$, the selected $z$ should be far enough from the nozzle to make sure that $L = b \propto z \gg D$. This requirement indicates that the present study is valid when the distance from the nozzle $z$ is bigger than about $z = 20D$ based on the following analysis. Hence $L = 100D$ was used in this study.

Table 1 Sediment and flow characteristics of experiments by Parthasarathy and Faeth [24] and Hall et al. [12]

Comparisons of the calculated and measured sediment concentration and velocity profile are shown in Figs. 2, 3, 4, 5, 6 and 7. Figures 2, 3, 4 and 5 show that: (1) the calculated concentration and velocity profile agree well with the experiments conducted by Hall et al. [12]; (2) the differences of the predictive velocity profiles between different cross-sections (z = 0.1 m and z = 0.6 m) are very small, which implies that the dependence of the velocity profile on $z$ is not remarkable in sediment-laden downward jets; (3) with the increasing of $\left| {{r \mathord{\left/ {\vphantom {r z}} \right. \kern-0pt} z}} \right|$, the difference of the concentration profile between different cross-sections becomes gradually obvious.

Fig. 2

Comparisons of calculated and measured concentration and velocity profiles for Run B1 [12] (lines: calculated result; markers: experimental data)

Fig. 3

Comparisons of calculated and measured concentration and velocity profiles for Run B2 [12] (lines: calculated result; markers: experimental data)

Fig. 4

Comparisons of calculated and measured concentration and velocity profiles for Run B3 [12] (lines: calculated result; markers: experimental data)

Fig. 5

Comparisons of calculated and measured concentration and velocity profiles for Run C1 [12] (lines: calculated result; markers: experimental data)

Fig. 6

Comparisons of calculated and measured concentration and velocity profiles for Case 1 [24] (lines: calculated result; markers: experimental data)

Fig. 7

Comparisons of calculated and measured concentration and velocity profiles for Case 2 [24] (lines: calculated result; markers: experimental data)

Figures 6, 7 show that the calculated concentration and velocity profile agree quite well with the experiments by Parthsarathy and Faeth [24]. However, it should be pointed out that Eq. (40) cannot be used to predict the concentration and velocity profile when $z$ is too small, such as $z = 8D$ and $z = 16D$, the reason for which is that when the nozzle Stokes number is large enough, sediments cannot fully diffuse in the zone near the nozzle, which did not satisfy the simplification condition of this study. It is found that the values of $St_{b}$ for experiments by Parthsarathy and Faeth [24] are much larger than that by Hall et al. [12]. Therefore, it is reasonable and understandable for the above results.

6 Discussions

6.1 Effect of particle inertia on concentration and velocity distributions

The effect of particle inertia on sediment-laden flows is significant which has been illustrated in turbulent open-channel flows by Greimann et al. [11], Greimann and Holly [10], Zhang and Prosperetti [38], and Zhang et al. [39]. Those results show that the classical diffusion theory for suspended sediment takes into account only the zeroth-order particle inertial effect, as implies that sediment distribution obtained by the diffusion theory can bring about obvious deviations from observations when the effect of particle inertia is prominent. The results shown in Sect. 5 reveal that particle inertia is also an important factor affecting sediment-laden downward jets by various ways. In this section we further discuss the effect of particle inertia on the movements of sediment-laden downward jets.

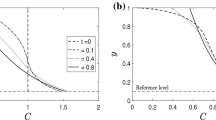
In order to illustrate the effect of particle inertia on the concentration and velocity distributions in sediment-laden jet flows, the runs of B1, Case 1, and Case 2 with different nozzle Stokes number were selected, results of which are shown in Figs. 8, 9. It should be pointed out that the cross-sections of $z = 0.6\,{\text{m}}\left( { \approx 39D} \right)$ for B1, and $z = 40D$ for Case 1 and Case 2 were selected here, because the distance to the nozzle for these three runs is almost the same, which are also far enough to make sure that sediment diffusion is fully developed. Results show that the sediment diffusion in sediment-laden jets decreases with increasing nozzle Stokes number (Fig. 8). However, The variation of the velocity profiles (Fig. 9) has not considerable relation with the various Stokes number for both the measured data and calculated results.

Fig. 8

Effect of Stokes number on the concentration distributions

Fig. 9

Effect of Stokes number on the velocity distributions

6.2 Effect of particle inertia on the sediment diffusion

Based on the above analysis, it is found that the effect of particle inertia on the concentration distribution is significant; therefore, here we further investigate the effect of particle inertia on the sediment diffusion coefficient, a key parameter for sediment diffusion. Equations (25) and (26) show that the sediment diffusion in sediment-laden jets consists of two parts, including the fluid turbulence and particle turbulence which closely depends on the particle inertia. To investigate the effect of particle inertia, Eq. (25) was expressed as

$$D_{pzz} = D_{zz} - \underbrace {{\frac{{\bar{\alpha }_{f} }}{{\rho_{p} }}\langle T_{pzz}^{{}} \rangle \langle \tau_{p}^{{}} \rangle }}_{{D_{pz} }}.$$

(61)

The contributions of these two factors to the sediment diffusion coefficient for the runs of B1, C1, Case 1, and Case 2 were presented, which are shown in Figs. 10, 11, 12 and 13 It can be seen that: (1) when the nozzle Stokes number is small, such as the case of the run B1 and C1, the effect of fluid turbulence on the sediment diffusion is dominant, the contribution of which to the sediment diffusion coefficient almost reaches 100%. This means that the effect of the particle turbulence is ignorable because of the small particle inertia; (2) comparing Case 1 and Case 2 with the run of B1 and C1, it is found that with the increasing of the nozzle Stokes number, the effect of fluid turbulence decreases, whereas the effect of particle turbulence gradually increases, the percentage of which can reach about 40%. This implies that the fluid turbulence is not the only driving force for sediment diffusion in sediment-laden jets; the effect of particle turbulence as well plays a significant role with increasing particle inertia; (3) it is also found that the contribution of the particle turbulence gradually decreases with the increasing value of $\left| {{r \mathord{\left/ {\vphantom {r z}} \right. \kern-0pt} z}} \right|$, which implies that the farther the sediment particle is away from the centerline, the smaller the effect of particle inertia is.

Fig. 10

Contribution of different factor to the sediment diffusion coefficient and the corresponding concentration distribution for run B1 (z = 0.6 m)

Fig. 11

Contribution of different factor to the sediment diffusion coefficient and the corresponding concentration distribution for run C1 (z = 0.6 m)

Fig. 12

Contribution of different factor to the sediment diffusion coefficient and the corresponding concentration distribution for run Case 1 (z = 40D)

Fig. 13

Contribution of different factor to the sediment diffusion coefficient and the corresponding concentration distribution for run Case 2 (z = 40D)

7 Conclusions

In this paper, the drift velocity, understood as the relative velocity of solid or liquid phase to the solid/liquid two phase mixtures underling downward jets, was derived by solving the two fluid equation for sediment-laden flows by the perturbation approach. With the help of the drift velocity, the numerical solutions of the concentration and velocity distribution were obtained by introducing the similarity function. Comparisons with experimental observations conducted by Parthsarathy and Faeth [24], and Hall et al. [12] were presented. Conclusions drawn from this study are as following:

• 1. The constitutive relation for the drift velocity in sediment-laden downward jets can be expressed as a power series in terms of the nozzle Stokes number (Eqs. (18)–(20)), which helps us to understand mechanisms of sediment diffusion induced by kinds of actions exerting on sediment particles in jets. The predicted concentration and velocity profile considering the effect of the first-order particle inertial correction agree well with experiments by Parthsarathy and Faeth [24] and Hall et al. [12]. It shows that the behavior of sediment-laden downward jets is not only affected by gravitational acceleration and flow turbulence, the effects of particle inertia, particle tensor, and other forces contained in the first-order particle inertial corrections are also of great importance.

• 2. Based on the relation for the sediment diffusion coefficient, the contributions of two mechanisms including fluid turbulence and particle turbulence which closely depends on particle inertia to the sediment diffusion were analyzed. Results show that fluid turbulence is not the only reason for the sediment diffusion in sediment-laden downward jets; the effect of particle turbulence on the sediment diffusion is also significant when the particle inertia is large enough. However, with the increasing of $\left| {{r \mathord{\left/ {\vphantom {r z}} \right. \kern-0pt} z}} \right|$, the fluid turbulence generally again becomes the dominant force for sediment diffusion in jets.

• 3. Because of the lack of information on turbulent closures for sediment-laden jets, the empirical relations based on experimental observations for the fluid and particle turbulence closures were adopted in this paper. This defect could cause certain errors during the application of the present study. Furthermore, in order to get the numerical solution of the concentration and velocity distributions for sediment-laden jets, some simplifications were adopted in this study. Therefore, how to improve the closures and these simplifications is still an important issue in the further study.